RBSE Class 11 Physics Important Questions Chapter 2 मात्रक एवं मापन

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 2 मात्रक एवं मापन Important Questions and Answers.

RBSE Class 11 Physics Chapter 2 Important Questions मात्रक एवं मापन

बहुचयनात्मक प्रश्न:

प्रश्न 1. 
एक नैनोमीटर तुल्य है:
(अ) 10⁹ मी.
(ब) 10⁶ मी.
(स) 10^-9 मी.
(द) 10^-7 मी.
उत्तर:
(अ) 10⁹ मी.

प्रश्न 2. 
एक प्रकाश वर्ष दूरी का मान:
(अ) 9.46 x 10¹⁰ किमी. 
(ब) 9.46 x 10¹² किमी.
(स) 9.46 x 10¹² मी. संकेत:
(द) 9.46 x 10¹⁵ सेमी.
एक प्रकाश वर्ष = 3 x 10⁸ x 365 x 24 x 60 x 60 मी.
= 9.46 × 10¹⁵ मी.
= 9.46 x 10¹² किमी.
अतः 
उत्तर:
(ब) होगा।

 

प्रश्न 3. 
यदि बल, लम्बाई तथा समय मूल मात्रक होते तो द्रव्यमान का विमीय सूत्र होता है:
(अ) [F¹ L^-1 T²]
(ब) [F¹ L¹ T^-2]
(स) [F¹ L¹ T^-1]
(द) [F¹ L¹ T¹]
उत्तर:
हम जानते हैं:
बल = द्रव्यमान × त्वरण

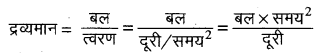
= [F¹ L^-1 T²]
अतः 
उत्तर:
(अ) होगा।

प्रश्न 4. 
एक भौतिक राशि y = Ma Lb T-c  द्वारा व्यक्त की जाती है। यदि M, L व T के मापन में क्रमशः α% व β%  γ% प्रतिशत त्रुटि हो तो कुल प्रतिशत त्रुटि होगी:
(अ) (aα + bβ + cγ)% 
(ब) (aα - bβ - cγ)%
(स) (aα + bβ + cγ) %
(द) (aα + bβ - cγ)%
हल - कुल अधिकतम आंशिक
\(\frac{\Delta \mathrm{y}}{\mathrm{y}}=\frac{\mathrm{a} \Delta \mathrm{M}}{\mathrm{M}}+\frac{\mathrm{b} \Delta \mathrm{L}}{\mathrm{L}}+\frac{\mathrm{c} \Delta \mathrm{T}}{\mathrm{T}}\)
∴ \(\frac{\Delta \mathrm{y}}{\mathrm{y}} \times 100=(\mathrm{a} \alpha+\mathrm{b} \beta+\mathrm{c} \gamma) \%\)
अतः 
उत्तर:
(स) होगा।

प्रश्न 5. 
निम्नलिखित युग्मों में से किस युग्म की राशियों की विमायें समान हैं:
(अ) कार्य और शक्ति
(ब) घनत्व तथा आपेक्षिक घनत्व
(स) संवेग और आवेग
(द) प्रतिबल और विकृति
उत्तर:
(स) संवेग और आवेग

प्रश्न 6. 
61,00,000 राशि में सार्थक अंकों की संख्या है:
(अ) 2
(ब) 5
(स) 7
(द) इनमें से कोई नहीं
उत्तर:
(अ) 2

प्रश्न 7. 
एक मीटर में kr6 की कितनी तरंगें होती हैं:
(अ) 1553164.13
(ब) 2347127.23
(स) 652189.63
(द) 1650763.73
उत्तर:
(द) 1650763.73

प्रश्न 8. 
एक मोल गैस के लिए PV = RT समीकरण में R का विमीय सूत्र होगा:
(अ) M¹L²T^-2K^-1
(ब) M¹L¹T^-2K^-2
(स) MLT²k^-1
(द) ML²T²
उत्तर:
(अ) M¹L²T^-2K^-1

प्रश्न 9. 
201,00,000 राशि में सार्थक अंकों की संख्या है:
(अ) 3
(ब) 5
(स) 8
(द) इनमें से कोई नहीं
उत्तर:
(अ) 3

रिक्त स्थानों की पूर्ति कीजिए:

प्रश्न 1.
जो मात्रक मूल मात्रकों पर आधारित होते हैं उन्हें ............................ मात्रक कहते हैं।
उत्तर:
व्युत्पन्न 

प्रश्न 2.
दूरी का सबसे बड़ा मात्रक ....................... सबसे बड़ा मात्रक चन्द्रशेखर सीमा (C.S. L.) है।
उत्तर:
पारसेक

प्रश्न 3.
अन्तर्राष्ट्रीय मात्रक पद्धति में .................... मूल राशियाँ हैं।
उत्तर:
सात

प्रश्न 4. 
किसी पिण्ड का वह द्रव्यमान जो उसके जड़त्व की माप है।
उत्तर:
a

प्रश्न 5.
\(m=\frac{\mathrm{F}}{\ldots \ldots \ldots}\)
उत्तर:
माध्य मान 

प्रश्न 6.
शक्ति का विमीय सूत्र ....................... है।
उत्तर:
ML²T^{- 3}

प्रश्न 7.
कोणीय संवेग का विमीय सूत्र ................................ है।
उत्तर:
 ML ² T ¹
 
प्रश्न 8.
यदि x = a + bt + ct² है तो जहाँ x मीटर में तथा सेकण्ड में दिये हैं तो c का मात्रक ...........................  होगा।
उत्तर:
मीटर / सेकण्ड ²

प्रश्न 9.
सबसे यथार्थ घड़ी .................. होती है।
उत्तर:
सीसीयम परमाणु घड़ी

प्रश्न 10.
1 जूल ऊर्जा का मान CGS पद्धति में ............................. होता है।
उत्तर:
10⁷ अर्ज 

नीचे दिये गये वाक्यों में कीजिए: सत्य / असत्य कथन का चयन:

प्रश्न 1.
किसी भौतिक राशि का मात्रक जितना छोटा होगा, किसी निश्चित राशि के मापन का आंकिक मान उतना ही अधिक होगा।
उत्तर:
सत्य 

प्रश्न 2.
किसी वृत्त की त्रिज्या के बराबर के चाप द्वारा वृत्त के केन्द्र पर अन्तरित कोण, 2 रेडियन के बराबर होता है।
उत्तर:
असत्य

प्रश्न 3.
1 पारसेक का मान 3.28 प्रकाश वर्ष होता है।
उत्तर:
सत्य 

प्रश्न 4. 
प्लांक. नियतांक का मात्रक जूल / सेकण्ड होता है।
उत्तर:
असत्य

प्रश्न 5.
वर्नियर केलीपर्स और स्क्रूगेज में स्क्रूगेज का मापन अधिक यथार्थ है।
उत्तर:
सत्य 

प्रश्न 6. 
तल की वक्रता मापने के लिये स्क्रूगेज उपकरण को काम में लेते हैं।
उत्तर:
असत्य

प्रश्न 7.
विमीय सूत्र M¹L²T^-2 कार्य, ऊर्जा भौतिक राशियों को प्रदर्शित करता है।
उत्तर:
सत्य 

प्रश्न 8.
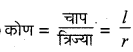होता है।
उत्तर:
सत्य 

प्रश्न 9.
समय का सबसे छोटा मात्रक शेक है।
उत्तर:
सत्य 

प्रश्न 10.
1 amu = 1/12 [cl² के परमाणु का द्रव्यमान]
उत्तर:
सत्य

कॉलम - A से कॉलम - B का सही मिलान कोजिए:

कॉलम - A 
1. 1amu का मान होता है
2. सबसे शुद्ध घड़ी कौनसी है?
3. चट्टानों की आयु ज्ञात करने की कौनसी विधि है?
4. 1 सेकण्ड में कितने नैनो सेकण्ड होते हैं?
5. कोणीय संवेग की विमा
6. बल आघूर्ण की विमा
7. ML ^-1T^-2 किसकी विमा है
8. गतिज ऊर्जा का विमीय मात्रक लिखिये
9. I का विमीय सूत्र है
10. 1/2mv² का मान किसके बराबर होता है?

कॉलम - B
(A) Mgh
(B) ML²
(C) किग्रा मी² से²
(D) शक्ति
(E) ML²T^-2 है
(F) ML²T¹ है 
(G) 10⁹
(H) रेडियोऐक्टिव डेटिंग
(I) सीसियम
(J) 1.66 x 10^-27 kg
उत्तर:
1. (J) 
2. (I) 
3. (H) 
4. (G) 
5. (F) 
6. (E) 
7. (D) 
8. (C) 
9. (B) 
10. (A)

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1. 
A, AU तथा u में क्या अन्तर है? 
उत्तर:
A = 10^-10 m
AU = 1.496 x 10¹¹ m जो खगोलीय मात्रक है।
1u = 1.66 x 10^-7kg (एकीकृत परमाणु संहति मात्रक)

प्रश्न 2.
0.00006 का कोटिमान बताइए।
उत्तर:
0.000066.0 x 10^-5
∵ 1 x 10 का वर्गमूल = \(\sqrt{1 \times 10}\) = 3.16 से संख्या बड़ी होती है तो 10 की घात में 1 जोड़ते हैं जबकि 3.16 से कम होने पर अपरिवर्तित रखते हैं।
∴ कोटिमान = 10 - 5 + 1 = 10^-4

प्रश्न 3. 
किसी यंत्र की यथार्थता की सीमा किस बात पर निर्भर करती है?
उत्तर:
यथार्थता की सीमा यंत्र के अल्पतमांक पर निर्भर करती है। यंत्र का अल्पतमांक कम होने पर यथार्थता बढ़ती है।

प्रश्न 4. 
वर्नियर केलीपर्स और स्क्रूगेज में किसका मापन अधिक यथार्थ है?
उत्तर:
स्क्रूज का

प्रश्न 5. 
SI पद्धति में प्रदीपन तीव्रता का मात्रक क्या होता है? 
उत्तर:
केन्डेला।

प्रश्न 6. 
पदार्थ की मात्रा का मूलं मात्रक क्या है?
उत्तर:
मोल

प्रश्न 7. 
तल की वक्रता मापने के लिए स्क्रूगेज़ और स्फेरोमीटर में से उपयुक्त उपकरण कौनसा है?
उत्तर:
स्फेरोमीटर

प्रश्न 8. 
एक जूल ऊर्जा कितने अर्ग के तुल्य है?
उत्तर:
10⁷ अर्ग 

प्रश्न 9. 
प्लांक नियतांक का मात्रक है।
उत्तर:
जूल सेकण्ड।

प्रश्न 10. 
एक C.S.L. सूर्य के द्रव्यमान का कितना गुना है?
उत्तर:
1.4 गुना।

प्रश्न 11. 
प्रकाश वर्ष किसका मात्रक है? 
उत्तर:
दूरीका।

प्रश्न 12. 
संख्या 0.0008 में कितने सार्थक अंक हैं?
उत्तर:
एक।

प्रश्न 13. 
अन्तर्राष्ट्रीय पद्धति में पूरक मात्रकों के नाम। 
उत्तर:
रेडियन, स्टेरेडियन।

प्रश्न 14. 
अन्तर्राष्ट्रीय पद्धति में कितने मूल मात्रक होते हैं? 
उत्तर:
मीटर (m), किलोग्राम (kg), सेकण्ड ( s), ऐम्पियर (I), कैल्विन (k), केन्डेला (cd) तथा मोल (mol)।

प्रश्न 15. 
एक मीटर में Kr की कितनी तरंगदैर्ध्य होती है? 
उत्तर:
1650, 763.73

प्रश्न 16. 
सेकण्ड की सीजियम 133 के कम्पनों के आधार पर परिभाषा दीजिये।
उत्तर:
सेकण्ड (Second ) - यह समय का मात्रक है। परिभाषा के अनुसार, 1 सेकण्ड यह समयान्तराल है जिसमें परमाणुक घड़ी (atomic clock) में सीजियम 133 परमाणु 9, 192, 631, 770 कम्पन करता है।

प्रश्न 17. 
एक व्यक्ति किसी प्रयोग में 100 प्रेक्षण लेता है। यदि वही प्रयोग वह 500 प्रेक्षणों से पुनरावृत्ति करता है तो किस प्रकार माध् य परम त्रुटि प्रभावित होगी?
उत्तर:
अतः माध्य परम त्रुटि प्रभावित होगी

प्रश्न 18. 
विद्युत ऊर्जा की वाणिज्यिक इकाई किलोवाट घण्टा (KWh) या यूनिट है, इसे जूल में परिवर्तित कीजिये।
उत्तर:
1 यूनिट या किलोवाट घण्टा
या
= 1000 × 60 x 60 वाट सेकण्ड 
= 3.6 x 10⁶ जूल उत

प्रश्न 19. 
इलेक्ट्रॉन का द्रव्यमान 9.11 x 10³¹ Kg. होता है तो 1 Kg. में इलेक्ट्रॉन की संख्या क्या होगी?
उत्तर:
दिया गया है। इलेक्ट्रॉन का द्रव्यमान
= 9.11 × 10^-31 Kg.
कुल द्रव्यमान =
1 Kg.

= 1.1 × 10³⁰

प्रश्न 20. 
यदि किसी परमाणु का आकार बड़ा करके पिन की तेज नोक के बराबर कर दिया जाये, तो एवरेस्ट पर्वत की शिखर की ऊँचाई कितनी होगी?
उत्तर:
10¹⁰ मीटर 

प्रश्न 21. 
यदि विश्व सिकुड़कर पृथ्वी के आकार का हो जाये तो इस पैमाने पर पृथ्वी कितनी बड़ी होगी ?
उत्तर:
परमाणु का आकार (10^-11 मीटर )।

प्रश्न 22. 
लेसर का अर्थ लिखिए।
उत्तर:
यह विकिरण को प्रेरित करके या उद्दीप्त करके प्रकाश संवर्धन के लिए पद है।

प्रश्न 23. 
एक प्रयोग में एक खोजकर्ता सावधानीपूर्वक 100 प्रेक्षण लेता है। यदि वह उसी प्रयोग को 400 प्रेक्षण लेकर पुनरावृत करता है, तो प्रायिक त्रुटि कितनी कम हो जायेगी? 
उत्तर:
4 घटक द्वारा या 4 गुणत्व 

प्रश्न 24. 
दो विमाहीन राशियों के नाम लिखिए।
उत्तर:
कोण, विकृति। द्वारा।

प्रश्न 25. 
परमाणु संहति मात्रक (amu) क्या है?
उत्तर:
⁶C₁₂ कार्बन परमाणु के द्रव्यमान का 1/12 (a.m.u.) या परमाणु संहति मात्रक कहलाता है।

प्रश्न 26. 
क्या वर्नियर कैलीपर्स द्वारा बाल की मोटाई ज्ञात कर सकते हैं?
उत्तर:
नहीं, बाल की मोटाई वर्नियर कैलीपर्स अल्पतमांक से कम होती है।

प्रश्न 27. 
यदि बल तथा लम्बाई के मात्रकों में प्रत्येक का मान दुगुना कर दिया जाये तो ऊर्जा के मात्रक का मान कितने गुना हो जायेगा?
उत्तर:
चार गुना।

प्रश्न 28. 
सबसे यथार्थ घड़ी कौन-सी होती है?
उत्तर:
सीसीयम परमाणु घड़ी।

प्रश्न 29. 
SONAR क्या दर्शाता है?
उत्तर:
यह पानी के जहाज में लगाने वाली एक युक्ति है। यह ध्वनि द्वारा नौसंचालन तथा जहाज से वस्तुओं की दूरी ज्ञात करने के लिए प्रयुक्त होता है।

प्रश्न 30. 
विमाओं का समांगता का सिद्धान्त क्या है?
उत्तर:
किसी भौतिक समीकरण के विमीय रूप से सही होने के लिये उसके समस्त पदों की विमायें एकसमान होनी चाहिये, इसे विमाओं की समांगता का सिद्धांत कहते हैं।

प्रश्न 31. 
भौतिक राशि की विमा किसे कहते हैं?
उत्तर:
किसी भौतिक राशि को M, L तथा T के रूप में व्यक्त करने के लिये उन पर लगाई गई घात (power) को उस भौतिक राशि की विमा (dimension) कहते हैं।

प्रश्न 32. 
विमीय सूत्र MI²T^-2 किन-किन भौतिक राशियों को प्रदर्शित करता है?
उत्तर:
कार्य, ऊर्जा।

प्रश्न 33. 
विमीय समीकरण का कोई एक उपयोग लिखिये। 
उत्तर:
भौतिक सूत्रों की सत्यता की जाँच करने के लिये। 

प्रश्न 34. 
विमीय समीकरण के सीमा बंधन बताइये।
उत्तर:
यदि कोई भौतिक राशि तीन राशियों पर निर्भर हो तो उसके लिये सूत्र इस विधि से प्राप्त नहीं किया जा सकता है। विमाहीन नियतांकों के बारे सूचना प्राप्त नहीं की जा सकती है।

प्रश्न 35. 
यदि x = a + bt + ct² है तो जहाँ x मीटर में तथा t सेकण्ड दिए हैं तो c का मात्रक क्या होगा?
उत्तर:
का मात्रक ms होगा।

प्रश्न 36. 
विमीय समीकरणों के संगति के सिद्धान्त को लिखिए। 
उत्तर:
किसी समीकरण के दोनों ओर के पदों की विमायें समान होनी चाहिए, यह सिद्धान्त है।

प्रश्न 37. 
क्या विमाहीन एवं मात्रकहीन भौतिक राशि का अस्तित्व सम्भव है?
उत्तर:
हाँ, जैसे आपेक्षिक घनत्व विकृति।

प्रश्न 38. 
गुरुत्वाकर्षण बल का विमीय समीकरण लिखिये। 
उत्तर:
M¹L¹ T^-2

प्रश्न 39. 
निम्न राशियों में ऐसे जोड़े छाँटिये जिनकी विमा एक ही हो संवेग, कोणीय वेग, बल-आघूर्ण, दाब, आवेग, पृष्ठ तनाव, प्रतिबल, कार्य आवृत्ति तथा बल नियतांक।
उत्तर:

1. संवेग तथा आवेग 
2. बल नियतांक तथा पृष्ठ तनाव 
3. दाब तथा प्रतिबल 
4. बल-आघूर्ण तथा कार्य 
5. आवृत्ति व कोणीय वेग।

प्रश्न 40. 
किसी तार में अनुप्रस्थ तरंग की चाल imm है. जहाँ T तनाव बल है, यदि m तार की एकांक लम्बाई का द्रव्यमान किग्रा. / मीटर में हो तथा वेग v मीटर / सेकण्ड में हो, तो तनाव बल T का मात्रक ज्ञात कीजिए।
उत्तर:
यहाँ पर mn तार की एकांक लम्बाई का द्रव्यमान है इसलिए तनाव बल ही बल के बराबर होगा और उसका मात्रक न्यूटन या किग्रा.मीटर होगा।

लघुत्तरात्मक प्रश्न:

प्रश्न 1. 
M. KS. एवं S. I पद्धति में अन्तर स्पष्ट कीजिये। 
उत्तर:
छ: मूल राशियों (लम्बाई, द्रव्यमान, समय, वैद्युत धारा, ताप तथा ज्योति तीव्रता ) के मात्रकों पर आधारित मात्रक पद्धति को 'अन्तर्राष्ट्रीय मात्रक पद्धति' (International System of Units) अथवा SI कहते हैं।
SI पद्धति के मूल मात्रक निम्नवत् हैं:

1. मीटर (m) - यह लम्बाई का मात्रक 
2. किलोग्राम (kg) - यह द्रव्यमान का मात्रक है। 
3. सेकण्ड ( s) - यह समय का मात्रक है।

यान्त्रिकी के उपर्युक्त तीन मूल मात्रकों पर आधारित मात्रक पद्धति को 'मीटर किलोग्राम- सेकण्ड पद्धति' (MKS System of Units) कहते हैं।

1. ऐम्पियर (A ) - यह वैद्युत धारा का मात्रक है।
2. केल्विन (K) - यह ताप का मात्रक है।
3. केन्डिला (ed ) - यह ज्योति तीव्रता का मात्रक है।

इनके अतिरिक्त दो पूरक मूल मात्रक भी हैं:

1. रेडियन (कोण का मात्रक) तथा 
2. स्टेरेडियन (घन कोण का मात्रक)। ये भी S. I. पद्धति के अन्तर्गत माने जाते हैं।

प्रश्न 2. 
M.K.S. एवं C.GS. पद्धति में श्यानता गुणांक के मात्रकों का अनुपात ज्ञात कीजिये।
उत्तर:
M.K.S पद्धति में श्यानता गुणांक का मात्रक

C.G.S. पद्धति में श्यानता गुणांक का मात्रक

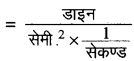
दोनों का अनुपात लेने पर = \(\frac{10^5}{100 \times 100}\)
= 10 

प्रश्न 3. 
निम्न सम्बन्ध में x का मान ज्ञात करो:
(वेग)^x = ( दाबान्तर) ^1/2 x (घनत्व)^-3/2
उत्तर:
यदि वेग को v से, दाबान्तर को P से और घनत्व को d से
निरूपित करें तब
(वेग)^x = (दाबान्तर) ^3/2 x (घनत्व)^-3/2
(v)^x = (P)^3/2  x (d)^-3/2
\((\mathrm{v})^{\mathrm{x}}=\left(\frac{\mathrm{P}}{d}\right)^{3 / 2}\)
R.H.S. का विमीय सूत्र लिखने पर
\(\left(\frac{\mathrm{F}}{\mathrm{A} \times \mathrm{d}}\right)^{3 / 2}=\left[\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}^2 \mathrm{ML}^{-3}}\right]^{3 / 2}\)
=> [L²T^-2]^3/2 = [LT^-1]³
लेकिन वेग (v) की विमा [LT^-1] होगी। अतः (v)³
=> (v)^x = (v)³
यहाँ पर आधार समान है घातें भी बराबर होंगी
∴x = 3

प्रश्न 4. 
निम्न राशियों की विमायें तथा मी. कि. से. पद्धति में इन राशियों के व्युत्पन्न मात्रक भी लिखिये:
(i) बल, 
(ii) शक्ति, 
(iii) दाब, 
(iv) प्रतिबल, 
(v) विकृति, 
(vi) प्रत्यास्थता गुणांक, 
(vii) आपेक्षिक घनत्व तथा 
(viii) गुरुत्वीय नियतांक।
उत्तर:
(i) बल = द्रव्यमान x त्वरण = [M] x [LT^-2]
= [MLT ^-2]
मात्रक - किग्रा. मी./से.2 या न्यूटन

(ii) शक्ति P = \(\mathrm{P}=\frac{\mathrm{W}}{\mathrm{t}}=\frac{\left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]}{[\mathrm{T}]}\) = [ML²T^-3]
मात्रक - kg.m²/s³ = जूल/सेकण्ड = वाट

(iii) दाब = 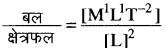 = [ML^-1T²]
मात्रक - किग्रा./ मी. से.² = न्यूटन / मी. ² = पास्कल

(iv) प्रतिबल = 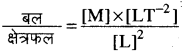= [ML^-1T^-2 ]
मात्रक - kg. / ms² = न्यूटन / मी. ²

(v) विकृति =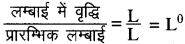
अतः यह एक विमा रहित राशि है।

(vi) प्रत्यास्थता गुणांक =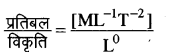
=  [ML^-1T^-2] मात्रक - न्यूटन / मी²

(vii) आपेक्षिक घनत्व =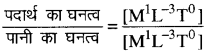
= [M⁰L⁰T⁰] = विमाहीन

(viii) गुरुत्वीय नियतांक G = \(\frac{F \times d^2}{m_1 \times m_2}\)
\(\mathrm{G}=\frac{\left[\mathrm{MLT}^{-2}\right] \times[\mathrm{L}]^2}{[\mathrm{M}] \times[\mathrm{M}]}\)
= [M^-1T^-2L³]

प्रश्न 5. 
निम्न सूत्रों की यथार्थता की जांच कीजिये:
(i) F = mv²/r
(ii) T = hrgd/2 
(iii) \(\mathrm{T}=2 \pi \sqrt{\frac{l}{g}}\)
\(\text { (iv) } \mathrm{Y}=\frac{\mathrm{MgL}}{\pi^2 l}\)यहाँ Y यंग का गुणांक है।
(v)  S = Ut + 1/2at²
(vi) 1/2mv² = mgh

(vii) v² = u² + 2as जहाँ v तथा u क्रमशः अंतिम तथा प्रारंभिक वेग हैं। a त्वरण व s तय की गई दूरी है।

(viii) \(n=\frac{1}{2 l} \sqrt{\frac{T}{m}}\) यहाँ n आवृत्ति, T तनाव बल, l लम्बाई तथा m एकांक लम्बाई का द्रव्यमान है।
उत्तर:
(i) F = mv²/r यहाँ पर F अभिकेन्द्रीय बल m कण का द्रव्यमान, वृत्ताकार पथ की त्रिज्या है और v कण का वेग है। समीकरण के बायें पक्ष की विमा = [M¹L¹T^-2] है।
एवं समीकरण के दायें पक्ष की विमा = \(\frac{\left[\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-2}\right]}{\left[\mathrm{L}^1\right]}\)
= [M¹L¹T²]
दायें पक्ष की विमा= [M¹L¹T^-2] है। 
दिया गया सूत्र विमा की दृष्टि से सत्य है।

(ii) T = hrgd/2
यहाँ पर T = पृष्ठ- तनाव है।
r = केशनली की त्रिज्या है।
h = केशनली के द्रव्य की ऊँचाई है।
d = द्रव्य का घनत्व है।
यदि सूत्र में दायीं ओर एवं बायीं ओर के मात्रकों की विमायें समान हों तो समीकरण यथार्थ मानी जाती है।
सूत्र में बायीं ओर की राशि = T = पृष्ठ तनाव = [MT^-2]
दायीं ओर की राशि = \(\frac{h r g d}{2}=\frac{[\mathrm{L}][\mathrm{L}]\left[\mathrm{LT}^{-2}\right]\left[\mathrm{ML}^{-3}\right]}{2}\)
= 1⁄2[MT^-2] = [MT^-2]
[1/2 एक विमाहीन राशि है ।]
∴ दोनों पक्षों में M तथा T की विमायें समान हैं, अतः समीकरण विमीय दृष्टि से सत्य है।

(iii) T = \(2 \pi \sqrt{\frac{l}{g}}\)
उपर्युक्त सूत्र में बायीं ओर की राशि T = आवर्तकाल
= [M⁰L⁰T¹]
अतः बायीं ओर की राशि में द्रव्यमान के मात्रक की विमा शून्य, लम्बाई के मात्रक की विमा शून्य एवं समय के मात्रक की विमा एक है।
दायीं ओर की राशि की विमा = \(2 \pi \sqrt{\frac{l}{g}}\)
\(=2 \pi \sqrt{\frac{\mathrm{L}^1}{\mathrm{~L}^{\mathrm{L}} \mathrm{T}^{-2}}}=\sqrt{\mathrm{T}^2}=\mathrm{T}\)
इसको इस प्रकार से भी लिख सकते हैं = [M⁰L⁰T¹]
अतः दोनों पक्षों की विमायें समान हैं, अतः उपर्युक्त सूत्र सही है।

(iv) \(\mathrm{Y}=\frac{\mathrm{MgL}}{\pi r^2 l}\) में
बायीं ओर की राशि (Y) (प्रत्यास्थता गुणांक) की विमायें = [M¹L^-IT^{- 2} ] तथा सूत्र के दायीं ओर की विमायें इस प्रकार हैं-
द्रव्यमान M = M,
लम्बाई L = L,
लम्बाई में वृद्धि l = L
यहाँ पर विमाहीन है।
गुरुत्वजनित त्वरण g = [LT²] 
त्रिज्या r = r
इसलिये पद \(\frac{\mathrm{MgL}}{\pi r^2 l}\) की विमायें \(\frac{\left[\mathrm{MLT}^{-2} \mathrm{~L}\right]}{[\mathrm{L}]^2 \mathrm{~L}}=\left[\mathrm{M}^{\mathrm{L}} \mathrm{L}^{-1} \mathrm{~T}^{-2}\right]\)
सूत्र के दोनों ओर की विमायें समान हैं, अतः विमीय दृष्टि से यह सूत्र सत्य है।

(v) सूत्र S = ut + 1⁄2at²
बायें पक्ष में स्थित राशि (S) दूरी है जिसकी विमा L है।
बायें पक्ष में स्थित राशि की विमा = [M⁰L¹ T⁰]
u वेग = समय a = त्वरण है। 
दायें पक्ष में स्थित प्रथम राशि की विमा
दायें पक्ष में स्थित द्वितीय राशि की विमा = 1/2at²
यहाँ पर 1/2 विमाहीन है।
∴ [LT^-2] [T²] = L = [M⁰L¹T⁰]
समीकरण S = ut + 1⁄2 at² में तीनों राशियों S, ut तथा 1⁄2at²' की विमायें समान हैं, अतः समीकरण विमीय दृष्टि से सत्य है।

(vi) सूत्र 1/2 mv² = mgh
सूत्र में बायें पक्ष में स्थित राशियाँ = 1/2 mv²
m = द्रव्यमान, V = वेग है।

mv² = M¹[L¹T^-1]² = [M¹L²T^-2]
दायें पक्ष की विमा mgh = M¹ [LT^-2] x L
= [M¹L²T^-2]
अतः समीकरण 1⁄/2 mv² = mgh में दोनों ओर की विमायें समान
हैं, अतः सूत्र सही है।

(vii) सूत्र
v² = ū₂ + 2as
बायें पक्ष में स्थित राशि v² की विमा = ( वेग की विमा)² 
v² = [M⁰L¹T^-1]²
= [M⁰L²T^-2]
दायें पक्ष में स्थित प्रथम राशि की विमा
u² = [M⁰L¹T^-1]²
= [M⁰L²T^-2]
दायें पक्ष में स्थित द्वितीय राशि की विमा = 2as
= [LT^-2] [L] (2 एक विमाहीन राशि है) 
= [L²T^-2] = [M⁰L²T^-2]
समीकरण V² = u²+ 2as में तीनों राशियों में v² u² तथा 2as की विमायें समान हैं, अतः समीकरण पूर्णतया वैध है।

(viii) सूत्र imm के बायें पक्ष में स्थित राशि
आवृत्ति (n) की विमा= [M⁰L⁰T^-1]
सूत्र के दायें पक्ष में स्थित राशियाँ = \(\frac{1}{2 l} \sqrt{\frac{\mathrm{Mg}}{m}}=\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{m}}\)
l की विमा = [L¹], 
M की विमा = [M¹]
g की विमा = [LT^-2 ] तथा m की विमा = [M¹L¹]
दायें पक्ष की विमा 
\(\begin{aligned} & =\frac{1}{2 L^1} \sqrt{\left(\frac{\mathrm{M}\left[\mathrm{LT}^{-2}\right]}{\mathrm{M}^1 \mathrm{~L}^{-1}}\right)} \\ & =\frac{1}{2 \mathrm{~L}^1} \sqrt{\mathrm{L}^2 \mathrm{~T}^{-2}}=\frac{1}{2} \mathrm{~T}^{-1} \end{aligned}\)
यहाँ 1/2 एक शुद्ध संख्या है, इसलिये इसकी कोई विमा नहीं है। अतः दायें पक्ष की विमा = T^-1 = बायें पक्ष की विमा, यह सूत्र पूर्णतया सही है।

प्रश्न 6. 
वायु में ध्वनि का वेग V, वायु के दाब P तथा वायु के घनत्व d पर निर्भर करता है। विमीय विधि द्वारा सम्भावित सूत्र की स्थापना कीजिये।
\(\mathrm{v}=\mathrm{K} \sqrt{\frac{\mathrm{P}}{d}}\)
उत्तर:
हम जानते हैं कि ध्वनि का वेग v, वायु के दाब P तथा घनत्व d पर निर्भर करता है अतः हम लिख सकते हैं:
V α P^xd^y
जहाँ पर x तथा y क्रमशः दाब व घनत्व की विमा है, यदि K एक स्थिरांक हो।
v = KP^xd^y .................(1)
बायें पक्ष की विमा (v) = [M⁰L¹T^-1] 
दाब की विमा = [M¹L^-1T^-2]
घनत्व की विमा = [M¹L^-3T0] तथा
K एक विमाहीन राशि है।
∴ दायें पक्ष की विमायें = [M¹L^-1T²] x [M¹L^-3T⁰]^Y 
= [M^x+y L^x-3y T^-2x]
हम जानते हैं कि बायें पक्ष की विमायें दायें पक्ष की विमायें
= [M⁰L¹T^-1] = [M^x+y L^x-3y T^-2x]
दोनों पक्षों में M, L तथा T की घातों की तुलना करने पर
x + y = 0  .....(2)
- x - 3y = 1 .....(3)
- 2x = - 1 .....(4)
∴ x = 12/2
x का मान समीकरण (2) में रखने पर
y =  -1/2
x तथा y के मान समीकरण (1) में प्रतिस्थापित करने पर 
v = KP^1/2d^-1/2
\(\mathrm{v}=\mathrm{K} \sqrt{\frac{\mathrm{P}}{d}}\)
विमीय विश्लेषण द्वारा K का मान ज्ञात नहीं किया जा सकता है। 

प्रश्न 7. 
एक फोटॉन की ऊर्जा E, उसकी आवृत्ति v सम्बन्ध E = ho द्वारा व्यक्त होता है। प्लांक नियतांक h की विमा एवं मात्रक बताइए।
उत्तर:
प्रश्नानुसार
E = hv
h की विमा =
ऊर्जा E की विमा = [ML²T^-2] 
आवृत्ति v की विमा = [T^-1]
प्लांक नियतांक h की विमा = \(\left[\frac{\mathrm{ML}^2 \mathrm{~T}^{-2}}{\mathrm{~T}^{-1}}\right]\)
= [ML²T^-1]

प्रश्न 8. 
यदि बल तथा लम्बाई के मात्रकों में से प्रत्येक को दुगुना कर दिया जाये, तो ऊर्जा के मात्रक का मान कितना गुना हो जायेगा ? ऊर्जा (= कार्य) = बल x विस्थापन
उत्तर:
ऊर्जा की विमा (= कार्य की विमा)
= बल की विमा x लम्बाई की विमा अतः बल तथा लम्बाई के मात्रकों को दुगुना कर देने पर ऊर्जा का मात्रक 4 गुना हो जायेगा।

प्रश्न 9. 
शून्य अंक किन परिस्थितियों में सार्थक अंक माना जाता है?
उत्तर:
शून्य अंक निम्न परिस्थितियों में सार्थक अंक माना जाता

1. दो अशून्य अंकों के बीच समस्त शून्य सार्थक अंक होते हैं।
2. यदि दशमलव के पूर्व कोई अशून्य अंक हो तो दशमलव के बाद के शून्य सार्थक अंक होते हैं। जैसे 3.005 में सभी शून्य सार्थक अंक हैं।
3. दशमलव के दायीं ओर किसी अशून्य अंक के बाद के सभी शून्य सार्थक अंक होते हैं। जैसे 4.6500 में दोनों शून्य सार्थक अंक हैं। 

प्रश्न 10. 
एक ठोस घन की भुजा मापने में 5% की त्रुटि तथा द्रव्यमानं मापने में 3% की त्रुटि होती है। उसके पदार्थ के घनत्व मापने में कितनी त्रुटि होगी?
उत्तर:

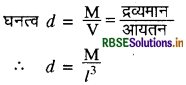
यदि माना ठोस घन की भुजा की लम्बाई = l 
घनत्व मापने में अधिकतम प्रतिशत त्रुटि
\(\left|\frac{\Delta d}{d}\right|_{\max } \times 100=\left(\frac{\Delta \mathrm{M}}{\mathrm{M}} \times 100\right)+\left(3 \times \frac{\Delta l}{l} \times 100\right)\)
= 3% + 3 x 5%
= 3% + 15% = 18%

प्रश्न 11. 
एक गोले की त्रिज्या के मापने में 0.5% की त्रुटि है। इसके पृष्ठीय क्षेत्रफल में स्वीकार्य त्रुटि ज्ञात करो। 
उत्तर:
गोले का पृष्ठीय क्षेत्रफल A = 4πr²
ऋणात्मक त्रुटि \(\frac{\Delta \mathrm{A}}{\mathrm{A}}=\frac{2 \dot{\Delta} r}{r}\)
% त्रुटि    \(\frac{\Delta \mathrm{A}}{\mathrm{A}} \times 100=2 \times\left(\frac{\Delta r}{r} \times 100\right)\)
= 2 x 0.5
% त्रुटि = 1.0% 

प्रश्न 12. 
एक छात्र प्रयोगशाला में सरल लोलक से आवर्तकाल का मान ज्ञात करने में 2% की त्रुटि लम्बाई ज्ञात करने में तथा 6% त्रुटि गुरुत्वीय त्वरण ज्ञात करने में करता है। T के मान में अधिकतम प्रतिशत त्रुटि ज्ञात करो।
उत्तर:

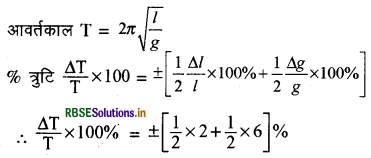
= +[1 + 3]% = +4%
आवर्तकाल में % त्रुटि = ± 4% 

प्रश्न 13. 
वायु में गतिमान किसी वस्तु पर वायु का घर्षण बल वस्तु के वेग के अनुक्रमानुपाती होता है, अनुक्रमानुपाती नियतांक (b) की विमायें क्या होंगी?
उत्तर:
यदि वायु का घर्षण बल F तथा वस्तु का वेग हो, तो
प्रश्नानुसार
F α V
या
F = bv
जिसमें b अनुक्रमानुपाती नियतांक है।
∴ b = F/V
बल की विमा = [M¹L¹T^-2] 
वेग v की दिशा = [LT^-1]
∴ b की विमा = \(\frac{\left[\mathrm{MLT}^{-2}\right]}{\left[\mathrm{LT}^{-1}\right]}=\left[\mathrm{MT}^{-1}\right]\)

आंकिक प्रश्न:

प्रश्न 1. 
एक प्रयोग में किसी छड़ की लम्बाई के प्रेक्षण क्रमशः 125 सेमी., 132 सेमी., 128 सेमी., 127 सेमी., 129 सेमी., 130 सेमी. एवं 126 सेमी. प्राप्त हुये। छड़ की औसत लम्बाई एवं प्रतिशत त्रुटि ज्ञात कीजिये। 
उत्तर:
औसत लम्बाई = (ā)

= 897/7 = 128.142  या 128 सेमी.
मापन में परम त्रुटि:
Δa1 = 128 - 125 = 3
Δa2 = 128 - 132 = -4
Δa3 = 128 - 128 = 0
Δa4 = 128 - 127 = 1
Δa5 = 128 - 129 = -1
Δa6 = 128 - 130 = -2
Δa7 = 128 - 126 = 2

प्रश्न 2. 
दो प्रतिरोध R₁ = (100 = 0.3) ओम तथा R₂ = (150° 0.5) ओम को श्रेणीक्रम में त्रुटि ज्ञात करो। जोड़ा जाता है। तुल्य प्रतिरोध एवं
उत्तर:
Rs = R₁ + R₂ = 100 + 150 = 250 ओम
Rs = ΔR₁ + ΔR₂ = 0.3 + 0.5 = 0.8 ओम
इसलिए तुल्य प्रतिरोध एवं त्रुटि = (250 = 0.8) ओम

प्रश्न 3. 
एक आयताकार पट्टिका की मीटर स्केल से लम्बाई इसी पट्टिका की चौड़ाई वर्नियर द्वारा 10.0 सेमी. प्राप्त होती है। 1.00 सेमी. प्राप्त होती है। मीटर स्केल एवं क्रमशः 0.1 सेमी. एवं 0.01 सेमी. हैं। इसके ज्ञात कीजिये।
उत्तर:
L = 10.0 सेमी.
B = 1.00 सेमी.
वर्नियर के अल्पतमांक
क्षेत्रफल में त्रुटि का मान
ΔL मीटर स्केल की अल्पतमांक = 0.1 सेमी.
ΔB = वर्नियर स्केल की अल्पतमांक = 0.01 सेमी. क्षेत्रफल में त्रुटि ज्ञात करने का सूत्र

प्रश्न 4. 
गुरुत्वीय त्वरण के सूत्र g = 4π²L/T2 तथा T के मान में क्रमश: +2% एवं +3% त्रुटि मापी गयी हैं। गुरुत्वीय त्वरण g के मान में प्रतिशत त्रुटि ज्ञात कीजिये।
उत्तर:
हम जानते हैं कि त्रुटि घात की राशियों के रूप में हो तो इस सूत्र को काम में लेते हैं। जैसे यदि
g = am/bm हो तो g में त्रुटि
\(\frac{\Delta g}{g}= \pm\left[\frac{n \Delta a}{a}+\frac{m \Delta b}{b}\right]\)
इसी सूत्र से हम उपर्युक्त सम्बन्ध को लिख सकते हैं।

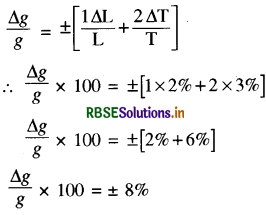
अतः g में प्रतिशत त्रुटि = + 8%

प्रश्न 5. 
किसी घनाभ की लम्बाई, चौड़ाई एवं ऊँचाई क्रमशः 4.234 मी., 1.005 मी. एवं 2.01 सेमी हैं। इसका क्षेत्रफल एवं आयतन सही सार्थक अंकों तक ज्ञात कीजिये।
उत्तर:
L = 4.234 मी.
B = 1.005 मी.
H = 2.01 सेमी. = 0.0201 मी.
क्षेत्रफल = ?
आयतन = ?
क्षेत्रफल और आयतन सही सार्थक अंकों तक ज्ञात करने हैं।
घनाभ का क्षेत्रफल
= 2 (L × B + B x H + H x L) = 2 (4.234 x 1.005 + 1.005 x 0.0201 0.0201 x 4.234)
= 2 (4.255 +0.0202 + 0.0851) = 2 x 4.360
= 8.720
सही सार्थक अंक में लेने पर = 8.72 मीटर²
तीन सार्थक अंक तक लेने पर
चूँकि सबसे कम सार्थक अंक ऊँचाई में तीन हैं। घनाभ का आयतन = L x B x H
= 4.234 x 1.005 x 0.0201 = 0.0855
पूर्णांकित करने पर 0.086 मी.³

प्रश्न 6. 
निम्नलिखित के सार्थक अंक लिखो:
(1) 0.046
(ii) 4.000
(iii) 0.060
(iv) 4.08 x 10⁶
(v) 600700
(vi) 24600
(vii) 600 मी.
(viii) 7432
(ix) 6212.0
(x) 427.071 
(xi) 0.0050
(xii) 0.00007032
(xiii) 0.4680
(xiv) 0.007
(xv) 0.046
(xvi) 946.860
(xvii) 0.04340N / m
(xviii) 46.000m
उत्तर:
(i) दो
(ii) चार
(iii) दो
(iv) तीन
(v) चार
(vi) तीन
(vii) तीन
(viii) चार
(ix) पाँच
(x) छः
(xi) दो
(xii) चार
(xiii) चार
(xiv) एक
(xv) दो
(xvi) छः
(xvii) चार
(xviii) पाँच।

प्रश्न 7. 
सार्थक अंकों के आधार पर 5.2 x 10⁶ को 8.3 x 10^-4 में से घटाओ।
उत्तर:
8.3 × 10^-4 - 5.2 x 10^-7
⇒ 8.3 x 10^-7  - 0.052 x 10⁴
⇒ 8.248 × 10^-4
⇒ 8.2 x 10^-4

प्रश्न 8. 
सार्थक अंकों के आधार पर 4.8 x 10 एवं 5.2 x 10⁷ का योग करो।
उत्तर:
4.8 x 10 + 5.2 x 10⁷
⇒ 0.48 × 10⁷ + 5.2 x 10⁷
⇒ 10⁷ [0.48 + 5.2]
⇒ 5.68 x 10^-7
⇒ 5.7 x 10⁷

प्रश्न 9. 
एक वायुमण्डलीय दाब 10⁶ डाइन / सेमी. 2 होता है। SI पद्धति में इसका मान ज्ञात कीजिए।
उत्तर: 
दाब का विमीय सूत्र = [M¹L^-1T^-2]
यहाँ पर a = 1, b = 1 तथा c = 2
पद्धति रूपान्तरण समीकरण से
\(\mathrm{n}_2=\mathrm{n}_1\left[\frac{\mathrm{M}_1}{\mathrm{M}_2}\right]^{\mathrm{a}}\left[\frac{\mathrm{L}_1}{\mathrm{~L}_2}\right]^{\mathrm{b}}\left[\frac{\mathrm{T}_1}{\mathrm{~T}_2}\right]^{\mathrm{c}}\)
दिया गया है:
CGS पद्धति
M = 1 ग्राम
L₁ = 1 सेमी.
T₁ = 1 सेकण्ड
n₁ = 10⁶ डाइन / सेमी.²

MKS पद्धति 
M₂ = 1 किग्रा. 
L₂ = 1 मीटर 
T₂ = 1 सेकण्ड 
n₂ = ?

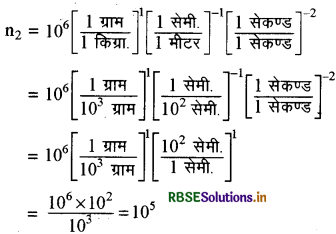
अतः SI मात्रकों में एक वायुमण्डलीय दाब = 10⁵ न्यूटन / मी. ² 

प्रश्न 10. 
1 जूल ऊर्जा के मान को CGS पद्धति में बदलिए। 
उत्तर: 
ऊर्जा का मात्रक SI पद्धति में जूल तथा CGS पद्धति में अ होता है:
ऊर्जा का विमीय सूत्र E = [M'L²T^-2 ] है।
यहाँ पर स्पष्ट है कि a = 1, b = 2 तथा c = - 2 है।
S. I. पद्धति में
C.G.S. पद्धति में
M₁ = 1 किग्रा.
Ly = 1 मीटर
T = 1 सेकण्ड
M₂ = 1 ग्राम
L₂ = 1 सेमी,
T₂ = 1 सेकण्ड
n₁ = 1 जूल
12 = ?
पद्धति रूपान्तरण समीकरण से

= 1 × 10³ × (10²)² = 10³ x 10⁴ = 10⁷
अतः 1 जूल = 10⁷ अर्ग

प्रश्न 11. 
ध्वनि का वायु में वेग imm सत्यता की जांच विमीय विधि द्वारा कीजिये। गुणांक एवं d घनत्व है।
उत्तर: 
दिया गया है:
ध्वनि का वायु में वेग (v) 
L.H.S. की विमा ज्ञात करने पर वेग (v) की विमा = [L¹T^-1] 
R.H.S. की विमा ज्ञात करने पर
है, इस सूत्र की
यहाँ E प्रत्यास्थता
प्रत्यास्थता गुणांक (E) की विमा = [M¹L^-1T^-2]
घनत्व d की विमा = [M¹L^-3T⁰]

= [LT^-1]
= L. H.S. की विमा का मान है।
L.H.S. = R.H.S.

प्रश्न 12. 
किसी स्वरित्र की आवृत्ति सूत्र \(\mathrm{n}=\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}}\) से दी जाती है। इसमें अनुनादी लम्बाई / भार के कारण उत्पन्न तनाव T एवं तार की एकांक लम्बाई का द्रव्यमान m है। इस सूत्र की सत्यता की जाँच विमीय विधि से कीजिए।
उत्तर: 
सूत्र \(\mathrm{n}=\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}}\)
बायें पक्ष में आवृत्ति की विमा = M⁰L⁰T¹ होगी।
दायें पक्ष में लम्बाई / का विमीय सूत्र [M⁰L¹T⁰] है, तनाव T का विमीय सूत्र [M¹L¹T²] है और एकांक लम्बाई के द्रव्यमान का विमीय सूत्र
होगा [M¹L^-1T⁰]
अतः \(\mathrm{n}=\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}}\) का विमीय सूत्र होगा:

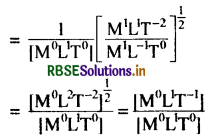
= [M⁰L⁰T¹]
अतः बायें पक्ष की विमा का मान दायें पक्ष की विमा का मान
अतः सूत्र विमीय दृष्टि से सही है।

प्रश्न 13. 
किसी उपग्रह का पलायन वेग पृथ्वी की सतह से ऊँचाई पर \(v=\sqrt{\frac{2 G M}{R}}\) हो तो सूत्र की सत्यता की जाँच कीजिए।
उत्तर: 
दिया गया है: \(v=\sqrt{\frac{2 G M}{R}}\)
बायें पक्ष की विमा वेगv = [M⁰L¹T^-1]
दायें पक्ष की विमा \(=\sqrt{\frac{2 G M}{R}}\)
\(=\sqrt{\frac{\left[\mathrm{M}^{-1} \mathrm{~L}^3 \mathrm{~T}^{-2} \|[\mathrm{M}]\right.}{[\mathrm{L}]}}\)
\(\left.=\sqrt{\left[\mathrm{M}^0 \mathrm{~L}^2 \mathrm{~T}^{-2}\right]}=\mid \mathrm{M}^0 \mathrm{~L}^1 \mathrm{~T}^{-1}\right]\)
दायें पक्ष की विमा = बायें पक्ष की विमा
अतः दिया गया सूत्र सही है।

प्रश्न 14. 
यदि किसी स्वरित्र की आवृत्ति (n), लम्बाई (1), घनत्व (d) तथा यंग के प्रत्यास्थता गुणांक y पर निर्भर करें तो सूत्र की स्थापना करो।
उत्तर:
माना कि
n α l^ad^dy^c
=> n = kl^ad^by^c .................. (1)
यहाँ विमाहीन समानुपाती नियतांक है। बायें पक्ष की विमा = \(\left|M^{10} L^0 \Gamma^1\right|\)
दायें पक्ष की विमा = \(\left|L^1\right|^{\mathrm{a}}\left|M^1 I^3\right|^b\left|M^1 L^{-1} T^2\right|^c\)
\(=\left[\left.\mathbf{M}^{\mathrm{b}+\mathrm{c}}\right|^{\mathrm{a}^{3 b}-\mathrm{c}} \mathrm{T}^{2 c}\right]\)
विमीय समांगता के सिद्धान्त के अनुसार
बायें पक्ष की विमा = दायें पक्ष की विमा 
[M⁰L⁰T^-1] = [M^b+c L^{a 3b-c} T^2c]
दोनों पक्षों में M L T की घातों की तुलना करने पर
b + c = 0
a - 3b - c = ( )
-2c = - 1
समीकरणों को हल करने पर
a = -1,b = 1⁄2 तथा c = 1/2
समीकरण (1) से
\(\begin{aligned} & \mathrm{n}=k l^{-1} \mathrm{~d}^{-\frac{1}{2}} \mathrm{y}^{\frac{1}{2}} \\ & \mathrm{n}=\frac{k}{l} \sqrt{\frac{\mathrm{y}}{\mathrm{d}}} \end{aligned}\)

गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न:

प्रश्न 1. 
समीकरण \(P=\frac{a-t^2}{b x}\) में P दाब x दूरी तथा समय है, तब a/b है की विमा होगी:
(a) [MT^-2]
(b) [M²LT ³]
(c) [ML³T^-2 ]
(d) [LT³]
उत्तर:
(a) [MT^-2]

प्रश्न 2. 
किसी दोलित्र पर अवमन्दक-बल वेग के समानुपाती होता है तो समानुपाती नियतांक का मात्रक है:
(a) kgms^-1
(b) kgms²
(c) kgs^-1
(d) kgs
उत्तर:
(c) kgs^-1

प्रश्न 3. 
वाण्डरबाल गैस समीकरण (P + a/v₂)(V-b) = RT  नियतांक 3 की विमायें होती हैं:
(a) [M¹L⁴T²] 
(b) [M¹L⁵T ²] 
(c) [M¹L³T²]
(d) [M¹L²T^-2]
उत्तर:
(b) [M¹L⁵T ²] 

प्रश्न 4. 
किसी नलिका से बहने वाले द्रव के क्रान्तिक वेग V की विमाओं को [nx py rz ] से निर्दिष्ट किया जाता है जहाँ n. p तथा क्रमशः द्रव का श्यानता गुणांक, द्रव का घनत्व तथा नलिका की त्रिज्या है। तो x y तथा 2 का क्रमशः मान है-
(a ) - 1 -1, I
(b) -1, -1, -1
(c) 1, 1, 1
(d) 1, −1, -1
उत्तर:
(d) 1, −1, -1

प्रश्न 5. 
R/L की विमा 
(a) [T²]
(b) [T]
(c) [T ^-1]
(d) [T^-2]
उत्तर:
(c) [T ^-1]

प्रश्न 6. 
एक प्रकाश फर्मी में कितने सेकण्ड होते हैं? 
(a) 10^-15 सेकण्ड
(b) 3.0 x 10⁸ सेकण्ड
(c) 3.33 x 10^-24 सेकण्ड
(d) 3.3 x 10^-7 सेकण्ड
उत्तर:
(c) 3.33 x 10^-24 सेकण्ड

प्रश्न 7.
\(\frac{1}{\mu_0 \epsilon_0}\) की विमा होगी, जहाँ प्रतीक का सामान्य अर्थ है:
(a) [LT^-1]
(b) [L^-1T]
(c) [L^-2T²]
(d) [L²T^-2]
उत्तर:
(d) [L²T^-2]
 

प्रश्न 8. 
प्लाँक नियतांक की विमायें (मात्रक ) किसके समान हैं:
(a) ऊर्जा
(b) रेखीय संवेग
(c) कार्य
(d) कोणीय संवेग
उत्तर:
(d) कोणीय संवेग

प्रश्न 9. 
संख्याओं 23.023 0.0003 तथा 2.1 x 10³ में सार्थक अंकों की क्रमश: संख्या है-
(a) 5, 1, 2
(b) 5, 1, 5
(c) 5, 5, 2
(d) 4, 4, 2
उत्तर:
(a) 5, 1, 2

प्रश्न 10. 
एक द्रव्यमान m स्प्रिंग से लटका है जिसका स्प्रिंग नियतांक K है। इस द्रव्यमान की आवृत्ति / निम्न सूत्र द्वारा दर्शायी जा रही है। f = Cmx Ky यहाँ पर C एक विमाहीन राशि है। x और y के मान होंगे:

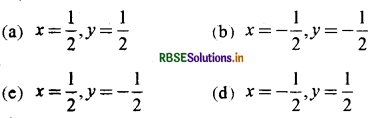
उत्तर:
\(\text { (d) } x=-\frac{1}{2}, y=\frac{1}{2}\)

प्रश्न 11. 
(μ0ε0)^-1/2 की विमा होगी:
(a) [L^1/2T^-1/2]
(b) [L^-1T]
(c) [LT^-1]
(d) [L^1/2T^1/2 ]
उत्तर:
(c) [LT^-1]
 

प्रश्न 12.
राशि (L/RCV) की विमा है:
(a) [A]
(b) [A₂] 
(c) [A^-1]
(d) इनमें से कोई नहीं
उत्तर:
(c) [A^-1]

प्रश्न 13. 
वोल्ट्जमैन नियतांक का विमीय सूत्र है:
(a) [ML²T^-2θ^-1]
(b) [ML²T^-2]
(c) [ML⁰T^-2θ^-1]
(d) [ML^-2T^-1θ^-1]
उत्तर:
(a) [ML²T^-2θ^-1]

प्रश्न 14.
\(\frac{e^2}{4 \pi \epsilon_0}\) से बनने वाली एक भौतिक राशि की विमायें वही हैं जो लम्बाई की हैं। [ जहाँ c प्रकाश का वेग, G सार्वत्रिक गुरुत्वीय स्थिरांक तथा आवेश हैं] यह भौतिक राशि होगी:

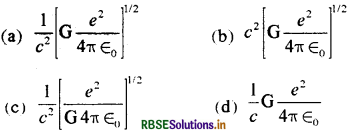
उत्तर:
\(\text { (b) } c^2\left[\mathrm{G} \frac{e^2}{4 \pi \epsilon_0}\right]^{1 / 2}\)

प्रश्न 15. 
यदि किसी गोले की त्रिज्या के मापन में त्रुटि 2% है, तो गोले के आयतन मापन में त्रुटि होगी:
(a) 8%
(b) 2%
(c) 4%
(d) 6%
उत्तर:
(d) 6%

प्रश्न 16. 
घन की आकृति वाले किसी पदार्थ का घनत्व, उसकी तीन भुजाओं एवं द्रव्यमान को माप कर निकाला जाता है। यदि द्रव्यमान एवं लम्बाई को मापने में सापेक्ष त्रुटियाँ क्रमश: 1.5% तथा 1% हो तो घनत्व को मापने में अधिकतम त्रुटि होगी-
(a) 3.5%
(b) 4.5%
(c) 6%
(d) 2.5%
उत्तर:
(b) 4.5%

प्रश्न 17. 
किसी छात्र ने इस्पात की लघु गेंद के व्यास की माप 0.001 cm अल्पतमांक वाले स्क्रू गेज द्वारा की मुख्य पैमाने की माप 5mm और वृत्तीय पैमाने का शून्य सन्दर्भ लेवल से 25 भाग ऊपर है। यदि स्क्रू गेज में शून्यांक त्रुटि 0.004 cm है, तो गेंद का
सही व्यास होगा:
(a) 0.521 cm
(b) 0.525 cm.
(c) 0.053 cm
(d) 0.529 cm
उत्तर:
(d) 0.529 cm

प्रश्न 18. 
व्यंजक 2d sin θ =  λ का उपयोग करते हुए हम 8 को माप कर d का मान जानना चाहते हैं। 8 का मान 0 व 90° के बीच में है। तरंगदैर्ध्य का मान हमें परिशुद्धतः ज्ञात है तथा 6 के मापने में त्रुटि के सभी मानों के लिए समान है। जैसे 8 का मान 0° से बढ़ता है तब:
(a) d में निरपेक्ष त्रुटि स्थिर रहती है।
(b) d में निरपेक्ष त्रुटि बढ़ती है।
(c) d में भिन्नात्मक त्रुटि स्थिर रहती है
(d) d में भिन्नात्मक त्रुटि घटती है।
उत्तर:
(d) d में भिन्नात्मक त्रुटि घटती है।

प्रश्न 19. 
एक छात्र के सरल आवर्त दोलन के 100 आवृत्तियों का समय 4 बार मापता है और उनको 90s, 95s और 92 5 पाता है। इस्तेमाल की गई घड़ी का न्यूनतम अल्पांश 15 है। तब मापे गये माध्य समय को उसे लिखना चाहिए-
(a) 92 + 5.0 s
(b) 92 + 1.8 s
(c) 92 ° 3 s
(d) 92 + 2 s
उत्तर:
(d) 92 + 2 s

प्रश्न 20. 
एक स्क्रू गेज का पिच 0.5mm है और उसके वृत्तीय स्केल पर 50 भाग हैं। इसके द्वारा एक पतली एल्यूमीनियम शीट की मोटाई मापी गई। माप लेने के पूर्व यह पाया गया कि जब स्क्रू गेज के दो जॉबों को सम्पर्क में लाया जाता है तब 45वाँ भाग मुख्य स्केल लाईन के सम्पाती होता है और मुख्य स्केल का शून्य (0) मुश्किल से दिखता है। मुख्य स्केल का पाठ्यांक यदि 0.5mm तथा 25वाँ भाग मुख्य स्केल लाईन के सम्पाती हो, तो शीट की मोटाई क्या होगी:
(a) 0.80mm
(b) 0.70 mm
(c) 0.50mm
(d) 0.75mm
उत्तर:
(a) 0.80mm

प्रश्न 21. 
एक व्यक्ति एक पत्थर को कुएँ में गिराते समय और कुएँ की तली में संघट से उत्पन्न ध्वनि के समय अन्तराल का मापन करके कुएँ की गहराई का पता लगाता है। वह समयान्तराल के मापन में त्रुटि ST = 0.01 सेकण्ड एवं कुएँ की गहराई L = 20 m मापता है। गुरुत्वाकर्षण त्वरण g = 10ms' एवं ध्वनि गति 300ms^-1 दी गई है। imm के मापन में निकटतम आंशिक त्रुटि
(a) 0.2%
(b) 3%
(c) 5%
(d) 1%
उत्तर:
(d) 1%

प्रश्न 22. 
एक मीटर स्केल द्वारा नापने पर किसी बेलन का व्यास और ऊँचाई क्रमशः 12.6 ° 0.1 cm और 34.2 ° 0.1 cm आते हैं। उपयुक्त सार्थक अंकों में इसके
(a) 4260 80 cm³
(b) 4300 ° 80 cm³
(c) 4264.4 ° 81.0cm³
(d) 4264 81 cm³
उत्तर:
(a) 4260 80 cm³

प्रश्न 23. 
यदि गति (V), त्वरण (A) तथा बल (F) मानें, तो यंग प्रत्यास्थता गुणांक की विमा होगी- आयतन का मान क्या होगा:
(a) V^-2A²F²
(b) V^-4A²F
(c) V^-4A^-2F
(d) V^-2A²4^-2
उत्तर:
(b) V^-4A²F

प्रश्न 24. 
एक पेचमापी की पिच तथा वृत्तीय पैमाने पर भागों की संख्या क्रमश: 0.5mm तथा 100 है जब पेचमापी को बिना किसी वस्तु के पूरी तरह कस दिया जाता है, तो इसके वृत्तीय पैमाने का शून्य मध्य रेखा से तीन भाग नीचे आता है। एक पतली चादर की मोटाई के लिए इस पेचमापी के मुख्य पैमाने तथा वृत्तीय पैमाने का पाठ्यांक क्रमश: 5.5 mm तथा 48 हैं तो चादर की मोटाई होगी.
(a) 5.755 m
(b) 5.725mm
(c) 5.740m
(d) 5.950mm
उत्तर:
(b) 5.725mm

प्रश्न 25. 
G (सार्वत्रिक गुरुत्वाकर्षण नियतांक) / (प्लांक नियतांक) तथा c (प्रकाश की गति) के रूप में समय का समतुल्य सम्बन्ध निम्न में से किसके समानुपाती होगा:

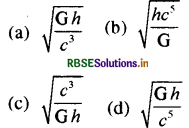
उत्तर:
\(\text { (b) } \sqrt{\frac{h c^5}{\mathrm{G}}}\)

प्रश्न 26.
एक वर्ग का क्षेत्रफल 5.29 cm² है। ऐसे सात वर्गों का क्षेत्रफल उचित सार्थक अंकों में होगा-
(a) 37 cm²
(b) 37.0 cm²
(c) 37.03 cm²
(d) 37.030 cm²
उत्तर:
(c) 37.03 cm²

प्रश्न 27. 
सूत्र X = 5YZ² में X तथा Z की विमायें, क्रमशः धारिता तथा चुम्बकीय क्षेत्र हैं। SI इकाई में Y की विमा क्या होगी:
(a) [M²L^-2T⁶A³]
(b) [M^-1L^-2T⁴A²]
(c) [M^-3L^-2T⁸A⁴]
(d) [M^-2L°T^-4A^-2]
उत्तर:
(a) [M²L^-2T⁶A³]

प्रश्न 28. 
निम्नांकित में से किस संयोजन की विमा वही है, जो विद्युत प्रतिरोध की है (यहाँ,  ε₀, निर्वात की विद्युतशीलता (परावैद्युतांक) तथा μ₀ निर्वात की चुम्बकशीलता है:

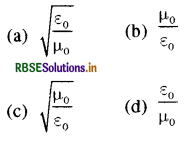
उत्तर:
\(\text { (d) } \frac{\varepsilon_0}{\mu_0}\)

प्रश्न 29. 
एक सरल दोलक के प्रयोग, जिसमें गुरुत्वीय त्वरण (g) मापना है, में 20 दोलनों का समय एक 1 sec अल्पतमांक वाली एक विराम घड़ी से मापते हैं। इस समय का माध्य मान 30s आता है । दोलक की लम्बाई को 1 mm अल्पतमांक के पैमाने से मापने पर 55.0 cm आती है। g के मापन में प्रतिशत त्रुटि का सन्निकट मान होगा
(a) 0.7%
(b) 0.2%
(c) 3.5%
(d) 6.8%
उत्तर:
(b) 0.2%

प्रश्न 30. 
किसी प्रयोग में भौतिक राशियों A, B, C और D की माप में होने वाली त्रुटि की प्रतिशतता क्रमशः 1% 2% 3% और 4% हैं। तब X की माप, जबकि \(\mathrm{X}=\frac{\mathrm{A}^2 \mathrm{~B}^{1 / 2}}{\mathrm{C}^{1 / 3} \mathrm{D}^3}\) है, में अधिकतम प्रतिशत त्रुटि होगी:
(a) (3/13)%
(b) 16%
(c) - 10%
(d) 10%
उत्तर:
(b) 16%

प्रश्न 31. 
प्लांक स्थिरांक 1, प्रकाश की चाल G को लम्बाई की इकाई L तथा द्रव्यमान की इकाई M बनाने के लिये प्रयोग किया जाता है। तब सही कथन है ( हैं ) - तथा गुरुत्वाकर्षण स्थिरांक

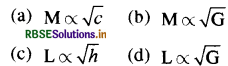
उत्तर:
\(\text { (d) } \mathrm{L} \propto \sqrt{\mathrm{G}}\)

प्रश्न 32. 
गुरुत्वीय त्वरण g के निर्धारण के एक प्रयोग में प्रयुक्त आवर्ती- गति का समयकाल का सूत्र imm है। R तथा r के मापा गया मान क्रमश: (60) + 1) mm तथा ( 10 ° 1) mm हैं। लगातार पाँच मापन में मापा गया समयकाल 0.52 s, 0.56 s, 0.57 s, 0.54 तथा 0.59s हैं। समयकाल के मापन के लिए प्रयोग में लायी गयी घड़ी का अल्पतमांक 0.01 s है। निम्नलिखित में से कौनसा / कौनसे कथन सत्य है/हैं:
(a) के मापन में त्रुटि 10% है
(b) T के मापन में त्रुटि 3.57% है
(c) T के मापन में त्रुटि 2% है
(d) g के निकाले गये मान में त्रुटि 11% है
उत्तर:
(d) g के निकाले गये मान में त्रुटि 11% है

प्रश्न 33. 
कॉलम: I को कॉलम-II से सुमेलित कीजिए और कॉलमों के नीचे दिये गये कोड का प्रयोग करके सही उत्तर चुनिये:

कॉलम-I	कॉलम-II
(A) बोल्ट्समान नियतांक	(p) [ML2T-1]
(B) श्यानता गुणांक	(q) [ML-1T-1]
(C) प्लांक नियतांक	(r) [MLT-3K-1]
(D) उष्मा चालकता	(s) [ML2T-2K-1]

उत्तर:

कॉलम-I	कॉलम-II
(A) बोल्ट्समान नियतांक	(s) [ML2T-2K-1]
(B) श्यानता गुणांक	(q) [ML-1T-1]
(C) प्लांक नियतांक	(p) [ML2T-1]
(D) उष्मा चालकता	(r) [MLT-3K-1]