RBSE Class 11 Physics Important Questions Chapter 2 Units and Measurements

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 2 Units and Measurements Important Questions and Answers.

RBSE Class 11 Physics Chapter 2 Important Questions Units and Measurements

Multiple Choice Questions

Question 1.
1 second is equivalent to:
(a) Time of 1650763.73 oscillations of krypton clock.
(b) Time of 652189.63 oscillations of krypton clock.
(c) Time of 1650763.73 oscillations of cesium clock.
(d) Time of 9,192,631,770 oscillations of cesium clock.
Answer:
(d) Time of 9,192,631,770 oscillations of cesium clock.

Question 2.
1 meter is equivalent to:
(a) 10¹⁰ Å
(b) 10⁸ Å
(c) 10⁶ Å
(d) 10 Å
Answer:
(a) 10¹⁰ Å

Question 3.
Maximum error in measuring the side of a cube and its mass is 2% and 3% respectively. Maximum error in estimating its density will be:
(a) 3%
(b) 27%
(c) 9%
(d) 6%
Answer:
(c) 9%

Question 4.
On heating the water, its temperature becomes (25.0 ± 0.3)°C from (20.0 ± 0.2)°C. Maximum possible error in rise in temperature will be:
(a) 2%
(b) 10%
(c) 10/9%
(d) 2/9%
Answer:
(b) 10%

Question 5.
If the unit of mass, length and time are halved, then what,will become the unit of pressure?
(a) one fourth
(b) half
(c) two times
(d) four times
Answer:
(d) four times

Question 6.
Errors in mass and speed of a body are 2% and 3%. Maximum error in estimating the kinetic energy of the body will be:
(a) 5%
(b) 8%
(c) 1%
(d) 7%
Answer:
(b) 8%

Question 7.
Error in measurement of arm of a cube is 2%, then error in calculation of its volume will be:
(a) 1%
(b) 2%
(c) 3%
(d) 6%
Answer:
(d) 6%

Question 8.
The number of significant figures in 0.02800 will be:
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(c) 4

Question 9.
A physical quantity Y is given by Y = am/n. If errors in measurement of a and b are respectively x and y, then maximum error in calculation of Y will be:
(a) m_x + n_y
(b) m_x - n_y
(c) m_x x n_y
(d) m_x + n_y
Answer:
(a) m_x + n_y

Question 10.
The errors in measurement of mass and radius of a spherical body are 2% and 3% respectively. The maximum error in calculation of its density will be:
(a) 5%
(b) 1%
(c) 6%
(d) 11%
Answer:
(d) 11%

Question 11.
If X = \(\frac{a \sin \theta+b \cos \theta}{a+b}\), then:
(a) Dimensions of X and a are same,
(b) Dimensions of a and b are not same,
(c) X is dimensionless
(d) None of these is correct
Answer:
(c) X is dimensionless

Question 12.
If pressure P, velocity V and time T are considered fundamental quantities, then dimension formula of force will be:
(a) [P¹V²T²]
(b) [P^-1V²T^-2]
(c) [P¹V¹T²]
(d) [P^-1V¹T²]
Answer:
(a) [P¹V²T²]

Question 13.
Dimensional formula of quantity \(\frac{L}{R C V}\) is:
(a) [A¹]
(b) [A²]
(c) [A^-1]
(d) None of these
Answer:
(c) [A^-1]

Question 14.
A student writes the angle of inclination θ as tanθ = \(\frac{r g}{v^2}\), then this formula:
(a) is numerically correct
(b) is dimensionally correct
(c) both (a) and (b) are correct
(d) both (a) and (b) are wrong
Answer:
(b) is dimensionally correct

Question 15.
A physical quantity P depends on time according to relation P = P₀e-^at2 where t is time and α and P₀ are constants, then constant α:
(a) will be dimensionless
(b) its dimensions will be [T^-2]
(c) its dimensions are those of P
(d) its dimensions are product of P and [T^-2]
Answer:
(b) its dimensions will be [T^-2]

Question 16.
Dimensional formula of pressure is:
(a) [M¹L¹T^-2]
(b) [M¹L^-1T^-2]
(c) [M¹L²T^-2]
(d) [M¹L²T^-3]
Answer:
(b) [M¹L^-1T^-2]

Question 17.
Dimensional formula of surface tension is:
(a) [M¹L¹T^-2]
(b) [M¹L²T^-2]
(c) [M¹L⁰T^-2]
(d) [M¹L¹T^-1]
Answer:
(c) [M¹L⁰T^-2]

Question 18.
dimensional formula of force constant of spring is:
(a) [M¹L¹T^-2]
(b) [M¹L¹T^-1]
(c) [M¹L²T^-2]
(d) [M¹L⁰T^-2]
Answer:
(d) [M¹L⁰T^-2]

Question 19.
In equation v = at + b, v is velocity and t is time. Dimensional formula of \(\frac{a}{b}\) will be:
(a) [M⁰L¹T^-1]
(b) [M⁰L⁰T^-1]
(c) [M⁰L^-1T^-1]
(d) [M⁰L^-1T¹]
Answer:
(d) [M⁰L^-1T¹]

Question 20.
In displacement equation of a wave y = a sin(ωt - kx), t is time and x is distance. Dimensional formula of \(\frac{w}{k}\) will be:
(a) [M⁰L⁰T⁰]
(b) [M⁰L¹T¹]
(c) [M⁰L¹T^-1]
(d) [M⁰L^-1T^-1]
Answer:
(c) [M⁰L¹T^-1]

Question 21.
Dimensional formula of gravitational potential is:
(a) [M^-2L²T^-2]
(b) [M^-1L²T^-2]
(c) [M⁰L²T^-2]
(d) [M¹L²T^-2]
Answer:
(c) [M⁰L²T^-2]

Question 22.
Dimensional formula of Planck’s constnat is equivalent to those of:
(a) Force
(b) Energy
(c) Linear momentum
(d) Angular momentum
Answer:
(d) Angular momentum

Question 23.
The velocity of following under gravity is proportional to g^xh^y; where g is gravitational acceleration and h is height, values of r and y are:
(a) x = 1; y = \(\frac{\mathrm{1}}{2}\)
(b) x = \(\frac{\mathrm{1}}{2}\); y = \(\frac{\mathrm{1}}{2}\)
(c) x = \(\frac{\mathrm{1}}{2}\); y = 1
(d) x = 1; y = 1
Answer:
(b) x = \(\frac{\mathrm{1}}{2}\); y = \(\frac{\mathrm{1}}{2}\)

Question 24.
Dimensional formula of Young’s modulus of elasticity is:
(a) [M¹L^-1T^-2]
(b) [M¹L²T^-2]
(c) [M¹L¹T^-2]
(d) [M¹L^-1T^-1]
Answer:
(a) [M¹L^-1T^-2]

Fill in the Blanks

Question 1.
The number of significant figures in 0.003403 is ...............................
Answer:
4.

Question 2.
The ............................... of a measurement is measure of ............................... the ............................... value is to the ............................... of the quantity.
Answer:
accuracy, how close, measured, actual value.

Question 3.
Momentum per unit volume has dimension ...............................
Answer:
[MLT^-2]

Question 4.
The dimensional formula of pressure gradient is ...............................
Answer:
[ML^-2T^-2]

Question 5.
The dimensional formula of Hubble constant is ...............................
Answer:
[M⁰L⁰T^-1]

Question 6.
The parallax method has been used for measuring ............................... which are ...............................
Answer:
distance of star, less than 100 ly away

Question 7.
Time taken by light to cross a distance of nuclear size is of the order of ...............................
Answer:
10^-22 second

Question 8.
Any phenomenon that ............................... can serve as a ...............................
Answer:
repeats itself regularly, clock.

Very Short Answer Questions

Question 1.
What is unit of luminous intensity in S.I. system?
Answer:
In S.I. system, the unit of luminous intensity is ‘Candela.’

Question 2.
How much times the solar mass is one C.S.L.?
Answer:
1.4 times.

Question 3.
Light year is the unit of which quantity?
Answer:
Light year is the unit of distance.

Question 4.
What is the fundamental unit of amount of substance?
Answer:
Mole

Question 5.
If error in measurement of physical quantity is ∆a, then what will be percentage error in an?
Answer:
Percentage error of quantity an will be n x \(\frac{\Delta a}{a}\) x 100.

Question 6.
1 A.U. is equivalent to how many meters?
Answer:
1 A.U. = 1496 x 10¹¹ m.

Question 7.
Parsec is unit of which quantity?
Answer:
Unit of distance.

Question 8.
Obtain the unit of Planck’s universal constant 'h'.
Answer:
Energy of photon is given by E= hv
where, v is the frequency
∴ h = \(\frac{\tilde{E}}{\mathrm{v}}\)
Hence, unit of h = \(\frac{\mathbf{J}}{s^{-1}}\) = J.s

Question 9.
How many fundamental and supplementary units are in international system?
Answer:
Seven fundamental units and two supplementary units.

Question 10.
Write the dimensional formula of Boltzmann constant.
Answer:
Boltzmann constnat k = \(\frac{\text { Energy }}{\text { Temperature }}\)
= \(\frac{\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-2}}{\theta^1}\) = [M¹L²T^-2θ^-1]

Question 11.
Write the dimensional formula of impulse.
Answer:
Impulse = Force x time interval
= M¹L¹T^-2 x T¹ = [M¹L¹T^-1]

Question 12.
Does the existence of dimensionless and unitless physical quantity is possible?
Answer:
Yes; for example relative density and strain.

Question 13.
Speed of transverse wave in a wire is v = \(\sqrt{\frac{T}{m}}\), where T is tension in the wire; m is mass per unit lenght in kg.m^-1, and velocity v in ms^-1, then what will be unit of tension T?
Answer:
Given: v = \(\sqrt{\frac{T}{m}}\) ⇒ T = v².m
But m = \(\frac{M}{L}\) ∴ T = v².\(\frac{M}{L}\)
∴ Unit of T = m²s^-2 x \(\frac{\mathrm{kg}}{\mathrm{m}}\) = kg.ms^-2 or Newton

Question 14.
Name two such constants which are not dimensionless.
Answer:
Planck’s constant; Gas constant.

Question 15.
Give the name of physical quantity which has same dimensions as those of linear momentum.
Answer:
Impulse; dimensional formula = [M¹L¹T^-1]

Question 16.
Write the dimension of coefficient of viscosity.
Answer:
Dimensional formula of coefficient of viscosity = [M¹L^-1T^-1]

Question 17.
Write the dimensions of gravitational acceleration (g) and universal constant of gravity (G).
Answer:
Dimensional formula of g = [M⁰L¹T^-2]
Dimensional formula of G = [M^-1L²T^-2]

Match the Following

Question 1.
Match the physical quantities with dimensional formulae expresed in disarray:

(i) Planck's constant	(a) [ML2T-3A-1]
(ii) Gravitational constant	(b) [M0L0T0]
(iii) Resistivity	(c) [ML2LT-1]
(iv) Joules Mechanical	(d) [M-1L3T-2]
(v) Potential difference	(e) [M1L3T-3A-2]

Answer:

(i) Planck's constant	(c) [ML2LT-1]
(ii) Gravitational constant	(d) [M-1L3T-2]
(iii) Resistivity	(e) [M1L3T-3A-2]
(iv) Joules Mechanical	(b) [M0L0T0]
(v) Potential difference	(a) [ML2T-3A-1]

Question 2.
Column I gives three physical quantities select the appropriate units for these form choices given in Column II. some of the physical quantities may have more than one choice.

Column I	Column II
(i) Capacitance	(a) Ohm-sec
(ii) Inductance	(b) Columb2-Joule-1
(iii) Magnetic Induction	(c) Columb-Volt-1
	(d) Newton-(Amp-m)-1
	(e) Volt-sec (Amp)-1

Answer:

Column I	Column II
(i) Capacitance	(c) Columb-Volt-1 (b) Columb2-Joule-1
(ii) Inductance	(a) Ohm-sec (e) Volt-sec (Amp)-1
(iii) Magnetic Induction	(d) Newton-(Amp-m)-1

Short Answer Questions

Question 1.
What do you understand by significant figure?
Answer:
Any physical quantity can be measured accurately by a measuring instrument upto a certain limit. Therefore every measurement involves errors. Therefore, it is reasonable to report the result of any measurement in such a way that indicates the precision of measurement. Normally the reported result of measurement is a number that includes all digits in the number that are known reliably plus one digit that is uncertain.

“The digits that are known reliably plus the first uncertain digit are known as significant digits or significant figures.” Significant figures can also be defined as, “The number of digits required to represent a physical quantity accurately, are called significant figures.”

At the time of measuring the length of a rod with the help of simple scale if it is found some what more than 5.8 cm but less than 5.9 cm, then on the basis of personal judgement writing its length 5.85 cm is scientifically wrong because least count of scale is 0.1 cm. This scale connot give any certain reading at second place after decimal point. Thus we can say that in this measurement only two digits 5 and 8 are significant while third digit 5 is doubtful. If the same measurement is carried out by vernier callipers and the length is found 5.87 cm. then third digit 7 will also be significant because the least count of vernier calliper is 0.01 cm.

It is clear from above discussion that in measurements 5.8 cm, 5.9 cm and 5.87 cm, the last digit of any measurement under limit of accuracy is doubtful or uncertain digit. More is the number of significant figures in a quantity, more accurate will be the measurement.

Question 2.
What is difference between accuracy and precission of a measurement?
Answer:
Difference between accuracy and precision:
Accuracy of any measurement is that how near is measurement value to its actual value while precision of any measurement means upto which resolving limit, the measurement of the quantity has been taken.
Precision of measurement ∝ \(\frac{1}{\text { Least count of measuring instrument }}\)
Accuracy of measurement depends upon various factors, e.g. instrumental errors, incompletion of experimental technique, sudden change in conditions during measurement and resolving limit of measuring instrument etc.

Question 3.
What do you understand by absolute and relative errors?
Answer:
Absolute error: Suppose n observatoins of measured quantity x are x₁ ,x₂,x₃,....., x_n, then arithmetic mean of these observations:
\(\bar{x}=\frac{x_1+x_2+x_3+\ldots+x_n}{n}\)
or \(\bar{x}=\sum_{i=1}^n \frac{x_i}{n}\)
Since actual value of measured quantity is unknown, therefore \(\bar{x}\) can be considered as actual value of x.
Difference of measured value and actual value is called absolute error. Therefore absolute error in various observations will be

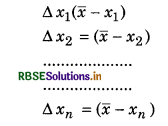
Therefore net absolute error will be obtained by arithmetical mean of magnitudes of these errors i.e. net absolute error,
\(\Delta \bar{x}=\frac{\left|\Delta x_1\right|+\left|\Delta x_2\right|+\left|\Delta x_3\right|+\ldots+\left|\Delta x_n\right|}{n}\)
or \(\Delta \bar{x}=\frac{\sum_{i=1}^n\left|\Delta x_i\right|}{n}\)

Relative or fractional error: Ratio of net absolute error and arithmetic mean of quantity, is called relative or fractional error.
∴ Relative error = \(\frac{\Delta \bar{x}}{\bar{x}}\)

Question 4.
What do you mean by fundamental and derived units?
Answer:
Fundamental Units: The units of fundamental quantities are called fundamental units.
There units represent fundamental quantities. For example: unit of mass is kilogram (kg), unit of length is meter (m), unit of time is second (s), unit of electric currennt is Ampere (A) etc.

Derived Units: Units of derived quantities are called derived units. For example,
Area = length x width
Unit of area = m x m = m²
or unit of area is m².
Similarly, derived unit of any derived physical quantity can be obtained.

Question 5.
Give standard definition of 1 second.
Answer:
Second: It is unit of time. " It defines the time interval in which cesium atom completes 9,192,631,770 vibrations in its ground state."

Question 6.
Write the definition of 1 Ampere.
Answer:
Ampere: It is unit of electric current. It is defined on the basis of force acting between two parallel currents. Force acting between two parallel currents is given by
F = 2 x 10^-7\(\frac{I_1 I_2}{r}\)l

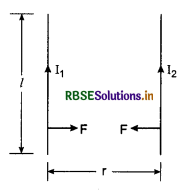
where I₁ and I₂ are currents flowing in wires placed parallel at distance r apart and l is the length of wire on which the force is acting.
If I₁ = I₂ = IA, l = 1m, r = 1m
then, F = 2 x 10^-7 N.m^-1
∴ From the relation
2 x 10^-7 = \(\frac{2 \times 10^{-7} \times I^2}{1}\)
∴ I₂ = 1
⇒ I = 1 Amp
i.e. "If equal current flows in two parallel wires placed at 1 m and force acting between them is 2 x 10^-7 N-m^-1, then each current in the wires will be 1 Ampere."

Question 7.
Define solar year.
Answer:
1 solar year is the time interval in which earth completes its one revolution in its orbit around the sun.
1 solar year = 365.25 solar days

Question 8.
Rotational energy of an object rotating with angular velocity ω, is represented by K = \(\frac{1}{2}\)Iω². Find the dimension of I by dimensional method.
Answer:
∵ K = \(\frac{1}{2}\)Iω² ⇒ I = \(\frac{2 K}{\omega^2}\)
∴ Dimensional formula of I = \(\frac{\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-2}}{\mathrm{~T}^{-2}}\) = [M¹L²T⁰]

Question 9.
Velocity of sound in air is given by v = \(\sqrt{\frac{E}{d}}\). Check the validity of this formula by dimensional method. Here E is modulus of elasticity and d is density of air.
Answer:
Given equation: v = \(\sqrt{\frac{E}{d}}\)
Dimensional formula of L.H.S = [M⁰L¹T^-1]
Dimensional formula of R.H.S.
= \(\sqrt{\frac{M^1 L^{-1} T^{-2}}{M^1 L^{-3}}}=\sqrt{L^2 T^{-2}}\)
= L¹T^-1
= [M⁰L₁T^-1]
Since the dimensions of both sides are the same, therefore the given formula is 'Correct' or 'True'

Question 10.
Find the ratio of unit of coefficient of viscosity in M.K.S and C.G.S. system.
Answer:
Dimensional formula of η = [M¹L^-1T^-1]
\(\therefore \frac{\text { Unit of } \eta \text { in M.K.S. system }}{\text { Unit of } \eta \text { in C.G.S. system }}\)
= \(\frac{\mathrm{kg} \cdot \mathrm{m}^{-1} \cdot \mathrm{s}^{-1}}{\mathrm{~g} \cdot \mathrm{cm}^{-1} \cdot \mathrm{s}^{-1}}=\frac{\mathrm{kg} \cdot \mathrm{cm}}{\mathrm{g} \cdot \mathrm{m}}\)
= \(\frac{1000 \mathrm{~g} \times \mathrm{cm}}{\mathrm{g} \times 100 \mathrm{~cm}}\) = 10

Question 11.
The velocity of a particle varies with time t according to relation v = at² + \(\frac{b}{c+t}\). Find out the dimensions of a,b and c.
Answer:
Dimensions of c = Dimensions of t = [M⁰L⁰T¹]
Dimensions of at² = Dimensions of v
∴ Dimensions of a = Dimensions of \(\frac{v}{t^2}\)
= \(\frac{\mathrm{L}^1 \mathrm{~T}^{-1}}{\mathrm{~T}^2}\) = L¹T^-3
= [M⁰L¹T^-3]
Similarly, dimensions of \(\frac{b}{(c+t)}\) = Dimensions of v
∴ Dimensions of b = Dimensions of v
= L¹T^-1 x T¹ = L¹
= [M⁰L¹T⁰]

Question 12.
What are the limitation of dimensional analysis?
Answer:
Some limitations of dimensional analysis are:
It doesn’t give information about the dimensional constant.
The formula containing trigonometric function, exponential functions, logarithmic function, etc. cannot be derived.
It gives no information about whether a physical quantity is a scalar or vector.

Question 13.
Write the uses of dimensional analysis.
Answer:
To check the correctness of a physical relation
To convert the value of a physical quantity from one system to another.
To derive relation between various physical quantities.
To find the dimensions of dimensional constants.

Question 14.
The displacement x of a particle is given by x = a + bt + ct², where t is time in second and displacement x is in meter. Find the dimensions of a,b and c.
Answer:
Dimensions of c = Dimensions of t = [M⁰L⁰T¹]
Dimensions of at² = Dimensions of v
∴ Dimensions of a = Dimensions of \(\frac{v}{t^2}\)
= \(\frac{\mathrm{L}^1 \mathrm{~T}^{-1}}{\mathrm{~T}^2}\) = L¹T^-3
= [M⁰L¹T^-3]
Similarly, dimensions of \(\frac{b}{(c+t)}\) = Dimensions of v
∴ Dimensions of b = Dimensions of v
= L¹T^-1 x T¹ = L¹
= [M⁰L¹T⁰]
Dimensions of a = [M⁰L¹T⁰]
Dimensions of b = [M⁰L¹T^-1]
Dimensions of c = [M⁰L¹T^-2]

Question 15.
Write the dimensional formula of equation y = a sin(ωt - kx).
Answer:
In given equation y = a sin(ωt - kx) the term (ωt - kx) represents the angle which is dimensionless.
∴ Dimensions of ωt = Dimensions of angle
∴ Dimensions of ω = Dimensions of \(\frac{\text { angle }}{t}\)
= \(\frac{\mathrm{M}^0 \mathrm{~L}^0 \mathrm{~T}^0}{\mathrm{~T}^1}\) = [M⁰L⁰T^-1]

Question 16.
Give the dimensions of x in relation, velocity = \(\sqrt{\frac{\text { Pressure }}{x}}\)
Answer:

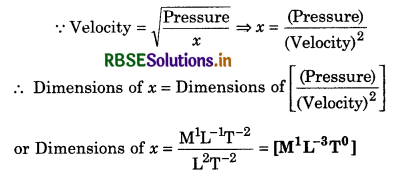
Question 17.
In formula T = 2π\(\sqrt{L Y}\), T is time and L is length. Obtain the dimensions of Y.
Answer:
Given formula: T = 2π\(\sqrt{L Y}\)

Long Answer Questions

Question 1.
What is called error? Describe various types of errors.
Answer:
Error: Measurements in Science and technology should be accurate and precise. There is some what uncertainty in measurements taken by measuring
instrument. This uncertainly only is called error.

1. Systematic errors: “The errors which are decided by a systematic law are called systematic errors.” This law can be found out and later on systematic error can be minimised. Sources of systematic errors are given below:
(a) Instrumental error: All instrumental errors are under systematic errors. Their exemples are given below:

• Errorfull calibration of scale: Due to errorful calibration of thermometer it may show the boiling point of water at NIP. as 95°C in place of 100°C.
• Zero-error of apparatus: Zero error of vernier calliper, screw gauge, index error of optical bench etc are systematic errors. For example zero of

main scale and zero of vernier scale are not coinciding in vernier calliper, meter scale is broken at starting end etc.

(b) Imperfection in experimental technique: During experiment, change in external conditions e.g. temperature, humidity, change in velocity of air etc are under systematic errors. Imperfect technique also comes under systematic errors. For example if the temperature of person is measured by pressing the thermometer under shoulder arm, then measured temperature is less than actual temperature.

(c) Personal errors: These errors are produced due to wrong setting of apparatus and carelessness in taking observations.

Elimination: To eliminate systematic errors, various methods are used in various situations.
(a) In same circumstances,the errors are decided before actual experiment. For example; zero error of apparatus is decided before performing the experiment and each observation is corrected accordingly.
(b) In some circumstances, errors are decided after the experiment. For example; in experiment of heat, the correction of heat due to radiation is done
after each observation according to observations of temperature.

2. Random errors: “The errors which are produced due to unknown reasons, are called ran1om errors”. Sources of random errors are as under:
(i) Sudden change in conditions during experiment. For example; sudden change in temperature and supply voltage.
(ii) Imperfect decision of observer in taking observations.
Gausss studied the random errors and he presented a law which is known as ‘normal law’ or “Gaussian law”. This law can be expressed by graph (fig. 2.10). In this graph N is the number of observations and X is error. From the graph it is clear that probability of less random errors is more and vice-versa.

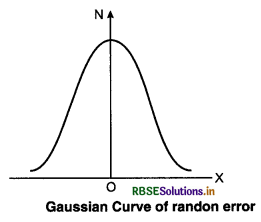
Elimination: From the graph it is also clear that positive and negative random errors are symmetrical. This law is obtained from it that, “Random error can be minimised by taking arithmetic mean of large number of observations taken in experiment.” This mean will be very close to actual value. If any observation differs very much from other observations, then this observation is not included in mean.

3. Gross-errors: The errors which occur due to carelessness of person, are called gross-errors. These are produced due to following reasons:

1. Taking observations without setting the apparatus.
2. Taking observation adopting wrong methods.
3. Comitting mistake while writing the observations
4. Wrong substitution of observations during calculation work.

Question 2.
What do you understand by least count of a measuring instrument? Calculate the percentage in addition and subtraction of two quantities.
Answer:
Least Count: Least count of an instrument is the minimum measurement which can be done by the instrument.
When two quantities are added or subtracted, the absolute error in the final result is the sum of the absolute errors in the individual quantities.
Z = A + B
We have by addition, Z ± ΔZ = (A ± ΔA) + (B ± ΔB).
The maximum possible error in Z
ΔZ = ΔA + ΔB
For the difference Z = A – B, we have
Z ± Δ Z = (A ± ΔA) – (B ± ΔB) = (A – B) ± ΔA ± ΔB
or, ± ΔZ = ± ΔA ± ΔB The maximum value of the error ΔZ is again ΔA + ΔB

Question 3.
Describe the maximum possible error in product and divison of two quantities.
Answer:
The result of an experiment is generally calculated by using some formulae which may contain many measured quantities and only one unknown quantity operations (e.g. addition, subtraction, multiplication, division etc.) may be carried out. Therefore errors in observations propagate to result.
(i) Error due to addition of quantities: Suppose two quantities A and B are related with third quantity Z as under:
Z = (A+B) .......................(1)
Errors in measurement of A&B are ± ∆A and ± ∆B respectively. Error propagated to Z is ± ∆Z.
Therefore equation (1) can be written as,
(Z ± ∆Z) = (A ± ∆A) ÷ (B ± ∆B)
or Z ± ∆Z = (A + B) ± (∆A + ∆B)
or Z ± ∆Z = Z± (∆A + ∆B)
or ± ∆Z = ± (∆A + ∆B)
∴ Maximum absolute error,


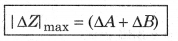
(ii) Error in difference of quantities: Suppose the difference of two quantities A and B is related with third quantity Z as under:
Z = (A - B)
Suppose errors in measurement of A and B are ∆A and ∆B respectively. The error propagated to Z is ∆Z.
∴ (Z ± ∆Z) = (A ± ∆A) - (B ± ∆B)
or Z ± ∆Z = (A - B) ± (∆A + ∆B)
or Z ± ∆Z = Z ± (∆A + ∆B)
or ± ∆Z = ±(∆A + ∆B)
∴|∆Z|max =  ∆A + ∆B

(iii) Error in product of quantities
Suppose two quantities A and B are related with quantity Z as under.
Z = A x B ..................(1)
If absolute errors in A, B and Z are ∆A, ∆B and ∆Z respectively, then equation (1) will become now:

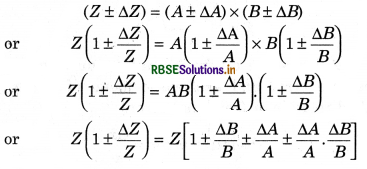
∵ \(\frac{\Delta A}{A} \times \frac{\Delta B}{B}\) is very small quantity, therefore it can be neglected.

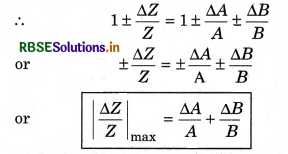
This is maximum relative error propagated to Z.

(iv) Error in quotientt of quantities


(v) Error due to measured quantity raised to power
Suppose Z = A² = A x A
∴ log Z = log A + log A
On differentiating both sides,

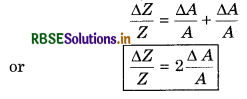
In general: If Z = Am
The log Z = log Am = m log A
On differentating both sides,

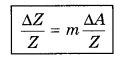
(vi) Maximum relative error in mixed quantities
Suppose, Z = \(\frac{a^p b^q}{c^x d^y}\)
On taking log on both sides, we have
Log Z = log[\(\frac{a^p b^q}{c^x d^y}\)]
= log a^p.b^p - log c^x d^y
= log a^p + log b^p - log c^x - log d^y
or log Z = p.log a + q log b - x log c - y log d
on differentiating both sides, we get

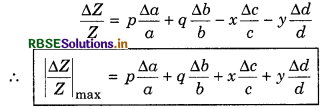
Question 4.
Describe some direct and indirect methods for measuring length.
Answer:
The measurement is the result of the comparison of standard and the unknown quantity. The result of the measured quantity is generally expressed in numeric forms. In other words, the measurement is the process through which the physical parameters like heat, displacement, force etc. is converted into the easily readable numeric value.

Methods of Measurement
The different methods of measurement are explained below in details.
Direct Method of Measurement – In this method of measurement, the unknown quantity is directly compared with the standard quantity. The result of the quantity is expressed in number. It is the most common method of measuring the physical quantities like length, temperature, pressure, etc.
Example: The physical balance directly measures the weight of the matter.

Indirect Method of Measurement – The direct measurement gives the inaccurate results in most of the cases. Hence, the direct method is rarely preferred for measurement. In indirect method of measurement, the physical parameters of the quantity are measured by the direct method, and then the numerical value of the quantity is determined by the mathematical relationship.
Example: The length, breadth and height of the substance is measured by the direct method and then by the help of the given relation the weight of the substance is known.
Weight = Length x Breadth x Height x Density

Method of Measurement without Contact - The sensor remains untouched with the object whose characters need to be measured.
Method of Combination measurement closed series - The result of the direct or indirect method of measurement are used for solving the equations.

Question 5.
What do you understand by intertial mass and gravitational mass? Describe the methods for measurement of these masses.
Answer:
Measurement of Length:
(a) Height of man is measured by scale.
(b) Diameter of a coil is measured by Vernier callipers.
(c) Diameter of a wire is measured by screw gauge.
(i) Measurement of Very Small Distances: Diameter of molecule is of order of 10^-8 m to 10^-10 m. A microscope has its own limit. In optical microscope,
wavelength of used light is 5 x 10^-7 m. Such microscope is useful only for resolving equivalent to wavelength of light. According to de-Broglie hypothesis, waves are also associated with electrons. If electron beams is accelerated by 150 volt then de-Broglie wavelength of waves associated with electron beam is found to be 1 Å = 10^-10 m. Also the electron beam can be focused with the help of electric and magnetic fields. On this basis, electron microscope was made in which electron beam is used in place of light waves.

Thus, the resolving limit of this microscope is reduced equivalent to 1 Å. Resolving of atoms and molecules would be possible by this microscope. Therefore indirect methods are useful to measure very short distances. Here we shall describe some such methods.

(1) Estimation of Size of very small distances like size of molecules:
(i) By oleic acid method: Oleic acid is a faty acid of molecular formula C₁₇H₃₂COOH.
This method is based on this fact that oleic acid makes monomolecular layer on water surface. Oleic acid is a liquid like soup. Which has its molecules of size of order 10^-9 m. (i.e. 10 Å).
First of all we take 1 m³ oleic acid and dissolve it in 20 cm³ of alcohol. 1 cm³ of this solution is again dissolved in 20 cm³ alcohol. Thus the concentration of oleic acid solution becomes \(\frac{1}{20 \times 20}=\frac{1}{400}\) cm^-3. Now water is taken in a big pot and some lycopodium powder is sprinkled on water surface. Now n drop of above final solution is poured on the water surface. This drop will spread out in the large, thin and almost circular film. The alcohol evaporates and oleic acid layer is left. If we assume that the film has one molecule thickness, then it becomes the diameter of oleic acid. Now measure the area (A) of the film using graph paper. If t be the thickness of the layer, then volume of oleic acid will be At cm³. Volume of oleic acid in n drops of solution will be \(\frac{n V}{400}\) cm³.
∴ At = \(\frac{n V}{400}\)
⇒ t = \(\frac{n V}{400 \mathrm{~A}}\) cm
[V = Volume of one drop of oleic acid]
If the film of oleic acid is monomolecular, then t will be the diameter of molecule of oleic acid.

(2) Estimation of Atomic Radius by Avogadro’s Hypothesis: An atom is a tiny sphere. When such atoms lie packed in any substance, empty spaces are left in between. By the Avogadro’s hypothesis, volume of all atoms in any mass of the substance is \(\frac{2}{3}\) of the volume occupied by that mass of
the substance.
Suppose the molar mass of an atomic substance is M i.e. number of atoms in M gram of substance will be equivalent to Avogadro’s number N.
Therefore, number of atoms in m gram substance = \(\frac{m N}{M}\).
If r be the radius of one atom, then volume of these atoms
V₀ = \(\frac{m N}{M} \times \frac{4}{3}\)πr³ .....................(1)
According to Avogadro's hypothesis, the actual volume of atoms is \(\frac{2}{3}\) of volume covered by atoms in solid state. Rest \(\frac{1}{3}\) part remains vacant. In real sense it structure. If volume of m gram substance be V, then

Thus value of r can be calculated if the values of M, ρ and N are known
∴ Distance between two nearest atoms in solid = 2r

Question 6.
How the units of physcial quantities are changed from unit system in other system. Give example.
Answer:
Product of numerical value of a physical quantity and its unit u remains constant
i.e., n.[u] = constant ........................(1)
Suppose the dimensions of a physical quantity Q are a, b and c then its dimensional formula will be [M^aL^bT^c]. In one system its unit is [M₁^aL₁^bT₁^c]
and its numerical value is n₁. Similarly in other system both are [M^a₂L₂^bT₂^c] and n₂ respectively. Therefore from equation (1)
Q = n₂u₂ = n₁u₁
or n₂ [M₂^aL₂^bT₂^c] = n₁ [M₁^aL₁^bT₁^c]
or n₂ = \(\frac{n_1\left[\mathrm{M}_1^a \mathrm{~L}_1^b \mathrm{~T}_1^c\right]}{\left[\mathrm{M}_2^a \mathrm{~L}_2^b \mathrm{~T}_2^c\right]}\)

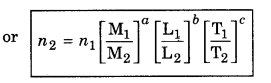
In this relation we consider n₁ and u₁ known parameters and n₂ and u₂ unknown parameters. Therefore the units in numerator are always converted in units of denominator.

Question 7.
What do you understand by dimensional equilibrium of physical equation? How the validity of a equation is checked with the help of this equilibrium of dimensions? Give example.
Answer:
For this purpose we obtain the dimensional formulae of both sides of the equation and then compare the dimensions of both sides. If the dimensions of both sides are same, the equation or formula will be correct or valid otherwise incorrect or invalid. This method is also called principle homogeneity. According to this law, if any quantity is added or subtracted from other quantity, then dimensions of both quantities must be same.
Example:
Check the validity of equation S = ut + \(\frac{1}{2}\)at² by dimensional method.
Given equation S = ut + \(\frac{1}{2}\)at²
Since in R.H.S. there is (+) sign. Therefore on preparing semi equations:
S = ut ............................(1)
and S = \(\frac{1}{2}\) at² ........................(2)
On writing the dimensional formula on both the sides of equation (1), we have
L¹ = L¹T^-1.T^-1 = L^-1
i.e. [M⁰L¹T⁰] = [M⁰L¹T⁰]
Since the dimensions on both sides of equation (2) we have:
L¹ = L¹T^-2.T² = L¹
or [M⁰L¹T⁰] = [M⁰L¹T⁰]
This equation is also dimensionally valid.
Since bothe semi-equations are dimensionally valid, therefore given equation S = ut + \(\frac{1}{2}\)at² is dimensionally valid.

Question 8.
Check the validity of following equations by dimensional method.
(i) S = \frac{h r \rho g}{2 \cos \theta}. where S is surface tension of the liquid; r is the radius of cappilary; ρ is density of the liquid; θ is angle of contact and h is the height of raised liquid column in the capillary.
(ii) Stoke's force acting on a spherical object in a liquid, F = 6πηrv where η is the coefficient of viscosity; r is the radius of the object; v is the velocity of the following object.
(iii) Time period of motion of an object suspended by a spring T = 2π\(\sqrt{\frac{m}{K}}\), where m is the mass of the object and K is spring constant.
Answer:
For this purpose we obtain the dimensional formulae of both sides of the equation and then compare the dimensions of both sides. If the dimensions of both sides are same, the equation or formula will be correct or valid otherwise incorrect or invalid. This method is also called principle homogeneity. According to this law, if any quantity is added or subtracted from other quantity, then dimensions of both quantities must be same. 
Example:
Check the validity of equation S = ut + \(\frac{1}{2}\)at² by dimensional method.
Given equation S = ut + \(\frac{1}{2}\)at²
Since in R.H.S. there is (+) sign. Therefore on preparing semi equations:
S = ut ............................(1)
and S = \(\frac{1}{2}\) at² ........................(2)
On writing the dimensional formula on both the sides of equation (1), we have
L¹ = L¹T^-1.T^-1 = L^-1
i.e. [M⁰L¹T⁰] = [M⁰L¹T⁰]
Since the dimensions on both sides of equation (2) we have:
L¹ = L¹T^-2.T² = L¹
or [M⁰L¹T⁰] = [M⁰L¹T⁰]
This equation is also dimensionally valid.
Since bothe semi-equations are dimensionally valid, therefore given equation S = ut + \(\frac{1}{2}\)at² is dimensionally valid.

Question 9.
Write the dimensional formulae of following quantities:
Gravitational constant; Young's modulus of elasticity, modulus of rigidity; gas constant; Boltzmann constant; coefficient of thermal conductivity; capacity; electric resistance; electric potential.
Answer:
Gravitational constant G = \(\frac{F r^2}{m_1 m_2}\)
= \(\frac{\mathrm{M}^1 \mathrm{~L}^1 \mathrm{~T}^{-2} \mathrm{~L}^2}{\mathrm{M}^1 \mathrm{M}^1}\) = [M^-1L³T^-2]

Young's modulus of elasticity:
Modulus of elasticity = \(\frac{\text { Stress }}{\text { Strain }}\)
= \(\frac{\mathrm{M}^1 \mathrm{~L}^{-1} \mathrm{~T}^{-2}}{\mathrm{M}^0 \mathrm{~L}^0 \mathrm{~T}^0}\) = [M¹L^-1T^-2]
Thus dimensions of pressure, stress and modulus of elasticity are the same i.e., [M¹L^-1T^-2].
Dimensions of all coefficients of elasticity e.g, Young’s modulus of elasticity, Bulk modulus of elasticity and modulus of Rigidity are the same i.e., [M¹L^-1T^-2].

modulus of rigidity:
By definition
Modulus of rigidity = \(\frac{\text { Shear stress }}{\text { Shear strain }} \frac{F / A}{x / L}\)
Dimensional formula of Modulus of rigidity are \(\frac{M L T^{-2}}{L^2}\) = ML^-1T^-2

gas constant (R)
∵ Gas equation for one mole PV = RT ⇒ R = \(\frac{P V}{T}\)
∴ R = \(\frac{M^1 L^{-1} T^{-2} L^3}{\theta^1}\) = [M¹L²T^-2θ^-1]

Boltzmann constant
∵ Energy E = \(\frac{3}{2}\)kT ⇒ k = \(\frac{2 E}{3 T}\)
k = \(\frac{E}{T}=\frac{\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-2}}{\theta^1}\) = [M¹L²T^-2θ^-1]

coefficient of thermal conductivity
Thermal conductivity K = \(\frac{Q l}{\text { At } \Delta \theta}\)
= \(\frac{M^1 L^2 T^{-2} L^1}{L^2 T^1 \theta^1}\) = [M¹L¹T^-3θ^-1]

capacity (C)
∵ Charge on capacity q = CV ⇒ C = \(\frac{q}{V}\)
∴ C = \(\frac{\mathrm{A}^1 \mathrm{~T}^1}{\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-3} \mathrm{~A}^{-1}}\) = [M^-1L^-2T⁴A²]

electric resistance (R)
∵ R = \(\frac{V}{I}=\frac{\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-3} \mathrm{~A}^{-1}}{\mathrm{~A}^1}\) = [M¹L²T^-3A^-2]

electric potential
Electric potential is defined as the work done to move per unit positive charge from one point to another point.
The SI unit of electric potential is volt (V).
V = \(\frac{\mathrm{W}}{\mathrm{Q}}\)
Hence dimension is \(\frac{\left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]}{[\mathrm{AT}]}\)
= [ML²T^-3A^-1]

Question 10.
Explain in detail the dimension, dimensional formula; dimensional equation and principle of homogeneity.
Answer:
When the unit of any physical quantity is represented in terms of funda mental units then the obtained expression is called the “Dimensional Formula” of the quantity and the raised powers on fundamental units, are called ‘Dimensions’ of the quantity. For example:
Speed = \(\frac{\text { Distance }}{\text { Time }}\)
∴ Unit of Speed = \(\frac{\text { Unit of distance }}{\text { Unit of time }}\)
= (Unit of distance)1 x (Unit of time)^-1
Thus it is clear that to obtain the unit of speed we have to raise power of 1 over the unit of distance and power of -1 over the unit of time. Thus the units of speed can be written in different systems as ms^-1, cms^-1, foot.s^-1. Hence, it is clear that the power i.e. dimensions remains unchanged even on changing the system of units i.e, “Dimensions of any physical quantity do not depend upon unit.”
Now, the dimensional formula of speed
= \(\frac{\text { Dimensional formula of distance }}{\text { Dimensional formula of time }}\)
= \(\frac{L^1}{T^1}\) = L¹T^-1
= [M⁰L¹T^-1]
Thus [M⁰L¹T^-1] is the dimensional formula of speed and (0,1,-1) are the dimensions of speed.
Dimensional equation: The equation obtained on equating the symbol of physical quantity with its dimensional formula is called dimesnional equation.
For example
Force = [M¹L¹T^-2]
or [F] = [M¹L¹T^-2] Dimensional equation

Principle of homogeneity of dimensions:
According to this principle, for a physical quantity, the dimensions of fundamental quantities on both the sides should be equal i.e., for equation
[M^aL^bT^c] = [M^xL^yT^z]. According to principle of homogeneity
x = a; y = b and z = c

Conceptual Questions

Question 1.
By which method the life of earth is determined?
Answer:
Life of earth can be determined by method of “Carbon Dating”. i.e. by dating of radioactive carbon (⁶C₁₄).

Question 2.
Does the measurement of an angle depend on the unit of length?
Answer:
No, because the angle is ratio of two lengths (Q = \(\frac{\Delta S}{r}\)). Hence the same units of ∆S and r cancel out each other.

Question 3.
Why the astronomical time was replaced by cesium atomic clock?
Answer:
Because the measurement of time by cesium atomic clock is 200 time more accurate than astronomical time.

Question 4.
Tell the relative error in the value of X if X is given by X = \(\frac{A^4 B^{1 / 3}}{C \cdot D^{3 / 2}}\)
Answer:
In terms of relative error,
\(\left|\frac{\Delta X}{X}\right|_{\max }=4 \frac{\Delta A}{A}+\frac{1}{3} \frac{\Delta B}{B}+\frac{\Delta C}{C}+\frac{3}{2} \frac{\Delta D}{D}\)

Question 5.
Tell the number of significant figure in following:
(a) 0.0020 x 10⁴ m
(b) 5.30 x 10⁶ kg
Answer:
(a) two
(b) three.

Question 6.
How many nano-seconds are there in 1 millisecond?
Answer:
1 ms = 10^-3 s and 1 ns = 10^-9 s
∴ \(\frac{1 \mathrm{~ms}}{1 \mathrm{n}}=\frac{10^{-3}}{10^{-9}}\) = 10⁶
∴ 1 ms = 10⁶ ns

Question 7.
Why cesium atomic clock was temporarily accepted by internationl standard?
Answer:
Because, invention of such a clock is in process which may prove itself more accurate than cesium atomic clock. For example error of 1 s is produced by Hydrogen Maser in 33,000,000 years.

Question 8.
α = \(\frac{F v^2}{\beta^2}\) log_e(\(\frac{2 \pi \beta}{v^2}\)), where F = force and v = velocity. Determine the dimensions of α and ß.
Answer:
Given relation: α = \(\frac{F v^2}{\beta^2}\) log_e(\(\frac{2 \pi \beta}{v^2}\))
Special fact:
1. log and powers of e are dimensionless.
2. Dimensionless quantity is equal to 1.

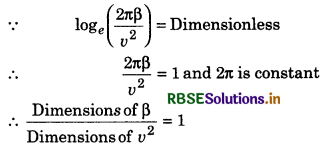
or Dimensional of ß = Dimensions of v₂
= [M⁰L²T^-2]

Question 9.
Force of air friction acting on an object moving in air is directly proportional to its velocity. Determine the dimensional formula of proportionality constant.
Answer:
If F be the force of air friction and v its velocity.
then F ∝ v (According to question)
or F = kV ⇒ k = \(\frac{F}{v}\)
∴ Dimensional formula of K = \(\frac{\text { Dimensions of } F}{\text { Dimensions of } v}\)
= \(\frac{M^1 L^1 T^{-2}}{L^1 T^{-2}}\) = [M¹L⁰T^-1]

Question 10.
Find the value of x when (velocity)^x = (pressure difference)^3/2 x (density)^3/2.
Answer:
Given relation (velocity)^x = (pressure - difference)^3/2 x (density)^3/2, writing the dimensional formula on both sides:
[M⁰L¹T^-1]^x = [M¹L^-1T^-2]^3/2.[M¹L^-3]^-3/2
or [M⁰L^xT^-x] = M^3/2L^-3/2T^-3. M^-3/2.L^9/2
or [M⁰L^xT^-x] = [M⁰L³T^-3]
On comparing the dimensions of both sides, we have
x = 3

Question 11.
Relation F = a + bx, where F is force and x is distance. Obtain the dimensions of a and b in this relation.
Answer:
Dimension of a = Dimension of F
= [M¹L¹T^-2]
Similarly, Dimensions of b = Dimensions of \(\frac{F}{x}\)
= \(\frac{M^1 L^1 T^{-2}}{L^1}\) = [M¹L⁰T^-2]

Question 12.
Displacement equation for a wave is y = a sin (At - B + C), where A, B and C are constants. Determine the dimensions of these constnats.
Answer:
∵ Angle is a dimensionless quantity.
∴ At - Bx + C = dimensionless quantity = 1
∴ At = dimensionless = 1
∴ A = \(\frac{1}{t}=\frac{1}{\mathrm{~T}^1}\) = T^-1
Hence, dimensional formula of A = [M⁰L⁰T^-1]
Similarly Bx = 1 ⇒ B = \(\frac{1}{x}\)
∴ Dimensional formula of B = [M⁰L^-1T⁰]
and C = 1
∴ Dimensional formula of C = [M⁰L⁰T⁰]

Question 13.
If velocity, force and time are considered as fundamental quantities, then obtain the dimensional formula of mass.
Answer:
From Newton’s law of motion,
m = \(\frac{F}{a}=\frac{F}{\frac{v}{t}}=\frac{F \cdot t}{v}\)
According to question F, t and v are fundamental quantities. Therefore,
Dimensional formula of m = [F¹v^-1t¹]

Question 14.
If units of force and length both are increased to 4 times, then how much time will become the unit of energy?
Answer:
∵ Energy = Work = Force x displacement.
∴ Dimension of energy = dimension of force x dimension of displacement.
Hence on changing the units of force and displacement to 4 times, the unit of energy will become 16 times.

Question 15.
E, M, L and G represent respectively energy, mass, angular momentum and constant of gravity. Determine the dimension of \(\frac{E L^2}{M^5 G^2}\).
Answer:
Dimension of energy E = [M¹L²T^-2]
Dimension of L = [M¹L²T^-1]
Dimension of M = [M¹]
Dimension of G = [M^-1L³T^-2]

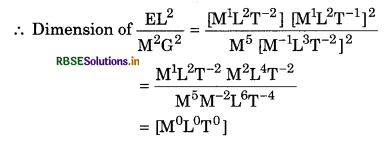
Thus the given quantity is dimensionless.

Question 16.
Four students were told to write the displacement particle executing harmonic motion. They wrote four different expressions given below:
(a) y = A sin ωt
(b) y = A sin vt
(c) y = \(\frac{A}{2}\) sin (2πλt)
(d) y = \(\frac{A \sin (\omega t / v)}{\sqrt{2}}\)
Here A is maximum displacement from mean position, ω is angular velocity, t is time, λ is wavelength and v is velocity of the particle. Explain which expression is correct?
Answer:
Special fact: Trigonometrical function is dimensionless ratio. Angular digit of trigonometric function is an angle which is dimensionless quantity. It means that ωt in formula (a), vt in formula (b), 2πλt in formula (c) and ωt/v in formula (d) should be dimensionless.
(a) Dimensions of ωt = [T^-1] x [T^-1] = [M⁰L⁰T⁰]. It is dimensionless.
(b) Dimensions of vt = [L¹T^-1]. [T^-1] = [M⁰L¹T⁰]. It is not dimensionless.
(c) Dimensions of 2πλt = [L¹] [T¹] = [M⁰L¹T¹]. It is also not dimensionless.
(d) Dimensions of \(\frac{\omega t}{v}=\frac{\left[\mathrm{T}^{-1}\right]\left[\mathrm{T}^1\right]}{\mathrm{L}^1 \mathrm{~T}^{-1}}\) = [M⁰E^-1T¹]. It is also not dimensionless.
Only in expresson (a), the angular digit is dimensionless therefore only expression (a) i.e. y = A sin ωt is correct and rest 3 i.e. (b), (c) and (d) are wrong.

Question 17.
The velocity of a particle is represented by equation v = at + \frac{b}{t}, where t is time. Find the dimensional formula of a and b.
Answer:
Given equation: v = at + \(\frac{b}{t}\)
According to principle of homogeneity the dimensions of v, at and \(\frac{b}{t}\) should be same.
∴ Dimensions of at = Dimensions of v
∴ Dimensions of a = Dimensions of \(\frac{v}{t}\)
= \(\frac{\mathrm{L}^1 \mathrm{~T}^{-1}}{\mathrm{~T}^1}\) = L¹T^-2
[M⁰L¹T^-2]
Similarly, dimensions of b = Dimensions of vt
= L¹T^-1T¹ = L¹
= [M⁰L¹T⁰]

Question 18.
In relation A + B = C, the dimensions of both A and C are [M¹L^-1T^-2]. Find the dimensions of B.
Answer:
According to principle of homogeneity, only the quantities of same dimensions can be added or subtracted. Therefore dimensions of B = Dimensions of A or C.
= [M¹L^-1T^-2]

Question 19.
Write the names of those quantities which have the dimensional formula [M¹L²T^-1].
Answer:
Angular momentum and Planck’s constant.

Question 20.
Unit of force in M.K.S. system is ‘Newton’. If somebody writes this unit as kg.m.s^-2, then is it correct?
Answer:
It is correct because the dimensional formula of force is [M¹L¹T^-2]. On writing the units we get kg. m.s^-2. Therefore in M.K.S. unit derived unit of force is kg.m.s^-2 which is called ‘Newton’.

Question 21.
In equation, E = at + bt², E is electromotive force (i.e. e.m.f.); t is temperature difference and a and b are constants. Here what will be unit of a?
Answer:
According to principle of homogeneity
Unit at = unit of E
∴ Unit of a = \(\frac{\text { Unit of } E}{\text { Unit of } t}=\frac{\text { volt }}{\text { degree }}\) = volt/degree.

Numerical Questions

Based on Measurement

Question 1.
Angular displacement of a body in space from two opposite ends of diameter of earth, is 60 second. If radius of earth be 6.4 x 106 m, then calculate the distance of the body from earth. Change this distance in A.U.
Answer:
Given: Radius of earth R = 6.4 x 10⁶ m
∴ Diameter of earth D = 2R
= 2 x 6.4 x 10⁶  = 12.8 x 10⁶ m
Parallax θ = 60 sec
= \(\left(\frac{60}{3600}\right)^{\circ}=\left(\frac{\pi}{180} \times \frac{1}{60}\right)\) rad.
∴ Diameter of body in space from earth

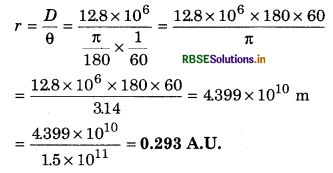
Question 2.
Size of hydrogen atom is nearby 0.4 Å. Determine the volume of 1 mole of hydrogen atom in m³. Given 1 Å = 10^-10 m.
Answer:
Given: Radius of hydrogen atom,
r = 0.4 Å
= 0.4 x 10^-10 m = 4 x 10^-11 m
Volume of hydrogen atom = \(\frac{4}{3}\)πr³
= \(\frac{4}{3}\) x 3.142 x (4 x 10^-11)³
= 2.68 x 10^-31 m³
∴ Volume of atoms in 1 mole of hydrogen = Number of atoms x Volume of 1 atom
= Avogadro's number x Volume of 1 atom
= 6.023 x 10²³ x 2.68 x 10^-31 m³
= 1.6 x 10^-7 m³

Question 3.
Radar signals are sent from earth to any planet. They are obtained on earth again after 7 minutes after reflecting from the planet. Distance between earth and planet is 6.3 x 10¹⁰ m. Calculate the speed of the signal.
Answer:
Given: Distance between earth and planet
S = 6.3 x 10¹⁰ m
Time taken by Radar signal to reach the planet,
t = \(\frac{7}{2}\) min = \(\frac{7}{2}\) x 60 s = 210 s
∴ Speed of Radar signal,
v = \(\frac{\text { distance }}{\text { time }}=\frac{6.3 \times 10^{10}}{210}\)
or v = 3 x 10⁸ ms^-1

Question 4.
A star is at a distance of a light years. What will be this distance in Parsec unit? When it is viewed from two different points situated at a distance of 3 x 10¹¹ m, then what will be its angular displacement?
Answer:
Given: 1 Ly = 9.46 x 10¹⁵ m
1 Parsec = 3.084 x 10¹⁶ m
∴ \(\frac{9 \mathrm{Ly}}{1 \text { Parsec }}=\frac{9 \times 9.46 \times 10^{15}}{3.084 \times 10^{16}}\)
or 9 Ly = 2.763 Parsec
Now displacement,
θ = \(\frac{l}{r}=\frac{3 \times 10^{11}}{2.763 \times 3.084 \times 10^{16}}\) radian
or θ = \(\frac{3 \times 10^{11}}{2.763 \times 3.084 \times 10^{16}} \times \frac{180 \times 3600}{3.14}\) sec.
or θ = 0.73 s

Question 5.
How many air molecules will there be in a room of volume 12 m³. At N.T.P. the volume of 1 mole of air is 22.4 litre.
Answer:
Given: Number of molecules in 1 mol of air = Avogadro's number = 6.023 x 10²³
Volume of 1 mol at N.T.P. = 22.4 litre = 22.4 x 10^-3 m³
∵ Number of air molecules in volume 22.4 x 10^-3 m³ = 6.023 x 10²³
∴ Number of air molecules in volume 12 m³
= \(\frac{6.023 \times 10^{23} \times 12}{22.4 \times 10^{-3}}\)
= 3.23 x 10²⁶

Based on Least Count

Question 6.
Least count of a screw gauge is 0.001 cm. Diameter of a wire is measured by this screw gauge as 0.225 cm. Determine percentage error, in this measurement.
Answer:
Percentage error = \(\frac{\text { Least count }}{\text { Measurement }}\) x 100
= \(\frac{0.001}{0.225}\) x 100
= 0.444%

Question 7.
Least count of Vernier calipers is 0.01 cm. Diameter of a sphere is measured by this instrument as 2.52 cm. Calculate the percentage error in this measurement.
Answer:
Percentage error = \(\frac{\text { Least count }}{\text { Measurement }}\) x 100
= \(\frac{0.01}{2.52}\) x 100
= 0.39%

Based on Error due to Product of Quantities

Question 8.
Following observations are obtained in experiment of surface tension of water by capillary rise method. Diameter of capillary D = 0.125 cm and height of raised water column h = 1.43 cm. Estimate the error in value of surface tension T using formula T = \(\frac{1}{2}\) hrg.
Answer:
Formula used, T = \(\frac{r h g}{2}\)
= \(\frac{D h g}{2 \times 2}=\frac{1}{4}\) Dhg
Since g is not measured, therefore for error purpose,

= [0.008 + 0.0069] x 100
= 0.0149 x 100
= 1.49
= 15%

Question 9.
Error of 2% takes place while measuring the radius of a sphere. What will be percentage error in estimating the volume of the sphere?
Answer:
Given: \(\frac{\Delta r}{r}\) x 100 = 2%
where r is the radius of sphere
\(\frac{\Delta V}{V}\) x 100 = ?
∵ V = \(\frac{4}{3}\)πr³
∴ \(\frac{\Delta V}{V}\) x 100 = 3\(\frac{\Delta r}{r}\) x 100 = 3 x 2% = 6%

Question 10.
There is error of 1.5% in measuring the radius of a circle. What will be maximum percentage error in estimating the area of the circle?
Answer:
Given: Error in radius of square 
\(\frac{\Delta r}{r}\) x 100 = 1.5%
Error in area, \(\frac{\Delta A}{A}\) x 100 = ?
∵ A = πr²
∴ \(\frac{\Delta A}{A}\) x 100 = 2 x \(\frac{\Delta r}{r}\) x 100 = 2 x 1.5% = 3%

Based on Error in Division

Question 11.
In experiment of simple pendulum, error of 0.1% is found in measuring the length l of the pendulum and that of 2% in measuring time period T of the pendulum. Calculate the maximum error in \(\frac{l}{T^2}\) using above measurements.
Answer:
Given: \(\frac{\Delta T}{T}\) x 100 = 0.1%
where l is length of the pendulum.
and \(\frac{\Delta T}{T}\) x 100 = 2%
where T is time period of pendulum.
Maximum error in \(\frac{l}{T^2}\) = ?
∴ Gravitational acceleration,
g = 4π² \(\frac{l}{T^2}\)
∴ \(\left|\frac{\Delta g}{g}\right|_{\max } \times 100=\frac{\Delta l}{l} \times 100+2 \frac{\Delta T}{T} \times 100\)
= 0.1% + 2 x 2%
= 0.1% + 4%
= 4.1%

Question 12.
In experiment of density measurement, a student measures the mass of the object and its volume as 7.34 g and 13.4 cm³ respectively. How much error is possible in his result?
Answer:
Given: Mass of an object m = 7.34 g
∴ ∆m = 0.1 g
Volume V = 13.4 cm³
∴ ∆V = 0.1 cm³

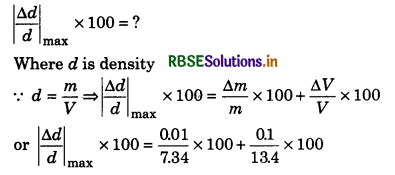
= [0.0013 x 0.0074] x 100
= 0.0088 x 100
= 0.88%

Question 13.
Speed of sound in a stretched string is given by v = \(\sqrt{\frac{T}{m}}\), where T = Mg. Measured values of M and m by experiment are M = 2.0 kg; m = 1.5 gm^-1. Determine the maximum error in value of v when calculated by given formula.
Answer:
Given: Velocity of sound in stretched string,

∵ M = 2.0 kg
∴ ∆M = 0.1 kg
and m = 1.5 gm^-1
∴ ∆m = 0.1 gm^-1
∴ \(\left|\frac{\Delta v}{v}\right|_{\max } \times 100=\frac{1}{2}\left[\frac{0.1}{2.0} \times 100+\frac{0.1}{1.5} \times 100\right] \%\)
= \(\frac{1}{2}\)[5 + 6.6]% = \(\frac{1}{2}\) x 11.6
= 5.8%

Question 14.
The measurements taken by a student in determining the value of g by simple pendulum, are as under:
Length of the pendulum l = 102.0 cm;
Time period T = 2.4 s
What will be maximum uncertainty in the value of g when it is calculated by formula g = 4π² \(\frac{l}{T^2}\) For more accuracy in result, which observation should be taken more accurately?
Answer:
Given: g = 4π² \(\frac{l}{T^2}\)
\(\left|\frac{\Delta g}{g}\right|\) = ?
l = 102.0 cm ∴ ∆l = 0.1 cm
T = 2.4 s ∴ ∆t = 0.1 s
For error purpose,

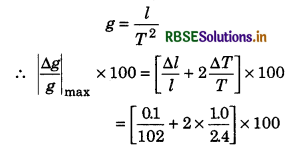
= [0.0083 + 0.0833] x 100
= 0.83% + 8.33%
= 9.2%
∵ Error in measurement of time period T is maximum.
∴ Measurement of time period should be done with more accuracy.

Question 15.
Value of g at any place is 9.8 ms while a student measures its value at that place 10 ms^-2 by experiment. Similarly the density of an object is 8.4 g cm^-3 and the student measures it 8.7 g.cm^-3 by experiment. Determine the percentage errors in results.
Answer:
Standard value of g = 9.8 ms^-2;
Experimental value of g = 10.0 ms^-2
∴ Percentage error in value of g
= \(\frac{\text { Standard value } \sim \text { Experimental Valve }}{\text { Standard Value }} \times 100\)
= \(\frac{9.8 \sim 10.0}{9.8} \times 100=\frac{0.2}{9.8} \times 100=\frac{0.2}{9.8} \times 100\)
= 2.04%
Similarly, percentage error in measurement of density
\(\frac{\Delta d}{d} \times 100=\frac{8.4 \sim 8.7}{8.4} \times 100=\frac{0.3}{8.4} \times 100\)
= \(\frac{100}{28}\) = 3.6%

Question 16.
Maximum errors in measurement of mass and arm of a cube are respectively 3% and 2%. What will be error in calculated value of density of substance of the cube?
Answer:
Given: \(\frac{\Delta m}{m}\) x 100 = 3% and \(\frac{\Delta l}{l}\) x 100 = 2%
\(\frac{\Delta d}{d}\) x 100 = ?
∵ Volume of the cube;
V = l³
∴ \(\frac{\Delta V}{V}\) x 100 = 3\(\frac{\Delta l}{l}\) x 100 = 3 x 2% = 6%
Now, density,
d = \(\frac{m}{V}\)
∴ \(\left|\frac{\Delta d}{d}\right|_{\max }\) x 100
= \(\frac{\Delta m}{m}\) x 100 + \(\frac{\Delta V}{V}\) x 100 = 3% + 6%
= 9%

Based on Error in Mixed Quantities

Question 17.
A physical quantity S is related with three quantities a, b and c according to formula S = \(\frac{a b^2}{c^3}\). If percentage errors in measurement of  a, b and c are respectively 1%, 2% and 3%, then calculate the possible error in S.
Answer:

= 1% + 2 x 2% + 3 x 3%
= 1% + 4% + 9%
= 14%

Question 18.
Voltage and current flowing through a wire are measured by a voltmeter of least count 0.1 volt and ammeter of least count 0.2 A. The observations obtained for those quantities are respectively 4.4 volt and 2.2 A. Determine: (i) resistance of wire with maximum permissible error and (ii) maximum percentage error in resistance.
Answer:
Given: V = 4.4 volt and ∆V = 0.1 volt
I = 2.2 A and ∆I = 0.2 A
∴ Resistance of the wire

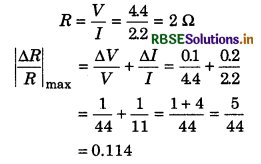
For percentage error = Relative error x 100
= 0.114 x 100
= 11.4%
∴ |∆R|_max = 0.114 x R = 0.114 x 2 = 0.228
or ∆R = 0.2Ω
∴ Resistance of the wire with maximum permissible error
R = (2 ± 0.2)Ω

Question 19.
A physical quantity X is related with quantities a, b, c and d by relation X = \(\frac{a^2 b^3}{c \sqrt{d}}\). The percentage errors in measurement of a, b, c and d are respectively 3%, 1%, 2% and 4%. What will be error in the value of X?
Answer:

= 2 x 3% + 3 x 1% + 2% + \(\frac{1}{2}\) x 4%
= 6% + 3% + 2% + 2% = 13%

Question 20.
Coefficient of viscosity (η) is represented by rate of flow of liquid in narrow tube according to following relation:
η = \(\frac{\pi P r^4}{8 V l}\)
where all quantities are in their usual meaning. 
Values of P, r, V and l are 76 cm of Hg, 0.28 cm, 1.2 cm³ s^-1 and 18.2 cm. If accurate measurement of these quantities is 0.1 cm of Hg, 0.01 cm cm³ s^-1 and 0.1 cm. Determine the percentage error in the value of q.
Answer:
Given: η = \(\frac{\pi P r^4}{8 V l}\)
\(\left|\frac{\Delta \eta}{\eta}\right|_{\max }\) x 100 = ?
P = 76.0 cm ⇒ ∆P = 0.1 cm
r = 0.28 cm ⇒ ∆r = 0.01 cm
V = 1.2 cm³ s^-1 ⇒ ∆V = 0.1 cm³ s^-1
l = 18.2 cm ⇒ ∆l = 0.1 cm

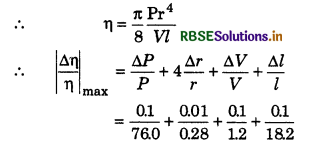
= 0.0013 + 0.1428 + 0.0833 + 0.0054
= 0.2328
∴ \(\left|\frac{\Delta \eta}{\eta}\right|_{\max }\) x 100 = 0.2328 x 100 = 23.28%

Based on conversion of unit from one system to another system

Question 21.
Density of water is 1 g.cm^-3. What will be its value in kg.m^-3?
Answer:
Fromula used:
n₂ = n₁\(\left[\frac{\mathrm{M}_1}{\mathrm{M}_2}\right]^a\left[\frac{\mathrm{L}_1}{\mathrm{~L}_2}\right]^b\left[\frac{\mathrm{T}_1}{\mathrm{~T}_2}\right]^c\)
Dimensional formula of density = [M¹L^-3T⁰]
∴ a = 1, b = -3, c = 0
Suppose 1 g cm³ = n₂ kg m^-3
∴ n₁ = 1 and n₂ = ?

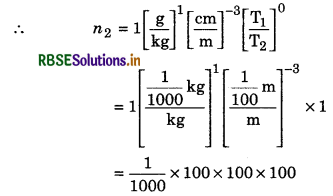
= 10³
∴ 1 g cm^-3 = 1 x 10³ kg.m^-3

Question 22.
Value of acceleration due to gravity is 9.8 ms^-2. Find its value in km. min^-2.
Answer:
Formula used: n₂ = n₁\(\left[\frac{\mathrm{M}_1}{\mathrm{M}_2}\right]^a\left[\frac{\mathrm{L}_1}{\mathrm{~L}_2}\right]^b\left[\frac{\mathrm{T}_1}{\mathrm{~T}_2}\right]^c\)
Dimensional formula of g = [M⁰L¹T^-2]
∴ a = 0, b = 1, c = -2
Suppose 9.8 ms^-2 = n₂ km.min^-2.
∴ n₁ = 9.8 and n₂ = ?

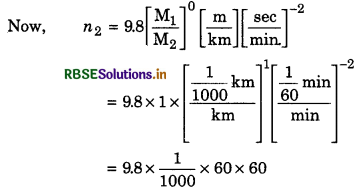
= 35.28
∴ 9.8 ms^-2 = 35.28 km.min^-2

Question 23.
Velocity of sound in water is 1440 ms^-1. It the unit of length is km and that of time is hour, then what will be the velocity of sound?
Answer:
Formula used: n₂ = n₁\(\left[\frac{\mathrm{M}_1}{\mathrm{M}_2}\right]^a\left[\frac{\mathrm{L}_1}{\mathrm{~L}_2}\right]^b\left[\frac{\mathrm{T}_1}{\mathrm{~T}_2}\right]^c\)
Dimensional form of speed = [M⁰L¹T¹]
∴ a = 0, b = 1, c = -1
Suppose 1440 ms^-1 = n₂ km.hr^-1
∴ n₁ = 1440 and n₂ = ?

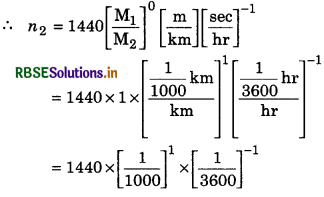
= 1440 x \(\frac{1}{1000}\) x 3600
= 144 x 36
= 5184
∴ 1440 ms^-1 = 5184 km-hr^-1

Question 24.
Young’s modulus of elasticity of steel is 19 x 10¹⁰ N.m^-2. What will be its value in dyne. cm^-2?
Answer:
Young's modulus of elasticity
Y = 19 x 10¹⁰\(\frac{N}{m^2}\) = 19 x 10¹⁰ x \(\frac{10^5 \text { dyne }}{100 \mathrm{~cm} \times 100 \mathrm{~cm}}\)
= 19 x 10¹¹ dyne/cm²

Question 25.
Surface tension of water 7.0 x 10^-2 N.m^-1. What will be its value in dyne, cm^-1?
Answer:
Surface tension of water is,
T = 7.0 x 10^-2\(\frac{\mathrm{N}}{\mathrm{m}}\)
= 7.0 x 10^-2 x \(\frac{10^5 \mathrm{dyne}}{10^2 \mathrm{~cm}}\) = 7.0 x 10¹\(\frac{\mathrm{dyne}}{\mathrm{~cm}}\)
= 70 dyne.cm^-1

Question 26.
Latent heat of ice is 80 cal.g^-1. Represent it in J.kg^-1.
Answer:
Latent heat of ice,
L = 80\(\frac{\mathrm{cal}}{\mathrm{g}}=\frac{80 \times 4.18 \mathrm{~J}}{10^{-3} \mathrm{~kg}}\)
= 8 x 418 x 10² J.kg^-1
= 3344 x 10² J.kg^-1
= 3.344 x 10⁵ J.kg^-1
= 3.34 x 10⁵ J.kg^-1

Based on relation between physical quantities

Question 27.
According to Einstein, the energy of a substance depends upon its mass (m) and speed of light (c). Derive the expression for energy by dimensional method.
Answer:
Suppose, E ∝ m^a and E ∝ c^b
∴ E ∝ m^ac^b
or E = km^a c^b ...........................(1)
Dimensional formula of L.H.S. = [M¹L²T^-2]
Dimensional formula of R.H.S = [M¹]^a [L¹T^-1]^b = [M^aL^bT^-b]
For the validity of formula (1), the dimensions of both sides should be equal. Therefore an comparing the dimensions,
a = 1 and b = 2
∴ From equation (1)
E = km¹c² = k.mc²
On the basis of parctical results, k = 1
∴ E = mc²

Question 28.
Suppose the speed of longitudinal waves (c) in a medium depends upon modulus of elasticity (E) and density of the medium (ρ). Obtain the expression for v adopting dimensional method.
Answer:
Suppose, v ∝ E^a where E is modulus of elasticity and v ∝ ρ^b. where ρ is density.
or v ∝ E^aρ^b
or v = k. E^aρ^b ..........................(1)
Dimensions of L.H.S. = [M⁰L¹T^-1]
Dimensions of R.H.S. = [M¹L^-1T^-2]^a [M¹L^-3]^b
= M^aL^-aT^-2aM^bL^-3b
= [M^a+bL^-a-3bT^-2a]
According to principle of homogencity, the dimensions of both sides of the equation should be same. Therefore on comparing the dimensions, we get
a + b = 0 ..........................(2)
-a - 3b = 1 ..........................(3)
-2a = -1 ..........................(4)
From equation (4)
a = \(\frac{1}{2}\)
Substituting the value of in equation (2), we have,
\(\frac{1}{2}\) + b = 0 ⇒ b = \(-\frac{1}{2}\)
∴ From equation (1)
v = KE^1/2ρ^-1/2 = K\(\sqrt{\frac{E}{\rho}}\)
On the basis of practical results,
k = 1
∴ v = \(\sqrt{\frac{E}{\rho}}\)

Question 29.
A particle is moving on a horizontal circular path and centripetal acceleration (a) acting on the particle depends upon the speed (v) of the particle and radius (r) of the path.
Establish the expressioin for ‘a’ by dimensional method.
Answer:
Supose centripetal acceleration
a ∝ v^x
and a ∝ r^y
∴ a ∝ v^xr^y
or a = kv^xr^y ..............................(1)
Dimensions of L.H.S. = [M⁰L¹T^-2]
Dimensions of R.H.S. = [L¹T^-1]^x[L¹]^y = L^xT^-xL^y
= [M⁰L^x+yT^-x]
On comparing the dimensions of both sides according to principle of homogeneity,
x + y = 1 .........................(2)
-x = -2 ........................(3)
⇒ x = 2
Substituting the value of x in equation (2),
2 + y = 1 ⇒ y = 1 - 2 = -1
∴ From equaiton (1)
a = k v²r^-1 = k.\(\frac{v^2}{r}\)
On the basis of parctical results,
k = 1

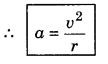
Question 30.
Centripetal force (F) acting on a particle moving on a horizontal circular path and it depends upon the mass (m) of the particle, velocity (v) of the particle and radius (r) of the circular path. Establish the expression for (F) adopting dimensional method.
Answer:
Suppose centripetal force F depends on m, v and r as under
F ∝ m^a
F ∝ v^b
F ∝ r^c
∴ F ∝ m^a v^b r^c
or F = k.m^a v^b r^c ...........................(1)
Dimensions of L.H.S. = [M¹L¹T^-2]
Dimensions of R.H.S . = [M¹]^a [L¹T^-1]^b [L¹]^c = M^aL^bT^-bL^c
= [M^aL^b+cT^-b]
On comparing the dimensions of both sides according to principle of homogeneity, we get
a = 1 .....................(2)
b + c = 1 .......................(3)
-b = -2 .......................(4)
From equation (4),
b = 2
From equation (3)
2 + c = 1 ⇒ c = 1 - 2 = -1
∴ From equation (1)
F = km¹v²r^-1 = k\(\frac{m v^2}{r}\)
On the basis of parctical results 
k = 1
∴ F = \(\frac{m v^2}{r}\)

Question 31.
Force (F) acting on a sphere falling in a liquid with constant velocity depends upon radius (r) of the sphere, terminal velocity (v) and coefficient of viscosity (η). Establish the expressioip for (F) by dimensional method.
Answer:
Force acting on falling body in liquid with constant velocity, depends on v, r and η as under:
F ∝ η^a
F ∝ r^b
F ∝ v^c
or F = k.η^a r^b v^c ........................(1)
Dimensions of L.H.S. = [M¹L¹T^-2]
Dimensions of R.H.S. = [M¹L^-1T^-1]^a [L¹]^b [L¹T^-1]^c
= M^aL^-aT^-aL^bL^cT^-c
= [M^aL^-a+b+cT^-a-c]
On comparing the dimensions of both sides on the basis of principle of homogeneity, we have
a = 1 .........................(2)
-a + b + c = +1 ...........................(3)
-a - c = -2 ......................(4)
From equation (4), we have
-1 - c = -2 ⇒ c = 1
From equation (3), -1 + b + 1 = +1
⇒ b = 1
∴ From equation (1), we have
F = k.η¹r¹v¹ = kηrv
On the basis of parctical results,
k = 6π
∴ F = 6πηrv

Based on the validity of equations

Question 32.
An object of mass m suspended by a spring is executing vibrational motion. If its time period is T and force constant of the spring is K, then prove that the relation T = 2π\(\frac{m}{K}\) is dimensionally incorrect. Obtain its correct form.
Answer:
Given equation T = 2π\(\frac{m}{K}\)
Dimensions of L.H.S. = [M⁰L⁰T¹]
Dimensions of R.H.S. = \(\frac{\mathrm{M}^1}{\mathrm{M}^1 \mathrm{~L}^0 \mathrm{~T}^{-2}}\) = [M⁰L⁰T²]
∵ The dimensions on both sides are different, therefore the given formula is wrong.
Derviation of correct equation
Suppose T ∝ m^a
T ∝ k^b
∴ T ∝ m^a k^b
or T = k' m^a k^b .........................(1)
Dimensions of L.H.S. = [M⁰L⁰T¹]
Dimensions of R.H.S. = [M¹]^a [M¹T^-2]^b = M^aM^bT^-2b
= [M^a+bL⁰T^-2b]
On comparing the dimensions of both sides.
a + b = 0 .....................(2)
-2b = 1 .....................(3)
⇒ b = \(-\frac{1}{2}\)
From equation (2)
a - \(\frac{1}{2}\) = 0 ⇒ a = \(\frac{1}{2}\)
∴ From equation (1)
T = k'. m^1/2 k^1/2 = k¹.\(\frac{m^{1 / 2}}{k^{1 / 2}}\)
or T = k'\(\sqrt{\frac{m}{k}}\)
On practical results
k' = 2π

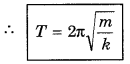
Higher Order Thinking Skills or HOTS

Question 1.
The pitch of screw gauge is 1 mm and there are 100 divisions on circular scale while measuring the diameter of wire, the linear scale reads 1 mm and 47 th division on circular scale coincides with reference line. The length of wire is 5.6 cm. Find the curved surface area of the wire in cm² to correct number of significant figures.
Solution:
Here, pitch = 1mm = 1 x 10^-1 cm
L = 5.6 cm
Least count of screw gauge = \(\frac{1 \mathrm{~mm}}{100}\) = 0.01 mm
Diameter of wire = MSR + CSR x LC
= 1 mm + 47 x 0.01 mm
= 1.47 mm = 0.147 cm
Curved surface area of wire = A = 2πrL
= 2π\(\frac{D}{2}\)L
= 2 x 3.14 x \(\frac{0.147}{2}\) x 5.6
= 2.5848 cm²
Rounding off to two significant figure = 2.6 cm²

Question 2.
Calculate the focal length of spherical mirror, with the halp of following observations: Distance of object from the mirror
u = (50.1 ± 0.5) cm ⇒ ∆u = 0.5 cm
Distance of image from the mirror
v = (20.1 ± 0.2) cm ⇒ ∆u = 0.2 cm
Solution:
Mirror formula for spherical mirror
\(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}=\frac{u+v}{u v}\)
∴ f = \(\frac{u v}{u+v}=\frac{50.1 \times 20.1}{50.1+20.1}=\frac{50.1 \times 20.1}{70.2}\)
or f = 14.3 cm
Now on differentiating formula \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\), we have

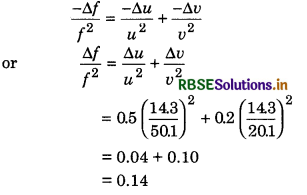
On rounding off, the digits upto first place after decimal point
∆f = 0.1 cm
∴ Focal length of spherical mirror
f = (14.3 ± 0.1) cm

Question 3.
In formula X = 3YZ², dimensions of X and Z are those of capacity and magnetic induction. What will be dimensions of Y in M.K.S. system?
Solution:
Dimensions of X = [M^-1L^-2T⁴A²] and dimensions of Z = [M¹L⁰T^-2A^-1]

Question 4.
Reynold’s number R decides that the flow in any pipe is streamlined or not? This constant is combination of velocity (v), density (ρ) and coefficient of viscosity (η). It is given that value of R is proportional to diameter (D) of the pipe. Establish the relation for R using dimensional method.
Solution:
Suppose the value of R depends upon v, ρ, η and D as under:
R ∝ D¹; R ∝ v^a
R ∝ ρ^b; R ∝ η^c
∴ R = k D¹v^aρ^bη^c .........................(1)
Dimensional fromula of L.H.S. = [M⁰L⁰T⁰]
Dimensional formula of R.H.S. = [L¹]¹ [L¹T^-1]^a [M¹L^-3]^b [M¹L^-1T^-1]^c
= L¹.L^aT^-aM^bL^-3bM^cL^-cT^-c
or Dimensional formula of R.H.S. = [M^b+cL^a-3b-c+1T^-a-c]
For the validity of formula (1), the dimensions on both sides should be equal. Therefore on comparing the dimensions, we get
b + c = 0 ......................(2)
a - 3b - c + 1 = 0 ...........................(3)
-a - c = 0 ........................(4)
On solving equations (2), (3) and (4), we get
a = 1; b = 1 and c = -1
∴ From equation (1)
R = \( \frac{k D v \rho}{\eta}\)
This is the required relation.

Question 5.
X is defined as under X = \(\frac{I F v^2}{W L^3}\). Which physical quantity is represented by X. In formula I is moment of inertia; F is force; v is velocity, L is length and W is work.
Solution:
According to question,
I = [M¹L²]; F = [M¹L¹T^-2]; v = [L¹T^-1] and L= [L¹]; W = [M¹L²T^-2]

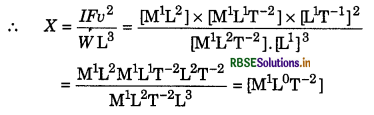
or X = [M¹L⁰T^-2]
This dimensional formula represents surface tension, force constant and work/area. Therefore X represent all these three quantities.

Question 6.
Suppose x and a represent distance. Determine whether following relation is dimensionally correct or not?
\(\int \frac{d x}{\sqrt{a^2-\log _2 x}}=\frac{1}{a} \sin ^{-1}\left(\frac{y}{a}\right)\)
Solution:
Dimensional formula of L.H.S.
= \(\int \frac{d x}{\sqrt{a^2-\log _2 x}}=\frac{\text { Dimension of } d x}{\sqrt{\text { dimension of } a^2}}\)
(Because log₂x is dimensionless)
= = L⁰
= [M⁰L⁰T⁰]
Now dimensional formula of R.H.S.
= \(\frac{1}{a} \sin ^{-1}\left(\frac{y}{a}\right)=\frac{1}{L^1}\)
(because sin^-1(\(\frac{y}{a}\)) is dimensionless)
= L^-1 = [M⁰L^-1T⁰]
∵ The dimensions of L.H.S. and R.H.S. are different. Therefore given equation is wrong.

Questions for Competitive Examinations

Objective Type Questions

Question 1.
In an experiment for measuring the diameter of a wire, the measurements are given below:
Reading of main scale is 0 mm and that of circular scale is 50 divisions. 1 mm of main scale is corresponding to loo divisions of circular scale. On the basis of above data, the diameter of the wire is:
(a) 0.52 cm
(b) 0.052 cm
(c) 0.026 cm
(d) 0.005 cm
Solution:
Least count of the screw gauge
= \(\frac{\text { Value of } 1 \text { division of main scale }}{\text { Number of divisions on circular scale }}\)
= \(\frac{1 \mathrm{~mm}}{100}\) = 0.01 mm
∴ Diameter of the wire = Reading of M.S. + Reading of C.S.
= 0.0 mm + 0.01 x 2
= 0.52 mm
= 0.052 cm
∴ Option (b) is correct.

Question 2.
The significant figure in numbers 23.023; 0.003 and 2.1 x 10^-3 are respectively:
(a) (5, 1, 2)
(b) (5, 1, 5)
(c) (5, 5, 2)
(d) (5, 4, 2)
Solution:
(a) (5, 1, 2)

Question 3.
In an xperiment, the measurement of angle by an apparatus is required. In this apparatus, 29 divisions of main scale are incident on 30 divisions
of vernier scale. If an division of main scale is equal to (0.5) degree. Then least count of the apparatus is:
(a) half min
(b) one degree
(c) half degree
(d) one min.
Solution:
One division of vernier scale = \(\frac{29}{30}\) divisions of M.S. or 1 V.S.D. = \(\frac{29}{30}\) x 0.5° = (\(\frac{29}{60}\))°
∴ L.C. of the apparatus = 1 MSD - 1 VSD
= \(\left(\frac{1}{2}\right)^{\circ}-\left(\frac{29}{60}\right)^{\circ}=\left(\frac{1}{60}\right)^{\circ}\)
= 1' (min)
∴ Option (d)  is correct.

Question 4.
Dimensions of magnetic field in M,L,T and C (coulomb) are:
(a) [M¹L¹T^-1C^-1]
(b) [M¹L⁰T²C^-2]
(c) [M¹L⁰T^-1C^-1]
(d) [M¹L⁰T^-2C^-2]
Solution:
∵ Magnetic force acting on moving charge in uniform magnetic field,
F = qvB ⇒ B = \(\frac{F}{q v}\)
∴ Dimensions of B = \(\frac{M^1 L^1 T^{-2}}{C^1 \cdot L^1 T^{-1}}\) = [M¹L⁰T^-1C^-1]
Hence, option (c) is correct.

Question 5.
Which unit of following units show the dimension [M¹L²/Q²]?
(a) Weber-m^-2
(b) Henry
(c) Henry-m^-2
(d) Weber-m^-2
Solution:
Induced e.m.f. across an inductor (numerically)
e = L\(\frac{\Delta I}{\Delta t}\) ⇒ L = \(\frac{e \Delta t}{\Delta I}=\frac{W}{q} \frac{\Delta t}{\Delta I}\)
or L = \(\frac{W \Delta t^2}{q \Delta I \Delta t}=\frac{W \Delta t^2}{q^2}\)
Here charge is denoted by Q
∴ L = \(\frac{W \Delta t^2}{Q^2}\)
∴ Dimensions of L = \(\frac{M^1 L^2 T^{-2} \cdot T^2}{Q^2}\) = M¹L²/Q²
∴ Unit of L is henry.
Hence; option (b) is correct.

Question 6.
Dimensional formula of coefficient of viscosity is:
(a) [M¹L^-1T^-1]
(b) [M¹L¹T^-2]
(c) [M¹L¹T^-1]
(d) [M¹L²T^-2]
Solution:
(a) [M¹L^-1T^-1]

Question 7.
Dimensional formula of modulus of elasticity is:
(a) M¹L^-1T^-2]
(b) [M⁰L¹T^-2]
(c) [M¹L¹T^-2]
(d) [M¹L²T^-2]
Solution:
(a) M¹L^-1T^-2]

Question 8.
There are divisions of 1 mm on main scale of vernier calliper. 20 divisions of vernier scale are equivalent to 16 divisions of main scale. The lesat count of vernier calliper will be:
(a) 0.02 mm
(b) 0.05 mm
(c) 0.005 mm
(d) 0.2 mm
Solution:
1 VSD = \(\frac{16}{20}\) MSD = \(\frac{16}{20}\) mm
∴ Least count = 1 mm - \(\frac{16}{20}\) mm
= \(\frac{4}{20}\) mm = \(\frac{1}{5}\) mm = 0.2 mm
Hence; option (d) is correct.

Question 9.
Dimension of planck's constant is equivalent to dimension of:
(a) Force
(b) Energy
(c) Linear momentum
(d) Angular momentum
Solution:
∵ E = hv ⇒ h = \(\frac{F}{v}\)
∴ Dimensions of h = \(\frac{M^1 L^2 T^{-2}}{T^{-1}}\) = [M¹L²T^-1]
Angular momentum
J = IW
∴ Dimenisons of J = [M^-1L²T^-1]
Hence the dimensions of planck's constant and angular momentum are same.
Hence; option (d) is correct.

Question 10.
The equatois of a wave is:
y = a sin (At - Bx + C)
Where A, B and C are constants. The dimensions of A,B and C are respectively.
(a) [T^-1], [L¹], [M⁰L⁰T⁰]
(b) [T^-1], [L^-1], [M⁰L⁰T⁰]
(c) [T¹], [L^-1], [M¹]
(d) [T^-1], [L^-1], [M^-1]
Solution:
Equation of wave:
y = a sin(At - Bx + C)
∵ The angle in trigonometrical function is dimensionless which can be taken to be 1.
∴ At = 1 ⇒ A = \(\frac{1}{t}=\frac{1}{T^1}\) = [T^-1]
Bx = 1 ⇒ B = \(\frac{1}{x}=\frac{1}{L^1}\) = [L^-1]
C = 1 = [M⁰L⁰T⁰]
Hence; option (b) is correct.

Question 11.
Dimensional formula of relative density is:
(a) [M¹T^-3]
(b) [M¹L^-3]
(c) Dimensionless
(d) [M²L^-6]
Solution:
(c) Dimensionless

Question 12.
Ratio of dimensions of plank’s constant and moment of inertia are the dimension of:
(a) Frequency
(b) Velcoity
(c) Angualr momentum
(d) Time
Solution:

= \(\frac{\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-1}}{\mathrm{M}^1 \mathrm{~L}^2}\) = [T^-1]
Hence; option (a) is correct.

Question 13.
The dimensions of which pair of following are different?
(a) Pressure, Young’s modulus of elasticity, stress.
(b) e.m.f., potential difference, electric potential
(c) Heat, work, energy
(d) Dipole moment, electric flux, electric field
Solution:
Answer (d) is correct which can be checked by determining the dimensions.

Question 14.
The dimension of \(\frac{1}{\mu_0 \varepsilon_0}\) (parameters are in the usual meaning) are:
(a) [L^-1]
(b) [L²T²]
(c) [L²T^-2]
(d) [L¹T^-1]
Solution:
∵ \(\sqrt{\mu_0 \varepsilon_0}\) = C ⇒ \(\frac{1}{\mu_0 \varepsilon_0}\) = C²
Hence the dimensions of \(\frac{1}{\mu_0 \varepsilon_0}\) = [L²T^-2]
Hence, option (c) is correct.

Question 15.
The spectrometer used in measurement of prism-angle, gives following measurements:
Measurement of main scale = 58.5°
Measurement of vernier scale = 09 divisions
Given one division of main scale is equal to 0.5°.
Total number of divisions on vernier scale are 30 and these divisions meet 29 divisions of main scale. The value of angle of prism according to above data is:
(a) 58.59°
(b) 58.77°
(c) 58.65°
(d) 59°
Solution:
Reading of main scale = 58.5°
Reading of vernier scale = 0.9 division
1 MSD = 0.5°
1 VSD = \(\frac{29}{30}\) MSD = \(\frac{29}{30}\) x 0.5 = (\(\frac{29}{60}\))°
∴ L.C. = 1 MSD - 1 VSD
= 0.5° - (\(\frac{29}{60}\))° = (\(\frac{1}{2}\))° - (\(\frac{29}{60}\))° = (\(\frac{1}{60}\))°
∴ Reading of spectrometer = Reading of M.S. + Reading of V.S.
= 58.5° + (\(\frac{1}{60}\) x 9)°
= 58.5° + 0.15°
= 58.65°
Hence; option (c) is correct.

Question 16.
Dimensions of (µ₀ε₀)^1/2 are:
(a) [L^1/2T^1/2]
(b) [L^-1T¹]
(c) [L¹T^-1]
(d) [L^1/2T^1/2]
Solution:
(µ₀ε₀)^-1/2 = \(\frac{1}{\left(\mu_0 \varepsilon_0\right)^{1 / 2}}=\frac{1}{\sqrt{\mu_0 \varepsilon_0}}\) = c
∴ Dimension of (µ₀ε₀)^-1/2 = [L¹T^-1]
Hence; option (c) is correct.

Question 17.
Retarding force on an oscillator is directly proportional to velocity, then unit of constant of proportionality is:
(a) kg.m.s^-1
(b) kg.m.s^-2
(c) kg.s^-1
(d) kg.s
Solution:
∵ F ∝ v or F = kv ⇒ k = \(\frac{F}{v}\)
∴ Dimensions of k = \(\frac{M^1 L^1 T^{-2}}{L^1 T^{-1}}\) = [M¹T^-1]
Hence unit of k = kg.s^-1
Hence; option (c) is correct.

Question 18.
In demonstration of an experiment, quantities a, b, c and d come in order and their percentage errors are 1%, 2%, 3% and 4% respectively. If quantity P is respected by percentage error in P will be:
(a) 14%
(b) 10%
(c) 7%
(d) 4%
Solution:

= 3 x 1% + 2 x 2% + 3% + 4%
= 3% + 4% + 3% + 4%
= 14%
Hence; option (a) is correct.

Question 19.
If [ε₀] represents the dimensional formula of permittivity of free space and mass = M, length = L and time = T, then.
(a) [ε₀] = [M^-1L^-3T²A¹]
(b) [ε₀] = [M^-1L^-3T⁴A²]
(c) [ε₀] = [M^-2L²T^-1A²]
(d) [ε₀] = [M^-1L²T^-1A²]
Solution:
Since electrostatic force between two charges,

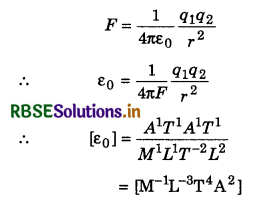
Hence; option (b) is correct.