RBSE Class 11 Physics Important Questions Chapter 15 Waves

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 15 Waves Important Questions and Answers.

RBSE Class 11 Physics Chapter 15 Important Questions Waves

Multiple Choice Questions

Question 1.
The distance between two consecutive crests is:
(a) \(\frac{\lambda}{4}\)
(b) \(\frac{\lambda}{2}\)
(c) λ
(d) 2λ
Answer:
(c) λ

Question 2.
The propagation constant of a wave is also called:
(a) wave number
(b) angular wave number
(c) wave length
(d) frequency
Answer:
(b) angular wave number

Question 3.
When temperature increases, the frequency of a tuning fork:
(a) increases
(b) decreases
(c) remains same
(d) increases or decreases depending on the matrial
Answer:
(b) decreases

Question 4.
Tube A has both ends open while tube B has one end closed, otherwise they are identical. The ratio of fundamental frequency of tube A and B is:
(a) 1:2
(b) 1:4
(c) 2:1
(d) 4:1
Answer:
(c) 2:1

Question 5.
Length of a string tied to two rigid supports is 40 cm. Maximum length (wavelength in cm) of a stationary wave produced on it is:
(a) 20
(b) 80
(c) 40
(d) 120
Answer:
(b) 80

Question 6.
A wave travelling in X direction with A = 0.2 m, velocity = 360 ms^-1 and λ = 60 m, then correct expression for the wave is:

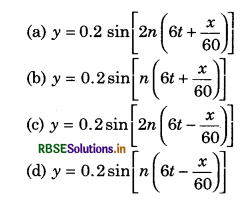
Answer:
(c) y = 0.2 sin[2n(6t - \(\frac{x}{60}\))]

Question 7.
A string in a musical instrument is 50 cm long and fundamental frequency is 800 Hz. If a frequency 100 Hz is produced, then required length of string is:
(a) 62.5 cm
(b) 50 cm
(c) 40 cm
(d) 37 cm
Answer:
(c) 40 cm

Question 8.
When a stationary wave is formed then its frequency is:
(a) same as that of the individual waves
(b) twice that of the individual waves
(c) half that of the individual waves
(d) \(\sqrt{2}\) that of the individual waves
Answer:
(b) twice that of the individual waves

Question 9.
For y₁ = 4 sin(ωt + kx), y₂ = -4 cos(ωt + kx), the phase difference is:
(a) π/2
(b) 3π/2
(c) π
(d) 0
Asnwer:
(b) 3π/2

Question 10.
Blowing air with open mouth is an example of:
(a) isochoric process
(b) isothermal process
(c) isobaric process
(d) adiabatic process
Answer:
(c) isobaric process

Very Short Answer Type Questions

Question 1.
Write Newton’s formula for speed of sound in a gas.
Answer:
Newton’s formula for speed of sound in a gas is given by
v = \(\sqrt{\left(\frac{P}{d}\right)}\)
where, P = pressure of the medium
d = density of the medium

Question 2.
Write formula for speed of sound in any gas.
Answer:
Speed of sound in a gaseous medium.
v = \(\sqrt{\left(\frac{\beta}{d}\right)}\)
where ß = coefficient of bulk modulus
d = density of the medium

Question 3.
For an ideal gas, write relation between pressure and density at a constant temperature.
Answer:
Ideal gas equation,
PV = RT
∵ V = \(\frac{M}{d}\), where M = molecular weight of the gas
d = density
∴ \(\frac{P M}{d}\) = RT
∴ \(\frac{P}{d}\) = \(\frac{R T}{M}\) = constant

Question 4.
Write formula for the speed of a transverse waves in a stretched string.
Answer:
The speed of a transverse wave in a stretched string is;
v = \(\sqrt{\left(\frac{T}{m}\right)}\)
where; T = tension in the string
m = mass per unit length of the string.

Question 5.
Write formula for the speed of sound in a rigid rod.
Answer:
v = \(\sqrt{\left(\frac{Y}{d}\right)}\)
where, Y = Young’s modulus
d = Density of the rod

Question 6.
What is the increase in the speed of sound in air when the temperature of air rises by 1° C?
Answer:
0.61 m s^-1.

Question 7.
What are matter waves?
Answer:
Matter waves are the waves associated with moving electrons, protons, neutrons and other fundamental particles, and even atoms and molecules.

Question 8.
What is the angle between particle velocity and wave velocity in (i) a transversse wave (ii) a longitudinal wave?
Answer:
Angle between particle velocity and wave velocity for a transverse wave is π/2. In case of a longitudinal wave it is either zero or π.

Question 9.
Amongst solids, liquids and gases, in which type of media, transverse wave motion is possible?
Answer:
Solids.

Question 10.
When the wire of a sonometer is plucked, what is the nature of the waves in (i) the string, (ii) in air?
Answer:
(i) In string-transverse,
(ii) In air-longitudinal.

Question 11.
A harmonic wave travelling in a medium has a period T and wavelength λ. How are λ and T related?
Answer:
Wave velocity v = \(\frac{\lambda}{T}\)
or λ = vT

Question 12.
The density of oxygen is 16 times the density of hydrogen. What is the relation between the speeds of sound in two gases?
Answer:
\(\frac{v_H}{v_0}=\sqrt{\frac{\rho_0}{\rho_H}}=\sqrt{\frac{16 \rho_H}{\rho_H}}=4\)
or v_H = 4v₀

Question 13.
What is the effect of pressure on the speed of sound in air?
Answer:
The increase of pressure has no effect on the speed of sound in air.

Question 14.
What is the phase difference between the particles being on either side of a node?
Answer:
π rad.

Question 15.
What will be the effect on the frequency of a sonometer wire if the tension is decreased by 2%?
Answer:
As V ∝ \(\sqrt{T}\), so frequency decreases by 1% when tension is decreased by 2%.

Question 16.
What is the minimum frequency with which a string of length L stretched under tension T can vibrate?
Answer:
Minimum frequency,
n = \(\frac{1}{2 l} \sqrt{\left(\frac{T}{m}\right)}\)
where m is the mass per unit length of the string.

Question 17.
Fundamental frequency of oscillation of a closed pipe is 400 Hz. What will be the fundamental frequency of oscillation of an open pipe of same length?
Answer:
800 Hz.

Question 18.
The frequency of the fundamental note of a closed organ pipe and that of an open organ pipe are the same. What is the ratio of their lengths?
Answer:
1:2.

Question 19.
An organ pipe produces a fundamental frequency of 128 Hz. When blown forcefully it produces first overtone of 384 Hz. Is the pipe open or closed?
Answer:
Closed pipe, because the first overtone is 3 times the fundamental frequency.

Question 20.
Where to pluck and where to touch a stretched string to excite its first overtone?
Answer:
The wire should be plucked at its one-fourth length and touched at its centre.

Question 21.
What are harmonics?
Answer:
Harmonics are the nodes of frequencies which are integral multiples of the fundamental frequency.

Question 22.
What is Doppler Effect?
Answer:
The apparent change in the frequency of a sound when the source, the observer and the medium are in relative motion is called Doppler Effect.

Question 23.
State the factors on which the speed of a wave travelling along a stretched ideal string depends.
Answer:
The speed of a wave travelling on a string depends on (i) the tension (T) in the string and (ii) its mass per unit length (m).
v = \(\sqrt{\left(\frac{T}{m}\right)}\)

Question 24.
Velocity of sound in air at NTP is 332 m/s. What will be the velocity, when pressure is doubled and temperature is kept constant?
Answer:
332 m/s, because pressure has no effect on the velocity of sound in air.

Question 25.
How are stationary waves produced?
Answer:
Stationary waves are produced when two indentical waves in opposite directions through a medium superpose each other.

Question 26.
What is the difference between a tone and a note?
Answer:
A sound of single frequency is called a tone. A combination of tones of different frequencies is called a note.

Question 27.
How does the frequency of a tuning fork change, when the temperature is increased?
Answer:
As the temperature increases, the length of the prong of the tuning fork increases. This increases the wavelength of the stationary waves set up in the
tuning fork. As frequency, v ∝ \(\frac{1}{\lambda}\), so frequency of the tuning fork decreases.

Question 28.
What physical change occurs when a source of sound moves and the listner is stationary?
Answer:
Wavelength of sound wave changes. 

Question 29.
Will there be Doppler effect, when the direction of motion of the source or observer is perpendicular to the direction of propagation of sound?
Answer:
No, there is no Doppler effect, when the source or observer moves perpendicular to the direction of propagation of sound.

Question 30.
What is the factor on which the pitch of a sound depends?
Answer:
The pitch of a sound depends on its frequency.

Question 31.
What is transferred in wave motion?
Answer:
In wave motion, energy is transferred through the motion of particles of the medium.

Question 32.
If the length of a stretched string is doubled and the tension is increased to four times then what would be the relation between new frequency and the old frequency?
Answer:

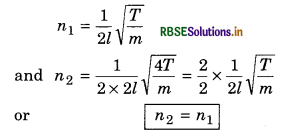
Question 33.
What does the number of vibrations executed by the particle of a medium in one second is called?
Answer:
Frequency

Question 34.
What is the velocity of sound in air at standard temperature and pressure?
Answer:
Velocity of sound in air at standard temperature and pressure is 332 m s^-1.

Question 35.
What will be the change in the intensity of a wave if its amplitude is reduced to half?
Answer:
∵ Intensity of wave I ∝ (Amplitude)²
or I ∝ a² or I = ka²
When amplitude is a/2, Intensity
I' ∝ \(\frac{a^2}{4}\) or I' = \(\frac{k a^2}{4}\)
or I' = \(\frac{I^{\prime}}{4}\)
Thus the intensity is reduced to one fourth of its original value.

Question 36.
From which medium a wave is reflected so that the phase changes by π for a reflected wave?
Answer:
When a wave is reflected from a denser medium, its phase changes by π.

Question 37.
What will be the frequency of the beats if two tuning forks of frequency 400 and 402 are vibrated together?
Answer:
Difference is the frequency of the turning forks
n = n₁ ~ n₂ = 400 ~ 402
or n = 2 beats/second

Question 38.
What will be the ratio of fundamental frequencies of an open and closed organ pipes of same length?
Answer:
Fundamental frequency of an open pipe n = \(\frac{v}{2l}\)
Fundamental frequency of an closed pipe n' = \(\frac{v}{4l}\)
or n' = \(\frac{1}{2} \times \frac{v}{2 l}=\frac{1}{2} n\)
∴ \(\frac{n^{\prime}}{n}=\frac{1}{2} \text { or } \frac{n}{n^{\prime}}=\frac{2}{1}\), ∴ n:n' = 2:1

Question 39.
In which closed or open organ pipe only odd harmonics are generated?
Answer:
In closed organ pipe.

Question 40.
What is the maximum displacement from mean position called?
Answer:
Amplitude

Question 41.
Is there transfer of energy by the standing waves?
Answer:
No.

Question 42.
Which waves are produced in a resonance air column?
Answer:
Longitudinal standing waves.

Question 43.
How much is the distance between an antinode and its consecutive node?
Answer:        

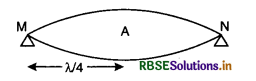
Distance between an antinode and its consecutive node = λ/4

Question 44.
What is the effect of temperature on velocity of sound?
Answer: 
v ∝ \(\sqrt{T}\) i.e., velocity increases with increase in temperature. Formula for variation in temperature.
vt = v₀ + 0.61 t

Question 45.
From loud or shrill sound whose pitch is more?
Answer:
Pitch is more for shrill sound.

Question 46.
Can Doppler’s effect be seen in the whistle of an aeroplane moving with the ultrasonic velocity?
Answer:
No, because to realise Doppler’s effect the velocity of the sound source and listener should be less than the velocity of sound.

Fill in the blanks:

Question 1.
Reflection of a travelling wave a a rigid boundary occurs with .............................
Answer:
phase change of 180°

Question 2.
The propagation constant of a wave is also called it’s .............................
Answer:
angular wave number

Question 3.
The temperature coefficient of velocity of sound in air is .............................
Answer:
0.61 m/s/K

Question 4.
Distacne between a compression and adjoining rarefaction in a pressure wave is .............................
Answer:
\(\frac{\lambda}{2}\)

Question 5.
Te speed of sound in a perfectly rigid rod will be .............................
Answer:
infinite

Short Answer Type Questions

Question 1.
Sound is simultaneously produced at the ends of the two strings of the same length, one of rubber and the other of steel. In which string will the sound reach the other end earlier and why?
Answer:
Speed of sound in a string, v = \(\sqrt{\left(\frac{Y}{\rho}\right)}\)
As the value of \(\frac{Y}{\rho}\) is larger for steel than for rubber, so sound will reach the other end earlier in the case of steel string.

Question 2.
Distinguish between harmonics and overtones.
Answer:
A vibrating system such as a stretched string, an air column etc., can vibrate with a number of frequencies. The mode with the lowest frequency is called ‘fundamental-mode’ and the others are called overtones.
When the frequencies of overtones are exact multiplies of the fundamental frequency, they are called harmonics. The fundamental itself is called the first harmonic. The presence of the harmonics makes a sound musical.

Question 3.
A source of sound moves towards a stationary observer. Is the increase in pitch due to (i) increase in the velocity of sound? (ii) actual or apparent change in wavelength? (iii) both?
Answer:
When a source of sound moves towards a stationary observer, the increase in pitch is due to the actual or apparent change in wavelength. It is so because due to motion of the source of sound towards the observer at rest, waves get compressed as the effective velocity of sound waves relative to source becomes less than the actual. As a result of it, the wavelength of sound wave decreases and hence the observed pitch increases.

Question 4.
Explain the factors on which the pitch of a tuning fork depends.
Answer:

1. Length of the prongs (l): The pitch (n) is inversely proportional to the square of the length (l) of the prongs, i.e., v ∝ \(\frac{1}{l^2}\).
2. Thickness of the prongs (b): The pitch (v) is directly proportional to the thickness (b) of the prongs i.e.,v ∝ b.
3. Elasticity of the material (Y): The pitch is directly proportional to the square root of the elasticity (Y) of the material i.e., v ∝ \(\sqrt{Y}\).
4. Density of the material (ρ): The pitch (v) is inversely proportional to the square root of the density of the material i. e., v ∝ \(\frac{1}{\sqrt{\rho}}\).

Question 5.
If the tension of a wire becomes 4 times of the previous value, then what will be the effect on the speed of a longitudinal wave.
Answer:

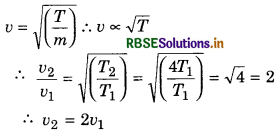
Question 6.
What are the essential properties which a medium must possess for the propagation of mechanical waves?
Answer:
Both transverse and longitudinal waves can propagate through those media which have the following properties:

1. Elasticity: The medium must possesses elasticity so that the particles can return to their mean positions after being disturbed.
2. Inertia: The medium must possess inertia or mass so that its particles can store kinetic energy.
3. Minimum friction: The frictional force amongst the particles of the medium should be negligibly small so that they continue oscillating for a sufficiently long time and the wave travels at sufficiently long distance through the medium.

Question 7.
What is a periodic wave function?
Answer:
A wave function y(x, t) of position following periodicity conditions is called periodic wave function:
(i) y(x + mλ, t) = y (x, t)
(ii) y(x,t + nT) = y(x,t)

Question 8.
What is a harmonic wave function?
Answer:
A periodic wave function, whose functional form is sine or cosine is called a harmonic wave function.

Question 9.
What will be the velocity of sound in a perfectly rigid rod? Give reason.
Answer:
The velocity of sound in a perfectly rigid rod will be infinite because the value of Young’s modulus of elasticity is infinite for a perfectly rigid rod.

Question 10.
If two sound waves of frequencies 500 Hz and 550 Hz superpose, will they produce beats? Would you hear the beats?
Answer:
Yes, the sound waves will produce 50 beats every second. But due to persistence of hearing, we will not be able to hear these beats. We would hear a continuous sound of frequency 50 Hz, called beat tone.

Question 11.
The length of a string rod tied to the rigid supports is 40 cm. What is the minimum length (wavelegth) (in cm) of the stationary wave produced on it?
Answer:
When the string vibrates in one segment
L = \(\frac{\lambda}{2}\)
or λ = 2L = 2 x 40 cm = 80 cm

Question 12.
An incident wave is represented by y(x, t) = 20 sin (2x - 4t), write the expression for the reflected wave:
(i) from a rigid boundary.
(ii) from an open boundary.
Answer:
(i) The wave reflected from a rigid boundary is
y(x, t) = -20sin (-2x - 4t)
20 sin (2x + 4t)
(ii) The wave reflected from an open boundary is y (x, t) = 20 sin (-2x - 4t)
= -20 sin (2x + 4t)

Question 13.
Set up a relation between the speed of the sound in a gas and root mean square velocity of the molecules of that gas.
Answer:
Speed of sound in a gas is v = \(\sqrt{\frac{\gamma P}{\rho}}\) ....................(1)
According to kinetic theory of gases, root mean square velocity (c) of molecules of gas is obtained from the relation
P = \(\frac{1}{3} \rho c^2, c=\sqrt{\left(\frac{3 P}{\rho}\right)}\) ......................(2)
Dividing (1) by (2), we get
\(\frac{v}{c}=\sqrt{\left(\frac{\gamma}{3}\right)} or v =  \sqrt{\left(\frac{\gamma}{3}\right)}\) x c

Question 14.
What will be the effect on speed of sound wave in a gas if absolute temperature become 4 times of its previous value.
Answer:

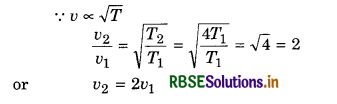
Question 15.
Write about the reflection of waves.
Answer:
We encounter situations involving the reflection of waves all around us, for example, in the phenomenon of echo, the sound reflected from a distant object reaches the listener with a little delay. In this section, we will learn more about the reflection of a wave from a fixed and a free end. In the image shown below, we can see what happens when a pulse or a travelling wave encounters a rigid boundary. We see how under such a situation the pulse or the wave gets reflected. When a wave is an incident on any surface, a part of the incident wave is reflected and a part is transmitted into the second medium. If the wave is incident obliquely on the boundary, the transmitted wave can also be termed as a reflected wave.

Question 16.
Differentiate between progressive and standing waves with their definitions.
Answer:

Progressive Waves	Standing Waves
1. Wave moves ahead. Disturbance moves ahead from one particle to another and thus energy is transferred.	1. These waves are stationary. Disturbance does not, move ahead in the form of medium particles. Therefore energy is not transferred.
2. In progressive waves; the amplitude is same at all the points.	2. In standing waves; amplitude is zero at nodes and maximum at antinodes.
3. In these waves, change of phase is in the same form as distance in the direction of propagation. Change of phase in unit distance is k = \(\frac{2 \pi}{\lambda}\).	3. In these waves, all the particles between two successive nodes are in the same phase but on both the sides of the node the particles are in the opposite phase.
4. Particles of progressive wave comes in the mean position or in the position of maximum displacement one by one.	4. All the particles of a standing wave are together in the mean position or in the position of maximum displacement.
5. In these, crest and trough or compress ion and rarefaction are propagated by a constant velocity which is called phase velocity.	5. In these, the wave image is not propagated in any direction but is formed and vanished at one place only.
6. In these waves, when velocity of the particle is maximum then strain is maximum but when velocity is zero then strain is also zero.	6. In these, the velocity is zero at nodes and strain is maximum and at antinodes velocity is maximum and strain is zero.
7. In these waves, all particles gain same maximum velocity respectively.	7. In these waves, maximum velocity value is different at different points.
8. In all the parts of the medium similar changes in pressure and density are observed i.e., in longitudinal wave at every point there is compression and rarefaction.	8. In longitudinal standing waves nodes are the points where there is maximum change in pressure and density and at antinodes pressure and density are equal in value.

Question 17.
What do you understand by superposition of waves? Explain.
Answer:
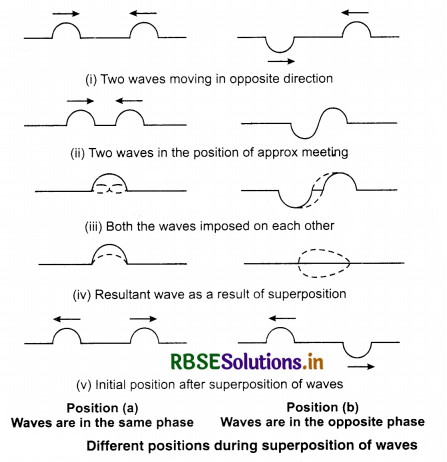
What would happen in a situation a progressive wave propagates in a medium and if we consider similarly many waves propagating in the same direction or opposite direction?

In this situation to study the displacement of the particle, we analyse two disturbances moving in the opposite direction at the same time in a stretched string as shown in the figure. According to the situation (a); two disturbances which are in the same phase, are moving towards each other in opposite direction and at the place of their meeting the displacement of the particle is different than the initial displacement. Since the waves are in the same phase it increases and the disturbances moving ahead then take the original position. Similarly according to situation (b); if the disturbances are in opposite phase and are imposed; then the resultant displacement in the diagram is different from the initial displacement and with time as the disturbance moves ahead then displacement takes its original position.

Hence, we can see that when on a particle at the same time two or more than two waves are imposed. then they effect the displacement of the particle. Therefore; “when more than one wave is imposed on a particle at the same time, it is called superposition of waves.” As a result of superposition of waves the particle instantaneously executes motion under the total resultant effect of the imposed waves and the resultant displacement is given by the principle of superposition.

Question 18.
Analyse the Laplace’s correction for the wave velocity expression in gas.
Answer:
According to Laplace when sound waves travel in air then there is compression and rarefaction of air. In the place of compression the air particles are closer hence become hot and in the position of rarefaction the particles are further apart hence temperature reduces; and this process of compression and rarefaction is so continuous that heat is not able to move out from the medium and control ‘its temperature. Hence, temperature is not constant in this process. From gas equation for adiabatic changes.

The value of γ for monoatomic gas molecule is 1.67 and for thatomic gas molecules is 1.41. Hence, by using the formula (15.63) at known temperature and pressure, the velocit of sound in air.
v_air = \(\sqrt{\frac{1.41 \times 1.01 \times 10^5}{1.29}}\) = 332 m/s (approximately)
Which is equal to the experimental value. From above study we see that in solid medium the velocity of sound is maximum and in gaseous medium it is minimum.

Question 19.
Write the rules for the transverse vibrations in a stretched string?
Answer:
We know that vibrations in a stretched string is an example of transverse standing waves. To understand it we study a string which is tied between two stationary points and is stretched. If T is the tension in the string and mass of unit length is m, then the velocity of waves produced in the string from equation (9.5). 
v = \(\sqrt{\frac{\mathrm{T}}{\mathrm{m}}}\)
When this string is stretched in the perpendicular direction slightly and then left. Then the transverse progressive waves start moving. These waves are reflected from the rigid ends of the string. Therefore, by superposition of incident and reflected waves transverse standing waves are generated and these waves remain till their energy is not destroyed due to friction, etc. Since both the ends of the string are tied up hence they are always nodes. 

When the string is stretched from middle and is left then the string vibrates in one part. Both the ends of the string are nodes and the middle point is antinode figure (9.15). This is the simple method of producing standing wave in a stretched string in which the string vibrates in a loop.

Question 20.
Define damped vibrations and maintained vibrations.
Answer:
When an object which execute vibration motion is slightly displaced from its stable position and is left then due to the effect of restitution force it vibrates with its natural (fundamental) frequency. This type of vibration is called the “free vibration”. In ideal free vibration the amplitude of the object is constant state of. But in reality when the object excutes free vibrations then it experiences some frictional force in the medium in which it is vibrating. As a result some part of its energy is lost as heat. Hence, the amplitude of the object decreases with time. Those types of vibrations whose amplitude decreases with time are called the “damped vibrations.”

If somehow we can provide the same energy to the vibrating object as to which it has lost; then the object keeps on vibrating with the same (constant) amplitude. This type of vibration is called the “maintained vibrations”.

A vibrating object forces another object (which has the tendency to vibrate) to vibrate. It is also possible if their fundamental frequencies are different. This type of vibration is called the “forced vibrations”. This type of vibrations end very soon because in this situation the second vibrating object does not vibrate with its fundamental frequency but vibrates with the frequency of the first vibrating object.
When the frequency of first vibrating object is equal to the fundamental frequency of the second vibrating object then the amplitude of forced vibrations increases relatively. This is called the “resonance”. Every impulse of frequency force helps the system state to vibrate. Due to this the amplitude of the system keeps on increasing.

Question 21.
If the wavelength of a wave is 2500 Å then what will be the wave number?
Answer:
Given λ = 2500 Å = 2500 x 10^-10 m
= 2.5 x 10^-7 m
∴ Wave number \(\bar{v}=\frac{1}{\lambda}=\frac{1}{2.5 \times 10^{-7}}=\frac{10}{25} \times 10^8\)
= 0.4 x 10⁸
or \(\bar{v}\) = 4.0 x 10⁷ m^-1

Question 22.
Define antinodes and nodes.
Answer:
1. Some medium particles (A₁, A₂, A₂, A₄ and A₅) always vibrate with the maximum amplitude on both the sides of the mean position. They are called antinode. Velocity (dy/dt) of particles at antinodes is, maximum and pressure or change in density is zero.
[∵ \(\frac{d y}{d x}\) = 0] 

2.Particles (N₁, N₂, N₃, N₄) between the consecutive antinodes are always stationary. These are called node. These are positioned at same distance. Velocity of particles [dy/dt] at nodes is zero and the pressure or density change is maximum. 

Question 23.
On what factors does the intensity of a wave depends upon?
Answer:
Intensity of a wave
I = 2π² n² a² ρ.v
∴ The intensity of wave depends on:
(i) Frequency; I ∝ n²
(ii) Amplitude I ∝ a²
(iii) Density of a medium I ∝ ρ
(iv) Velocity of a wave I ∝ v

Question 24.
How can the frequency of a tuning fork be calculated by the methods of beats?
Answer:
In incidents related to sound, beats are very important and has many uses. For tuning of musical instruments this is used. If we wish to listen only one type of note from the musical instrument then it is only possible if it does not have beats. When beats are not present the musical instrument become sametone. With the help of this the frequency of unknown tuning fork is also known. By the method of beats the calculation of the frequency of unknown tuning fork.

To calculate the frequency of unknown tuning fork, an approximately same but known frequency tuning fork is taken beoause to observe the beats of sound waves is necessary that the difference in the frequency of both the forks is not much otherwise beats will be formed so fast that to hear them will not be possible. Both the’ tuning forks are, vibrated together and per second the number of beats is calculated. Suppose known frequency of the tuning fork is n and the obtained beats is ∆v then the frequency of unknown tuning would be ∆v or v₁ - ∆n.

To calculate that whether the frequency of unknown tuning fork is ∆v or v - ∆v, we put some wax on the arm of the unknown tuning fork due to the increase in arm weight its frequency will reduce. Now again both tuning forks are vibrated together and the number of beats is calculated. If more beats are noticed from earlier then the frequency of unknown tuning fork is v - ∆v and if the number of beats noticed is less than before; then the frequency of unknown tuning fork is v +  ∆v. Its reason is clear that when wax is put on the arm of unknown frequency (v - ∆v) tuning fork then its frequency will reduce more from v - ∆v and as the difference increases between known and unknown frequency of tuning forks the number of beats will increase.

In second case if unknown frequency of tuning fork is v + ∆v then after putting wax its frequency will reduce more from v + ∆v and hence less difference between the frequencies of known and unknown tuning forks the number of beats will also reduce. In this way by putting wax on unknown frequency tuning fork of unknown frequency and analysing the increase or decrease the number of beats the frequency of unknown tuning fork can be calculated.

Question 25.
What are the limitations of Doppler’s Effect?
Answer:
To observe (view) Doppler’s effect it is necessary that for the source, the observer and the medium, the velocity of all should be less than the velocity of sound. If their velocity is more than the velocity of sound then the wave velocity graph is distorted and shocking waves are generated. Its example is Jet plane, when the speed of jet plane is more than the speed of sound then Doppler’s effect is not seen.

Question 26.
On what factors, does the Doppler’s effect in sound waves depend upon?
Answer:
Doppler’s effect in sound waves depends upon the following factors:

1. Velocities of the source and the observer.
2. Relative velocities of the source and the observer.
3. Whether the source or/and the observer is in motion.
4. Velocity of the medium.

Question 27.
With what velocity does source move towards the observer such that the apparent frequency become double?
Answer:
When the source moves towards the stationary observer, the apparent frequency is.

∴ Velocity of source should be half the velocity of the sound.

Question 28.
How can we calculate the velocity of submarine by Doppler’s effect?
Answer:
The most important use of Doppler’s Effect in sound is to calculate the velocity of submarines. Sound waves are sent from the sea shore towards the sea; they are reflected back from the enemy submarines and are gained back at sea-shore (SONAR station). Now by calculating the change in the wavelength of the reflected wave the velocity of submarine is calculated as follows.

There is no change in the wavelength of the waves reaching the submarine from the SONAR station because in this case source is statibnary but there is change in the wavelength of the reflected waves because for the reflected waves submarine will act as sound source. If submarine (sound source) is coming towards the SONAR station then the apparent wavelength will be:

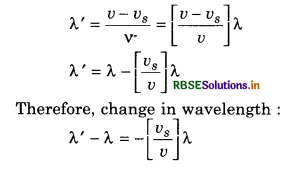
Where v_s is the velocity of source means that of submarine and v is the velocity of sound in water and λ is the original wavelength of the sound waves. Negative sign means submarine is coming closer and the wavelength of the reflected waves from it decreases. If submarine is going away from SONAR station then there would be positive sign. Hence, simple formula for change in wavelength will be;
∆λ = λ' - λ = ±[\(\frac{v_s}{v}\)]λ ..........................(15.98)
By using this formula, the velocity of submarine (v_s) is calculated and the position of the submarine relative to the SONAR station is also calculated.

Conceptual Questions

Question 1.
Why are the longitudinal waves also called pressure waves?
Ans. Longitudinal waves travel in a medium as series of alternate compressions and rarefactions i.e., they travel as variations in pressure and hence are called pressure waves.

Question 2.
Sound travels faster on a rainy day than on a dry day. Why?
Answer:
The amount of water vapours present in the atmosphere is much higher on a rainy day than on a dry day. As the water vapours are lighter than dry air, hence density of wet air becomes less than that of dry air. Now, because the speed of sound is inversely proportional to the square root of the density hence sound travels faster on a rainy day than on a dry day.

Question 3.
Why in a sound wave, a displacement node is a pressure antinode and vice-versa?
Answer:
At a displacement node (the point of zero displacement), the variation of pressure is maximum. Hence, the displacement node is the pressure antinode and vice-versa.

Question 4.
Solids can support both longitudinal and transverse waves, but only longitudinal waves can propagate in gases. Why?
Answer:
Solids have both volume and shear elasticity. So, both longitudinal and transverse waves can propagate through them. On the other hand, gases have only volume elasticity and not shear elasticity. So, only longitudinal waves can propagate through them.

Question 5.
When we start filling an empty bucket with water, the pitch of sound produced goes on changing. Why?
Answer:
A bucket can be treated as a pipe closed at one end. The frequency of the note produced = \(\frac{v}{4 L}\), where v is the velocity of the sound in air and L is the length of the air column, which is equal to the depth of the water level from the open end. As the bucket is filled with water, L decreases. Therefore, frequency of sound produced goes on increasing.

Question 6.
The organ pipes of same length, open at both the ends produce sound of different pitch, if their radii are different, Why?
Answer:
Due to end correction, the frequency of an open organ pipe depends on its radius (r) and is given by
v = \(\frac{v}{2(L+1 \cdot 2 r)}\)
So, the pitch will be of different radii.

Question 7.
All harmonics are overtones but all overtones are not harmonics. Why?
Answer:
The overtones with frequencies which are integral multiples of the fundamental are called harmonics. Hence all harmonics are overtones. But overtones which are non-integral multiples of the fundamental are not harmonics.

Question 8.
Will there be any Doppler effect if both the sound and the listner are moving with the same velocity and in the same direction?
Answer:
The apparent frequency is given by v' = \(\frac{v-v_0}{v-v_s}\) x v
As, v₀ = v_s, there v'= v, i.e., there is no Doppler Effect.

Question 9.
Will there be Doppler effect, when the direction of motion of the source or observer is perpendicular to the direction of propagation of sound?
Answer:
No, there is no Doppler Effect, when the source or observer moves perpendicular to the direction of propagation of sound.

Question 10.
Why are strings of different thickness and materials are used in a sitar or a violin?
Answer:
Fundamental frequency of a stretched string, v = \(\frac{1}{2 l} \sqrt{\left(\frac{T}{m}\right)}\)
When we use strings of different thicknesses and materials, they have different values of mass per unit length (m). So the strings will produce notes of different frequencies.

Question 11.
A tuning fork is in resonance with a closed pipe. But the same tuning fork cannot be in resonance with an open pipe of same length, why?
Answer:
As the tuning fork of frequency v is in resonance with a closed pipe of length L, so v = \(\frac{v}{4 L}\)
But an open pipe of length L produces a frequency of \(\frac{v}{2L}\). Hence it canot be in resonance with the tuning fork of frequency v(= \(\frac{v}{4 L}\)).

Question 12.
If a person places his ear to one end of a long iron pipeline, he can distinctly hear two sounds when a workman hammers the other end of the pipeline. How?
Answer:
Sound travels sixteen times faster in iron than in air, so the person hears two sounds, the first one travelling through the iron pipeline and the second travelling through air.

Question 13.
Explain why sound travels faster in warm air than in cold air?
Answer:
Velocity of sound is directly proportional to the square root of the temperature of the air
i.e., v ∝ \(\sqrt{T}\)
As temperature of the warm air is more than that of the cold air so sound travels faster in warm air than in cool air.

Question 14.
Two astronauts on the surface of the moon cannot talk to each other. Why?
Answer:
Sound waves require material medium for their propagation. As there is no atmosphere on the moon, hence the sound wave cannot propagate on the moon.

Question 15.
Why does sound travel faster in solids than in gases?
Answer:
The speed of sound through any medium of bulk modulus ß and density ρ is given by
v = \(\sqrt{\left(\frac{\beta}{\rho}\right)}\)
The value of the ratio ß/ρ is much higher for solids than that for gases. That is why sound travels faster in solids than in gases.

Match the following:

There are equations for the displacement of a particle in column I and the type of motion in column II

Column-I	Column-II
(A) y = 1 + cos 2ωt	(p) Simple harmonic motion
(B) Y = a sin ωt + b cos ωt	(q) Periodic motion
(C) Y = ae-ωt	(r) A periodic motion
(D) Y = a sin (ωt + Φ) and X = b cosωt	(s) Harmonic but elliptical motion

Answer:

Column-I	Column-II
(A) y = 1 + cos 2ωt	(q) Periodic motion
(B) Y = a sin ωt + b cos ωt	(r) A periodic motion
(C) Y = ae-ωt	(s) Harmonic but elliptical motion
(D) Y = a sin (ωt + Φ) and X = b cosωt	(p) Simple harmonic motion

Long Answer Type Questions

Question 1.
What do you understand by wave motion? Clearly explain. Establish the expression and the one dimensional differential equation for a progressive wave.
Answer:
In the physical world it is compulsory for us to transfer energy from one place to another in many cases. “Wave motion is a technique which transfers energy from one point to another, often with no permanent displacement of the particles of the medium: that is, with little or no associated mass
transport.” Almost all the branches of Physics have their relation with the wave motion. Waves can be broadly classified into three types:

1. Electromagnetic Waves: Those waves which do not require any medium to transport their energy from one place to another are called electromagnetic waves. Thermal radiation, light waves, X-rays, radio waves, gamma rays, etc. are examples of electromagnetic waves.

2. Matter Waves: When the matter particles like electron, proton, neutron, etc, are in motion, then the waves related to these moving particles are called matter waves. In electron microscope the matter waves associated with electron are used.

3. Mechanical Waves: Those waves which require the material medium for their propagation or transfer of energy are called mechanical waves. Sound waves are an example of mechanical waves.
In this chapter we will study about mechanical waves which will be called waves with reference to this chapter. There are mainly two methods for transfer of energy in Mechanics.

In the first method the particles of the substance themselves take the energy from one place to another i.e., in this method there is physical transfer of the substance. For example, when a stone hits on a window pane then the kinetic energy given to the stone reaches the window pane together with the
stone. Where as in the second method the propagation or transfer of energy takes place from one medium particle to another till the energy reaches the last particle and the medium particles remain at their places. In this method there is no physical transfer of the substance. This method of energy transfer is called ‘wave motion’.

For example, ifa stone is dropped in a lake, then there is disturbance on the surface of water which executes three-dimensional motion and by wave motion the energy is transferred to the sides of the lake. If an empty cap is dropped in the lake then it would float on the surface of water and we would notice that after the stone is dropped in the lake the cap moves up and down on the same place; which shows that the medium particles are not moving. Similarly, the propagation of waves with the help of an elastic string; waves generated from vibration of a tuning fork are some examples of wave motion. Generally, wave is a type of disturbance which is propagated from one part to the other by the harmonic vibration motion of the partîcles. This wave is propagated in a direction with a constant velocity (which is dependent on the medium).

Properties of Wave Motion:
1. It is the disturbance generated by the harmonic motion of the medium particles.

2. Only wave (energy) moves ahead and it is in the direction of the propagation of the wave; where as the medium particles vibrate around the mean position.

3. The phase of the medium particles changes constantly i.e., the different particles have different positions other than the mean position at any instant. The former particles vibrate after some time than the previous particle.

4. The velocity with which the disturbance moves ahead is called the velocity of the wave. The velocity of the wave is different from the velocity of the medium particles. The velocity of the wave is constant where as the velocity of the particles is different in different positions. Their velocity is maximum at the mean point and zero in position of maximum displacement. The wave takes a definite time in reaching from one place to another.

5. It is the property of a wave that it can be reflected or refracted after reaching the boundary of another medium.

6. It has the property of interference and diffraction.

For the effective propagation of the waves, the medium should have the following properties:
1. The medium should have the elasticity property so that if a particle is displaced then it comes back to the original (initial) position and displaces the particle close to it.

2. For efficient transfer of energy the material medium should have the property of inertia so that it can collect the energy otherwise the energy would be lost.

3. Every medium resists the disturbance of the motion; which is called resistance; due to this the energy of oscillation of the particle reduces. If this resistance is more than the dimension of disturbance then disturbance becomes zero which means that the propagation of energy is for a very small distance.
Hence, the resistance of the medium should be very small.

The above properties are for the motion of mechanical wave. If the wave is electromagnetic then it can travel without any medium or in vacuum; and all the properties of wave motion are in-built in it.

When in any medium the wave propagates then the medium particle vibrates and this vibrational motion is called simple harmonic motion. Medium particles vibrate in same or different phases. Suppose a wave is moving as shown in diagram from point O to the right hand side.

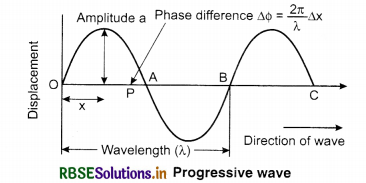
Particles on the right hand side of O are disturbed after sorne time hence due to this their motion is lagging. Displacenwnt equation for a particle at point P which is at a distance x from origin O is;
y = a sin(ωt - Φ) ......................(15.7)
Here, Φ is the phase difference between particles at O and P. Since, point P is at a distance x from O and the phase difference between particles at distance λ is 2π.
Hence, phase difference between the particles at distance x is
Φ = \(\frac{2 \pi}{\lambda}\) x (x) ....................(15.8)
Putting the value of Φ in equation (15.7)

Equations (15.9) and (15.10) represent progressive wave equation in the positive x direction.
Similarly, progressive wave equation in negative x direction will be given by: y = a sin (ωt + kx).
Again from equation (15.9)
y = a sin(ωt - kx)
Differentiating the above equation with respect to time;
v = \(\frac{d y}{d t}\) = ω a cos (ωt - kx) .........................(15.11)
This is the expression for velocity of the particle. Hence, it is clear that the velocity of the particle is different from wave velocity. Velocity of the particle is dependent on time (t) and position (x) of the particle, whereas wave velocity is constant. From equation (15.11) the maximum value of the velocity of a particle is ωa.
Again differentiating equation (15.11) with respect to time:

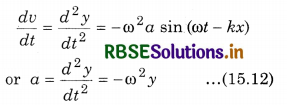
Here, a = \(\frac{d^2 y}{d t^2}\) is the acceleration of the particle.
Equation (15.12) shows that the acceleration of a particle is directly proportional to displacement and is in opposite direction. This is the necessary condition of simple harmonic motion. Differentiating equation (15.9) twice relative to position (x)
\(\frac{d^2 y}{d x^2}\) = -k² a sin (ωt - kx) = -k²y ............................(15.13)
From equations, (15.12) and (15.13)

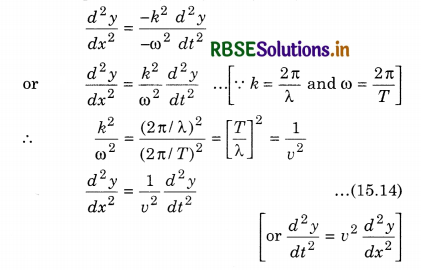
Equation (15.14) is called one dimensional differential equation of the wave.

Question 2.
Derive the formula for velocity of wave in liquid.
Answer:
To calculate the velocity and propagation of longitudinal waves we take a tube having a piston containing, compressed liquid, which can be divided into similar lines in many layers of same liquid. Where the lines are closer the pressure and density of the liquid is more and where the lines are farther apart the pressure and density of the liquid is less. Here we consider the liquid as a continuous medium and will ignore that in reality it is made up of atoms which are moving in different directions with different velocities.

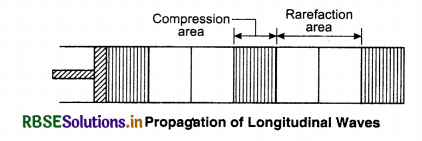
If the piston is pushed inside the tube then the liquid will be compressed and it would thus increase the pressure and density. This layer of the compressed liquid will move ahead and would generate compression in another layer. If the piston is again pulled outwards then due to this the liquid will spread and its pressure and density will decrease which means there would be rarefaction. This way if piston is continuously pulled and pushed then the disturbance would move ahead in the tube in the form of rarefaction and compression. Hence, it behaves as a longitudinal wave.

Suppose the piston is pushed inside and a disturbance is generated which moves in the form of a compression and is moving towards the right with v velocity. For simplicity, we assume that in this compression area, the pressure and density of the liquid is constant. Now if the observer is also considered to be moving in the direction of compression with same velocity then the liquid medium will be assumed to be moving in opposite direction to the compression with the v velocity and for observer the compression would be at rest. In this situation when liquid with velocity v moving towards the compression area collides with the compression area then the pressure at front end will be more than the pressure at the last end. Suppose that ∆P is the pressure difference between both the ends. Due to this in this area B this element (liquid medium) would be compressed and in this area its velocity is some less v - ∆v and when this element will come out of compression area then it would again gain its volume. Due to this ∆P will move backwards and accelerated and due to this its velocity will again become v. This is how this small part will reach position C.
When liquid element enters the compression area then the working resultant force on it (right side),
F = Pressure (P) x Area (A)
= (P + ∆P)A - PA
= ∆PA
where, A is the cross sectional area of the tube.
Out of compression area the length of this small part is v ∆t, where ∆t is the time taken by the small part to pass a point. Hence, volume of small part is v ∆t x A and mass ρ v A ∆t, where ρ is the density of the liquid outside compression area. When this small part enters the compression area then acceleration experienced by it is;
a = -\(\frac{\Delta v}{\Delta t}\)
(∵ Velocity reduces hence acceleration is negative)
Now by Newton's second law of motion;
Force (F) = mass (m) x acceleration (a)

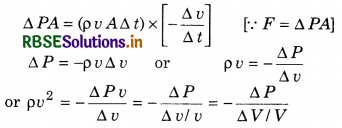
Since, volume of liquid outside compression area
V = A v ∆t and decrease in volume in compression area is ∆V = A ∆v ∆t.
∴ \(\frac{\Delta V}{V}=\frac{A \Delta v \Delta t}{A v \Delta t}=\frac{\Delta v}{v}\)
or v = \(\sqrt{\frac{E}{\rho}}\) ............................(15.6)
where, E = -\(\frac{\Delta P}{\Delta V / V}\) = volume elasticity coefficient
Hence, velocity of longitudinal wave in liquid medium

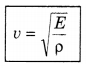
It is clear that velocity of wave is dependent on property of the medium, elasticity constant and density.

Question 3.
Derive the formula for velocity of the transverse waves in a uniform stretched string.
Answer:
We have studied earlier that due to disturbance in stretched string transverse waves are generated. Hence, to calculate the velocity of transverse waves, let us assume a string, whose unit length mass is m, and tension is T. A disturbance is in motion from left towards right with velocity v.We can also assume that the observer is moving in the direction of disturbance with the same velocity v, then the vibration will appear stable to the observerand the string will appear moving in the opposite direction. Now analyse the small part δl; due to disturbance if there is small displacement in the string then this small part δl; can be considered as a part of the circle with radius R and the mass of this small part will be m δ l.
On this small part as shown in the diagram, the component of tension towards the center is 2Tsinθ which will provide the necessary centripetal force.
Therefore;
2 T sinθ = \(\frac{M v^2}{R}\) where M = mass = m δ l
When, θ is very small then sinθ ≅ θ
Therefore; 2 T θ = \(\frac{m \delta l v^2}{R}\) .............................(15.3)
Again from the figure, formula for arc PQ.
Angle = Arc/Radius
2 θ = \(\frac{\delta l}{R}\) ...................(15.4)

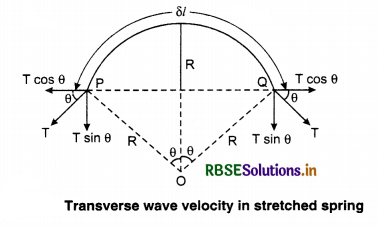
Putting values from equation (15.4) and (15.3) we get;

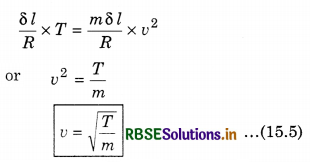
This is the equation for velocity of a transverse wave which shows that the velocity of the wave in a string is dependent on the tension and the mass of unit length and is not dependent on amplitude of the wave and its wavelength. In the above situation string is considered to be ideal (that is totally elastic and same density) and while doing vibration motion there is no change in the length of the string.

Question 4.
Prove that in a string the ratio of velocity of longitudinal waves and transverse waves is \(\frac{1}{\sqrt{\text { strain }}}\).
Answer:
To calculate the velocity and propagation of longitudinal waves we take a tube having a piston containing, compressed liquid, which can be divided into similar lines in many layers of same liquid. Where the lines are closer the pressure and density of the liquid is more and where the lines are farther apart the pressure and density of the liquid is less. Here we consider the liquid as a continuous medium and will ignore that in reality it is made up of atoms which are moving in different directions with different velocities.

If the piston is pushed inside the tube then the liquid will be compressed and it would thus increase the pressure and density. This layer of the compressed liquid will move ahead and would generate compression in another layer. If the piston is again pulled outwards then due to this the liquid will spread and its pressure and density will decrease which means there would be rarefaction. This way if piston is continuously pulled and pushed then the disturbance would move ahead in the tube in the form of rarefaction and compression. Hence, it behaves as a longitudinal wave.

Suppose the piston is pushed inside and a disturbance is generated which moves in the form of a compression and is moving towards the right with v velocity. For simplicity, we assume that in this compression area, the pressure and density of the liquid is constant. Now if the observer is also considered to be moving in the direction of compression with same velocity then the liquid medium will be assumed to be moving in opposite direction to the compression with the v velocity and for observer the compression would be at rest. In this situation when liquid with velocity v moving towards the compression area collides with the compression area then the pressure at front end will be more than the pressure at the last end.

Suppose that ∆P is the pressure difference between both the ends. Due to this in this area B this element (liquid medium) would be compressed and in this area its velocity is some less v - ∆v and when this element will come out of compression area then it would again gain its volume. Due to this ∆P will move backwards and accelerated and due to this its velocity will again become v. This is how this small part will reach position C.

When liquid element enters the compression area then the working resultant force on it (right side),
F = Pressure (P) x Area (A)
= (P + ∆P)A - PA
= ∆PA
where, A is the cross sectional area of the tube.
Out of compression area the length of this small part is v ∆t, where ∆t is the time taken by the small part to pass a point. Hence, volume of small part is v ∆t x A and mass ρ v A ∆t, where ρ is the density of the liquid outside compression area. When this small part enters the compression area then acceleration experienced by it is;
a = -\(\frac{\Delta v}{\Delta t}\)
(∵ Velocity reduces hence acceleration is negative)
Now by Newton's second law of motion;
Force (F) = mass (m) x acceleration (a)

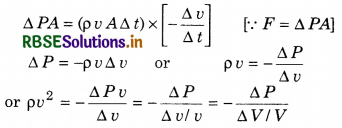
Since, volume of liquid outside compression area
V = A v ∆t and decrease in volume in compression area is ∆V = A ∆v ∆t.
∴ \(\frac{\Delta V}{V}=\frac{A \Delta v \Delta t}{A v \Delta t}=\frac{\Delta v}{v}\)
or v = \(\sqrt{\frac{E}{\rho}}\) ............................(15.6)
where, E = -\(\frac{\Delta P}{\Delta V / V}\) = volume elasticity coefficient
Hence, velocity of longitudinal wave in liquid medium

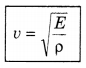
It is clear that velocity of wave is dependent on property of the medium, elasticity constant and density.

Question 5.
Derive the relationship between the amplitude of a wave and its intensity.
Answer:
When in any medium a progressive wave propagates then it transmits the energy to the other particles of the medium gradually, due to which these particles successively start harmonic vibration. This energy is provided by wave source. This way energy is transferred from one part of the medium to another successively by progressive wave. Since, the medium particles execute simple harmonic motion hence the total energy of the particle is equal to the sum of its potential energy and kinetic energy. Therefore first we calculate the energy of unit volume i.e., energy density. 

We know that the displacement equation of the particle moving with a velocity u towards the x axis of a progressive wave is given as follows.
y = asin[\(\frac{2 \pi}{\lambda}\)(vt - x)]
where; a = amplitude of the particle.
λ = wavelength, t = time, x = distance of the particle from the origin. 
Hence, velocity of this particle,
u = \(\frac{d y}{d t}\) (where; u is the velocity of particle and v is the velocity of the wave)
u = \(\frac{d}{d t}\left[\alpha \sin \frac{2 \pi}{\lambda}(v t-x)\right]\)
u = \(\frac{2 \pi v \alpha}{\lambda} \cos \frac{2 \pi}{\lambda}(v t-x)\)
and acceleration
= \(\frac{d u}{d t}=\frac{d^2 y}{d t^2}=-\alpha\left[\frac{2 \pi v}{\lambda}\right]^2 \sin \frac{2 \pi}{\lambda}(v t-x)\)
∴ Acceleration = -[\(\frac{2 \pi v}{\lambda}\)]² y

Question 6.
What are standing waves? Derive the resultant wave equation for standing waves.
Answer:
When two progressive waves having equal amplitude and frequency moving in opposite directions along the same line in a bounded medium and are superimposed then the wave produced as a result of this superposition is not seen moving in any direction. These type of waves are called standing waves. Similar to progressive waves, standing waves are also of two types: transverse and longitudinal. Transverse standing waves are generated in stretched strings and longitudinal standing waves are generated in air columns. The music from musical instruments is produced due to standing waves. Sitar, Violin. Piano,  Guitar. Iktara, etc. produce transverse standing waves and Flute, Whistle, Tabla, etc. produce longitudinal standing wave.

The medium in which the wave moves along a constant line is called linear medium and if the length of linear medium is not infinity, meaning it is finite, then the medium is called bounded (fixed) medium. In linear bounded medium at the end a wave is incident and the second wave is obtained by the reflection of the first wave. Superposition of those two waves leads to the formation of standing waves. To understand the formation of such waves we will study figure 15.14.

Here two waves of same frequency and amplitude propagation in opposite directions are shown. One wave is shown from left side to right side and second wave is shown from right side to left side by constant line and dotted line respectively. Initially (at t = 0) both waves are superimposed
in opposite phases due to this all the medium particles are in the mean position. After t = T/4 (where T is the time period of both the waves) time both the waves move ahead by λ/4 in opposite directions. Additional path difference or π phase difference is generated and therefore both the waves meet in the same phase. It is clear from the resultant wave diagram that in this position displacement of some particles [A₁, A₂, A₃, A₄, A₅] is maximum and some particles (N₁, N₂, N₃, N₄) are still in the mean position. After t = T/2 time again the waves are superimposed in opposite phases; now the resultant displacement of all the particles will be zero.

After time t = 3T/4 waves are in the same phase. At this time the displacement of the medium particles A₁, A₂, A₃, A₄ and A₅ is again maximum, but their phase is opposite. It is clear from the diagram, after t = T again the initial position is reached.
From the above discussion we can get the conclusion that:

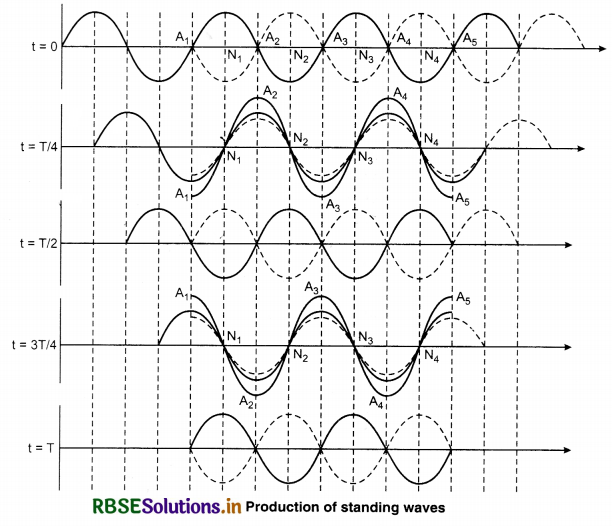
1. Some medium particles (A₁, A₂, A₃, A₄ and A₅) always vibrate with the maximum amplitude on both the sides of the mean position. They are called antinode. Velocity (dy/dt) of particles at antinodes is maximum and pressure or change in density is zero.
[∵ \(\frac{d y}{d x}\) = 0]

2. Particles (N₁, N₂, N₃, N₄) between the consecutive antinodes are always stationary. These are called node. These are positioned at same distance. Velocity of particles [dy/dt] at nodes is zero and the pressure or density change is maximum.

3. Distance between two successive antinodes or two successive nodes is λ/2 and the distance between a node and the consecutive nearest antinode is λ/4; where λ is the wavelength.

4. Antinode’s energy is not transferred to nodes meaning these waves do not transfer energy and the waves do not propagate in the medium, but remain in their position and diverge and compress in the boundaries of the medium. Due to this property of the waves they are called standing waves.

5. In standing waves the time period of all the particles is same but the amplitude of all the particles is different. Similarly: the particles between two successive nodes vibrate in the same phase but their amplitudes are different.

6. Particles on both the sides of a node vibrate in opposite phase and particles on both the sides of an antinode vibrate in the same phase.

7. Two times in a time period all the particles of the medium come together in their equilibrium position. Meaning in one time period the displacement of all the particles is zero twice.

Question 7.
What is resonance? By drawing the diagram of resonance tube calculate the formula for velocity of sound in air.
Answer:
When an object which execute vibration motion is slightly displaced from its stable position and is left then due to the effect of restitution force it vibrates with its natural (fundamental) frequency. This type of vibration is called the ‘free vibration”. In ideal free vibration the amplitude of the object is constant state of. But in reality when the object excutes free vibrations then it experiences some frictional force in the medium in which it is vibrating. As a result some part of its energy is lost as heat. Hence, the amplitude of the object decreases with time. Those types of vibrations whose amplitude decreases with time are called the “damped vibrations.”

If somehow we can provide the same energy to the vibrating object as to which it has lost; then the object keeps on vibrating with the same (constant) amplitude. This type of vibration is called the “maintained vibrations”.

A vibrating object forces another object (which has the tendency to vibrate) to vibrate. It is also possible if their fundamental frequencies are different. This type of vibration is called the “forced vibrations”. This type of vibrations end very soon because in this situation the second vibrating object does not vibrate with its fundamental frequency but vibrates with the frequency of the first vibrating object.

When the frequency of first vibrating object is equal to the fundamental frequency of the second vibrating object then the amplitude of forced vibrations increases relatively. This is called the “resonance”. Every impulse of frequency force helps the system state to vibrate. Due to this the amplitude of the system keeps on increasing.

As a result of Laplace’s correction we know that the velocity of sound in air is given by the following formula;
v = \(\sqrt{\frac{\gamma P}{\rho}}\) ............................(15.64)
where, γ = \(\frac{C_P}{C_v}\) = constant
P = pressure
ρ = denstiy of gas
We also know that for any gas if density and pressure are kept constant then its density is inversely proportional to the temperature.
ρ ∝ \(\frac{1}{T}\) ...........................(15.65)
We can say from equations (15.64) and (15.65) that in air or in any gas the velocity of sound is directly proportional to the square root its absolute temperature.
v ∝ \(\sqrt{T}\)
or \(\frac{v_1}{v_2}=\sqrt{\frac{T_1}{T_2}}\) .......................(15.66)
If at 0°C the velocity of sound is v₀ and at t°C temperature it is v_t then by equation (15.66):

It is clear from this equation that if there is 1°C change in temperature then the velocity of sound is changed by 0.61 m/s.
Effect of Density: The velocity of sound in a gas is inversely proportional to the square root of density of the gas.
∵ v = \(\sqrt{\frac{\gamma \rho}{\rho}}\)
∴ \(\frac{v_1}{v_2}=\sqrt{\frac{\rho_2}{\rho_1}}\)
Effect of pressure: The formula for velocity of sound in a gas is:

When T = constant
then PV = constant
∴ v = constant
Hence velocity of sound is independent of the change pressure of gas, provided temperature remains constant.
Effect of humidity: The presence of water vapour in air changes in its density. That is why the velocity of sound changes with humidity of air.
∴ ρ_m < ρ_d
∴ v_m > v_d

Question 8.
What are beats? By mathematical analysis prove that the number of beats per second is equal to the difference of frequencies of the sources.
Answer:
If two waves are taken into consideration which are totally not similar but there is sorne difference in their frequency meaning the wavelength of both is not same but somewhat different. This type of two waves are if superimposed at some point then at sorne instant they can produce high sound being in same phase but at another instant there can be phase difference in them and there can be an instant at which at the same point they can be in opposite phase and produce zero intensity sound. After sometime they can be in the same phase and will produce high frequency sound. Similarly, at any point the phase difference will keep on changing and the intensity of sound will be high and low: would increase and decrease.

Figure (15.17) shows two waves superposition at the same place as per the time and formation of beats. For convenience the frequency of one wave is taken 5 and that of the other is taken 4. The wave with frequency 5 is shown by dotted line and wave with frequency 4 is shown by a straight line. Vertical axis shows displacement of particles from the mean position and horizontal axis shows time. Wave formed by the superposition of both is shown by thick black line.

At instant A, both the waves are in the same phase and hence resultant displacement will be maximum and intensity of sound will be highest. After small time difference B, both the waves will be in opposite phase and hence will deduct the effect of each other and will make zero displacement and zero sound. Again at instant C, both the waves will be in same phase with maximum displacement and loud sound. Similarly, according to time at any place sound will be maximum or minimum. Hence, we can say as conclusion;

“Superposition of two slightly different frequencies waves produce sometimes high or low intensity sounds, this harmonic cycle is called beats.”

Phase difference of two high intensity sounds or two low intensity sounds is called time of beat, meaning in this time one beat is produced.

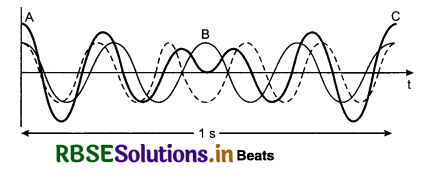
From the above figure one more conclusion is drawn that if first wave produces 5 vibrations in 1 second and second wave produces 4 vibrations in 1 second then in 1 second 1 beat is heard meaning frequency of beats is equal to the difference of the frequencies of two waves.

Question 9.
Describe Doppler’s effect for sound waves and calculate the formula for experienced frequency when:
(a) Source is moving towards the stationary observer.
(b) Observer is moving towards the stationary source.
Answer:
(a) Source is moving towards the stationary observer.
We all know that when a moving train with high speed comes closer then the sound of its whistle is sharper in comparison to the sound of the whistle when it moves away. If sound is heard sharper then it means that its pitch (frequency) has increased and if it is heard coarse (thick) then it means that the frequency has decreased. But in reality there is no change in the pitch of the whistle.

Pitch: The quality of sound or the degree of highness or lowness of a tone dependent on frequency. High frequency source generates sharp sound meaning its pitch is high whereas low frequency source generates low or flat sound whose pitch is less (low). Children and women have high pitch sound because its frequency is more where as man of more age has low pitch voice. Therefore, for normal loud sounds pitch is dependent on frequency. But both are not equal. Pitch’s physical measurement is not possible but people can only tell by their experience that pitch of the sound is high or low. On the other hand frequency is per second completed vibrations; whose physical measure is possible. Therefore, we view pitch in terms of frequency.

This change was first noticed by Doppler hence it is known as Doppler’s Effect. According to this, “When there is relative motion between the observer and the source of sound then the sound heard by the observer is relatively different from the sound produced by the source of sound i.e., the observer experiences some change in frequency of sound due to the relative motion.”

Therefore Doppler Effect is a phenomena, it is not only applicable on sound waves but also works for electro-magnetic waves. Here we will only study sound waves and the changes in frequency at different situations of the source and observer. Suppose sound source is S and observer is O and source S is vibrating with a frequency v and u is the velocity of sound in stable medium then:
1. When source and observer both are stationary:
In one second y waves are generated in the medium by source S and they will spread at a distance v in the medium. When 1^st wave reaches v distance then last nth wave is generated at the source. If wavelength is λ then;
λ = \(\frac{v}{n}\)

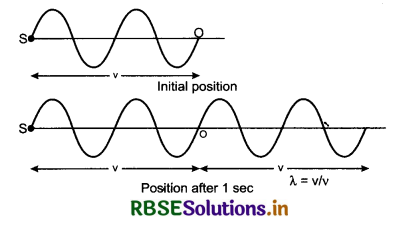
Since, these waves pass through the ears of the observer O by y velocity hence the first wave reaching the ear of the observer will move y distance ahead in 1 s and the waves which are at a distance y will only pass through the ears in 1 s.
This will be the frequency heard by the observer v'. Therefore;
v' = \(\frac{v}{\lambda}=\frac{v}{v / n}\) = n ...........................(15.82)
or v' = v
Hence, in this case the sound heard by the observer is the same as the sound generated by the source.

(b) Observer is moving towards the stationary source.
Now we study the effect of motion of the observer. Suppose sound source S is stationary and observer is moving with velocity v₀ in the direction of propagation of the sound away from the source. If v is the frequency of the sound source and v is the velocity of sound then wavelength λ = \(\frac{v}{v}\). If the observer was also stationary then he/she could hear the n waves coming from the sound source. But he is himself moving v₀ distance away from the source hence he would only hear the waves in v - v₀ distance meaning the effect of motion of the observer changes the number of waves passing
through it in 1 s and source is stationary so the wavelength of waves generated from it will not change. Hence, if frequency experienced is v₁ then;

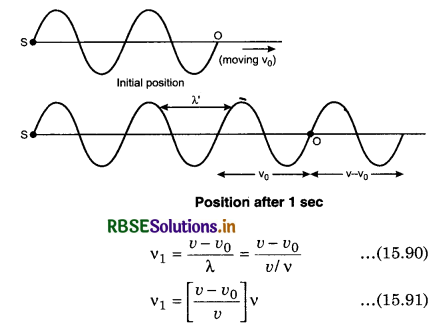
It is clear from above that v₁ < v i.e., if observer is moving away from the source then he will experience less frequency.
Similarly, if observer is moving with velocity v0 towards the source then the frequency experienced;
v₂ = [\(\frac{v+v_0}{v}\)]v ...............................(15.92)
It is clear from above that v₂ > v i.e., if observer is moving towards the source then he will experience an increase in frequency.
If the observer passes through the stationary source then change in apparent frequency is ∆v then;

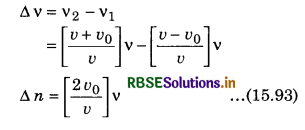
Question 10.
Write Newton’s formula for the speed of sound in gases. Why and what correction was applied by Laplace in this formula? Also deduce modified formula for speed of sound.
Answer:
When any object vibrates then due to its vibration sound is produced. When vibration through air or any other elastic medium reaches the ear membrane then the membrane of the ear starts vibrating; whose sensation is caught by the brain and we experience sound.

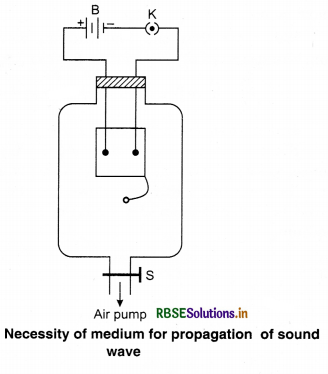
Normally, sound travels in air and it can he reflected and refracted. It can also produce irterference. These properties show that sound propagates in the form of a wave and these waves are the longitudinal progressive waves. Sound takes time to travel and requires medium for its propagation; which can be understood by following:

As shown in the figure 15.22 we take a jar and place an electric bell in ‘it, the wires of the bell are taken out and on the mouth of the jar an air-resistant cork is placed. The other end of the jar is joined by an air pump. Now when it is joined by battery, current flows and we can hear the sound of the ball. Now when the air of the jar is slowly taken out with the help of the air pump the sound reduces but the electric current is the same. After some time when there is very less air pressure in the jar then very low sound is heard. If there is complete vacuum then no sound is heard; but complete vacuum is not possible. Hence, we can say that medium is necessary for the propagation of sound waves.

We cannot listen all the disturbances of elastic medium. Normally, human ear can listen the waves of frequency of approximately 20 vibrations/second to 20,000 vibrations/second. Frequency of sounds above or below this range is not audible to normal human ear. This is known as audible range. The average frequency of woman sound is 280 vibrations/second and that of man is 140 vibrations/second. Sounds having frequency above the audible range are called ultrasonic and sounds having frequency below audible range are called infrasonic. Generally, all the waves generated in the elastic medium solid, liquid or gaseous are called sound waves, whether they are heard or not.
We know that the longitudinal wave velocity from equation (15.6)) is given as follows:
v = \(\sqrt{\frac{\beta}{\rho}}\) where ß = volume modulus of elasticity and
ρ = density of the substance.
Sounds waves are also longitudinal waves. Hence, velocity of sound waves is also given by above formula (equation). But we know that the velocity of sound is dependent on the medium. Hence, for solid medium,
v_solid = \(\sqrt{\frac{\beta}{\rho}}=\sqrt{\frac{Y}{\rho}}\)
v_solid = \(\sqrt{\frac{E}{\rho}}=\sqrt{\frac{Y}{\rho}}\)
where Y is the modulus of elasticity.
For example; for velocity of sound in steel,
For steel, Y = 2 x 10¹¹ N/m²,
Density of steel ρ = 7800 kg/m³
Therefore;
v_steel = \(\sqrt{\frac{2 \times 10^{11}}{7800}}\) = 5600 m/s
Similarly, for the liquid medium;
v_liquid = \(\sqrt{\frac{E}{\rho}}=\sqrt{\frac{\beta}{\rho}}\)
where B = volume elasticity constant.
For example, for water B = 2.04 x 10⁹ N/m²
and ρ = 1000 kg/m³
Therefore; v_water = \(\sqrt{\frac{2.04 \times 10^9}{1000}}\) = 1430 m/s
Again for gaseous medium;
v_gaseous = \(\sqrt{\frac{E}{\rho}}\)
But, for velocity of sound in gas Newton has assumed that when sound waves propagate in gaseous medium; then temperature of the medium is constant.
Therefore, by Boyle’s law
PV = (P + ∆P)(V + ∆V)
= PV + P ∆V + V ∆P + ∆P ∆V
or P ∆V = -V ∆P [∆P ∆V are very and small so negligible]
or P = -∆P \(\frac{V}{\Delta V}\) ........................(15.58)
∴ From equations (15.6) and (15.62)
ρv² = P
or v = \(\sqrt{\frac{P}{\rho}}\) .......................(15.59)
Where P is pressure and ρ is density.
But air pressure at normal temperature and pressure is P = 1.01 x 10⁵ N/m² and density ρ = 1.29 kg/m³.
Therefore, velocity of sound in air;
v_air = \(\sqrt{\frac{1.01 \times 10^5}{1.29}}\) = 280 m/s
But by experiments velocity of sound in air comes 332 m/s. Hence, there was something missing in the formula for gases hence scientist Laplace corrected it.

Laplace Correction
According to Laplace when sound waves travel in air then there is compression and rarefaction of air. In the place of compression the air particles are closer hence become hot and in the position of rarefaction the particles are further apart hence temperature reduces; and this process of compression and rarefaction is so continuous that heat is not able to move out from the medium and control ‘its temperature. Hence, temperature is not constant in this process. From gas equation for adiabatic changes.

The value of γ for monoatomic gas molecule is 1.67 and for thatomic gas molecules is 1.41. Hence, by using the formula (15.63) at known temperature and pressure, the velocit of sound in air.
v_air = \(\sqrt{\frac{1.41 \times 1.01 \times 10^5}{1.29}}\) = 332 m/s (approximately)
Which is equal to the experimental value. From above study we see that in solid medium the velocity of sound is maximum and in gaseous medium it is minimum.

Question 11.
What are stationary waves? Explain the formation of stationary waves graphically.
Answer:
When two progressive waves having equal amplitude and frequency moving in opposite directions along the same line in a bounded medium and are superimposed then the wave produced as a result of this superposition is not seen moving in any direction. These type of waves are called standing waves. Similar to progressive waves, standing waves are also of two types: transverse and longitudinal. Transverse standing waves are generated in stretched strings and longitudinal standing waves are generated in air columns. The music from musical instruments is produced due to standing waves. Sitar, Violin. Piano,  Guitar. Iktara, etc. produce transverse standing waves and Flute, Whistle, Tabla, etc. produce longitudinal standing wave.

The medium in which the wave moves along a constant line is called linear medium and if the length of linear medium is not infinity, meaning it is finite, then the medium is called bounded (fixed) medium. In linear bounded medium at the end a wave is incident and the second wave is obtained by the reflection of the first wave. Superposition of those two waves leads to the formation of standing waves. To understand the formation of such waves we will study figure 15.14.

Here two waves of same frequency and amplitude propagation in opposite directions are shown. One wave is shown from left side to right side and second wave is shown from right side to left side by constant line and dotted line respectively. Initially (at t = 0) both waves are superimposed
in opposite phases due to this all the medium particles are in the mean position. After t = T/4 (where T is the time period of both the waves) time both the waves move ahead by λ/4 in opposite directions. Additional path difference or π phase difference is generated and therefore both the waves meet in the same phase. It is clear from the resultant wave diagram that in this position displacement of some particles [A₁, A₂, A₃, A₄, A₅] is maximum and some particles (N₁, N₂, N₃, N₄) are still in the mean position. After t = T/2 time again the waves are superimposed in opposite phases; now the resultant displacement of all the particles will be zero.

After time t = 3T/4 waves are in the same phase. At this time the displacement of the medium particles A₁, A₂, A₃, A₄ and A₅ is again maximum, but their phase is opposite. It is clear from the diagram, after t = T again the initial position is reached.
From the above discussion we can get the conclusion that:

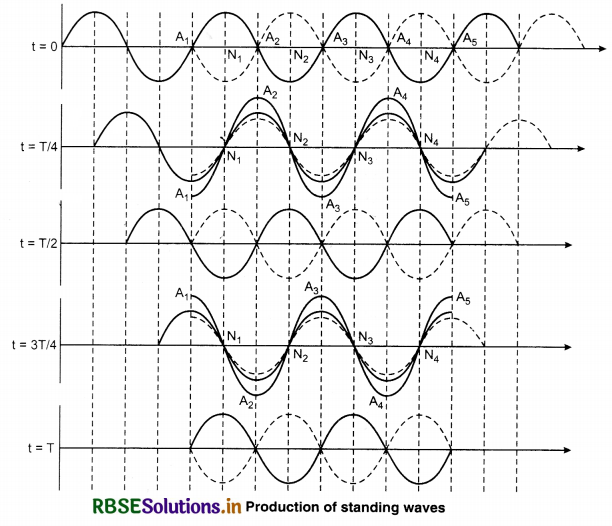
1. Some medium particles (A₁, A₂, A₃, A₄ and A₅) always vibrate with the maximum amplitude on both the sides of the mean position. They are called antinode. Velocity (dy/dt) of particles at antinodes is maximum and pressure or change in density is zero.
[∵ \(\frac{d y}{d x}\) = 0]

2. Particles (N₁, N₂, N₃, N₄) between the consecutive antinodes are always stationary. These are called node. These are positioned at same distance. Velocity of particles [dy/dt] at nodes is zero and the pressure or density change is maximum.

3. Distance between two successive antinodes or two successive nodes is λ/2 and the distance between a node and the consecutive nearest antinode is λ/4; where λ is the wavelength.

4. Antinode’s energy is not transferred to nodes meaning these waves do not transfer energy and the waves do not propagate in the medium, but remain in their position and diverge and compress in the boundaries of the medium. Due to this property of the waves they are called standing waves.

5. In standing waves the time period of all the particles is same but the amplitude of all the particles is different. Similarly: the particles between two successive nodes vibrate in the same phase but their amplitudes are different.

6. Particles on both the sides of a node vibrate in opposite phase and particles on both the sides of an antinode vibrate in the same phase.

7. Two times in a time period all the particles of the medium come together in their equilibrium position. Meaning in one time period the displacement of all the particles is zero twice.

Question 12.
What are standing waves? Derive an expression for the standing waves. Also define the terms node and antinode.
Answer:
When two progressive waves having equal amplitude and frequency moving in opposite directions along the same line in a bounded medium and are superimposed then the wave produced as a result of this superposition is not seen moving in any direction. These type of waves are called standing waves. Similar to progressive waves, standing waves are also of two types: transverse and longitudinal. Transverse standing waves are generated in stretched strings and longitudinal standing waves are generated in air columns. The music from musical instruments is produced due to standing waves. Sitar, Violin. Piano,  Guitar. Iktara, etc. produce transverse standing waves and Flute, Whistle, Tabla, etc. produce longitudinal standing wave.

The medium in which the wave moves along a constant line is called linear medium and if the length of linear medium is not infinity, meaning it is finite, then the medium is called bounded (fixed) medium. In linear bounded medium at the end a wave is incident and the second wave is obtained by the reflection of the first wave. Superposition of those two waves leads to the formation of standing waves. To understand the formation of such waves we will study figure 15.14.

Here two waves of same frequency and amplitude propagation in opposite directions are shown. One wave is shown from left side to right side and second wave is shown from right side to left side by constant line and dotted line respectively. Initially (at t = 0) both waves are superimposed
in opposite phases due to this all the medium particles are in the mean position. After t = T/4 (where T is the time period of both the waves) time both the waves move ahead by λ/4 in opposite directions. Additional path difference or π phase difference is generated and therefore both the waves meet in the same phase. It is clear from the resultant wave diagram that in this position displacement of some particles [A₁, A₂, A₃, A₄, A₅] is maximum and some particles (N₁, N₂, N₃, N₄) are still in the mean position. After t = T/2 time again the waves are superimposed in opposite phases; now the resultant displacement of all the particles will be zero.

After time t = 3T/4 waves are in the same phase. At this time the displacement of the medium particles A₁, A₂, A₃, A₄ and A₅ is again maximum, but their phase is opposite. It is clear from the diagram, after t = T again the initial position is reached.
From the above discussion we can get the conclusion that:

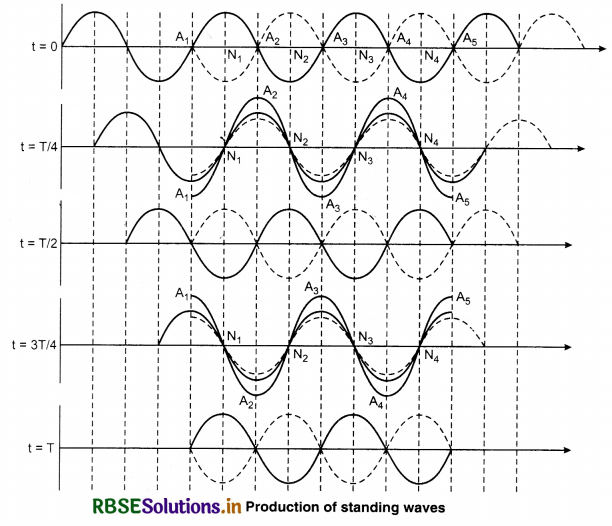
1. Some medium particles (A₁, A₂, A₃, A₄ and A₅) always vibrate with the maximum amplitude on both the sides of the mean position. They are called antinode. Velocity (dy/dt) of particles at antinodes is maximum and pressure or change in density is zero.
[∵ \(\frac{d y}{d x}\) = 0]

2. Particles (N₁, N₂, N₃, N₄) between the consecutive antinodes are always stationary. These are called node. These are positioned at same distance. Velocity of particles [dy/dt] at nodes is zero and the pressure or density change is maximum.

3. Distance between two successive antinodes or two successive nodes is λ/2 and the distance between a node and the consecutive nearest antinode is λ/4; where λ is the wavelength.

4. Antinode’s energy is not transferred to nodes meaning these waves do not transfer energy and the waves do not propagate in the medium, but remain in their position and diverge and compress in the boundaries of the medium. Due to this property of the waves they are called standing waves.

5. In standing waves the time period of all the particles is same but the amplitude of all the particles is different. Similarly: the particles between two successive nodes vibrate in the same phase but their amplitudes are different.

6. Particles on both the sides of a node vibrate in opposite phase and particles on both the sides of an antinode vibrate in the same phase.

7. Two times in a time period all the particles of the medium come together in their equilibrium position. Meaning in one time period the displacement of all the particles is zero twice.

 
Question 13.
Discuss the formation of standing waves in a string fixed at both the ends and the different modes of vibrations.
Answer:
We know that vibrations in a stretched string is an example of transverse standing waves. To understand it we study a string which is tied between two stationary points and is stretched. If T is the tension in the string and mass of unit length is m, then the velocity of waves produced in the string from equation (9.5). 
v = \(\sqrt{\frac{\mathrm{T}}{\mathrm{m}}}\)
When this string is stretched in the perpendicular direction slightly and then left. Then the transverse progressive waves start moving. These waves are reflected from the rigid ends of the string. Therefore, by superposition of incident and reflected waves transverse standing waves are generated and these waves remain till their energy is not destroyed due to friction, etc. Since both the ends of the string are tied up hence they are always nodes. 

When the string is stretched from middle and is left then the string vibrates in one part. Both the ends of the string are nodes and the middle point is antinode figure (9.15). This is the simple method of producing standing wave in a stretched string in which the string vibrates in a loop.

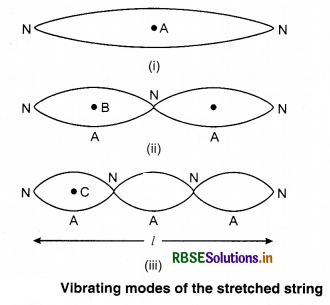
In this state the string produces minimum frequency sound which is called the orignal (fundamental) sound. In this state the length of the string is;
l = \(\frac{\lambda}{2}\) or λ = 2l ............................(15.48)
And frequency of the fundamental sound;
v₁ = \(\frac{v}{\lambda}=\frac{\sqrt{T / m}}{2 l}\) [From equations (15.47) and (15.48)]
or v₁ = \(\frac{1}{2 l} \sqrt{\frac{T}{m}}\) .........................(15.49)
If the string is left from point B (at a distance l/4 from one end) by touching the middle point and then the string vibrates in two parts. In this situation;
l = \(\frac{\lambda}{2}+\frac{\lambda}{2}=\frac{2 \lambda}{2}\) or λ = \(\frac{2 l}{2}\) .........................(15.50)
If in this situation, the frequency of the string is v₂ then;
v₂ = \(\frac{v}{\lambda}=\frac{\sqrt{T / m}}{2 l / 2}\)
From equations (15.47) and (15.50)
v₂ = \(\frac{2}{2 l} \sqrt{\frac{T}{m}}\) .............................(15.51)
or v₂ = 2n₁ ...........................(15.52)
[From equations (15.49) and (15.51)]
In this situation the frequency of the vibrations of the string is twice the frequency of the fundamental sound. This is known as the first overtone or the second harmonic.

Similarly, if the string vibrates in 3, 4, 5, ... etc. parts then the frequency would be three times, four times, 5 times, etc. These are known as the second overtone or the third harmonic, the third overtone or the fourth harmonic, the fourth overtone or the fifth harmonic. In this series if the string vibrates in P segments then the frequency will be;
V_P = \(\frac{P}{2 l} \sqrt{\frac{T}{m}}\) ........................(15.53)
It is clear from the above description that there is a following relationship in frequencies;
v₁:v₂:v₃:............... = 1:2:3:....................
i.e., that both even and odd harmonics are produced in a string. We also get the result that all possible frequencies in a harmonic system has their value equal to the collection of all the fundamental frequencies. The system cannot vibrate with its own frequency. These frequencies are called the normal modes of vibration.

Laws for transverse vibrations of a string:
From the above study, following laws are given for transverse vibrations:
First law: For a given string of constant m and tension T, vibration frequency is inversely proportional to the length i.e.
v ∝ \(\frac{1}{l}\), where T and m are constant.
Second law: For a given string of constant m and length. vibration frequency is directly proportional to the square root of tension (T).
v ∝ T, where l and m are constant.
Third law: Stringsof same length and tension have their vibration frequency inversely proportional to the square root of mass of unit length (m) i.e.,
V ∝ \(\sqrt{\frac{1}{m}}\) where T and l are constant.
Here, m is the mass of unit length = πr² x 1 x d,
where r is the radius of the string and d is its density.

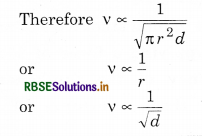
Question 14.
Discuss the formation of harmonics in a stretched string. Show that in case of a stretched string the first four harmonics are in the ratio 1 : 2 : 3 : 4.
Answer:
We know that vibrations in a stretched string is an example of transverse standing waves. To understand it we study a string which is tied between two stationary points and is stretched. If T is the tension in the string and mass of unit length is m, then the velocity of waves produced in the string from equation (9.5). 
v = \(\sqrt{\frac{\mathrm{T}}{\mathrm{m}}}\)
When this string is stretched in the perpendicular direction slightly and then left. Then the transverse progressive waves start moving. These waves are reflected from the rigid ends of the string. Therefore, by superposition of incident and reflected waves transverse standing waves are generated and these waves remain till their energy is not destroyed due to friction, etc. Since both the ends of the string are tied up hence they are always nodes. 

When the string is stretched from middle and is left then the string vibrates in one part. Both the ends of the string are nodes and the middle point is antinode figure (9.15). This is the simple method of producing standing wave in a stretched string in which the string vibrates in a loop.

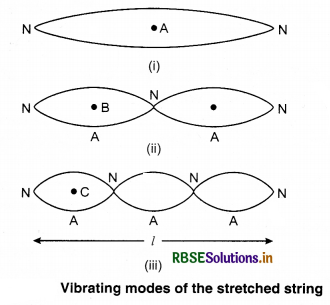
In this state the string produces minimum frequency sound which is called the orignal (fundamental) sound. In this state the length of the string is;
l = \(\frac{\lambda}{2}\) or λ = 2l ............................(15.48)
And frequency of the fundamental sound;
v₁ = \(\frac{v}{\lambda}=\frac{\sqrt{T / m}}{2 l}\) [From equations (15.47) and (15.48)]
or v₁ = \(\frac{1}{2 l} \sqrt{\frac{T}{m}}\) .........................(15.49)
If the string is left from point B (at a distance l/4 from one end) by touching the middle point and then the string vibrates in two parts. In this situation;
l = \(\frac{\lambda}{2}+\frac{\lambda}{2}=\frac{2 \lambda}{2}\) or λ =\(\frac{2 l}{2}\) .........................(15.50)
If in this situation, the frequency of the string is v₂ then;
v₂ = \(\frac{v}{\lambda}=\frac{\sqrt{T / m}}{2 l / 2}\)
From equations (15.47) and (15.50)
v₂ = \(\frac{2}{2 l} \sqrt{\frac{T}{m}}\) .............................(15.51)
or v₂ = 2n₁ ...........................(15.52)
[From equations (15.49) and (15.51)]
In this situation the frequency of the vibrations of the string is twice the frequency of the fundamental sound. This is known as the first overtone or the second harmonic.

Similarly, if the string vibrates in 3, 4, 5, ... etc. parts then the frequency would be three times, four times, 5 times, etc. These are known as the second overtone or the third harmonic, the third overtone or the fourth harmonic, the fourth overtone or the fifth harmonic. In this series if the string vibrates in P segments then the frequency will be;
V_P = \(\frac{P}{2 l} \sqrt{\frac{T}{m}}\) ........................(15.53)
It is clear from the above description that there is a following relationship in frequencies;
v₁:v₂:v₃:............... = 1:2:3:....................
i.e., that both even and odd harmonics are produced in a string. We also get the result that all possible frequencies in a harmonic system has their value equal to the collection of all the fundamental frequencies. The system cannot vibrate with its own frequency. These frequencies are called the normal modes of vibration.

Laws for transverse vibrations of a string:
From the above study, following laws are given for transverse vibrations:
First law: For a given string of constant m and tension T, vibration frequency is inversely proportional to the length i.e.
v ∝ \(\frac{1}{l}\), where T and m are constant.
Second law: For a given string of constant m and length. vibration frequency is directly proportional to the square root of tension (T).
v ∝ T, where l and m are constant.
Third law: Stringsof same length and tension have their vibration frequency inversely proportional to the square root of mass of unit length (m) i.e.,
V ∝ \(\sqrt{\frac{1}{m}}\) where T and l are constant.
Here, m is the mass of unit length = πr² x 1 x d,
where r is the radius of the string and d is its density.

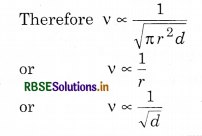
Question 15.
What are beats? Explain their formation analytically. Prove that the beat frequency is equal to the difference in frequencies of the two superposing waves.
Answer:
If two waves are taken into consideration which are totally not similar but there is sorne difference in their frequency meaning the wavelength of both is not same but somewhat different. This type of two waves are if superimposed at some point then at sorne instant they can produce high sound being in same phase but at another instant there can be phase difference in them and there can be an instant at which at the same point they can be in opposite phase and produce zero intensity sound. After sometime they can be in the same phase and will produce high frequency sound. Similarly, at any point the phase difference will keep on changing and the intensity of sound will be high and low: would increase and decrease.

Figure (15.17) shows two waves superposition at the same place as per the time and formation of beats. For convenience the frequency of one wave is taken 5 and that of the other is taken 4. The wave with frequency 5 is shown by dotted line and wave with frequency 4 is shown by a straight line. Vertical axis shows displacement of particles from the mean position and horizontal axis shows time. Wave formed by the superposition of both is shown by thick black line.

At instant A, both the waves are in the same phase and hence resultant displacement will be maximum and intensity of sound will be highest. After small time difference B, both the waves will be in opposite phase and hence will deduct the effect of each other and will make zero displacement and zero sound. Again at instant C, both the waves will be in same phase with maximum displacement and loud sound. Similarly, according to time at any place sound will be maximum or minimum. Hence, we can say as conclusion;

“Superposition of two slightly different frequencies waves produce sometimes high or low intensity sounds, this harmonic cycle is called beats.”
Phase difference of two high intensity sounds or two low intensity sounds is called time of beat, meaning in this time one beat is produced.

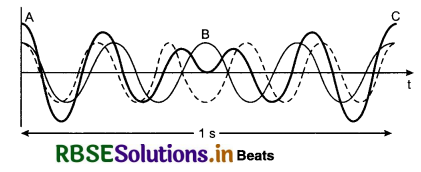
From the above figure one more conclusion is drawn that if first wave produces 5 vibrations in 1 second and second wave produces 4 vibrations in 1 second then in 1 second 1 beat is heard meaning frequency of beats is equal to the difference of the frequencies of two waves.

Question 16.
Draw the fundamental modes of vibration of a statioary waves in (i) Closed pipe, (ii) An open pipe.
Answer:
Standing waves in air column is an example of longitudinal standing waves. When any source of sound is brought near the air column then there is generation of compression and rarefaction in the column. These waves are reflected from the other end of air column. By the superposition of incident waves and reflected waves longitudinal standing waves are produced. Air columns are of two types:

• If one end of the pipe is closed and the other is open, then it is called closed organ pipe and its air column is called closed air column.
• If both the ends of the pipe are open, it is called open organ pipe or open air column.

To know about the modes of vibration in an air column, following facts have to be known:

• At the closed end of the pipe the air particles cannot vibrate hence this end should have node.
• The open end of the pipe is in contact of the atmosphere hence the change in density at this end should be zero or we can say that the strain here should be zero and there should be antinode at the open end.
• There should be an antinode between two nodes and a node between two antinodes.

Question 17.
What is Doppler effect in sound? Obtain an expression for the observed frequency of sound produced by a source when both the observer and the source are in motion and medium is at rest.
Answer:
Doppler effect is a common phenomenon that we observe in our everyday lives. For instance, if you are standing on the footpath, you hear a police vehicle approaching in the distance. First, the sound of the siren is faint and it gets louder as the vehicle reaches closer to you. Once the police car crosses you and goes ahead the sound gradually decreases again. This effect is basically known as the Doppler effect.

Generally, the doppler effect can be defined as the change in wave frequency (whether it is light or sound) during relative motion between the source of the wave and the observer. This effect can be observed every time a source wave is moving in relation to the observer. The Doppler effect was discovered in the year 1842 by an Austrian mathematician and physicist named Christian Johann Doppler. The effect was named after him.

When the source and observer are moving relative to each other, the frequency observed by the observer (f_a) is different from the actual frequency produced by the source (f₀). This is basically the definition of the Doppler effect in Physics. Here, when the source of waves is moving towards the observer they will have an upward shift in frequency. As for the observers from whom the source is receding, there will be a downward shift in frequency.

However, it should be noted that the effect does not occur as a result of the actual change in the frequency of the wave source. The Doppler effect can be observed in both sound waves and light waves. While we have already described the effect in sound waves, the following is an example of the Doppler effect for light waves.

If we observe the light of a star from earth it usually shifts toward the red end of the spectrum (lower frequency or longer wavelength) when the earth and star are moving away from each other. This is also known as red-shift. On the other hand, it tends to move toward the violet side (higher frequency or shorter wavelength) if both earth and the star are coming close to each other. This is also called the blue shift. As a result of this phenomenon, the doppler effect is used in studying the motion of stars. It is also an integral part of modern theories of the universe.

The main reason that we experience the Doppler effect is that as the wave source moves toward the observer, each new wave crest that is formed from the source is emitted from a location that is closer to the observer. Therefore, as the source moves closer and closer the waves will now take less time to reach the observer or the time between the arrivals of new wave crests is reduced. This further causes an increase in frequency. Similarly, when the source of waves is going away, the waves are emitted from a farther location thus increasing the arrival time between each new wave. This leads to a reduction in frequency.

Nonetheless, from what we have learnt above, we can summarize that the Doppler effect could result from several factors such as;
the motion of the observer
the motion of the source
the motion of the medium.
This is mainly true for sound waves. Whereas, for waves that can travel in any medium, such as light, we need to consider only the relative difference in velocity between the source and the observer.

Question 18.
What is a plane progressive harmonic wave? Establish displacement relation for a harmonic wave travelling along the positive direction of X-axis.
Answer:
When in any medium the wave propagates then the medium particle vibrates and this vibrational motion is called simple harmonic motion. Medium particles vibrate in same or different phases. Suppose a wave is moving as shown in diagram from point O to the right hand side.

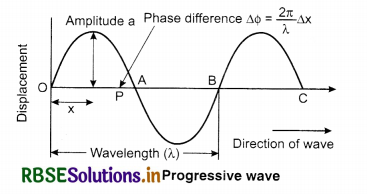
Particles on the right hand side of O are disturbed after sorne time hence due to this their motion is lagging. Displacement equation for a particle at point P which is at a distance x from origin O is;
y = a sin (ωt - Φ) ..........................(15.7)
Here, Φ is the phase difference between particles at O and P. Since, point P is at a distance x from O and the phase difference between particles at distance λ is 2π.
Hence, phase difference between the particles at distance x is
Φ = \(\frac{2 \pi}{\lambda}\) x (x) .......................(15.8)
Putting the value of Φ in equation (15.7)

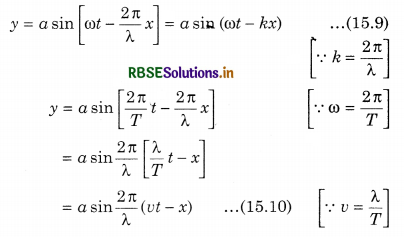
Equations (15.9) and (15.10) represent progressive wave equation in the positive x direction. Similarly, progressive wave equation in negative
x direction will be given by: y = a sin (ωt + kx).
Again from equation (15.9)
y = asin (ωt - kx)
Differentiating the above equation with respect to time;
v = \(\frac{d y}{d t}\) = ω a cos (ωt - kx) .............................(15.11)
This is the expression for velocity of the particle. Hence, it is clear that the velocity of the particle is different from wave velocity. Velocity of the particle is dependent on time (t) and position (x) of the particle, whereas wave velocity is constant. From equation (15.11) the maximum value of the velocity of a particle is ωa.
Again differentiating equation (15.11) with respect to time:
\(\frac{d v}{d t}=\frac{d^2 y}{d t^2}=-\omega^2 a \sin (\omega t-k x)\)
or a = \(\frac{d^2 y}{d t^2}\) = -ω² y ..............................(15.12)
Here, a = \(\frac{d^2 y}{d t^2}\) is the acceleration of the particle. Equation (15.12) shows that the acceleration of a particle is directly proportional to displacement and is in opposite direction. This is the necessary condition of simple harmonic motion. Differentiating equation (15.9) twice relative to position (x)
\(\frac{d^2 y}{d x^2}\) = -k² a sin (ωt - kx) = -k² y .................................(15.13)
From equations, (15.12) and (15.13)

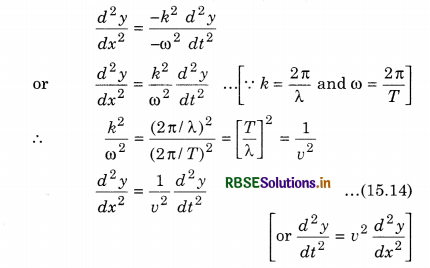
Equation (15.14) is called one dimensional differential equation of the wave.

Question 19.
What is a progressive wave? Derive an expression which represents a progressive wave.
Answer:
When in any medium the wave propagates then the medium particle vibrates and this vibrational motion is called simple harmonic motion. Medium particles vibrate in same or different phases. Suppose a wave is moving as shown in diagram from point O to the right hand side.

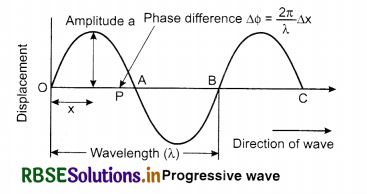
Particles on the right hand side of O are disturbed after sorne time hence due to this their motion is lagging. Displacement equation for a particle at point P which is at a distance x from origin O is;
y = a sin (ωt - Φ) ..........................(15.7)
Here, Φ is the phase difference between particles at O and P. Since, point P is at a distance x from O and the phase difference between particles at distance λ is 2π.
Hence, phase difference between the particles at distance x is
Φ = \(\frac{2 \pi}{\lambda}\) x (x) .......................(15.8)
Putting the value of Φ in equation (15.7)

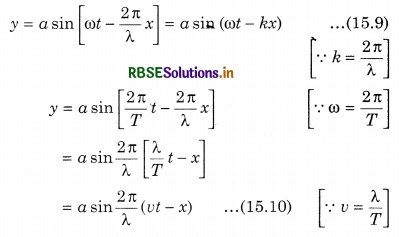
Equations (15.9) and (15.10) represent progressive wave equation in the positive x direction. Similarly, progressive wave equation in negative
x direction will be given by: y = a sin (ωt + kx).
Again from equation (15.9)
y = asin (ωt - kx)
Differentiating the above equation with respect to time;
v = \(\frac{d y}{d t}\) = ω a cos (ωt - kx) .............................(15.11)
This is the expression for velocity of the particle. Hence, it is clear that the velocity of the particle is different from wave velocity. Velocity of the particle is dependent on time (t) and position (x) of the particle, whereas wave velocity is constant. From equation (15.11) the maximum value of the velocity of a particle is ωa.
Again differentiating equation (15.11) with respect to time:
\(\frac{d v}{d t}=\frac{d^2 y}{d t^2}=-\omega^2 a \sin (\omega t-k x)\)
or a = \(\frac{d^2 y}{d t^2}\) = -ω² y ..............................(15.12)
Here, a = \(\frac{d^2 y}{d t^2}\) is the acceleration of the particle. Equation (15.12) shows that the acceleration of a particle is directly proportional to displacement and is in opposite direction. This is the necessary condition of simple harmonic motion. Differentiating equation (15.9) twice relative to position (x)
\(\frac{d^2 y}{d x^2}\) = -k² a sin (ωt - kx) = -k² y .................................(15.13)
From equations, (15.12) and (15.13)

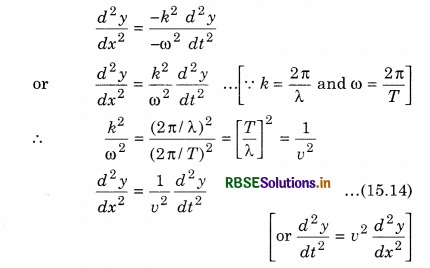
Equation (15.14) is called one dimensional differential equation of the wave.

Question 20.
Describe a simple experiment for showing the formation of beats.
Answer:
When in any medium the wave propagates then the medium particle vibrates and this vibrational motion is called simple harmonic motion. Medium particles vibrate in same or different phases. Suppose a wave is moving as shown in diagram from point O to the right hand side.

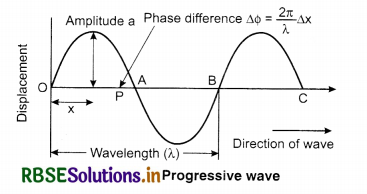
Particles on the right hand side of O are disturbed after sorne time hence due to this their motion is lagging. Displacement equation for a particle at point P which is at a distance x from origin O is;
y = a sin (ωt - Φ) ..........................(15.7)
Here, Φ is the phase difference between particles at O and P. Since, point P is at a distance x from O and the phase difference between particles at distance λ is 2π.
Hence, phase difference between the particles at distance x is
Φ = \(\frac{2 \pi}{\lambda}\) x (x) .......................(15.8)
Putting the value of Φ in equation (15.7)

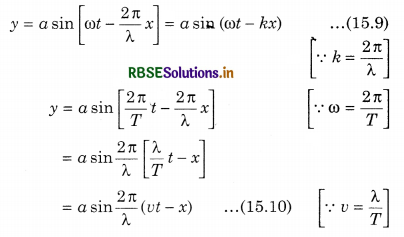
Equations (15.9) and (15.10) represent progressive wave equation in the positive x direction. Similarly, progressive wave equation in negative
x direction will be given by: y = a sin (ωt + kx).
Again from equation (15.9)
y = asin (ωt - kx)
Differentiating the above equation with respect to time;
v = \(\frac{d y}{d t}\) = ω a cos (ωt - kx) .............................(15.11)
This is the expression for velocity of the particle. Hence, it is clear that the velocity of the particle is different from wave velocity. Velocity of the particle is dependent on time (t) and position (x) of the particle, whereas wave velocity is constant. From equation (15.11) the maximum value of the velocity of a particle is ωa.
Again differentiating equation (15.11) with respect to time:
\(\frac{d v}{d t}=\frac{d^2 y}{d t^2}=-\omega^2 a \sin (\omega t-k x)\)
or a = \(\frac{d^2 y}{d t^2}\) = -ω² y ..............................(15.12)
Here, a = \(\frac{d^2 y}{d t^2}\) is the acceleration of the particle. Equation (15.12) shows that the acceleration of a particle is directly proportional to displacement and is in opposite direction. This is the necessary condition of simple harmonic motion. Differentiating equation (15.9) twice relative to position (x)
\(\frac{d^2 y}{d x^2}\) = -k² a sin (ωt - kx) = -k² y .................................(15.13)
From equations, (15.12) and (15.13)

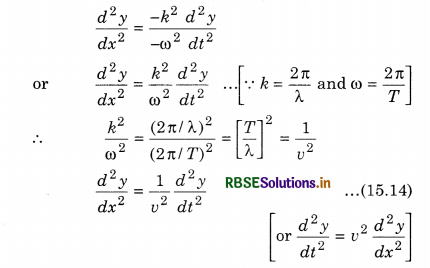
Equation (15.14) is called one dimensional differential equation of the wave.

Numerical Problems

Based on Wavelength and Wave Motion

Question 1.
The frequency of a radio transmission centre is 60 MHz. Find out the wavelength produced from the centre. (Speed of light = 3 x 10⁸ m s^-1)
Solution:
Given: v = 60 MHz = 60 x 10⁶ Hz;
c = 3 x 10⁸ ms^-1; λ = ?
∵ c = vλ ⇒ λ = \(\frac{c}{v}\)
or λ = \(\frac{3 \times 10^8}{6 \times 10^7}=\frac{1}{2}\) x 10 = 5 m
λ = 5 m

Question 2.
On standing near the sea-shore a man sees that in 1 minute 70 waves reach at the shore. If the wavelength is 12 m, then find out their velocity.
Solution:
Given: Frequency v = \(\frac{70}{60}=\frac{7}{6}\) Hz; λ = 12 m
v = ?
∵ v = nλ
∴ v = \(\frac{7}{6}\) x 12 = 14 m s^-1
or v = 14 ms^-1

Question 3.
The distance between two crests in sea waves is 12 m and if per minute 20 crests are produced, then find out the wave velocity.
Solution:
Given: λ = distance between two crest = 12 m;
Frequency v = \(\frac{20}{60}\) = \(\frac{1}{3}\) Hz; v = ?
∵ v = nλ
∴ v = \(\frac{1}{3}\) x 12 = 4 ms^-1

Speed of Wave In a Stretched String

Question 4.
The mass of 4.0 m long wire is 0.1 kg. It is pulled by a force of 400 N. Determine the speed of wave in the wire.
Solution:
m = \(\frac{M}{L}=\frac{0.01}{4}=\frac{1}{400}\) kg m^-1; T = 400 N; v = ?
∵ v = \(\sqrt{\frac{T}{m}}\)
∴ v = \(\sqrt{\frac{400}{1 / 400}}=\sqrt{400 \times 400}\)
or v = 400 m s^-1

Based on Speed of Mechanical Waves

Question 5.
The Young’s modulus for steel is 2.9 x 10¹¹ N m^-2 and density is 8 x 10³ kg m^-3. Find out speed of the longitudinal waves in steel.
Solution:
Given: Y = 2.9 x 10¹¹ N m²; ρ = 8 x 10³ kg m^-3; v = ?

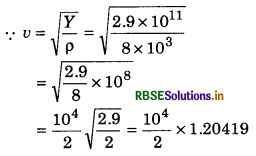
= 6020.8
= 6.02 x 10³ ms^-1

Question 6.
At 10⁵ N m^-2 atmospheric pressure, the density of air is 1.29 kg m^-3. If for air (γ = 1.41), then determine the speed of sound in air.
Solution:
Given: P = 10⁵ N m^-2; ρ = 1.29 kg m^-3; γ = 1.41; v = ?
∵ v = \(\sqrt{\frac{\gamma P}{\rho}}=\sqrt{\frac{1.41 \times 10^5}{1.29}}\)
= 10²\(\sqrt{\frac{14.1}{1.29}}\) = 10² \(\sqrt{10.93}\)
= 10² x 3.306
= 330.6 m s^-1

Question 7.
Speed of sound in water is 1346 ms^-1 and density of water is 1.0 x 10³ kg m^-3. Determine the bulk modulus of water.
Solution:
v = 1346m s^-1; ρ = 1.0 x 10³ kg m^-3; ß = ?
∵ v = \(\sqrt{\frac{\beta}{\rho}}\) ⇒ v² = \(\frac{\beta}{\rho}\) = ß = v².ρ
∴ ß = (1346)² x 1.0 x 10³ = (1.346)² x 10⁶ x 10³
or ß = 1.81 x 10⁹ N m^-2

Question 8.
Volumetric strain of water is 5 x 10^-5 at 10 N m^-2 pressure. If density of water is 1 x 10³ kg m^-3, then determine the speed of sound in water.
Solution:
P = 10⁵ N m^-2;
Volumetric strain = 5 x 10⁵; ρ = 1 x 10³ kg m^-3; v = ?
Bulk modulus of the water
ß = \(\frac{\text { Volume stress }}{\text { Volumetric strain }}=\frac{10^5}{5 \times 10^{-5}}\) = 0.2 x 1010
= 2 x 10⁹ N m^-2
∴ v = \(\sqrt{\frac{\beta}{\rho}}=\sqrt{\frac{2 \times 10^9}{10^3}}=\sqrt{2 \times 10^6}\)
= 1.4142 x 10³
= 1414.2 ms^-1

Based on Speed of Sound in Gases

Question 9.
Speed of sound is 330 ms^-1 at 0°C. At which temperature the speed of sound will be 495 m s^-1?
Solution:
v₀ = 330 m s^-1; v_t = 495 m s^-1; t = ?

Question 10.
At 0°C and 1092 K temperature determine the ratio of speeds of sound.
Solution:
\(\frac{v_1}{v_2}=\sqrt{\frac{T_1}{T_2}}=\sqrt{\frac{273+0}{273+1092}}=\sqrt{\frac{273}{4 \times 273}}=\sqrt{\frac{1}{4}}=\frac{1}{2}\)
or v₁:v₂ = 1:2

Question 11.
At which temperature the speed of sound at 25°C in air becomes 1.6 times the speed of sound in air?
Solution:

or 273 + t = 2.56 x 298 = 762.88
∴ t = 762.88 - 273
or t = 489.88 = 489.9°C

Question 12.
At which temperature the speed of sound in oxygen will be same as the speed of sound in nitrogen at 28°C? The molecular weight of oxygen and nitrogen are 32 and 28 respectively.
Solution:
(v_t)_O2 = (v₂₈)_N2

∴ t = 344 - 273
or t = 71°C

Based on Progressive Waves

Question 13.
The equation of a wave is y = 0.5 sinπ (100x - 3t). y and x are in metre and t is in second. Find out propagation speed of this wave.
Solution:
Given: y = 0.5 sinπ (0.01x - 3t)
or y = -0.5 sinπ (3t - 0.01x)
or y = -0.5 sinπ x 0.01 (\(\frac{3}{0.01}\)t - x)
or y = -0.5 sin\(\frac{2 \pi}{200}\) (300t - x)
Standard equation y = a sin\(\frac{2 \pi}{\lambda}\) (vt - x)
On comparing v = 300 m s^-1

Question 14.
Determine wavelength from this equation y = 0.4sin (120πt - \(\frac{4 \pi}{5}\)x), where distance are in m and time in second.
Solution:
Given: y = 0.4 sin (120πt - \(\frac{4 \pi x}{5}\))
but y = a sin (ωt - kx)
On comparing
k = \(\frac{4 \pi}{5} \Rightarrow \frac{2 \pi}{\lambda}=\frac{4 \pi}{5}\)
∴ λ = \(\frac{2 \times 5}{4}\) = 2.5 m

Question 15.
The amplitude of a progressive wave is 0.05 m, speed 330 ms^-1 and frequency is 110 Hz. Write the equation of this wave.
Solution:
Given: a = 0.05 m; v = 330 ms^-1; v = 110 Hz
∴ λ = \(\frac{v}{v}=\frac{330}{110}\) = 3 m
∴ Equation of progessive wave

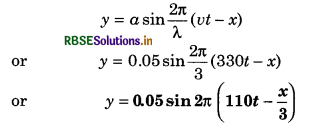
Question 16.
The distance between two particles of a medium is 5 cm. If the phase difference between them is \(\frac{\pi}{3}\), then find out the wavelength.
Solution:
∆x = 5 cm; ∆Φ = \(\frac{\pi}{3}\); λ = ?
∵ Phase difference due to path difference
∆Φ = \(\frac{2 \pi}{\lambda} \cdot \Delta x\)
\(\frac{\pi}{3}=\frac{2 \pi}{\lambda} \times 5 \mathrm{~cm} \Rightarrow \frac{1}{3}=\frac{10}{\lambda}\)
∴ λ = 30 cm = 0.30 m

Question 17.
The equation of a plane progressive wave is y = 0.04sin (157t - 3.14x), where x, y distance are in m, t in second. Determine the wave-amplitude, frequency and wave length. In the same way, the equation of another wave is y'= 0.30 sin (157t - 3.14x + 3.14). Then find out the phase difference between both the waves.
Solution:
y = 0.04 sin (157t - 3.14x) ......................(1)
y' = 0.30 sin (157t - 3.14x + 3.14) ............................(2)
From equation (1)
y = 0.04 sin3.14(\(\frac{157}{3.14}\)t - x)
or y = 0.04 sin\(\frac{2 \pi}{2}\)(50t - x)
Comparing this equation with y = a sin\(\frac{2 \pi}{\lambda}\)(vt - x)
Amplitude a = 0.04 m
Wavelength λ = 2 m
Velocity v = 50 m s^-1
∴ Frequency n = \(\frac{v}{\lambda}=\frac{50}{2}\) = 25 Hz
Φ₁ = (157t - 3.14x)
Φ₂ = (157t - 3.14x + 3.14)
∴ Phase difference
∆Φ = Φ₁ - Φ₂ = 157t - 3.14x + 3.14 - 157t + 3.14x
or ∆Φ = 3.14 = π rad = 180°

Question 18.
The ratio of amplitude of two waves is 2 : 3. Find out the ratio of their intensities.
Solution:
Given: \(\frac{a_1}{a_2}=\frac{2}{3}\)
∵ Intensity I ∝ a²
∴ \(\frac{I_1}{I_2}=\left(\frac{a_1}{a_2}\right)^2=\left(\frac{2}{3}\right)^2=\frac{4}{9}\)
or I₁:I₂ = 4:9

Question 19.
The equation of a plane progressive wave is y = 0.4sin8π (t - \(\frac{x}{20}\)). If wave is reflected from a surface, and its amplitude remains half of previous value, then determine the equation of the reflected wave if (i) it is reflected from a rigid plane, (ii) free plane.
Solution:
Incident wave y = 0.4 sin8π(t - \(\frac{x}{20}\))
(i) From rigid surface path difference of π will be produced. Amplitude of the reflected wave
a' = \(\frac{a}{2}=\frac{0.4}{2}\) = 0.2
∴ Equation of the reflected wave

Question 20.
The equation of a standing wave is y = 12 cos\(\frac{\pi x}{5}\) sin20πt, where x and y are in cm and 5 t is in second. Determine:
(i) Wavelength and frequency of progressive wave.
(ii) Velocity and amplitude.
Solution:
(i) Given: y = 12 cos\(\frac{\pi x}{5}\) sin 20πt
Standard equation y = 2 a cos\(\frac{2 \pi x}{\lambda}\) sin 2πnt
On comparing
\(\frac{2 \pi x}{\lambda}=\frac{\pi x}{5} \Rightarrow \frac{2}{\lambda}=\frac{1}{5}\)
or Wavelength λ = 10 cm
2πv = 20π ⇒ v = 10 Hz
∴ Frequency v = 10 Hz

(ii) Amplitude 2a = 12 ⇒ a = 6 cm
or a = 6 cm
Wave velocity v = vλ = 10 x 10 = 100 cm s^-1

Question 21.
The equation of a standing wave in a closed organ pipe is 7cos \(\left(\frac{\pi x}{6}\right)\) sin (30πt), where x and y are in cm and t is in second. Find out the frequency of the progressive wave, which produce it, also find speed, amplitude and wavelength of the progressive wave.
Solution:
y = 7 cos(\(\frac{\pi x}{6}\)) sin(30πt)
Standard equation
y = 2a cos\(\frac{2 \pi x}{\lambda}\) sin2πnt
On comparing,
2a = 7 ⇒ a = 3.5 cm
\(\frac{2 \pi x}{\lambda}=\frac{\pi x}{6} \Rightarrow \frac{2}{\lambda}=\frac{1}{6}\) ⇒ λ = 12 cm
∴ Wavelength λ = 12 cm
2πv = 30π ⇒ v = 15 Hz
or frequency = 15 Hz
∴ v = vλ = 15 x 12 = 180 cm s^-1

Question 22.
The frequency of the fundametal tone of a closed tube is 200 Hz. Find out the frequency of the fundamental tone of an open pipe of the same length?
Solution:
Given: Fundamental frequency of the closed tube n = 200 Hz
Fundamental frequency of open pipe v' = ?
∵ v = \(\frac{v}{4 l}\) and v' = \(\frac{v}{2 l} \)
∴ v = \(\frac{1}{2} v \frac{v}{2 l}=\frac{1}{2} \cdot v^{\prime}\)
∴ v' = 2n = 2 x 200 = 400 Hz
∴ v' = 400 Hz

Question 23.
The frequency of the fundamental overtone of a closed organ pipe and frequency of the fundamental overtone of an open pipe are equal. Determine the ratio of their lengths.
Solution:
Frequency of fundamental overtone of a closed pipe = Frequency of the fundamental overtone of an open pipe
\(\frac{v}{4 l_1}=\frac{v}{2 l_2}\)
∴ \(\frac{l_1}{l_2}=\frac{1}{2}\)

Question 24.
Two tuning forks A and B when vibrating together produce 8 beats per second. A resonates with a 32 cm long closed organ pipe while B resonates with a 33 cm long closed organ pipe. Find out the frequencies of the tuning forks.
Solution:

Question 25.
A tuning fork of frequency 341 Hz is vibrated on a tube of 1 m length. Water is slowly adding to tube. What height of water will be necessary for resonance?
Solution:
v = 341 m s^-1; v = 341 Hz
∴ λ = \(\frac{v}{v}=\frac{341}{341}\) = 1 m = 100 cm
Length of resonance from upper side
l₁ = \(\frac{\lambda}{4}=\frac{100}{4}\) = 25 cm
Length of second resonance
l₂ = \(\frac{3}{4} \lambda=\frac{3}{4} \times 100\) = 75 cm
So, positions of resonance
= 75 cm, 25 cm

Question 26.
100 cm long glass tube is filled with water in vertical position. The water exit from the lower side of the tube. If a tuning fork of 495 Hz is vibrated over the tube. Then at 0°C, on which layer, resonance will occur? At 0°C, the speed of sound in air is 330 ms^-1.
Solution:
v = 330 m s^-1; v = 495 Hz
∴ λ = \(\frac{v}{v}=\frac{330}{495}=\frac{30}{45}=\frac{2}{3} \mathrm{~m}=\frac{200}{3} \mathrm{~cm}\)
∴ Length of first resonance l₁ = \(\frac{\lambda}{4}=\frac{200}{4 \times 3}=\frac{50}{3}\)
= 16\(\frac{2}{3}\) cm
Length of second resonance
l₂ = \(\frac{3}{4}\) x λ = 3.\(\frac{\lambda}{4}\) = 3 x \(\frac{50}{3}\)
= 50 cm
Length of third resonance
l₃ = \(\frac{5}{4}\)λ = 5.\(\frac{50}{3}\) = \(\frac{250}{3}\) = 83\(\frac{1}{3}\) cm

Question 27.
The fundamental frequency of a stretched string is 500 Hz. If tension becomes 4 times, then determine its fundamental frequency.
Solution:
Fundamental frequency n = 500Hz; Tension = T
v' = ?; Tension = 4T
∵ v = \(\frac{1}{2 l} \sqrt{\frac{T}{m}}\); ∴ v ∝ \(\sqrt{T}\)
∴ \(\frac{\mathrm{v}^{\prime}}{\mathrm{v}}=\sqrt{\frac{T^{\prime}}{T}}=\sqrt{\frac{4 T}{T}}\) = 2
∴ v' = 2 x n = 2 x 500 = 1000 Hz
or v' = 1000 Hz

Question 28.
Two strings of same length are equally stretched by the same tension. Strings are made of the same material. If ratio of their diameter is 3 : 2, then determine, the ratio of their fundamental frequencies.
Solution:

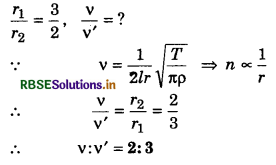
Question 29.
A stretched string loaded with 2.5 kg weight has a longitudinal wave velocity equal to 340 m s^-1. If tension in the string becomes 3.6 kg weight, then find the speed of the longitudinal wave.
Solution:
M₁ = 2.5 kg; v₁ = 340 m s^-1;
M₂ = 3.6 kg; v₂ = ?

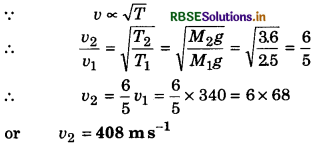
Question 30.
Two wires are similar and they are in the same tone. When there is increase of 1% in the tension of one wire, then on sounding both at the same time, 3 beats are heard in 2 s. Find the initial frequency of both the wire.
Solution:
Beat frequency = \(\frac{3}{2}\) per second

Based on Beats

Question 31.
When two tuning forks are sound together the sound of maximum intensity is heard at time interval of 2 second. Find out the difference in the frequencies of tuning forks.
Solution:
Beats T = 0.2 s
∴ Beat frequency v₂ - v₁ = \(\frac{1}{T}=\frac{1}{0.2}\) = 5
v₂ - v₁ = 5 Hz
v₂ = 260 Hz

Question 32.
If frequencies of two tuning forks are 256 and 260 Hz respectively, then how much beats will be heard in 3 s?
Solution:
v₁ = 256 Hz;
∴ Beat frequency
v = v₁ ~ v₂ = 260 ~ 260 = 4 per second
∴ Number of beats in 3 seconds
= 3v = 3 x 4 = 12 beats

Question 33.
Two tuning forks when sounded together produce 4 beats per second. The frequency of one tuning fork is 256 Hz. When some wax is loaded on the arm of the second tuning fork, then 6 beats per second are produced. Find out the frequency of the second tuning fork.
Solution:
v₁ = 256 Hz; b = 4 beat/second
On loading wax on arm of the second tuning fork
v₂ = ?
we consider v₂ = 200 Hz, then after loading with wax, its frequency will be little less than 260 Hz. So with the first tuning fork the beat frequency will decrease, which is according to the question.
∴ v₂ ≠ 260 Hz
∴ v₂ = 252 Hz

Question 34.
16 tuning forks are arranged in ascending form of frequencies. Each tuning fork produce 2 beats per second with its previous tuning fork. If the frequency of last tuning fork is 3 times of the first, then find out the frequency of the first tuning fork.
Solution:
v, (v + 2 x 1), (v + 2 x 2), ........................, (v + 2 x 15)
Given: Frequency of the last tuning fork
= 3 x frequency of the first tuning fork
or (v + 2 x 15) = 3v
or v + 30 = 3v
or 3v - v = 3 ⇒ 2v = 30
∴ v = \(\frac{30}{2}\) = 15 Hz

Based on Doppler Effect

Question 35.
A motor car is going towards crossing with a velocity 72 km h^-1. A policeman standing on crossing hear the frequency of sound of horn as 260 Hz.    ,
Find out real frequency of horn. (Speed of sound = 332 m s^-1)
Solution:
v_s = 72 km h^-1 = 72 x \(\frac{5}{18}\) = 20 m s^-1; v = 332 m s^-1
v' = 260 Hz; n = ?
∵ Source is approaching towards the observer

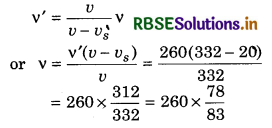
= 244.33
or v ≃ 244 Hz

Question 36.
A railway engine passing through a still observer with a speed of 60 m s^-1. The original frequency of the whistle of engine is 400 Hz. Determine apparent frequency: (i) When engine is going towards observer, (ii) When engine is going away from observer. (v = 330 ms^-1)
Solution:
v_s = 60 m s^-1; v = 400 Hz; v' = ?; v = 330 m s^-1

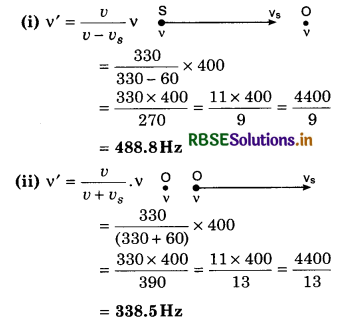
Question 37.
An observer is coming towards a still source of sound of frequency 90 Hz with a velocity of 33 m s^-1. Determine the frequency heard by the observer. (Speed of sound = 330 m s^-1)
Solution:
v₀ = 33m s^-1; v = 90 Hz; v = 330m s^-1; v' = ?
∵ The observer is coming towards the still sound source, so apparent frequency
v' = \(\frac{v+v_0}{v} \cdot \mathrm{v}=\frac{330+33}{333} \times 90=\frac{363}{333} \times 90\)
= \(\frac{121}{111} \times 90=\frac{10890}{111}\) = 98.11 Hz ≈ 99 Hz

Question 38.
With how much velocity should an observer approach towards a still sound source such that he hear twice the frequency of the original frequency. (Speed of sound = 330 m s^-1)
Solution:
v₀ = ?; v' = 2n; v = 330m s^-1
v' = \(\frac{v+v_0}{v} \cdot v\) ⇒ 2v = \(\frac{v+v_0}{v} \cdot v\)
or 2 = \(\frac{v+v_0}{v}\) or v + v₀ = 2v
∴ v₀ = 2v - v
or v₀ = v = 330m s^-1

Question 39.
A railway engine whose velocity is 72 km/h blows a whistle. The frequency of the whistle is 600 Hz. If a man, who is travelling in another train hears the frequency of sound as 673 Hz. Then determine the velocity of the second train. (Speed of sound = 332 m s^-1)
Solution:
v_s = 72 km h^-1 = 72 x \(\frac{5}{18}\) = 20m s^-1; v = 600 Hz; v₀ = ?

or v₀ = 350 - v = 350 - 332 = 18m s^-1
or v₀ = 18m s^-1

Question 40.
The frequency of the whistle of a engine is 500 Hz. It is going towards a bridge with velocity 2 m s^-1. The sound of the whistle after reflection from the bridge/reaches back to the driver of the engine. What frequency will be heard by the driver? (Speed of sound in air = 330 m s^-1)
Solution:
v = 500 Hz; v_s = 2m s^-1; v₀ = 2m s^-1; v = 330m s^-1
The nature of the reflected sound from bridge will be same as the source and the observer are approaching towards each other.

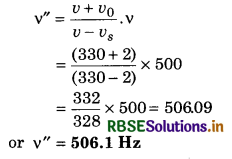
Questions for Competitive Examinations 

Objective Type Questions

Question 1.
The two nearest harmonics of a tube closed at one end and open at the other end are 220 Hz and 260 Hz. What is the fundamental frequency of the system?
(a) 20 Hz
(b) 30 Hz
(c) 40 Hz
(d) 10 Hz
Solution:
Difference between any two consecutive frequencies of a closed organ pipe
= \(\frac{2 v}{4 l}\) = 260 - 220 = 40 Hz
⇒ \(\frac{v}{4 l}\) = 20 Hz
So, fundamental frequency = 20 Hz

Question 2.
Two cars moving in the opposite directions approach each other with a speed of 22 m/s and 16.5 m/s respectively. The driver of the first car blows a horn having a frequency 400 Hz. The frequency heard by the driver of the second car is (velocity of sound 340 m/s):
(a) 361 Hz
(b) 411 Hz
(c) 448 Hz
(d) 350 Hz
Solution:

As we know for given condition
f_opp. = f₀(\(\frac{v+v_{\text {observer }}}{v-v_{\text {source }}}\))
= 400(\(\frac{340+16.5}{340-22}\))
f_opp. = 448 Hz

Question 3.
A siren emitting a sound of frequency 800 Hz moves away from an observer towards a cliff at a speed of 15 m s^-1. Then the frequency of sound that the observer hears in the echo reflected from the cliff is:
(Take velocity of sound in air = 330 m s-1)
(a) 800 Hz
(b) 838 Hz
(c) 885 Hz
(d) 765 Hz
Solution:

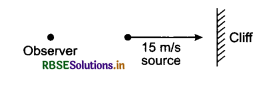
Frequency of sound that the observer hear in the echo reflected from the cliff is given by
f' = (\(\frac{v}{v-v_s}\))
So, f' = (\(\frac{330}{330-15}\)) x 800 = 838 Hz

Question 4.
An air column, closed at one end and open at the other, resonates with a tuning fork when the smallest length of the column is 50 cm. The next larger length of the column resonating with the same tuning fork is:
(a) 100 cm
(b) 150 cm
(c) 200 cm
(d) 667 cm
Solution:
The smallest length of the air column is associated with fundamental mode of vibration of the air column as shown in the diagram.

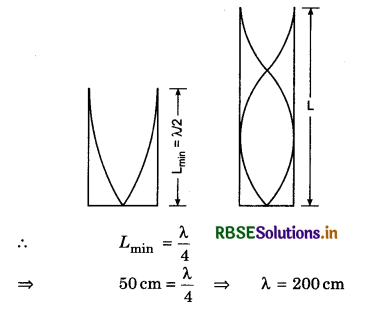
The next higher length of the air column is
L = \(\frac{\lambda}{4}+\frac{\lambda}{2}=\frac{\lambda+2 \lambda}{4}=\frac{3 \lambda}{4}\)
= \(\frac{3}{4}\) x 200 = 150 cm

Question 5.
A source of sound S emitting frequency 100 Hz and an observer O are located at some distance from each other. The source is moving with a speed of 19.4 m s^-1 at an angle of 60° with the source observer line as shown in the figure. The observer is at rest. The apparent frequency observed by the observer (velocity of sound in air is 330m s^-1) is:

(a) 100 Hz
(b) 103 Hz
(c) 106 Hz
(d) 97 Hz
Solution:

The apparent frequency heard by observer
f_o = f_s[\(\frac{v}{v-v_s \cos 60^{\circ}}\)] = 100[\(\frac{330}{330-19.4 \times \frac{1}{2}}\)]
= 100[\(\frac{330}{300-9.7}\)] = 100[\(\frac{300}{320.3}\)]
= 103.02 Hz

Question 6.
A string is stretched between fixed points separated by 75.0 cm. It is observed to have resonant frequencies of 420 Hz and 315 Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this string is:
(a) 155 Hz
(b) 205 Hz
(c) 10.5 Hz
(d) 105 Hz
Solution:
f₁ = \(\frac{n v}{2 l}\) and f₂ = \(\frac{(n+1)}{2 l}\)
⇒ f₂ - f₁ = 420 - 315
⇒ \(\frac{(n+1) v}{2 l}-\frac{n v}{2 l}\) = 105 Hz
⇒ \(\frac{v}{2 l}\) = 105 Hz
Thus, lowest resonant frequency of a string is 105 Hz.

Question 7.
The fundamental frequency of a closed organ pipe of length 20 cm is equal to the second overtone of an organ pipe at both the ends. The length of organ pipe open at both the ends is:
(a) 80 cm
(b) 100 cm
(c) 120 cm
(d) 140 cm
Solution:
v_c = \(\frac{v}{4 l}\), v₀ = \(\frac{v}{2 l}\)
Given the second overtone (i.e., third harmonic) of open pipe is equal to the fundamental frequency of closed pipe.
i.e., 3v₀ = v_c
⇒ \(\frac{3 v}{2 l^{\prime}}=\frac{v}{4 l}\)
⇒ l' = 6l = 6 x 20 = 120 cm

Question 8.
If n₁,n₂ and n₃ are the fundamental frequencies of three segments into which a string is divided, then the original fundamental frequency n of the string is given by:

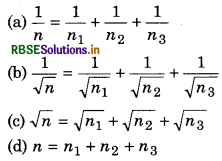
Solution:

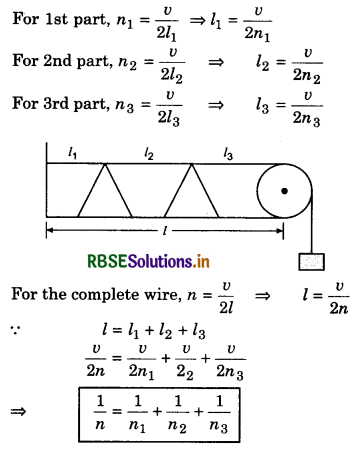
Question 9.
The number of possible natural oscillations of an air column in a pipe closed at one end of length 85 cm whose frequencies lie below 1250 Hz are (velocity of sound = 340 ms^-1):
(a) 4
(b) 5
(c) 7
(d) 6
Solution:
For a closed pipe at one end,
f_n = n(\(\frac{v}{4 l}\)), here n is an odd number
= n(\(\frac{340}{4 \times 85 \times 10^{-2}}\)) = n(100)
Here, n is an odd number, so for the given condition, n can go upto n = 11
i.e., n = 1, 3, 5, 7, 9, 11
So, number of possible natural oscillations could be 6, which are below 1250 Hz.

Question 10.
A speeding motorcyclist sees traffic jam ahead of him. He slows down to 36 km/h. He finds that the traffic has eased and a car moving ahead of him at 18 km/h horns at a frequency of 1392 Hz. If the speed of sound is 343 m/s, the frequency of the horn as heard by him will be:
(a) 1332 Hz
(b) 1372 Hz
(c) 1412 Hz
(d) 1454 Hz
Solution:

Here both the observer and the source are moving, we can use the formula of apparent frequency, as
f = f₀(\(\frac{v+v_0}{v+v_s}\)) = 1392 (\(\frac{343+10}{343+5}\))
= 1392 (\(\frac{353}{348}\)) = 1412 Hz

Question 11.
A wave travelling in the positive x-direction having displacement along y-direction as 1 m, wavelength 2π m and frequency of \(\frac{1}{\pi}\) Hz is
represented by:
(a) y = sin (x - 2t)
(b) y = sin (2πx - 2πt)
(c) y = sin (10πx - 20πt)
(d) y = sin (2πx + 2πd)
Solution:
y = a sin(ωt - kx)
= sin (\(\frac{2 \pi}{2 \pi} x-2 \pi \times \frac{1}{\pi} \)t)
= sin (x - 2t) [∵ a = 1 m]

Question 12.
If we study the vibration of a pipe open at both the ends, which of the following statements is not true?
(a) Open end will be antinode.
(b) Odd harmonics of the fundametal frequency will be generated.
(c) All harmonics of the fundamental frequency will be generated.
(d) Pressure change will be maximum at both the ends.
Solution:
At the open ends pressure change will be zero.

Question 13.
A source of unknown frequency gives 4 beat/second when sounded with a source of known frequency 250 Hz. The second harmonic of the source of the unknown frequency gives 5 beat/second when sounded with a source of frequency 513 Hz. The unknown frequency is:
(a) 254 Hz
(b) 246 Hz
(c) 240 Hz
(d) 260 Hz
Solution:
Given

Question 14.
When a string is divided into three segments of lengths l₁, l₂ and l₃, the fundamental frequencies of these three segments are v₁,v₂ and v₃ respectively. The original fundamental frequency (v) of the string is:

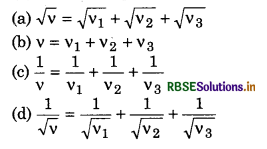
Solution:
∵ v = \(\frac{1}{2 l} \sqrt{\left(\frac{T}{m}\right)}\)
∴ n₁l₁ = n₂l₂ = n₃l₃ = k
∴ l₁ = \(\frac{k}{n_1}\), l₂ = \(\frac{k}{n_2}\) and l₃ = \(\frac{k}{n_3}\)
Original length, l = \(\frac{k}{v}\)
Here, l = l₁ + l₂ + l₃
\(\frac{k}{v}=\frac{k}{\mathrm{v}_1}+\frac{k}{\mathrm{v}_2}+\frac{k}{\mathrm{v}_3}\)
∴ \(\frac{1}{v}=\frac{1}{v_1}+\frac{1}{v_2}+\frac{1}{v_3}\)

Question 15.
Two sources of sound placed closed to each other, are emitting progressive waves given by y₁ = 4 sin 600 πt and y₂ = 5 sin 608πt. An observer located near these two sources of sound will hear:
(a) 4 beats/second with intensity ratio 25 : 16 between waxing and waning
(b) 8 beats/second with intensity ratio 25 : 16 between waxing and waning
(c) 8 beate/second with intensity ratio 81 : 1 between waxing and waning
(d) 4 beate/second witji intensity ratio 81:1 between waxing and waning
Solution:
y₁ = 4 sin 600πt
y₂ = 5 sin608πt
Comparing with the general equation
y = a sin 2πft
We get, f₁ = 300 Hz, f₂ = 304 Hz
So, number of beats = f₂ - f₁ = 4 s-1
We know that,
\(\frac{I_{\max }}{I_{\min }}=\left(\frac{a_1+a_2}{a_1-a_2}\right)^2\)
= \(\left(\frac{4+5}{4-5}\right)^2\) = 81

Question 16.
Two waves are represented by the equations y₁ = a sin (ωt + kx + 0.87) m and y₂ = a cos (ωt + kx) m, where x is in metre and t in second. The phase difference between them is:
(a) 1.25 rad
(b) 1.57 rad
(c) 0.57 rad
(d) 1 rad
Solution:
y₁ = a sin (ωt + kx + 0.57)
and y₂ = a cos (ωt + kx)
or y₂ = a sin (\(\frac{\pi}{2}+\omega t+k x\))
As, ∆Φ = Φ₂ - Φ₁
= \(\frac{\pi}{2}\) - 0.57
= 1.57 - 0.57
= 1 rad.

Question 17.
Sound waves travel at 350 m/s through warm air and at 3500 m/s through brass. The wavelength of a 700 Hz acoustic wave as it enters brass from warm air:
(a) increases by a factor 20
(b) increases by a factor 10
(c) decreases by a factor 20
(d) decreases by a factor 10
Solution:
Velocity of a wave is given by
v = vλ
For two different cases
v₁ = v₁λ₁
v₂ = v₂λ₂
λ₂ = \(\lambda_1 \frac{v_2}{v_1}=\lambda_1 \times \frac{3500}{350}=\lambda_1 \times 10\) [∵ v₁ = v₂]
λ₂ = 10 λ₁

Question 18.
An observer is moving with half the speed of light towards a stationary microwave source emitting waves at frequency 10 GHz. What is the frequency of the microwave measured by the observer?
(Speed of light = 3 x 10⁸ m s^-1)
(a) 12.1 GHz
(b) 17.3 GHz
(c) 15.3 GHz
(d) 10.1 GHz
Solution:
The relativistic Doppler formula is
v_observed = v_actual\(\sqrt{\left(\frac{1+\beta}{1-\beta}\right)}\)
where ß = _{\(\frac{v}{c}\)}
v is the relative velocity of the observer w.r.t the source and is taken to be positive if the observer and the source are moving towards each other, so
vobserved = (10 GHz) \(\sqrt{\frac{1+\frac{1}{2}}{1-\frac{1}{2}}}\) = 17.3 GHz

Question 19.
A uniform string of length 20 m is suspended from a rigid support. A short wave pulse is introduced at its lowest end. It starts moving up through the string. The time taken to reach the support is (take g = 10m s-2):
(a) 2 s
(b) 2\(\sqrt{2} \)s
(c) \(\sqrt{2}\) s
(d) 2π\(\sqrt{2}\) s
Solution:
Let mass per unit length be λ.

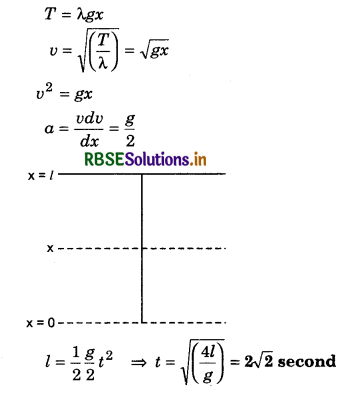
Question 20.
A pipe open at both the ends has fundamental frequency f in air. The pipe is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column is now:
(a) \(\frac{3 f}{4}\)
(b) 2f
(c) f
(d) \(\frac{f}{2}\)
Solution:
For an open pipe
f = \(\frac{v}{2 l}\)
For a closed organ pipe
f' = \(\frac{v}{4\left(\frac{l}{2}\right)}=\frac{v}{2 l}\) = f

Question 21.
A train is moving on a straight track with speed 20 m s^-1. It is blowing its whistle at the frequency of 1000 Hz. The percentage change in the frequency heard by a person standing near the track as the train passes him is (speed of sound = 320 m s^-1) close to:
(a) 12%
(b) 18%
(c) 24%
(d) 6%
Solution:

Question 22.
A pipe of length 85 cm is closed from one end. Find the number of possible natural oscillations of air column in the pipe whose frequencies lie below 1250 Hz.The velocity of sound in air is 340 m/s:
(a) 6
(b) 4
(c) 12
(d) 8
Solution:
In fundamental mode
\(\frac{\lambda}{4}\) = 0.85
λ = 4 x 0.85
f = \(\frac{v}{\lambda}=\frac{340}{4 \times 0.85}\) = 100 Hz
∴ Possible frequencies = 100 Hz, 300 Hz, 500 Hz, 700 Hz, 900 Hz, 1100 Hz, below 1250 Hz.

Question 23.
A sonometer wire of length 1.5 m is made of steel. The tension in it produces an elastic strain of 1%. What is the fundamental frequency of steel if density and elasticity of steel are 7.7 x 10³ kg/m³ and 2.2 x 10¹¹ N/m² respectively?
(a) 178.2 Hz
(b) 200.5 Hz
(c) 770 Hz
(d) 188.5 Hz
Solution:

Question 24.
A cylindrical tube, opened at both the ends, has fundamental frequency f, in air. The tube is dipped vertically in water so that half of it is in water. The fundametal frequency of the air column is now:
(a) f
(b) \(\frac{f}{2}\)
(c) \(\frac{3 f}{4}\)
(d) 2f
Solution:
f₀ = \(\frac{v}{2 l}\), f_c = \(\frac{v}{2 l}\)

Question 25.
The transverse displacement y (x, t) of a wave in a string is given by y (x, t) = e^{-(ax2 + bt2 + 2\(\sqrt{a b}\) x t)}. This represents a:
(a) Wave moving in -x direction with speed \(\sqrt{\left(\frac{b}{a}\right)}\)
(b) Standing wave of frequency \(\sqrt{b}\)
(c) Standing wave of frequency \(\frac{1}{\sqrt{b}}\)
(d) Wave moving in +x direction with \(\sqrt{\left(\frac{a}{b}\right)}\)
Solution:
y(x, t) = e^{-(\(\sqrt{a}\) x+\(\sqrt{b}\) t)2}
v = \(\frac{d y}{d t}=\sqrt{\left(\frac{b}{a}\right)}\)
The wave is moving in -ve x direction.

Question 26.
Two loudspeakers M and N are located 20 m apart and emit sound at frequencies 118 Hz and 121 Hz, respectively. A car is initially at a point P, 1800 m away from the midpoint Q of the line MN and moves towards Q constantly at 60 km/h along the perpendicular bisector of MN. It crosses Q and eventually reaches a point R 1800 m away from Q. Let v(t) represent the best frequency measured by a person sitting in the car at time t. Let v_P, v_Q and v_R be the beat frequencies measured at locations P, Q and R, respectively. The speed of sound in air is 330 ms^-1. Which of the following statement(s) is (are) true regarding the sound heard by the person:
(a) v_P + v_R = 2v_Q
(b) The rate of change in beat frequency is maximum when the car passes through Q
(c) The plot below represents schematically the variation of beat frequency with time

(d) The plot below represents schematically the variation of beat frequency with time

Solution:

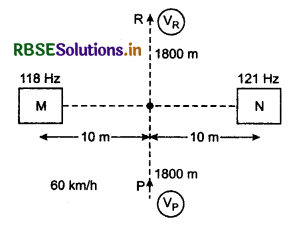
Apparent frequency of M and N at P

Apparent frequency of M, N at R

Question 27.
One end of a tight string of length 3 m along the x-axis is fixed at x = 0. The speed of the waves in the string is 100 m s^-1. The other end of the string is vibrating in the y-direction so that stationary waves are set up in the string. The possible waveform(s) of these stationary waves is (are):

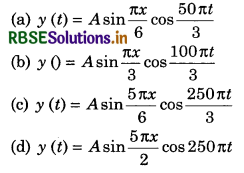
Solution:
There should be a node at x = 0 and an antinode at x = 3 m.
Also, v = \(\frac{\omega}{k}\) = 100 m/s

∴ y = 0 at x = 0
and y = ± A at x = 3 m
only (a), (c) and (d) satisfy the condition.

question 28.
A horizontal stretched string, fixed at two ends, is vibrating in its fifth harmonic according to the equation, y (x, t) = (0.01 m) [sin (62.8 m^-1) x] cos [(6.28 s^-1) t].
Assuming, π: = 3.14 the correct statement(s) is (are):
(a) The number of nodes is 5.
(b) The length of the string is 0.25 m.
(c) The maximum displacement of the mid-point of the string from its equilibrium position is 0.01 m.
(d) The fundamental frequency is 100 Hz.
Solution:

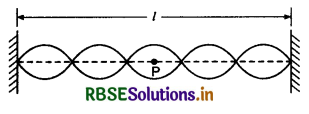
Number of nodes = 6
From the given equation, we can see that

The midpoint of the string is P, an antinode.
∴ Maximum displacement = 0.01 m
ω = 2πf = 628 s^-1
∴ f = \(\frac{628}{2 \pi}\) = 100 Hz
But this is the fifth harmonic frequency,
∴ Fundamental frequency f₀ = \(\frac{f}{5}\) = 20 Hz

Question 29.
A student is performing the experiment of a resonance column. The diameter of the column tube is 4 cm. The frequency of the tuning fork is 512 Hz. The air temperature is 38°C in which the speed of sound is 336 m/s. The zero of the meter scale coincides with the top end of the resonance column tube. When the first resonance occurs, the reading of the water level in the column is:
(a) 14.0 cm
(b) 15.2 cm
(c) 16.4 cm
(d) 17.6 cm
Solution:
With the end correction,
f = n[\(\frac{v}{4(l+e)}\)], (where n = 1, 3, .......................)
= n[\(\frac{v}{4(l+0.6 r)}\)]
Because, e = 0.6r, where r is the radius of the pipe.
For the first resonance, n = 1
∴ f = \(\frac{v}{4(l+0.6 r)}\)
or l = \(\frac{v}{4 f}-0.6 r=\left[\left(\frac{336 \times 100}{4 \times 512}\right)-0.6 \times 2\right] cm\)
= 15.2 cm

Question 30.
A hollow pipe of length 0.8 m is closed at one end. At its open end a 0.5 m long uniform string is vibrating in its second harmonic and it resonates with the fundamental frequency of the pipe. If the tension in the wire is 50 N and the speed of sound is 320 ms^-1, then mass of the string is:
(a) 5 g
(b) 10 g
(c) 20 g
(d) 40 g
Solution:

Given, 2nd harmonic of I = fundamental of II
∴ 2\(\left(\frac{v}{2 l_1}\right)=\frac{v_2}{4 l_2} \Rightarrow \frac{\sqrt{T / \mu}}{l_1}=\frac{v_2}{4 l_2}\)
⇒ µ = \(\frac{16 T l_2^2}{v_2^2 l_1^2}\)
= \(\frac{16 \times 50 \times(0.8)^2}{(320)^2 \times(0.5)^2}\)
= 0.02 kg/m
∴ m₁ = µl₁ = (0.02) (0.5)
= 0.01 kg = 10 g

Question 31.
A tuning fork is used to produce resonance in a glass tube. The length of the air column in this tube can be adjusted by a variable piston. At room temperature of 27°C two successive resonances are produced at 20 cm and 73 cm of column length. If the frequency of the tuning fork is 320 Hz, the velocity of sound in air at 27°C is.
(a) 330 ms^-1
(b) 339 ms^-1
(c) 350 ms^-1
(d) 300 ms^-1
Solution:

Question 32.
A turning fork with frequency 800 Hz produces resonance in a resonance column tube with upper end open and lower end closed by water surface. Successive resonances are observed at length 9.75 cm, 31.25 cm and 52.75 cm. The speed of sound in air is
(a) 500 m/s
(b) 156 m/s
(c) 344 m/s
(d) 172 m/s
Solution:
v = 800 Hz
v = 2v (l₂ - l₁)
l₁ = 9.75 cm, l₂ = 31.25 cm
∴ v = 2 x 800 (31.25 - 9.75)
= 344 m/s