RBSE Class 11 Physics Important Questions Chapter 14 Oscillations

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 14 Oscillations Important Questions and Answers.

RBSE Class 11 Physics Chapter 14 Important Questions Oscillations

Other Important Questions 

Question 1.
If a spring has time period T, and is cut into n equal parts, then the time period will be.
(a) T\(\sqrt{n}\)
(b) T
(c) T/\(\sqrt{n}\)
(d) nT
Answer:
(a) T\(\sqrt{n}\)

Question 2.
When the displacement is one-half the amplitude in SHM, the fraction of the total energy that is potential.
(a) 1/4
(b) 1/ 2
(c) 1/8
(d) 3/4
Answer:
(a) 1/4

Question 3.
In a simple harmonic oscillator, at mean position.
(a) Kinetic energy is minimum, potential energy is maximum
(b) Kinetic energy is maximum, potential energy is minimum.
(c) Both kinetic and potential energies are minimum
(d) Both kinetic and potential anergies are maximum
Answer:
(b) Kinetic energy is maximum, potential energy is minimum.

Question 4.
The mass and radius of a planed are twice that of earth. Then, period of oscillation of a second pendulum on that planet will be
(a) 1/\(\sqrt{2}\) second
(b) \(\sqrt{2}\) second
(c) 2 second
(d) 1/2 second
Answer:
(b) \(\sqrt{2}\) second

Question 5.
The length of a simple pendulum executing simple harmonic motion is increased by 21%. The percentage increase in the time period of the pendulum of increased length is:
(a) 10%
(b) 11%
(c) 21%
(d) 42%
Answer:
(a) 10%

Question 6.
Two particles A and B of equal masses are suspended from two massless spring of spring constant k₁ and k₂ respectively. If the maximum velocities, during oscillation, are equal, the ratio of amplitudes of A and B is:
(a) k₁/k₂
(b) \(\sqrt{k_1 / k_2}\)
(C) k₂/k₁
(d) \(\sqrt{k_2 / k_1}\)
Answer:
(d) \(\sqrt{k_2 / k_1}\)

Question 7.
The equation of motion of a simple harmonic oscillation is

Answer:
(a) \(\frac{d^2 x}{d t^2}=-\omega^2 x\)

Question 8.
The total energy of particle, exceuting simple harmonic motion is
(a) ax
(b) ax²
(c) independent of x
(d) ax^1/2
Answer:
(b) ax²

Question 9.
A simple pendulum has time period T. The bob is given negative charge and surface below it is given positive charge. The new time period will be.
(a) Less than T
(b) greater than T
(c) Equation to T
(d) Infinite
Answer:
(a) Less than T

Question 10.
In simple harmonic motion maximum velocity is at
(a) extreme position
(b) half of extreme position
(c) equilibrium position
(d) between extreme and equilibrium position
Answer:
(c) equilibrium position

Fill in the Blanks 

Question 1.
The frequency of total energy of a particle in S.H.M. is ........................
Answer:
Zero

Question 2.
The acceleration in S.H.M. is always in ........................ to that of displacement.
Answer:
opposite phase

Question 3.
The motion which do not repeat with time are called ........................ motion.
Answer:
non-repetitive

Question 4.
Two simple harmonic motions are represented by y₁ = 4 sin(4πt + π/2) and y₃ = 3cos4πt. The resultant amplitude is ........................
Answer:
7

Question 5.
The tension in the string of a simple pendulum is ........................
Answer:
Variable

Very Short Answer Questions

Question 1.
Write displacement equation of a simple harmonic motion.
Answer:
Displacement equation
y = a sinω₀t
If initial phase of the particle is Φ, then
y = asin(ω₀t + Φ)

Question 2.
For a particle executing simple harmonic motion, write the formula for velocity and acceleration of the particle in terms of displacement of the particle.
Answer:
Velocity of the particle
v = ω₀\(\sqrt{a^2-y^2}\)
and acceleration a = -ω₀²y
where y is displacement, a amplitude and ω₀ is angular frequency.

Question 3.
Write the formula for periodic time of a particle executing simple harmonic motion.
Answer:
T = 2π\(\sqrt{\left(\frac{\text { displacement }}{\text { acceleration }}\right)}\)

Question 4.
Write down the relation between acceleration, displacement and frequency of the particle executing simple harmonic motion.
Answer:
f = -ω₀²y = -(2πn)² y
or f = -4π²n²y

Question 5.
The equation of motion of a particle executing simple harmonic motion is represented by the equation a = -bx, where a is acceleration, x is displacement, b any constant. Find out the time period of the particle.
Answer:
Acceleration, a = -bx
numerically a = bx

Question 6.
A girl is swinging in the sitting position. How will the period of the swing change if she stands up.
Answer:
The girl and the swing together constitute a pendulum of time period.
T = 2π \(\sqrt{\left(\frac{l}{g}\right)}\)
As the girl stands up, her C.G. is raised. The distance between the point of suspension and the C.G. decreases i.e., the length l decreases. Hence, the time period T decreases.

Question 7.
If the length of a simple pendulum is increased by 4%, what is the percentage increase in its time period?
Answer:

Question 8.
Will a pendulum clock close or gain time when taken to the top of a mountain?
Answer:
On the top of the mountain, the value of g is less than that on the surface of the earth. The decrease in the value of g increases the time period of the pendulum on the top of the mountain. So the pendulum clock loses time.

Question 9.
What will the period of oscillation if the length of a second’s pendulum is halved?
Answer:

Question 10.
Can we use a pendulum which in an artificial satellite?
Answer:
No, in an artificial satellite, a body is in a state of weightlessness, i.e., g = 0
T = 2π\(\sqrt{\left(\frac{l}{g}\right)}\) = ∞
Inside the satellite, the pendulum does not oscillate. Hence, a pendulum watch cannot be used in an artificial satellite.

Question 11.
What will be the change in the time period of a loaded spring, when taken on moon?
Answer:
Time period of a loaded spring,
T = 2π\(\sqrt{\left(\frac{m}{k}\right)}\)
As T is independent of g it will not be affected when the loaded spring is taken to the moon.

Question 12.
What determines the natural frequency of a body?
Answer:
Natural frequency of a body depends upon (i) elastic properties of the material of the body and (ii) dimensions of the body.

Question 13.
What fraction of the total energy is kinetic when the displacement of a simple harmonic oscillator is half of its amplitude?
Answer:
\(\frac{\text { kinetic energy }}{\text { total energy }}=\frac{\frac{1}{2} m \omega^2\left(A^2-\frac{A^2}{4}\right)}{\frac{1}{2} m \omega^2 A^2}=\frac{3}{4}\)

Question 14.
Why does the amplitude of an oscillating pendulum go on decreasing?
Answer:
Due to frictional resistance between air and bob, the amplitude of oscillations of the pendulum gradually decreases and finally the bob stops.

Question 15.
When are the displacement and velocity in the same direction in S.H.M.?
Answer:
When a particle moves from mean position to extreme position, its displacement and velocity are in the same direction.

Question 16.
Is spring constant a dimensional or non-dimensional constant?
Answer:
Spring constant,
k = \(\frac{F}{x}=\frac{\text { Restoring force }}{\text { Displacement }}\)
= \(\frac{\left[\mathrm{MLT}^{-2}\right]}{[\mathrm{L}]}\) = [ML⁰T^-2]
Hence, spring constant is a dimensional constant.

Match the Following

Question 1.

Column I	Column II
A. Orbital motion of the planet around the sun	P. Forced Motion
B. Oscillations of the bob of a simple pendulum in air	Q. Simple Harmonic
C. Up and down motion of a suspended spring in vacuum	R. Damped Oscillations
D. Vibrations of a table when its top is pressed with the stem of the vibrating tuning took	S. Periodic Motion

Answer:

Column I	Column II
A. Orbital motion of the planet around the sun	S. Periodic Motion
B. Oscillations of the bob of a simple pendulum in air	R. Damped Oscillations S. Periodic Motion
C. Up and down motion of a suspended spring in vacuum	Q. Simple Harmonic S. Periodic Motion
D. Vibrations of a table when its top is pressed with the stem of the vibrating tuning took	P. Forced Motion R. Damped Oscillations

Short Answer Type Questions

Question 1.
The maximum acceleration of a simple harmonic oscillator is a₀ and the maximum velocity is v₀. What is the displacement amplitude?
Answer:
Let A be the displacement amplitude and ω be the angular frequency of S.H.M., Then,
Maximum velocity, v₀ = ωA; ω = v₀/A
Maximum acceleration,
a₀ = ω² A = (\(\frac{v_0}{A}\))² A = \(\frac{v_0^2}{A}\)
∴ Displacement amplitude, A = \(\frac{v_0^2}{a_0}\)

Question 2.
Are the functions tan ωt and cotωt periodic? Are they harmonic?
Answer:
Both tan ωt and cot ωt are periodic functions each with time period, T = π/ω because.
tan[ω(t + \(\frac{\pi}{\omega}\))] = tan(ωt + π) = tan ωt
and cot[ω(t + \(\frac{\pi}{\omega}\))] = cot (ωt + π) = cotωt
But these functions are not harmonic because they can take any value between 0 and ∞.

Question 3.
A simple pendulum is hung in a stationary lift and its periodic time is T. What will be the effect on its periodic time T if:
(i) The lift goes up with a uniform velocity v,
(ii) The lift goes up with a uniform acceleration a and
(iii) The lift comes down with a uniform acceleration a?
Answer:
(i) When the lift goes up (Fig. a) with uniform velocity v, tension in the string, T = mg. The value of g remains unaffected. The period T remains same as that in stationary lift, i.e.,
T = 2π\(\sqrt{\left(\frac{l}{g}\right)}\)
(ii) When the lift goes up with acceleration a [Fig.(b)], the net upward force on the bob is
T' - mg = ma
or T' = m(g + a)
The effective value of g is (g + a) and time period is
T₁ = 2π\(\sqrt{\left(\frac{l}{g+a}\right)}\)

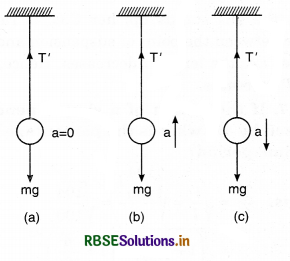
clearly, T₁ < T i.e., time period decreases.
(iii) When lift comes down with acceleration a [Fig. (c)], the net downward force on the bob is
mg - T' = ma ∴ T' = m(g - a)
The effective value of g becomes (g - a) and time period is T₂ = 2π\(\sqrt{\left(\frac{l}{g-a}\right)}\)
clearly, T₂ > T, i.e., time period increases.

Question 4.
A simple harmonic motion is repersented by \(\frac{d^2 x}{d t^2}\) + ax = 0, What is its time period?
Answer:
\(\frac{d^2 x}{d t^2}\) = -ax or a = -ax
Time period, T = 2π\(\sqrt{\left(\frac{x}{a}\right)} = 2π\sqrt{\frac{x}{\alpha x}}=\frac{2 \pi}{\sqrt{2}}\)

Question 5.
You have a light spring, a meter scale and a known mass. How will you find the time period of oscillation of mass without the use of a clock?
Answer:
Suspend the known mass m from the spring and note the extension l of the spring with the metre scale. If k is the force constant of the spring, then in equilibrium,
kl = mg or \(\frac{m}{k}\) = \(\frac{l}{g}\)
Time period of the loaded spring
T = 2π\(\sqrt{\frac{m}{k}}\) = 2π\(\sqrt{\frac{l}{g}}\)
So, by knowing the value of extension l, time period T can be determined.

Question 6.
The bob of a vibrating pendulum is made of ice. How will the time period change when the ice starts melting?
Answer:
If the ice bob is of very small size, the position of its C.G. will remain same as the ice melts. Hence, its time period will remain same. If the size of the ice bob is large, then
T = 2π\(\sqrt{\left(\frac{\frac{2 r^2}{5 l^{-}}+l}{g}\right)}\)
as ice melts, the radius r of the bob decreases and hence the time period T will decrease. The pendulum will oscillate faster.

Question 7.
A particle is executing S.H.M. of amplitude A. At what displacement from the mean position, is half the kinetic energy equal to half potential?
Answer:
As E_k = E_p
∴ \(\frac{1}{2}\) mω² (A² - y²) = \(\frac{1}{2}\) mω² y²
or A² - y² = y² or 2y² = A²
or y² = \(\frac{A^2}{2}\) or y = \(\pm \frac{A}{\sqrt{2}}\)
Thus, the energy will be half kinetic and half potential at displacement A/\(\sqrt{2}\) on either side of the mean position.

Question 8.
At a time when the displacement is half the amplitude? What fraction of the total energy is kinetic and what fraction is potential in S.H.M.?
Answer:

Question 9.
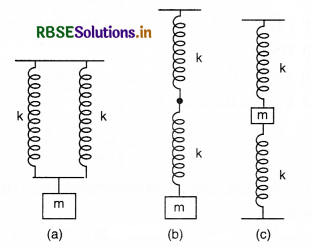
Two identical springs, each of spring factor k, may be connected in the following ways. Deduce the spring factor of the oscillation of the body in each case.
Answer:
For each spring
F = -ky .......................(i)
where, F = restoring force, k = spring factor and y = displacement of the spring
(i) In Fig. (a), let the mass m produce a displacement y in each spring and F be the restoring force in each spring, if k₁ be the spring factor of the combined systems, then
2F = -k₁y
or F = -\(\frac{k_1}{2}\)y ..................(ii)
Comparing (i) and (ii), we get
\(\frac{k_1}{2}\) = k or  k₁ = 2k
(ii) If Fig. (b), as the length of the spring is doubled, the mass m will produce double the displacement (2y). If k₂ be the spring factor of the combined system then
F = -k₂ (2y) = -2 k₂y ......................(iii)
Comparing (i) and (iii), we get
2k₂ = k or k₂ = \(\frac{k}{2}\)
(iii) In Fig. (c), the mass m stretches the upper spring and compresses the lower spring, each giving rise to a restoring force F in the same direction. If k₃ be the spring factor of the combined system, then
2F = -k₃ y
or F = -\(\frac{k_3}{2}\) y ..........................(iv)
Comparing (i) and (iv)
\(\frac{k_3}{2}\) = k or k₃ = 2k

Question 10.
The frequency of oscillations of a mass m suspended by a spring is v₁. If the length of the spring is cut to one-half, the same mass oscillates with frequency v₂. Determine the value of v₂/v₁.

Answer:
Let k be the force constant of the full spring.
Then frequency of oscillation of mass m will be
v₁ = \(\frac{1}{2 \pi} \sqrt{\left(\frac{k}{m}\right)}\)
When the spring is cut to one half of its length, its force constant is doubled (2k), frequecny of oscillation of mass m will be v₂ = \(\frac{1}{2 \pi} \sqrt{\frac{2 k}{m}}\)
∴ v₂/v₁ = \(\sqrt{2}\)

Conceptual Questions

Question 1.
For a simple harmonic motion what is the relationship between acceleration and displacement?
Answer:
For a simple harmonic motion, acceleration is directly proportional to the displacement of the object from its mean position and always points towards the mean position (f = -ω² y).

Question 2.
What will be the initial phase angle of a body starting its simple harmonic motion from the extreme end?
Answer:
The time taken by the body starting its simple harmonic motion from the extreme end to the mean position is 774 and accordingly the phase angle is π/2. Hence, the initial phase angle is π/2.

Question 3.
In simple harmonic motion the value of displacement is how much phase angles ahead of its acceleration value?
Answer:
In a simple harmonic motion, the displacement and acceleration are in the opposite direction, displacement is ahead of acceleration by a phase angle π.

Question 4.
In simple harmonic motion which physical quantity is conserved?
Answer:
Total mechanical energy is conserved in simple harmonic motion.

Question 5.
What is the relation between oscillating frequency and total energy of a simple pendulum?
Answer:
For a simple pendulum
E_total = \(\frac{1}{2}\) mω² a² = \(\frac{1}{2}\) m (2πn)² a²
= \(\frac{1}{2}\) m 4π² n² a²
= 2 π² mn² a²
Here, E_total = total energy
m = mass of the pendulum (bob)
ω = angular frequency = 2πn = 2π/T
n = linear frequency
a = amplitude.

Question 6.
What will be the effect on time period on using soft spring of same length instead of hard spring?
Answer:
The relation between the time period and the spring constant of an oscillating body is
T = 2π\(\sqrt{\frac{m}{k}}\)
k = spring constant
The spring constant for a softer spring is less than that for a harder one.
i.e., k_soft < k_hard
Hence from the above equation
T_soft > T_hard
i.e, the time period will increase.

Question 7.
What will be the value of the time period of a simple pendulum if the amplitude is reduced to half of its original value?
Answer:
Formula for the time period of a simple pendulum,
T = 2π\(\sqrt{\frac{l}{g}}\)
In this expression, there is no term ‘a’, hence the time period is independent of the amplitude of oscillation. Thus, the time period remains unaffected.

Question 8.
For a simple pendulum why is a spherical bob chosen.
Answer:
A spherical bob is chosen for a simple pendulum for the following reasons:

1. For a given value of density, the spherical shape has minimum volume.
2. The air friction is minimum due to spherical shape.

Question 9.
While crossing a bridge the soldiers stepping together are asked not to put their steps together. Why?
Answer:
While crossing the bridge, due to soldiers stepping together, the bridge is set into forced vibrations. If by chance the frequency of forced vibration of bridge becomes equal to the natural frequency of the bridge, a resonance will occur. The amplitude of vibration will become very high and there is a high probability that the bridge will break.

Long Answer Type Questions

Question 1.
With suitable examples, explain the meaning of a periodic function. Define the terms harmonic oscillator, displacement, amplitude, cycle, time period, frequency angular frequency and phase with reference to an oscillatory system.
Answer:
(i) Periodic Motion: When a moving object returns back to its original position after a particular interval of time and repeats its motion then this motion is called the periodic motion. A motion that repeats itself after regular intervals of time is known as the periodic motion. Example: Motion of planets around the Sun, motion of hands of a clock motion of the blades of a fan, Moon revolving around the Earth. To complete a full cycle the body takes a definite time which is called time period and is denoted by T.

(ii) Non-periodic Motion: When an object does not repeat its motion after a definite time interval then its motion is called non-periodic motion. Example: Throwing a ball, shooting an arrow from a bow, etc.

(iii) Oscillatory Motion: If a body moves to and fro repeatedly about a mean position; then the motion of the body is called vibratory motion or oscillatory motion. It is a special form of periodic motion.
Example:
(i) When guitar strings are vibrated then they oscillate around its mean position.

(ii) A piece of wood which is floating on the surface of water, if slightly pushed and left then it does up and down vibration motion.

(iii) An iron plate clamped at one end if pushed on one side and left then it does vibrational motion around the equilibrium position.

(iv) A weight tied (hanged) from a spring if pulled and left, then it does up and down periodic motion.
Every oscillatory motion is periodic motion, but  all periodic motions are not oscillatory motions.

(iv) Time Period: The time taken to complete one oscillation by a body is called its time period. It is generally represented by T. Its SI unit is second (s). Time period is that minimum time interval after which the body again starts repeating its vibration motion.

(v) Frequency: The number of periodic motions in one second(s) i.e. the number of completed oscillations is called frequency. It is generally represented as n or y. Its SI unit is Hertz (Hz). 
Relationship between Frequency and Time Period
1f the time period of a body executing periodic motion is T and frequency is n.
Number of oscillations completed in T second = 1.
Hence, number of oscillations completed in 1 second
= \(\frac{1}{T}\)
But, the number of oscillations completed in 1 second is called frequency (n).
∴ n = \(\frac{1}{T}\) ........................(14.1)

(vi) Displacement and Amplitude: We consider a physical quantity in normal oscillatory motion which changes with time and whose measure is possible. The change in this physical quantity relative to its mean position is called displacement and in oscillatory motion, the displacement at any instant relative to the mean position is called instantaneous displacement. The value of instantaneous displacement changes with time.

The maximum displacement of a particle from its mean position when a particle does oscillatory or vibratory motion is called amplitude. In linear oscillatory motion linear amplitude is represented as ‘a’ and in angular oscillatory motion angular amplitude is represented as θ₀.


(vii) Phase Angle: The physical quantity representing the nature (state) of vibrating particle’s motion at any instant is called phase angle.
From instantaneous displacement
y= a sin(ω₀t + Φ);
(ω₀t + Φ) is known as phase angle or phase. By knowing the phase the instantaneous position of the oscillating system can be calculated. In phase angle keeping the value of t = 0, then the value of phase angle Φ is called the First (Initial) Phase Angle in simple recurring (periodic) motion or is also known as phase constant. The difference in the phase angles of two particles executing simple periodic motion is called “phase difference”. It is represented as ∆Φ.

When phase difference is ∆Φ = π then, both simple periodic motions are called in opposite phases. Whereas, when ∆Φ = 0 or 2π then the two particles are said to be in same phase. In same phase position both the particles do motion in the same direction.

(viii) Periodic Function: Periodic function is that function whose repetition is after a definite time interval. Periodic function is that function which is used to represent periodic motion.
If there is any function F(θ);
F(θ + T) = F(θ) ......................(14.2)
Then, F(θ) is called periodic function.
Here, T is time period and θ is the argument of a function.
It is clear from Eq.(14.2) that if the value of the argument changes from θ to θ + T then the value of the function does not change. Similarly, if θ is increasesd by one more period then also the value of the function does not change.
F(θ + 2T) = F(θ)
F(θ + kT) = F(θ)
where, k = 0, ±1, ±2, .....................
A simple periodic function is a sine or cosine function.
f(t + T) = f(t)
g(t + T) = g(t)
where, f(t) = A sin ωt and g(t) = A cos ωt can be taken as the periodic functions.

Question 2.
Show that simple harmonic function may be regarded as the projection of uniform circular motion along a diameter of the circle. Hence derive an expression for the displacement of a particle in S.H.M.
Answer:
Using Newtons second law of motion and the expression for acceleration of a particle undergoing S.H.M., the force acting on a particle of mass M in S.H.M. is:
f(t) = ma
= -mω² (xt)
i.e., f(t) = -kx (t)
where k = mω²
or ω = \(\sqrt{\frac{k}{m}}\)
Like acceleration, force is always directed towards mean position.

Question 3.
Explain the relation in phase between displacement, velocity and acceleration in graphically as well as theoretically.
Answer:
Let displacement X = Asinωt
Velocity v = ωAcosωt
acceleration a = -ω² AsinωT = ω² Asin(ωT + π)
Displacement and velocity have phase difference of π/2 radians.
v and α has \(\frac{\pi}{2}\) radians of phase difference. α and x has π radians of phase difference.
Assume ω > 1

Question 4.
Derive expressions for the kinetic and potential energies of a harmonic oscillator. Hence show that total energy in conserved in S.H.M.
Answer:
(i) Oscillations due to a Spring
Suppose there is a weightless spring whose length is l and it is hanged from a rigid base. This is shown in fig. 14.12 (a). At one end of it, a mass m is hanged due to which there is stretch in the spring and there is increase in its length y. Due to elasticity in the spring a restoring force F is acting upwards. According to Hooke’s law restoring force is directly proportional to displacement i.e., F = -ky ....................(14.21)

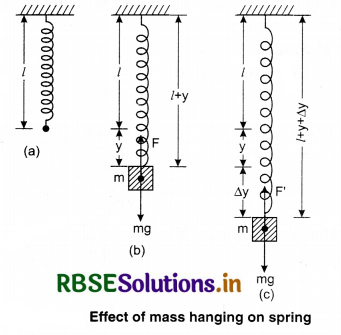
Where, k = spring force constant whose unit is Newton/meter (N/m). Negative sign in Eq. (14.21) shows that restoring force is acting in opposite direction of displacement. Zero equilibrium position as shown in fig. 14.12(b) the resultant force is zero due to zero acceleration on mass.
i.e., F + mg = 0
F = -mg
or -ky = -mg
ky = mg ...........................(14.22)
Now, if the piece of mass m is pulled and left then it performs up and down oscillation. As shown in fig. 14.12 (c). Suppose in pulling there is increase of ∆y in the length of the spring.
Hence, restoring force:
F = -k(y + ∆y)
= -ky - k ∆y
The weight mg is hanged on the spring. Hence, the resultant force on the particle = F + mg
= -ky - k ∆y + mg
∴ ky = mg
= -k ∆y [By using Eq. (14.22)]
Hence, resultant acceleration of the piece of mass m.
Force/Mass = -\(\frac{k \Delta y}{m}\)
Resultant acceleration (f) = \(\frac{-k}{m}\) ∆y ....................(14.23)
It is clear from Eq. (14.23) that resultant acceleration is directly is opposite to displacement. Hence, definitely the motion of mass m will be simple harmonic motion.
Time period:
We know that S.H.M.
f = -ω₀² ∆y
This equation is compared by the equation 14.23.
From Eq. (14.23),

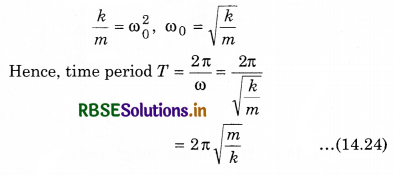
(ii) Simple Pendulum
An ideal simple pendulum is that which has the following properties:
(i) Point mass: The mass of the bob of the simple pendulum should be centered at one point. It is only possible if its shape is zero. Shapeless mass is called point mass. Point mass is imaginary. 

(ii) The string through which the point mass is suspended should be weightless and it should not be extended by the pendulum’s weight.

(iii) Rigid Base: The base from which it is hanged should be rigid.

(iv) Frictionless: The external and internal frictions will be zero for its various parts.
Here, we discuss an ideal simple pendulum and its nature.
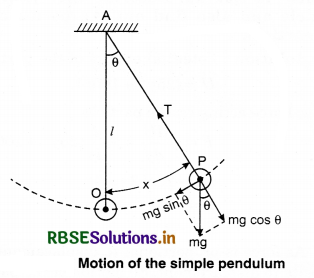
According to the figure (14.13) a small ball of heavy metal meaning bob is hanged from a thin string. Point O (centre of gravity center of the bob) and point A are the point of oscillation and point of suspension respectively. The distance between these two points is called the working length.

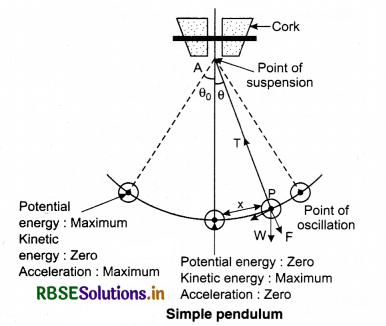
Bob is pulled slightly towards right and then left, it starts oscillating.

Generally, due to loss of energy against the frictional forces, the amplitude reduces slowly.
The working force on the bob at the displacement position AP of the particle:

(i) Weight of bob, W = mg, towards the center of the Earth where m is the mass of the bob and g is acceleration due to gravity.

(ii) The tension force T in the string, works in the PA direction. Weight W is divided into two components; component mgcose which is along the length of the string and works in the opposite direction of T and component mgsinθ which is working perpendicular to the string. Component mgcosθ balances the tension T in the string but component mgsinθ is imbalance. Component mg sinθ tries to bring the pendulum in the equilibrium position. This is called restoring force.
Restoring force on bob, F = -mg sinθ
Negative sign shows that force is in opposite direction to the displacement, meaning towards mean position. If angular displacement θ is very less then;
sin θ = θ = Arc/Radius = \(\frac{OP}{AP}\) = \(\frac{x}{l}\)
∴ F = -mg\(\frac{x}{l}\)
From Newton's law, IInd law of motion
Force = Mass x Acceleration
mf = -mg\(\frac{x}{l}\) where (f = acceleration)
f = -[\(\frac{g}{l}\)]x ......................(14.25)
f ∝ -x
The acceleration of the bob is directly proportional to its displacement and its direction is is opposite to that of displacement. Therefore, definitely. The motion of bob is simple harmonic
From Eq. (14.25);
ω² = \(\frac{g}{l}\)
Therefore, time period of the motion
T = 2π\(\sqrt{\frac{l}{g}}\) ......................(14.26)
This is the formula for time period of a simple pendulum. It is clear from Eq. (14.26) that;
(i) Time period is not dependent on mass: If a girl is swinging in a swing; then if another girl comes and sits in the same swing then there is no effect on the time period.

(ii) Dependency of the time-period of the pendulum on amplitude: It is clear from Eq. (14.26) that value of time period is not dependent on amplitude. But it is only true for smell angular amplitude.

(iii) Time period is directly proportional to the square root of length: If the girl swinging on the swing stands up then center of gravity will shift upwards and the effective length of the swing will reduce. As a result time period will reduce.

(iv) Dependency on gravitational acceleration: Time period is inversely proportional to the square root of gravitational acceleration g. When any pendulum clock is taken to a mountain or in a cave then the value of g reduces; hence time period increases; meaning the clock becomes slow.

(v) Seconds Pendulum: It is a simple pendulum whose time period is of 2 s. The length of a seconds pendulum by Eq. (14.26) is;
l = [\(\frac{T}{2\pi}\)]² g
T = 2 s, π = 3.14, g = 9.8 m/s²
Then length of seconds pendulum;
l = 99.4 cm
(vi) Since, T = \(\frac{1}{\sqrt{g}}\) and gpoles > gequator
Hence, relative to poles the time period at equator will be more
i.e., T_poles < T_equator

Question 5.
What is a simple pendulum? Show that motion executed by the bob of the pendulum is S.H.M. Derive an expression for its time period.
Answer:
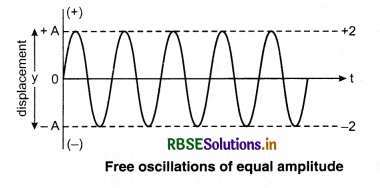
If there is only restoring force acting on a vibrating object for example simple pendulum or tuning fork then that object can vibrate till infinity. This  type of vibration or oscillation is called ‘free oscillation’ and this type of vibration is called ‘free vibration’. Its frequency is called ‘Natural Frequency’. There is only restoring force working in free vibration, Its amplitude and energy both are constant with time as shown in figure (14.20).

Naturally, one object can oscillate till infinite time. If we study the simple pendulum then we get to know that due to frictional forces there is loss in energy due to which the amplitude of the oscillation reduces gradually, and at the end the simple pendulum comes to the position of rest. This frictional force resists the motion of the body hence the energy provided to the object at initial displacement, gradually but continuously changes to heat against frictional force. This energy is not gained by the object any more hence due to energy loss the amplitude of oscillations reduces slowly and at the end amplitude is zero and the body comes in the position of rest. The gradual decrease in the amplitude of oscillations due to the energy loss is called damping.

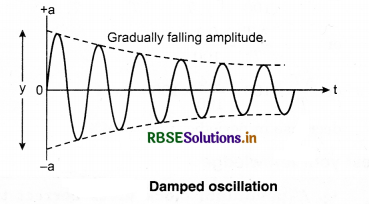
Damping force is generally directly proportional to the velocity of the oscillator and it acts in the opposite direction to the direction of velocity.
i.e. Fd ∝ -v 
Fd = -bv .................(14.32)
‘b’ is known as the damping constant in Eq. (14.32). Hence, the total working force on the oscillator is shown by the sum of the restoring force and the damped force.

Question 6.
Show that when a body is suspended from a spring and is pulled down a little and released, it executes S.H.M. Also find an expression for its time period. Does it depend on acceleration due to gravity?
Answer:
In simple harmonic motion; when the particle is displaced then the potential energy is obtained in the form of negative value of the work done opposite to the restoring force F = -ky. Hence, increase in the potential energy of the particle;
∆U = -F dy
Hence, potential energy in displacing the particle to a distance y from the mean position is;

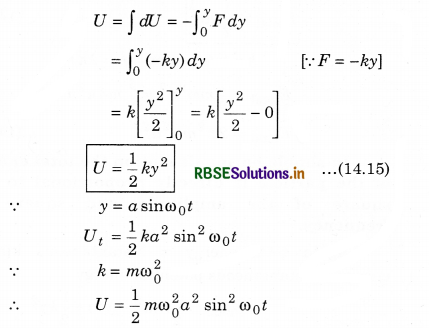
Average potential energy per unit time period

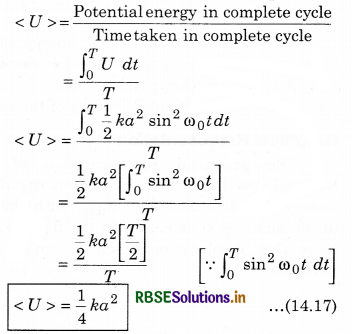
It is clear from Eqs.(14.14) and (14.17) that the value of average kinetic energy and average potential energy per unit time period is \(\frac{1}{4}\)ka².

Question 7.
What are free, damped and maintained oscillation? Define and explain.
Answer:
We have noticed that when the motor of flour mill, or motor of well is started then the objects closer to it like windows, doors also vibrate. This is called forced vibrations. According to fig. 14.17 if four simple pendulums A, B, C and D are hanged and out of these pendulum A is vibrated; then we will notice that B. C and D also vibrate with the frequency of A. Vibrations of B, C and D are called forced vibrations.

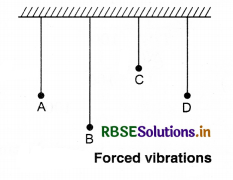
In this situation A is initiator which produces vibrations in B, C and D. When initiator’s frequency is equal to the natural frequency of the object to be initiated then the maximum energy is transferred to the object to be initiated and its amplitude is also maximum.

Question 8.
With the help of an example, differentiate between free oscillations and forced oscillations.
Answer:
We have noticed that when the motor of flour mill, or motor of well is started then the objects closer to it like windows, doors also vibrate. This is called forced vibrations. According to fig. 14.17 if four simple pendulums A, B, C and D are hanged and out of these pendulum A is vibrated; then we will notice that B. C and D also vibrate with the frequency of A. Vibrations of B, C and D are called forced vibrations.

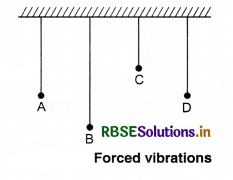
In this situation A is initiator which produces vibrations in B, C and D. When initiator’s frequency is equal to the natural frequency of the object to be initiated then the maximum energy is transferred to the object to be initiated and its amplitude is also maximum.

Question 9.
Draw a graphical representation of simple harmonic motion, showing the:
(a) displacement-time curve,
(b) velocity-time curve and
(c) acceleration-time curve
Answer:
(a)Displacement-time graphs show how the displacement of a moving object changes with time. A horizontal line on a displacement-time graph shows that the object is stationary (not moving because the displacement does not change). A sloping line on a displacement-time graph shows that the object is moving. In a displacement-time graph, the slope or gradient of the line, is equal to the velocity of the object. The steeper the line (and the greater the gradient) the faster the object is moving.

(b) velocity-time curve
When the acceleration is increasing with time, the velocity-time graph will be a curve as predicted from the equation:
v = u + at
Since u = 0
v = at
Since acceleration is a function of time, the velocity-time graph will be a curve.
Note: Since the acceleration continuously increases with time, the magnitude of the slope will also continuously increase with time.

(c) Acceleration-Time Graph shows the acceleration plotted against time for a particle moving in a straight line. The acceleration-time plots acceleration values on the y-axis and time values on the x-axis.

Acceleration-Time Graph Explanation
Vertical Axis
The vertical axis in the acceleration-time graph represents the acceleration of the object. In the given graph below, reading the value of the graph at a particular time will fetch you the acceleration of the object in meters per second squared for that moment.

Slope of the acceleration graph
The slope of the acceleration graph represents a quantity known as a jerk. Jerk is the rate of change of acceleration. In the given acceleration graph as shown below, the slope can be calculated as follows:
slope = \(\frac{\text { rise }}{\text { run }}=\frac{a_2-a_1}{t_2-t_1}=\frac{\Delta a}{\Delta t}\)

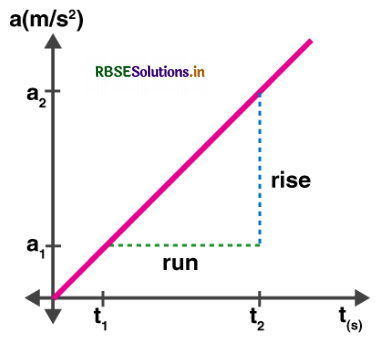
Area Under the Acceleration Graph
The area under the acceleration graph represents the change in velocity. In other words, the area under the graph for a certain time interval is equal to the change in velocity during that time interval.
Area = ∆V
Let us consider the below example to understand better:
The graph below shows a constant acceleration of 4 m/s² for a time of 9 s.

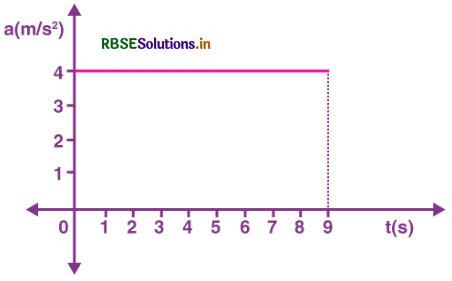
Acceleration is defined as,
∆a = \(\frac{\Delta v}{\Delta t}\)
By multiplying both sides of the equation by the change in time ∆t, we get
∆v = a∆t
Substituting the values in the above equation, we get
∆v = a∆t = (4 m/s²)(9s) = 36 m/s
Multiplying the acceleration by the time interval is equivalent to finding the area under the curve. The area under the curve is a rectangle. This area can be found by multiplying height and width. The height, in this case, is 4 m/s2 and the width is 9 s.
area = 4 m/s2 x 9 s = 36 m/s
The area under any acceleration graph for a certain time interval gives the change in velocity for that time interval.
 
Numerical Questions

Based on displacement, velocity and acceleration of simple harmonic motion

Question 1.
A particle executing simple harmonic motion has displacement equation y = 0.50 sin (500t + 0.5), where distance is in cm, time is in s, angular frequency and initial phase of the particle.
Solution:
Given: y = 0.50 sin (500t + 0.5)cm
Displacement equation in simple harmonic motion
y = a sin (ωt + Φ)
On comparing:
amplitude a = 0.50 cm
angular frequency ω = 500 rad s^-1
initial phase Φ = 0.5 rad

Question 2.
A simple harmonic motion has an amplitude A and time period T. What is the time taken to travel from x = A to x = A/2?
Solution:
Equation of simple harmonic motion
x = A cos ωt = A cos\(\frac{2 \pi}{T}\)t
when x = A
then A = A cos\(\frac{2 \pi}{T}\)t₁

Question 3.
The displacement of a particle is given by the equation x = 4cos (3πt + 7t), where x is in metre, t is in second. Find out:
(a) Time period and frequency of the motion
(b) Amplitude of the motion
(c) Phase constant
(d) Position of the particle at t = 0.
Solution:
Given: x = 4 cos(3πt + π) m ...........................(1)
displacement equation of S.H.M.
x = a cos(ω₀t + Φ) .......................(2)
comparing (1) and (2)
amplitude a = 4 m
phase constant Φ = π rad
angular frequency ω₀ = 3π
∴ If periodic time is T then \(\frac{2 \pi}{T}\) = 3π ⇒ T = \(\frac{2}{3}\)
or T = 0.67 s
If frequency is n then 2 π n = 3π
∴ n = \(\frac{3}{2}\) = 1.5 Hz
Displacement at t = 0
x = 4 cos(3π x 0 + π) = 4 cosπ = 4(-1)
or x = -4 m

Question 4.
A particle executing simple harmonic motion has maximum velocity 1.0 m s^-1 and maximum acceleration 1.57 ms^-2, Find out the periodic time of the particle.
solution:
Given: v_max = 1.00 m s^-1 and maximum acceleration f_max = 1.57 m s^-2; T = ?

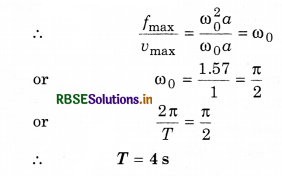
Question 5.
A particle is executing simple harmonic motion whose amplitude is 0.15 m and frequency is 4 Hz. Find out:
(i) Maximum acceleration
(ii) Velocity of the particle when displacement is 0.10 m.
Solution:
a = 0.15 m; n = 4 Hz; f_max = ?; when y = 0.10 m then v = ?
∴ ω₀ = 2π n = 2π x 4 = 8π rad s^-1
∵ Maximum acceleration
f_max = ω₀² x a = (8π)² x 0.15 = 64π² x 0.15
= 64 x 9.86 x 0.15
= 94.6 ms^-2

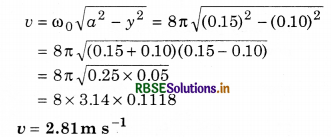
Based on simple pendulum

Question 6.
Find out periodic time of the simple pendulum of length \(\frac{9.8}{\pi^2}\) m.
Solution:
Given: l = \(\frac{9.8}{\pi^2}\); T = ?
∵ T = 2π\(\sqrt{\frac{l}{g}}\) = 2π\(\sqrt{\frac{9.8}{\pi^2 \times 9.8}}=\frac{2 \pi}{\pi}\)
or T = 2 s

Question 7.
The time period of a simple pendulum is 2 s and vibration amplitude is 5 cm. Write its equation of motion. After start of motion at 1.5 s find out displacement and velocity of the particle. Assume that the particle starts its motion from the mean position.
Solution:
Given: T = 2 s; a = 5 cm; after t = 1.5 s; y = ?; v = ?
∵ As motion starts from mean position so
y = a sin ω t
∵ ω = \(\frac{2 \pi}{T}\) ∴ ω = \(\frac{2 \pi}{2}\) = π rad s^-1
∴ y = (5 sin π t) cm
After t = 1.5 s
y = 5 sin π x 1.5 = 5 sin \(\frac{3 \pi}{2}\) = 5 sin(\(\pi+\frac{\pi}{2}\))
= -5 sinπ/2
v = ω\(\sqrt{a^2-y^2}=\pi \sqrt{(5)^2-(5)^2}=\pi \sqrt{25-25}\)
or v = 0 (zero)

Question 8.
The time taken to complete 100 vibration by a simple pendulum is 8 min 9 s at a place and 8 min 20 s on another place. Find the ratio of acceleration due to gravity at both the places.
Solution:
t₁ = 8 min + 9 s = 8 x 60 + 9 = 480 + 9 = 489 s
T₁ = \(\frac{t_1}{1000}=\frac{489}{1000}\)
or T₁ = 0.489 s
t₂ = 8 min + 20 s
= 8 x 60 + 20 = 480 + 20 = 500 s
∴ T₂ = \(\frac{t_2}{1000}=\frac{500}{1000}\) = 0.5 s
∵ Time period of the simple pendulum
T = 2π\(\sqrt{\frac{l}{g}}\)
If l is constant then T ∝ \(\frac{1}{\sqrt{g}}\)

Question 9.
A simple pendulum is so formed that its time period at that place is 1 s where g = 9.8 ms^-2. If at another place g = 8.813 ms^-2, then to maintain time period to Is, what change is required in its length.
Solution:
Given: T₁ = 1 s; g₁ = 9.8 m s^-2; l₁ = ?
T₂ = 1 s; g₂ = 8.813 m s^-2; l₂ = ?

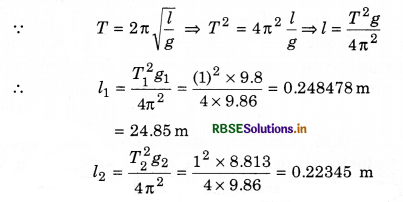
= 22.345 cm
= 22.35 cm
∴ Change in length
∆l = l₁ - l₂ = 24.85 - 22.35
or ∆l = 2.50 cm (less)

Question 10.
The length of a simple pendulum is 2 m and it is suspended from the roof of a lift. If lift is going with an acceleration of 2 m s^-2 upward. Then what will be the time period of the simple pendulum? If the rope of the lift is broken and it falls freely, then what will be the time period of the simple pendulum in this position. (g = 9.8 ms^-2)
Solution:
l = 2 m; a = 2.0 m s^-2 (on upper side); T = ?
Lift is going upwards

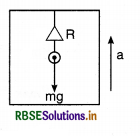
R - mg = ma
or R = mg + ma = m(g + a)
= m(9.8 + 2)
= m x 11.8
If apparent acceleration is g', then
Apparent weight
R = mg'
∴ mg' = m x 11.8
or g' = 11.8 m s^-2
∴ Time period of pendulum in lift
T = 2π\(\sqrt{\frac{l}{g}}=2 \pi \sqrt{\frac{2}{11.8}}=2 \pi \sqrt{0.16949}\)
= 2 x 3.14 x 0.41169
or T = 2.58 s
If the rope of the lift is broken, then lift falls freely
∴ pendulum will be in position of weightlessness,
or g' = 0
∴ T = 2π\(\sqrt{\frac{2}{0}}\) = ∞ (Infinite)

Based on spring-block system

Question 11.
Two mass m₁ = 2.0 kg and m₂ = 10 kg are suspended by a spring of force constant k = 25Nm^-1. When both are in equilibrium then m₁ is removed, then find out the angular frequency and amplitude of m₂. (g = 10ms_-2)
Solution:
m₁ = 2.0 kg; m₂ = 1.0 kg; k = 25 N. m^-1
g = 10 m s^-2
After removing m₁ angular frequency of m₂
ω = \(\sqrt{\frac{k}{m_2}}=\sqrt{\frac{25}{1}}\) = 5
or ω = 5 rad s^-1
After removing m₁, decrease in displacement of the spring amplitude of oscillations m₂.
F = m₁g = ka
∴ a = \(\frac{m_1 g}{k}=\frac{2 \times 10}{25}=\frac{4}{5}\) = 0.8 m
or a = 0.8 m

Question 12.
On suspending a 1.0 kg mass by a massless spring, there is increase of 1.0 cm in its length. Find: (i) Force constant of the spring (ii) Time period of the vibration of the spring.
Solution:
m = 1.0 kg; l = 1.0 cm = 0.01 m; g = 9.8 m s^-2
(i) ∵ F = ky
or mg = ky ⇒ k = \(\frac{m g}{y}=\frac{1.0 \times 9.8}{0.01}\)
or k = 980 N m^-1
(ii) ∵ T = 2π\(\sqrt{\frac{m}{k}}\)
∴ T = 2π\(\sqrt{\frac{1}{980}}=\frac{2 \times 3.14}{31.3049}\)
= \(\frac{6.28}{31.3049}\)
T = 0.2006 s

Question 13.
The time period of a mass m suspended by a spring is 2 s. If a mass of 2 kg is also added to it, then the periodic time increases by 1 second, find mass of m.
Solution:
Mass m; T = 2 s
mass (m + 2 kg); T' = 3 s; m = ?

Based on energy in simple harmonic motion

Question 14.
A mass of 0.50 kg is executing simple harmonic motion. Its time period is 0.1 s and amplitude is 10 cm. When block is 5 cm from the equilibrium position, then find its acceleration, force imposed on it and its potential energy.
Solution:
m = 0.50 kg; T = 0.1 s; a = 10 cm = 0.10 m
y = 0.05 m; f = ?; F = ?; U = ?
ω₀ = \(\frac{2 \pi}{T}=\frac{2 \pi}{0.1}\) = 20π rad s^-1
∴ acceleration f = ω₀².y = 20π x 20π x 0.05
= 4π² x 5 = 20π² = 20 x 9.86
= 2 x 98.6
f = 197.2 m s^-2
force F = mf = 0.5 x 197.2 = 98.6 m
or F = 98.6 N
potential energy, U = \(\frac{1}{2}\)mω²y² = \(\frac{1}{2}\) x 0.5 x 400π² x 0.05 x 0.05
U = 0.5 x 200π² x 0.005
U = 0.5 x 2π² x 0.25
U = 0.125 x 2 x 9.86
U = 2.465 J

Question 15.
A block of mass 2 kg is moving with a velocity 10 ms^-1 and strikes with a massless spring and produces a compression of 25 cm. Find the spring constant of the spring.
Solution:
m = 2 kg; v = 10 m s^-1; x = 25 cm = 0.25 m; k = ?
Potential energy of the spring = kinetic energy of body
U = K

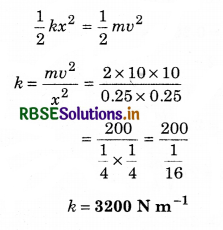
Question 16.
A body of mass 0.5 kg is suspended by an ideal spring is oscillating up and down. The amplitude of oscillation is 0.5 m and time period is 3.14 seconds. Find:
(i) Maximum velocity of the body
(ii) Maximum kinetic energy
(iii) Total energy
Solution:
m = 0.5 kg; a = 0.5 m; T = 3.14 s
v_max = ?; K_max = ?; E_total = ?
ω = \(\frac{2 \pi}{T}=\frac{2 \times 3.14}{3.14}\) = 2 rad s^-1
∴ v_max = ω₀a = (2) x 0.5 = 2 x 0.5 = 1 ms^-1
v_max = 1 m s^-1
K_max = \(\frac{1}{2}\)mω₀²a² = \(\frac{1}{2}\) x 0.5 x 4 x 0.25
K_max = 0.25 J
E_total = K_max = 0.25 J

Competition Corner 

Question 1.
A particle executes linear simple harmonic motion with an amplitude of 3 cm. When the particle is at 2 cm from the mean position, the magnitude of its velocity is equal to that of its acceleration.Then its time period in seconds is

Solution:
Amplitude A = 3 cm
when particle is at x = 2 cm
its |velocity| = |acceleration|

Question 2.
When two displacements represented by y₁ = a sin ωt and y₂ = b cos ωt are superimposed, then the motion is
(a) Not a simple harmonic
(b) Simple harmonic with amplitude a/b
(c) Simple harmonic with amplitude \(\sqrt{\left(a^2+b^2\right)}\)
(d) Simple harmonic with amplitude \(\frac{(a+b)}{2}\)
Solution:
Given y₁ = a sin ωt
y₂ = b sin ωt
= b sin (ωt + \(\frac{\pi}{2}\))
The resultant displacement is given by
y = y₁ + y₂
= \(\sqrt{\left(a^2+b^2\right)} \sin (\omega t+\phi)\)
Hence the motion of superimposed wave is simple harmonic with amplitude \(\sqrt{\left(a^2+b^2\right)}\)

Question 3.
The oscillation of a body on a smooth horizontal surface is represented by the equation
X = Acos(ωt)
Where, X = displacement at time t
ω = frequency of oscillation
Which one of the following graph shows correctly the variation of a with t?
Here, a = acceleration at time t
T = time period.

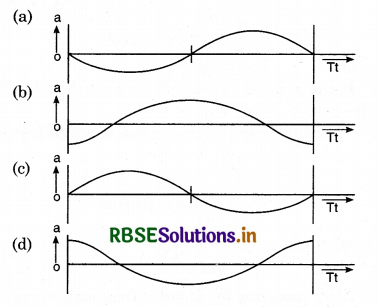
Solution:
As x = A cos ωt
∴ v = \(\frac{d x}{d t}\) = -Aω sinωt .......................(i)
and, a = \(\frac{d^2 x}{d t^2}\) = -Aω² cos ωt ...........................(ii)
We can find the correct graph by putting different values of t in Eq. (ii),
At, t = 0, a = -Aω²

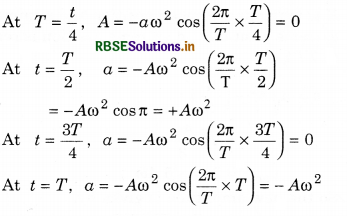
This condition represented by the graph is option (c).

Question 4.
The damping force on an oscillator is directly proportional to the velocity. The units of the constant of proportionality are
(a) kg ms^-1
(b) kg m s^-2
(c) kg s^-1
(d) kg s
Solution:
Given, Damping force α velocity
F ∝ v
F = kv ⇒ k = \(\frac{F}{v}\)
Unit of k = \(\frac{\text { unit of } F}{\text { unit of } v}=\frac{\mathrm{kg} / \mathrm{m} \mathrm{s}^{-2}}{\mathrm{~ms}^{-1}}\)
= kg s^-1

Question 5.
Out of the following functions representing motion of a particle which represents S.H.M.?
I. y = sinωt - cosωt
II. y = sin³ ωt
III. y = 5 cos(\(\frac{3 \pi}{4}-3 \omega t\))
IV. y = 1 + ωt + ω²t²
(a) only (IV) does not represent S.H.M.
(b) (I) and (III)
(c) (I) and (II)
(d) only (I)
Solution:
For a simple harmonic motion,
a ∝ \(\frac{d^2 y}{d t}\) ∝ -y
Hence, equations y = sinωt - cosωt and y = 5 cos (\(\frac{3 \pi}{4}-3 \omega t\)) are satisfying the condition and equation y = 1 + ωt + ω²t² is not periodic and y = sin3 ωt is periodic but not simple harmonic motion.

Question 6.
The period of oscillation of a mass M suspended from a spring of negligible mass is T. If along with it another mass M is also suspended, the period of oscillation will now be.
(a) T
(b) T/\(\sqrt{2}\)
(c) 2T
(d) \(\sqrt{2}\) T
Solution:
The period of spring pendulum
T = 2π\(\sqrt{\left(\frac{M}{k}\right)}\)
If mass is doubled then time period
T' = 2π\(\sqrt{\left(\frac{2 M}{k}\right)}\) = \(\sqrt{2}\) T

Question 7.
The displacement of a particle along the x-axis is given by x = a sin^-2 ωt. The motion of the particle corresponds to
(a) Simple harmonic motion of frequency ω/π
(b) Simple harmonic motion of frequency 3ω/2π
(c) Non-simple harmonic motion
(d) Simple harmonic motion of frequency ω/2π
Solution:
For a particle executing S.H.M.,
Acceleration (a) α - ω² displacement (x) ......................(i)
Given, x = a sin² ωt .........................(ii)
Differentiating the above equation w.r.t. we get,
\(\frac{d x}{d t}\) = 2aω (sin ωt) (cos ωt)
Again, differentiating, we get
\(\frac{d^2 x}{d t^2}\) = a = 2aω² [cos² ωt - sin² ωt]
= 2aω² cos²ωt
The given equation does not satisfy the condition for S.H.M. [Eq. (i)]. Therefore motion is not simple harmonic.

Question 8.
A particle is executing simple harmonic motion with a time period T. At time t = 0, it is at its position of equilibrium. The kinetic-energy-time graph of the particle will look like.

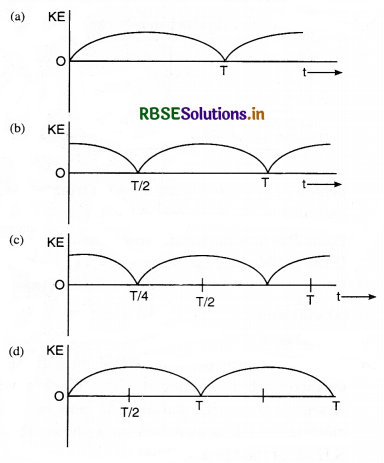
Solution:
K is maximum at mean position and minimum at extreme position and extreme position is reached at T/4.

Question 9.
A particle performs simple harmonic motion with amplitude A When it is at distance \(\frac{2 A}{3}\) from equilibrium position its speed is tripled. The new amplitude of the motion is
(a) 3A
(b) A\(\sqrt{3}\)
(c) \(\frac{7 A}{3}\)
(d) \(\frac{A}{3}\sqrt{41}\)
Solution:

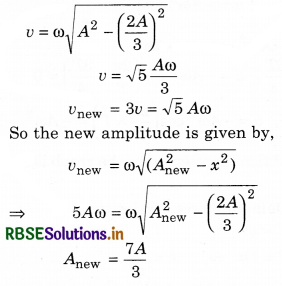
Question 10.
A pendulum made of a uniform wire of cross-secional area A has time period T. When an additional mass M is added to its bob, the time period changes to Tm. If the young’s modulus of the material of the wire is Y, then 1/Y is equal to (g = acceleration due to gravity.)

Solution:
Time period T = 2π\(\sqrt{\left(\frac{l}{g}\right)}\)
When additional mass M is added to its bob

Question 11.
For a simple pendulum, a graph is plotted between its kinetic energy (KE) and potential energy (PE) against its displacement d. Which one of the following represents these correctly?

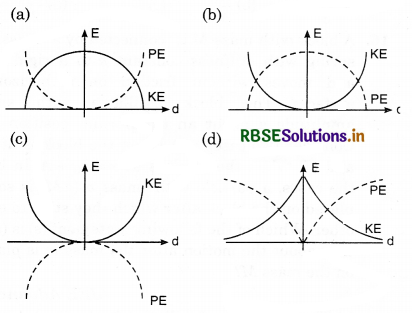
Solution:
At mean position, K.E. is maximum where as P.E. is minimum.

Question 12.
A particle moves with simple harmonic motion in a straight line. In first τ s, after starting from rest it travels a distance a, and in next τ it travels 2a, in same direction, then
(a) Amplitude of motion is 4a
(b) Time period of oscillations is 6τ
(c) Amplitude of motion is 3a
(d) Time period of oscillation is 8τ
Solution:
A(1 - cos ωτ) = a
A (1 - cos² ωτ) = 3a

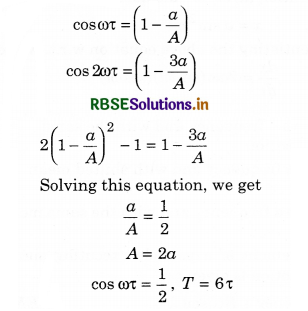
Question 13.
The amplitude of a damped oscillator decreases to 0.9 times its original magnitude in 5 s. In another 10 s, it will decrease to α times its orignal magnitude, where a equals
(a) 0.81
(b) 0.729
(c) 0.6
(d) 0.7
Solution:
A = A₀e^-kt
⇒ 0.9 A₀ = A₀ e^-5k
and α A₀ = A₀ e^-15k
Solving ⇒ α = 0.729

Question 14.
If a simple pendulum has significant amplitude (upto a factor of 1/e of original) only in the period between t = 0 s to t = τ s, then τ may be called the average life of the pendulum. When the spherical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity, with ‘b’ as the constant of proportionality, the average life time of the pendulum in (assuming damping is small) is seconds.
(a) \(\frac{0.693}{b}\)
(b) b
(c) \(\frac{1}{b}\)
(d) \(\frac{2}{b}\)
Solution:
As retardation = bv
retardation force = mbv
∴ net restoring torque when angular displacement θ is given by

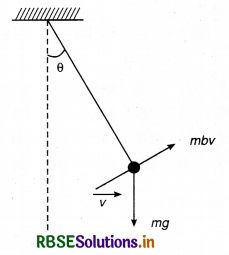
= -mgl sinθ + mbvl
∴ Iα = -mgl sinθ + mbvl
where, I = ml²
∴ \(\frac{d^2 \theta}{d t^2}=\alpha=-\frac{g}{l} \sin \theta+\frac{b v}{l}\)
for small damping, the solution of the above differential equation will be
θ = θ₀e^-bt/2 sin (ωt + Φ)
According to question, in τ time (average life time),
angular amplitude drops to 1/e value of its orginal value (θ)
∴ \(\frac{\theta_0}{e}=\theta_0 e^{-6 \tau / 2}\)
\(\frac{2 \tau}{2}\) = 1
∴ τ = \(\frac{2}{b}\)

Question 15.
Two particles are executing simple harmonic motion of the same amplitude A and frequency ω along the x-axis. Their mean position is separated by distance X₀ (X₀ > A). If the maximum separation between them is (X₀ + A), the phase difference between their motion is

Solution:
Φ₁ = 0
Φ₂ = \(\frac{\pi}{2}\)

Question 16.
A block with mass M is connected by a massless spring with stiffness constant k to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude a about an equilibrium position X₀. Consider two cases: (i) When the block is at x₀; and (ii) when the block is at x = x₀ + A In both the cases, a particle with mass m (< M) is softly placed on the block after which they stick to each other. Which of the following statement (s) is (are) true about the motion after the mass m is placed on the mass M?
(a) The amplitude of ocillation in the first case changes by a factor of \(\sqrt{\frac{M}{m+M}}\), whereas in the second case it remains unchanged
(b) The final time period of oscillation in both the cases in same
(c) The total energy decreases in both the cases

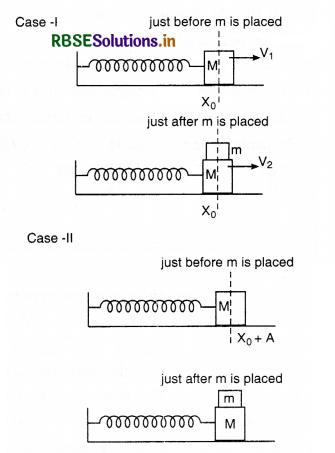
(d) The instantaneous speed at x₀ of the combined masses decreases in both the cases.
Solution:
In first condition,

In first condition, total energy decreases while in second condition, it remains constant. At x0 instantaneous speed in both condition decreases.

Question 17.
A small block is connected to one end of a massless spring of unstretched length 4.9 m. The other end of the spring (see the figure) is fixed. The system lies on a horizontal frictionless surface. The block is stretched by 0.2 m and released from rest at t = 0. It then executes simple harmonic motion with angular frequency ω = \(\frac{\pi}{3}\) rad/s. Simultaneously at t = 0, a small

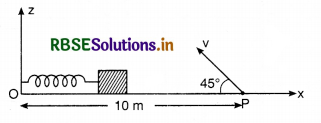
pebble is projected with speed v from point P at an angle of 45° as shown in the figure Point P is at a horizontal distance of 10 m from O, If the pebble hits the block at t = 1 s, the value of v is

Solution:
t = time of flight of projectile

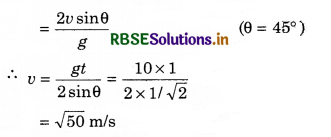
Question 18.
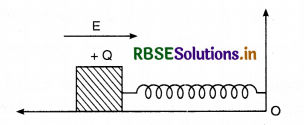
A wooden block performs SHM on a frictionless surface with frequency v₀. The block carries a charge +Q on its surface. If now a uniform electric field E is switched, on a shown them the S.H.M. of the block will be

(a) of the some frequency and with shifted mean position
(b) of the same frequency and with the same mean position
(c) of the change frequency and with shifted mean position
(d) of changed frequency and with the same mean position
Solution:
Frequency or time period of S.H.M. depends on variable forces. It does not depend on constant external force. Constant external force can only change the mean position. For example, in the given question mean position is at natural length of spring in the absence of electric field. Whereas in the presence of electric field mean position will be obtained after a compression of x₀.
where x₀ is given by,
kx₀ = QE
or x₀ = \(\frac{Q E}{k}\)
∴ correct answer is (a)

Question 19.
The displacement of a particle executing simple harmonic motion is given by
y = A₀ + A sinωt + Bcosωt
Then the amplitude of its oscillation is given by:

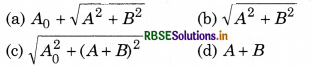
Solution:
(b)

Question 20.
A pendulum is hung from the roof of a sufficiently high building and is moving freely to and fro like a simple harmonic oscillator. The acceleration of the bob of the pendulum is 20 m/s² at a distance of 5 m from the mean position. The time period of oscillation is:
(a) 2 π s
(b) π s
(c) 2 s
(d) 1 s
Solution:
a = ω² x
20 = ω² x 5
ω² = \(\frac{20}{5}\) = 4
∴ ω = 2
\(\frac{2 \pi}{T}\) = 2
∴ T = \(\frac{2 \pi}{2}\) = π second.