RBSE Class 11 Physics Important Questions Chapter 13 Kinetic Theory

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 13 Kinetic Theory Important Questions and Answers.

RBSE Class 11 Physics Chapter 13 Important Questions Kinetic Theory

Multiple Choice Questions

Question 1.
A gas at 300 K has pressure 45 x 10^-10 N/m². If K = 1.38 x 10^-23 J/K, the number of molecules/cm³ is of the order of:
(a) 10
(b) 10⁵
(c) 10⁷
(d) 10¹¹
Answer:
(b) 10⁵

Question 2.
A gas is found to obey the law P²V = constant. The initial temperature and volume are T₀ and V₀. If the gas expands to a volume 3 V₀, its final temperature becomes:
(a) \(\sqrt{3}\) T₀
(b) 3 T₀
(c) \(\frac{T_0}{3}\)
(d) \(\frac{T_0}{\sqrt{3}}\)
Answer:
(a) \(\sqrt{3}\) T₀

Question 3.
Boyle's law is applicable for an:
(a) Isothermal process
(b) Adiabatic process
(c) Isochoric process
(d) Isobaric process
Answer:
(a) Isothermal process

Question 4.
The specific heat of the mixture of two gases at constant volume is \(\frac{13}{6}\) R. The ratio of the number of moles of the first gas to the second gas is 1:2. The respective gases are:
(a) He, Ne
(b) He, N₂
(c) O₂, H₂
(d) N₂, He
Answer:
(b) He, N₂

Question 5.
When the temperature of a gas filled in a closed vessel is increased by 1°C, its pressure increases by 0.4%. The initial temperature of gas was:
(a) 25°C
(b) 250°C
(c) 25 K
(d) 250 K
Answer:
(d) 250 K

Question 6.
1 mole of H₂ gas is contained in a box of volume V = 1.00 m³ at T = 300 K. The gas is heated to a temperature of T = 3000 K and the gas gets converted to a gas of hydrogen atoms. The final pressure would be (considering all gases to be ideal):
(a) Same as the pressure initially
(b) 2 times the pressure initially
(c) 10 times the pressure initially
(d) 20 times the pressure initially
Answer:
(d) 20 times the pressure initially

Question 7.
An inflated rubber balloon contains one mole of an ideal gas, has a pressure P, volume V and temperature T. If the temperature rises to 1.1 T, and the volume is increased to 1.05 V, the final pressure will be:
(a) 1.1 P
(b) P
(c) less than P
(d) between P and 1.1 P
Answer:
(d) between P and 1.1 P

Question 8.
A gas is filled in a container at pressure P₀. If the mass of molecules is halved and their rms speed is doubled, then the resultant pressure would be:
(a) \(\frac{P_0}{2}\)
(b) \(\frac{P_0}{4}\)
(c) 2P₀
(d) 4P₀
Answer:
(c) 2P₀

Question 9.
Three moles of oxygen are mixed with 2 moles of helium. What will be the ratio of specific heats at constant pressure and constant volume for the mixture?
(a) 1.5
(b) 4
(c) 6.7
(d) none of these
Answer:
(a) 1.5

Question 10.
The root mean square velocity of hydrogen molecules at 300 K is 1930 ms^-1. The rms velocity of oxygen molecules at 1200 K will be:
(a) 765 ms^-1
(b) 865 ms^-1
(c) 965 ms^-1
(d) 1065 ms^-1
Answer:
(c) 965 ms^-1

Fill in the blanks

Question 1.
The number of degrees of freedom associated with 2 gram of helium at N.T.P. is .........................
Answer:
9.03 x 10²³

Question 2.
All curves for real gases approach the ideal gas behaviour at .........................
Answer:
Low pressures and high temperature

Question 3.
Avogadro’s number NA is    .........................
Answer:
6.023 x 10²³

Question 4.
The ratio of most probable speed, average speed and rms speed of gas molecule is .........................
Answer:
\(\sqrt{2}: \sqrt{\frac{8}{\pi}}: \sqrt{3}\)

Question 5.
Average straight distance covered between two successive collisions of molecules, is called .........................
Answer:
mean free path of molecule

Very Short Answer Questions

Question 1.
What is the value of root mean square speed at a temperature T for an ideal gas?
Answer:
Root mean square speed at a temperature 'T' for an ideal gas.
v_rms = \(\sqrt{\frac{3 R T}{M}}\)
where M = molar mass of the gas; T = absolute temperature of the gas; R = universal gas constant.

Question 2.
What is the unit of gas constant (R)?
Answer:
Ideal gas equation
PV = nRT
⇒ R = \(\frac{P V}{n T}\)
∴ Unit of R = \(\frac{\mathrm{Nm}^{-2} \mathrm{~m}^3}{\mathrm{molK}}=\frac{\mathrm{Nm}}{\mathrm{molK}}\) = J mol^-1 K^-1

Question 3.
How much would the root mean square speed become when the absolute temperature of a gas is increased by 16 times?
Answer:
Root mean square speed

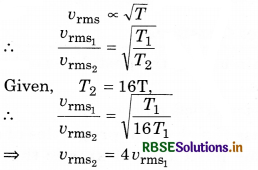
Question 4.
According to the kinetic theory of gas, what is the speed of gas molecules at absolute zero temperature?
Answer:
According to the kinetic theory of gas, the root mean square speed of gas molecules is
v²_rms = \(\frac{3 R T}{M}\)
At absolute zero temperature i.e., T = 0
v²_rms = 0 or v_rms = 0

Question 5.
Given the relation between degree of freedom (f) and γ.
Answer:
γ = (1 + \(\frac{2}{f}\)) where f = degree of freedom.

Question 6.
What is the degree of freedom for an airplane flying in the sky?
Answer:
An airplane can have independent velocities in three directions (X, Y, Z). Hence, the degree of freedom is 3.

Question 7.
Given the value of C_p for a distance gas.
Answer:
C_p = \(\frac{7}{2}\) R, where R = Universal gas constant.

Question 8.
Write the relation for pressure by kinetic theory of gases.
Answer:
P = \(\frac{1}{3} \frac{m n \bar{v}^2}{V}\)
where m is molar mass; n is number density of molecules; \(\overline{v^2}\) mean square speed; V = volume of the gas; ρ = density of the gas.

Question 9.
What is the value of Avogadro's number?
Answer:
N_A = 6.023 x 10²³.

Question 10.
At what temperature all molecules of the gas becomes speedless?
Answer:
At absolute zero temperature.

Question 11.
What is the volume of 1 mol of gas at N.T.P?
Answer:
22.4 litre.

Question 12.
What will be the relation between pressure P and density ρ for an ideal gas at constant temperature?
Answer:
Gas pressure P = \(\frac{1}{3} \rho \bar{v}^2\)
or \(\frac{P}{\rho}=\frac{1}{3} \bar{v}^2\)
∵ Temperature is constant so, \(\bar{v}^2\) will be constant, 
∴ \(\frac{P}{\rho}\) = constant.

Question 13.
Ideal gas cannot be converted into solid or liquid, why?
Answer:
Attraction force between the molecules of an ideal gas is zero, so it cannot be converted into solid or liquid.

Question 14.
Write S.I. unit of gas constant.
Answer:
J mol^-1K^-1.

Question 15.
At which temperature does all molecules motion cease?
Answer:
At zero kelvin.

Question 16.
What is the nature of graph between pressure (P) and volume (K) for a given mass of a gas at a fixed temperature?
Answer:
It is a rectangular hyperbola.

Question 17. 
What is the lowest temperature attainable according to Charles’ law?
Answer:
-273.15°C.

Question 18.
Does the average K.E. per molecule of the gas depend upon the mass of the molecule?
Answer:
No.

Question 19.
Define absolute zero, according to kinetic interpretation of temperature.
Answer:
Absolute zero is the temperature at which all molecular motion ceases.

Question 20.
How is the average K.E. of a gas molecule related to the temperature of the gas?
Answer:
Average K.E. of a gas molecule
\(\frac{1}{2} m\bar{v}^2 = \frac{3}{2} kB T\)

Question 21.
The absolute temperature of a gas is increased four times its original value, what will be the change in r.m.s. velocity of its molecules?
Answer:

Change in r.m.s. velocity of molecules
= v'_rms - v_rms = v_rms
Thus, the change in r.m.s. velocity will be equal to its initial value.

Question 22.
A gas enclosed in a vessel has pressure P, volume V and absolute temperature T. Write the formula for the number of molecules N of the gas.
Answer:
N = \(\frac{P V}{k_B T}\)

Question 23.
The velocities of three molecules are 3v, 4v and 5v. Determine the root mean square velocity.
Answer:
v_rms = \(\sqrt{\frac{(3 v)^2+(4 v)^2+(5 v)^2}{3}}\)
= \(\sqrt{\frac{50}{3}}\)v = 4.08 v

Question 24.
A mixture of He and hydrogen gases is filled in a vessel at 30°C. Compare the root mean square velocities of the molecules of these gases at this temperature. Atomic weight of hydrogen = 4.
Answer:
\(\frac{\left(v_{\mathrm{rms}}\right)_{\mathrm{He}}}{\left(v_{\mathrm{rms}}\right)_{\mathrm{H}}}=\sqrt{\frac{M_{\mathrm{H}}}{M_{\mathrm{He}}}}=\sqrt{\frac{2}{4}}=1: \sqrt{2}\)

Question 25.
What is the mean translational kinetic energy of a perfect gas molecule at temperature T?
Answer:
K.E. = \(\frac{3}{2}\) k_B T.

Question 26.
What is the translational K.E. per unit volume of a gas whose pressure is P?
Answer:
E = \(\frac{3}{2}\)P.

Question 27.
What is the mean translational kinetic energy of a perfect gas molecule at temperature T?
Answer:
A perfect gas molecule has only translational K.E., E = \(\frac{3}{2}\)k_BT.

Question 28.
Name two factors on which the degrees of freedom of a gas molecules depends.
Answer:
Degrees of freedom of a gas depends upon;

• Atomicity of the gas molecules
• Shape of the molecules
• Temperature of the gas

Short Answer Questions

Question 1.
Explain briefly the postulates of kinetic theory of gases.
Answer:
The law of equipartition of energy states that, “for any dynamical system in a thermal equilibrium, the total energy is equally divided among the degrees of freedom.” The energy related with a molecule for one degree of freedom is \(\frac{1}{2}\)kBT where kB is Boltzmann’s constant and T is absolute temperature.
According to kinetic theory of gases, the average kinetic energy per molecule is

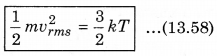
where, k = \(\frac{R}{N}\)
A monoatomic gas has three degrees of freedom. So, average kinetic energy per degree of freedom is \(\frac{1}{2}\)kT. Let N atoms be there in one mole of a gas. So, total energy per mole of the gas
= 3 x \(\frac{1}{2} \)kT x N = \(\frac{3}{2}\)RT. .........................(13.59)
In diatomic gas, there are five degrees of freedom. The average kinetic energy per molecule
= \(\frac{5}{2}\)kT x N = \(\frac{5}{2} \)kT.
The total energy per mole of the gas
= \(\frac{5}{2} \) kT x N = \(\frac{5}{2} \)NkT
= \(\frac{5}{2}\) RT .................(13.60)
In non-linear triatomic molecule, there are six degrees of freedom. So, average kinetic energy per molecule = 6 x \(\frac{1}{2}\) kT
= 3kT .....................(13.61)
The total energy per molecule
= 3kT x N = 3 NkT = 3 RT ........................(13.62)

Question 2.
Discuss the physical properties of a gas according to the postulates of kinetic theory of gases.
Answer:
The law of equipartition of energy states that, “for any dynamical system in a thermal equilibrium, the total energy is equally divided among the degrees of freedom.” The energy related with a molecule for one degree of freedom is \(\frac{1}{2}\)kBT where kB is Boltzmann’s constant and T is absolute temperature.
According to kinetic theory of gases, the average kinetic energy per molecule is

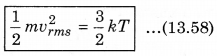
where, k = \(\frac{R}{N}\)
A monoatomic gas has three degrees of freedom. So, average kinetic energy per degree of freedom is \(\frac{1}{2}\)kT. Let N atoms be there in one mole of a gas. So, total energy per mole of the gas
= 3 x \(\frac{1}{2}\) kT x N = \(\frac{3}{2}\)RT. .........................(13.59)
In diatomic gas, there are five degrees of freedom. The average kinetic energy per molecule
= \(\frac{5}{2}\)kT x N = \(\frac{5}{2}\) kT.
The total energy per mole of the gas
= \(\frac{5}{2}\) kT x N = \(\frac{5}{2}\) NkT
= \(\frac{5}{2}\) RT .................(13.60)
In non-linear triatomic molecule, there are six degrees of freedom. So, average kinetic energy per molecule = 6 x \(\frac{1}{2}\) kT
= 3kT .....................(13.61)
The total energy per molecule
= 3kT x N = 3 NkT = 3 RT ........................(13.62)

Question 3.
Describe the temperature according to the kinetic theory of gases.
Answer:
The law of equipartition of energy states that, “for any dynamical system in a thermal equilibrium, the total energy is equally divided among the degrees of freedom.” The energy related with a molecule for one degree of freedom is \(\frac{1}{2}\)kBT where kB is Boltzmann’s constant and T is absolute temperature.
According to kinetic theory of gases, the average kinetic energy per molecule is

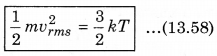
where, k = \(\frac{R}{N}\)
A monoatomic gas has three degrees of freedom. So, average kinetic energy per degree of freedom is \(\frac{1}{2}\)kT. Let N atoms be there in one mole of a gas. So, total energy per mole of the gas
= 3 x \(\frac{1}{2}\) kT x N = \(\frac{3}{2}\)RT. .........................(13.59)
In diatomic gas, there are five degrees of freedom. The average kinetic energy per molecule
= \(\frac{5}{2}\)kT x N = \(\frac{5}{2}\) kT.
The total energy per mole of the gas
= \(\frac{5}{2}\) kT x N = \(\frac{5}{2}\) NkT
= \(\frac{5}{2}\) RT .................(13.60)
In non-linear triatomic molecule, there are six degrees of freedom. So, average kinetic energy per molecule = 6 x \(\frac{1}{2}\) kT
= 3kT .....................(13.61)
The total energy per molecule
= 3kT x N = 3 NkT = 3 RT ........................(13.62)

Question 4.
What do you understand by degree of freedom?
Answer:
The number of independent ways in which a molecule of gas can move is called the degree of freedom. It is an independent physical parameter in the formal description of the state of a physical system. The degrees of freedom refers to the number of ways a molecule in the gas phase may move, rotate, or vibrate in space. The number of degrees of freedom a molecule possesses plays a role in estimating the values of various thermodynamic variables using the equipartition theorem. There are three types of degrees of freedom, such as translational, rotational, and vibrational. The number of degrees of freedom of each type possessed by a molecule depends on both the number of atoms in the molecule and the geometry of the molecule, with geometry referring to the way in which the atoms are arranged in space.

Question 5.
Explain Boyle’s law from kinetic theory of gases.
Answer:
According to kinetic theory, the average kinetic energy of molecules of a gas is directly proportional to the absolute temperature of gas. So,
\(\frac{1}{2} m \bar{v}^2\) = αT
Where a = proportionality constant
∴ From we get PV = \(\frac{1}{3} m N_A \bar{v}^2\)
PV = \(\frac{2}{3}\) N_AαT
If temperature T is constant, then PV = constant
i.e., the product of pressure and volume of gas at constant temperature is constant. This is Boyle's law.

Question 6.
Determine the values of C_P, C_V and γ for a monoatomic, diatomic and polyatomic gas.
Answer:
For a given mass of a gas, the amount of heat required to produce temperature difference is different for different substances. Let Q be the heat required to increase temperature by ∆T of a gas of mass m, then the specific heat can be defined as follows:

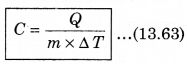
The unit of specific heat in CGS system is cal g^-1 C^-1 and in MKS unit, it is represented as J kg^-1K¹. For example the specific heat for water is 4.2 x 10³ J kg^-1 K^-1. The specific heat for gas can be from zero to infinity because if we compress a gas without heating it, then it increases the temperature.
For an adiabatic process,
Q = 0 and ∆T = positive, then C = 0
If on heating the gas, the gas expands such that there is no increase in the temperature, i.e., for isothermal process, then, from equation (13.63)
C = \(\frac{Q}{m \times 0}\) = ∞ [∵ ∆T = 0] ......................(13.64)
Generally, to determine the amount f specific heat of a gas, pressure or volume is kept constant.

Generally, there are two types of specific heats:
1. Specific Heat at Constant Volume: The amount of heat required to increase the temperature by 1°C of a gas of mass 1 g at constant volume is called
specific heat at constant volume (C_V).

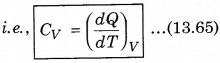
2. Specific Heat at Constant pressure: At constant pressure, the amount of heat required to raise the temperature by 1°C is called specific heat at constant pressure (C_P)

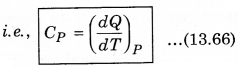
It is important to note that for a gas, the value of C_P is more than C_V, because the heat given at constant pressure, to increase the temperature by 1°C of a gas of mass 1 gm is more than that at constant volume. The difference of the two (C_P - C_V) is equal to the universal gas constant R, i.e.,

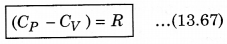
The above relation is called Mayer’s relation.
Consider 1 g molecules of an ideal gas to be at absolute temperature T, and total energy of its molecules is equal to its total kinetic energy. If N_A is Avogadro’s number, then internal energy.
U = N x Average kinetic energy of one molecule. If degree of freedom of each molecule of gas is f, then the internal energy of the gas,
U = N_A x f x \(\frac{1}{2}\)k_BT
or, U = \frac{f}{2}RT ..................(13.68)
Substituting the value of U from equation (13.68) to equation (13.67), specific heat at constant volume (here dQ = dU, from first law of thermodynamics)
C_V = \(\left(\frac{d U}{d T}\right)_V=\frac{d}{d t}\left(\frac{f}{2} R T\right)=\frac{f}{2} R\) ......................(13.69)
From equation (13.67) and (13.68),
C_P - f\(\frac{R}{2}\) = R

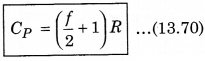
We know that, the ratio of C_P and C_V is represented in γ as:

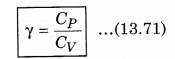
From equation (13.69) and (13.70), putting the values of C_P and C_V in equation (13.71)

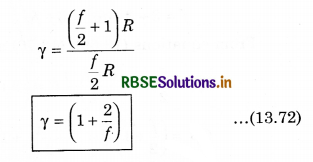
Question 7.
Explain mean free path for a gas molecule.
Answer:
A gas molecule’s mean free path λ is its average path length between collisions.
Mathematically the mean free path can be represented as follows:
λ = \(\frac{1}{\sqrt{2} \pi d^2 \frac{N}{V}}\)
Let’s look at the motion of a gas molecule inside an ideal gas; a typical molecule inside an ideal gas will abruptly change its direction and speed as it collides elastically with other molecules of the same gas. Though between the collisions, the molecule will move in a straight line at some constant speed, this is applicable for all the molecules in the gas. It is difficult to measure or describe this random motion of gas molecules thus, we attempt to measure its mean free path λ.

As its name says, λ is the average distance travelled by any molecule between collisions, we expect λ to vary inversely with N/V, which is the number of molecules per unit volume or the density of molecules because if there are more molecules, more are the chances of them colliding with each other hence reducing the mean free path, and also λ would be inversely proportional to the diameter d of the molecules, because if the molecules were point masses, then they would never collide with each other, thus larger the molecule smaller the mean free path. It should be proportional to π times the diameter square and not the diameter itself because we consider the circular cross-section and not the diameter itself.

Question 8.
What would be the change in pressure if the number of molecules in a container gets doubled?
Answer:
Pressure of the gas
P = \(\frac{1}{3} \frac{m n}{V} \bar{v}^2\)
When the number of molecules gets doubled i.e., n' = 2 n, the new pressure
P' = \(\frac{1}{3} \frac{m 2 n}{V} \bar{v}^2=2 \times \frac{1}{3} \frac{m n \bar{v}^2}{V}\)
∴ P' = 2P
∴ The pressure also double.

Question 9.
Although the root mean square speed of gas molecules is of the order of the speed of sound in that gas, yet on opening a bottle of ammonia in one corner of a room its smell takes time in reaching the other corner. Why?
Answer:
The molecules of ammonia have random motion. They frequently collide with one another. Consequently, their net speed in any particular direction is low, so gas takes several seconds to go from one corner to the other corner of the room.

Question 10.
The ratio of vapour densities of two gases at the same temperature is 8 : 9. Compare the r.m.s. velocities of their molecules.
Answer:

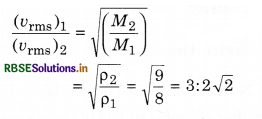
Question 11.
At what temperature does all molecular motion ceases? Explain.
Answer:
All molecular motion ceases at absolute zero or at 0 K. According, to the kinetic interpretation of temperature,
\(\bar{E}=\frac{3}{2} k_B T\)
or T = \(\frac{2}{3} \frac{\bar{E}}{k_B}\)
or Absolute temperature a Average K.E. of molecules
∴ at temperature = 0 K, average K.E. = 0
Thus, at 0 K the velocity of molecules becomes zero.

Question 12.
For an ideal gas, the internal energy can only be translational kinetic energy. Explain.
Answer:
In an ideal gas, the molecules can be considered as point masses with no intermolecular forces between them. So there can neither be internal potential energy nor the internal energy due to rotation or vibration. The molecules can have only translational kinetic energy.

Question 13.
Deduce the dimensional formula for R used in an ideal gas equation PV = nRT
Answer:

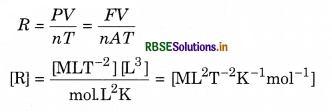
Question 14.
A sample of an ideal gas occupies a volume V at a pressure P and absolute temperature T. The mass of each molecule is m. If kB is the Boltzmann’s constant, then write the expression for the density of the gas.
Answer:
According to kinetic theory of gases,

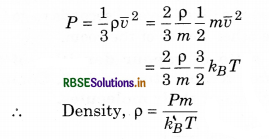
Question 15.
Write the equation of state for 16 g of O₂.
Answer:
Number of mol in 32 g of O₂ = 1
∴ Number of moles in 16 g of O₂ = \(\frac{1}{32}\) x 16 = \(\frac{1}{2}\)
As PV = nRT and n = \(\frac{1}{2}\)
so PV = \(\frac{1}{2}\)RT

Question 16.
Should the specific heat of monoatomic gas be less than, equal to or greater than that of a diatomic gas at room temperature? Justify your answer.
Answer:
The specific heat of a gas at constant volume is equal to \(\frac{f}{2} \)R.
For monoatomic gases, f = 3, so C_V = \(\frac{3}{2}\)R
For diatomic gases, f = 5, so C_V = \(\frac{5}{2} \)R
Hence, the specific heat for monoatomic gas is less than that for a diatomic gas.

Question 17.
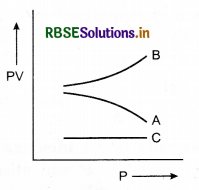
Figure shows variation of the product PV with respect to the pressure (P) of given masses of three gases A, B and C. The temperature is kept constant. State with proper arguments which of these gases is ideal.
Answer:
Gas C is ideal, because PV is constant for it, that is, gas C obeys Boyle’s law at all pressures.

Question 18. 
In an experiment a gas obeys an

additional law VP² = constant. Initially the temperature of the gas is T and volume is V. After expansion, its temperature becomes 2V, then what will be its temperature?
Answer:
Ideal gas equation PV = RT
Applicable to all processes.
Additional condition is
VP² = constant ........................(1)
From, ideal gas equation

Question 19.
N molecules of gas A (each of mass m) and 2N molecules of gas B (each of mass 2m) are put in a pot at temperature T. Mean square velocity of molecules of gas B is \(\bar{v}^2\) and x-component of mean square velocity of molecules of gas A is l², then calculate \(\frac{l^2}{v^2}\).
Answer:
Root mean square velocity of gas molecules = \(\frac{3 k T}{m}\)
For gas A, x-component of root mean square velocity of molecules = l²
∴ Square mean velocity
= 3l² = \(\frac{3 k T}{m}\) .........................(1)
For gas B, root mean square velocity
\(\bar{v}^2=\frac{3 k T}{2 m}\) ..................(2)
From equations (1) and (2)
\(\frac{3 l^2}{v^2}=\frac{2}{1}\)
∴ \(\frac{l^2}{v^2}=\frac{2}{3}\)

Question 20.
A pot is filled with a gas at pressure P₀. If mass of molecules become half and speed is doubled, then what will be the resultant pressure?
Answer:
From molecular theory,

Question 21.
In pot A, pressure of a gas is P, volume V and temperature is T. While in another pot B, pressure of the same gas is 2P, volume \(\frac{V}{4}\) and temperature is 2T. Then calculate ratio of the number of molecules in pot A and pot B.
Answer:
From ideal gas equation,

Match the following

Question 1.

Column I	Column II
(A) Avogadro’s number	(p) ms-1
(B) Gas constant	(q) [ML2T-2K-1]
(C) Most probable speed	(r) µ-1
(D) Root mean square speed	(s) J/K-1

Answer:

Column I	Column II
(A) Avogadro’s number	(r) µ-1
(B) Gas constant	(q) [ML2T-2K-1]
(C) Most probable speed	(p) ms-1
(D) Root mean square speed	(s) J/K-1

Question 2.
Match the following:
In V-T graph shown in figure 9(f).6, match the following:

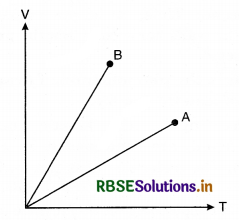
Column I	Column II
(A) \(\frac{n_B}{n_A}\)	(p) > 1
(B) \(\frac{P_B}{P_A}\)	(q) < 1
(C) \(\left(\frac{n}{P}\right)_A>\left(\frac{n}{P}\right)_B\)	(r) cannot say
(D) A is monotomic; B is diatomic	(s) true

Answer:

Column I	Column II
(A) \(\frac{n_B}{n_A}\)	(r) cannot say
(B) \(\frac{P_B}{P_A}\)	(r) cannot say
(C) \(\left(\frac{n}{P}\right)_A>\left(\frac{n}{P}\right)_B\)	(s) true
(D) A is monotomic; B is diatomic	(r) cannot say

Conceptual Questions

Question 1.
Two different gases have exactly the same temperature. Does this mean that their molecules have the same rms speed?
Answer:
When two different gases have exactly the same temperature, then their molecules do not have the same rms speed as the different gases may have molecules of different masses.

Question 2.
A gas is filled in a cylinder fitted with a piston at a definite temperature and pressure. Explain on the basis of kinetic theory, the pressure of the gas increses by raising its temperature.
Answer:
When temperature is raised, the average velocity of the gas increases. The larger number of molecules collide with the walls of the cylinder and thus, greater momentum is transferred per second to the walls. The pressure increases as
P = \(\frac{m n C^2}{3 V}\)

Question 3.
On reducing the volume of the gas at constant temperature, the pressure of the gas increases. Explain on the basis of kinetic theory.
Answer:
On reducing the volume, the number of molecules per unit volume increases. Hence, more number of molecules collide with the walls of the vessel per second. Thus, a larger momentum is transferred to the walls per second. So, the pressure of the gas increases.

Question 4.
Explain the phenomenon of evaporation on the basis of kinetic theory.
Answer:
According to the kinetic theory, the molecules (in liquid) are continuously in a state of random motion. The molecules near the surface have kinetic energy to overcome the intermolecular attraction of other molecules on the surface and hence leaves. These molecules (left) move freely above the liquid. This happens in evaporation.

Question 5.
Why cooling is caused by evaporation?
Answer:
Evaporation takes place because of faster molecules that escape from the liquid surface. So, the liquid is left with slow moving molecules. The reduction in the average speed of the molecules results in lower temperature. So, cooling is caused by evaporation.

Question 6.
Explain the rise temperature on heating on the basis of kinetic theory.
Answer:
When a gas is heated, the rms speed of the molecules in gas increases. So, the temperature of the gas increases.

Long Answer Questions

Question 1.
Give the laws of Boyle, Charles, Gay-Lussac and Dalton by writing the postulates of kinetic theory of gases.
Answer:
Boyle’s Law
According to the kinetic theory, the average kinetic energy of molecules of a gas is directly proportional to the absolute temperature of the gas. So, from equation (13.21).
\(\frac{1}{2} m \overline{v^2}=\alpha T\) ......................(13.24)
where α is a proportional constant.
From equation (13.17), we get

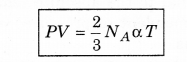
If temperature (T) is constant, then

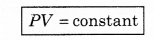
i.e., the product of pressure and volume of gas at constant temperature is constant. This is Boyle's law.

Charles’ Law
From equation (13.25), if pressure (P) of a gas is constant, then
V ∝ T ................(13.25)
i.e., for a gas of a given mass, volume of gas is directly proportional to the temperature at constant pressure. This is Charles’ law.

Gay Lussac's Law
From equation (13.17),
P = \(\frac{1}{3} \frac{m N}{V} \overline{v^2}\) ..........................(13.27)
Since, from equation (13.20),
\(\overline{v^2}=\frac{3 k_B T}{m}\)
By putting the value of \(\overline{v^2}\) in equation (13.27), we have

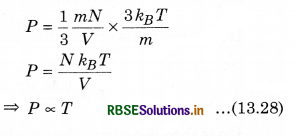
So, at constant volume for a gas of given mass, the pressure of a gas is directly proportional to the temperature of gas. This is Gay Lussac's law.

Dalton's Law of Partial Pressure
According to Dalton’s law ot partial pressure, in thermal equilibrium state, the total pressure of each gas is equal to the sum of the different pressures of each gas for a mixture of unreactive gases filled in a container, i.e., if P₁, P₂, P₃, ... respectively are the different pressure of gases, then, the total pressure (P)
P = P₁ + P₂ + P₃ + ..........................(13.41)
Let the gases be filled in a container with volume V in which the number of molecules are n₁, n₂, n₃, .......................... respectively, \(\frac{m_1}{2}, \frac{m_2}{2}, \frac{m_3}{2}, ..................\) be the mass of each molecules, and v₁, v₂, v₃, ............... respectively be the mean square speed.
Now, according to the kinetic theory, the pressure on the first gas

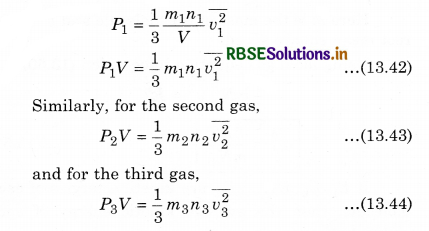
Similarly, we can write equation for other gases. Since the mixture of all the gases are in thermal equilibrium state. i.e.,the temperature is same. Then, average kinetic energy of each molecule of a gas will be equal, i.e.,

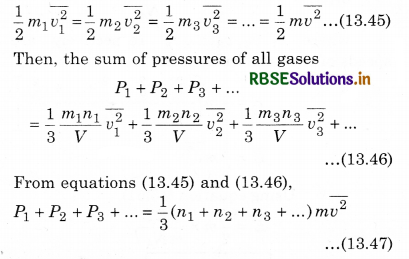
If the total pressure of container is P and the total number of molecules are (n₁ + n₂ + n₃ + ...), then the total applied pressure,
P = \(\frac{1}{3}\)(n₁ + n₂ + n₃ + .................) m \(\overline{v^2}\) .........................(13.48)
i.e., P = P₁ + P₂ + P₃ + ....................... (13.49)
This is Dalton's law of partial pressure.

Question 2.
Calculate the pressure on the walls of container filled with gas according to kinetic theory.
Answer:
Consider a gas enclosed in a cube. Let the axes be parallel to the sides of the cube (Fig. 13.3).

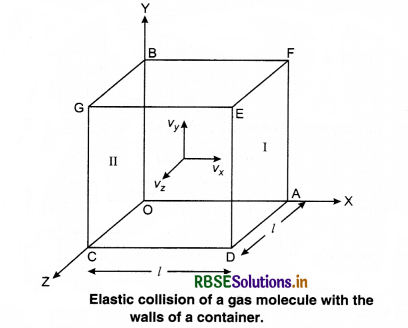
A molecule having velocity (V_x, V_y, V_z) hits the planar wall parallel to yz plane of area A(l²). As the collision is elastic, the molecule rebounds with the same velocity, y and z components of velocity do not change in the collision but the sign of x-component is reversed. Then, the velocity of collision is (-V_x, V_y, V_z). 
The change in momentum of molecule,
= -mV_x - (mV_x) = -2 mV_x .........................(13.9)
According to the principle of conservation of momentum, the momentum imported to wall (in collision) = 2mV. Consider a small time interval ∆t, a molecule with velocity V_x will hit the wall when it is within the volume of AV_x ∆t and can hit the wall in time ∆t. The number of molecules with velocity (V_x, V_y, V_z) hitting the wall in time ∆t is AV_x ∆t n where n is the number of molecules per unit volume.
The total momentum transferred to wall by these molecules in time ∆t is:

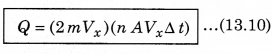
The force on the wall is the rate of momentum transfer Q/∆t and pressure = \(\frac{\text { Force }}{\text { Area }}\)
∴ P = \(\frac{Q}{A \Delta t}\) = n m V_x² ..........................(13.11)
There is a distribution in velocities. So, equation (13.11) stands for pressure due to the group of molecules having velocity V in x-direction and n is the number density of these molecules. 
The total pressure is

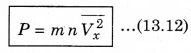
Here \(\overline{V_x^2}\) is average of V_x².
If the gas is isotropic, i.e., the velocity of molecules in the vessel has no preferred direction.
So, by symmetry,

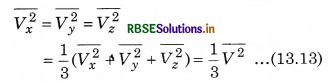
where V is speed and \(\overline{V^2}\) is the root mean square speed.

Remarks:
1. The shape of the vessel is immaterial. We always choose an infinitesimal (planar) area.
2. In the derivation, we have ignored many collisions. The number of molecules hitting the wall in time ∆t was n AV_x ∆t. The collisions are random and the gas is in a steady state. So, if a molecule having velocity (V_x, V_y, V_z) acquires a different velocity due to the collision with some molecule, then some other molecules with different initial velocity will acquire velocities (V_x, V_y, V_z) after collision. If it were not so, the distribution of velocities won’t be steady.

Question 3.
What is meant by degree of freedom. Explain the specific heats for monoatomic, diatomic and polyatomic gases.
Answer:
A degree of freedom is an independent physical parameter in the formal description of the state of a physical system. In three-dîmensional space, three degrees of freedom are associated with the movement of a particle.

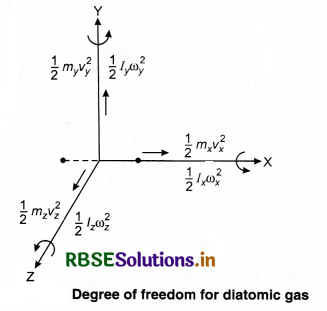
A diatomic gas molecule thus has six degrees of freedom. This set may be split in terms of translations, rotations, and vibrations of the molecule. The centre of mass motion of the whole molecule accounts for three (3) degrees of freedom. Also, the molecule has two rotational degrees of motion and one vibrational degree of freedom.
For a non-linear molecule with N > 2 atoms, 3 rotational degrees of freedom are taken that results in the decomposition
3N = 3 + 3 + (3N - 6)
We can also count the degree of freedom using the minimum number of coordinates needed to specify a position.

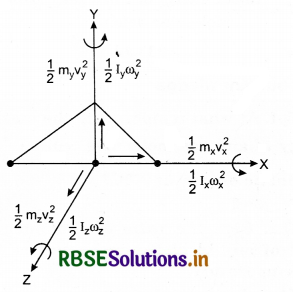
1. For a single particle, we require two coordinates in 2 - D plane and three coordinates in 3 - D plane, to specify its position. Thus, in a 3 - D space, its degree of formation is 3.
2. For a body consisting of two particles (a diatomic molecule) in a 3 - D space with constant distance between them. Its degree of freedom is 5.

For a given mass of a gas, the amount of heat required to produce temperature difference is different for different substances. Let Q be the heat required to increase temperature by ∆T of a gas of mass m, then the specific heat can be defined as follows:

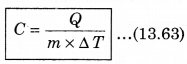
The unit of specific heat in CGS system is cal g^-1 C^-1 and in MKS unit, it is represented as J kg^-1K¹. For example the specific heat for water is 4.2 x 10³ J kg^-1 K^-1. The specific heat for gas can be from zero to infinity because if we compress a gas without heating it, then it increases the temperature.
For an adiabatic process,
Q = 0 and ∆T = positive, then C = 0
If on heating the gas, the gas expands such that there is no increase in the temperature, i.e., for isothermal process, then, from equation (13.63)
C = \(\frac{Q}{m \times 0}\) = ∞ [∵ ∆T = 0] ......................(13.64)
Generally, to determine the amount f specific heat of a gas, pressure or volume is kept constant.
Generally, there are two types of specific heats:
1. Specific Heat at Constant Volume: The amount of heat required to increase the temperature by 1°C of a gas of mass 1 g at constant volume is called specific heat at constant volume (C_V).

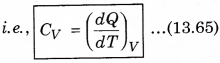
2. Specific Heat at Constant pressure: At constant pressure, the amount of heat required to raise the temperature by 1°C is called specific heat at constant pressure (C_P)

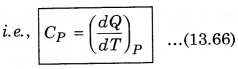
It is important to note that for a gas, the value of C_P is more than C_V, because the heat given at constant pressure, to increase the temperature by 1°C of a gas of mass 1 gm is more than that at constant volume. The difference of the two (C_P - C_V) is equal to the universal gas constant R, i.e.,

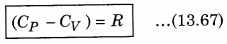
The above relation is called Mayer’s relation.
Consider 1 g molecules of an ideal gas to be at absolute temperature T, and total energy of its molecules is equal to its total kinetic energy. If N_A is Avogadro’s number, then internal energy.
U = N x Average kinetic energy of one molecule. If degree of freedom of each molecule of gas is f, then the internal energy of the gas,
U = N_A x f x \(\frac{1}{2}\)k_BT
or, U = \(\frac{f}{2}\)RT ..................(13.68)
Substituting the value of U from equation (13.68) to equation (13.67), specific heat at constant volume (here dQ = dU, from first law of thermodynamics)
C_V = \(\left(\frac{d U}{d T}\right)_V=\frac{d}{d t}\left(\frac{f}{2} R T\right)=\frac{f}{2} R\) ......................(13.69)
From equation (13.67) and (13.68),
C_P - f\(\frac{R}{2}\) = R

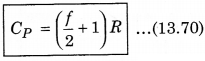
We know that, the ratio of C_P and C_V is represented in γ as:

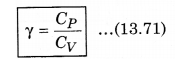
From equation (13.69) and (13.70), putting the values of C_P and C_V in equation (13.71)

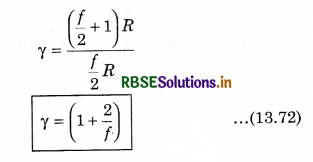
Question 4.
Derive the relation between kinetic energy of ideal gas and temperature.
Answer:
The law of equipartition of energy states that, “for any dynamical system in a thermal equilibrium, the total energy is equally divided among the degrees of freedom.” The energy related with a molecule for one degree of freedom is \(\frac{1}{2}\)k_BT where k_B is Boltzmann’s constant and T is absolute temperature.
According to kinetic theory of gases, the average kinetic energy per molecule is

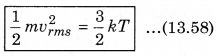
where, k = \(\frac{R}{N}\)
A monoatomic gas has three degrees of freedom. So, average kinetic energy per degree of freedom is \(\frac{1}{2}\)kT. Let N atoms be there in one mole of a gas. So, total energy per mole of the gas
= 3 x \(\frac{1}{2}\) kT x N = \(\frac{3}{2}\)RT. .........................(13.59)
In diatomic gas, there are five degrees of freedom. The average kinetic energy per molecule
= \(\frac{5}{2}\)kT x N = \(\frac{5}{2}\) kT.
The total energy per mole of the gas
= \(\frac{5}{2} \)kT x N = \(\frac{5}{2}\) NkT
= \frac{5}{2} RT .................(13.60)
In non-linear triatomic molecule, there are six degrees of freedom. So, average kinetic energy per molecule = 6 x \(\frac{1}{2}\) kT
= 3kT .....................(13.61)
The total energy per molecule
= 3kT x N = 3 NkT = 3 RT ........................(13.62)

Question 5.
What are the basic assumptions of kinetic theory of gases? On their basis derive an expression for the pressure exerted by an ideal gas.
Answer:
The main assumptions of kinetic theory of gases are:
1. A gas is made up of a large number of sub microscopic particles called atoms.
2. Gases consist of particles in constant random motion. They continue to move in a straight line until they collide with each other on the walls of their container.
3. Gas pressure is due to the molecules colliding with the walls of the container. All of these collisions are perfectly elastic. This means that there is no change in energy of either the particles or the wall upon collision. So, no energy is lost or gained fram collisions i.e.,the collisions are perfectly elastic.
4. No molecular forces are at work. The potential energy of molecules is zero. So, whole of the energy in an ideal gas is kinetic energy only. There is no attraction or repulsion between the particles.
5. The time taken for the collision is negligible as compared with the time between collisions. i.e., The collisions are almost instantaneous.
6. The kinetic energy of a gas is a measure of its kelvin temperature. Each gas molecule has different speed but the temperature and kinetic energy of gas refer to the average of these speeds.
7. The average kinetic energy of an atom of gas is directly proportional to the temperature. An increase in temperature increases the speed in which the gas molecules move.
8. AIl gases at a given temperature have same average kinetic energy.
9. Lighter molecules of a gas move faster than the heavier molecules.

Explanation of Physical Properties of Gases on the Basis of Kinetic Theory
The physical properties of gases on the basis of kinetic theory can be explained as:
1. According to the kinetic theory of gases, the gas molecules have free space between them as they are far away from each other. So, gases can be easily compressed, and if two gas containers are joined, then .the density in both the gas containers will become equal.
2. As there is no force of attraction between the gas molecules and there is more kinetic energy due to which gas molecules move to the free space available. That is why, gases have no fixed shape and no fixed volume. Thus, gases get completely filled in the container in which they are kept. Example : When the lid of a perfume bottle is open, the aroma gets filled in the room.

Consider a gas enclosed in a cube. Let the axes be parallel to the sides of the cube (Fig. 13.3).

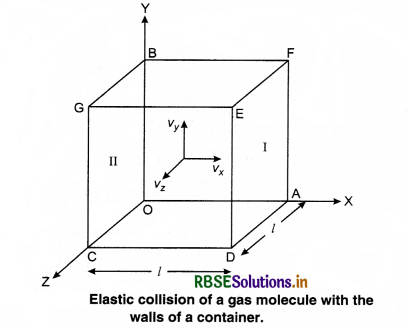
A molecule having velocity (V_x, V_y, V_z) hits the planar wall parallel to yz plane of area A(l²). As the collision is elastic, the molecule rebounds with the same velocity, y and z components of velocity do not change in the collision but the sign of x-component is reversed. Then, the velocity of collision is (-V_x, V_y, V_z). 
The change in momentum of molecule,
= -mVx - (mV_x) = -2 mV_x .........................(13.9)
According to the principle of conservation of momentum, the momentum imported to wall (in collision) = 2mV. Consider a small time interval ∆t, a molecule with velocity V_x will hit the wall when it is within the volume of AV_x ∆t and can hit the wall in time ∆t. The number of molecules with velocity (V_x, V_y, V_z) hitting the wall in time ∆t is AV_x ∆t n where n is the number of molecules per unit volume.
The total momentum transferred to wall by these molecules in time ∆t is:

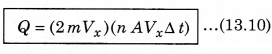
The force on the wall is the rate of momentum transfer Q/∆t and pressure = \(\frac{\text { Force }}{\text { Area }}\)
∴ P = \(\frac{Q}{A \Delta t}\) = n m V_x² ..........................(13.11)
There is a distribution in velocities. So, equation (13.11) stands for pressure due to the group of molecules having velocity V in x-direction and n is the number density of these molecules. 
The total pressure is

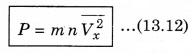
Here \(\overline{V_x^2}\) is average of V_x².
If the gas is isotropic, i.e., the velocity of molecules in the vessel has no preferred direction.
So, by symmetry,

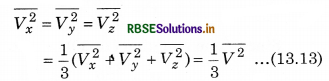
where V is speed and \(\overline{V^2}\) is the root mean square speed.

Remarks:
1. The shape of the vessel is immaterial. We always choose an infinitesimal (planar) area.
2. In the derivation, we have ignored many collisions. The number of molecules hitting the wall in time ∆t was n AV_x ∆t. The collisions are random and the gas is in a steady state. So, if a molecule having velocity (V_x, V_y, V_z) acquires a different velocity due to the collision with some molecule, then some other molecules with different initial velocity will acquire velocities (Vx, Vy, Vz) after collision. If it were not so, the distribution of velocities won’t be steady.

Question 6.
Define ideal gas and find out the phase equation of an ideal gas.
Answer:
It is easier to understand the properties of gases than those of solids and liquids, as the molecules in a gas are far apart and their mutual interactions are quite negligible except when the two molecules collide. But which gas hydrogen, nitrogen or oxygen should be chosen? Because the nature of all these gases is different. From experiments we know that if equal volume of 1 mole of different gases is filled in different containers at the same temperature, then their pressure is almost equal but not completely equal. If these observations are repeated for less dense gases, then the difference measured in the pressure is almost zero. From experiments, it is known that at less density, all the real gases obey the following relation:

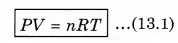
where P is absolute pressure, V is the volume of container (gas), n is the number of moles present in the gas and T is the maximum temperature (in K). In the above expressimi, R is a constant known as universal gas constant, and its value is same for all gases. In numerical form, in SI unit (when unit of pressure is pascal and volume is measured in m 3), the value of R is,

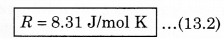
If pressure is in atmospheric unit 'atm' and volume is taken in litre, then
R = 0.82 1 L atm/mol K
In thermodynamic calculations, the value of R = 1.98 cal/mol K is also used.
Equation (13.1) is called ideal gas equation or state equation of ideal gas.

Question 7.
Explain the concept of temperature, pressure of an ideal gas and Graham diffusion law, on the basis of kinetic theory of gases.
Answer:
From ideal gas equation,

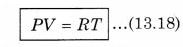
From equations (13.17) and (13.18)

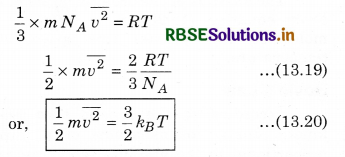
where k_B is Boltzmann's constant. From equation (13.20),

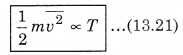
This means that the average kinetic energy of a molecule is proportional to the absolute temperature of the gas. It is independent of pressure, volume or nature of the ideal gas. This is a fundamental result that relates temperature (a macroscopic measurable of a gas) to the average kinetic energy of a molecule (a molecular quantity). Equation (13.20) tells us that the internal energy of an ideal gas depends only upon temperature, and not on pressure or volume. From this, we can say that the kinetic theory of an ideal gas is completely consistent with the ideal gas equation and with the different laws based on it. For a mixture of non-reactive ideal gases, the total pressure gets the contribution from all of the gas in the mixture. Equation (13.15) becomes
P = \(\frac{1}{3}\left(n_1 m_1 \overline{v_1^2}+n_2 m_2 \overline{v_2^2}+\ldots\right)\) .........................(13.22)
In equilibrium, the average kinetic energy of the molecules of different gases will be equal, i.e.,
\(\frac{1}{2} m_1 \overline{v_1^2}=\frac{1}{2} m_2 \overline{v_2^2}=\frac{3}{2} k_B T\)
P = (n₁ + n₂ + ......................) k_B T ............................(13.23)
This is Dalton’s law of partial pressures.
From equation (13.20), the root mean square speed of a molecule in nitrogen gas at temperature, T = 300 K can be calculated as:

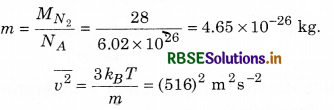
\(\overline{v^2}\) is root mean square (rms) speed and is denoted by v_rms.
So, v_rms = 516 m s^-1
The speed is of the order of speed of sound in air. From equation (13.20), it is followed that lighter molecules have greater rms speed, at the same temperature.

Graham’s Diffusion Law
According to Graham’s thffusion law, at equal pressure. the rate of diffusion (r) for a gas and the square root density of gas (p) are inversely proportional to each other, i.e.,

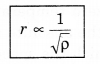
According to kinetic theory of ideal gases, pressure of gas and mean square speed \(\left(\overline{v^2}\right)\) are related as:

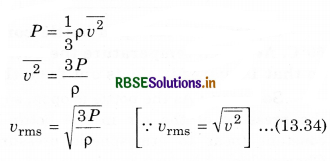
So, if pressures are equal. Then
v_rms ∝ \(\sqrt{\frac{1}{\rho}}\) ..........................(13.35)
Since the rate of diffusion will be directly proportional to the root mean square speed (v_rms), i.e.,
r ∝ v_rms ....................(13.36)
Then, from equations (13.35) and (13.36),
r ∝ \(\frac{1}{\sqrt{\rho}}\) .....................(13.37)
This is Graham's diffusion law.
If two gases A and B at same pressure have mean square speeds of \(\overline{v_1^2}\) and \(\overline{v_2^2}\) respectively, and ρ₁ and ρ₂ are densities respectively, then from equation (13.34),

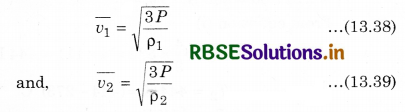
Then, from equations (13.38) and (13.39),
\(\frac{\overline{v_1}}{\overline{v_2}}=\sqrt{\frac{\rho_2}{\rho_1}}\) ...........................(13.40)
This is another form of Graham's diffusion law.

Consider a gas enclosed in a cube. Let the axes be parallel to the sides of the cube (Fig. 13.3).

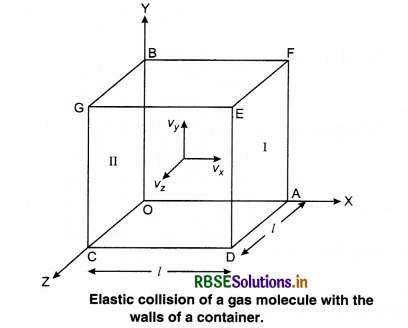
A molecule having velocity (V_x, V_y, V_z) hits the planar wall parallel to yz plane of area A(l²). As the collision is elastic, the molecule rebounds with the same velocity, y and z components of velocity do not change in the collision but the sign of x-component is reversed. Then, the velocity of collision is (-V_x, V_y, V_z). 
The change in momentum of molecule,
= -mV_x - (mV_x) = -2 mV_x .........................(13.9)
According to the principle of conservation of momentum, the momentum imported to wall (in collision) = 2mV. Consider a small time interval ∆t, a molecule with velocity V_x will hit the wall when it is within the volume of AV_x ∆t and can hit the wall in time ∆t. The number of molecules with velocity (V_x, V_y, V_z) hitting the wall in time ∆t is AV_x ∆t n where n is the number of molecules per unit volume.
The total momentum transferred to wall by these molecules in time ∆t is:

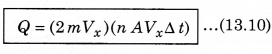
The force on the wall is the rate of momentum transfer Q/∆t and pressure = \(\frac{\text { Force }}{\text { Area }}\)
∴ P = \(\frac{Q}{A \Delta t}\) = n m V_x² ..........................(13.11)
There is a distribution in velocities. So, equation (13.11) stands for pressure due to the group of molecules having velocity V in x-direction and n is the number density of these molecules. 
The total pressure is

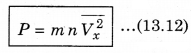
Here \(\overline{V_x^2}\) is average of V_x².
If the gas is isotropic, i.e., the velocity of molecules in the vessel has no preferred direction.
So, by symmetry,

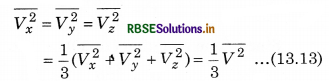
where V is speed and \(\overline{V^2}\) is the root mean square speed.

Remarks:
1. The shape of the vessel is immaterial. We always choose an infinitesimal (planar) area.
2. In the derivation, we have ignored many collisions. The number of molecules hitting the wall in time ∆t was n AV_x ∆t. The collisions are random and the gas is in a steady state. So, if a molecule having velocity (V_x, V_y, V_z) acquires a different velocity due to the collision with some molecule, then some other molecules with different initial velocity will acquire velocities (V_x, V_y, V_z) after collision. If it were not so, the distribution of velocities won’t be steady.

Question 8.
Derive theorem between kinetic energy and temperature of an total Ideas gas.
Answer:
The law of equipartition of energy states that, “for any dynamical system in a thermal equilibrium, the total energy is equally divided among the degrees of freedom.” The energy related with a molecule for one degree of freedom is \(\frac{1}{2}\)k_BT where k_B is Boltzmann’s constant and T is absolute temperature.
According to kinetic theory of gases, the average kinetic energy per molecule is

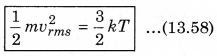
where, k = \(\frac{R}{N}\)
A monoatomic gas has three degrees of freedom. So, average kinetic energy per degree of freedom is \(\frac{1}{2}\)kT. Let N atoms be there in one mole of a gas. So, total energy per mole of the gas
= 3 x \(\frac{1}{2}\) kT x N = \(\frac{3}{2}\)RT. .........................(13.59)
In diatomic gas, there are five degrees of freedom. The average kinetic energy per molecule
= \(\frac{5}{2}\)kT x N = \(\frac{5}{2} \)kT.
The total energy per mole of the gas
= \(\frac{5}{2}\) kT x N = \(\frac{5}{2}\) NkT
= \(\frac{5}{2} \)RT .................(13.60)
In non-linear triatomic molecule, there are six degrees of freedom. So, average kinetic energy per molecule = 6 x \(\frac{1}{2}\) kT
= 3kT .....................(13.61)
The total energy per molecule
= 3kT x N = 3 NkT = 3 RT ........................(13.62)

Question 9.
Explain law of equipartition of energy.
Answer:
The law of equipartition of energy states that, “for any dynamical system in a thermal equilibrium, the total energy is equally divided among the degrees of freedom.” The energy related with a molecule for one degree of freedom is \(\frac{1}{2}\)k_BT where k_B is Boltzmann’s constant and T is absolute temperature.
According to kinetic theory of gases, the average kinetic energy per molecule is

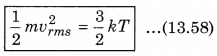
where, k = \(\frac{R}{N}\)
A monoatomic gas has three degrees of freedom. So, average kinetic energy per degree of freedom is \(\frac{1}{2}\)kT. Let N atoms be there in one mole of a gas. So, total energy per mole of the gas
= 3 x \(\frac{1}{2}\) kT x N = \(\frac{3}{2}\)RT. .........................(13.59)
In diatomic gas, there are five degrees of freedom. The average kinetic energy per molecule
= \(\frac{5}{2}\)kT x N = \(\frac{5}{2} \)kT.
The total energy per mole of the gas
= \(\frac{5}{2}\) kT x N = \(\frac{5}{2}\) NkT
= \(\frac{5}{2} \)RT .................(13.60)
In non-linear triatomic molecule, there are six degrees of freedom. So, average kinetic energy per molecule = 6 x \(\frac{1}{2} \)kT
= 3kT .....................(13.61)
The total energy per molecule
= 3kT x N = 3 NkT = 3 RT ........................(13.62)

Question 10.
What do you mean by mean free path? Derive a relation for it.
Answer:
According to the kinetic theory, the molecules of a gas move in different directions and collide with each other. The mean free path is the average distance travelled by a moving particle (such as an atom, a molecule, a photon) between successive collisions, that modify its direction.

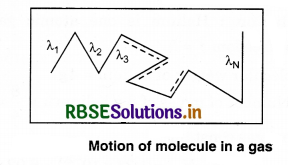
Let the distances covered by molecules of gas in N collisions be λ₁, λ₂, λ₃ ....................λ_N, then, the mean free path can be defined as
λ = \(\frac{\lambda_1+\lambda_2+\lambda_3+\ldots+\lambda_N}{N}\) .........................(13.73)
If t is the time taken to cover the path and \bar{v} is the mean speed of molecule, then
λ = \(\frac{\bar{v} t}{N}\) ........................(13.74)

Expression for Mean Free Path
Assumptions:
1. Each molecule of gas is a solid sphere of diameter, (d)
2. All molecules of gas except the molecule ‘A’ under consideration are at rest.

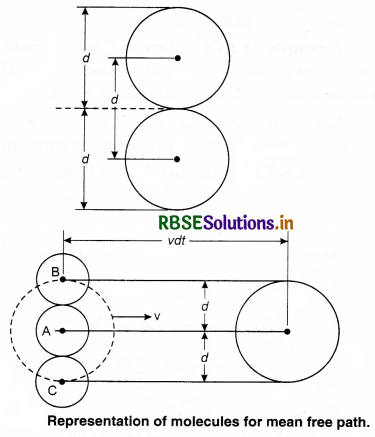
Let the number density of the gas molecules be n and d be the diameter of each molecule. The moving molecule will collide with a stationary molecule when the area of the moving molecule overlaps the area of one of the stationary molecules. 
Volume of such a cylinder = π d² vdt
Number of molecules in the cylinder = Volume of cylinder x Number of molecules per unit volume
= π d² v dt x n
= π d² v n dt
Number of collision by the molecule in time dt N,
N = π d² v n dt ...........................(13.75)
Since mean free path (λ)
λ = \(\frac{v d t}{N}\)
Using equation (13.754),
λ = \(\frac{v d t}{\pi d^2 v n d t}\)
λ = \(\frac{1}{\pi d^2 n}\) ....................(13.76)
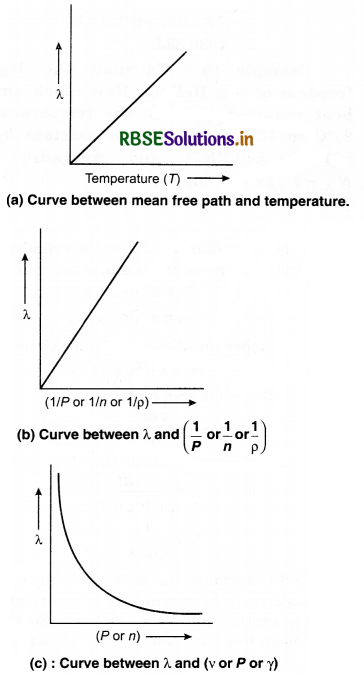
To determine the value of λ, only one molecule is considered to be moving while others are stationary, but in real, all the molecuks move. So, the expression for mean free path can be precisely written as
λ = \(\frac{1}{\sqrt{2} \pi d^2 n}\) .........................(13.77)
i.e., λ is inversely proportional to n. So, the gas molecules are inversely proportional to the density.
Again, from ideal gas equation,

i.e., Mean free path of gas molecules is directly proportional to the absolute temperature (T) and inversely proportional to the gas pressure.

Numerical Questions

Based on ideal gas equation and its laws

Question 1.
During the seal of an electric bulb of volume 250 cm³ at temperature 27°C pressure was 10^-3 mm. Find out the number of molecules in the bulb?
Solution:
Given: V = 250 cm³ = 250 x 10^-6 m³;
T = 27 + 273 = 300 K;
P = 10^-3 mm = 10^-6 m = 10^-6 x 13.6 x 10³ x 9.8 N m^-2
k_B = 1.38 x 10^-23 J K^-1

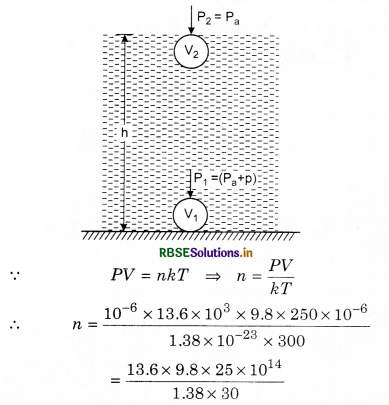
= 80.48 x 10¹⁴
= 8.048 x 10¹⁵ = 8.05 x 10¹⁵

Question 2.
An air bubble of volume 1 x 10^-6 m³ is at depth of 40 m from surface of a lake, where temperature is 283 K. When the bubble reaches at the surface of water, calculate its volume. Temperature at the surface of water is 27°C. (Atmospheric pressure = 1.01 x 10⁵ Pa)
Solution:
Given: v₁ = 1 x 10^-6 m³, h = 40 m; P_a = 1.01 x 10⁵ Pa
∴ p = h.ρ_w.g = 40 x 10³ x 9.8
= 39.2 x 10⁴ = 3.92 x 10⁵ Pa
∴ P₁ = P_a + p = (1.01 + 3.92) x 10⁵
= 4.93 x 10⁵ Pa
T = 283 K; T2 = 27 + 273 = 300 K
P₂ = P_a = 1.01 x 10⁵ Pa; V₂ = ?
∵ From ideal gas equation 

= 5.1744 x 10^-6 m³
or V₂ = 5.17 x 10^-6 m³

Question 3.
The pressure of a gas at fixed volume becomes 3000 N m^-2 from 2000 Nm^-2. If the initial temperature was 350 K, then find out the last temperature.
Solution:
P₁ = 2000 N m^-2; P₂ = 3000 N m^-2
T₁ = 350 K; T₂ = ?
From Gay Lussac's law

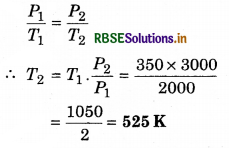
Question 4.
An empty barometer tube 1 m long is lowered vertically (mouth downwards) into a tank of water. What will be the depth above the water level in the tube, when the water has risen 20 cm inside the tube? Take 1 atm = 10.4 m column of water.
Solution:
2.6 m

Based on molecular speed

Question 5.
At constant pressure, at which temperature hydrogen gas at 327°C temperature be cooled, so that root mean square speed of the molecules becomes half of its previous value.
Solution:
T₁ = 327°C = 327 + 273 = 600 K; T₂ = ?

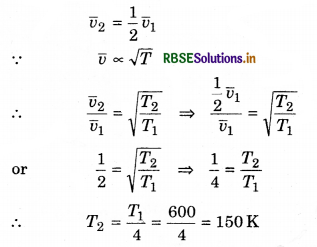
or T₂ = 150 - 273 = -123°C
or T₂ = -123°C

Question 6.
The speed of four molecules are v, 2v, 3v and 4v. Calculate the root mean square speed of the molecules.
Solution:
Root mean square speed

Question 7.
The root meah square speed of oxygen at any temperature is 150 ms^-1. Find out the root mean square speed of hydrogen at the same temperature. [M_O = 32, M_H = 2]
Solution:
v_O = 150 m s^-1; v_H = ?; M_O = 32; M_H = 2
∵ AT the same temperature E_H = E_O
∴ \(\left(\frac{v_{\mathrm{H}}}{v_{\mathrm{O}}}\right)^2=\frac{M_{\mathrm{O}}}{M_{\mathrm{H}}} \Rightarrow \frac{v_{\mathrm{H}}}{v_{\mathrm{O}}}=\sqrt{\frac{M_{\mathrm{O}}}{M_{\mathrm{H}}}}=\sqrt{\frac{32}{2}}=\sqrt{16}\)
or v_H = v_O ⇒ v_H = 4 x 150 = 600 ms^-1
or v_H = 600 m s^-1

Question 8.
The mass of dust particles performing Brownian motion in the air are 5x 10^-17 kg. Calculate the root mean square speed of these molecules. (Boltzmann constant, k = 1.38 x 10^-23 JK^-1)
Solution:
m = 5 x 10^-17 kg; T = 273 K; v_rms = ?
k = 1.38 x 10^-23 J K^-1

= 15 x 10^-3 m s^-1
= 1.5 x 10^-2 m s^-1
= 1.5 cm s^-1

Based on energy of molecules

Question 9.
Calculate for hydrogen at 27°C:
(i) Kinetic energy of 1 g molecule of gas.
(ii) Kinetic energy of 1 g of gas.
(Molecular weight of hydrogen = 2, R = 8.31 J mol^-1 K^-1)
Solution:
T = 27°C = 27 + 273 = 300 K; R = 8.31 J mol^-1 K^-1
(i) Kinetic energy of 1 g molecule or 1 mol of hydrogen
E = \(\frac{3}{2}\) RT = \(\frac{3}{2} \) x 8.31 x 300
= 3 x 8.31 x 150
= 3739.5 J
= 3.74 x 10³ J
(ii) Molecular weight of hydrogen M = 2
∵ 2 g kinetic energy of hydrogen = 3.74 x 10³ J
∴ 1 g kinetic energy of hydrogen = \(\frac{3.74 \times 10^3}{2}\)
= 1.87 x 10³ J

Question 10.
Calculate the kinetic energy of 1 g molecule of gas at N.T.P. and what will be its value at 273°C?
Solution:
Kinetic energy of 1 mol
E = \(\frac{3}{2}\) RT
At T = 273 K
E = \(\frac{3}{2}\) x 8.31 x 273 = 3402.9 J
or E = 3.40 x 10³ J
E₁ = 3.40 x 10³ J, T₁ = 273 K
E₂ = ?; T₂ = 273 + 273 = 2 x 273 K
∵ \(\frac{E_2}{E_1}=\frac{T_2}{T_1}=\frac{2 \times 273}{273}\) = 2
∴ E₂ = 2E₁ = 2 x 3.40 x 10³
or E₂ = 6.80 x 10₃ J

Question 11.
The temperature of any gas is - 68°C. At what temperature should it be heated that (i) mean kinetic energy of molecules becomes double?
(ii) Root mean square velocity of molecules becomes double?
Solution:
(i) T₁ = -68°C = -68 + 273 = 205 K; T₂ = ?
E₂ = 2E₁

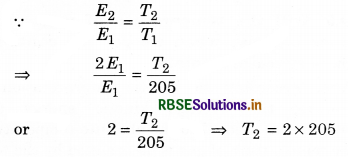
or T₂ = 410 K
= 410 - 273 = 137°C
(ii)

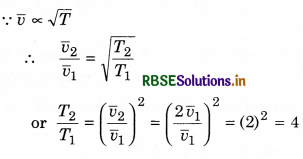
∴ T₂ = 4T₁ = 4 x 205 = 820 K
or T₂ = 820 - 273 = 547°C

Question 12.
What will be the mean kinetic energy of the molecules of any gas at 300 K temperature? At the same temperature calculate the root mean square speed of any molecule of hydrogen gas? (R = 8.31 J mole^-1 K^-1, N = 6.02 x 10²³ mol^-1, mass of hydrogen molecule = 3. 34 x 10^-27 kg)
Solution:
Mean kinetic energy of any molecule of gas
E = \(\frac{3}{2}\)k_BT = \(\frac{3}{2}\) x 1.388 x 10^-23 x 300
= \(\frac{9}{2}\) x 1.38 x 10^-21
E = 6.21 x 10^-21 J

= 1.928 x 10³
= 1.93 x 10³ m s^-1

Based on mean free path

Question 13.
Calculate the mean free path of water molecule in water vapour at 100°C and 1 atm pressure. Diameter of water molecule = 4 Å, Boltzmann constant kg = 1.38 x 10^-23 J K^-1]
Solution:
T = 100 + 273 = 373 K
P = 1 atm = 1.01 x 10⁵ N m^-2
d = 4 Å = 4 x 10^-10 m; λ = ?
∵ Mean free path

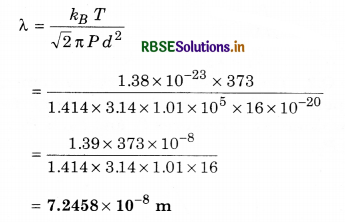
Question 14.
Calculate mean free path of nitrogen molecule at 27°C temperature while pressure is 1.5 atmosphere. (Diameter of nitrogen molecule = 1.5 Å, k= 1.38 x 10^-23 JK^-1)
Solution:
T = 27 + 273 = 300 K;
P = 1.5 atm = 1.5 x 1.01 x 10⁵ N.m^-2
d = 1.5 Å = 1.5 x 10^-10 m; k = 1.38 x 10^-23; λ = ?

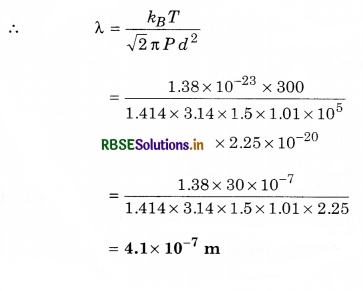
High Order Thinking Skills or Hots

Question 1.
The following graph shows the variation of pressure. P with reciprocal of volume V of an ideal gas at two constant temperatures T₁ and T₂. What inference can you draw from the graphs?
(a) T₁ > T₂, (b) T₁ < T₂, (c) T₁ = T₂.

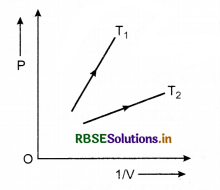
Answer:
Slope of curve PV is greater for T₁ than that for T₂.
\(\frac{P V}{T}\) = constant
⇒ \(\frac{P}{1 / V}\) ∝ T
∴ T₁ > T₂.

Question 2.
The graph shows the volume V us temperature T for a certain mass of a perfect gas at two constant pressures P₁ and P₂. Is P₁ > P₂ or P₁<P₂?

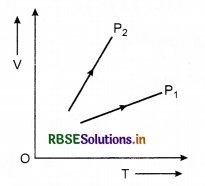
Answer:
Slope of curve (\(\frac{V}{T}\)) for P₂ is greater than that of P.
\(\frac{P V}{T}\) = constant
or \(\frac{V}{T} \propto \frac{1}{P}\)
⇒ P₁ > P₂.

Question 3.
Is Boyle’s law perfectly obeyed at all temperatures and pressures?
Answer:
No, Boyle’s law is perfectly obeyed at high temperature and low pressure of a gas.

Question 4.
The following graph shows the variation of pressure P with absolute temperature T of a certain mass of an ideal gas at two constant volume V₁ and V₂. What inference can you draw from the graphs?

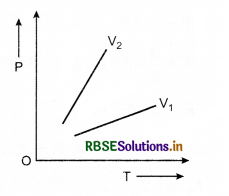
(i) V₁ > V₂, (ii) V₁ < V₂, (iii) V₁ = V₂
Answer:
Slope of (\(\frac{P}{T}\)) curve is greater for V₂ that for V₁.
\(\frac{P V}{T}\) = constant
⇒ \(\frac{P}{T} \propto \frac{1}{V}\)
⇒ V₁ > V₂.

Question 5.
Will the temperature of a gas in a container increase when we put the container on a moving train? Explain.
Answer:
According to kinetic interpretation of temperature, the average kinetic energy (per molecule) is proportional to the absolute temperature. But, the temperature of gas is determined by the total translational kinetic energy which is measured w.r.t. to the centre of the mass of the gas, and not the motion. So, there will be no change in temperature of the gas.

Question 6.
Two molecules of a gas have speeds of 9 x 10⁶ ms^-1 and 1 x 10⁶ ms^-1, respectively. What is the rms speed of these molecules?
Answer:
V_rms = \(\sqrt{\frac{V_1^2+V_2^2}{2}}\)
Here, V₁ = 9 x 10⁶ ms^-1
and, V₂ = 1 x 10⁶ ms^-1

Question 7.
Explain why:
(a) There is no atmosphere on moon?
(b) There is fall in temperature with altitude?
Answer:
(a) There is small escape velocity in case of moon, as there is small gravitational force. The rms speed of the air molecules is smaller than the escape velocity on moon, but a significant number of molecules had greater speed than the escape velocity, and hence they escaped. Now, the other molecules arranged the speed distribution for equilibrium temperature. Again a significant number of molecules escaped, because their speed exceeded the escape velocity. So, over a long time, the moon lost most of its atmosphere.

(b) When the potential energy of molecules increases, the molecules move higher, and thus kinetic energy reduces. This results in lowering of temperature. With altitude, the gas expands and hence cooling occurs.

Question 8.
An insulated container containing monoatomic gas of molar mass m is moving with a velocity V₀. If the container is suddenly stopped, find the change in temperature.
Answer:
Loss in kinetic energy of the gas, ∆E = \(\frac{1}{2}\) (mn) V₀²
where, n is number of moles
If the temperature changes by ∆T, then
\(\frac{3}{2}\) n R ∆T = \(\frac{1}{2}\)mnV₀²
∴ Change in temperature, ∆T = \(\frac{m v_0^2}{3 R}\)

Question 9.
When air is pumped into a cycle tyre, the volume and pressure of the air in the tyre both are increased. What about Boyle’s law in this case?
Answer:
When air is pumped, then more molecules are pumped in Boyle’s law is applicable when the number of molecules are constant.

Question 10.
A gas mixture consists of 2.0 moles of oxygen and 4.0 moles of neon at temperature T. Neglecting all vibrational modes, calculate the total internal energy of the system. (Oxygen has two rotational moles.)
Answer:
Oxygen has 5 degrees of freedom.
∴ Energy per mole = \(\frac{5}{2}\)RT
For 2 moles of O₂, energy = 5 RT
Neon has 3 degrees of freedom.
∴ Energy per mole = \(\frac{3}{2}\)RT
For 4 moles of Ne, energy = 4 x \(\frac{3}{2}\) RT = 6RT
∴ Total energy = 11RT 

Questions for Competitive Examinations 

Question 1.
Increase in temperature of a gas filled in a container would lead to:
(a) Increase in its mass
(b) Increase in its kinetic energy
(c) Decrease in its pressure
(d) Decrease in intermolecular distance
Solution:
(a) Kinetic energy E ∝ Temperature T
∴ With increase in temperature, K.E. increases.

Question 2.
One mole of an ideal monoatomic gas is compressed isothermally in a rigid vessel to double its pressure at room temperature 27°C. The work done on the gas will be:
(a) 300 R In 6
(b) 300 R
(c) 300 R In 7
(d) 300 R In 2
Solution:
(d) Work done on gas = nRT ln(\(\frac{P_F}{P_i}\))
= R (300) ln 2
∵ \(\frac{P_F}{P_i}\) = 2 (given)

Question 3.
A gas mixture consists of 2 moles of O₂ and 4 mol of Ar at temperature T. Neglecting all vibrational modes, the total internal energy of the system is:
(a) 15 RT
(b) 9 RT
(c) 11 RT
(d) 4 RT
Solution:
(c) U = \(\frac{f}{2} \)nRT
U_total = \(\frac{5}{2}\)(2) RT + \(\frac{3}{2}\) (4) RT
U_total = 11RT

Question 4.
The molecules of a given mass of a gas have r.m.s. velocity of 200 m s^-1 at 27°C and 1.0 x 10 N m^-2 pressure. When the temperature and pressure of the gas are respectively, 127°C and 0.05 x 10⁵ Nm^-2, the r.m.s. velocity of its molecules in m s^-1 is:

Solution:
(a) It is given that,
v_rms = 200 m s^-1; T₁ = 300 K, P₁ = 10⁵ N/m²
T₂ = 400 K, P₂ = 0.05 x 10⁵ N/m²
As r.m.s. velocity of gas molecules,

Question 5.
4 g of a gas occupies 22.4 L at N.T.P. The specific heat capacity of the gas at constant volume is 5.0 J K^-1 mol^-1. If the speed of sound in this gas at NTP is 952 ms^-1, then the heat capacity at constant pressure is:
(Take gas constant R = 8.3 JK^-1 mol^-1)
(a) 8.0 J K^-1 mol^-1
(b) 7.5 J K^-1 mol^-1
(c) 7.0 J K^-1 mol^-1
(d) 8.5 J K^-1 mol^-1
Solution:
(a) Given, m = 4g, V = 22.4 L, C_V = 5 JK^-1 mol^-1
v_sound = 952 m/s, C_P = ?

= \(\frac{20}{22.4}\) x (952)² x 10⁵
= 809.200 x 10^-5
= 8.09 J/mol K

Question 6.
The ratio of the specific heats \(\frac{C_P}{C_V}\) = γ in terms of degrees of freedom (n) is given by:

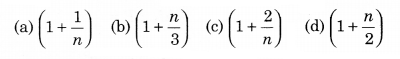
Solution:
(c) The specific heat of gas at constant volume in terms of degree of freedom n is

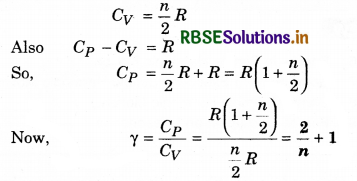
Question 7.
If the radius of molecules of any gas is r, then its mean free path will be proportional to:
(a) r³
(b) r^-2
(c) r
(d) \(\sqrt{r}\)
Solution:
(b) \(\bar{\lambda}=\frac{1}{n \pi r^2}\)
⇒ \(\bar{\lambda} ∝ \frac{1}{r^2}\)

Question 8.
For an ideal gas, the molar specific heat at constant volume and pressure are C_V and C_P respectively. If γ = C_P/C_V and R is universal gas constant, then C_V = ?:

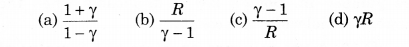
Solution:
(b) C_V = \(\frac{R}{\gamma-1}\)

Question 9.
During adiabatic process, the pressure of a gas is proportional to power of three of temperature. Then for gas the value of C_P/C_V will be:
(a) \(\frac{4}{3}\)
(b) 2
(c) \(\frac{5}{3}\)
(d) \(\frac{3}{2}\)
Solution:
(d) According to the question,
p ∝ T³
but pV = nRT
p ∝ T³
∴ p ∝ (pV)³
⇒ p² V³ = constant
pV^3/2 = constant
∵ pV^γ = constant
∴ γ = 3/2

Question 10.
C_P and C_V are specific heats at constant pressure and constant volume respectively. It is observed that:
C_P - C_V = a for hydrogen gas
C_P - C_V = b for nitrogen gas
(a) a = \(\frac{1}{14}\) b
(b) a = b
(c) a = 14b
(d) a = 28b
Solution:
(c) C_P - C_V = R
But if C_P and C_V are specific heats i.e., gram-specific heats, then
C = MS_g
{Q = 1 C∆T ⇒ Q = MS_g ∆T ⇒ C = MS_g]
S_g = \(\frac{C}{M}\)
MS_gp - MS_gv = R
S_gp - S_gv = R/M
∴ R/2 = a [As M = 2 for hydrogen]
∴ R/2 = b [As M = 28 for nitrogen]
∴ 14 = \(\frac{a}{b}\)
∴ a = 14b

Question 11.
The temperature of an open room of volume 30 m³ increases from 17°C to 27°C due to the sunshine. The atmospheric pressure in the room remains 1 x 10⁵ Pa. If n_i and n_f are the number of molecules in the room before and after heating, then n_f - n_i will be:
(a) -1.61 x 10²³
(b) 1.38 x 10²³
(c) 2.5 x 10²⁵
(d) - 2.5 x 10²⁵
Solution:
(d) pV = nRT
n = \(\frac{P V}{R T}\)
T_i = 273 + 17 = 290 K
T_f = 273 + 27 = 300 K

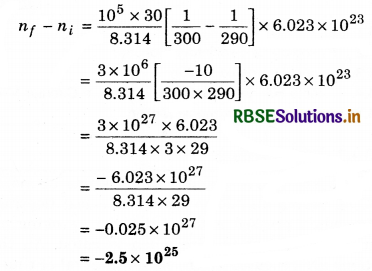
Question 12.
Consider an ideal gas confined in an isolated closed chamber. As the gas undergoes an adiabatic expansion the average time of collision between the molecules increases as Vq; where V is the volume of the gas. The value of q is (γ = C_P/C_V):

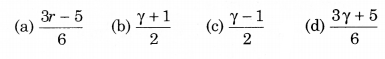
Solution:
(b) Average time between collision