RBSE Class 11 Physics Important Questions Chapter 12 Thermodynamics

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 12 Thermodynamics Important Questions and Answers.

RBSE Class 11 Physics Chapter 12 Important Questions Thermodynamics

Multiple Choice Questions

Question 1.
Which of the following parameters does not characterize the thermodynamic state of matter?
(a) Temperature
(b) Pressure
(c) Work
(d) Volume
Answer:
(c) Work

Question 2.
If C_P and C_V denote the specific heats of nitrogen per unit mass at constant pressure and constant volume respectively, then:
(a) C_P - C_V = \(\frac{R}{28}\)
(b) C_P - C_V = \(\frac{R}{14}\)
(c) C_P - C_V = R
(d) C_P - C_V = 28R
Answer:
(a) CP - CV = \(\frac{R}{28}\)

Question 3.
A carnot engine takes 3 x 10⁶ cal of heat from a reservoir at 627°C and gives it to a sink at 27°C and give it to a sink at 27°C, The work done by the engine is:
(a) Zero
(b) 8.4 x 10⁶ J
(c) 4.2 x 10⁶ J
(d) 16.8 x 10⁶ J
Answer:
(b) 8.4 x 10⁶ J

Question 4.
First law of thermodynamics corresponds to:
(a) Conservation of energy
(b) Heat flows from hotter to cooler body
(c) Law of conservation of angular momentum
(d) Newton’s law of cooling
Answer:
(a) Conservation of energy

Question 5.
Which one of the following is not a state function?
(a) Temeprature
(b) Entropy
(c) Pressure
(d) Work
Answer:
(d) Work

Question 6.
Which one is correct?
(a) In an isobaric process, ∆ P = 0
(b) In an isochoric process, ∆ W = 0
(c) In an isothermal process, ∆ T = 0
(d) In an isothermal process, ∆ Q ≠ 0
Answer:
(d) In an isothermal process, ∆ Q ≠ 0

Question 7.
In an adiabatic process, the state of a gas is changed from P₁,V₁, T₁ to P₂,V₂,T₂. Which of the following relations is correct?
(a) T₁V₁^γ-1 = T₂V₂^γ-1
(b) P₁V₁^γ-1 = P₂V₂^γ-1
(c) T₁P₁^γ = T₂P₂^γ
(d) T₁V₁^γ = T₂V₂^γ
Answer:
(a) T₁V₁^γ-1 = T₂V₂^γ-1

Question 8.
The efficiency of a Carnot engine when source temperature is T₁ and sink temperature is T₂ will be:

Answer:
(a) \(\frac{T_1-T_2}{T_1}\)

Question 9.
The temperature of sink of Carnot engine is 27°C. Efficiency of engine is 25% Temperature of source is:
(a) 227°C
(b) 327°C
(c) 127°C
(d) 27°C
Answer:
(c) 127°C

Question 10.
Which of the following is path dependent?
(a) V
(b) PdV
(c) P
(d) V
Answer:
(b) PdV

Question 11.
In an adiabatiic process, the quantity which remains constant is:
(a) Volume
(b) Pressure
(c) Temperature
(d) Total heat of the system
Answer:
(d) Total heat of the system

Question 12.
The gas law (\(\frac{P V}{T}\) = constant) is true for:
(a) Isothermal charge only
(b) Adiabatiic charge only
(c) Both isothermal and adiabatic changes
(d) Neither isothermal nor adiabatic changes
Answer:
(c) Both isothermal and adiabatic changes

Question 13.
The increase in internal energy of a system is equal to the work done on the system, which process does the system undergo?
(a) Isochoric
(b) Adiabatic
(c) Isobaric
(d) Isothermal
Answer:
(b) Adiabatic

Question 14.
A sample of gas expands from volume V₁ to V₂. The amount of work done by the gas is greatest, when the expansion is:
(a) Isothermal
(b) Isobaric
(c) Adiabatic
(d) Equal in all cases
Answer:
(b) Isobaric

Question 15.
Which of the following is not thermodynamical function?
(a) Enthalpy
(b) Work done
(c) Gibb’s energy
(d) Internal energy
Answer:
(b) Work done

Question 16.
For a certain gas, the ratio of specific heats is given to be γ = 1.5. For this gas:

Answer:
(b) C_P = \(\frac{3 R}{J}\)

Question 17.
The P-T relation for an adiabatiic expansion is:
(a) P^γT^γ-1 = constant
(b) P^γ-1T^γ = constant
(c) P^γT^γ-1 = constant
(d) P^1-γ T^γ = constant
Answer:
(d) P^1-γ T^γ = constant

Question 18.
Which of the following process is reversible?
(a) Transfer of heat by conduction
(b) Transfer of heat by radiation
(c) Isothermal compression
(d) Electrical heating of a nichrome wire
Answer:
(c) Isothermal compression

Question 19.
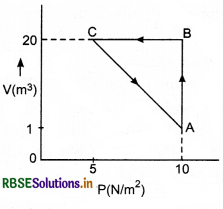
In the cyclic process shown in figure, the work done by the gas in one cycle is:
(a) 28P₁V₁
(b) 14P₁V₁
(c) 18P₁V₁
(d) -9P₁V₁

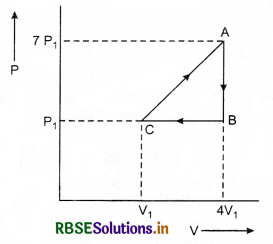
Answer:
(d) -9P₁V₁

Question 20.
During adiabatic compression of a gas, its temperature:
(a) Falls
(b) Remains constant
(c) Rises
(d) becomes zero
Answer:
(c) Rises    

Fill in the Blanks

Question 1.
Efficiency of Carnot’s engine working between the point and stem points is ..............................
Answer:
26.8%

Question 2.
During an adiabatic change, speific heat of gas is ..............................
Answer:
zero

Question 3.
Specific heat of a gas during an isothermal change is ..............................
Answer:
infinity

Question 4.
Expansion of hot gases in an internal combustion engine is ..............................
Answer:
an example of adiabatic change

Question 5.
Melting process and boiling process are ..............................
Answer:
some example of isothermal change

Very Short Answer Questions

Question 1.
If two systems A and B are in thermal equilibrium with C, then will A and B also be in thermal equilibrium?
Answer:
Yes; according to Zeroth law of Thermodynamics.

Question 2.
On which law is the first law of thermodynamics based on?
Answer:
Law of conservation of energy.

Question 3.
Write the P-V relation for adiabatic expansion of ideal gas.
Answer:
PV^γ = constant, where γ = \(\frac{C_P}{C_V}\) which is known as atomicity of gas.

Question 4.
What is the effect on pressure on change of state in a system in an isobaric process?
Answer:
In an isobaric process, the pressure remains constant hence the change in pressure ∆P = 0.

Question 5.
Can heat be supplied without increasing the temperature of gas?
Answer:
Yes, when the gas is allowed to do the work on the surroundings.

Question 6.
Which thermodynamical variable is defined by the Zeroth law of Thermodynamics?
Answer:
Temperature.

Question 7.
What is the specific heat of a gas in isothermal and adiabatic process?
Answer:
Specific heat s = \(\frac{Q}{m \Delta T}\)
In isothermal process ∆T = 0 ∴ s = ∞ (infinity)
and in adiabatic process Q = 0 ∴ s = 0 (zero)

Question 8.
What type of process is a Carnot’ cycle?
Answer:
Reversible cyclic process.

Question 9.
On what factors does the efficiency of a Carnot engine depend?
Answer:
Efficiency of a Carnot heat engine,
η = 1 - \(\frac{T_2}{T_1}\)
It depends on the temperatures of source and sink.

Question 10.
Can temperature of a body be raised without heating it? Is the converse true?
Answer:
Yes; e.g, in adiabatic compression. Converse is also true. For example, when a solid melts, temperature does not rise, although heat is given.

Question 11.
Is it possible to convert internal energy into work?
Answer:
Yes; for example in explosion of a bomb chemical energy (which is a form of internal energy) is converted into kinetic energy.

Question 12.
Which molecules, ice at 0°C or water at 0°C have greater potential energy and why?
Answer:
The potential energy of water molecules at 0°C is more, because heat spent in melting is used up increasing the P.E.

Question 13.
An ideal gas is compressed at a constant temperature, will its internal energy increase or decrease?
Answer:
No, because internal energy of an ideal gas depends only on temperature of the gas.

Question 14.
Does the internal energy of an ideal gas change in an isothermal process and in an adiabatic process?
Answer:
In an isothermal process, T = constant
dT = 0, ∴ dU = 0
In an adiabatic process, Q = constant
dQ = 0 ∴ dV = -dW ≠ 0

Question 15.
If on giving 40 joule of heat to a system, work done on the system is 10 joule, What will be the change in the internal energy of the system?
Answer:
Internal energy of the system will increase by 40 + 10 = 50 joule.

Question 16.
In a thermodynamical process, 300 joule of heat is supplied to a gas and 200 joule of work is done by the gas, what is the change in the internal energy of the system?
Answer:
There will be a net increase in internal energy of the system by 300 - 200 = 100 joule.

Question 17. 
Can two isothermal curves can intersect each other?
Answer:
No, if they intersect, then at two different temperatures (of the isothermals), volume and pressure of gas will be same, which is not possible.

Question 18.
In summer, when the valve of a bicycle tube is removed, the escaping air appears cold. Why?
Answer:
This happens due to adiabatic expansion of the air of the tube of the bicycle.

Question 19.
When air of the atmosphere rises up, it cools. Why?
Answer:
When air rises up, it expands due to decrease in the atmospheric pressure. Therefore temperature falls.

Question 20.
Does the internal energy of a gas change in (i) an isothermal process, (ii) an adiabatic process?
Answer:

• No, because temperature remains constant.
• Yes, because temperature changes.

Question 21.
Why does a gas gets heated on compression?
Answer:
Because work done in compressing the gas increases the internal energy of the gas.

Question 22.
Give one example of a heat pump.
Answer:
A refrigerator is an example of a heat pump.

Question 23.
Can we decide whether change in the internal energy of a system is due to heating or performance of work?
Answer:
No, as internal energy might change due to both heating or performance of work.

Question 24.
Can the temperature of a system be increased without heating it?
Answer:
Yes, for example in adiabatic compression.

Question 25.
Can whole of work be converted into heat?
Answer:
Yes, through friction.

Question 26.
Can whole of heat be converted into work?
Answer:
No, in accordance with the second law of thermodynamics.

Short Answer Questions

Question 1.
A thermos flask containing tea is shaken vigorously. Considering tea as a system:
(a) Has heat been added to tea?
(b) Has work been done on it?
(c) Has its internal energy changed?
(d) Does its temperature rise?
Answer:
(a) No, heat is not transferred as the flask is insulated from the surroundings,
∴ dQ = 0
(b) Yes, work is done in shaking (against the viscous force) i.e, dW is negative.
(c) Yes, internal energy of tea increases, as dU = dQ - dW = 0 - dW, and dW is negative, therefore dU is positive.
(d) Yes, temperature of tea rises because of increase in internal energy.

Question 2.
Can a room be cooled by opening the door of a refrigerator in a closed room?
Answer:
No, when a refrigerator is working in a closed room with its door closed, it is rejecting heat from inside to the air in the room. So temperature of room increases gradually.
When the door of refrigerator is kept open, heat rejected by the refrigerator to the room will be more than the heat taken by the refrigerator from the room (by an amount equal to work done by the compressor). Therefore, temperature of room will increase at a slower rate compared to the first case.

Question 3.
First law of thermodynamics does not forbid flow of heat from lower temperature, comment.
Answer:
First law of thermodynamics tells only about the conversion of mechanical energy into heat energy and vice-versa. As such, it does not put any condition as to why heat can not flow from lower temperature to higher temperature.

Question 4.
Can you design a heat engine of 100% efficiency? Explain your answer.
Answer:
The efficiency of heat engine η = 1 - \(\frac{T_2}{T_1}\), the efficiency will be 100%, or 1 if T₂ = 0K or T₁ = ∞. Since, both these conditions can not be attained practically a heat engine can not have 100% efficiency.

Question 5.
During adiabatic changes, the volume of a gas is found to depend inversely on the square of its absolute temperature. Find out how its pressure will depend on the absolute temperature.
Answer:

Question 6.
If PV = RT is valid for all types of thermodynamically processes, what do the relations PV = a constant and PV^γ = a constant, signify?
Answer:
The relations PV = a constant and PV^γ = a constant, are the relations between pressure and volume in the isothermal and adiabatic processes respectively. They are derived from the equation PV = RT.

Question 7.
How many specific heats does a gas possess?
Answer:
A gas can possess infinite number of specific heats, depending upon the conditions of temperature and pressure. However, generally we consider only two specific heats, one at constant pressure and the other at constant volume.

Question 8.
Why a gas has two principle specific heat capacities?
Answer:
When the gases are heated, there occurs an appreciable change in their volume. So energy is required for expansion and we have two specific heats one at constant pressure and the other at constant volume. In case of solids and liquids, expansion is negligible, so they have only one specific heat i.e., at constant volume.

Question 9.
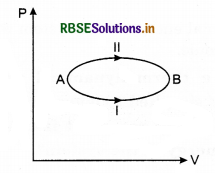
A system goes from state A to B via two processes I and II, as shown in figure. How are ∆U₁ and ∆U₂ (the changes in internal energies in the processes I and II) related to each other?
Answer:
Since, the initial and final states are same for both processes I and II and the change in internal energy is path independent, therefore,
∆U₁ = ∆U₂

Question 10.
A gas expands in such a manner that its pressure and volume comply with the condition PV2 = constant, will the gas cool or get heated on expansion?
Answer:

That is the expansion of the gas will result in the decrease of temperature.

Question 11.
What happens to the change in internal energy of a gas during (i) isothermal expansion and (ii) adiabatic expansion?
Answer:
(i) Isothermal expansion: Temperature remains constant during an isothermal change. As internal energy is a function of temperature only, so it will remain constant during an isothermal change.
As, ∆T = 0, so ∆U = C_V ∆T = 0
(ii) Adiabatic expansion: For an adiabatic change, ∆Q = 0, so from first law of Thermodynamics,
∆Q = ∆U + ∆W = 0
or ∆W = -∆U
During expansion, work is done by a gas i.e., ∆W is positive, so ∆U must be negative. Hence external energy of a gas decreases during an adiabatic expansion.

Question 12.
Show that the slope of an adiabatic curve at any point is γ times the slope of an isothermal curve at the corresponding point.
Answer:
For an isothermal change PV = K
Differentiating both the sides, we get
P.dV + V.dP = 0 or V.dP = -PdV
∴ Slope of an isothermal curve,
\(\left(\frac{d P}{d V}\right)_{\text {iso }}=-\frac{P}{V}\)
For an adiabatic change, PV^γ = K'
Differentiating both sides, we get
P.^γV^γ-1.dV + V^γ.dP = 0
or γPdV + VdP = 0 or VdP = -γPdV
Slope of an adiabatic curve,
\(\left(\frac{d P}{d V}\right)_{\mathrm{adia}}=-\frac{\gamma P}{V} \)
Clearly, slope of an adiabatic curve = γ x slope of an isothermal curve
As, γ > 1, so an adiabatic P - V curve is steeper than the corresponding isothermal P - V curve.

Question 13.
The volume versus temperature T graphs for a certain amount of perfect gas at two pressures P₁ and P₂ are shown in figure. Which one is greater -P₁ or P₂?

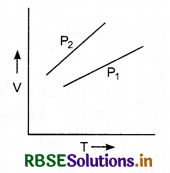
Answer:
For a perfect gas,
PV = µRT
∴ V = \(\frac{\mu R}{P}T\)
∴ Slope of V - T graph with T-axis = \(\frac{\mu R}{P}\)
For a given amount of gas, slope ∝ \(\frac{1}{P}\)
Hence, P₁ > P₂

Question 14.
In figure (a), (b) and (c) given below, identify the isothermal and adiabatic process in each diagram.
Answer:
For the same values of pressure and volume, the slope of an adiabatic curve is greater than the slope of an isothermal curve.

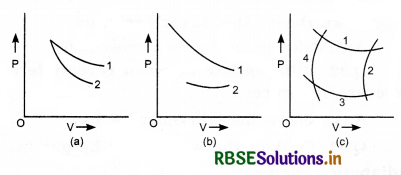
Using this fact, we find.
(a) 1-isothermal; 2-adiabatic.
(b) 1-adiabatic; 2-isothermal.
(c) 1, 3-isothermal; 2, 4-adiabatic.

Question 15.
An ideal gas is taken through the cycle A → B → C → A, as shown in figure. If the net heat supplied to the gas in the cycle in 5 J,what is the work done by the gas is the process C → A?

Answer:
For the cyclic process,
∆Q = ∆W
or ∆Q = W_AB + W_BC + W_CA
or  5 = 10(2 - 1) + 0 + W_CA
or W_CA = 5 - 10 = -5J

Question 16.
Explain the efficiency of heat engine.
Answer:
Heat engine is a device which converts heat energy into mechanical energy. For example, steam engine, diesel engine, petrol engine etc.
Construction: Heat engine consists of the following parts:
1. Source: A hot body maintained at very high temperature T₁ (say) which supplies heat energy is called source or supplies.
2. Sink: A cold body maintained at law temperature T₂ (say) which absorbs the rejected heat is called sink.
3. Working substance: A material which absorbs heat energy from the source and converts it into mechanical energy (useful work) by rejecting the heat to the sink is called the working substance.

Working and efficiency of heat engine: The working substance of the engine absorbs heat energy from the source. A part of this absorbed heat energy is converted into mechanical energy (useful work) and the remaining heat energy is rejected to the sink, thus, the temperature of the working substance remains as it was before the absorption of heat energy. Therefore, the working substance is now again ready to absorb the heat energy from the source and to repeat the process continuously. This process is continuous and we get the continuous amount of mechanical energy.

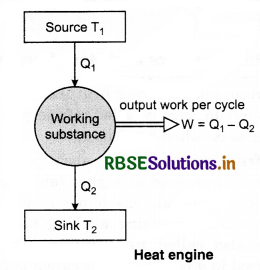
Let, Q₁ = Amount of heat absorbed by working substance from the source
Q₂ = Amount of heat rejected to the sink
W = Mechanical energy or work performed in each cycle.
Since, there is no change in the temperature of the working substance is zero.
i.e., dU = U_f - U_i = 0
According to first law of thermodynamics,
dQ = dU + W
dQ = W (∵ dU = 0)
or W = Q₁ - Q₂ = dQ
The efficiency of heat engine is defined as the ratio of the mechanical work done per cycle (i.e., output) to the heat absorbed per cycle (i.e., input).
i.e., Efficieny η = \(\frac{W}{Q_1}=\frac{Q_1-Q_2}{Q_1}\)
or  η = 1 - \(\frac{Q_2}{Q_1}\) .....................(1)
From equation (1), it is clear that efficiency of heat engine is less than one (i.e. η < 1).

Question 17.
What is thermodynamics? Explain the Zeroth law of thermodynamics and give its importance.
Answer:
Thermodynamics is the branch of Physics that deals with the concept of heat and temperature and the inter-conversion of heat and other forms of energy. Thermodynamics is a macroscopic study and it deals with bulk system and does not deal with the molecular constitution of matter. The system which is studied using Thermodynamics is called Thermodynamic system. Here system means a group of particles.

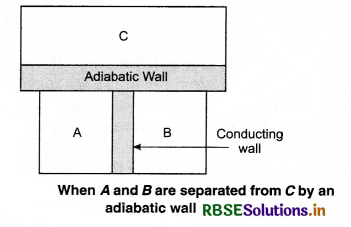
Principle: It is based on the principle of temperature.
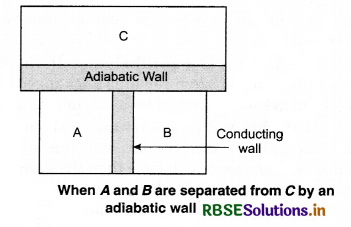
To understand this law, consider two systems A and B, separated by an adiabatic wall, each of these are in contact with a third system C by a conducting wall. The states of the system will change until A and B are in equilibrium with C. Now, let the adiabatic wall between A and B be replaced by a conducting wall and C is insulated from A and B by an adiabatic wall. It is found that A and B are in thermal equilibrium with each other. This is the basis of Zeroth law of thermodynamics. This law states that the two systems are in thermal equilibrium with a third system separately, then both are in thermal equilibrium with each other.

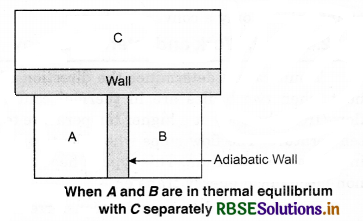
The zeroth law apparently suggests that when two systems A and B are in thermal equilibrium, then, there must be a physical quantity that has the same value for both. The thermodynamic variable whose value is equal for the two systems (in thermal equilibrium) is called temperature (T). If A and B are separately in equilibrium with C. then, T_A = T_C and T_B = T_C. This means that T_A = T_B. So, the systems A and B are in thermal equilibrium.

Question 18.
Explain heat, work and internal energy of a system.
Answer:
Temperature determines the direction of flow of heat when two bodies are in thermal contact. Heat flows from the body at a higher temperature to a lower temperature. The flow stops when the two bodies are in thermal equilibrium. This type of heat transfer is a non-mechanical energy transfer. When thermal energy is transferred from an object into the atmosphere then the thermal energy of the object is taken to be negative while on giving heat to an object from the atmosphere the therma1 energy of the object is taken to be positive. If the temperature of the object remains constant then due to the exchange of heat in the object the state of the object changes.
Concept:
1. Heat absorbed by a system is positive.
2. Heat given out by a system is negative.

Question 19.
Explain the work done in an isothermal process.
Answer:
Temperature determines the direction of flow of heat when two bodies are in thermal contact. Heat flows from the body at a higher temperature to a lower temperature. The flow stops when the two bodies are in thermal equilibrium. This type of heat transfer is a non-mechanical energy transfer. When thermal energy is transferred from an object into the atmosphere then the thermal energy of the object is taken to be negative while on giving heat to an object from the atmosphere the therma1 energy of the object is taken to be positive. If the temperature of the object remains constant then due to the exchange of heat in the object the state of the object changes.
Concept:
1. Heat absorbed by a system is positive.
2. Heat given out by a system is negative.

Question 20.
Explain the First Law of thermodynamics.
Answer:
The first law of thermodynamics states the equivalence of heat and work. This law is based on the principle of conservation of energy.
The internal energy U of a system can change through two modes of energy transfer: heat and work.
Let ∆Q = Heat supplied to the system by the surroundings,
∆W = Work done by the system on the surroundings.
∆U = Change in internal energy of the system.
From the general principle of conservation of energy, i.e.,
∆Q = ∆U + ∆W ......................(1)
The energy ∆Q, supplied to the system goes in partly to increase the internal energy of the system (∆U) and work (∆W). Equation (1) is called the first law of Thermodynamics. This is the general law of conservation of energy applied to any system in which the energy transfer from or to the surroudnings. We can write equation (1) as
∆Q - ∆W = ∆U ......................(2)
Now, the system go from an initial state to final state in a number of ways. To change the state of a gas from (P₁, V₁) to (P₂, V₂), we first change the volume from V₁ to V₂, keeping the pressure constant. This means that we first go to state (P₁, V₂). Changing the pressure from P₁ and P₂, keeping volume constant to the state (P₂, V₂). We can also first keep the volume constant and then keep the pressure constant. U is a state variable. ∆U depends only on the initial and final states and not on the path taken by the gas to move from one to the other. However, ∆Q and ∆W depends on the path in moving from initial to final states.
From equation (2), (∆Q - ∆W) is path independent for a system with ∆U = 0,
∆Q = ∆W
This implies that heat supplied to the system is completely used up by the system in doing work on the environment. Work done by the system against a constant pressure P is

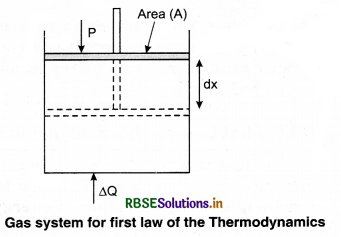
∆W = P ∆V
Here, ∆V is the small change in volume of gas.
So equation (2) gives
∆Q = ∆U + P∆V ........................(3)

Question 21.
Derive the Mayer’s relation.
Answer:
Let an amount of heat ∆Q be supplied to a substance that changes its temperature from T to T + ∆T. We define specific heat capacity as:
s = \(\frac{d Q}{m d T}\) .....................(1)
Specific heat depends up on the nature of the substance and its temperature. The unit of specific heat capacity is J/kg-K. Specific heat is that heat that raises the temperature of 1. gm of a substance through the temperature of 1°C. If the amount of substance is given in terms of (µ) moles we define molar specific heat capacity as
C = \(\frac{1}{\mu} \frac{d Q}{d T}\) ......................(2)
There are two specific heats for a gas: Specific heat capacity at constant volume and specific heat capacity at constant pressure.
(a) Molar specific heat at constant volume: The amount of heat required to raise the temperature of 1°C of one mole of gas, keeping the volume constant. It is denoted by C_V.
C_V = \(\left(\frac{d Q}{d T}\right)_V\) ...........................(3)
(b) Molar specific heat at constant pressure: The amount of heat required to raise the temperature of 1°C of one mole of gas, keeping the pressure constant. It is denoted by C_P.
C_P = \(\left(\frac{d Q}{d T}\right)_P\) ......................(4)

Question 22. 
Differentiate between reversible and irreversible process.
Answer:

Reversible process	Irreversible process
1. A reversible process is change that can be retraced in a reverse (opposite) direction.	An irreversible process is a change that cannot be retraced in a reverse (opposite) direction.
2. The path of a reversible process is the same in the forward and reverse direction.	The path of an irreversible process is not the same in the forward and reverse direction.
3. Reversible changes are very slow and there is no loss of any energy in the process.	There is a permanent loss of energy from the system due to friction or other dissipative forces in an irreversible process.
4. The system comes back to its initial state after it is taken along the reverse path.	The change of state depends upon the path taken to change the state during an irreversible process.
5. Reversible processes are ideal processes.	Irreversible processes are real processes.

Question 23.
Explain the work done by gas in an adiabatic expansion.
Answer:
For this step (B to C), the piston and cylinder are assumed to be thermally insulated. So, they neither gain nor loose heat. The gas continues to expand, doing work on the surroundings, loses an equivalent amount of internal energy. The gas expansion causes it to cool to the cold temperature, T_C. The entropy remains unchanged.

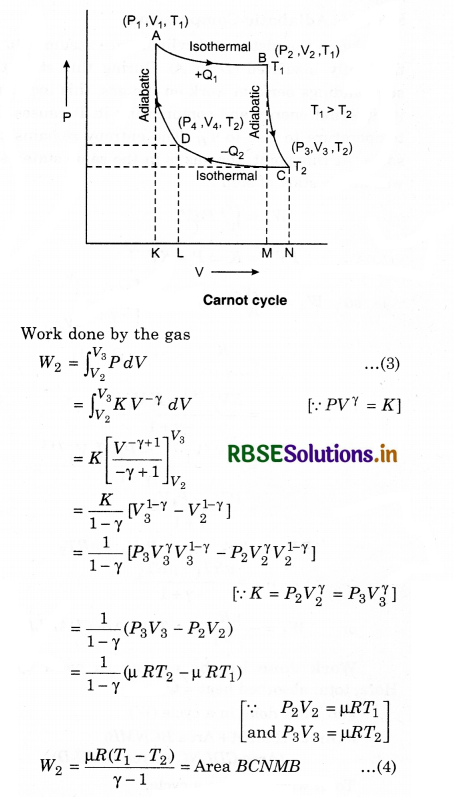
Question 24.
Derive the formula for efficiency of Carnot engine.
Answer:
Heat engine is a device which converts heat energy into mechanical energy. For example, steam engine, diesel engine, petrol engine etc.
Construction: Heat engine consists of the following parts:
1. Source: A hot body maintained at very high temperature T₁ (say) which supplies heat energy is called source or supplies.
2. Sink: A cold body maintained at law temperature T₂ (say) which absorbs the rejected heat is called sink.
3. Working substance: A material which absorbs heat energy from the source and converts it into mechanical energy (useful work) by rejecting the heat to the sink is called the working substance.

Working and efficiency of heat engine: The working substance of the engine absorbs heat energy from the source. A part of this absorbed heat energy is converted into mechanical energy (useful work) and the remaining heat energy is rejected to the sink, thus, the temperature of the working substance remains as it was before the absorption of heat energy. Therefore, the working substance is now again ready to absorb the heat energy from the source and to repeat the process continuously. This process is continuous and we get the continuous amount of mechanical energy.

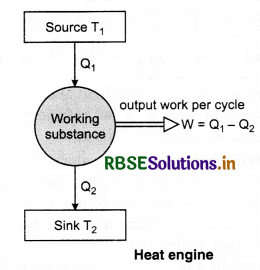
Let, Q₁ = Amount of heat absorbed by working substance from the source
Q₂ = Amount of heat rejected to the sink
W = Mechanical energy or work performed in each cycle.
Since, there is no change in the temperature of the working substance is zero.
i.e., dU = U_f - U_i = 0
According to first law of thermodynamics,
dQ = dU + W
dQ = W (∵ dU = 0)
or W = Q₁ - Q₂ = dQ
The efficiency of heat engine is defined as the ratio of the mechanical work done per cycle (i.e., output) to the heat absorbed per cycle (i.e., input).
i.e., Efficieny η = \(\frac{W}{Q_1}=\frac{Q_1-Q_2}{Q_1}\)
or  η = 1 - \(\frac{Q_2}{Q_1}\) .....................(1)
From equation (1), it is clear that efficiency of heat engine is less than one (i.e. η < 1).

Question 25.
Derive the formula for the efficiency of carnot heat engine and explain it.
Answer:
Heat engine is a device which converts heat energy into mechanical energy. For example, steam engine, diesel engine, petrol engine etc.
Construction: Heat engine consists of the following parts:
1. Source: A hot body maintained at very high temperature T₁ (say) which supplies heat energy is called source or supplies.
2. Sink: A cold body maintained at law temperature T₂ (say) which absorbs the rejected heat is called sink.
3. Working substance: A material which absorbs heat energy from the source and converts it into mechanical energy (useful work) by rejecting the heat to the sink is called the working substance.

Working and efficiency of heat engine: The working substance of the engine absorbs heat energy from the source. A part of this absorbed heat energy is converted into mechanical energy (useful work) and the remaining heat energy is rejected to the sink, thus, the temperature of the working substance remains as it was before the absorption of heat energy. Therefore, the working substance is now again ready to absorb the heat energy from the source and to repeat the process continuously. This process is continuous and we get the continuous amount of mechanical energy.

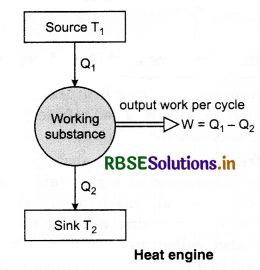
Let, Q₁ = Amount of heat absorbed by working substance from the source
Q₂ = Amount of heat rejected to the sink
W = Mechanical energy or work performed in each cycle.
Since, there is no change in the temperature of the working substance is zero.
i.e., dU = U_f - U_i = 0
According to first law of thermodynamics,
dQ = dU + W
dQ = W (∵ dU = 0)
or W = Q₁ - Q₂ = dQ
The efficiency of heat engine is defined as the ratio of the mechanical work done per cycle (i.e., output) to the heat absorbed per cycle (i.e., input).
i.e., Efficieny η = \(\frac{W}{Q_1}=\frac{Q_1-Q_2}{Q_1}\)
or  η = 1 - \(\frac{Q_2}{Q_1}\) .....................(1)
From equation (1), it is clear that efficiency of heat engine is less than one (i.e. η < 1).

Long Answer Type Questions

Question 1.
Explain briefly the zeroth, first and second law of thermodynamics.
Answer:
Principle: It is based on the principle of temperature.
To understand this law, consider two systems A and B, separated by an adiabatic wall, each of these are in contact with a third system C by a conducting wall. The states of the system will change until A and B are in equilibrium with C. Now, let the adiabatic wall between A and B be replaced by a conducting wall and C is insulated from A and B by an adiabatic wall. It is found that A and B are in thermal equilibrium with each other. This is the basis of Zeroth law of thermodynamics. This law states that the two systems are in thermal equilibrium with a third system separately, then both are in thermal equilibrium with each other.

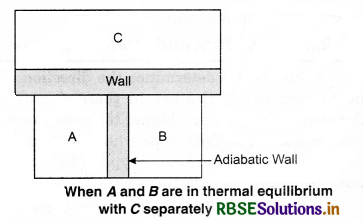
The zeroth law apparently suggests that when two systems A and B are in thermal equilibrium, then, there must be a physical quantity that has the same value for both. The thermodynamic variable whose value is equal for the two systems (in thermal equilibrium) is called temperature (T). If A and B are separately in equilibrium with C. then, T_A = T_C and T_B = T_C. This means that T_A = T_B. So, the systems A and B are in thermal equilibrium.

The first law of thermodynamics states the equivalence of heat and work. This law is based on the principle of conservation of energy.
The internal energy U of a system can change through two modes of energy transfer: heat and work.
Let ∆Q = Heat supplied to the system by the surroundings,
∆W = Work done by the system on the surroundings.
∆U = Change in internal energy of the system.
From the general principle of conservation of energy, i.e.,
∆Q = ∆U + ∆W ......................(1)
The energy ∆Q, supplied to the system goes in partly to increase the internal energy of the system (∆U) and work (∆W). Equation (1) is called the first law of Thermodynamics. This is the general law of conservation of energy applied to any system in which the energy transfer from or to the surroudnings. We can write equation (1) as
∆Q - ∆W = ∆U ......................(2)
Now, the system go from an initial state to final state in a number of ways. To change the state of a gas from (P₁, V₁) to (P₂, V₂), we first change the volume from V₁ to V₂, keeping the pressure constant. This means that we first go to state (P₁, V₂). Changing the pressure from P₁ and P₂, keeping volume constant to the state (P₂, V₂). We can also first keep the volume constant and then keep the pressure constant. U is a state variable. ∆U depends only on the initial and final states and not on the path taken by the gas to move from one to the other. However, ∆Q and ∆W depends on the path in moving from initial to final states.
From equation (2), (∆Q - ∆W) is path independent for a system with ∆U = 0,
∆Q = ∆W
This implies that heat supplied to the system is completely used up by the system in doing work on the environment. Work done by the system against a constant pressure P is

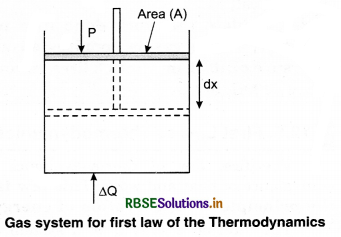
∆W = P ∆V
Here, ∆V is the small change in volume of gas.
So equation (2) gives
∆Q = ∆U + P∆V ........................(3)

The second law of thermodynamics states that the total entropy of an isolated system increases over time, or it remains same in ideal cases (where the system undergoes a reversible process or when it is in a steady state). The first law of thermodynamics tells the basic definition of internal energy and states the law of conservation of energy. The second law of thermodynamics deals with the direction of natural process. It states that a natural process is not reversible. For e.g., heat flows from hot to cold region, and never the reverse, unless some external work is done on the system.

In Terms of Entropy
In a reversible process, a very small increase inthe entropy (dS) of a system is defined to result from a small heat transfer to a closed system divided by the common temperature (T) of the system and the surroundings that supply of the heat:
dS = \(\frac{d Q}{T}\) (closed system)
If teh temperature is changed from T₁ and T₂
∴ Integration both side:

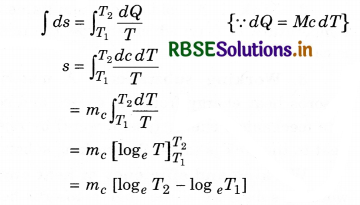
= m_c log(\(\frac{T_2}{T_1}\))
= 2.303 m_c log₁₀[\(\frac{T_2}{T_1}\)]

Various Statements of the Planck’s Law
1. Statement of keivn: According to this statement “It is not possible to make an engine in which the working substance can take heat from the source and change it completely into work and remain unchanged itself in one complete cycle.” It is concluded from this statement that it is not possible to get work continuously from heat source. Actually the sink is necessary and it is necessary to release some heat to the sink. This statement is based on the principle of Carnot heat engine.

2. Statement of Clausius: According to this statement, “It is an impossible process that in cyclic process the working substance transfers heat from low temperature object to high temperature object directly in the absence of external work.” It is concluded from this statement that transfer of heat from a low temperature object to a high temperature object on its own is not possible. For this it is important that external work be done on the working substance. This statement is based on the principle of refrigerator.

Equivalence of Clausius and Kelvin Statements
Let there be an engine violating the Kelvin statement: i.e., one that drains heat and converts it completely into work in a cyclic manner without any other result. Now, pairing it with a reverse Carnot engine.

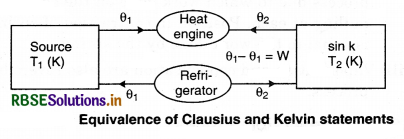
The newly created engine (consists of two engines) transfers heat ∆Q = Q(\(\frac{1}{\eta}\) - 1) from the colder region (sink) to the hotter region (source), which violates the statement of Clausius. Thus, violation of Kelvin statement means violation of Clausius statement i.e., the Clausius statement implies the Kelvin statement. Similarly, we can prove that the Kelvin statement implies the Clausius statement and hence both the statements are equivalent.

Question 2.
Explain the various processes of thermodynamics and work done in these processes.
Answer:
Every equilibrium state of a thermodynamical system is completely described by specific values of some macroscopic variables. If in a thermodynamic system, variables like temperature (T), pressure (P), volume (V), etc. changes with time, then the process is called thermodynamical process. There are various types of thermodynamical processes:

1. Isothermal process
2. Isochoric process
3. Isobaric process
4. Adiabatic process
5. Cyclic process

Question 3.
Differentiate between the isothermal and adiabatic processes and calculate the work done in these process.
Answer:
An isothermal process is a change of a system, in which the temperature remains constant, ∆T = 0. This typically occurs when a system is in contact with an outside thermal reservoir and the change takes place slowly to allow the system to continually adjust to the reservoir’s temperature through heat exchange.

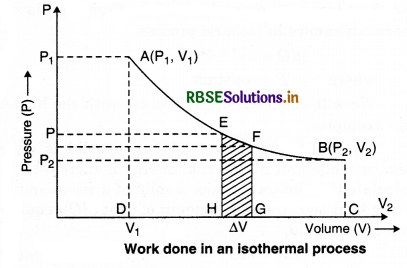
Isothermal process takes place in any type of system that regulates the temperature. In the thermodynamic analysis of chemical reactions, it is first analyzed what happens under isothermal conditions. In an isothermal process, the internal energy of an ideal gas is constant. This is due to the fact that there are no intermolecular forces in an ideal gas. In the isothermal compression of a gas, there is work done on the system to decrease the volume and increase the pressure. Doing work on the gas, can increase the internal energy and increase the temperature. For constant temperature, energy must leave the system. For an ideal gas, the amount of energy entering the environment is equal to the amount of work done on the gas, as the internal energy does not vary.

Adiabatic process is that process in which temperature (T), pressure (P) and volume (V) can be changed, but there is no transfer of heat between a thermodynamical system and its surroundings. In this process, energy is transferred only as work. This process provides a rigorous conceptual basis to explain the first law of thermodynamics. A process in which transfer of heat is not involved in the system, so that Q = 0, is called an adiabatic process. For example, the compression of a gas within an engine’s cylinder is assumed to take place so fast that on the time scale of the process of compression, little energy of the system can be transferred out as heat. Essential conditions for an adiabatic process:

• The process of expansion or compression should be sudden, so that heat does not get time to get exchanged with the surroundings.
• The walls of the container must be perfectly insulated so that there can not be any exchange of heat between the gas and surroundings.

Question 4.
Write the working principle of Carnot’s reversible engine and plot the P-V curve for work in each process, and obtain the formula for efficiency.
Answer:
In this cycle four processes are done on working substance. In these, two processes are isothermal and two are adiabatic. The order of these processes is as follows:

Step-I: Isothermal Expansion
During this step (A to B in figure 12.14), the gas is allowed to expand and it does work on the surroundings. The temperature of the gas does not change during the process and the expansion is thus, called isothermal. 
The gas expansion is propelled by absorption of heat energy Q₁ and of entropy  ∆SH = QH/TH from the high-temperature reservoir


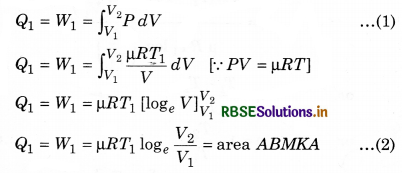
Step-II: Adiabatic Expansion
For this step (B to C), the piston and cylinder are assumed to be thermally insulated. So, they neither gain nor loose heat. The gas continues to expand, doing work on the surroundings, loses an equivalent amount of internal energy. The gas expansion causes it to cool to the cold temperature, T_C. The entropy remains unchanged.

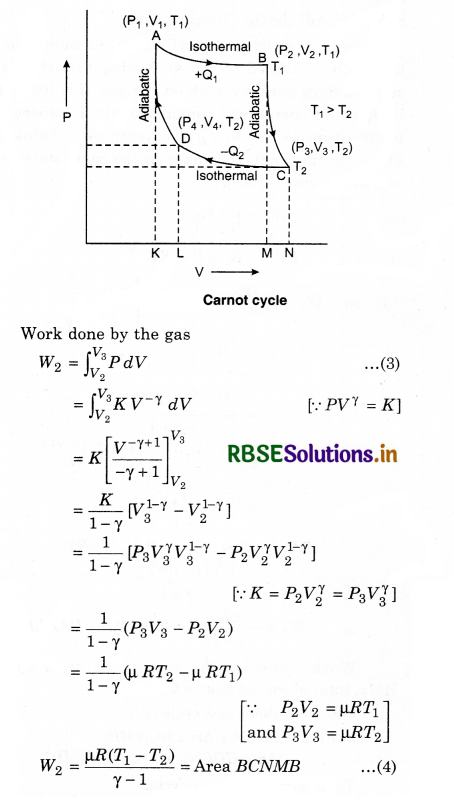
Step-III: Isothermal Compression
For C to D, the surroundings perform work on the gas, which causes an amount of heat energy Q₂ and of entropy ∆SC = \(\frac{Q_C}{T_C}\) to flow out of the gas to the low temperature reservoir. If heat given to the system is Q₂, then the work done on the substance (W₃),


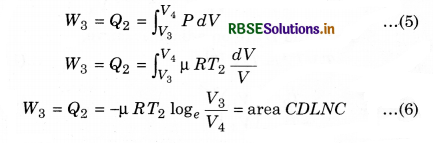
Step IV: Adiabatic Compression
Again the piston and cylinder are assumed to be thermally insulated (D to A). During this step, the surroundings perform work on the gas, this increases its internal energy and compressing it. It causes the temperature to rise to TH. The entropy remains the same. At this point, the gas is in the sam state as it was at the start of step I.

Work done by the engine in each cycle:
Here, total absorbed heat = Q₁ - Q₂
and work done in a cycle (W)
= (Area ABMKA + Area BCNMB) - (Area CDLNC + Area DAKLD) .........................(9)
Total work done in a cycle,
W = W₁ + W₂ + W₃ + W₄

Similarly, B and C are on adiabatic curve, then

Efficiency of the Engine
For a heat engine, the total thermodynamical process is generally irreversible. The ratio of work done to convert heat and the heat absorbed by the source is called efficiency. 
This means that,

From the above relation, it is clear that the efficiency of engine depends upon the temperature of source (T₁) and sink (T₂).
Here T₁ > (T₁ - T₂). Efficiency is always less than one, i.e., less than 100%.
If T₁ = T₂, then η = 0, which represents that when source and sink are at same temperature. Then, in this situation, heat energy can not be transformed to mechanical energy. It is to be noted here that the value of η will be 100% in two situations: if T₁ = ∞ or T₂ = 0, and both these situations are not possible. So, efficiency can not be 100%.

Question 5.
Write the statements of Kelvin-Planck and Clausius of second law of Thermodynamics and show the equivalence of the two statements.
Answer:
The second law of thermodynamics states that the total entropy of an isolated system increases over time, or it remains same in ideal cases (where the system undergoes a reversible process or when it is in a steady state). The first law of thermodynamics tells the basic definition of internal energy and states the law of conservation of energy. The second law of thermodynamics deals with the direction of natural process. It states that a natural process is not reversible. For e.g., heat flows from hot to cold region, and never the reverse, unless some external work is done on the system.

In Terms of Entropy
In a reversible process, a very small increase inthe entropy (dS) of a system is defined to result from a small heat transfer to a closed system divided by the common temperature (T) of the system and the surroundings that supply of the heat:
dS = \(\frac{d Q}{T}\) (closed system)
If teh temperature is changed from T₁ and T₂
∴ Integration both side:

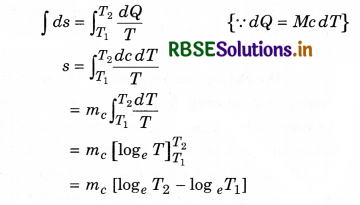
= m_c log(\(\frac{T_2}{T_1}\))
= 2.303 m_c log₁₀[\(\frac{T_2}{T_1}\)]

Various Statements of the Planck’s Law
1. Statement of keivn: According to this statement “It is not possible to make an engine in which the working substance can take heat from the source and change it completely into work and remain unchanged itself in one complete cycle.” It is concluded from this statement that it is not possible to get work continuously from heat source. Actually the sink is necessary and it is necessary to release some heat to the sink. This statement is based on the principle of Carnot heat engine.

2. Statement of Clausius: According to this statement, “It is an impossible process that in cyclic process the working substance transfers heat from low temperature object to high temperature object directly in the absence of external work.” It is concluded from this statement that transfer of heat from a low temperature object to a high temperature object on its own is not possible. For this it is important that external work be done on the working substance. This statement is based on the principle of refrigerator.

Equivalence of Clausius and Kelvin Statements
Let there be an engine violating the Kelvin statement: i.e., one that drains heat and converts it completely into work in a cyclic manner without any other result. Now, pairing it with a reverse Carnot engine.

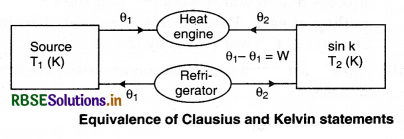
The newly created engine (consists of two engines) transfers heat ∆Q = Q(\(\frac{1}{\eta}\) - 1) from the colder region (sink) to the hotter region (source), which violates the statement of Clausius. Thus, violation of Kelvin statement means violation of Clausius statement i.e., the Clausius statement implies the Kelvin statement. Similarly, we can prove that the Kelvin statement implies the Clausius statement and hence both the statements are equivalent.

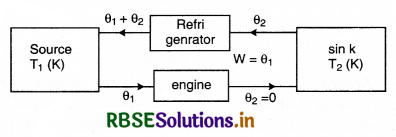
Question 6.
Write and obtain the Carnot’s theorem.
Answer:
Carnot’s theorem states:
(a) All heat engines between two heat reservoirs are less efficient than a Carnot heat engine operating between the same reservoirs. The efficiency of Carnot (reversible) engine is maximum.
(b) The efficiency of every Carnot heat engine working between a pair of heat reservoirs are equal, regardless of the working substance employed. 
Proof:
Figure 12.13 shows two reservoirs of different temperatures. The engine with less efficiency is being driven as a heat pump and hence it is a reversible engine. If the less efficient engine is not reversible, then the device could be built, but the expressions for work and heat flow would not be valid.

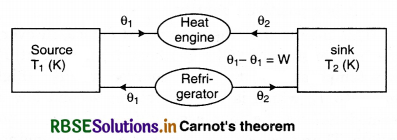
If one of the engines is irreversible, it must be the engine (I), placed so that it reverse drives the less efficient but reversible engine (R). But if the irreversible engine is more efficient than the reversible engine, then the second law of thermodynamics is violated.
Efficiency of irreversible engine (ηI)
η_I = \(\frac{W}{Q_1}\)
If the reversible engine takes the heat Q'₁ from the source at temperature T₁ and does work W and provides heat (Q'₁ - W) to the sink. Then, the efficiency of reversible process (ηR),
η_R = \(\frac{W}{Q_1^{\prime}}\)
Let η_I > I_R
i.e., \(\frac{W}{Q_1}>\frac{W}{Q_1^{\prime}}\)
Q'₁ > Q₁
i.e., (Q'₁ - Q₁) is a positive quantity.
According to figure 12.13. both the engines are connected so that the irreversible engine does work in the same direction and the reversible engihe performs work in the opposite direction, then the reversible engine does the work as the refrigerator (working on irreversible engine). The temperature T₂ takes the heat (Q'₁ - W) from the sink and work W is done on it. Here at temperature T₁ it gives Q'₁ heat to the source. Work done (W) on the reversible engine is fulfilled by the irreversible engine; and irreversible engine and refrigerators works as an automated device. Since, the source provides Q₁ heat to the irreversible engine and takes Q'₁ heat from the reversible engine. Then,
Heat taken by the source = Q'₁ - Q₁
Similarly, the sink takes (Q₁ - W) heat from the irreversible engine and gives (Q'₁ - W) heat to the reversible engine. Then, loss in heat by the sink,
= (Q'₁ - W) - (Q₁ - W) = Q'₁ - Q₁
Since, Q'₁ > Q₁
∴ It is positive quantity.
This means that the automated device, in every cycle, is transferring (Q'₁ - Q₁) heat from sink at T₂ (low temperature) to the source at T₁ (high temperature), which is not possible as second law of thermodynamics, i.e., our assumption η_I > η_R is not possible. Therefore, we can say that of all the engines working between similar temperature, reversible engines have maximum efficiency.

For the second statement of Carnot’s theorem, we replace the irreversible engine with another reversible engine (R'), i.e., two reversible engines are working between similar temperatures T₁ (High) and T₂ (low). Now, if we consider the efficiency of R engine (η_R) to be greater than that of engine R'(η_R').
Then, the result again violates the second law of Thermodynamics. This implies the transfer of heat from low temperature to high temperature without heat loss. Therefore η_R > η_R' then the result is same and violation is obtained, i.e., it must be η_R = η_R'. So, we can say that all the reversible engines working at similar temperatures will have similar efficiency.

Question 7.
Define C_P and C_V. For an ideal gas, prove that C_P - C_V = P.
Answer:
(a) Molar specific heat at constant volume: The amount of heat required to raise the temperature of 1°C of one mole of gas, keeping the volume constant. It is denoted by C_V.
C_V = \(\left(\frac{d Q}{d T}\right)_V\) .......................(1)
(b) Molar specific heat at constant pressure: The amount of heat required to raise the temperature of 1°C of one mole of gas, keeping the pressure constant. It is denoted by C_P.
C_P = \(\left(\frac{d Q}{d T}\right)_P\) ........................(2)
Consider one mole of an ideal gas. Let dQ be the amount of heat is given to the system to raise the dT, and change in internal energy be dV. Then, from first law of Thermodynamics,
dQ = dU + PdV ....................(3)
If heat is supplied to one mole at constant volume, i.e.,
V = constant,
then, dV = 0
From equation (3),
dQ = dU .................(4)
Molar specific heat (C_V) at constant volume,
C_V = \(\left(\frac{d Q}{d T}\right)_V\)
From equation (4),
dQ = dU = C_V dT ........................(5)
If one mole of gas is supplied heat at constant pressure, i.e., from equation (2) of molar specific heat C_P at constant pressure,
C_P = \(\left(\frac{d Q}{d T}\right)_P\)
or, dQ = C_P dT
From equation (3),
dQ = C_P dT = dU + PdV
Again, from equation (5), substituting
dU = C_V dT
C_P dT = C_V dT + PdV ......................(6)
For one mole of gas (µ = 1), from ideal gas equation,
PV = RT
PdV = RdT ........................(7)
From equations (6) & (7),
(C_P - C_V)dT = RdT
or C_P - C_V = R ............................(8)
The above expression is called Mayer's relation where R = 8.31 J/mol¹K¹. This relation is for one mole of gas.

Question 8.
Define the terms related to thermodynamics, and define thermodynamic equilibrium.
Answer:
Thermodynamics is the branch of Physics that deals with the concept of heat and temperature and the inter-conversion of heat and other forms of energy. Thermodynamics is a macroscopic study and it deals with bulk system and does not deal with the molecular constitution of matter. The system which is studied using Thermodynamics is called Thermodynamic system. Here system means a group of particles.

Some important definitions for the study of Thermodynamics are as follows:
Thermodynamic System: A thermodynamic system is the material and radiative content of a macroscopic volume in space that can be adequately described by thermodynamic state variables such as temperature, entropy, internal energy and pressure.
Surroundings: Everything external to a thermodynamic system is called surroundings. System and surroundings are separated by a definite border called boundary. The universe is constituted by the system, surroundings and boundary.

Types of Thermodynamic System:
Thermodynamic systems are mainly classified into three types. These are:

1. Open system
2. Closed system
3. Isolated system

1. Open system: An open system is a thermodynamic system which allows both matter and energy to flow in and out of it, across the boundary. An example of open system is boiling water in an open vessel, where transfer of heat as well as mass in the form of steam takes place between the vessel and surrounding.

2. Closed System: The system in which the transfer of energy takes place across its boundary with the surrounding, but no transfer of matter takes place is called closed system. This type of system is fixed mass system. An example of closed system is the fluid like air or gas being compressed in the piston and cylinder arrangement, Another example of closed system is the water being heated in the closed vessel, where water will get heated but its mass will remain same.

3. Isolated System: An isolated system is a thermodynamic system that cannot exchange either energy or matter outside the boundaries of the system.
Example : If the piston and cylinder arrangement in which the fluid like air or gas is being compressed or expanded is insulated, it becomes isolated system.

Homogeneous System: A homogeneous system is defined as the one whose chemical composition and physical properties are the same in all parts of the system. For example: pure solid, pure liquid, pure gas etc.

Heterogeneous System: A heterogeneous system is defined as one consisting of two or more homogeneous bodies. The heterogeneous bodies are separated from each other by boundaries. An example of a heterogeneous system is water with ice floating in it.

The state of a system is in equilibrium state if the macroscopic variables that characterise the system do not change in time. A gas in a closed container, which is completely insulated from its surroundings, with fixed values of pressure, volume, temperature, mass and composition that do not change with time is in thermodynamic equilibrium state.

Whether a system is in thermal equilibrium or not depends upon the surroundings and nature of the wall that separates the system from the surroundings. Consider two gases A and B are filled in two different containers. We know that pressure and volume of a given mass of gas can be chosen to be its two independent variables. Let the pressure and volume of the gases be (P_A, V_A) and (S_B, V_B) respectively. Let us assume that the two systems are closed but are separated by an adiabatic wall that does not allow the flow of heat from one to another. Figure. 12.1 (a).

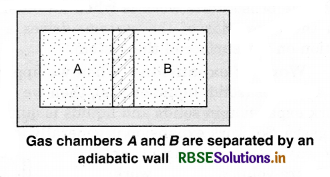
Now, let the adiabatic wall be replaced by a diathermic wall, i.e., a wall that conducts heat from one to another. It is found that the macroscopic variables of A and B system changes spontaneously until they achieve equilibrium states. After that, no change of states take place.

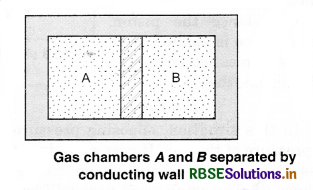
The pressure and volume variables of the two gases change to (P'_B, V'_B) and (P'_A, V'_A) so that the new states of A and B are in equilibrium. Then, we say that A and B are in thermal equilibrium.

1. Mechanical equilibrium: If no unbalanced force acts between the different parts of the system and the system and surroundings then the system is said to be in mechanical equilibrium with the surroundings.
2. Chemical equilibrium: If the chemical constitution of a system remains unchanged with time then the system is said to be in chemical equilibrium.
3. Thermal equilibrium: If the temperature of each part of the system and the surroundings remains unchanged with time then the system and the surroundings are said to be in thermal equilibrium.
4. Thermodynamical equilibrium: If a system is in mechanical, chemical and thermal i.e., all three equilibrium states then it is said to be in thermodynamic equilibrium.

Question 9.
What is first law of thermodynamics? With its help define internal energy.
Answer:
The first law of thermodynamics states the equivalence of heat and work. This law is based on the principle of conservation of energy.
The internal energy U of a system can change through two modes of energy transfer: heat and work.
Let ∆Q = Heat supplied to the system by the surroundings,
∆W = Work done by the system on the surroundings.
∆U = Change in internal energy of the system.
From the general principle of conservation of energy, i.e.,
∆Q = ∆U + ∆W ......................(1)
The energy ∆Q, supplied to the system goes in partly to increase the internal energy of the system (∆U) and work (∆W). Equation (1) is called the first law of Thermodynamics. This is the general law of conservation of energy applied to any system in which the energy transfer from or to the surroudnings. We can write equation (1) as
∆Q - ∆W = ∆U ......................(2)
Now, the system go from an initial state to final state in a number of ways. To change the state of a gas from (P₁, V₁) to (P₂, V₂), we first change the volume from V₁ to V₂, keeping the pressure constant. This means that we first go to state (P₁, V₂). Changing the pressure from P₁ and P₂, keeping volume constant to the state (P₂, V₂). We can also first keep the volume constant and then keep the pressure constant. U is a state variable. ∆U depends only on the initial and final states and not on the path taken by the gas to move from one to the other. However, ∆Q and ∆W depends on the path in moving from initial to final states.
From equation (2), (∆Q - ∆W) is path independent for a system with ∆U = 0,
∆Q = ∆W
This implies that heat supplied to the system is completely used up by the system in doing work on the environment. Work done by the system against a constant pressure P is

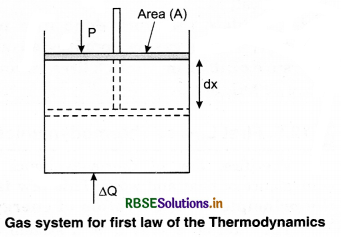
∆W = P ∆V
Here, ∆V is the small change in volume of gas.
So equation (2) gives
∆Q = ∆U + P∆V ........................(3)

Question 10.
What do you mean by indicator diagram. From indicator diagram define external work, prove that external work depends on the path of change.
Answer:
Indicator diagram: When the thermodynamical state of a system is expressed by pressure and volume variables, then in some process, the curve showing the change in thermodynamic state of the system is called pressure volume curve or indicator diagram. The volume of work can be found by drawing a graph between pressure (P) and volume (V) which is called indicator graph. It shows the change of state of the system. When pressure (P) remains constant the P - V graph is obtained as follows:

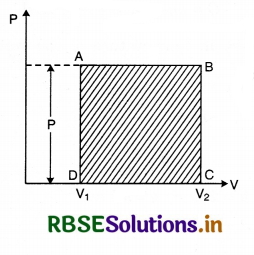
From this the area ABCD below the line AB and between V₁ and V₂ can be found and the value of work done by the gas can be obtained.
∴ Work done by the system at constant pressure.
W = P(V₂ - V₁)
= Area ABCD ......................(1)

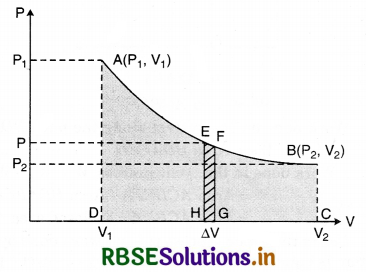
When pressure (P) is not constant then P - V graph is obtained as follows:
Area ABCD can be divided into rectangular strip of very small widths. Consider one such rectangular strip EFGH with length P and width ∆V.
Area of a rectangular strip = P∆V
Work done in elementary changing the volume ∆V of the system.
∆W = P∆V = Area EFGH
∴ Complete area ABCD = ∑ Area EFGH
= ∑P∆V
If ∆V is very small ∑V → 0 then
Work W = \(\underset{\Delta V \rightarrow 0 V_1}{\operatorname{Limit}} \sum_{V_2}^{V_2} P \Delta V\)
= \(\int_{V_1}^{V_2} P d V\)
= Area ABCD
So work done by the system along AB
W = \(\int_{V_1}^{V_2} P d V\) .............................(2)
So work done by a thermodynamic system is equivalent to the area surrounded between P - V curve and volume axis.

Question 11.
Define isochoric and isobaric process. Calculate the work done in these processes.
Answer:
¡fin a physical change of thermodynamic system, there is change in pressure (P) and temperature but volume remains constant, then, it is called an isochoric process. So, no work is done by the gas in this process. No work is done on the gas because V is constant. Then, dV = 0
Explanation of isochoric process using first law of thermodynamics: From first law of Thermodynamics,
dQ = dU + dW
dQ = dU + PdV
V = constant for isochoric process,
dV = 0
then, dQ = dU .......................(5)
This means that the total heat absorbed by gas is consumed in changing the internal energy and the temperature of the system by gas. At constant volume, molar specific heat,
C_V = \(\left(\frac{d Q}{d T}\right)_V\)
then, C_V dT = dU ........................(6)

If temperature (T) and volume (V) changes in a physical change in a thermodynamic system and pressure (P) is constant, the process is called isobaric i.e, when the state of the substance changes, then the pressure (P) is constant. For example, freezing of water, formation of steam, etc.

Matrix Matching Type Questions

Match Column I with Column II

Column I	Column II
A. Work done in an isothermal process	P. nR(T2 - T1)
B. Work done in an adiabatic process	Q. P(\(\frac{\Delta V}{\Delta T})\)P
C. CP - CV	R. 2.303µRTlog\(\frac{P_1}{P_2}\)
D. Work done in an isobaric process	S. \(\frac{\mu R}{\gamma-1}\) (T1 - T2)

Answer:

Column I	Column II
A. Work done in an isothermal process	R. 2.303µRTlog\(\frac{P_1}{P_2}\)
B. Work done in an adiabatic process	S. \(\frac{\mu R}{\gamma-1}\) (T1 - T2)
C. CP - CV	Q. P(\(\frac{\Delta V}{\Delta T}\))P
D. Work done in an isobaric process	P. nR(T2 - T1)

Conceptual Questions

Question 1.
Can water be made to boil without heating?
Answer:
Yes, by reducing pressure on water. Boiling point of water water can be brought down to room temperature.

Question 2.
Does the mass of a body change when it is heated or cooled?
Answer:
Yes, in heating or cooling, a body absorbs or loses energy. The mass will, therefore, increase or decrease accordingly as per the relation E = mc².

Question 3. 
A piece of lead is hammered. Does its internal energy increase? Does the heat enter the lead from outside?
Answer:
Yes, internal energy of lead increases. No heat energy from outside enters the load.

Question 4.
Is the internal energy of a gas a function of the pressure? Explain.
Answer:
The internal energy of an ideal gas depends only on the temperature of the gas, while that of a real gas depends on the temperature and volume, which in turn is dependent on pressure.

Question 5. 
Can the Carnot engine be realised in practice?
Answer:
No, because Carnot engine is an ideal heat engine, whose conditions are not realized in practice.

Question 6.
Why is conversion of heat into work not possible without a sink at lower temperature? 
Answer:
For converting heat energy into work continuously, a part of heat energy absorbed from the source has to be rejected. The heat energy can be rejected only if there is a body, whose temperature is less then that of the source. This body at lower temperature is the sink.

Question 7. 
An electric refrigerator transfers heat from the cold cooling coils to the warm surroundings. Is it against the second law of Thermodynamics? Justify your answer.
Answer:
No, it is not against the second law. This is done by the compresser for this transfer of heat.

Question 8.
Reversibility is the basis of an ideal engine. Briefly explain the statement.
Answer:
In a reversible process, the system and its surroundings return to the original states if the forward cycle is followed by the reverse cycle. Carnot engine is a theoretical thermodynamical cycle proposed by Leonard Carnot. It gives the estimate of the maximum possible efficiency that a heat engine during the conversion process of heat into work and conversely, working between two reservoirs can possess. Thus we can say that reversibility is the basis of an ideal engine.

Numerical Questions

Based on Work, Internal Energy and First Law of Thermodynamics

Question 1.
In the given figure, if at position A, the internal energy of a system is 10 J and during the change from A to B the heat given to the system is 50J then calculate the internal energy at position B.

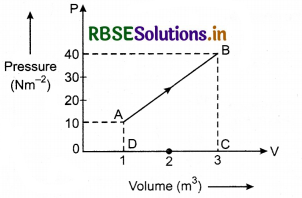
Solution:
Given: U_A = 10J; for process A → B, dQ = 50 J; U_B = ?; For process A → B
dW = Area of trapezium ABCDA

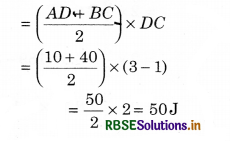
From first law of Thermodynamics-
dQ = dU + dW
∴ dU = dQ - dW = 50 - 50 = 0
∴ dU = 0
but dU = U_B - U_A
∴ U_B - U_A = 0
or U_B - U_A = 10 J

Question 2.
In a thermodynamical process for a gas heat given is 300 J and 200 J work is done on the gas. Calculate the change in internal energy of the gas.
Solution:
Given: dQ = 300 J; dW = -200 J; dU = ?
∵ From first law of Thermodynamics
dQ = dU + dW
or dU = dQ - dW
∴ dU = 300 - (-200)
= 300 + 200
or dU = 500 J

Question 3.
In the given figure, the pressure-volume graph for a cyclic process of an ideal gas is shown. The value of internal energy of gas in state A is 150J, in state B is 100J and in state C is 250J, then calculate:

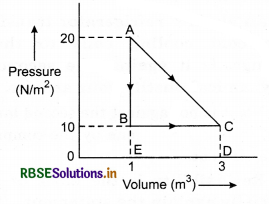
(i) Heat given by the gas in process A → B.
(ii) Work done by the gas in process B → C.
(iii) Heat taken by the gas in process B → C.
Solution:
U_A = 150J; U_B = 100 J; U_C = 250J
(i) For process A → B
dW = PdV = 0, as volume in constant dV = 0
dU = U_B - U_A = 100 - 150 = -50J
∴ dQ = dU + dW = (-50J + 0)
or dQ = -50J
∴ Heat liberated = 50J

(ii) For process B → C
dW = +area BCDE
= +BC x BE
= (3 - 1) x 10
= 2 x 10
= 20J

(iii) For process B → C
dW = 20J
dU = U_C - U_B
= 250 - 100
= 150J
∴ dQ = dU + dW
= 150 + 20
or dQ = 170J

Question 4.
The mass of a man is 60 kg. If he receives 10⁵ cal heat from food and his body’s efficiency is 28%, then how much height he can climb? (g = 9.8 ms , J = 4.2 J/cal¹).
Solution:
M = 60 kg; Q = 10⁵ cal = 4.2 x 10⁵ J
∵ Efficiency of human body = 28% = \(\frac{28}{100}\)
∵ Efficiency η = \(\frac{W}{Q}\)
∴ W = η x Q = \(\frac{28}{100}\) x 4.2 x 10⁵
W = 28 x 4.2 x 10³ J
∵ W = mgh
∴ h = \(\frac{W}{m g}=\frac{28 \times 4.2 \times 10^3}{60 \times 9.8}=\frac{28 \times 42}{6 \times 98}\) x 10²
= 2 x 10² = 200 m
h = 200 m

Question 5.
A bullet of lead moving with 150 ms^-1 stops after striking a target. If 80% kinetic energy remains in the bullet, then calculate the rise in temperature of the bullet. Specific heat of lead is 30 cal/kg¹°C¹. (J = 4.2 J/cal¹)
Solution:
v = 150 ms^-1; ∴ E_k = \(\frac{1}{2}\) mv²
Heat absorbed by bullet
Q = \(\frac{80}{100} \times \frac{1}{2} m v^2=\frac{2}{5} m v^2\)
s = 30 cal kg.°C^-1
= 30 x 4.2 J kg^-1°C^-1
If increase in the temperature is ∆θ
Q = ms∆θ

Question 6.
In the given figure, the P - V graph of thermodynamical process of an ideal gas is shown. Calculate from this graph work done in the processes.

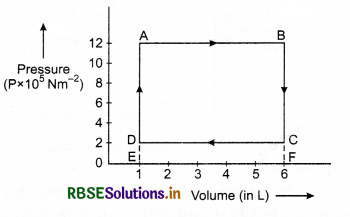
(i) A → B
(ii) B → C
(iii) C → D
(iv) D → A
Solution:
(i) For process A → B
dW = +Area of ▭ ABFE
= AB x BF
= (6 - 1) x 10^-3 x 12 x 10⁵
= 5 x 12 x 10²
= 60 x 10²
= 6000 J

(ii) For process B → C; volume is constant, so dV = 0
∴ dW = PdV = 0
or dW = 0

(iii) For process C → D
dW = - Area ▭ CDEF = -DE x EF
= -(2 x 105) x (6 - 1) x 10^-3 = -2 x 5 x 10²
= -10 x 10²
= -1000 J

(iv) For process D → A, volume is constant, so dV = 0
∴ dW = PdV = 0

Based on Isothermal Process

Question 7.
The volume of 1 mole of O₂ gas at 0°C and 1 atmospheric pressure is 22.4 litre. It is compressed isothermally. Due to this volume decreases upto 11.2 litre. Calculate work done in this process.
Solution:
V₁ = 22.4 litre; V₂ = 11.2 litre; T = 273 K;
µ = 1 mole; R = 8.31 J.mol^-1.K^-1
∴ Work done W = µRT x log_e\(\frac{V_2}{V_1}\)
or W = 1 x 8.31 x 273 x 2.303log₁₀(\(\frac{11.2}{22.4}\))
= 5224.65log₁₀(\(\frac{1}{2}\))
= 5224.65 [log 1 - log 2]
= 5224.65 [0 - 0.3010]
W = -1572.6 J

Question 8.
2 mole ideal gas is expanded at 27°C isothermally. Due to which its volume increases and becomes three times of its initial volume. Calculate work done by the gas and current of heat absorbed by the gas. (R = 8.31J/mol¹K¹).
Solution:
µ = 2; T = 273 + 27 = 300K; V₂ = 3V₁; W = ?; Q = ?
W = 2.303 µRTlog₁₀(\(\frac{V_2}{V_1}\))
= 2.303 x 2 x 8.31 x 300 log₁₀(\(\frac{3V_1}{V_1}\))
= 2.303 x 2 x 8.31 x 300 x 0.4771
= 2739.2 x 2
= 5478.4J
= 5.478 x 10³ J
= 5.48 x 10³ J
∴ Heat absorbed
Q = W = 5.48 x 10³ J
= \(\frac{5478.4}{4.2}\) = 1304.38 cal
= 1.31 x 10³ cal

Based on Adiabatic Process

Question 9.
At 27°C, 2 mole of an ideal and one atomic gas occupy volume V. Gas expands upto volume 2V by adiabatic process. Calculate:
(i) Final temperature of the gas.
(ii) Change in the internal energy of the gas,
(iii) Work done by the gas in this process.
(R = 8.31 J/mol¹ K¹)
Solution:
(i) T₁ = 27°C = 27 + 273 = 300K; V₁ = V; V₂ = 2V;
γ = \(\frac{5}{3}\) (For one atomic gas); T₂ = ?
∵ T₂V₂^γ-1 = T₁V₁^γ-1
∴ T₂ = T₁\(\left(\frac{V_1}{V_2}\right)^{\gamma-1}=\left(\frac{V}{2 V}\right)^{5 / 3-1}=\left(\frac{1}{2}\right)^{2 / 3}\)
= \(\frac{300}{(2)^{2 / 3}}=\frac{300}{1.587}\) = 189K
or T₂ = 189K

(ii) Change in internal energy


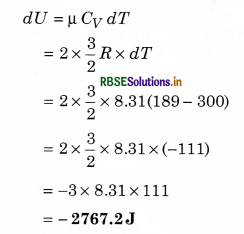
(iii) In adiabatic process dQ = 0 and dQ = dU + dW
∴ dW = -dU
= - (-2767.2)
= 2767.2J

Based on Mayer’s Formula

Question 10.
At N.T.P. volume of 1 mole oxygen gas is 22.4 litre. Calculate the both molar heat capacities of the oxygen.
Solution:
P = 1.01 x 10⁵ N/m²; V = 22.4 x 10^-3 m³; µ = 1; T = 273K
∵ PV = µRT
⇒ R = \(\frac{P V}{\mu T}=\frac{1.01 \times 10^5 \times 22.4 \times 10^{-3}}{1 \times 273}\)
or R = 8.31 J/mol¹K¹
∵ By Mayer's relation
C_P - C_V = R
∴ C_P - C_V = 8.31 ........................(1)
For diatomic gas γ = 1.4
and \(\frac{C_P}{C_V}\) = γ, ∴ C_P = γC_V = 1.4C_V
∴ From equation (1),
1.4C_V - C_V = 8.31 or 0.4C_V = 8.31
∴ C_V = \(\frac{8.31}{0.4}\) = 20.775 J/mol¹K¹
∴ C_P = 1.4 x C_V = 1.4 x 20.775
or C^P = 29.085 J/mol¹ K¹

Based on Carnot’s Engine

Question 11.
The efficiency of a Carnot’s engine is 50% and temperature of the sink is at 27°C. If its efficiency is increased by 10%, then how much increase in the temperature of the source?
Solution:
T₂ = 7 + 273 = 280K; η = 50% = \(\frac{1}{2}\)
∴ T₁ = ?
∴ η = 1 - \(\frac{T_2}{T_1}\)
⇒ \(\frac{T_2}{T_1}=1-\eta=1-\frac{1}{2}=\frac{1}{2}\)
∴ T₁ = 2T2 = 2 x 280 = 560K
or T₁ = 560K
If the efficiency is increased by 10%, then new efficiency
η' = 60% = \(\frac{60}{100}=\frac{3}{5}\)
If new temperature of the source is T₁', then

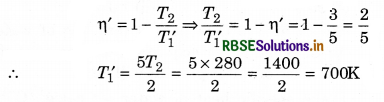
∴ Rise in the temperature of the source
∆T₁ = T₁' - T₁ = 700 - 560
or ∆T₁ = 140K

Question 12.
A Carnot engine working between temperatures 500K and 400K, is absorbing heat 2000 cal in each cycle from source, then calculate:
(i) In each cycle heat rejected in sink.
(ii) Work done by the engine in each cycle.
(iii) Efficiency of the engine
Solution:
T₁ = 500K; T₂ = 400K; Q₁ = 2000 cal,

(i) Q₂ = ?
∵ η = 1 - \(\frac{T_2}{T_1}=1-\frac{Q_2}{Q_1}\)


(ii) W = Q₁ - Q₂ = 2000 - 1600 = 400 cal
= 400 x 4.2J
= 40 x 42 = 1680 J

(iii) Efficiency of the engine

Objective Type Questions

Question 1.
In which of the following process, heat is neither absorbed nor released by a system?
(a) isothermal
(b) adiabatic
(c) isobaric
(d) isochoric
Solution:
For adiabatic process
∆Q = 0

Question 2.
A Carnot’s engine works as a refrigerator between 2250 K and 300 K. It receives 500 cal heat from the reservoir at low temperature. The amount of work done in each cycle to operate the refrigerator is:
(a) 420 J
(b) 772 J
(c) 2100 J
(d) 2500 J
Solution:
The coefficient of performance of a refrigerator is

Question 3.
One mole of an ideal monoatomic gas is compressed isothermally in a rigid vessel to double its pressure at room temperature, 27°C. The work done on the gas will be:
(a) 300 R
(b) 300 R log 6
(c) 300 R log 2
(d) 300 R log 7
Solution:
Let's assume initial pressure to be P₁. Thus, the final pressure is P₂ = 2P₁ (since the pressure has doubled)
Work done in isothermal process
W = µRT log(\(\frac{P_2}{P_1}\))
= 1 x R x 300 x log(\(\frac{2P_1}{P_1}\))
⇒ W = 300 R log2 (since P₂ = 2P₁)

Question 4.
The efficiency of an ideal heat engine working between the freezing point and boiling point of water is:
(a) 26.8%
(b) 12.5%
(c) 6.25%
(d) 20%
Solution:
Efficiency of ideal heat engine

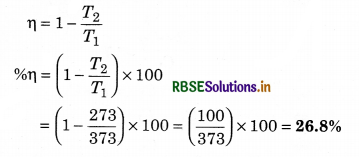
Question 5.
The thermodynamical processes are indicated in the following diagram:
Match the following

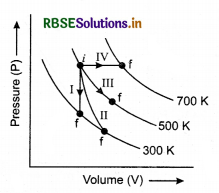
Column I	Column II
P. Process I	a. Adiabatic
Q. Process II	b. Isobaric
R. Process III	c. Isochoric
S. Process IV	d. Isothermal

(1) P → c, Q → a, R → d, S → b
(2) P → c, Q → d, R → b, S → a
(3) P → d, Q → b, R → a, S → c
(4) P → a, Q → c, R → d, S → b
Solution:
I - volume constant → isochoric P → c
II - Adiabatic → Q → a
III - Temperature constant → Isothermal R → d
IV - Pressure constant → Isobaric S → b

Question 6.
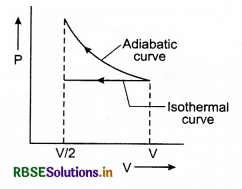
A gas is compressed isothermally to half of its initial volume. The same gas is compressed separately through an adiabatic process until its volume is again reduced to half. Then:
(a) Compressing the gas through adiabatic process will require more work to be done.
(b) Compressing the gas isothermally or adiabatically will require the same amount of work.
(c) Which of the case (whether compression through isothermal or through adiabatic process) requires more work will depend upon the atomicity of the gas.
(d) Compressing the gas isothermally will require more work to be done.
Solution:
The solution of this question can be understood by plotting a p - V graph for the compression of a gas isothermally and adiabatically simultaneously to half of its initial volume, i.e., since the isothermal curve is less steeper than the adiabatic curve. So area under the p - V curve for adiabatic process will be more than in isothermal process.

Question 7.
The coefficient of performance of a refrigerator is 5. If the temperature inside freezer is -20°C, the temperature of the surroundings to which it rejects heat is:
(a) 31°C
(b) 41°C
(c) 11°C
(d) 21°C
Solution:
Given, coefficient of performance of a refrigerator ß = 5, temperature of surface i.e., inside freezer
T₂ = -20°C = -20 + 273 = 253 K
Temperature of surroundings i.e., heat rejected outside, T₁ = ?
So, ß = \(\frac{T_2}{T_1-T_2}\)
⇒ 5 = \(\frac{253}{T_1-253}\)
⇒ 5T₁ - 1265 = 253
⇒ 5T₁ = 1518
T₁ = \(\frac{1518}{5}\) = 303.6 K
T₁ = 303.6 - 273 = 31°C

Question 8.
Figure below shows two paths that may be taken by a gas to go from a state A to a state C. In process AB, 400J of heat is added to the system and in process BC, 100J of heat is added to the system. The heat absorbed by the system in the process AC will be:
(a) 380 J
(b) 500 J
(c) 460 J
(d) 300 J

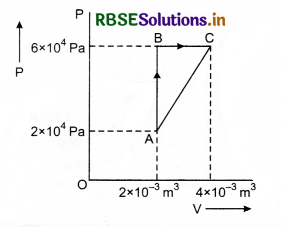
Solution:
Since, initial and final points are same.
So, \(\Delta U_{A \rightarrow B \rightarrow C}=\Delta U_{A \rightarrow C}\) .....................(1)
Also, A → B is isochoric process.

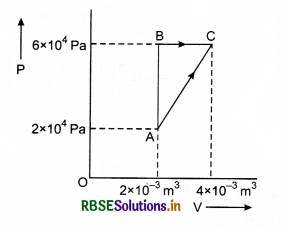
so, dW_{A → B} = 0
and, dQ = dU + dW
so, dQ_{A → B} = dU_{A → B} = 400 J
Next B → C is isobaric process.
so, dQ_{B → C} = dU_{B → C} + dW_{B → C}
= dU_{B → C} + p∆U_{B → C}
⇒ 100 = dU_{B → C} + 6 x 10⁴ (2 x 10^-3)
⇒ dU_{B → C} = 100 - 120 = -20 J
From eqn. (1)
∴ ∆U _{A → B → C} = ∆U_{A → C}
⇒ ∆U_{A →B} + ∆U_{B → C} = dQ_{A → C} - dW_{A → C}
⇒ 400 + (-20) = dQ_{A → C} - (p∆V_A + Area of ∆ABC)
⇒ dQ_{A → C} = 380 + [2 x 10⁴ x 2 x 10^-3 + \(\frac{1}{2}\) x 2 x 10^-3 x 4 x 10⁴]
= 380 + (40 + 40)
dQ_{A → C} = 460 J

Question 9.
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in figure.

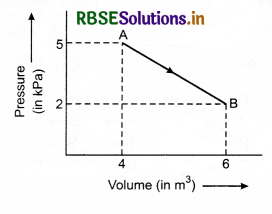
The change in internal energy of the gas during the transition is:
(a) 20 kJ
(b) - 20 kJ
(c) 20 J
(d) - 12 kJ
Solution:
For a diatomic gas

The change in internal energy of gas in the transition from A to B is

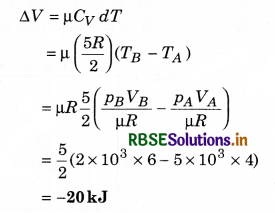
Question 10.
A Carnot engine, having an efficiency of η = \(\frac{1}{10}\) as heat engine, is used as a refrigerator. If the work done on the system is 10 J, the amount of energy absorbed from the reservoir at lower temperature is
(a) 100 J
(b) 99 J
(c) 90 J
(d) 1 J
Solution:

Question 11.
Steam at 100°C is passed into 20g of water at 10°C. When water acquires a temperature of 80°, the mass of water present will be:
[Take specific heat of water = 1 cal g¹°C^-1 and latent heat of steam = 540 cal g^-1]
(a) 24 g
(b) 31.5 g
(c) 42.5 g
(d) 22.5 g
Solution:
According to principle of calorimetry,
Heat lost by steam = Heat gained by water
Let m' be the amount of steam that converts into water,
m' x L + m's ∆T = ms∆t
m' x 540 + m' x 1 x (100 - 80) = 20 x 1 x 70
m' = \(\frac{20 \times 70}{560}\)
= 2.5 g
Now, net mass of water = 20 + 2.5 = 22.5 g

Question 12.
A monoatomic gas at a pressure p, having a volume V expands isothermally to a volume 2V and then adiabatically to a volume 16V. The final
pressure of the gas is (take γ = \(\frac{5}{3}\)):
(a) 64p
(b) 32p
(c) \(\frac{p}{64}\)
(d) 16p
Solution:
For isothermal expansion process,
pV = p' x 2V [∴ V' = 2V]
p' = \(\frac{p}{2}\)
For adiabatic expansion

Question 13.
A thermodynamic system undergoes cyclic process ABCDA as shown in figure. The work done by the system in the cycle is:

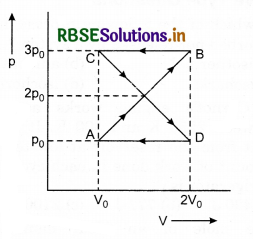
(a) p₀V₀
(b) 2p₀V₀
(c) \(\frac{p_0 V_0}{2}\)
(d) zero
Solution:
Work done in the cyclic process = Area bounded by the closed configuration
= Area of closed configuration
= \(\frac{1}{2}\) x V₀ x p₀ - \(\frac{1}{2}\)V₀p₀ = 0

Question 14.
The molar specific heats of an ideal gas at constant pressure and volume are denoted by C_P and C_V respectively. If γ = \(\frac{C_p}{C_V}\) and R is the universal gas constant then C_V is equal to:

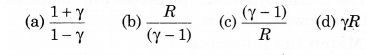
Solution:
∵ C_P - C_V = R
C_P = R + C_V
and \(\frac{C_p}{C_V}\) = γ (given)
So, \(\frac{R+C_V}{C_V}\) = γ
⇒ γC_V = R + C_V
⇒ γ C_V - C_V = R
⇒ C_V = \(\frac{R}{\gamma-1}\)

Question 15.
A gas is taken through the cycle A → B → C → A as shown. What is the net work done by the gas?

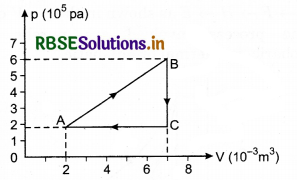
(a) 2000 J
(b) 1000 J
(c) zero
(d) -2000 J
Solution:
Net work done = Area enclosed in p - V curve = Area of ∆ABC
Area of ∆ABC = \(\frac{1}{2}\) x 5 x 10^-3 x 4 x 10⁵ J
= 10³ J = 1000 J

Question 16.
During an adiabatic process, the pressure of a gas is found to be proportional to the cube of its temperature. The ratio of \(\frac{C_p}{C_V}\) for the gas is:
(a) \(\frac{4}{3}\)
(b) 2
(c) \(\frac{5}{3}\)
(d) \(\frac{3}{2}\)
Solution:
According to question,
p ∝ T³
We know that pV = nRT
and pV ∝ T
∴ p ∝ (pV)³
⇒ p²V³ = constant
⇒ pV^3/2 = constant
Comparing it with pV^γ = constant,
We have γ = \(\frac{3}{2}\)

Question 17.
In the given (V - T) diagram, what is the relation between pressures p₁ and p₂?

(a) p₂ = p₁
(b) p₂ > p₁
(c) p₂ < p₁
(d) Cannot be predicted
Solution:
According to question,
Slope of the graph ∝ \(\frac{1}{\operatorname{Pressure}(p)}\)
So, p₂ < p₁.

Question 18.
The amount of heat energy required to raise the temperature of 1g of helium at NTP, from T₁K to T₂K is:

Solution:
We know that, Q = \(\frac{\mu f R T}{2}\)
∴ Amount of heat required
Q = \(\frac{3}{2}\) x \(\frac{1}{4}\) x k_B N_a ∆T
= \(\frac{3}{8}\) N_a k_B (T₂ - T₁)

Question 19.
A thermodynamic system is taken through the cycle ABCD as shown in the figure. Heat rejected by the gas during the cycle is:

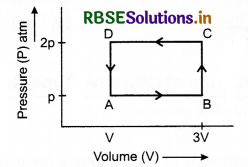
(a) 2pV
(b) 4 pV
(c) \(\frac{1}{2}\) pV
(d) pV
Solution:
For given cyclic process,
∆U = 0
∴ Q = W
Also, W = -Area enclosed by the curve
= -AB x AD
= -(2p - p) (3V - V)
= -p x 2V
∴ Heat rejected = 2 pV

Question 20.
One mole of an ideal gas goes from an initial state A to final state B via two processes. It first undergoes isothermal expansion from volume V to 3V and then its volume is reduced from 3V to V at constant pressure. The correct p - V diagram representing the two processes is:

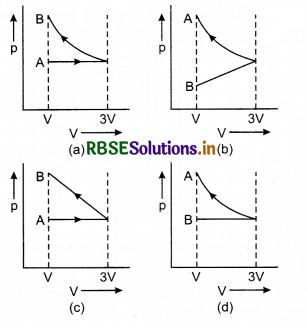
Solution:
According to question, first gas goes from volume V to 3V and after this volume is reduced from 3V to V at constant pressure. In isothermal expansion, p - V curve is rectangular hyperbola.

Question 21.
Liquid oxygen at 50K is heated to 300K at constant pressure of 1 atm. The rate of heating is constant. Which one of the following graphs repersents the variation of temperature with time?

Solution:
Graph (a) shows the variation of temperature with time. At first temperature will increase than there will be state change from liquid to gas.

Question 22.
'µ' moles of an ideal gas undergoes a process A → B as shown in the figure. The maximum temperature of the gas during the process will be:

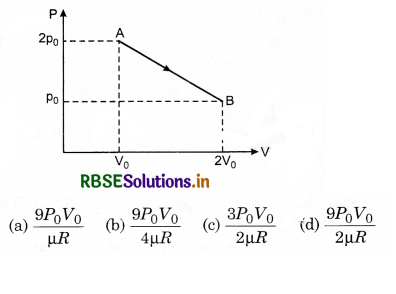
Solution:
T will be maximum where product of PV is maximum.
Equation of line

Question 23.
One mole of diactomic ideal gas undergoes a cyclic process ABC as shown in the figure. The process BC is adiabatic. The temperature at A, B and C are 400K, 800K and 600K respectively. Choose the correct statement:

(a) The change in internal energy in the process AB is -350 R
(b) The change in internal energy in the process BC is -500 R
(c) The change in internal energy in whole cyclic process is 250 R
(d) The change in internal energy in the process is 700 R
Solution:
∆U_AB = µC_V (T_B - T_A)
= 1 x \(\frac{5R}{2}\) (800 - 400) = 1000R
∆U_BC = µC_V (T_C - T_B)
= 1 x \(\frac{5R}{2}\) (600 - 800) = -500R
∆U_total = 0
∆UC_A = µ C_V (T_A - T_C)
= 1 x \(\frac{5R}{2}\) (400 - 6000) = -500R

Question 24.
The p - V diagram represents the thermodynamic cycle of an engine, operating with an ideal monoatomic gas. The amount of heat extracted from the source in a single cycle is:

(a) (\(\frac{13}{2}\)) P₀V₀
(b) (\(\frac{11}{2}\)) P₀V₀
(c) 4P₀V₀
(d) P₀V₀
Solution:
Heat extracted from the source in path DA and AB
∆Q = \(\frac{3}{2} R\left(\frac{P_0 V_0}{R}\right)+\frac{5}{2} R\left(\frac{2 P_0 V_0}{R}\right)\)
= \(\frac{13}{2}\) P₀V₀

Question 25.
A Carnot engine operating between temperatures T₁ and T₂ has efficiency 1/6. When T₂ is lowered by 62K, its efficiency increases to 1/3. Then T₁ and T₂ are, respectively:
(a) 372 K and 310K
(b) 372 K and 330K
(c) 330 K and 268 K
(d) 310 K and 248 K
Solution:
Here, η = 1 - \(\frac{T_2}{T_1}=\frac{1}{6} or \frac{T_2}{T_1}=\frac{5}{6}\)
When T₂ is lowered by 62K,

Question 26.
One mole of a monatomic ideal gas is taken along two cyclic processes E → F → G → E and E → F → H → E as shown in the p - V diagram. The process involved are purely isochoric, isobaric, isothermal or adiabatic.

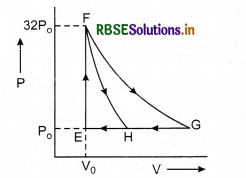
Match the paths in List I with the magnitudes of the work done in List II and select the correct answer using the codes given below the lists:

List I	List II
P. G → E	1. 160 p0V0In 2
Q. G → H	2. 36 p0V0
R. F → H	3. 24 p0V0
S. F → G	4. 31 p0 V0

Codes

P	Q	R	S
(a) 4	3	2	1
(b) 4	3	1	2
(c) 3	1	2	4
(d) 1	3	2	4

Solution:
In F → G, work done in isothermal process is
µRT log (\(\frac{V_f}{V_i}\)) = 32 p₀ V₀ log (\(\frac{32 V_0}{V_0}\))
= 32 p₀ V₀ log 25
= 160 p.V₀ log 2

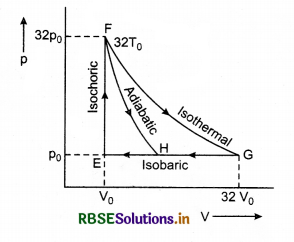
In G → E, ∆W = p₀ ∆V = p₀ (31 V₀) = 31 p₀ V₀
In G → H, work done in less than 31 p₀V₀ i.e., 24 p₀ V₀.
In F → H work done is 36 p₀ V₀.

Question 27.
5.6 L of helium gas at STP is adiabatically compressed to 0.7 L. Taking the initial temperature to be T₁, the work done in the process is:
(a) \(\frac{9}{8}\) RT₁
(b) \(\frac{3}{2}\) RT₁
(c) \(\frac{15}{8}\) RT₁
(d) \(\frac{9}{2}\) RT₁
Solution:
I STP, 22.4 L of any gas is 1 mole
∴ 5.6 L = \(\frac{5.6}{22.4}=\frac{1}{4}\) moles = µ
In adiabatic process,
TV^γ-1 = constant
∴ T₂V₂^γ-1 = T₁V₁^γ-1 or T₂ = T₁ (\(\frac{V_1}{V_2}\))^γ-1
γ = \(\frac{C_P}{C_V}=\frac{5}{3}\) for monoatomic He gas
∴ T₂ = T₁\(\left(\frac{5.6}{0.7}\right)^{5 / 3-1}\) = 4T₁
Further in adiabatic process, Q = 0
∴ W + ∆U = 0

∴ Correct option is (a).