RBSE Class 11 Physics Important Questions Chapter 11 Thermal Properties of Matter

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 11 Thermal Properties of Matter Important Questions and Answers.

RBSE Class 11 Physics Chapter 11 Important Questions Thermal Properties of Matter

Multiple Choice Questions

Question 1.
Heat given to a body, which raises its temperature by 1°C is:
(a) water equivalent
(b) temperature
(c) thermal capacity
(d) specific heat
Answer:
(c) thermal capacity

Question 2.
According to Newton's law of cooling, the rate of cooling of a body is proportional to (∆θ)n, where ∆θ is the difference of the temperature of the body and the surroundings and n is equal to:
(a) two
(b) three
(c) four 
(d) one
Answer:
(d) one

Question 3.
On a hilly region, water boils at 95°C, the temperature expressed is Fahrenheit is:
(a) 100°F
(b) 203°F
(c) 150°F
(d) 203°F
Answer:
(d) 203°F

Question 4.
50 g of ice at 0°C is mixed with 50 g of water at 80°C, final temperature of mixture will be:
(a) 0°C
(b) 40°C
(c) 60°C
(d) 4°C
Answer:
(a) 0°C

Question 5.
In determining the temperature of a distant star, one makes use of:
(a) Kirchhoffs law
(b) Stefan’s law
(c) Wien’s displacement law
(d) None of the above
Answer:
(c) Wien’s displacement law

Question 6.
The wavelength of radiation emitted by a body depends upon:
(a) The nature of the surface
(b) The area of the surface
(c) The temperature of the surface
(d) All of the above factors
Answer:
(c) The temperature of the surface

Question 7.
A quantity of heat required to change the unit mass of a solid substance, from solid state to liquid state, while the temperature remains constant is:
(a) Latent heat
(b) Sublimation
(c) Hoar frost
(d) Latent heat of fusion
Answer:
(d) Latent heat of fusion

Question 8.
When a solid is converted into a gas, directly by heating, then this process is known as:
(a) Boiling
(b) Sublimation
(c) Vapourisaton
(d) Condensation
Answer:
(b) Sublimation

Question 9.
The density of a substance at 0°C is 10 g/cm and at 100°C its density is 9.7 g/cm³. The coefficient of linear expansion of the substance is:
(a) 10^-4
(b) 10^-2
(c) 10^-3
(d) 10²
Answer:
(a) 10^-4

Question 10.
Calorimeters are made of which of the following?
(a) Glass
(b) Metal
(c) Wood
(d) Either (a) or (c)
Answer:
(b) Metal

Question 11.
Heat travels through vacuum by:
(a) Conduction
(b) Convection
(c) Radiation
(d) Both (a) and (b)
Answer:
(c) Radiation

Question 12.
A black body is at a temperature 300 K, emits energy at a rate, which is proportional to:
(a) 300
(b) 300²
(c) 300³
(d) 300⁴
Answer:
(d) 300⁴

Question 13.
On a cold morning, a metal surface will feel colder to touch than a wooden surface, because:
(a) Metal has high specific heat
(b) Metal has high thermal conductivity
(c) Metal has low specific heat
(d) Metal has low thermal conductivity
Answer:
(b) Metal has high thermal conductivity

Question 14.
According to Wien's displacement law:
(a) λ_mT = constant
(b) λ_m ∝ \(\frac{1}{T}\)
(c) λ_m/T = constant
(d) both (a) and (b)
Answer:
(b) λ_m ∝ \(\frac{1}{T}\)

Question 15.
The presence of gravitational field is required for the heat transfer by:
(a) Stirring liquids
(b) Conduction
(c) Natural convection
(d) Radiation
Answer:
(c) Natural convection

Question 16.
Mercury thermometer can be used to measure temperature upto:
(a) 260°C
(b) 100°C
(c) 360°C
(d) 500°C
Answer:
(c) 360°C

Question 17.
When a body is heated, then maximum rise will be in its:
(a) Length
(b) Surface area
(c) Volume
(d) Density
Answer:
(c) Volume

Question 18.
In order that the heat flows from one part of a solid to another part, what is required?
(a) Uniform density
(b) Temperature gradient
(c) Density gradient
(d) Uniform temperature
Answer:
(b) Temperature gradient

Question 19.
At which temperature, the centigrade and Fahrenheit scales are equal?
(a) 40°
(b) -40°
(c) 37°
(d) -80°
Answer:
(b) -40°

Question 20.
A body cools from 80°C to 64°C in 5 minutes and same body cools from 80°C to 52°C in 10 minutes, what is the temeprature of surroundings?
(a) 24°C
(b) 28°C
(c) 22°C
(d) 25°C
Answer:
(a) 24°C

Fill in the Blanks

Question 1.
...................... is the best conductor of heat.
Answer:
silver

Question 2.
If the process of transfer of heat is slow, then it can be ...................... process.
Answer:
conduction or convection

Question 3.
Sea freeze is caused by ......................
Answer:
convection process

Question 4.
Themetal rods of same length and same area of cross-section are connected in series. If their conductivities are 120 ωm^-1k^-1 and 240 ωm^-1K^-1, the effective conductivity of the combination is ......................
Answer:
160 ωm^-1k^-1

Question 5.
Stain less cooking pans are preferred with extra ...................... bottoms.
Answer:
copper

Very Short Answer Questions

Question 1.
At what temperature does degree centigrade and Fahrenheit scale become equal?
Answer:

Question 2.
At what point, the three states of matter for a substance (solid, liquid or gas) coexist?
Answer:
Triple point.

Question 3.
In which mode of heat transfer, no medium is required?
Answer:
Radiation.

Question 4.
Absorpotion coefficient for an ideal black body is zero. Is this statement true or false?
Answer:
False.

Question 5.
According to Wien’s displacement law, what is the product of Wavelength for maximum emission and absolute temperature?
Answer:
λ_mT = b = 2.9 x 10^-3 mK.

Question 6.
What are the SI and CGS units of heat? How are they related?
Answer:
SI unit of heat is joule and CGS unit of heat is calorie.
1 calorie = 4.18 joule

Question 7.
The temperature of a gas is increased by 10°C. What is the corresponding change in the Kelvin scale?
Answer:
10 K.

Question 8.
What is the value of 0°F on the Kelvin scale?
Answer:
0°F = 255.23 K.

Question 9.
What are the values of the triple point of water on the centigrade, Fahrenheit and absolute scales of temperature?
Answer:
0.01°C, 32.018°F, 273.16K.

Question 10.
How are the three coefficients of expansion related to each other?
Answer:
\(\frac{\alpha}{1}=\frac{\beta}{2}=\frac{\gamma}{3}\)

Question 11.
Define Joule’s mechanical equivalent of heat. Give its value.
Answer:
Joule’s mechanical equivalent of heat may be defined as the amount of work that must be done to produce a unit quantity of heat. Its value is 4.18 J/cal.

Question 12.
Write the SI unit of specific heat.
Answer:
SI unit of specific heat = J/kg K.

Question 13.
Which substance has the highest specific heat?
Answer:
Water.

Question 14.
What is the relation between heat capacity and water equivalent of a body?
Answer:
The heat capacity and water equivalent of a body are numerically equal.

Question 15.
Arrange the metals Cu, Al and Ag in the order of their increasing thermal conductivity.
Answer:
Al < Cu < Ag.

Question 16.
Write the unit and dimensional formula of thermal resistance.
Answer:
SI unit of thermal resistance = K/W. Dimensional formula of thermal resistance is [M^-1L^-2T^-3K].

Question 17.
What is the nature of heat radiations?
Answer:
Heat radiations are electromagnetic waves having wavelength range from 1 pm to 100 pm. These are also called infrared waves.

Question 18.
What is the absorbity of a perfect black body?
Answer:
1.

Question 19.
What is the effect of decrease of pressure on the fusion and boiling points of CO₂?
Answer:
Both the boiling point and freezing point of CO₂ decrease if pressure decreases.

Question 20.
Why a small gap is left between the iron rails of railway tracks?
Answer:
If no gap is left between the iron rails, the rails may bend due to expansion in summer and the train may get derailed.

Question 21.
Why are loops provided in long metal pipes used for carrying oil and any other liquid over long distances?
Answer:
The loops in metal pipes are provided in order to avoid the strain that would develop in the pipes when the temperature changes and hence the pressure of liquids in them changes.

Question 22.
Pendulum clocks generally run fast in winter and slow in summer. Why?
Answer:
The time period of a simple pendulum is given by,
T = 2π\(\sqrt{\left(\frac{l}{g}\right)}\) i.e., T ∝ \(\sqrt{l}\)
In winter, l decreases with the fall in temperature, so T decreases and clocks run fast. In summer l increases with, the increase in temperature so T increases and clock runs slow.

Question 23.
Why must telephone or power lines necessarily slag a little?
Answer:
The slag is allowed for contraction in winter. If no slag is allowed, the wire may snap in extremely cold weather.

Question 24.
A tightened glass stopper can be taken out easily by pouring hot water around the neck of the bottle. Why?
Answer:
The neck expands but not the stopper due to poor conductivity of glass. Thus the stopper can be taken out easily. 

Question 25.
Thick bottomed drinking glasses frequently crack if hot water is poured into them. Why?
Answer:
Glass is a bad conductor of heat. It does not pass down the heat quickly to the lower surface. Different layers of the bottom are at different temperatures and expand differently. I'his causes breakage of the glass at the bottom.

Question 26.
Why iron rims are heated red hot before being put on the cart wheels?
Answer:
The iron ring to be put on the rim of a cart wheel is always of slightly smaller diameter than that of the wheel. When the iron ring is heated to become red hot, it expands and slips on the wheel easily. When it is cooled, it contracts and grips the wheel firmly.

Question 27.
A thermos bottle containing water is vigorously shaken. What will be the effect on the temperature of water?
Answer:
The temperature of the water will increase slightly. This is because some of the work done against opposing viscous force will be converted into heat.

Question 28.
If an electric fan be switched in a closed room, will the air of the room be cooled? If not, why do we feel cold?
Answer:
The air will not be cooled. In fact, it will get heated up due to the increase in the speed of its molecules. We feel cold due to faster evaporation of sweat.

Question 29.
Why do the metal utensils have wooden handles?
Answer:
Wood is a bad conductor of heat. Wooden handle does not allow heat to be conducted from the hot utensil to the hand. So we can easily hold the hot utensil with its help.

Question 30.
Why are two thin blankets warmer than a single blanket of double the thickness?
Answer:
The air enclosed between two blankets prevents the transfer of heat from our body to outside. Thus it provides a better insulation than a single blanket of double thickness.

Question 31.
Woolen clothes are worn in winter, why?
Answer:
Woolen fibres enclose a large amount of air in them. Both wool and air are bad conductors of heat. The small coefficient of thermal conductivity prevents the loss of heat from our body due to conduction, so we feel warm in wooden clothes.

Question 32.
Usually a good conductor of heat is a good conductor of electricity also. Give reason. 
Answer:
Electrons contribute largely both towards the flow of electricity and the flow of heat. A good conductor contains a large number of free electrons, so it is both a good conductor of heat and the electricity.

Short Answer Questions

Question 1.
Explain the change of state of ice through heat.
Answer:
To understand this take some ice cubes in a beaker and note the temperature of ice. Slowly heat it. It is observed that there is no change in temperature as long as there is ice in the beaker.

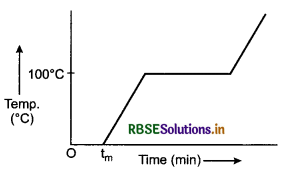
In this process, even though the heat is continuously supplied, but the temperature does not change. The heat supplied is used in changing the state from solid to liquid (ice → water).
The temperature remains 0°C until the ice melts. At this point, further heat transfer will produce a temperature increase of liquid phase till it reaches 100°C, the boiling point of water. It remains at 100°C till all the water change into gass (steam).

Question 2.
Explain the conduction mode of heat transfer.
Answer:

1. In conduction, the heat transfer takes place at the molecular level without actual movement of molecules, from the hottest to the coldest surface.
2. In the process of heat transfer, the molecules pump into their neighbours and transfer the energy to them which continues as long as heat is still being added.
3. The transfer between bodies continues until the temperature difference decays and a state known, as thermal equilibrium occurs.
4. Greater the value of thermal conductivity K of a body better is its heat conducting capability.
5. For insulator this value of K is zero.

Question 3.
Why is displacement term used in Wien’s displacement law?
Answer:
According to Wien’s displacement law λ_mT = b = 2.90 x 10^-3 mK.
That is on increasing the temperature λm moves towards the lower part of spectrum and when the temperature decreases, λ_m gets displaced towards the higher end of the spectrum. This is why it is called Wien’s displacement law.

Question 4.
Give a brief note on black body.
Answer:
The energy radiated by a hot body depends on the nature of the radiating surface. A black body absorbs all the radiations falling on it and emits radiation that are independent of the shape, size, material and nature of the surface selected for the body and depends on its temperature.

A black body is an ideal abstraction and cannot be realised in practice. For rough work, we use surface coated with lamp-black or platinum black; but for more accurate work, black body designed by Fery is used. 

Ferry constructed an enclosure having a hole. The hole O should be placed against the conical projection P of the enclosure and the enclosure should be coated black from inside. Any radiation falling on the hole passes through it and is completely absorbed due to successive reflections.

When we heat the enclosure, the black-body radiations come out from the hole and not the enclosure, that acts as a black body. A black-body is most convenient reference for the study of radiation emitted by hot bodies.

Question 5.
Differentiate between emissive and absorption power.
Answer:

Absorption Power	Emissive Power
1. It is the ability of a body to absorb radiant energy.	1. It is the ability of a body to emit radiation.
2. Total absorptive power of a body is the ratio	2. Total emissive power of a radiating body is the total amount of energy radiated per second per unit area of the surface.
3. Spectral absorptive power for perfectly black body is 1.	3. The total emissive power of a black body (at same temperature) has the maximum value.

Question 6.
Why do animals curl into a ball, when they feel very cold?
Answer:
The total energy radiated by a body depends on its surface area. Thus when the animals feel very cold, they curl their bodies into a ball so as to decrease the surface area of their bodies which in turn helps to reduce the amount of heat lost by them.

Question 7.
Why a body with large reflectivity is a poor emitter?
Answer:
A body whose reflectivity is large would naturally absorbs less heat. So, a body with large reflectivity is a poor emitter.

Question 8.
Two stars radiate maximum energy at wavelengths 3.6 x 10^-7 m and 4.8 x 10^-7 m respectively, what is the ratio of their temperatures?
Answer:
Here, λ_m = 3.6 x 10^-7 m,λ'_m = 4.8 x 10^-7 m
By Wien’s law,
λ_mT = λ'_mT'
∴ \(\frac{T}{T^{\prime}}=\frac{\lambda_m^{\prime}}{\lambda_m}=\frac{4.8 \times 10^{-7}}{3.6 \times 10^{-7}}\) = 4 : 3

Question 9.
Is it necessary that all black coloured objects should be considered black bodies?
Answer:
No. A polished black surface is not a black body because it reflects radiation incident on it, on the other hand, the sun, which is a dazzling white body, is a black body.

Question 10.
Why are clear nights colder than cloudy nights?
Answer:
Clouds are opaque to heat radiations. So on a cloudy night, radiations from the earth’s surface fail to escape but on a clear night, the surface of the earth is cooled due to excessive radtation, so, a clear night is colder than a cloudy night.

Question 11.
A hole in the cavity of a radiator is a black body. Why?
Answer:
A hole in the cavity of a radiator does not reflect any radiation and absorbs all the radiation incident on it. So it is a black body.

Question 12.
Which object will cool faster when kept in open air, the one at 300°C or the one at 100°C? Why?
Answer:
The object at 300°C will cool faster then the object at 100°C. This is in accordance with Newton’s law of cooling.
Rate cooling of an object is proportional temperature difference between the object and its surroundings. 

Question 13.
What is the effect of pressure on melting point of a solid?
Answer:
The melting point of a solid may increase or decrease depending on the nature of solid. For solids such as ice which contracts on melting, it is lowered while for solids such as- sulphur and wax which expands on melting, it increases.

Question 14.
What is the significance of negative slope of ice line of water?
Answer:
It indicates that the melting point of ice decreases with increase in pressure (on ice line). This is because volume of water formed on melting is less than the volume of ice (before melting).

Question 15.
What are the critical temperature and pressure for CO₂? What is their significance?
Answer:
The critical temperature and pressure of CO₂ are 31.1°C and 73.0 atm respectively. Above this temperature, CO₂ will not liquify even it is compressed to high pressures.

Question 16.
Ice of 0° is converted into steam at 100°C. State the isothermal changes in the process.
Answer:
The isothermal changes are:
(i) The conversion of ice at 0°C into water at 0°C.
(ii) Conversion of water at 100°C into steam at 100°C.

Question 17.
Two bodies of specific heat c₁ and c₂ having same heat capacities are combined to form a single composite body. What is the specific heat of the composite body?
Answer:
As the heat capacities are equal, so m₁s₁ = m₂s₂.
Let s be the specific heat of the composite body.
Then,
(m₁ + m₂) s = m₁s₁ + m₂s₂ = m₁s₁ + m₁s₁ = 2m₁s₁
or s = \(\frac{2 m_1 s_1}{m_1+m_2}=\frac{2 m_1 s_1}{m_1+m_1 \frac{s_1}{s_2}}=\frac{2 s_1 s_2}{s_1+s_2}\)

Question 18.
How does tea in a thermos flask remains hot for a long time?
Answer:
The air between the two walls of the thermos flask is evacuated. This prevents heat loss due to conduction and convection. The loss of heat due to radiation is minimised by silvering the inside surface of the double wall. As the loss of heat due to the three processes is minimised, the tea remains hot for a long time.

Question 19.
Two rods A and B are of equal length, each rod has the ends at temperatures T₁ and T₂. What is the condition that will ensure equal rates of flow of heat through the rods A and B?
Answer:

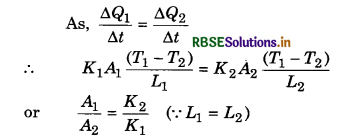
Question 20.
Why does a gas not have a unique value of specific heat?
Answer:
This is because a gas can be heated under different conditions of pressure and volume. The amount of heat required to raise the temperature of unit mass through unit degree is different under different conditions of heating.

Question 21.
On a hot day, a car is left in sunlight with all the windows closed. After sometimes, it is found that inside of the car is considerably warmer than the air outside. Explain why?
Answer:
Glass transmits about 50% of heat radiation coming from a hot source like the sun but does not allow the radiation from moderately hot bodies to pass through it. Due to this, when a car is left is the sun, heat radiation from the sun get into the car but as the temperature inside the car is moderate, they do not pass back through its windows. Hence, inside of the car becomes considerably warmer.

Long Answer Questions

Question 1.
Explain the three modes of heat transfer.
Answer:
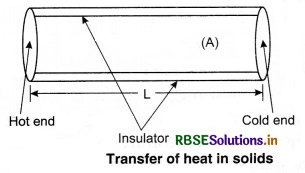
Transfer of heat, takes place from high temperature to low temperature. There are three modes of heat transfer: (i) conduction, (ii) convection, and (iii) radiation. In solids, conduction is common. In liquids and gases, convection takes place. For radiation, no medium is required.

Conduction:
In conduction heat is transferred without actual movement of molecules. The molecules that are in contact with the heat sources, take heat from the source directly and transfer it to the surrounding molecules by increasing the amplitude of their vibrations during collision between the adjacent atoms. So, region of increasing temperature extends it along the length.
Assume a slab of thickness x and cross-sectional

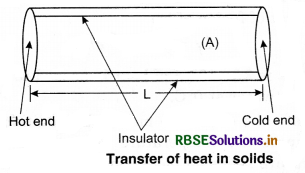
area A. Let the temperature of its two faces be T₁ and T₂, so that T₁ > T₂. The quantity of heat (∆Q) transmitted from hot face (with temp. T₁) through cold face in time ∆t is directly proportional to time (∆t), the area of cross-section (A) and the difference in temperature (T₁ - T₂); and inversely proportional to thickness (x).
⇒ ∆Q ∝ \(\frac{A\left(T_1-T_2\right)}{x} \)∆t

where K is constant of propotionality and is called coefficient of thermal conductivity.
Thermal current: The flow of rate of heat is known as thermal current.

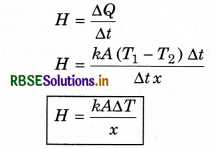
The term \(\frac{T_1-T_2}{x}=\frac{\Delta T}{x}\) is called temperature gradient. Eqn (16) is called Fourier's law and it defines as the coefficient of thermal conductivity K as:

Hence the coefficient of thermal conductivity is equal to the amount of heat when the temperature gradient, area of cross section and time are take as unity.
The unit of K is \(\frac{\text { Watt }}{\text { meter } \times \text { kelvin }}\)
Thermal resistance: Thermal resistance is defined as the temperature difference per unit thermal current:

Convection:
The liquids and gases transmit large fraction of heat by a process in which a part of the hot medium moves from one place to another place. This type of transfer of heat is called convection. Within the hot medium, the movement takes place in the form of currents. Hot current of gas or liquid moves upwards, and its place is taken by cold current of gas or liquid (it moves downwards).

Two Kinds of Convection
1. Forced Convection: Convection in which heated substance is forced to move.
2. Natural Convection: Convection in which heated substance moves without any help of external agency, because of the difference in density of hot and
cold material.
The rate of flow of heat due to convection is,
H = hA(Tsurface - Tfluid)
Here A → area
(Tsurface - Tfluid) → Temperature difference
h → Convective heat transfer constant.
Fluids (liquids and gases) are heated mainly by the process of convection in which buoyancy and gravity play on important role. As shown in figure 11.17, when a fluid is heated from below, the hot position at the bottom expands and becomes less dense. Because of buoyancy, this lighter portion rises up. The denser colder fluid takes its place by moving downwards. Thus convection current is set up in the fluid. The actual movement of a liquid can be seen by colouring the liquid with potassium permanigarate crystals placed at the bottom of the vessel.

1. In maintaining comfortable room temperature in cold countries: In cold during winter, the outside temperature is much below 0°C while the room temperature is comfortably maintained around 20°C. However, the inside air close to the glass window is cooler than 20°C while the outside close to the window is warmer than the chilling temperature of the atmosphere. Thus heat is continuously transferred from the room to the outside by convection of air inside the room. Conduction across the glass pane and again convection of air outside. But this heat loss is compensated by the heating system provided in the room.

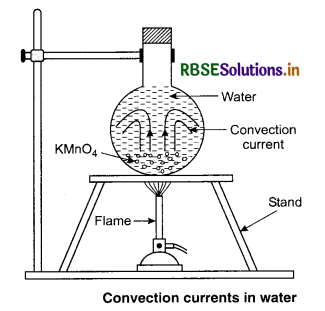
These are local convection currents. Specific heat of water is higher than that of soil. So land and breeze air above it is heated faster in summer during day time than air above the sea. The air above land expands and rises and its place is taken up by the colder air from sea to land and is called sea breeze. At night the land gets cooled faster than water. So, colder air flows from land to sea and is called land breeze.

Radiation:
The process of the transfer of heat from one place to another place without heating the intervening medium is called radiation. Heat from the sun reaches the earth through radiation mode.
Thermal radiation or heat radiation: Everybody emits energy in the form of waves (i.e. electromagnetic waves) due to its temperature. These waves are known as thermal radiation or heat radiation.
When a body emits heat radiation it loses heat. On the other hand, the body gains heat whenever it absorbs thermal radiation. Thermal radiation have wavelength ranging from 8 x 10^-7 m to 4 x 10^-4 m. This wavelength range lies in the infra-red region of electromagnetiic spectrum. Therefore, thermal radiations are also known as infra-red radiations.
According to Prevost all bodies whose temperature is above 0 K or -273°C emit thermal radiations continuously.
Thermal radiations require no material medium for their propogation, so they can travel in vacuum also. They travel with speed of light. They travel in straight lines. They can be reflected and refracted like light waves. They do not affect the intervening medium through which they pass.

Question 2.
State and prove Newton’s law of cooling.
Answer:
A hot body left to itself slowly cools down to the surrounding’s temperature. It was Newton who found that the rate of cooling depends on the temperature difference between the hot body and the surrounding. Newton’s law of cooling states that, the rate of energy loss by a hot body is directly proportional to the temperature difference of hot body and surrounding (if the temperature difference is small), i.e.,
-\(\frac{\Delta Q}{\Delta t}\) ∝ (T - T₀)
where ∆Q is the amount of heat lost in ∆t seconds by a hot body. Consider a hot body at temperature T. Let T₀ be the temperature of its surroundings. According to Newton’s law of cooling.
Rate of loss of heat ∝ Temperature difference between the body and its surroundings

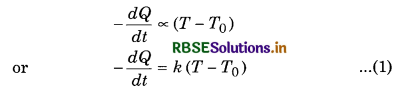
Where k is a proportionality constant depending upon the area and nature of the surface of the body. Let m be the mass and s the specific heat of the body at temperature T. If the temperature of the body falls by small amount dT in time dt. then the amount of heat lost is
dQ = msdT ......................(2)
∴ Rate of loss of heat is given by
\(\frac{d Q}{d t}=m s \frac{d T}{d t}\) .........................(3)
Putting the value of \(\frac{d Q}{d t}\) from equation (3) into (1)

Using equation (7) we can calculate the time of cooling of a body through a particular range of temperature.
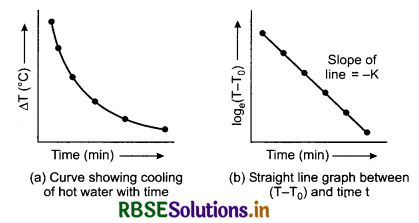
If we plot a graph by taking different values of temperature difference ∆T = T - T₀ along y-axis and the corresponding values of t along x-axis, we get a curve of the form shown in figure 11.21 (a). It clearly shows that the rate of cooling is higher initially and then decreases as the temperature of the body falls.

Morever the equation is of the form y = mx + c. So, if we plot a graph by taking log(T - T₀) along y-axis and time t along x-axis, we must get a straight line, as shown in figure 11.21 (b). It has a negative slope equal to -K and intercept on y-axis equal to c.

Concept: All the numerical are solved from the equation (7).
Experimental Verification of Newton’s Law of Cooling: The experimental set-up used for verifying Newton’s law of cooling is shown in figure 11.22. The set-up consists of a double walled vessel (V) containing water in between the two walls. A copper calorimeter (C) containing hot water is placed inside the double walled vessel. Two thermometers through the corks are used to note the temperatures T of hot water in calorimeter and T₀ of water in between the double walls respectively.

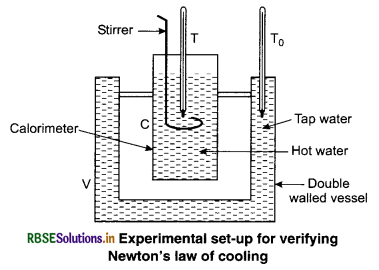
Temperature of hot water in the calorimeter is noted after fixed intervals of time, say after everyone minute of stirring the water gently with a stirrer. Continue noting its temperature about 5°C above that of surroundings. Plot a graph between loge(T - T₀) and time (t) shown in a figure 11.21. The nature of the graph is observed to be a straight line, having a negative slope. This verifies Newton’s law of cooling.

Question 3.
Explain the change of state of substances.
Answer:
Normally, matter exists in three states: solid, liquid and gas. A change from one of these states to another can be done. These changes take place when there is exchange of heat between the substance and its surroundings.

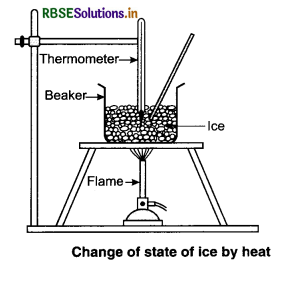
Take some ice-cubes in a beaker. Note the temperature of ice. Slowly heat it. Observe the temperature after every minute and stir the mixture of water and ice continuously. We will see that there is no change in temperature as long as there is ice in the beaker.
In this process, even though the heat is continuously supplied, but the temperature does not change. The heat supplied is used in changing the state from solid to liquid (ice → water).

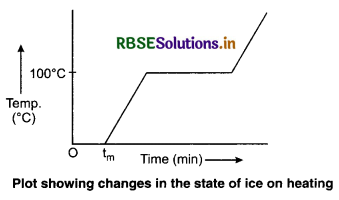
The change of state from solid to liquid is called melting and that from liquid to solid is called fusion. The temperature remains 0°C until all the ice melts. At this point, further heat transfer will produce a temperature increase of liquid phase till it reaches 100°C, the boiling point of water. It remains at 100°C till all the water changes into gas (steam).

Melting Point: The temperature at which the solid and liquid state of substance (in thermal equilibrium) coexist with each other is called its melting point. The melting point of a substance depends on the nature of the substance. It also depends upon the pressure.

Boiling Point: The temperature at which the liquid and the vapour states of the substance coexist.
Sublimation: It is the change from solid to vapour state without passing through the liquid state. The substances showing sublimation are called sublime. For e.g. ,Dry ice (solid CO₂) and iodine. In this process, both solid state and gaseous state co-exist.

Question 4.
What do you mean by temperature and heat? Distinguish between them.
Answer:
Temperature is a physical quantity that measures hotness or coldness of the body. The body that feels hot has a higher temperature than the body that feels cold. The device used to measure temperature is called thermometer. We have experienced that a glass of ice cold water placed on a table (at room temperature) on a hot summer day eventually becomes warm; but a cup of hot coffee placed on the table cools down. So, an exchange of energy has taken between-water or coffee and the surrounding. This transfer of energy takes place till thermal equilibrium is reached.

So, temperature is that physical quantity of an object which tells whether an object is in thermal equilibrium with the other object or not. If the two objects kept in contact are not in thermal equilibrium, then heat will flow from object at high temperature to the object at lower temperature. When the temperature of both the objects becomes equal, the heat flow stops. So, temperature is that physical quantity of an object which decides thedirection of flow of heat.
The S.I unit of temperature is Kelvin and its value is \(\frac{1}{273.16}\) point of water. Temperature is a scalar quantity.
Other than Kelvin scale, temperature can be measured in degree Celsius, Fahrenheit, etc. 

Heat: Heat is a form of energy. The hotness or coldness of any object is felt by it. When a hot object and a cold object are brought in contact with each other then the energy flows from hot to cold object. The energy transferred in this process is heat. The unit of heat is joule (J) or calorie. One calorie is defined as the quantity of heat energy required to raise the temperature of one gram (1g) of water from 14.5°C to 15.5°C.
1 kcal = 10³ Calorie
1 calorie = 4.186 Joule.

Question 5.
What do you mean by thermo measurement? What are temperatures scale? How can we obtain these? Derive formulae for different temperature scales and write the relation between them.
Answer:
Thermometer is used to measure the temperature of a body. Many physical properties of materials changes with temperature. These properties are used as the basis for constructing thermometers. Such a property is variation of the volume of liquid with temperature. For e.g., in liquid-in-glass type (common) thermometer, mercury and alcohol are used. Thermometers are made so that a numerical value may be assigned at a given temperature. For a standard scale, two fixed reference points are required. These fixed points may be correlated to physical phenomena that always take place at the same temperature. The freezing and boiling points of water are such points. These are called lower fixed point (LFP) and upper fixed point (UFP) respectively. These temperatures are given arbitrary numerical values and the difference of these values are divided into equal parts. Each part is called degree which is the unit of temperature.

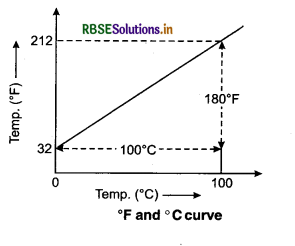
Celsius temperature scale, Fahrenheit temperature scale and Reaumur temperature scale are the familiar temperature scales. The ice and steam points (freezing and boiling points respectively) on the Celsius scale are 0°C and 100°C, 32°F and 212°F on the Fahrenheit scale and 0° to 80°R on Reaumur scale. On the Celsius scale, there are loo equal intervals between two reference points, and on the Fahrenheit scale, there are 180 equal intervals.

The ice and steam points on the Reaumur scale are 0°R and 80°R respectively and there are 80 equal intervals between the two reference points. A relationship for conversion of the two scales is obtained from the graph of Fahrenheit temperature (F) versus Celsius temperature C (see fig. 11.1). The
equation is
\(\frac{F-32}{180}=\frac{C-0}{100}\)
The version of different scales into one another is related as:
\(\frac{C-0}{100}=\frac{F-32}{180}=\frac{R-0}{80}=\frac{K-273}{100}\) ......................(1)
where R is the Reaumur temperature and K is the Kelvin temperature.

Question 6.
What is ideal scale of temperature. Explain.
Answer:
The liquid-in-glass thermometers exhibit different readings for temperatures other than the points due to different expansion properties. However, the thermometer using a gas provides same readings. Experiments show that the gases at low densities show same expansion behaviour. The quantities that describe the behaviour of a given mass of gas are pressure (P), volume (V) and temperature (T). Here T is in Kelvin scale.
Boyle’s Law
When temperature is kept constant, the relationship between the pressure and volume of gas at a given mass is
PV = constant

Charle’s Law
When pressure is kept constant, the relationship between volume of a quantity of gas and temperature is
\(\frac{V}{T}\) = constant
Combining the above two laws, we get
\(\frac{PV}{T}\) = constant
This relationship is called ideal gas law.
Ideal gas equation:
\(\frac{PV}{T}\) = nR
or Pv = n RT .........................(2)
where n → number of moles in the sample of gas
R → Universal gas constant = 8.31 J mol^-1 K^-1
From equation (2),
PV ∝ T
This relationship is used to measure temperature in a constant volume gas thermometer. For constant volume, P ∝ T. Hence, temperature is measured in terms of pressure.

The measurements on real gases deviate from these predicted measurements by the ideal gas law at low temperature. Over a large temperature range, the relationship is linear and on decreasing temperature, the pressure might reach zero. The absolute minimum temperature for an ideal gas is found to be -273.15°C and is called absolute zero. At low pressure and high temperature, all real gases almost behave as ideal gases. In an ideal gas, there is no intermolecular force. An ideal gas follows the law PV = µRT, where P, V and T are the pressure, volume and temperature of the gas respectively, µ is
the number of moles in as ideal gas and R = 8.31 J mol^-1 K^-1 is known as universal gas constant. The equation, PV = µRT is known as ideal gas equation.
If volume of a given gas is constant, then P ∝ T. This shows that the chalkge in pressure of the gas at constant volume is directly proportional to the change in temperature.
The variation, of P and T at constant V is shown in figure.

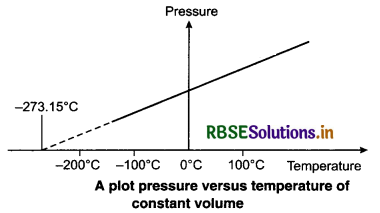
This variation of P with T at constant V is used to measure the temperature of a gas using constant volume gas thermometer. Results have shown that the readings of constant volume gas thermometer are independent of the type of gases used as long as the pressure of the gases is low and the temperature is high. The variation of pressure with temperature of different amounts of a given gas in the bulb of a constant volume thermometer is shown in figure.

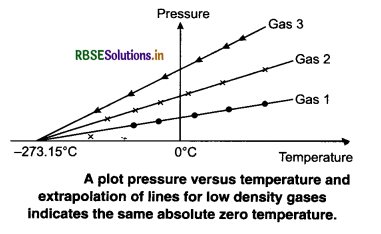
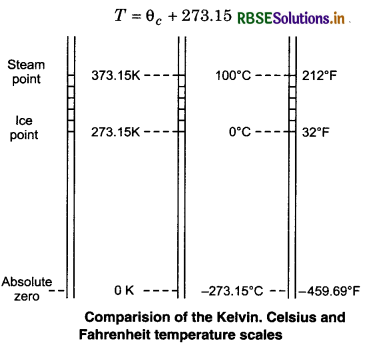
When these lines of gases are extended, (extraploting), they meet at a point on the temperature axis. This point corresponds to -273.15°C. Thus, the pressure of a gas becomes zero at -273.15°C. It is designated as absolute zero. Absolute zero is the foundation of the Kelvin temperature after the British Scientist Lord Kelvin. On this scale -273.15°C is taken as the zero point, that is 0 K.
Kelvin scale and Celsius scale are related to each other as follow:

Question 7.
What are linear coefficient of expansion and volume coefficient of expansion? Obtain derivations for them.
Answer:
The tightly screwed lids or sealed bottles are first put in hot water so that the lid expands. ¡n case of liquids, when the thermometer is put in a slightly warm water, the mercury in it rises. When the thermometer is taken out, mercury falls again. In case of gases, a balloon partially inflated in a room (cool) expands when put in warm water. Also, a fully inflated balloon when placed in cold water starts shrinking.

Most of the substances expand on heating while contract on cooling. Change in the temperature of a body causes change in the dimensions of the body. The increase in dimensions of a body because of increase in its temperature is known as thermal expansion. The change in length is called linear expansion. The increase in area is called area expansion. The expansion in volume is called volume expansion. When the substance is in the form of a long rod, then for small change in temperature (∆T), the fractional change in length (∆l/l₀) is directly proportional to ∆T.
\(\frac{\Delta l}{l o}\) ∝ ∆T
∴ ∆T = α l₀ ∆T

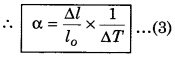
Where α is called the coefficient of linear expansion and it is a characteristic of the material.
From equation (3),

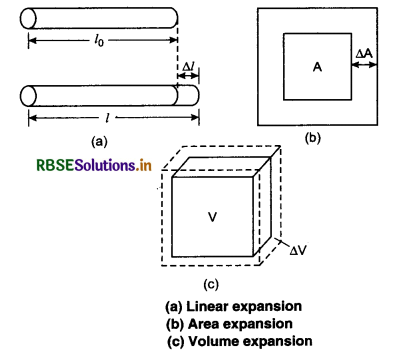
l₀ ∆T α = ∆l = l - l₀
⇒ l = l₀ + l₀α ∆T
or  l = l₀(1 + α ∆T) .......................(4)
Now considering the fractional change in area \(\frac{\Delta A}{A}\); the coefficient of areal expansion or superficial expansion (ß) is

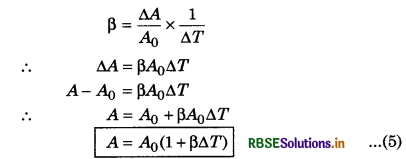
Now, considering the fractional change in volume (∆V/V), the coefficient of volume expansion ß is
γ = \(\left(\frac{\Delta V}{V}\right) \times \frac{1}{\Delta T}\) ......................(6)
where V is the initial volume of the substance. The unit of ß and γ is K^-1.
is also a characteristic of the substance. Generally, it depends on the temperature. It becomes constant only at a high temperature. The value of γ is more for those metals whose melting point is low. The value of γ is least for solid, more than solids in liquids, maximum in gases.
From ideal gas equation, we know that
PV = nRT .....................(7)
At constant pressure,
P ∆V = nR ∆T
or, ∆V = \(\frac{n R}{P} \Delta T\)

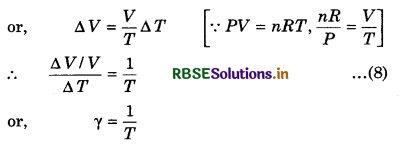
Now, we will establish the relation between α and γ.
Consider a rectangular cuboid of length l₁, l₂ and l₃ and on increasing the temperature by ∆T, the length changes to l'₁, l'₂ and l'₃ respectively. Then, according to equation (4),
l'₁ = l₁(1 + α ∆T) ..................(9)
l'₂ = l₂(1 + α ∆T) ..................(10)
and l'₃ = l₃(1 + α ∆T) ....................(11)
Then, with increase in temperature ∆T we represent the volume as:
V + ∆V = l'₁ l'₂ l'₃
or V + ∆V = l₁(1 + α ∆T) x l₂(1 + α ∆T) x l₃(1 + α ∆T)
or, V + ∆V = l₁ l₂ l₃ (1 + α ∆T) ....................(11)
or, V + ∆V = V (1 + 3α ∆T + 3α² ∆T₂ + α³ ∆T₃)
[∵ V = l₁ l₂ l₃ and (a + b)³ = a³ + b³ + 3ab(a + b)]
Neglecting the higher powers of α, i.e., α² and α³, we have
V + ∆V ≈ V(1 + 3 α ∆T)
or, V + ∆V ≈ V + 3α V ∆T
or, \(\frac{\Delta V / V}{\Delta T}\) ≈ 3α
Using equation (8), we have

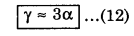
This means that the coefficient of volume expansion is thrice the coefficient of linear expansion.
Similarly we can say ß = 2α

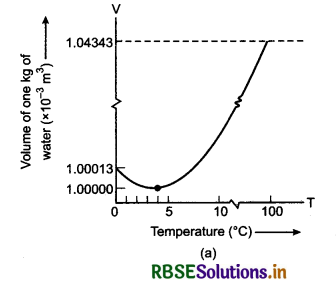
The anomalous behaviour of water:
Water shows unsual behaviour or anomalous behaviour when heated from 0°C to 4°C. Water does not expand when heated from 0°C to 4°C. If the temperature of water is increased beyond 4°C, then it expands. The variation of volume of water with increase in temperature is shown in figure 11.6.

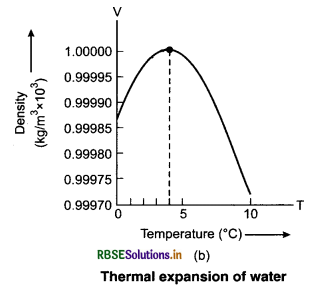
So, water has maximum density at 4°C. This property of water has an important effect on the environment. Lakes and ponds freeze at the top first. A lake starts cooling around 4°C, water near to the surface losses energy and becomes denser and sinks. The warmer water near the bottom rises. When the colder water on the top reaches below 4°C, then it becomes less dense. This way, animal and plant life is saved in cold region.

Gases, at ordinary temperature, expand more than solids and liquids. For liquids, the coefficient of volume expansion is relatively independent of the temperature. However, for gases it is dependent as temperature. For an ideal gas, the coefficient of volume expansion at constant pressure can be found from the ideal gas equation.

Question 8.
Define specific heat. Explain change of state.
Answer:
The heat required to raise the temperature by 1°C of unit mass of a substance is called specific heat (s). Its SI unit is J kg^-1 K^-1 and C.G.S. unit is cal g^-1°C^-1. Specific heat epends upon the nature and temperature of a substance. If M is the mass of the substance to raise the temperature ∆T and ∆Q is the required heat. Then, specific heat can be defined as

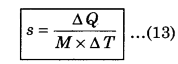
Clearly the amount of heat required to raise the temperature of M mass of a substance through ∆T is
∆Q = Ms ∆T
Molar specific heat: The molar specific heat of a substance is defined as the amount of heat required to raise the temperature of one mole of substance thruogh one degree. It depends on the nature of the substance and it’s temperature. If ∆Q amount of heat raises the temperature by ∆T of µ mol of a substance, then the molar specific heat can be defined as:

The SI unit of molar specific heat is J mol^-1 K^-1.
In this case, heat transfer can be done by keeping either pressure or volume constant. If the gas is kept at constant pressure, then it is called molar specific heat at constant pressure and is represented by C_P. If the volume of the gas is kept constant, then it is called molar specific heat at constant volume and is represented by C_V.

Normally, matter exists in three states: solid, liquid and gas. A change from one of these states to another can be done. These changes take place when there is exchange of heat between the substance and its surroundings.

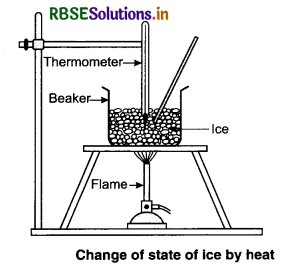
Take some ice-cubes in a beaker. Note the temperature of ice. Slowly heat it. Observe the temperature after every minute and stir the mixture of water and ice contînuously. We will see that there is no change in temperature as long as there is ice in the beaker.
In this process, even though the heat is continuously supplied, but the temperature does not change. The heat supplied is used in changing the
state from solid to liquid (ice → water).

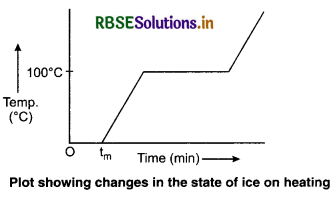
The change of state from solid to liquid is called melting and that from liquid to solid is called fusion. The temperature remains 0°C until all the ice melts. At this point, further heat transfer will produce a temperature increase of liquid phase till it reaches 100°C, the boiling point of water. It remains at 100°C till all the water changes into gas (steam).

Melting Point: The temperature at which the solid and liquid state of substance (in thermal equilibrium) coexist with each other is called its melting point. The melting point of a substance depends on the nature of the substance. It also depends upon the pressure.

Boiling Point: The temperature at which the liquid and the vapour states of the substance coexist.

Sublimation: It is the change from solid to vapour state without passing through the liquid state. The substances showing sublimation are called sublime. For e.g. ,Dry ice (solid CO₂) and iodine. In this process, both solid state and gaseous state co-exist.

Question 9.
What is the effect of pressure on melting point and boiling point? Explain.
Answer:
We know that for a constant value of pressure, the melting point of a pure substance is constant, but if there is change in the value of  ressure, then the value of melting point also changes. To understand his process, we will perform an experiment. Take a slab of ice and put a wire (metallic) holding equal weights (say 5 kg) tied at the two ends. After some time, we will observe that the metallic wire passes through the slab. It is due to the fact the pressure on the slab just below the wire increases and hence the slab melts and the wire passes through it, and then the water above the wire again freezes.

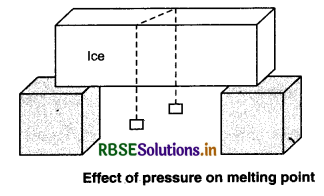
This phenomenon of refreezing is called regelation. So, the phenomenon in which ice melts when pressure is increased and again freezes when pressure is removed is called regelation.
Applications of regelation
(i) By pressing snow in our hand, we can transform it into a snow-ball. When snow is pressed by our hand its crystals melt. As the pressure is released, water refreezes forming a snow ball.
(ii) Skating on ice is possible due to the formation of water layer below the skates. Water is formed due to increase in pressure and it acts as lubricant.
(iii) When the wheels of cast pass over snow, ice melts due to increase in pressure exerted by the wheels, when pressure is released, water so formed refrezes on the wheels. That is why wheels are covered with ice.
Variation of density with temperature:
When a given mass of solid or liquid is heated, it’s volume increases and hence density decreases. If V and V' are the volumes and ρ and ρ' are the densities of given mass M at temperatures T and (T + ∆T) respectively, then:
V' = V(1 + γ ∆T)
\(\frac{M}{\rho^{\prime}}=\frac{M}{\rho}(1+\gamma \Delta T)\)
or ρ' = ρ(1 + γ ∆T)^-1
By the binomial theorem and neglecting the term containing higher power of γ. ∆T, we get
ρ' = ρ(1 - γ ∆T) ........................(15)
Clearly, the density of a solid or a liquid decreases with the increase in temperature.

Effect of Pressure on Boiling point
Increase in atmospheric pressure also increases the boiling point of a liquid by increasing the vapour pressure of water above the liquid. This raises the amount of heat required to increase the vapour pressure of the water. The vapour pressure of a liquid tells how quickly molecules leave out the liquid state and converts to gas under normal conditions, the vapour pressure is low for water. This results in few molecules leaving the liquid by evaporation. Heating the liquid increases the kinetic energy of the molecules and increases the vapour pressure of the liquid. As soon as the vapour pressure is equal to the pressure of the outside atmosphere the water gets converted into gas quickly. Take a round bottom flask more than half filled with water. Keep it over a burner and fix a thermometer and steam outlet through the cork of the flask. As water gets heated in the flask, note first that the air, which was dissolved in the water, will come out as small bubbles. Later bubbles of steam will form at the bottom but as they rise to the cooler water near the top, they condense and disappear. Later, as the temperature of the entire mass of the water reaches 100°C, bubbles of steam occur.

Initially the  steam in the flask is not visible but as it comes out of the flask, it condenses but it condenses as ting droplets of water giving a foggy appearance. If we close the steam outlet for a few seconds and let the increase in the pressure in the flask, we notice that boiling stops. More heat is required to raise the temperature before boiling begins again. Thus boilings point increases with increase in pressure. Now we remove the burner and allow water to cool to about 80°C. Removing the thermometer and steam outlet and closing the flask with the airtight cork. Keep the flask turned upside down on the stand. Now we pour ice-cold water on the flask. We notice water vapours in the flasks condense reducing the pressure on the water surface inside the flask. Here water begins to boil again, now at a lower temperature. Thus boiling point decreases with decrease in pressure.

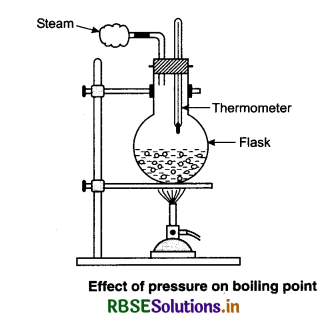
Pressure cookers make advantage of this L. As 212°F is the boiling point of water under 1 atm, boiling water can not cook food to more than that temperature. By increasing the pressure inside the cooker, food cooks much faster. High-altitude cooking takes into account the lower pressure and lower boiling points at elevation.

Question 10.
What is principle of thermometry? Describe the method to determination of specific heat of a liquid by calorimeter.
Answer:
A device in which heat measurement can be done is called a calorimeter. It consists of a cylindrical vessels of copper or aluminium. The vessel is kept inside a wooden jacket which contains heat insulating material, like glass wool etc. This outer jacket acts as heat shield and reduces the heat loss from the inner vessel. There is an opening in the outer jacket through which a mercury thermometer can be inserted into the calorimeter. The lid is provided with holes for inserting a thermometer and a stirrer into the calorimeter.
When bodies at different temperatures are mixed together in the calorimeter, heat is excharged between the bodies as well as with calorimeter. If there is no heat lost to the surroundings, then according to the calorimetry principle.

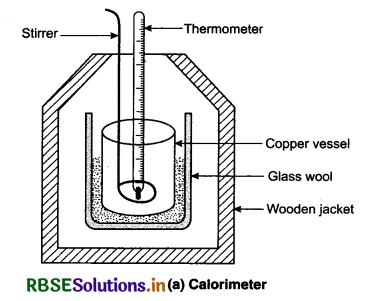
Heat gained by cold bodies Heat lost by hot bodies. From this equation we can determine the specific heat and latent heat of different bodies.

Question 11.
Explain the steady and variable state of heat conduction and give definition of coefficient of thermal conductivity. Write its unit and dimensional formula.
Answer:
In conduction heat is transferred without actual movement of molecules. The molecules that are in contact with the heat sources, take heat from the source directly and transfer it to the surrounding molecules by increasing the amplitude of their vibrations during collision between the adjacent atoms. So, region of increasing temperature extends it along the length.
Assume a slab of thickness x and cross-sectional

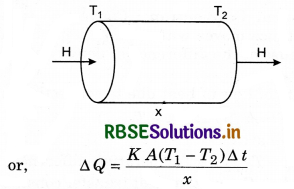
area A. Let the temperature of its two faces be T₁ and T₂, so that T₁ > T₂. The quantity of heat (∆Q) transmitted from hot face (with temp. T₁) through cold face in time ∆t is directly proportional to time (∆t), the area of cross-section (A) and the difference in temperature (T₁ - T₂); and inversely proportional to thickness (x).
⇒ ∆Q ∝ \(\frac{A\left(T_1-T_2\right)}{x} \)∆t

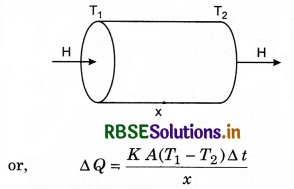
where K is constant of propotionality and is called coefficient of thermal conductivity.
Thermal current: The flow of rate of heat is known as thermal current.

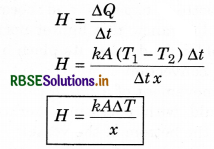
The term \(\frac{T_1-T_2}{x}=\frac{\Delta T}{x}\) is called temperature gradient. Eqn (16) is called Fourier's law and it defines as the coefficient of thermal conductivity K as:

Hence the coefficient of thermal conductivity is equal to the amount of heat when the temperature gradient, area of cross section and time are take as unity.
The unit of K is \(\frac{\text { Watt }}{\text { meter } \times \text { kelvin }}\)
Thermal resistance: Thermal resistance is defined as the temperature difference per unit thermal current:

Question 12.
Explain convection with the help of an experiment. Draw light on its examples.
Answer:
The liquids and gases transmit large fraction of heat by a process in which a part of the hot medium moves from one place to another place. This type of transfer of heat is called convection. Within the hot medium, the movement takes place in the form of currents. Hot current of gas or liquid moves upwards, and its place is taken by cold current of gas or liquid (it moves downwards).

Two Kinds of Convection
1. Forced Convection: Convection in which heated substance is forced to move.
2. Natural Convection: Convection in which heated substance moves without any help of external agency, because of the difference in density of hot and
cold material.
The rate of flow of heat due to convection is,
H = hA(Tsurface - Tfluid)
Here A → area
(Tsurface - Tfluid) → Temperature difference
h → Convective heat transfer constant.
Fluids (liquids and gases) are heated mainly by the process of convection in which buoyancy and gravity play on important role. As shown in figure 11.17, when a fluid is heated from below, the hot position at the bottom expands and becomes less dense. Because of buoyancy, this lighter portion rises up. The denser colder fluid takes its place by moving downwards. Thus convection current is set up in the fluid. The actual movement of a liquid can be seen by colouring the liquid with potassium permanigarate crystals placed at the bottom of the vessel.

1. In maintaining comfortable room temperature in cold countries: In cold during winter, the outside temperature is much below 0°C while the room temperature is comfortably maintained around 20°C. However, the inside air close to the glass window is cooler than 20°C while the outside close to the window is warmer than the chilling temperature of the atmosphere. Thus heat is continuously transferred from the room to the outside by convection of air inside the room. Conduction across the glass pane and again convection of air outside. But this heat loss is compensated by the heating system provided in the room.

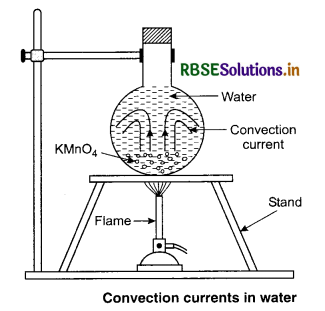
These are local convection currents. Specific heat of water is higher than that of soil. So land and breeze air above it is heated faster in summer during day time than air above the sea. The air above land expands and rises and its place is taken up by the colder air from sea to land and is called sea breeze. At night the land gets cooled faster than water. So, colder air flows from land to sea and is called land breeze.

Question 13.
What do you mean by black body radiation? Explain’s Ferry’s ideal black body.
Answer:
The energy radiated by a hot body depends on the nature of the radiating surface. A black body absorbs all the radiations falling on it and emits radiation that are independent of the shape, size, material and nature of the surface selected for the body and depends on its temperature. A black body is an ideal abstraction and can not be realised in practice. For rough work, we use surface coated with lamp-black or platinum black; but for more accurate work, black body designed by Ferry is used.

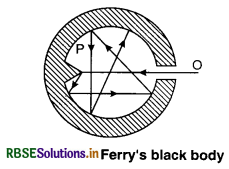
Ferry constructed an enclosure having a hole. The hole O should be placed against the conical projection P of the enclosure and the enclosure should be coated black from inside. Any radiation falling on the hole passes through it and is completely absorbed due to successive reflections. When we heat the enclosure, the black-body radiations come out from the hole and not the enclosure, that acts as a black body. A black-body is most convenient reference for the study of radiation emitted by hot bodies.
Absorption Power
When radiant energy faIts on a body, a part of energy is absorbed. Absorptive power is the ability of a body to absorb radiant energy. The total absorptive power of a body is the ratio of energy absorbed to energy falling.
The absorptive power (a) is defined as the fraction of incident energy which is absorbed for a perfect black body, a = 1.
When there is an ability of a body to absorb radiations of given wavelength, then, the term spectral absorptive power (a_λ) is used. Spectral absorptive power for perfectly black body, a_bλ = 1.
If the radiant energy dQ in wavelength range and λ + dλ is incident on a body of absorptive power a_λ, then amount of radiant energy absorbed by the body = a_λ aQ.
Emissive Power
Different bodies at same temperature emit energy. The ability of a hot body to emit radiation is called emissive power.
The total emissive power of a radiating body is the total amount of energy radiated per second per unit area of the surface. It depends on the body’s temperature. The unit of emissive power is J/m² s.
The total emissive power of a black-body (at same temperature) has the maximum value.
Emissivity is the ratio of total emissive power of a real body (e_λ) to the total emissive power of a black-body (E_λ) at the same temperature.
i.e., Emissivity, ε = \(\frac{e_\lambda}{E_\lambda}\)
or, e_λ = ε E_λ
e_λ and E_λ both depends on temperature. Emissivity is not a constant and shows a small variation in temperature. The radiations emitted by hot bodies spread over a long region of electromagnetic spectrum. Considering a small range of wavelength, say λ, and λ + ∆λ.
e = Number of emitted radiation in the wavelength = \(\frac{\text { Range } \lambda \text { and } \lambda+\mathrm{d} \lambda}{d \lambda}\)
∴ e = \(\int_0^{\infty} e_\lambda d \lambda\)
The spectral emissive power (E_λ) for a particular wavelength λ of a body is the amount of energy radiated per second per unit area between λ and (λ + ∆λ) divided by ∆λ.
The energy radiated per second unit area between λ and λ + ∆λ is (E_λ . ∆λ) for a non-black body and by (E_b - ∆λ) for a black body.

Question 14.
Explain radiation curve obtained by Lununer and Pringsheim related to black body radiation spectrum distribution. Draw inference from these curves.
Answer:
Spectrum Energy Distribution for Black Body
Energy radiated per second per unit area in a small range of wavelength λ and (λ + ∆λ) divided by ∆λ is called spectral emissive power E_bλ of a black body at λ wavelength.
So, the energy radiated per second per unit area (in wavelength λ → λ + ∆λ) = E_bλ ∆λ.
E_bλ depends on the wavelength (λ) and temperature (T) of the black body.
The area beneath the radiation curve between λ and λ + ∆λ (See fig. 11.20)
= E_bλ ∆λ

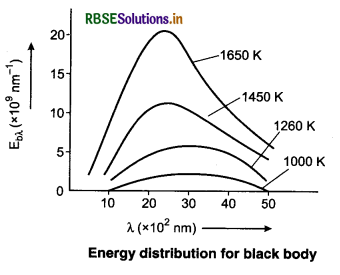
The important results obtained from the curves are as follows:
1. The emission spectrum of black body at each temperature is continuous but the amount of radiation is different at different wavelengths.
2. There is increase in radiation of each wavelength on increasing the temperature.
3. The value of E_λ first increases on increasing λ at a temperature. At λ_m, it becomes maximum and then it decreases.
4. The value of λ_m decreases on increasing the temperature, i.e., λ_m and temperature T are inversely proportional to each other.
This means the value of λ_mT is constant. This is called Wien’s displacement law.

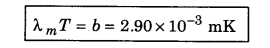
5. The peak emissive power (E_bλ (max)) is directly proportional to the fifth power of temperature,

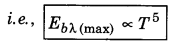
6. The total energy emitted by a black body per second per unit area is directly proportional to the fourth power of its absolute temperature, i.e.,
E_b ∝ T⁴

Conceptual Questions

Question 1.
Why white clothes are more comfortable in summer while colourful clothes are more comfortable in winter?
Answer:
White clothes absorb very little heat radiation and hence they are comfortable in summer. Coloured clothes absorb almost whole of the incident radiation and keep the body warm in winter.

Question 2.
Explain why cooking utensils are often blackened at the bottom and polished at the top.
Answer:
Black surfaces are good absorbers of heat radiations. The bottom of the cooking utensils is blackened so that it absorbs maximum heat radiations. Polished white surfaces are bad absorbers and hence bad emitters of heat radiations. By polishing the upper parts of the cooking utensils, the loss of heat by radiation is minimised.

Question 3.
A sphere, a cube and a thin circular plate all made of the same material and having the same mass are initially heated to a temperature of 200°C. Which of these objects will cool fastest and which one slowest when left in air at room temperature. Give reasons.
Answer:
The thin circular plate has the largest surface area. The sphere has the smallest surface area. Thus the plate will radiate maximum heat while the sphere will radiate minimum heat. Hence the plate will cool fastest and the sphere will cool slowest.

Question 4.
A blackened platinum wire, when gradually heated, first appears dull red, then blue and finally white. Explain why?
Answer:
According to Wien’s displacement law, when blackened platinum wire is gradually heated, it first emits radiations of longer wavelengths, so it appears red. At higher temperatures, it emits blue radiations more strongly than red and appears blue. At very high temperatures, it emits all radiations strongly and appears white.

Question 5.
Explain why a brass tumbler feels much colder than a wooden tray on a chilly day?
Answer:
When we touch a brass tumbler on a chilly day, heat flows from our body to the tumbler quickly (as thermal conductivity of brass is very high) and as a result, it appears colder. On the other hand, as the wood is a bad conductor, heat does not flow to the wooden tray from our body, on touching it.

Matrix Matching Type Questions

Match the column I with column II

Column I	Column II
A. Coefficient of linear expansion	P. \(\frac{K A \Delta \theta}{l}\)
B. Coefficient of volume expansion	Q. \(\frac{\Delta l}{l_0 \Delta T}\)
C. Thermal current	R. \(m s \frac{d T}{d t}\)
D. Specific heat	S. 3α
E. Newton's law of cooling	T. \(\frac{\Delta Q}{M . \Delta T}\)

Answer:

Column I	Column II
A. Coefficient of linear expansion	Q. \(\frac{\Delta l}{l_0 \Delta T}\)
B. Coefficient of volume expansion	S. 3α
C. Thermal current	P. \(\frac{K A \Delta \theta}{l}\)
D. Specific heat	T. \(\frac{\Delta Q}{M . \Delta T}\)
E. Newton's law of cooling	R. \(m s \frac{d T}{d t}\)

Numerical Questions

Based on thermal measurement

Question 1.
The difference between temperatures of two bodies is 63°F, what will be this difference in Celsius scale?
Solution:
∵ Difference of 180°F = Difference of 100°C
∴ Difference of 1°F = Difference of \(\frac{100}{180}\)°C
∴ Difference of 63°F
= Difference of \(\frac{100 \times 63}{180}{ }^{\circ} \mathrm{C}\) = difference of 35°C

Question 2.
The fixed point of ah impure thermometer are 5°C and 95°C. The temperature measured by this of an object is 59°. What will be the pure value at Celsius scale?
Solution:
Let for impure scales 59°C reading, the correct reading is C, then
\(\frac{C-0}{100}=\frac{59-5}{95-5}=\frac{54}{90}=\frac{3}{5}\)
or C = \(\frac{3}{5}\) x 100
or C = 60°C

Based on thermal expansion

Question 3.
The length of arm of a cube of brass is 10 cm at 15°C temperature. When it is heated to 60°C temperature, calculate length of its arm and volume. Coefficient of linear expansion is 1.9 x 10^-5 °C^-1.
Solution:
L₂ = L₁(1 + α ∆T)
Given: L₁ = 10 cm; α = 1.9 x 10^-5°C^-1
∆T = 60 -15 = 45°C
∴ L₂ = 10 cm (1 + 1.9 x 10^-5 x 45)
= 10 (1 + 85.5 x 10^-5)
= 10 (1 + 0.000855) cm
= 10.0085 cm
∴ Volume of the cube
V = L₂³ = (10.0085)³ cm³
= 1002.55 cm³
= 1002.5 cm³

Question 4.
The volume of a flask at 0°C is 100 cm³. What will be its volume at 100°C? Given coefficient of volume expansion of glass = 2.5 x 10^-5 °C^-1.
Solution:
V₀ = 100 cm³; T = 100°C; V_T = ?; γ = 2.5 x 10^-5
∵ V_T = V₀ (1 + γ_T)
∴ V₁₀₀ = 100(1 + 2.5 x 10-5 x 100) cm³
= 100(1 + 0.0025)
= 100(1.0025)
= 100.25 cm³

Based on thermometry

Question 5. 
How much heat will be required to convert 5 kg of ice at 20°C to steam at 100°C? The specific heat of ice = 0.5 kcal kg^-1 °C^-1, latent heat of ice = 80 kcal/kg, latent heat of steam = 540 kcal/kg.
Solution:
Specific heat of ice S_i = 0.5 kcal/kg; m = 5 kg
Latent heat of ice L_f = 80 kcal/kg;
S_w = 1 kcal/kg
Latent heat of steam L_v = 540 kcal.kg^-1
Necessary heat to increase the temperature of ice from -20°C to 0°C
Q₁ = mS_i ∆T = m x 0.5 x 20 kcal
Heat required to melt ice
Q₂ = mL_f
Heat required to increase temperature of ice water upto 100°C
Q₃ = mS_w x 100 kcal
Heat required to convert water into steam at 100°C
Q₄ = mL_v
∴ Total heat
Q = Q₁ + Q₂ + Q₃ + Q₄
= m x S_i x 25 + mL_f + mS_w x 100 + mL_v
= m[0.5 x 20 + 80 + 1 x 100 + 540]
= 5[10.0 + 80 + 100 + 540]
= 5 x 730
= 3650 kcal

Question 6.
Water fall at Narora dam from 200 m height. If during fall whole energy converts into heat and it is absorbed by falling water, then calculate increase in temperature.
Solution:
h = 200 m
If mkg water falls on the earth, then absorbed heat by water.
Q = m g h J
If temperature increase is ∆θ, then
Q = mS ∆θ
∴ mS ∆θ = mgh

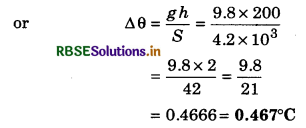
Based on thermal conduction and thermal current

Question 7.
The cross-sectional area of a 2 cm thick iron plate is 5 x 10^-4 m². The surface temperature of the plate are 150°C and 140°C. If thermal conduction coefficient is 1.115 x 10^-2 K- calm^-1 s^-1 °C^-1, then calculate the heat flow per second in the plate.
Solution:
l = 2 cm = 2 x 10^-2 m; A = 5 x 10^-4 m²;
∆T = 150 - 140 = 10°C;
K = 1.115 x 10^-2 kcal m^-1 s^-1°C^-1; t = 1 s;
Q = ?
Q = \(\frac{K A \Delta T t}{l}=\frac{1.115 \times 10^{-2} \times 5 \times 10^{-4} \times 10 \times 1}{2 \times 10^{-2}}\)
= 1.115 x 25 x 10^-4
= 27.875 x 10^-4
= 2.7875 x 10^-3 kcal

Question 8.
The thickness of the sheet of nickel is 4 x 10^-3 m. The temperature difference between its two layers is 32°C. If they emit 200 kcal heat per hour from 5 x 10^-4 m² area, then calculate the coefficient of thermal conductivity of nickel.
Solution:
l = 4 x 10^-3 m; ∆T = 32°C; A = 5 x 10^-4 m²; Q = 200 kcal; t = 1 hr = 3600 s; K = ?

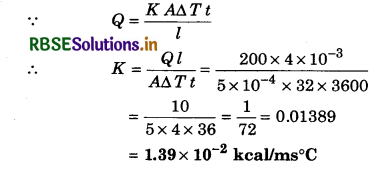
Question 9.
The temperature difference between two surfaces of a glass sheet is 10°C. If the area of the glass sheet is 2 x 10^-4 m² and thickness is 4.0 mm, then calculate rate of heat flow, coefficient of thermal conductivity of glass = 2 x 10^-4 kcal m^-1 °C^-1 s^-1.
Solution:
∆T = 10°C; A = 2 x 10^-4 m₂; l = 4.0 mm = 4.0 x 10^-3 m;
H = ?; K = 2 x 10^-4 kcal/ms°C
∵ H = \(\frac{K A \Delta T}{l}=\frac{2 \times 10^{-4} \times 2 \times 10^{-4} \times 10}{4 \times 10^{-3}}\)
= 1 x 10^-4 kcal/s

Question 10.
A window in a room fitted with a glass of 3 mm thickness and of 5 m2 area. If inside temperature of the room is 10°C more comparatively to outside, then how much heat will transmit in 1 hour? If the thickness of glass become 12 mm, then how much heat it will stop in going outside? Coefficient of thermal conductivity of glass = 2x 10^-4 kcal m^-1 °C^-1s^-1.
Solution:
l₁ = 3 mm = 3 x 10^-3 m; A = 5 m²; ∆T = 10°C; t = 1 hr = 3600 s; K = 2 x 10^-4 kcal/ms°C

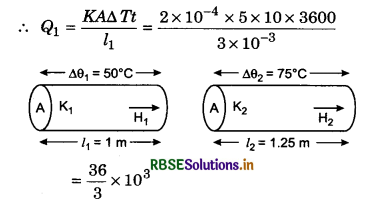
= 12000 kcal.
If l₂ = 12 mm = 12 x 10^-3 m
then Q₂ = \(\frac{K A \Delta T t}{l_2}=\frac{1}{4} \frac{K A \Delta T t}{l_1}\)
= \(\frac{1}{4}\) Q₁ = \(\frac{12000}{4}\) = 3000 kcal.
Heat stopped
∆Q = Q₁ - Q₂ = 12000 - 3000 = 9000 kcal.

Question 11.
Two plates of equal area are placed in contact to each other. Their thickness are 2.0 cm and 3.0 cm. The temperature of the outer surface of one plate is -25° C and temperature of the outer surface of second plate is 25°C, what will be the temperature of the common surface of these plates. It (i) both plates are made of same substance, (ii) coefficient of thermal conductivity of two plates may of 2 : 3.
Solution:
l₁ = 2.0 cm = 2.0 x 10^-2 m;
l₂ = 3.0 cm = 3.0 x 10^-2 m
(i) K₁ = K₂ = K

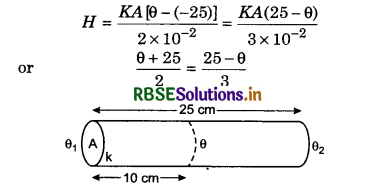
or 3θ + 75 = 50 - 2θ or 5θ = -25
∴ θ = -5°C

(ii) When K₁ = 2K and K₂ = 3K
then H = \(\frac{2 K A(\theta+25)}{2 \times 10^{-2}}=\frac{3 K A(25-\theta)}{3 \times 10^{-2}}\)
or θ + 25 = 25 - θ
2θ = 25 - 25 = 0
∴ θ = 0°C

Question 12.
The heat is flowing in a rod of 25.0 cm length and 8.80 cm² cross sectional area. The coefficient of thermal conductivity of the rod is 920 x 10^-4 kcal m^-1 s^-1 °C^-1 and in steady state the temperature of the ends of rod are 125°C and 0°C. Calculate: (i) temperature gradient in rod, (ii) temperature at 10.0 cm distance from hot end of rod, (iii) rate of transfer of neat.
Solution:
l = 25 cm = 25 x 10^-2 m;
A = 8.80 cm² = 8.80 x 10^-4 m²;
K = 920 x 10^-4 = 9.2 x 10^-2 kcal/ms°C
θ₁ = 125°C; θ₂ = 0°C
(i) Temperature gradient in rod = \(\frac{\Delta \theta}{l}\)
= \(\frac{(125-0)}{25 \times 10^{-2}}{ }^{\circ} \mathrm{C} / \mathrm{m}\)
= 5 x 10²°C/m

(ii) Temperature gradient at 10 cm distance from hot end
= \(\frac{125-\theta}{10 \times 10^{-2}}\) = 5 x 10²
∴ 125 - θ = 5 x 10² x 10 x 10^-2 = 50
or θ = 125 - 50 or θ = 75°C

(iii) Rate of transfer of heat
H = \(\frac{K A\left(\theta_1-\theta_2\right)}{l}\)
= \(\frac{9.20 \times 10^{-2} \times 8.80 \times 10^{-4}(125-0)}{25 \times 10^{-2}}\)
= 9.2 x 8.8 x 5 x 10^-4
= 404.8 x 10^-4
= 4.048 x 10^-2
= 4.1 x 10^-2 kcal.s^-1

Question 13.
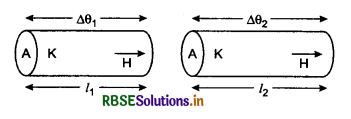
The length of two rods of same material are 0.5 m and 0.8 m. The temperature difference between the ends of two first rod is 40°C. Calculate the temperature difference between ends of second rod. If rate of heat conduction is same in both the rods.
Solution:
l₁ = 0.5 m; l₂ = 0.8 m
∆θ₁ = 40°C; ∆θ₂ = ?
∵ H₁ = H = H
∴ H = \(\frac{K A \Delta \theta_1}{l_1}=\frac{K A \Delta \theta_2}{l_2}\)
∴ ∆θ₂ = ∆θ₁ x \(\frac{l_2}{l_1}\) = 40 x \(\frac{0.8}{0.5}\)
∆θ₂ = 64°C

Based on Stefan’s law

Question 14.
Earth receives radiation energy at the rate of 1400 W/m2 from the sun. The distance of sun from earth’s surface is 1.5 x 10¹¹ m and radius of the sun is 7.0 x 10⁸ m. Assuming sun to be perfectly black body, calculate its surface temperature,
(Stefan’s constant = 5.67 x 10^-8 W m^-2K^-4 )
Solution:
Given: P = 1400 Watt/m²; r = 1.5 x 10¹¹ m;
R_S = 7.0 x 10⁸ m;
T = ?; σ = 5.67 x 10^-8 Watt/m² K⁴
Rate of emission of radiation energy from sun's surface
Q = P 4πr²
but Q = σ T₄ 4 π R_s²
∴ σ T₄ 4 π R_s² = P4πr²
∴ T₄ = \(\frac{P r^2}{\sigma R_s^2}=\frac{1400}{5.67 \times 10^{-8}} \times\left(\frac{1.5 \times 10^{11}}{7 \times 10^8}\right)^2\)
= \(\frac{1400 \times 10^8}{5.67} \times\left(\frac{1.5}{7} \times 10^3\right)^2\)
= 2.469 x 10¹⁰ x (0.21428 x 10³)²
= 2.469 x 10¹⁰ x 0.045918 x 10⁶
T₄ = 0.113373 x 10¹⁶
∴ T = 10⁴ x 0.58026
= 5802.6 K
= 5803 K

Question 15.
The temperature of the black body is 1727°C and surface area is 0.1 m². Calculate energy emitted per minute by black body. (Stefan’s constant, σ = 5.67 x 10^-8 watt m^-2K^-4)
Solution:
T = 1727 + 273 = 2000 K; A = 0.1 m²; t = 60 s
Q = ?; σ = 5.67 x 10^-8 Watt/m²K⁴
Q = EAt = σ T₄ A x t
= 5.67 x 10^-8 x (2000)⁴ x 0.1 x 60
= 5.67 x 10^-8 x 16 x 10¹² x 6
= 544.32 x 10⁴
= 5.44 x 10⁶ J/mol

Based on Newton law of cooling

Question 16.
A liquid cools from 80°C to 70°C in 5 minutes, then how much time it will take to cool from 70° C to 60°C? Temperature of the surrounding is fixed at 40°C.
Solution:
T₁ = 80°C; T₂ = 70°C; t₁ = 5 min
T₂ = 70°C; T₃ = 60°C; t₂ = ?; T₀ = 40°C
By Newton's law of cooling

Question 17.
A body cools from 60°C to 40°C in 10 minutes. It temperature of the surrounding is 5°C, then what will be its temperature after 10 minutes?
Solution:
T₁ = 60°C; T₂ = 40°C; t₁ = 10 min; T₀ = 5°C
T₂ = 40°C; T₃ = ?; t₂ = 10 min.
By Newton's law of cooling,
\(\frac{d T}{d t}=K\left[T_{a v}-T_0\right]\)

∴ T₃ = \(\frac{300}{11}\) = 27.27°C
T₃ = 27.27°C

Based on Wien’s Displacement law

Question 18.
Two stars X and Y emit maximum radiation at 4800 Å and 6000 Å wavelength. If temperature of Y is 5800 K, then what will be the temperature of X?
Solution:
λm₁ = 4800 Å; λm₂ = 6000 Å; T₁ = ?; T₂ = 5800 K
By Wien's displacement law
λ_m1 T₁ = λ_m2 T₂
T₁ = \(\frac{\lambda_{m_2}}{\lambda_{m_1}} T_2=\frac{6800 \AA}{4800 \AA}\) x 5800 K
= \(\frac{5}{4}\) x 5800 = 5 x 1450 = 7250 K

Question 19.
If maximum spectrals energy is received at 5800 Å wavelength of a star, then what will be temperature of that star?
(Wien’s constant = 2.90 x 10^-3 mK)
Solution:
λ_m = 5800 Å; b = 2.9 x 10^-3 mK; T = ?
∵ λ_m T = b ⇒ T = \(\frac{b}{\lambda_m}\)
∴ T = \(\frac{2.9 \times 10^{-3}}{5.8 \times 10^{-7}}=\frac{2.9}{5.8}\) x 10⁴ = 0.5 x 10⁴
or T = 5000 K

Questions for Competitive Examinations

Objective Type Questions

Question 1.
A copper rod of 88 cm and an aluminium rod of, unknown length have their increase in length independent of increase in temperature. The length of aluminium rod is: (α_Cu =1.7 x 10^-5 K^-1 and α_Al = 2.2 x 10^-5 K^-1):
(a) 6.8 cm
(b) 113.9 cm
(c) 88 cm
(d) 68 cm
Solution:
At any temperature
(∆l)_Cu = (∆l)_Al
l₁α₁ ∆T = l₂α₂ ∆T
88 x 1.7 x 10^-5 = l₂ x 2.2 x 10^-5
∴ l₂ = 68 cm

Question 2.
The power radiated by a black body is P and it radiates maximum energy at wavelength λ₀. If the temperature of the black body is now changed so that it radiates maximum energy of wavelength \(\frac{3}{4}\) λ₀, the power radiated by it becomes nP. The value of n is:
(a) \(\frac{3}{4}\)
(b) \(\frac{81}{256}\)
(c) \(\frac{256}{81}\)
(d) \(\frac{4}{3}\)
Solution:
λ_m T = constant (Wein's law)
So, λ_max1. T₁ = λ_max2. T₂

Question 3.
The power of a black body at temperature 200 K is 544 W. Its surface area is (σ = 5.67 x 10^-8 Wm^-2K^-4)
(a) 6 m²
(b) 6 x 10² m²
(c) 6 x 10^-2 m²
(d) 6 x 10^-6 m²
Solution:
P = σAT₄
∴ A = \(\frac{P}{\sigma T^4}=\frac{544}{5.67 \times 10^{-8} \times 16 \times 10^8}\)
= 5.99 = 6 m²

Question 4.
A spherical black body with K radius of 12 cm radiates 450 watt power at 500 K. If the radius were halved and the temperature doubled, the power radiated in watt would be:
(a) 450
(b) 1000
(c) 1800
(d) 225
Solution:
P ∝ r²T₄
⇒ \(\frac{P_1}{P_2}=\left(\frac{r_1}{r_2}\right)^2\left(\frac{T_1}{T_2}\right)^4\)
P₂ = 1800 watt

Question 5.
A black body is at a temperature of 5760 K. The energy of radiation emitted by the body at wavelength 250 ran is U₁, at wavelength 500 run is U₂ and that at 1000 run is U₃. Wien's constant, b = 2.88 x 10⁶ nmK. Which of the following is correct?
(a) t/3 = 0
(b) U₁ > U₂
(c) U₂ > U₁
(d) U₁ = 0
Solution:
λ_mT = b
λ_m = \(\frac{b}{T}\)
⇒ λ_m = \(\frac{2.88 \times 10^6 \mathrm{nmK}}{5760 \mathrm{~K}}\)
⇒ λ_m = 500 nm
∵ λ_m = wavelength corresponding to maximum energy, so
U₂ > U₁.

Question 6.
The two ends of a metal rod are maintained at temperatures 100°C and 110°C. The rate of heat flow in the rod is found to be 4 J/s. If the ends are maintained at temperatures 200°C and 210°C, the rate of heat flow will be:
(a) 44 J/s
(b) 16.8 J/s
(c) 8 J/s
(d) 4 J/s
Solution:
Here ∆T₁ = 110 - 100 = 10°C
\(\frac{d Q_1}{d t}\) = 4 J/s, ∆T₂ = 210 - 200 = 10°C
\(\frac{d Q_2}{d t}\) = ?
As the rate of heat flow is directly proportional to the temperature difference and the temperature difference in both the cases is same i.e.,10°C. So the same rate of heat will flow in the second case
Hence, \(\frac{d Q_2}{d t}\) = 4 J/s

Question 7.
Steam at 100°C is passed into 20g of water at 10°C. When water acquires a temperature of 80°C, the mass of water present will be: [Take specific heat of water = 1 cal g^-1°C^-1 and latent heat of steam = 540 cal/g]
(a) 24g
(b) 31.5g
(c) 42.5g
(d) 22.5g
Solution:
Heat lost by steam = Heat gained by water
Let m' be the amount of steam that converts into water,
m' x L + m' s∆T = ms∆t
m' x 540 + m' x 1 x (100 - 80) = 20 x 1 x (80 - 10)
m' = \(\frac{20 \times 70}{560}\)
= 2.5 g
Now net mass of water = 20 + 2.5 = 22.5 g

Queston 8.
Certain quantity of water cools from 70°C to 60°C in the first 5 min and to 54°C in the next 5 min. The temperature of the surroundings is:
(a) 45°C
(b) 20°C
(c) 42°C
(d) 10°C
Solution:
Let the temperature of the surrounding be t°C for first case,

so t = 45°C

Question 9.
A piece of iron is heated in a flame. If first becomes dull red then becomes reddish yellow and finally turns to white hot. The correct explanation for the above observation is possible by using:
(a) Stefan’s law
(b) Wien’s displacement law
(c) Kirchhoff s law
(d) Newton’s law of cooling
Solution:
∵ λ_mT = constant.

Question 10.
If the radius of a star is R and it acts as a black body, what would be the temperature of the star, in which the rate of energy production is Q?
(σ stands for Stefan’s constant)
(a) Q/4πR²σ
(b) (Q/ 4πR²σ)^-1/2
(c) (4πR²Q/σ)^1/4
(d) (Q/4πR²σ)^1/4
Solution:
From Stefan's law
E = σT₄
So, rate of energy production
Q = E x A
Q = σT₄ x 4πR²
Temperature of star
T = (\(\frac{Q}{4 \pi R^2 \sigma}\))^1/4

Question 11.
Liquid oxygen at 50K is heated to 300 K at constant pressure of 1 atm. The rate of heating is constant. Which one of the following graphs represents the variation of temperature with time?
Solution:
Graph (a) shows the variation of temperature with time. At first temperature will increase then there wifl be state change from liquid to gas.

Question 12.
A copper ball of mass 100 gm is at a temperature T. It is dropped in a copper calorimeter of mass 100 gm, filled with 170 gm of water at room temperature. Subsequently, the temperature of the system is found to be 75°C. T is given by: (Given: room temperature = 30°C, specific heat of copper = 0.1 cal/gm°C)
(a) 885°C
(b) 1250°C
(c) 825°C
(d) 800°C
Solution:
Heat gained by (water + calorimeter) = Heat lost by copper ball
⇒ 100 x 0.1 x (75 - 30) + 170 x 1 x (75 - 30)
= 100 x 0.1 x (T - 75)
⇒ 450 + 7650 = 10(T - 75)
⇒ T - 75 = 810
⇒ T = 885°C

Question 13.
Parallel rays of light of intensity 1 = 912 W/m² are incident on a spherical black body kept in surroundings of temperature 300 K. Take Stefan constant σ = 5.7 x 10^-8 W/m²K⁴ and assume that the energy exchange with the surroundings is only through radiation. The final steady state temperature of the black body is close to:
(a) 330 K
(b) 660 K
(c) 990 K
(d) 1550 K
Solution:
In steady state
Energy incident per second = Energy radiated per second
∴ IπR² = σ(T⁴ - T₀⁴) 4πR² ⇒ I = 4σ(T⁴ - T₀⁴)

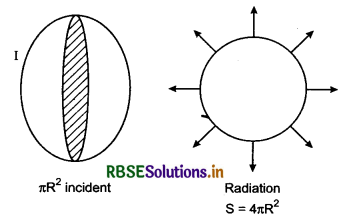
⇒T⁴ - T₀⁴ = 40 x 10⁸
⇒ T⁴ - 81 x 10⁸ = 40 x 10⁸
⇒ T⁴ = 121 x 10⁸ ⇒ T ≈ 330 K

Question 14.
Three rods of copper, brass and steel are welded together to form a Y-shaped structure. Area of cross-section of each rod is 4 cm². End of copper rod is maintained at 100°C whereas ends of brass and steel are kept at 0°C. Lengths of the copper, brass and steel rods are 46, 13 and 12 cm respectively.
The rods are thermally insulated from surroundings except at ends. Thermal conductivities of copper, brass and steel are 0.92, 0.26 and 0.12 in CGS units, respectively. Rate of heat flow through copper rod is:
(a) 1.2 cal/s
(b) 2.4 cal/s
(c) 4.8 cal/s
(d) 6.0 cal/s
Solution:
In thermal conduction, it is found that in steady state the heat current is directly proportional to the area of cross section A which is proportional to the change in temperature (T₁ - T₂).

Question 15.
If a piece of metal is heated to temperature θ and then allowed to cool in a room which is at temperature θ0. The graph between the temperature T of the metal and time t will be closed to:

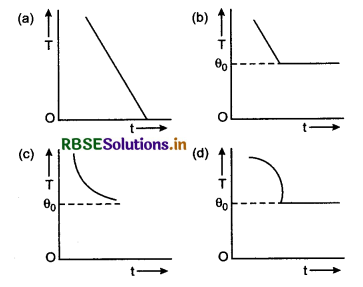
Solution:

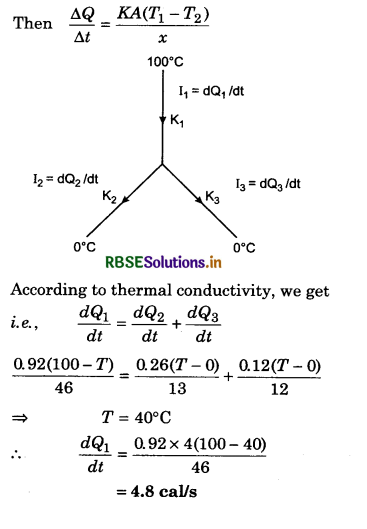
Question 16.
Two rectangular blocks, having indentical dimensions, can be arranged either in configuration I or in configuration II as shown in the figure. One of the blocks has thermal conductivity K and the other 2K. The temperature difference between the ends along the x-axis is the same in both the configurations. It takes 9s to transport a certain amount of heat from the hot end to the cold end in the configuration I. The time to transport the same amount of heat in the configuration II is:
(a) 2.0 s
(b) 3.0 s
(c) 4.5 s
(d) 6.0 s

Solution:
R_Th = R₁ + R₂

Since, thermal resistance R_Th ρ is 4.5 times less than thermal resistance R_Th S
∴ t_Th ρ = \(\frac{t_{\mathrm{Th} S}}{4.5}=\frac{9}{4.5}\) = 2s