RBSE Class 11 Physics Important Questions Chapter 10 तरलों के यांत्रिकी गुण

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 10 तरलों के यांत्रिकी गुण Important Questions and Answers.

RBSE Class 11 Physics Chapter 10 Important Questions तरलों के यांत्रिकी गुण

बहुचयनात्मक प्रश्न:

प्रश्न 1. 
द्रव का श्यानता गुणांक किस पर निर्भर करता है:
(अ) द्रव की प्रकृति पर
(स) दाब पर
(ब) ताप पर
(द) उपर्युक्त सभी पर 
हल: द्रव का श्यानता गुणांक द्रव की प्रकृति, ताप व दाब पर निर्भर करता है।
अतः सही विकल्प (द) है।
उत्तर:
(द) उपर्युक्त सभी पर 

प्रश्न 2. 
असमान त्रिज्या की नली का दो स्थानों पर अनुप्रस्थ काट का अनुपात 1 : 2 हो तो असम्पीड्य द्रव के लिए नली में प्रवेश कर रहे तथा बाहर निकल रहे द्रव के द्रव्यमान का अनुपात होगा:
(अ) 1 : 2
(ब) 2 : 1
(स) 1 : 4
(द) 1 : 1
हल : सांतत्य समीकरण से जितना द्रव प्रवेश करेगा उतना ही द्रव बाहर निकलेगा।
अत: सही विकल्प (द) है।
उत्तर:
(द) 1 : 1

प्रश्न 3. 
असमान त्रिज्या की नली का दो स्थानों पर अनुप्रस्थ काट का अनुपात 12 हो तो असम्पीड्य द्रव के लिए नली में प्रवेश कर रहे तथा बाहर निकल रहे द्रव के वेगों का अनुपात होगा:
(अ) 1 : 2
(ब) 2 : 1
(स) 1 : 4
(द) 1 : 1
हल: सांतत्य समीकरण से A₁v₁ = A₂v₂
\(\therefore \frac{A_1}{A_2}=\frac{v_2}{v_1} \quad \therefore \frac{v_2}{v_1}=\frac{1}{2}\)
या
v₁/v₂ = 2/1 = 2 : 1
अतः सही विकल्प (ब) है।
उत्तर:
(ब) 2 : 1

प्रश्न  4. 
बरनूली की प्रमेय आधारित है:
(अ) ऊर्जा संरक्षण सिद्धान्त पर 
(ब) संवेग संरक्षण सिद्धान्त पर
(स) द्रव्यमान संरक्षण सिद्धान्त पर
(द) उपर्युक्त सभी पर
उत्तर:
(अ) ऊर्जा संरक्षण सिद्धान्त पर 

प्रश्न  5. 
किसी बहते हुए द्रव की ऊर्जा होती है:
(अ) केवल दाब ऊर्जा
(ब) केवल गतिज ऊर्जा
(स) केवल स्थितिज ऊर्जा
(द) उपर्युक्त सभी
हल: बहते हुये द्रव में दाब ऊर्जा, गतिज ऊर्जा व स्थितिज ऊर्जा सभी हो सकती हैं।
अतः सही विकल्प (द) है।
उत्तर:
(द) उपर्युक्त सभी

प्रश्न  6. 
कौन सा कथन अशुद्ध है:
(अ) द्रव के ऊपरी मुक्त तल पर द्रव का दाब शून्य होता है। 
(ब) किसी पात्र में भरे द्रव का दाब सभी बिन्दुओं पर समान रहता है। 
(स) किसी क्षैतिज तल में द्रव का दाब सभी बिन्दुओं पर समान रहता है।
(द) किसी तल पर द्रव का दाब क्षेत्रफल पर निर्भर नहीं करता है।
उत्तर:
(ब) किसी पात्र में भरे द्रव का दाब सभी बिन्दुओं पर समान रहता है। 

प्रश्न  7. 
द्रव दाब निर्भर करता है:
(अ) केवल गहराई पर
(ब) केवल घनत्व पर
(स) केवल गुरुत्वीय त्वरण पर
(द) गहराई, घनत्व तथा गुरुत्वीय त्वरण तीनों पर
उत्तर:
(द) गहराई, घनत्व तथा गुरुत्वीय त्वरण तीनों पर

प्रश्न  8. 
सर्वाधिक श्यानता होगी:
(अ) पारे की
(ब) जल की
(स) ऑक्सीजन की
(द) हाइड्रोजन की
उत्तर:
(अ) पारे की

प्रश्न  9. 
ताप बढ़ने पर गैस की श्यानता:
(अ) बढ़ती है।
(ब) घटती है
(स) अपरिवर्तित रहती है
(द) इनमें से कोई नहीं
उत्तर:
(अ) बढ़ती है।

प्रश्न  10. 
बरनौली प्रमेय का निष्कर्ष है:
(अ) पास्कल का नियम
(ब) टोरीसैली प्रमेय
(स) हुक का नियम
(द) स्टोक का नियम 
उत्तर:
(ब) टोरीसैली प्रमेय

प्रश्न  11. 
रेनॉल्ड्स के अनुसार क्रांतिक वेग का मान क्या होगा?

उत्तर:
\(\text { (ब) } \frac{R D}{\rho \eta}\)

प्रश्न  12. 
संकीर्ण नली के लिये रेनॉल्ड्स संख्या का मान होता है:
(अ) 10
(ब) 100
(स) 1000
(द) 10000
हल: संकीर्ण नली में धारा रेखीय प्रवाह के लिये रेनॉल्ड्स संख्या 1000 होती है।
अत: सही विकल्प (स) है।
उत्तर:
(स) 1000

प्रश्न  13. 
एक नली में दाब P पर प्रवाहित जल की दर Q है। यदि नली की त्रिज्या पहले से आधी कर दी जाये तथा दाब को 2P कर दिया जाये तो प्रवाह दर होगी:
(अ) 4Q
(ब) Q2/4
(स) Q/4
(द) Q/8
उत्तर:
(द) Q/8

प्रश्न  14. 
बरनौली प्रमेय का संबंध है:
(अ) श्यानता से
(ब) पृष्ठ तनाव से
(स) तरलों के प्रवाह से
(द) द्रवों की आण्विक संरचना से
उत्तर:
(स) तरलों के प्रवाह से

प्रश्न  15. 
एक पाइप A पर जल वेग से प्रवेश करता है तथा पाइप के ऊर्ध्वाधर भाग में / ऊँचाई तक चढ़ता है। यदि जल का घनत्व d हो तो वेग v होगा:
(अ) 2gh
\(\text { (ब) } \sqrt{d g h}\)
\(\text { (स) } \sqrt{2 g h}\)
\(\text { (द) } \sqrt{g h}\)
उत्तर:
\(\text { (ब) } \sqrt{d g h}\)

प्रश्न  16. 
असमान परिच्छेद के पाइप की त्रिज्या r₁ से r₂ तक बदलती है। पाइप में द्रव के प्रवाह का वेग यदि v₁ से v₂ तक बदले ता v₁/v₂ 'बराबर
(अ) r₁²/r₂²
(ब) r₂²/r₁²
(स) r₁/r₂
(द) 1
उत्तर:
(ब) r₂²/r₁²

प्रश्न  17. 
द्रव का पृष्ठ तनाव
(अ) क्षेत्रफल के साथ बढ़ता है 
(ब) क्षेत्रफल के साथ घटता है।
(स) ताप के साथ बढ़ता है
(द) ताप के साथ घटता है।
उत्तर:
(द) ताप के साथ घटता है।

प्रश्न  18. 
ताप कम करने पर पृष्ठ तनाव होता है.
(अ) बढ़ता है
(ब) कम होता है।
(स) अपरिवर्तित रहता है
(द) इनमें से कोई नहीं।
उत्तर:
(अ) बढ़ता है
 
प्रश्न  19. 
असमान अनुप्रस्थ परिच्छेद के क्षैतिज पाइप में जल बह रहा है। पाइप में सँकरे स्थान पर होगा:
(अ) वेग अधिक, दाब अधिक 
(ब) वेग कम दाब अधिक
(स) वेग अधिक दाब कम
(द) वेग कम, दाब कम
उत्तर:
(स) वेग अधिक दाब कम

प्रश्न  20. 
द्रव में अपमार्जक मिलाने से सम्पर्क कोण:
(अ) बढ़ता है
(ब) घटता है
(स) अपरिवर्तित रहता है 
(द) कुछ निश्चित नहीं कर सकते।
उत्तर:
(ब) घटता है

प्रश्न  21. 
एक द्रव ठोस की सतह को नहीं भिगोएगा, यदि स्पर्श कोण है:
(अ) 0°
(ब) 45°
(स) 60°
(द) अधिक कोण
उत्तर:
(द) अधिक कोण

प्रश्न  22. 
दो द्रव की बूंदों की त्रिज्याओं का अनुपात 1 : 2 है तो उनके दाब आधिक्यों का अनुपात होगा:
(अ) 1 : 2
(ब) 2 : 1
(स) 1 : 4
(द) 4 : 1
हल: P = 2T/r
\(\frac{P_1}{P_2}=\frac{r_2}{r_1}=\frac{2}{1} \therefore P_1: P_2=2: 1\)
अत: सही विकल्प (ब) है।
उत्तर:
(ब) 2 : 1

प्रश्न  23. 
जब केशनली को पानी में डाला जाता है तो नवचन्द्रक के ऊपर व नीचे के बिन्दुओं के बीच दाबांतर का मान होगा:
(अ) 4T/r
(ब) 2T/r
(स) 2.Tr
(द) 4Tr
उत्तर:
(ब) 2T/r

प्रश्न  24. 
साबुन के घोल का बुलबुला, जिसकी त्रिज्या है, को बनाने में कितना कार्य करना होगा?
(अ) 4πr²T
(ब) 8πr²T
(स) 2πr²T
(द) πr²T
हल: साबुन के बुलबुले में दो पृष्ठ होते हैं।
इस कारण से 44 = 2 x 4πr² = 8πr²
∴ W = T × M = T x 8πr² = 8πr²T
अतः सही विकल्प (ब) है।
उत्तर:
(ब) 8πr²T

प्रश्न  25. 
किसी केशिका में चढ़े हुये पानी की ऊँचाई होगी:
(अ) 4°C पर अधिकतम
(ब) 2°C पर अधिकतम
(स) 4°C पर न्यूनतम
(द) 0°C पर न्यूनतम 
उत्तर:
(स) 4°C पर न्यूनतम

प्रश्न  26. 
चॉक द्वारा श्यामपट्ट पर लिखना किस गुण के कारण सम्भव है?
(अ) ससंजक 
(ब) आसंजक बल
(स) पृष्ठ तनाव
(द) श्यानता
उत्तर:
(ब) आसंजक बल

प्रश्न  27. 
क्रान्तिक ताप पर पृष्ठ तनाव हो जाता है:
(अ) अनन्त
(ब) शून्य
(स) ऋणात्मक एवं निश्चित
(द) धनात्मक एवं निश्चित
उत्तर:
(ब) शून्य

प्रश्न  28. 
यदि साबुन के घोल से आयतन का वायु का एक बुलबुला बनाने में W कार्य करना पड़ता हो तो उसी घोल से 21 आयतन का बुलबुला बनाने में किये गये कार्य का मान होगा:
(अ) W
(ब) √2W
(स) 41/3 W
(द) 2 w
उत्तर:
(स) 41/3 W

प्रश्न  29. 
अगर कोई द्रव केशनली में न गिरता है न चढ़ता है तो उस द्रव व केशनली पदार्थ के लिये सम्पर्क कोण होगा:
(अ) 0°
(ब) 45°
(स) 90°
(द) 120°
उत्तर:
(स) 90°

प्रश्न  30. 
पृथ्वी पर एक केशनली में द्रव स्तम्भ की ऊँचाई 1⁄2 है। चन्द्रमा पर 1/6 जहाँ गुरुत्वीय त्वरण पृथ्वी का है। यह ऊँचाई
(अ) 1/6
(ब) 6h
(स) h
(द) शून्य
हल: चूँकि \(h \propto \frac{1}{g} \therefore \frac{h_1}{h_2}=\frac{g_2}{g_1}\) से
उत्तर:
(ब) 6h

रिक्त स्थानों की पूर्ति कीजिए:

प्रश्न  1.
क्षेत्रफल का मान अधिक होने पर दाब ......................  होगा।
उत्तर:
दाब

प्रश्न  2.
4°C पर पानी का घनत्व ...................... तथा इसका मान ................ kg m³ होता है।
उत्तर:
अधिकतम 1.0 x 10³

प्रश्न  3.
द्रव के भीतर ऊर्ध्वाधर रेखा में किन्हीं दो बिन्दुओं का दावान्तर केवल ......................... के कारण होता है।
उत्तर:
गुरुत्व प्रभाव

प्रश्न  4.
हाइड्रोलिक मशीन ...................... नियम पर आधारित है।
उत्तर:
पास्कल

प्रश्न  5. 
वायुमण्डलीय दाब को ऊँचाई का प्रभाव, ताप का प्रभाव, ................. प्रभावित करते हैं।
उत्तर:
जल वाष्प का प्रभाव

 प्रश्न  6.
किसी द्रव का प्रवाह धारा रेखीय तब तक ही रहता है जब तक कि उसके बहने का वेग एक निश्चित मान से कम ......................... हो। वेग के इस मान को
उत्तर:
क्रांतिक वेग

प्रश्न  7. 
ताप बढ़ने से द्रवों की श्यानता ..................... जाती है परन्तु गैसों की श्यानता जाती है।
उत्तर:
घट बढ़

प्रश्न  8.
R का मान 3000 से अधिक होने पर द्रव प्रवाह .................. होता है।
उत्तर:
प्रक्षुब्ध

प्रश्न  9.
बरनौली का प्रमेय एक प्रकार से बहते हुए द्रव (अथवा गैस) के लिए. ............................. का सिद्धान्त है।
उत्तर:
ऊर्जा संरक्षण

प्रश्न  10.
पृष्ठ तनाव व पृष्ठ ऊर्जा में सम्बन्ध ...................... होता है।
उत्तर:
T = W/∆ A

नीचे दिये गये वाक्यों में सत्य / असत्य कथन का चयन कीजिए:

प्रश्न  1.
क्षेत्रफल कम होने पर दाब कम और क्षेत्रफल अधिक होने पर दाब अधिक होता है।
उत्तर:
असत्य

प्रश्न  2.
किसी तरल (द्रव अथवा गैस) के / ऊँचाई के स्तम्भ के कारण दाब का सूत्र है। P = hpg 
उत्तर:
सत्य

प्रश्न  3.
यदि g = 0 अर्थात् गुरुत्व प्रभाव अनुपस्थित हो तो P2 ≠ P1
उत्तर:
असत्य

प्रश्न  4.
श्यानता गुणांक का एक अन्य (CGS) मात्रक प्वाइज (Poise) भी होता है
उत्तर:
सत्य

प्रश्न  5.
संकीर्ण बेलनाकार नलियों के लिए R2000 हो तो द्रव का प्रवाह धारा रेखीय होता है।
उत्तर:
असत्य

प्रश्न  6.
बरनौली के सिद्धान्त में दाब ऊर्जा, गतिज ऊर्जा ऊर्जा का योग एक नियतांक नहीं होता है।
उत्तर:
असत्य

प्रश्न  7.
पृष्ठ ऊर्जा में वृद्धि को पृष्ठ तनाव कहते हैं।
पृष्ठ तनाव T = W/A जूल/मी.²
उत्तर:
सत्य

प्रश्न  8.
साबुन के बुलबुले के अन्दर दाब आधिक्य P = T/r होता है।
उत्तर:
असत्य

प्रश्न  9.
केशनली में चढ़े द्रव स्तम्भ की ऊँचाई तथा केशनली की त्रिज्या का गुणनफल नियत रहता है।
उत्तर:
सत्य

प्रश्न  10.
असमान अनुप्रस्थ परिच्छेद के क्षैतिज पाइप में जल बह रहा है। पाइप में संकरे स्थान पर वेग अधिक, दाब कम होगा।
उत्तर:
सत्य

कॉलम - A से कॉलम B का सही मिलान कीजिए:

प्रश्न  1.

कॉलम-A	कॉलम-B
1. द्रव स्तम्भ का भार	(A) घनत्वों के
2. 1 बार (bar)	(B) dv/dx
3. विभिन्न द्रवों में समान गहराई पर दाब उनके में होता है।	(C) पास्कल
4. द्रव चालित लिफ्ट का कार्य सिद्धान्त किस नियम पर आधारित है?	(D) परिवर्तित
5. वेग प्रवणता =	(E) विपरीत
6. श्यान बल की दिशा द्रव प्रवाह की दिशा के होती है।	(F) R = 2000
7. द्रव का दाब परिवर्तित करने पर श्यानता गुणांक भी होता है।	(G) स्थिरांक (इकाई आयतन के लिए)
8. श्यान बल का मान F =	(H) Ahpg
9. द्रव का प्रवाह धारा रेखीय तब	(I) 6πηVtr
10. \(\frac{\mathrm{P}}{\rho}+\frac{1}{2} \mathrm{~V}^2+g h=\)	(J) 105 पास्कल (Pa)

उत्तर:

कॉलम-A	कॉलम-B
1. द्रव स्तम्भ का भार	(H) Ahpg
2. 1 बार (bar)	(J) 105 पास्कल (Pa)
3. विभिन्न द्रवों में समान गहराई पर दाब उनके में होता है।	(A) घनत्वों के
4. द्रव चालित लिफ्ट का कार्य सिद्धान्त किस नियम पर आधारित है?	(C) पास्कल
5. वेग प्रवणता =	(B) dv/dx
6. श्यान बल की दिशा द्रव प्रवाह की दिशा के होती है।	(E) विपरीत
7. द्रव का दाब परिवर्तित करने पर श्यानता गुणांक भी होता है।	(D) परिवर्तित
8. श्यान बल का मान F =	(I) 6πηVtr
9. द्रव का प्रवाह धारा रेखीय तब	(F) R = 2000
10.\(\frac{\mathrm{P}}{\rho}+\frac{1}{2} \mathrm{~V}^2+g h=\)	(G) स्थिरांक (इकाई आयतन के लिए)

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1. 
पास्कल तथा न्यूटन / मीटर ? में क्या सम्बन्ध है? 
उत्तर:
1 न्यूटन / मीटर = 1Pa

प्रश्न 2. 
एक आदमी व एक बच्चे ने अपनी-अपनी हथेली पर 2 किग्रा का बाँट रखा हुआ है। किसकी हथेली पर अधिक दाब लगेगा? 
उत्तर:
बच्चे की।
[ चूँकि आदमी की हथेली का क्षेत्रफल बच्चे की हथेली की तुलना में अधिक होता है।]

प्रश्न 3. 
द्रव का दाब किस पर निर्भर करता है?
उत्तर:
द्रव स्तम्भ की ऊँचाई पर।

प्रश्न 4. 
यदि किसी वस्तु का वायु में भार W ग्राम और जल में भार W1 ग्राम है, तो वस्तु के ऊपर जल का उत्प्लावन बल कितना होगा? 
उत्तर:
(W - W1)

प्रश्न 5. 
वायुमण्डल में बहुत अधिक ऊपर जाने पर मानव रक्त नलिकाओं का फटने का डर क्यों रहता है?
उत्तर:
वायुदाब कम होने से इसका रक्त दाब से सन्तुलन बिगड़ने के कारण।

प्रश्न 6. 
हाइड्रोलिक प्रेस तथा हाइड्रोलिक ब्रेक का कार्य सिद्धान्त किस नियम पर आधारित है?
उत्तर:
पास्कल के नियम पर।

प्रश्न 7. 
पास्कल नियम के दो अनुप्रयोग लिखिये।
उत्तर:
द्रवचालित ब्रेक, द्रवचालित लिफ्ट।

प्रश्न 8. 
श्यानता पर ताप का क्या प्रभाव पड़ता है? 
उत्तर:
ताप बढ़ने पर श्यानता कम हो जाती है।

प्रश्न 9. 
क्षैतिज नली के लिए बरनौली का सिद्धान्त क्या है? 
उत्तर:
क्षैतिज नली के लिए बरनौली का सिद्धान्त-
(P1 - P2) = 1/2P(v₂² - v₁²)

प्रश्न 10. 
M. KS पद्धति में श्यानता गुणांक का मात्रक क्या है? 
उत्तर:
श्यानता का मात्रक न्यूटन सेकण्ड / मी.'।

प्रश्न 11. 
किसी टंकी में पानी के धरातल से / मीटर नीचे रंध्र में बहि:स्राव वेग का सूत्र क्या है?
उत्तर:
वेग \(v=\sqrt{2 g h}\)

प्रश्न 12. 
एक फ्लास्क में ग्लिसरीन तथा दूसरे फ्लास्क में जल है। दोनों को तेजी से घुमाया जाता है और मेज पर रख दिया जाता है। किस फ्लास्क का द्रव पहले विराम अवस्था में आयेगा और क्यों?
उत्तर:
ग्लिसरीन पहले विरामावस्था में आयेगी क्योंकि इसकी श्यानता अधिक होती है।

प्रश्न 13. 
m द्रव्यमान तथा p घनत्व की एक छोटी गेंद को • घनत्व के एक श्यान द्रव में गिराया जाता है। थोड़ी देर बाद गेंद एक नियत वेग से नीचे जाती है, तब गेंद पर लगने वाला श्यान बल कितना लगता है?
उत्तर:
श्यान बल = गेंद का भार - उत्प्लावन बल
\(=\operatorname{mg}\left(1-\frac{\sigma}{\rho}\right)\)

प्रश्न 14. 
द्रव में किसी बिन्दु पर दाब किन-किन बातों पर निर्भर करता है?
उत्तर:
द्रव में किसी बिन्दु पर दाब सभी दिशाओं में समान होता है तथा यह दाब द्रव के घनत्व व गहराई पर निर्भर नहीं करता है।

प्रश्न 15. 
एक असमान परिच्छेद वाले क्षैतिज पाइप में जल बह रहा है। जल का किसी बिन्दु A पर वेग एक अन्य बिन्दु B पर जल के वेग का चार गुना है। बिन्दु A पर पाइप का व्यास बिन्दु B के सापेक्ष कितना होगा?
उत्तर:
A पर पाइप का व्यास बिन्दु B के सापेक्ष आधा होता है। 

प्रश्न 16. 
यदि हम धागे की रील के छेद में ऊपर से फूँक मारें तो उसके निचले सिरे पर रखा कार्ड नीचे नहीं गिरता, क्यों?
उत्तर:
रील व कार्ड के बीच वायु वेग अधिक होने के कारण उनके बीच दाब वायुमण्डलीय दाब से कम हो जाता है।

प्रश्न 17. 
ताजे जल से भरी एक टंकी की दीवार में एक छिद्र है जिससे जल बाहर निकल रहा है। यदि छिद्र कुछ बड़ा हो जाये तो क्या जल के बाहर निकलने का वेग बदल जाएगा? क्या प्रति सेकण्ड निकलने वाले जल का आयतन बदल जाएगा?
उत्तर:
वेग कम होगा, आयतन बदल जाएगा।

प्रश्न 18. 
यदि टंकी में ताजे जल के स्थान पर समुद्री जल भर दें तो क्या छिद्र से निकलने वाले जल का वेग बदल जाएगा?
उत्तर:
नहीं, बहिःस्राव वेग घनत्व पर निर्भर नहीं करता। 

प्रश्न 19. 
गोली A का व्यास गोली B के व्यास से आधा है। जल के भीतर उनके सीमान्त वेगों में क्या अनुपात होगा? 
उत्तर:
सीमान्त वेग v α r²
सीमान्त वेगों में अनुपात = 1 : 4 होगा।

प्रश्न 20. 
एक क्षैतिज पाइप में जल के प्रवाह का वेग 15 मीटर / सेकण्ड है, जल का वेग शीर्ष ज्ञात कीजिए। (g = 10 मीटर/से.²)
उत्तर:
वेग शीर्ष
= v²/2g = \(\frac{\mathrm{v}^2}{2 g}=\frac{15 \times 15}{2 \times 10}\)
= 45/4 = 11.25 मीटर/सेकण्ड

प्रश्न 21. 
बरनौली सिद्धान्त के क्या-क्या उपयोग हैं? 
उत्तर:

1. क्षैतिज धरातल पर रखी हुई नली में द्रव का प्रवाह ज्ञात करना।
2. किसी नली में बहते हुए द्रव की प्रवाह दर Q ज्ञात करना। 
3. रॉकेट से निकलने वाली गैस के कारण रॉकेट पर लगने वाला प्रतिक्रिया बल ज्ञात करना।

प्रश्न 22. 
किसी बाँध में गुरुत्व शीर्ष 100 मीटर है। उसके पेंदे से लगे पाइप से पानी बाहर आता है, पानी का वेग ज्ञात करो। (g= 10 मी./से².) 
उत्तर:
\(\mathrm{v}=\sqrt{2 \mathrm{gh}}=\sqrt{2 \times 10 \times 100}\)
= 20/5 मी. सेकण्ड

प्रश्न 23. 
स्टोक का नियम क्या है?
उत्तर:
स्टोक के नियम के अनुसार यदि कोई पिण्ड त्रिज्या का एक गोला है और वह उपयुक्त माध्यम में जिसका विस्कासित गुणांक n है, v वेग से गति कर रहा है तो इस गोलाकार पिण्ड पर लगने वाला विरोधी विस्कासिता बल F = 6πnav होगा।

प्रश्न 24. 
ताप बढ़ाने पर स्पर्श कोण के मान पर क्या प्रभाव पड़ता है?
उत्तर:
स्पर्श कोण कम हो जाता है।

प्रश्न 25. 
एक सुई साफ पानी में तैरती है, लेकिन साबुन के पानी में डूब जाती है। क्यों?
उत्तर:
साफ पानी का पृष्ठ तनाव साबुन मिले पानी से अधिक होता है, अतः साफ पानी का पृष्ठ तनाव सुई के भार को संतुलित कर सकता है।

प्रश्न 26. 
केशिका नली में पारा भरने में कठिनाई क्यों होती है? 
उत्तर:
काँच के लिए पारे का स्पर्श कोण 140 है, अतः यह केशिका नली में अवनमन दिखाता है।

प्रश्न 27. 
जब छोटी-छोटी बूंदें मिलकर बड़ी बूँद बनाती हैं तो उसके ताप में क्या अंतर होता है?
उत्तर:
बूँद का ताप बढ़ जायेगा।

प्रश्न 28. 
केशिका नली की लम्बाई यदि आवश्यकता से कम हो तो क्या पानी उसमें से बाहर निकल जाएगा?
उत्तर:
नहीं, पानी ऊपर पहुँचकर पानी तल की वक्रता त्रिज्या इस प्रकार से समंजित कर लेता है कि नली की लम्बाई के लिए अनुबंध - पूरा हो जाये।

प्रश्न 29. 
किसी बेलनाकार नली में बहते हुये द्रव में किस पर्त का वेग सर्वाधिक होता है?
उत्तर:
नली की अक्ष के अनुदिश पर्त का।

प्रश्न 30. 
किसी केश नली में द्रव प्रवाह की दर का प्वाँजली का सूत्र लिखिये।
उत्तर:
प्वॉजली का सूत्र \(Q=\frac{\pi \operatorname{Pr}^4}{8 \eta l}\)

प्रश्न 31. 
रेनॉल्ड संख्या का कितना मान होने पर द्रव का प्रवाह विक्षुब्ध हो जाता है?
उत्तर:
3000 से अधिक।

प्रश्न 32. 
किसी श्यान द्रव में स्वतन्त्रतापूर्वक गिरती हुई एक छोटी गोली के सीमान्त वेग के लिये सूत्र लिखिये।
उत्तर:
\(-v_t=\frac{2 r^2(\rho-\sigma) g}{9 \eta}\)

प्रश्न 33. 
बहते हुये द्रव में कौन-कौनसी ऊर्जायें होती हैं? 
उत्तर:
दाब ऊर्जा, गतिज ऊर्जा, स्थितिज ऊर्जा।

प्रश्न 34. 
बेंच्यूरोमीटर किस प्रयोग में आता है?
उत्तर:
किसी पाइप में द्रव प्रवाह की दर ज्ञात करने में।

प्रश्न 35. 
किसी पात्र में द्रव के स्वतन्त्र तल से h गहराई पर एक छिद्र बना है जिसकी त्रिज्या r है इस छिद से निकलने वाले द्रव जेट के निष्कासन वेग का सूत्र लिखिये।
उत्तर:
v = √2gh

प्रश्न 36. 
भारहीनता की अवस्था में यदि केशिका नली को पानी में डुबोया जाये तो क्या होगा?
उत्तर:
भारहीनता की स्थिति में द्रव नली की पूरी लम्बाई तक चढ़ जायेगा।

प्रश्न 37. 
शुद्ध पानी की बजाय साबुन के घोल से कपड़े धोना आसान है, क्यों?
उत्तर:
साबुन के घोल का पृष्ठ तनाव शुद्ध पानी की तुलना में कम होता है।

प्रश्न 38. 
पारे की छोटी-छोटी बूँदों को पास लाने पर वे आपस में मिलकर एक बड़ी बूँद बना लेती हैं, क्यों?
उत्तर:
ससंजक बलों के कारण।

प्रश्न 39. 
यदि पानी की कुछ बूँदें मिलकर एक बड़ी बूँद बनाती हैं तो पृष्ठ ऊर्जा घटेगी या बढ़ेगी?
उत्तर:
पृष्ठ ऊर्जा घटेगी।

प्रश्न 40. 
जब एक सीधी केशनली को जल में ऊर्ध्वाधर खड़ा करते हैं तब उसमें पानी 5 सेमी. तक चढ़ता है। अब यदि केशनली को 45° कोण पर झुका दिया जाये तब द्रव तल से किस ऊँचाई तक पानी चढ़ेगा? 
उत्तर:
5 सेमी. तक ही।

प्रश्न 41. 
खेतों में बरसात के तुरन्त बाद जुताई कर दी जाती है, क्यों?
उत्तर:
जुताई करने से मिट्टी में बनी केशनलियाँ टूट जाती हैं और इसके कारण मिट्टी के अंदर का पानी ऊपर आकर व्यर्थ में वाष्पित नहीं होता है।

प्रश्न 42. 
एक केशनली में पानी 6 सेमी. ऊँचाई तक चढ़ता है। एक दूसरी केशनली जिसका व्यास पहले के व्यास का 2/3 है, में पानी किस ऊँचाई तक चढ़ेगा?
उत्तर:
सूत्र r₁h₁ = r₂h₂
\(\begin{aligned} & h_2=\frac{r_1 h_1}{r_2} \\ & h_2=\frac{r \times 6}{\frac{2}{3} r}=\frac{6 \times 3}{2} \end{aligned}\)
h₂ = 3 x 3 = 9 सेमी.

प्रश्न 43. 
तेल से भरे दीपक में कपास की बत्ती क्यों जलती रहती है?
उत्तर:
कपास की बत्ती में बनी असंख्य केशनलियों में केशिकात्व के कारण तेल ऊपर चढ़ता है।

प्रश्न 44. 
यदि किसी द्रव व ठोस के बीच स्पर्श कोण 90° से अधिक हो तो क्या वह द्रव ठोस को भिगोयेगा? इसका उस ठोस से बनी केशनली में पृष्ठ कैसा होगा? क्या द्रव केशनली में चढ़ेगा?
उत्तर:
नहीं भिगोयेगा, उत्तल, नहीं बल्कि केशनली में नीचे उतरेगा। 

प्रश्न 45. 
पृष्ठ तनाव किसे कहते हैं तथा इसकी इकाई क्या होती है?
उत्तर:
द्रव का वह गुण जिसके कारण द्रव की सतह खिंची हुई झिल्ली की तरह व्यवहार करती है, पृष्ठ तनाव कहलाता है। अर्थात् द्रव अपनी सतह को न्यूनतम करना चाहता है पृष्ठ तनाव का मात्रक न्यूटन / मी. होता है।

प्रश्न 46. 
साबुन के बुलबुले में अन्दर तथा बाहर के कारण दाब आधिक्य के मान को ज्ञात करने का सूत्र लिखिए।
उत्तर:
p = 4T/r

प्रश्न 47. 
किसी संकीर्ण नली में धारा रेखीय द्रव प्रवाह के लिये रेनॉल्ड्स संख्या का मान क्या होना चाहिये?
उत्तर:
धारा रेखीय प्रवाह के लिये R सामान्यतः 1000 लिया जाता है।

प्रश्न 48. 
गर्म सूप ठंडे सूप की अपेक्षा स्वादिष्ट क्यों लगता है? 
उत्तर:
गर्म सूप का पृष्ठ तनाव कम हो जाने से वह जीभ के अधिक पृष्ठ क्षेत्रफल पर फैल जाता है व स्वादिष्ट लगता है।

प्रश्न 49. 
खेतों में बरसात के तुरन्त बाद जुताई कर दी जाती है, क्यों?
उत्तर:
जुताई करने से मिट्टी में बनी केशनलियाँ टूट जाती हैं, जिससे मिट्टी के अन्दर का पानी ऊपर चढ़कर वाष्पित नहीं हो पाता। 

प्रश्न 50. 
जल के पृष्ठ तनाव को कैसे कम कर सकते हैं? 
उत्तर:
गर्म करके, तेल अथवा साबुन का घोल डालकर। 

प्रश्न 51. 
क्या वर्षा की सभी बूँदें (बड़ी और छोटी) एक ही अन्तिम वेग से पृथ्वी पर पहुँचती हैं?
उत्तर:
नहीं, चूँकि अतः बड़ी बूँद का अन्तिम वेग अधिक होता है।

लघुत्तरात्मक प्रश्न:

प्रश्न 1. 
जब आप बालू पर खड़े होते हैं तो आपके पैर अधिक गहराई तक इसमें धँस जाते हैं लेकिन जब आप लेट जाते हैं तो आपका शरीर बालू में कम धँसता है, क्यों?
उत्तर:
खड़े होने की स्थिति में क्षेत्रफल कम होता है लेकिन जब आप लेट जाते हैं तो क्षेत्रफल अधिक होता है। जबकि दोनों स्थितियों में भार बल समान है। अतः खड़े होने की स्थिति की तुलना में लेटने की स्थिति में
दाब P = (F/A) कम होने के कारण शरीर कम धँसता है।

प्रश्न 2. 
भारी वाहनों के पहियों के टायर अधिक चौड़े क्यों बनाये जाते हैं?
उत्तर:
भारी वाहनों के पहियों के टायर चौड़े होने से (क्षेत्रफल (A) का मान अधिक है) सड़क अथवा जमीन पर लगने वाला दाब (P = F/ A) कम हो जाता है क्योंकि वाहन का भार अधिक क्षेत्रफल पर लगता है। इसलिये वाहन के पहिये सड़क पर धँसने से बच जाते हैं।

प्रश्न 3. 
चाय की केतली के ढक्कन में सूराख होता है, क्यों?
उत्तर:
चाय की केतली के ढक्कन में सूराख न होने पर चाय से भरी केतली के भीतर का दाब वायुमण्डल के दाब से कम होगा। स्पष्ट है, केतली को टेढ़ा करने पर उसकी टोंटी से चाय सरलता से नहीं निकलेगी क्योंकि बाहर का दाब केतली के अन्दर के दाब से अधिक होगा।

प्रश्न 4. 
पास-पास लटकी दो हल्की गेंदों के बीच फूँक मारने. पर गेंदें एक-दूसरे की ओर आकर्षित हो जाती हैं, क्यों?
उत्तर:
फूँक मारने पर उनके बीच वायु वेग बढ़ जाता है इसके कारण दाब कम हो जाता है।

प्रश्न 5. 
सन्तुलित भौतिक तुला के एक पलड़े के नीचे तेजी से हवा चलाने पर भौतिक तुला के सन्तुलन पर क्या प्रभाव पड़ेगा?
उत्तर:
पलड़े के नीचे वायु वेग बढ़ने के कारण दाब कम हो जायेगा। अतः पलड़ा कुछ नीचे झुक जायेगा।

प्रश्न 6. 
हिमखण्ड जल पर क्यों तैरता है?
उत्तर:
हिमखण्ड का घनत्व जल के घनत्व से कम होता है, जिससे हिमखण्ड के आयतन के बराबर जल का उत्क्षेप बल हिमखण्ड के भार से अधिक हो जाता है और हिमखण्ड जल पर तैरता रहता है। तैरते समय हिमखण्ड का केवल उतना आयतन ही जल में डूबता है, जितने आयतन के द्वारा हटाये गये जल का भार हिमखण्ड के भार के बराबर होता है।

प्रश्न 7. 
एक पात्र में ग्लिसरीन है और दूसरे पात्र में जल है। दोनों को तेजी से हिला कर मेज पर रख दिया जाता है। किस पात्र का द्रव पहले विरामावस्था में आ जायेगा और क्यों?
उत्तर:
ग्लिसरीन पहले विरामावस्था में आ जायेगी चूँकि ग्लिसरीन की श्यानता जल की अपेक्षा अधिक होती है।

प्रश्न 8. 
नदी के किनारे जल का वेग कम तथा बीच में अधिक होता है, क्यों?
उत्तर:
स्थिर पृष्ठ से दूर जाने पर जल परतों का वेग बढ़ता है। 

प्रश्न 9. 
क्या वर्षा की गिरती बूँदों का वेग लगातार बढ़ता जाता है? क्या बड़ी व छोटी बूँदें पृथ्वी पर एक ही वेग से पहुँचती हैं? 
उत्तर:
वर्षा की बूँदें वायु की श्यानता के कारण सीमान्तं वेग ( नियत वेग) से नीचे गिरती हैं, अतः उनका वेग लगातार बढ़ता नहीं है चूँकि सीमान्त वेग V1 α R2 अतः बड़ी बूँद छोटी बूँद की तुलना में अधिक वेग से पहुँचेगी।

प्रश्न 10. 
जल का घनत्व वायु के घनत्व से अधिक है फिर भी जल की छोटी बूँदों से युक्त बादल गिरता नहीं है बल्कि आकाश में तैरता रहता है। क्यों?
उत्तर:
जल की छोटी बूँदों से युक्त बादल वायु की श्यानता के कारण नीचे की ओर सीमान्त चाल प्राप्त कर लेता है। यह चाल बूंदों की त्रिज्या, जो बहुत छोटी है, के वर्ग के अनुक्रमानुपाती होती है, इसलिये बूँदों से युक्त बादल की चाल इतनी कम होती है कि ये वायु में तैरते प्रतीत होते हैं।

प्रश्न 11. 
धारा रेखीय प्रवाह किसे कहते हैं?
उत्तर:
जब कोई द्रव इस प्रकार बहता है कि किसी एक ही बिन्दु में से होकर गुजरने वाले द्रव के सभी कण एक ही मार्ग पर चलते हैं तो द्रव के प्रवाह को 'धारा रेखीय प्रवाह' कहते हैं तथा उस मार्ग को 'धारा रेखा' कहते हैं। धारा रेखा के किसी भी बिन्दु पर खींची गई स्पर्श रेखा उस बिन्दु पर द्रव के वेग की दिशा को प्रदर्शित करती है।

प्रश्न 12. 
विक्षुब्ध प्रवाह की परिभाषा लिखिए।
उत्तर:
विक्षुब्ध प्रवाह जब किसी तरल के प्रवाह का वेग क्रांतिक वेग से अधिक होता है तब तरल प्रवाह में कणों की गति व्यवस्थित नहीं रहकर अनियमित टेढ़ी-मेढ़ी हो जाती है एवं तरल के अंदर भंवर धाराएँ उत्पन्न हो जाती हैं। तरल के इस प्रकार के प्रवाह को 'विक्षुब्ध प्रवाह' कहते हैं।

प्रश्न 13. 
धारा रेखीय प्रवाह तथा विक्षुब्ध प्रवाह में अंतर बताइये।
उत्तर:

धारा रेखीय प्रवाह	विक्षुब्ध प्रवाह
1. यह द्रव का व्यवस्थित और नियमित रूप से प्रवाह है।	यह द्रव का अव्यवस्थित व अनियमित प्रवाह है।
2. धारा रेखीय प्रवाह में द्रव का वेग क्रान्तिक वेग से कम होता है।	इस प्रवाह में द्रव का वेग क्रान्तिक वेग से अधिक होता है।
3. किसी बिन्दु से गुजरने वाले कणों के वेग की दिशा नियत रहती है।	इस प्रवाह में किसी बिन्दु से गुजरने वाले कणों के वेग की दिशा परिवर्तित होती रहती है।
4. इस प्रवाह में द्रव के अन्दर भंवर धाराएँ उत्पत्र नहीं होती हैं।	इस प्रवाह में द्रव के अंदर भंवर धाराएँ उत्पन्र होती हैं।

प्रश्न 14. 
क्रांतिक वेग की परिभाषा दीजिये।
उत्तर:
क्रांतिक वेग- किसी तरल के प्रवाह का वह वेग है, जिससे कम वेग पर तरल प्रवाह धारा रेखीय तथा जिससे अधिक वेग पर तरल प्रवाह विक्षुब्ध हो जाता है, 'क्रांतिक वेग' कहलाता है।
क्रांतिक वेग तरल के श्यानता गुणांक (n) के समानुपाती, घनत्व (p) के व्युत्क्रमानुपाती एवं नली के व्यास (D) के व्युत्क्रमानुपाती होता है।
अतः
\(\begin{aligned} \mathrm{V}_{\mathrm{C}} & \propto \frac{\eta}{\rho D} \\ \therefore \mathrm{v}_{\mathrm{C}} & =\frac{\mathrm{R \eta}}{\rho \mathrm{D}} \end{aligned}\)
हम जहाँ R = 2000 रेनॉल्ड्स संख्या है।

प्रश्न 15. 
आदर्श द्रव के धारा रेखीय प्रवाह में कौन-कौन-सी ऊर्जायें होती हैं? संक्षेप में समझाइये।
उत्तर:
आदर्श द्रव के धारा रेखीय प्रवाह में तीन प्रकार की ऊर्जायें होती हैं
(i) दाब ऊर्जा (Pressure Energy ): यदि किसी द्रव के 4 क्षेत्रफल पर P दाब पड़ रहा हो और यह द्रव इस दाब के कारण l दूरी चले
तो
द्रव की दाब ऊर्जा = किया गया कार्य = बल x दूरी
= दाब x क्षेत्रफल x दूरी = P x A x l
द्रव का आयतन = क्षेत्रफल x दूरी = A x l
∴ द्रव के एकांक आयतन की दाब ऊर्जा \(=\frac{\mathbf{P} \times \mathbf{A} \times l}{\mathbf{A} \times l}=\mathbf{P}\)

(ii) गतिज ऊर्जा (KE.) यदि m द्रव्यमान व V आयतन का द्रव, v वेग से बह रहा हो तो उसकी गतिज ऊर्जा 1/2 mv² होगी।
∴ द्रव के एकांक आयतन की दाब ऊर्जा imm
\(=\frac{1}{2} \frac{m}{\mathrm{~V}} \cdot v^2=\frac{1}{2} \rho \times v^2\)
जहाँ पर द्रव का घनत्व है

(iii) स्थितिज ऊर्जा (Potential Energy ): यदि m द्रव्यमान का द्रव्य पृथ्वी तल से ऊँचाई पर हो तो उसकी स्थितिज ऊर्जा mgh होगी।
∴ द्रव के एकांक आयतन की स्थितिज ऊर्जा = \(\frac{m}{\mathrm{~V}} g h=\rho \mathrm{g} h .\)

प्रश्न 16. 
चक्रण गति करती हुई गेंद के पथ में परिवर्तन का कारण समझाइये।
उत्तर:
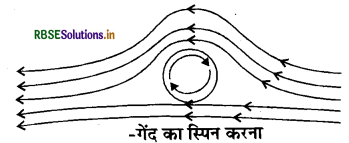
चित्रानुसार जब क्रिकेट की गेंद स्पिन करती हुई हवा में फेंकी जाती है तब गेंद के घूर्णन के साथ वायु परत भी घूमने लगती है। इस कारण गेंद के एक ओर वायु का परिणामी वेग बढ़ जाता है, जबकि दूसरी ओर परिणामी वेग कम हो जाता है।
बरनूली के प्रमेय के अनुसार जहाँ वेग अधिक होगा वहाँ दाब कम होगा। गेंद के दोनों ओर उत्पन्न दाबान्तर के कारण गेंद के एक ओर बल लगेगा जिससे गेंद स्विंग कर जाएगी। चक्रण करती हुई गेंद पर इस प्रकार के प्रभाव को मेगनस प्रभाव कहते हैं।

प्रश्न 17. 
धमनियों में बरनूली सिद्धान्त से रक्त के प्रवाह को समझने में किस प्रकार सहायता मिलती है?
उत्तर:
धमनी की भीतरी दीवार पर प्लाक (Plaque) का जमाव होने के कारण धमनी भीतर से संकीर्ण हो जाती है। इन संकरी धमनियों से रक्त प्रवाहित कराने के लिए हृदय की गतिविधि पर अधिक बोझ पड़ जाता है। इस क्षेत्र में रक्त के प्रवाह की चाल बढ़ जाती है और भीतरी दाब घट जाता है तथा बाह्य दाब के कारण धमनी दब जाती है। हृदय इस धमनी को खोलने के लिये रक्त को धक्का देता है। जैसे ही रक्त इसे खोलकर बाहर की ओर तीव्र गति से प्रवाहित होता है, आंतरिक दाब पुनः गिर जाता है और धमनी पुनः दब जाती है, इससे हार्ट अटैक हो सकता है

प्रश्न 18. 
विस्कासिता किसे कहते हैं?
उत्तर:
बहते हुए द्रव में वेग ग्रेडिएन्ट या वेग प्रवणता होती है। जिससे ऊपर की परत नीचे की परत से अधिक वेग से प्रवाहित होती है। इस प्रकार उत्तरोत्तर परतों में आपेक्षिक वेग होता है। जिस प्रकार दो आपेक्षिक वेग से चलने वाले धरातलों के बीच घर्षण बल कार्य करता है, उसी प्रकार द्रव की उत्तरोत्तर परतों में आपेक्षिक वेग होने के कारण एक प्रकार का घर्षण होता है। इसी कारण अधिक वेग से चलने वाली परत पर धीरे चलने वाली परत रुकावट डालती है। इस रुकावट को जीत कर प्रवाह कायम रखने के लिए ऊर्जा की आवश्यकता होती है। रुकावट डालने वाले बलों को विस्कासिता बल और इस गुण को विस्कासिता कहते हैं।

प्रश्न 19. 
विस्कासिता गुणांक की विमा क्या है?
उत्तर:
हम जानते हैं:
F = -nA dv/dx
यहाँ समानुपात का स्थिरांक है। इसे विस्कासिता गुणांक कहते है। इसका मान द्रव की प्रकृति पर निर्भर करता है। इसकी विमा के लिये

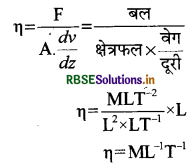
स. ग.स. पद्धति में विस्कासिता गुणांक का मात्रक ग्राम प्रति सेमी. प्रति सेकण्ड है, इसे पॉइज (Poise) भी कहा जा सकता है। 

प्रश्न 20. 
विस्कासिता के अनुप्रयोग लिखिये।
उत्तर:
विस्कासिता के अनुप्रयोग निम्नलिखित हैं:

1.  मशीनों में स्नेहक तेल देना आवश्यक है। किसी भी स्नेहक तेल को चुनते समय उसके विस्कासिता गुणांक का ध्यान रखना पड़ता है, साथ ही साथ यह भी देखना पड़ता है कि ताप वृद्धि से उसमें न्यूनतम परिवर्तन हो । अलग-अलग मशीनों में, ऋतु के अनुसार अलग-अलग स्नेहक तेल देना होता है। साइकिल और मोटर में दिये जाने वाले स्नेहक तेल भिन्न होते हैं।
2.  किसी वेग से चलने वाली वस्तु में मन्दन पैदा करने के लिए उसके वेग को एकसमान करने के लिये, विस्कासिता गुण का उपयोग होता है।
3. विस्कासिता गुणांक के मान से अणुभार भी निकाला जाता है, साथ ही जटिल यौगिकों की संरचना ज्ञात करने में भी इसका उपयोग होता है।

प्रश्न 21. 
स्टोक का नियम क्या है? इसके सूत्र के अनुप्रयोग लिखिए।
उत्तर:
उत्तर-स्टोक का नियम-इस नियम के अनुसार r त्रिज्या का गोला, जो श्यानत η के तरल में, v वेग से गतिमान है, द्रव की श्यानता के कारण एक श्यानाकर्षण बल \(\overrightarrow{\mathrm{F}}\) अनुभव करता है जो \(\overrightarrow{\mathrm{F}}\) = -6πηrv द्वारा व्यक्त किया जा सकता है।

1. जब वर्षा की बूँदें अपने भार के कारण नीचे गिरती हैं तब वायु के श्यान बल के कारण अन्ततः बूँदें नियत अन्तिम वेग से नीचे गिरने लगती हैं। बूँदों का अन्तिम वेग बूँदों की त्रिज्या पर निर्भर करता है; क्योंकि बूंदों की त्रिज्या बहुत छोटी होती है, अतः यह वेग भी बहुत कम होता है।
2. जब कोई छाताधारी पैराशूट से नीचे गिरता है तब उसका प्रारम्भ में वेग तेजी से बढ़ता है, उसके बाद वायु में श्यान बल के कारण नियत होकर अन्तिम वेग प्राप्त कर लेता है।
3. जब जल की वाष्प धूल कणों पर संघनित होकर बादल बनाती है तब प्रारम्भ में बूंदें बहुत छोटी होती हैं। इस कारण इनका वेग इतना कम होता है कि ये आकाश में तैरती हुई प्रतीत होती हैं।
4. इलेक्ट्रॉन आवेश का मान ज्ञात करने के लिए मिलिकन तेल- बूँद प्रयोग में अन्तिम वेग ज्ञात करने के लिए स्टोक्स सूत्र का प्रयोग किया जाता है।

प्रश्न 22. 
सिद्ध कीजिये कि R त्रिज्या की एक बड़ी बूँद की r त्रिज्या की n छोटी-छोटी बूँदों में विभक्त करने के लिये आवश्यक ऊर्जा का मान 4πT(r²n - R²) है, जहाँ T पृष्ठ तनाव है।
उत्तर:
पृष्ठीय क्षेत्रफल में वृद्धि 
∆A = n x 4πr² - 4πR²
= 4πr² - 4πR²
∴ आवश्यक ऊर्जा  W = T x ∆A
= T(4πr² - 4πR²)
= 4πT(r² - R²)

प्रश्न 23. 
काँच की छड़ के सिरे को उच्च ताप पर गर्म करने पर सिरा गोल क्यों हो जाता है?
उत्तर:
जब काँच को गर्म करते हैं तो वह पिघलकर द्रव बन जाता है। यह द्रव का पृष्ठ कम-से-कम क्षेत्रफल घेरने का प्रयत्न करता है। हम जानते हैं कि दिये हुए आयतन के लिये गोले के पृष्ठ का क्षेत्रफल सबसे कम होता है। अतः पिघला हुआ काँच गोले का रूप लेने का प्रयत्न करता है जिससे कि नली के किनारे गोल हो जाते हैं।

प्रश्न 24. 
अपर्याप्त लम्बाई की केशनली में से जल बाहर नहीं फैलता, क्यों?
उत्तर:
एक अपर्याप्त लम्बाई की केशनली का एक सिरा द्रव में डुबोते हैं तब द्रव नली में उसके ऊपरी सिरे तक द्रव चढ़ जाता है और ऊपरी सिरे पर एक ऐसी त्रिज्या की बूंद में बदल जाता है जिसका आंतरिक दाब और नली में द्रव स्तम्भ का परिणामी दाब नली के बाहरी द्रव की सतह पर लगने वाले दाब के बराबर हो जाता है। जिससे नली के ऊपरी सिरे से नली के अपर्याप्त लम्बाई का होते हुए भी द्रव बाहर नहीं निकलता है।

प्रश्न 25. 
पृष्ठ तनाव को प्रभावित करने वाले कारक लिखिए। 
उत्तर:
द्रव का पृष्ठ तनाव कई कारकों से प्रभावित होता है। कुछ उदाहरण नीचे दिये जा रहे हैं

1.  ताप का प्रभाव - ताप बढ़ाने पर द्रव का पृष्ठ तनाव घट जाता है। एक निश्चित ताप (क्रांतिक ताप) पर पृष्ठ तनाव का मान शून्य हो जाता है।
2. विलेय का प्रभाव - यदि विलेयक बहुत घुलनशील (Soluble) है तो द्रव का पृष्ठ तनाव बढ़ जाता है, जैसे- जल में नमक डालने पर जल का पृष्ठ तनाव बढ़ जाता है। यदि विलेयक कम घुलनशील है तो पृष्ठ तनाव घट जाता है, जैसे- साबुन या फिनोल डालने पर जल का पृष्ठ तनाव घट जाता है।
3. संदूषण का प्रभाव- यदि जल की सतह पर धूल, कोई चिकनाई ( ग्रीज या तेल) हो तो इससे जल का पृष्ठ तनाव घट जाता है। 

प्रश्न 26. 
साबुन मिला जल शुद्ध जल की अपेक्षा कपड़ों की अच्छी धुलाई करता है, समझाइये।
उत्तर:
डिटर्जेंट व साबुन के घोल से कपड़ों का स्वच्छ होना- जब कपड़ों पर ग्रीज व तेल. के. धब्बे लगे हों तो वे पानी से साफ नहीं होते हैं। इसका कारण है कि चिकने कपड़े पर पानी फैलकर उसे गीला नहीं करता, वरन् उसके ऊपर पारे की तरह गोल बूंदें बनाता है। जब पानी में साबुन का घोल या डिटर्जेन्ट पाउडर मिलाया जाता है तो उसका पृष्ठ तनाव कम हो जाता है। इससे घोल कपड़े को गीला कर देता है और ग्रीज और कपड़े के बीच एक परत बनाकर ग्रीज को कपड़े से पृथक् कर देता है। 

प्रश्न 27. 
जल की छोटी बूंदें फुहारने (Spraying) से ठंडक क्यों उत्पन्न होती है?
उत्तर:
छोटी बूंदों में फुहारने पर पृष्ठ क्षेत्रफल बढ़ता है। अतः पृष्ठ ऊर्जा में वृद्धि होती है लेकिन इस कार्य में आंतरिक ऊर्जा में कमी आती है (क्योंकि कुल ऊर्जा संरक्षित रहती है) अतः ताप गिरने से ठण्डक उत्पन्न होती है, जिसे हम दैनिक जीवन में अनुभव करते हैं। पानी के फव्वारे के नीचे नहाने में अधिक ठण्डक का अनुभव होना इसी का उदाहरण है।

प्रश्न 28. 
केशनली का व्यास कम होने पर केशनली में दव अधिक ऊँचाई तक चढ़ता है, इसका कारण समझाइये। 
उत्तर:
केशिकत्व के जूरिन नियम से r त्रिज्या के केशनली में द्रव स्तम्भ की ऊँचाई h α 1/r होता है, अतः नली का व्यास अर्थात् त्रिज्या r का मान कम होने पर h का मान अधिक होगा अर्थात् द्रव अधिक ऊँचाई तक चढ़ेगा।

प्रश्न 29. 
यदि किसी द्रव व ठोस के बीच स्पर्श कोण का मान (अ) 90° से कम है (ब) 90° से अधिक है तो क्या द्रव ठोस को भिगोयेगा? उस ठोस से बनी केशनली में द्रव का तल कैसा होगा? क्या वह द्रव केशनली में ऊपर चढ़ेगा?
उत्तर:
(अ) भिगोयेगा, अवतल, चढ़ेगा।
(ब) नहीं भिगोयेगा, उत्तल, नहीं चढ़ेगा बल्कि नली के बाहर द्रव तल की तुलना में नीचे उतरेगा।

प्रश्न 30. 
समुद्र की लहरों को शान्त करने के लिये उन पर तेल डाला जाता है, क्यों?
उत्तर:
तेल डाल देने पर तेज हवा तेल को जल के पृष्ठ पर हवा की दिशा में दूर तक फैला देती है। बिना तेल वाले जल का पृष्ठ तनाव तेल वाले जल से अधिक होता है। अतः बिना तेल वाला जल तेल वाले जल की वायु की विपरीत दिशा में खींचता है, जिससे समुद्र की लहरें शान्त हो जाती हैं।

प्रश्न 31. 
भारहीनता की स्थिति में यदि किसी केशनली को जल में डुबोया जाये तो उसमें जल का चढ़ना सामान्य अवस्था में जल के चढ़ने से किस प्रकार भिन्न होगा?
उत्तर:
सामान्य स्थिति में पृष्ठ तनाव का बल ( जिसके कारण जल केशनली में चढ़ता है) केशनली में चढ़े जल-स्तम्भ के भार के बराबर हो जाता है तो जल का चढ़ना रुक जाता है। भारहीनता की स्थिति में चढ़ने वाले जलस्तम्भ का प्रभावी भार शून्य होगा। अतः जल केशनली के दूसरे सिरे तक पहुँच जायेगा चाहे केशनली कितनी ही लम्बी क्यों न हो।

आंकिक प्रश्न:

प्रश्न 1. 
एक व्यक्ति का द्रव्यमान 30 किग्रा. है तथा उसके पैर के तलवे का क्षेत्रफल 0.01 मीटर है। यदि g-10 मीटर / सेकण्ड' हो, तो व्यक्ति द्वारा फर्श पर लगने वाले दाब की गणना कीजिये। 
(i) जब व्यक्ति एक पैर पर खड़ा हो, पैरों पर खड़ा हो।
(ii) जब व्यक्ति दोनों
उत्तर:
(i) दिया है: तलवे का क्षेत्रफल A = 0.01 मीटर
फर्श पर आरोपित बल = व्यक्ति का भार
= mg = 30 किग्रा. x 10 मी./से. ² 
= 300 न्यूटन
फर्श पर लगने वाला दाब P =
P  \(=\frac{300}{0.01}\) = 3 x 10⁴ न्यूटन / मीटर

(ii) दोनों पैरों पर खड़े मनुष्य के दोनों तलवों का क्षेत्रफल
A = 2 × 0.01 = 0.02 मीटर
फर्श पर आरोपित बल = व्यक्ति का भार
= 300 न्यूटन
फर्श पर लगने वाला दाब P = 

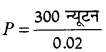
= 1.5 x 10⁴ न्यूटन / मीटर

प्रश्न 2. 
एक आयताकार टंकी की लम्बाई 4.0 मीटर तथा चौड़ाई 3.0 मीटर है। इसमें 2.5 मीटर की ऊँचाई तक पानी भरा हुआ है। टंकी की तली पर पानी द्वारा सम्पूर्ण बल एवं पानी का दाब ज्ञात कीजिये। ( पानी का घनत्व 1000 किग्रा./ मीटर तथा g-10 मीटर / सेकण्ड)
उत्तर:
टंकी में भरे हुये पानी का आयतन
= लम्बाई × चौड़ाई x ऊँचाई
= 30.0 मीटर
(4.0 मीटर ) x ( 3.0 मीटर ) x (2.5 मीटर)
∴ पानी का घनत्व = 10³ किग्रा./मी.³ 
∴ पानी का द्रव्यमान M आयतन घनत्व
= (30.0 मीटर³) x ( 1000 किग्रा./मीटर) 
= 30000 किग्रा. = 3 x 10⁴ किग्रा.
टंकी में पानी का भार द्रव्यमान गुरुत्वीय त्वरण (g)
= 3 x 10⁴ x 10
= 3 x 10⁵ न्यूटन
∴ टंकी की तली पर कुल बल F =  पानी का भार 
= 3 x 10⁵ न्यूटन
तली का क्षेत्रफल A लम्बाई × चौड़ाई
= ( 4.0 मीटर ) x ( 3.0 मीटर)
= 12.0 मीटर²
तली पर पानी का दाब =
\(=\frac{3 \times 10^5}{12}\)
= 2.5 x 10⁴ न्यूटन/मीटर

प्रश्न 3. 
यदि पृथ्वी पर वायुमण्डलीय दाब पारे के 75.0 सेमी. स्तम्भ के बराबर हो तो 250 मीटर ऊँची पर्वत की चोटी पर दाबमापी की माप क्या होगी ? (वायु का औसत घनत्व 1.29 किग्रा./मी.³) 
उत्तर:
माना मीनार की चोटी पर दाब का मान पारा स्तम्भ की ऊँचाई के मान के बराबर है। अतः पर्वत की तली पर वायुमण्डलीय दाब का मान 250 मीटर ऊँचे वायु स्तम्भ के दाब तथा h पारा स्तम्भ के दाब के योग के बराबर होगा।
0.75 × 13.6 × 10³ x g = 1.29 x g x 250 + h × 13.6 x 10³ x g
⇒ 0.75 × 13.6 × 10³ = 1.29 × 250 + h × 13.6 × 10³
⇒ 0.75 × 13.6 × 10³ - 1.29 × 250 = h × 13.6 × 10³
\(\Rightarrow \frac{0.75 \times 13.6 \times 10^3}{13.6 \times 10^3}-\frac{1.29 \times 250}{13.6 \times 10^3}=h\)
⇒ 0.75 - 0.02371 = h
⇒ 0.72629 = h
अत: h = 0.72629 मीटर = 72.63 सेमी.

प्रश्न 4. 
एक वस्तु जिसका आयतन 100 सेमी. है, को पानी पूर्णतः डुबा दिया जाता है। वस्तु पर उत्प्लावन बल ज्ञात कीजिये।
उत्तर:
वस्तु पर उत्प्लावन बल-वस्तु द्वारा हटाये गये समान आयतन
के पानी का भार
= V x p x g
= 200 सेमी.3 x (1 ग्राम / सेमी³)  x 9.8 मी./से.²
= 200 ग्राम x 98 मी./से.²
= 200 × 10^-3 Kg × 9.8 मी./से.²
= 1.96 न्यूटन

प्रश्न 5. 
सीमेण्ट की 1 मीटर मोटी दीवार 105 न्यूटन/मीटर2 का दाब सहन कर सकती है। 200 मीटर गहरे पानी के बाँध के आधार पर दीवार की मोटाई कितनी होनी चाहिए?
(जल का घनत्न = 10 किग्रा./ मी.' तथा गुरुत्वीय त्वरण = 9.8 मी./से.²)
उत्तर: 
बाँध के निकट की दीवार पर दाब (P) का मान = hpg
= 200 × 10 x 9.8
= 19.6 x 10⁵ न्यूटन / मी.²
चूँकि 10⁵ न्यूटन / मीटर² का दाब सहन करने के लिये दीवार की
आवश्यक मोटाई = 1 मीटर
∴ 19.6 x 10⁵ न्यूटन / मीटर का दाब सहन करने के लिये दीवार की वांछित मोटाई
= (1/10⁵) x 19.6 × 10⁵
= 19.6 मीटर

प्रश्न 6. 
दो मीटर लम्बी एक नली में 0.8 × 10³ किग्रा./मी.³ घनत्व वाला एक द्रव भर कर नली को झुकाकर एक दीवार के सहारे टिका दिया गया है जिससे द्रव की ऊपरी सतह की नली की तली से ऊर्ध्वाधर ऊँचाई 1.8 मीटर रह जाती है। यदि वायुमण्डलीय दाब 1.01 x 10⁵ न्यूटन / मी.' हो तो नली की तली पर कुल दाब ज्ञात कीजिये। 
उत्तर:
द्रव के ऊपरी तल की ऊर्ध्वाधर ऊँचाई h = 1.8 मीटर
द्रव का घनत्व = 0.8 × 10 किग्रा./मी.³ 
नली की तली पर कुल दाब
= वायुमण्डलीय दाब + द्रव स्तम्भ का दाब

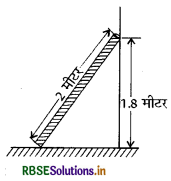
p' = Pa + hpg
= (1.01 × 10) + 1.8 × 0.8 × 10³ × 9.8
= 1.01 × 10⁵ + 0.14
= 1.15 x 10⁵ न्यूटन / मी.²

प्रश्न 7. 
एक हाइड्रोलिक लिफ्ट में 800 किग्रा. भार के पत्थर को उठाने के लिये कितने भार की आवश्यकता होगी? दिया है दोनों पिस्टनों की अनुप्रस्थ काट के क्षेत्रफलों का अनुपात 4 हो तो क्या मशीन द्वारा किया गया कार्य मशीन पर किये गये कार्य से अधिक है? समझाइये।
उत्तर:
पास्कल के नियम के आधार पर
हाइड्रोलिक लिफ्ट के सिद्धान्त से,

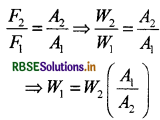
यहाँ दिया गया है W₂ = 800 किग्रा. भार
A2/A1 = 4 अर्थात् A1/A2 = 1/4
W1 = ?
इसलिये आवश्यक भार W1 = 800 x 1/4 = 200 किग्रा. भार
परन्तु मशीन का यांत्रिक लाभ
\(\frac{W_2}{W_1}=\frac{A_2}{A_1}=4\)
अर्थात्
W2/W1 > 1 ⇒ W2 > W1
अर्थात् मशीन द्वारा किया गया कार्य > मशीन पर किया गया कार्य

प्रश्न 8. 
किसी खाली नाव का भार 500 किग्रा. है। जब यह तैरती है तो इसका 1/3 भाग पानी में डूबता है। ज्ञात कीजिये कि नाव पर अधिक से अधिक कितना भार लादा जा सकता है?
उत्तर:
माना नाव का आयतन v मी³ तथा जल का घनत्व p है।
चूँकि खाली नाव का (1/3v) भाग जल में डूबता है।
अतः नाव के डूबे भाग द्वारा हटाये जल का भार = v/3 x p x g
तैरने के सिद्धान्त से
नाव का भार = नाव द्वारा हटाये गये पानी का भार
⇒ 500 × g = Vpg/3
⇒ 1500g = Vpg .......... (1)
माना नाव पर W किग्रा अधिक से अधिक भार लादा जा सकता है तब नाव द्वारा हटाये गये जल का भार नाव के कुल भार के बराबर होगा।
अर्थात् हटाये गये जल का आयतन नाव के कुल आयतन के बराबर होगा।
अत: (W + 500) g = Vpg ............ (2)
समी. (1) तथा (2) की तुलना करने पर
(W + 500 ) g = 1500g
∴ W = 1500 - 500 = 1000 किग्रा.
अतः नाव पर अधिक से अधिक 1000 किग्रा भार लादा जा सकता है।

प्रश्न 9. 
धातु का 200 ग्राम का एक टुकड़ा जब शुद्ध जल में तौला जाता है, तब इसका भार 160 ग्राम प्राप्त होता है। धातु का आपेक्षिक घनत्व व टुकड़े का आयतन ज्ञात कीजिये।
उत्तर:
धातु का आपेक्षिक घनत्व = 
\(=\frac{200}{200-160}=\frac{200}{40}\)
∴ धातु का घनत्व =  धातु का आपेक्षिक घनत्व x जल का घनत्व
= 5 x 1 = 5 ग्राम / सेमी³
∴ द्रव्यमान =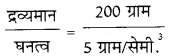
= 40 सेमी3

प्रश्न 10. 
रक्त 0.1 सेमी. लम्बी तथा 2 × 10⁴ सेमी. त्रिज्या की नली में बह रहा है। इस नली के खून का श्यानता गुणांक 0.5 × 10³ किग्रा. मीटर^-1/सेकण्ड^-1है। रक्त प्रवाह की दर ज्ञात कीजिये।
उत्तर:
दिया है
l = 0.1 सेमी = -3 मीटर, त्रिज्या r = 2 x 10^-4 सेमी.
r = 2 x 10^-6 मीटर
दाबान्तर p= 20 मिमी पारा = 20 x 10^-3 मी. पारा
= 20 × 10^-3 × (13.6 × 10³) x 9.8 न्यूटन/मी²
n = 0.5 x -3 किग्रा./मी. से.
अतः नली में रक्त प्रवाह की दर
\(Q=\frac{\pi \operatorname{Pr}^4}{8 \eta l}\)
मान रखने पर
\(Q=\frac{3.14 \times\left(20 \times 10^{-3} \times 13.6 \times 10^3 \times 9.8\right) \times\left(2 \times 10^{-6}\right)^4}{8 \times 0.5 \times 10^{-3} \times 10^{-3}} \) मी³/से.
Q = 3.42 x 10^-15 मी³/से.

प्रश्न 11.
4 मिमी. त्रिज्या की काँच की एक गोली समुद्र में छोड़े जाने पर 52.3 मी./से. के वेग से गति आरम्भ करती है। यदि समुद्री जल घनत्व 1.015 × 10³ किग्रा./ मी.' हो तो गोली पर कार्य करने वाले श्यान बल का मान क्या होगा? ज्ञात कीजिये। समुद्र के पानी का श्यानता गुणांक = 0.01 प्वॉइज
उत्तर:
दिया है = 4 मिमी. = 4 x 10^-3 मी. 
v = 523 मी./से.
n = 0.01 प्वॉइज = 0.01/10 किग्रा./मी. से
n = 10^-3 किग्रा./मी. से
इसलिये श्यान बल F = 6πnrv
मान रखने पर
F = 6 x 3.14 × 10³ × 4 x 10³ x 52.3 = 9.84 × 10^-4 न्यूटन

प्रश्न 12. 
4 x 10⁴ न्यूटन / मीटर दाब का जल 2 मीटर / सेकण्ड के वेग से 0.02 मीटर² अनुप्रस्थ परिच्छेद के पाइप से प्रवाहित होता है जिसका अनुप्रस्थ परिच्छेद घटकर 0.01 मीटर' हो जाता है। पाइप के छोटे अनुप्रस्थ में कितना दाब है?
उत्तर:
दिया गया है:
P = 4 x 10⁴ न्यूटन / मी.²
V₁ = 2 मीटर/सेकण्ड
A₁ = 0.02 मीटर²
A₂ = 0.01 मीटर²
P₂ = ? और v₂ = ?
हम जानते हैं:
A₁v₁ = A₂V₂
\(\mathrm{v}_2=\frac{A_1 v_1}{A_2}\)
या
\(=\frac{0.02 \times 2}{0.01}\)
= 4 मीटर / से.
पाइप क्षैतिज है, इसलिये बरनौली के समीकरण से
p₂ + 1/2pv₂² = p₁ + 1/2pv₁²
मान रखने पर
p₂ + 1/2 x 10³ x (4)² = 4 x 10⁴ + 1/2 x 10³ + (2)²
p₂ + 8 x 10³ = 4 x 10⁴ + 2 x 10³
⇒ p₂ = 4 x 10⁴ + 2 x 10³ - 8 x 10³
= 4 x 10⁴ - 6 x 10³
= 40 x 10³ - 6 x 10³
= (40 - 6) x 10³
p₂ = 34 x 10³
या
P₂ = 3. 4 x 10⁴ न्यूटन/मीटर²
अतः पाइप के छोटे अनुप्रस्थ में दाब 3.4 x 10⁴ न्यूटन/मी² है।

प्रश्न 13. 
क्षैतिज वायुयान पंख के पास से होकर तीव्र वायु इस प्रकार बह रही है कि पंख की ऊपरी सतह पर उसका वेग 120 मीटर/सेकण्ड है तथा निचली सतह पर 90 मीटर / सेकण्ड है। यदि वायु का घनत्व 1.3 किग्रा./ मीटर हो तो पंख के ऊपर और नीचे के मध्य दाबान्तर ज्ञात कीजिये। यदि पंख 10 मीटर लम्बा और औसत चौड़ाई 2 मीटर हो तो इस पर कुल उत्प्लावक बल की गणना कीजिये। 
उत्तर:
वायुयान के नीचे बहने वाली वायु का वेग
v₁ = 90 मीटर/से.
और यहाँ पर दाब P₁ माना है।
पंख के ऊपर बहने वाली वायु का वेग v₂ = 120 मी./से. है और 
इसके कारण दाब माना P₂ है। तब बरनौली प्रमेय से
p₁ + 1/2pv₁² = p₂ + 1/2pv₂²
यहाँ p = वायु का घनत्व है।
⇒ p₁ - p₂ = 1/2pv₂² - pv₁²
⇒ p₁ - p₂ = 1/2p(v₂² - v₁²)
⇒ p₁ - p₂ = 1/2p(v₂ + v₁) (v₂ - v₁)
= 1/2p(120 + 90) (120 - 90)
= 1/2p210 x 30
= 3150 x p
p का मान रखने पर
⇒ (p₁ - p₂) = 3150 x 1.3
(p₁ - p₂) = 4095न्यूटन/मीटर²
(P₁ - P₂) = 4095 न्यूटन / मीटर
अतः पंख के ऊपर और नीचे के मध्य दाबान्तर का मान 4095
न्यूटन/मीटर² होगा।
पंख का क्षेत्रफल = L x B
= 10 x 2 = 20 मीटर²
∴ वायुयान पर कुल उत्प्लावक बल का मान
= 20 x 4095
= 8.19 × 10⁴ न्यूटन

प्रश्न 14. 
एक क्षैतिज पाइप में एक सिरे पर जल का दाब एक वायुमण्डल के दाब के बराबर है। जल का दाब शीर्ष ज्ञात कीजिये। (g = 9.8 मी./से.²)
उत्तर:
माना कि जल का दाब शीर्ष = h मीटर है। 
दाब = 1 x 10⁵ न्यूटन / मी.² 
हम जानते हैं p = hpg
h = p/pg
\(h=\frac{1 \times 10^5}{10^3 \times 10}\)
चूँकि पानी का घनत्व p = 10³ किग्रा./मी.³
\(h=\frac{10^5}{10^4}\)
= 10 मीटर
अतः जल का दाब शीर्ष 10 मीटर है।

प्रश्न 15. 
एक क्षैतिज पाइप में जल के प्रवाह का वेग 10 मीटर / सेकण्ड है। जल का वेग शीर्ष ज्ञात कीजिये। (g = 9.8 मी./से.²)
उत्तर:
यदि पाइप में द्रव का वेग होने पर
वेग शीर्ष = 1/2v²/g
यहाँ पर = 10 मी./से. और g = गुरुत्वीय त्वरण 9.8 मी./से.²
∴ पानी का वेग शीर्ष = 1/2 x (10)²/9.8
\(\frac{100}{19.6}=\frac{1000}{196}=5.102\)
= 5 मी.

प्रश्न 16. 
एक असमान परिच्छेद के पाइप में जल बह रहा है। जिस स्थान पर पाइप की त्रिज्या 1 सेमी. है वहीं जल का वेग 10 सेमी./सेकण्ड है। किसी अन्य स्थान पर जहाँ पाइप की त्रिज्या 2 सेमी. हो, जल का वेग ज्ञात कीजिये।
उत्तर:
दिया गया है
r₁ = 1 सेमी.
V₁ = 10 सेमी./सेकण्ड
r₂ = 2 सेमी.
माना जल का वेग (v₂) = ?
हम जानते हैं
A₁v₁ = A₂V₂
πr₁²v₁ = πr₂²v₂
या
r₁²v₁ = r₂²v₂
मान रखने पर
(1)² x 10 = (2)² x v²
10 = 4v²
⇒ v² = 10/4
= 2.5 सेमी./से.

प्रश्न 17. 
1 सेमी. तथा 2 सेमी. त्रिज्या के दो क्षैतिज पाइप आपस में जुड़े हैं और इनमें पानी बह रहा है। पहले पाइप में पानी का वेग 8 मीटर/सेकण्ड तथा दाब 1 x 10 न्यूटन / मीटर है तो दूसरे पाइप में पानी का वेग और दाब ज्ञात करो।
उत्तर:
दिया गया है:
r₁ = 1 सेमी.
r₂ = 2 सेमी. 
V₁ = 8 मी./सेकण्ड
P = 1 x 10⁵ न्यूटन/मी²
माना दूसरे पाइप में पानी का वेग (v) = ?
माना दूसरे पाइप में पानी का दाब P = ?
सूत्र
A₁V₁ = A₂V₂
या
πr₁²v₁ = πr₂²v₂
या
r₁²v₁ = r₂²v₂
मान रखने पर
(1) × 8 = (2)² x v₂
⇒ v₂ = 8/4
= 2 मी./से.
बरनौली के समीकरण से
p₁ + 1/2p₁v₁² = p₂ + 1/2p₂v₂²
⇒ 1 × 10⁵ + 1/2 × 10³ × (8)² = p₂ + 1/2 × 10³ × (2)²
चूंकि पानी का घनत्व = 10³ किलोग्राम / मी. होता है।
=> 10⁵ + 32 × 10³ = P₂ + 2 × 10³
⇒ 10⁵ + 32 × 10³ - 2 × 10³ = P₂
⇒ 10⁵ + 30 × 10³ = P₂
=> 10⁵ + 0.30 × 10⁵ = P₂
10⁵ (1 + 0.30 ) = P₂
P₂ = 1.30 × 10⁵ न्यूटन/मी.²
अतः दूसरे पाइप में दाब = 1.30 x 10⁵ न्यूटन/मी²

प्रश्न 18. 
किसी टंकी में H मीटर की ऊँचाई तक पानी भरा है। तथा उसमें पेंदे से 1⁄2 ऊँचाई पर एक छेद है। उस छेद में से निकलने वाले पानी का वेग ज्ञात करो तथा वह टंकी से कितनी दूर जमीन पर गिरेगा? 
उत्तर: 
टंकी में पानी H मीटर ऊंचाई तक भरा हुआ है। 
छेद पेंदे से h मी. ऊँचाई पर है।
∴ पानी के धरातल से पृष्ठ तक की ऊँचाई (Hh) मीटर होगी। 
उस छेद में से निकलने वाले पानी का वेग
\(\begin{aligned} & \mathrm{v}=\sqrt{2 g \times(\mathrm{H}-h)} \\ & \mathrm{v}=\sqrt{2 g(\mathrm{H}-h)} \end{aligned}\)
माना टंकी से दूरी x मीटर तथा गिरने का समय t से है।
सूत्र
h = ut + 1/2gt²
h = 0 + 1/2gt²
∴ t² = 2h/g
या
\(t^2=\sqrt{\frac{2 h}{g}}\)
इसी समय में v वेग से पार की गई क्षैतिज दूरी होगी
∴ x = vt
\(\begin{aligned} & =\sqrt{2 g(\mathrm{H}-h)} \times \sqrt{\frac{2 h}{g}} \\ x & =2 \sqrt{h(\mathrm{H}-h)} \end{aligned}\)
अत: वह टंकी से \(2 \sqrt{h(\mathrm{H}-h)}\) दूरी पर जाकर गिरेगा। 

प्रश्न 19. 
असमान बोर के एक क्षैतिज पाइप से 2 सेमी. Hg स्तम्भ वाले दाब के एक बिन्दु पर 40 सेमी./सेकण्ड के वेग से पानी प्रवाहित हो रहा है। उस बिन्दु पर दाब की गणना करो जहां पर पानी के प्रवाह का वेग 60 सेमी./सेकण्ड है।
उत्तर: 
पाइप क्षैतिज है। 
बरनौली समीकरण से
p₁ + 1/2pv₁² = p₂ + 1/2pv₂²
यहाँ पर
P₁ = 2 × 13.6 x 980 = 26656
P₁ = 26656 डाइन/सेमी²
V₁ = 40 सेमी./से.
V₂ = 60 सेमी./से., P₂ = ?
मान रखने पर समी. (1) में
26656 + 1/2 × 1 × (40)² = P₂ + 1/2 × 1 × (60)²
26656 + 800 = P₂ + 1800
P₂ = 25656 डाइन/सेमी² 
hgd = 25656 डाइन / सेमी
पारे के स्तम्भ में बदलने पर
\(\mathrm{h}=\frac{25656}{\mathrm{~d} g}=\frac{25656}{13.6 \times 980}\)
= 1.92 सेमी. पारे के स्तम्भ के समान 

प्रश्न 20. 
पानी के बंद नल में दाबमापी का पाठ्यांक 3.5 x 10⁵ न्यूटन / मी² है। नल के वाल्व को खोल देने पर दाबमापी का पाठ्यांक 3.0 x 10⁵ न्यूटन / मी² रह जाता है। नल में प्रवाहित पानी के वेग की गणना कीजिए।
उत्तर:
बरनौली के प्रमेय से
p₁ + 1/2pv₁² = p₂ + 1/2pv₂²
या
1/2p(v₂² - v₁²) = p₁ - p₂
चूंकि प्रारम्भ में नल बंद है, इसलिए v₁ = 0 इस प्रकार
\(\mathrm{v}_2^2=\frac{2}{\rho}\left(\mathrm{P}_1-\mathrm{P}_2\right)\)
\(=\frac{2}{1 \times 10^3}(3.5-3.0) \times 10^5\)
= 2 × 0.5 × 10² = 100
∴ V₂ = \(\sqrt{100}=\) 10 मी./से. 

प्रश्न 21. 
100 वर्ग सेमी. क्षेत्रफल की एक समतल प्लेट तथा एक बड़ी प्लेट के बीच ग्लिसरीन की 1 मिमी. मोटी तह है। यदि ग्लिसरीन का श्यानता गुणांक 1.0 किग्रा. ( मीटर सेकण्ड ) हो तो प्लेट को 7 सेमी./सेकण्ड के वेग से चलाने के लिए कितना बल चाहिए?
उत्तर:
प्लेट को एक निश्चित वेग से चलाने के लिए आवश्यक बल प्लेट पर कार्यशील विरोधी बल F के बराबर होगा।
सूत्रानुसार

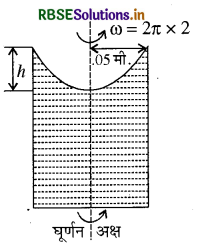
लेकिन यहाँ पर दिया गया है:
1 = 1.0 किग्रा./ ( मीटर - सेकण्ड )
A = 100 सेमी = 10^-2 मीटर^-2
∆v = 7 × 10^-2 मी./से.
तथा ∆x = 1 मिमी. = 10^-3 मीटर
∴ \(h=\frac{0.04 \times 9.86}{19.6}=\frac{0.3944}{19.6}\)
F = 0.7 न्यूटन

प्रश्न 22. 
कोई द्रव एक बेलनाकार पात्र में रखा है जिसे अपने अक्ष के परितः घुमाया जा रहा है। दीवारों के सहारे का द्रव ऊंचा उठ जायेगा। यदि पात्र की त्रिज्या 0.05 मीटर है और घुमाने की गति 2 चक्कर प्रति सेकण्ड है तो पात्र के केन्द्र और पाश्र्व के बीच द्रव की ऊंचाई का अन्तर ज्ञात कीजिये।
उत्तर:
बरनौली की प्रमेय के अनुसार,
P₁ + 1/2pv² = नियतांक।
दीवार के सहारे वेग अधिक है। अतः दाब कम होगा। परन्तु एक ही क्षैतिज तल में दाब समान होना चाहिये। अतः किनारों पर द्रव चढ़ जाता है।

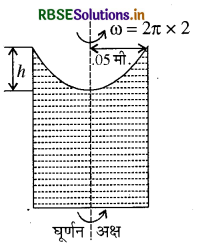
1/2 pv² = pgh
अथवा h = v2/2g
परन्तु
v = rω = 2лnr
v = 2 x л x 2 x 0.05
घूर्णन अक्ष
v = 0.2 मीटर/सेकण्ड
∴  \(h=\frac{(0.2 \pi)^2}{2 \times 9.8}=\frac{0.04 \pi^2}{19.6}\)
लेकिन л² = 9.86 होता है।
∴ \(h=\frac{0.04 \times 9.86}{19.6}=\frac{0.3944}{19.6}\)
h = 0.02 मीटर = 2 सेमी.

प्रश्न 23. 
एक केशनली में जल 10 सेमी. ऊँचाई तक चढ़ता है। यदि जल का पृष्ठ तनाव 73 x 10⁵ न्यूटन / मी. तथा घनत्व 1 x 10³ किग्रा./ मी.' हो तथा g = 9.8 मी./से.² हो तो केशनली की त्रिज्या ज्ञात करो।
उत्तर:
यदि कोई p घनत्व का द्रव त्रिज्या की केशनली में h ऊँचाई तक चढ़ता है, तब
पृष्ठ तनाव T =  hrpg/2  यहाँ g गुरुत्वीय त्वरण है।
यहां
h = 10 सेमी = 0.1 मीटर
T = 73 x 10^-3 न्यूटन / मी.
P = 1 x 10^-3  किलोग्राम / मीटर और
8 = 9.8 मीटर / से² है।
∴ \(73 \times 10^{-3}=\frac{0.1 \times\left(1 \times 10^3\right) \times 9.8 \times r}{2}\)
2 x 73 x 10^-3 = 980r 
\(r=\frac{146 \times 10^{-3}}{980}\)मीटर
= 0.1489 × 10^-3 मीटर
r = 0.1489 × 10^-3 x 10 सेमी.
= 0.1489 × 10^-1 सेमी.
r = 0.015 सेमी. (Round off करने पर)

प्रश्न 24. 
साबुन के घोल की एक आयताकार फिल्म जो 6 सेमी. व 4 सेमी. चौड़ी है, का आकार यदि 8 सेमी. x 5 सेमी. करना हो तो पृष्ठ तनाव के विरुद्ध कितना कार्य करना पड़ेगा, यदि साबुन के घोल का पृष्ठ तनाव 40 × 10^-3 न्यूटन / मी. है?
उत्तर:
दिया गया है:
A = 2 × 6 × 10^-2 × 4 × 10^-2
= 48 × 10^-4 वर्ग मी.
A + ∆A = 2 × 8 × 10^-2 x 5 x 10^-2
= 80 × 10^-4 वर्ग मी.
∆ A = (A + ∆ A) – (A)
= 80 × 10^-4
= 48 × 10^-4
= 32 x 10^-4 वर्ग मी.
हम जानते हैं:
W = T∆A
=40 x 10^-3 x 32 x 10^-4
= 1280 x 10^-7
= 1.2 × 10^-4 जूल

प्रश्न 25. 
दो साबुन के बुलबुले जिनकी त्रिज्यायें क्रमश: 2 सेमी. तथा 3 सेमी. हैं, को नजदीक लाने से सम्पर्क स्थल पर बनी उभयनिष्ठ सतह की वक्रता त्रिज्या कितनी होगी?
उत्तर:
उभयनिष्ठ सतह पर कुल दाब आधिक्य माना 4T/r दोनों बुलबुलों के दाब आधिक्यों 4T/r1 4T/r2 के अंतर के बराबर होगा,
अतः
\(\frac{4 \mathrm{~T}}{r}=\frac{4 \mathrm{~T}}{r_1}-\frac{4 \mathrm{~T}}{r_2}\)
या
\(\begin{aligned} & \frac{1}{r}=\frac{1}{r_1}-\frac{1}{r_2} \\ & \frac{1}{r}=\frac{r_2-r_1}{r_1 r_2} \end{aligned}\)
जहाँ उभयनिष्ठ सतह की वक्रता त्रिज्या है।
अतः
\(r=\frac{2 \times 3}{3-2}=\frac{6}{1}\)
= 6 सेमी.

प्रश्न 26. 
साबुन के बुलबुले के भीतर दाब आधिक्य जल के 0.8 सेमी. स्तम्भ के बराबर है। बुलबुले की त्रिज्या 0.35 सेमी. है। साबुन के घोल का पृष्ठ तनाव ज्ञात कीजिए।
उत्तर: 
दिया गया है:
h = 0.8 सेमी.
= 8 x 10^-3 मीटर
जल का घनत्व
P = 1 x 10³ किग्रा./मी³ तथा
= 0.35 सेमी. 35 × 10^-4 मीटर
जल स्तम्भ का दाब
P = hpg
= 8 × 10^-3 × 1 × 10³ × 9.8
P = 78.4 न्यूटन /मी²
बुलबुले में दाब आधिक्य,
अतः
\(\begin{aligned} T & =\frac{\operatorname{Pr}}{4} \\ T & =\frac{78.4 \times 35 \times 10^{-4}}{4} \\ & =\frac{2744 \times 10^{-4}}{4} \end{aligned}\)
= 686 × 10^-1 न्यूटन / मीटर
= 68.6 x 10^-3 न्यूटन / मी.

गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न:

प्रश्न 1. 
झील की तली की गहराई से आधी गहराई पर स्थित किसी बिन्दु पर दाब झील की तली पर दाब का 2/3 है। झील की गहराई होगी:
(a) 10m
(b) 20m
(c) 60m
(d) 30 m
उत्तर: 
(b) 20m

प्रश्न 2. 
एक दूसरे में मिश्रित न होने वाले दो द्रव्य, जिनके घनत्व p तथा np(n>1) हैं, किसी पात्र में भरे हैं। प्रत्येक द्रव की ऊँचाई h है। लम्बाई L और घनत्व d के किसी बेलन को इस पात्र में रखा जाता है। यह बेलन पात्र में इस प्रकार तैरता है कि इसका अक्ष ऊर्ध्वाधर रहता है तथा इसकी लम्बाई pL(p < 1) सघन द्रव में होती है। घनत्व d का मान है:
(a) {1 + (n+1) p}p
(b) {2 + (n+1) p}p
(c) {2 + (n-1) p}p
(d) {1 + (n-1) p}p
उत्तर: 
(d) {1 + (n-1) p}p

प्रश्न 3. 
पतली चादर से बने एकसमान बेलनाकार कोश (shell) के दोनों सिरे बन्द हैं। उसमें आंशिक रूप से पानी भरा है। यह कोश आधी डूबी अवस्था में पानी में ऊर्ध्वाधर (vertically) तैर रहा है। जिस पदार्थ से कोश निर्मित है उसका घनत्व पानी की तुलना में pc है। सही प्रकथन चुनें:
(a) कोश आधे से अधिक भरा है, यदि pc 0.5 से कम है
(b) कोश आधे से अधिक भरा है, यदि pc 1.0 से अधिक है
(c) कोश आधा भरा है, यदि pc 0.5 से अधिक है
(d) कोश आधे से कम भरा है, यदि pc 0.5 से कम है
उत्तर: 
(d) कोश आधे से कम भरा है, यदि pc 0.5 से कम है

प्रश्न 4. 
ग्लिसरीन की आयतन प्रसार गुणांक 5 x 10^-4JK^-1 है। तब ग्लिसरीन के ताप में 40°C की वृद्धि करने पर उसके, घनत्व में कितना आंशिक परिवर्तन होगा:
(a) 0.020
(b) 0.025
(c) 0.010
(d) 0.015
उत्तर: 
(a) 0.020

प्रश्न 5. 
किसी व्यक्ति का हृदय धमनियों के माध्यम से 150mm पारद दाब पर 5 लीटर रक्त प्रति मिनट पम्प करता है। यदि पारद का 13.6 × 10³ kg/m³ तथा g = 10ms² है तो हृय की शक्ति (वाट में) होगी:
(a) 2.35
(b) 3.0
(c) 1.50
(d) 1.70
उत्तर: 
(d) 1.70

प्रश्न 6. 
किसी जल कुण्ड के बाँध की मोटाई पैंदें पर अधिक होती है, क्योंकि:
(a) गहराई के साथ जल की मात्रा बढ़ती है
(b) गहराई के साथ जल का घनत्व बढ़ता है
(c) गहराई के साथ जल का दाब बढ़ता है
(d) गहराई के साथ जल का ताप बढ़ता है
उत्तर: 
(c) गहराई के साथ जल का दाब बढ़ता है
 
प्रश्न 7. 
एक खुली काँच की नली को पारे में इस प्रकार डुबोया जाता है कि पारे के स्तर से 8cm ऊपर काँच की नली की लम्बाई है। नली के खुले सिरे को अब बन्द कर सील कर दिया जाता है और नली को ऊर्ध्वाधर अतिरिक्त 46Cm से ऊपर उठाया जाता है। नली में पारे के ऊपर वायु स्तम्भ की लम्बाई अब क्या होगी(वायुमण्डलीय दाब = Hg का 76cm
(a) 16 cm
(b) 22 cm
(c) 38 cm
(d) 6 cm
उत्तर: 
(a) 16 cm

प्रश्न 8. 
समान द्रव्यमान के तीन द्रवों को तीन एक समान घनाकार पात्र A, B व C में रखा जाता है। इनके घनत्व क्रमशः PA, PB, PC और PC हैं। किन्तु PA < PB < PC है। घनाकार पात्रों के आधार पर द्रव द्वारा आरोपित बल होगा:
(a) पात्र C में अधिकतम
(b) पात्र C में न्यूनतम
(c) सभी पात्रों में समान
(d) पात्र A में अधिकतम
उत्तर: 
(c) सभी पात्रों में समानु

प्रश्न 9. 
दोनों सिरों पर खुली एक यू-नलिका को पानी से आंशिक भरा गया है। इसकी एक भुजा में पानी में मिश्रित न होने वाला एक तेल इतना डाला गया है कि यह दूसरी नली में पानी के तल से 10mm ऊँचा हो जाता है तथा दूसरी भुजा में पानी का तल उसके प्रारम्भिक तल से 65mm ऊँचा चढ़ जाता है। (आरेख देखिये) तो इस तेल का आपेक्षिक घनत्व है:

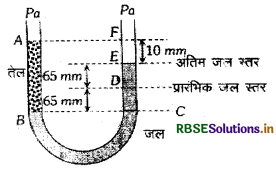
(a) 650 kg m^-3
(b) 425 kg m^-3
(c) 800 kg m^-3
(d) 928 kg m^-3
उत्तर: 
(d) 928 kg m^-3

प्रश्न 10. 
120 kg द्रव्यमान के लकड़ी के ब्लाक को पानी में डुबोने के लिए इस पर रखे जा सकने वाले भार का मान क्या होना चाहिए ( लकड़ी का घनत्व = 600 kg/m³ है):
(a) 80kg
(b) 50kg
(c) 60 kg
(d) 30 kg
उत्तर: 
(a) 80kg

प्रश्न 11. 
एल्युमिनियम के गुटके का द्रव्यमान 1 kg तथा आयतन 3.6 x 10⁴ m³ है। इसे डोरी से लटकाकर जल से भरे पात्र में पूर्णतः डुबा दिया जाता है। डुबाने के पश्चात् डोरी के तनाव में कमी है:
(a) 9.8N
(b) 6.2 N
(c) 3.6 N
(d) 1.0 N
उत्तर: 
(c) 3.6 N

प्रश्न 12. 
एक समान अनुप्रस्थ परिच्छेद की एक वस्तु किसी द्रव में तैर रही घनत्व से तीन गुना हो तब द्रव है। यदि द्रव का घनत्व वस्तु के की ऊँचाई का भिन्नात्मक व्यक्त मान होगा:
(a) 2/3 
(b) 5/6
(c) 1/6
(d) 1/3
उत्तर: 
(a) 2/3 

प्रश्न 13. 
एक बहुत संकीर्ण नली से जल प्रवाहित हो रहा है। तब जल का वेग जिससे कम प्रवाह पर प्रवाह धारा रेखीय होता है, जाना जायेगा:
(a) आपेक्षिक वेग
(b) सीमान्त वेग
(c) क्रान्तिक वेग
(d) वस्तुत: वेग
उत्तर: 
(c) क्रान्तिक वेग

प्रश्न 14. 
एक वृत्ताकार नली ऊर्ध्वाधर तल में है। दो द्रव, जो एक-दूसरे से मिश्रित नहीं होते तथा जिनका घनत्व d₁ एवं d₂ है, नली में भरे गये हैं। प्रत्येक द्रव केन्द्र पर 90° का कोण अन्तरित करता है। उनके अन्तःपृष्ठ को जोड़ने वाली त्रिज्या ऊर्ध्वाधर से α कोण बनाती है। अनुपात d₁/d₂ है:

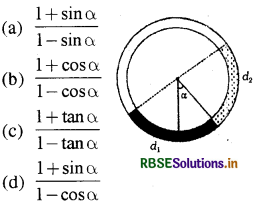
उत्तर: 
\(\text { (c) } \frac{1+\tan \alpha}{1-\tan \alpha}\)

प्रश्न 15. 
किसी पात्र में H ऊँचाई तक जल भरा है। जल की मुक्त सतह से D गहराई पर छिद्र P से जल बह रहा है। क्षैतिज परास x को H व D के पदों में किस सम्बन्ध द्वारा व्यक्त किया जायेगा:

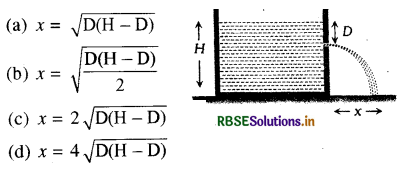
उत्तर: 
\(\text { (c) } x=2 \sqrt{\mathrm{D}(\mathrm{H}-\mathrm{D})}\)

प्रश्न 16. 
बरनोली प्रमेय निम्न में किसके संरक्षण नियम पर आधारित है:
(a) कोणीय संवेग
(b) रेखीय संवेग
(c) द्रव्यमान
(d) ऊर्जा
उत्तर: 
(d) ऊर्जा

प्रश्न 17. 
त्रिज्या '' का कोई लघु गोला विरामावस्था से किसी श्यान द्रव में गिरता है। श्यान बल के कारण इसमें ऊष्मा उत्पन्न होती है। गोले के अन्तिम (टर्मिनल) वेग पर उत्पन्न ऊष्मा की दर निम्नलिखित में से किसके अनुक्रमानुपाती होती है:
(a) r³
(b) r²
(c) r⁵
(d) r⁴
उत्तर: 
(c) r⁵

प्रश्न 18. 
4 सेमी. व्यास के एक पाइप से प्रवाहित हो रहे जल का वेग 3 मी./से. है। तत्पश्चात् जल 2 सेमी व्यास की नलिका में प्रवेश करता है। नलिका में प्रवाहित जल का वेग है:
(a) 3 मी./से.
(b) 6 मी./सै.
(c) 12 मी./सै.
(d) 8 मी./से.
उत्तर: 
(c) 12 मी./सै.

प्रश्न 19. 
एक समरूप लम्बी नलिका को R त्रिज्या के वृत्त में मोड़ा जाता है तथा यह ऊर्ध्वाधर तल में स्थित है। समान आयतन किन्तु घनत्व p तथा 8 के दो द्रव आधी नलिका में भरे जाते हैं। तब, कोण θ होगा:

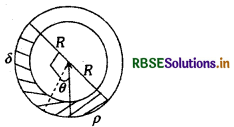
(a) tan^-1 \(\left(\frac{\rho-\delta}{\rho+\delta}\right)\)
(b) tan^-1 \(\frac{\rho}{\delta}\)
(c) tan^-1 \(\frac{\delta}{\rho}\)
(d) tan^-1 \(\left(\frac{\rho+\delta}{\rho-\delta}\right)\)
उत्तर:  
(a) tan^-1 \(\left(\frac{\rho-\delta}{\rho+\delta}\right)\)

प्रश्न 20. 
पानी की एक टंकी ऊपर से खुली हुई है तथा इसमें पानी का स्तर स्थिर है। इसकी दीवार में एक 2 cm त्रिज्या के वृत्ताकार छेद से पानी 0.74m³/ min. की दर से बह रहा है। इस छेद के केन्द्र की पानी की सतह से गहराई का निकटतम मान होगा:
(a) 9.6m
(b) 4.8m
(c) 2.9 m
(d) 6.0 m
उत्तर: 
(b) 4.8m

प्रश्न 21. 
एक समतल तली के बड़े टैंक में पानी 10⁴ms^-1 से भर रहा है और इसकी तली में बने 1 cm² क्षेत्रफल के एक छेद से पानी बाहर भी बह रहा है। यदि पानी की टैंक में ऊँचाई स्थिर है, तो इस ऊँचाई का मान होगा:
(a) 4 cm
(b) 2.9cm
(c) 1.7 cm
(d) 5.1 cm
उत्तर: 
(d) 5.1 cm

प्रश्न 22. 
द्रव से आधा भरा लम्बा बेलनाकार पात्र को अपनी ऊर्ध्व अक्ष के संगत घुमाते हैं तो द्रव पात्र की दीवार के समीप ऊपर उठता है। यदि पात्र की त्रिज्या 5 cm तथा इसकी घूर्णन गति 2 चक्कर प्रति सेकण्ड है, तो पात्र के मध्य तथा किनारे पर द्रव की ऊँचाई में अन्तर का मान cm में होगा:
(a) 1.2
(b) 0.1
(c) 2.0
(d) 0.4
उत्तर: 
(c) 2.0

प्रश्न 23. 
एक नल से पानी का ऊर्ध्वाधर नीचे की ओर 1.0 ms^-1 का आरम्भिक गति से निकलता है। नल के अनुप्रस्थ काट का क्षेत्रफल 10^-4m² है। पानी की धारा में दाब को नियत तथा बहाव को धारारेखीय मानिये। नल में 0.15m नीचे धारा का अनुप्रस्थ काट का क्षेत्रफल होगा (g = 10 ms^-2 लीजिए ):
(a) 1 x 10⁵m²
(b) 5 x 10^-5 m²
(c) 2 x 10⁵ m²
(d) 5 x 10⁴m²
उत्तर: 
(b) 5 x 10^-5 m²

प्रश्न 24. 
बराबर त्रिज्या वाले दो गोलों P तथा Q के घनत्व क्रमश: p तथा P2 हैं। गोलों को एक द्रव्यमान रहित डोरी से जोड़कर 0) एवं 02 घनत्व वाले तथा n एवं T2 श्यानता गुणांकों वाले द्रव । एवं L1 में डाला जाता है। साम्यावस्था में गोला P द्रव L2 में तथा गोला Q द्रव L1 में तैरता है तथा डोरी तनी रहती है (चित्र देखें)। यदि गोले P को अलग से L2 में डालने पर उसका सीमान्त वेग V होता है तो गोले Q को L1 में अलग से डालने पर सीमान्त वेग Vo है, तब

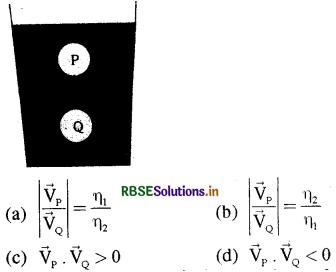
उत्तर:
\(\text { (a) }\left|\frac{\vec{V}_{\mathrm{P}}}{\overrightarrow{\mathrm{V}}_{\mathrm{Q}}}\right|=\frac{\eta_1}{\eta_2}\)

प्रश्न 25. 
एक सपाट प्लेट अल्प दबाव के गैस में, अपने तल की अभिलम्ब दिशा में, बाह्य बल F के प्रभाव में अग्रसरित है। प्लेट की गति V, गैस अणुओं के औसत गति u से बहुत कम है। निम्न में से कौनसा (से) कथन सही है/हैं:
(a) प्रतिगामी एवं अनुगामी पृष्ठ के दबाव का अन्तर MV के समानुपाती है।
(b) कुछ समय के बाद बाह्य बल F और प्रतिरोधक बल सन्तुलित हो जाएँगे
(c) प्लेट द्वारा अनुभव हुआ प्रतिरोधक बल V के समानुपाती है 
(d) प्लेट सदैव अशून्य नियत त्वरण से चलती रहेगी
Passage-III
चित्र में दिखाई गई पिचकारी में एक पिस्टन वायु को एक चंचू (noble) द्वारा बाहर धकेलता है। चंचू के सामने एकसमान अनुप्रस्थ काट वाली पतली नली लगी है। नली का दूसरा सिरा द्रव से भरे एक छोटे पात्र में है। जब पिस्टन वायु को चंचू से बाहर धकेलता है, तब पात्र में द्रव उठकर चंचू में आ जाता है। और फुहार के रूप में बाहर निकलता है। चित्र में दिखाई गई पिचकारी में पिस्टन तथा चंचू की त्रिज्याएँ क्रमश: 20mm तथा हैं। पात्र का ऊपरी भाग वातावरण में खुला है।

उत्तर: 
(a) प्रतिगामी एवं अनुगामी पृष्ठ के दबाव का अन्तर MV के समानुपाती है।
(b) कुछ समय के बाद बाह्य बल F और प्रतिरोधक बल सन्तुलित हो जाएँगे
(c) प्लेट द्वारा अनुभव हुआ प्रतिरोधक बल V के समानुपाती है 

प्रश्न 26. 
पिस्टन को 5ms^-1 की गति से धकेलने पर चंचू से बाहर वाली वायु की गति है:
(a) 0.1ms^-1
(b) 1ms^-1
(c) 2 ms^-1
(d) 8ms^-1
उत्तर: 
(c) 2 ms^-1

 प्रश्न 27. 
वायु तथा द्रव का घनत्व क्रमशः Pa और pl मानिये। पिस्टन की एक नियत गति के द्रव का भी (आयतन प्रति समय) से फुहार होता है वह दर नीचे दिये गये विकल्पों में से किसके अनुक्रमानुपाती है:

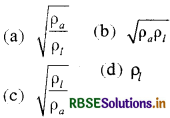
उत्तर: 
\(\text { (a) } \sqrt{\frac{\rho_a}{\rho_t}}\)

प्रश्न 28. 
पानी को गर्म करने पर, बर्तन की तली में बुलबुले बनते हैं और विलग्न होकर ऊपर की ओर उठते हैं। बुलबुलों को त्रिज्या R का गोला मान लें और बर्तन की तली से वृत्तीय स्पर्श की त्रिज्या लें। यदि << R और पानी का पृष्ठ तनाव T है, तब बुलबुलों के पास विलग्न होने से जरा पहले का मान है (पानी का घनत्व pω है) 

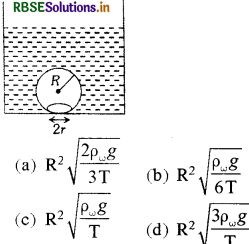
उत्तर:
\(\text { (a) } \mathrm{R}^2 \sqrt{\frac{2 \rho_\omega g}{3 \mathrm{~T}}}\)

प्रश्न 29. 
ताप के बढ़ने पर द्रव का पृष्ठ तनाव:
(a) बढ़ता है
(b) कम होता है
(c) अपरिवर्तित रहता है
(d) पहले बढ़ता है, फिर घटता है
उत्तर:
(b) कम होता है

प्रश्न 30. 
साबुन के बुलबुले (त्रिज्या = ४) को फूँक मारकर इतना बड़ा बनाया गया है कि इसकी त्रिज्या दोगुना हो जाये, यदि साबुन के घोल का पृष्ठ तनाव T हो, तो इस कार्य में आवश्यक ऊर्जा होगी:
(a) 4πr²T
(b) 2πr²T
(c) 12πr²T
(d) 24πr²T
उत्तर:
(d) 24πr²T

प्रश्न 31. 
5 न्यूटन / मी. पृष्ठ तनाव वाले द्रव की फिल्म एक रिंग पर बनाई गई है, जिसका क्षेत्रफल 0.02 मी. है, उसकी पृष्ठ ऊर्जा होगी:
(a) 5 x 10² J
(b) 2.5 x 10^-2 J
(c) 2 x 10^-1J
(d) 5 x 10^-1 J
उत्तर:
(c) 2 x 10^-1J

प्रश्न 32. 
जब 10⁶ छोटी बूंदें मिलकर एक बड़ी बूंद बनाती हैं, तब बूंद का:
(a) घनत्व बढ़ जाता है
(b) घनत्व कम हो जाता है
(c) ताप बढ़ जाता है
(d) ताप घट जाता है
उत्तर:
(c) ताप बढ़ जाता है

प्रश्न 33. 
यदि किसी द्रव का पृष्ठ तनाव T हो, तो द्रव की सतह को A से बढ़ाने पर उसकी पृष्ठ ऊर्जा में वृद्धि होगी:
(a) AT^-1
(b) AT
(c) A2T
(d) A2T2
उत्तर:
(b) AT

प्रश्न 34. 
किसी द्रव की आयताकार झिल्ली (फिल्म) के क्षेत्रफल में वृद्धि (4 cm x 2 cm) से 5 cm x 4 cm की जाती है। यदि इस प्रक्रिया में किया गया कार्य 3 x 10 J हो, तो द्रव के पृष्ठ तनाव का मान होगा:
(a) 8.0 Nm^-1
(b) 0.250 Nm^-1
(c) 0.125 Nm^-1
(d) 0.2Nm^-1
उत्तर:
(c) 0.125 Nm^-1

प्रश्न 35. 
तीन द्रवों के घनत्व क्रमश: P1. Pa तथा P3(P1 > P2 > P3) हैं। तीनों द्रवों का पृष्ठ तनाव T समान है। तीन सर्वसम केशिकाओं में तीनों द्रव समान ऊँचाई तक चढ़ते हैं। यदि इन द्रवों के लिए स्पर्श कोण क्रमश: 01 02 तथा 63 है, तो निम्नलिखित में से कौनसा सम्बन्ध ठीक होगा:
(a) π > θ1 > θ2 > θ3 < π/2
(b) π/2 > θ1 > θ2 > θ3 > 0
(c) 0 < θ1 < θ2 < θ3 < π/2
(d) π/2 < θ1 < θ2 > θ3 < π
उत्तर:
(c) 0 < θ1 < θ2 < θ3 < π/2

प्रश्न 36. 
0° स्पर्श कोण वाले द्रव के चन्द्रतल की प्रकृति होगी:
(a) समतल
(b) परवलयाकार
(c) अर्द्ध-गोलाकार
(d) बेलनाकार
उत्तर:
(c) अर्द्ध-गोलाकार

प्रश्न 37. 
किसी सतह (पृष्ठ ) का किसी द्रव से गीला होना मुख्यत: निर्भर करता है:
(a) पृष्ठ तथा द्रव के बीच स्पर्श कोण पर
(b) श्यानता पर
(c) पृष्ठ तनाव पर
(d) घनत्व पर
उत्तर:
(a) पृष्ठ तथा द्रव के बीच स्पर्श कोण पर

प्रश्न 38. 
छिन्न शंकु (truncated cone) की आकृति वाली काँच की एक केशनली, जिसका शीर्ष कोण है, के दो अन्तःसिरों के अनुप्रस्थ काट की त्रिज्याएँ भिन्न हैं। केशनली को पानी में ऊर्ध्वतः डुबोने पर केशनली में पानी / ऊँचाई तक चढ़ जाता है, जहाँ इसकी अनुप्रस्थ काट की त्रिज्या b है। यदि पानी का पृष्ठ तनाव (surface tension) S, घनत्व तथा काँच के साथ इसका स्पर्श कोण e हो, तब 1⁄2 का मान है (g गुरुत्वीय त्वरण है)

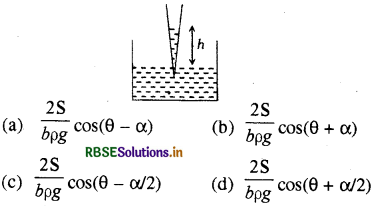
उत्तर:
\(\text { (d) } \frac{2 \mathrm{~S}}{b \rho g} \cos (\theta+\alpha / 2)\)

प्रश्न 39. 
साबुन के किसी गोलीय बुलबुले के अन्दर तथा बाहर के दाब में अन्तर होता है:
(a) 2T/r
(b) 4T/r
(c) T/2r
(d) T/r
उत्तर:
(b) 4T/r

प्रश्न 40. 
साबुन के एक बुलबुले में दाब आधिक्य दूसरे साबुन के बुलबुले के दाब आधिक्य से दोगुना है। यदि पहले बुलबुले का आयतन दूसरे बुलबुले के आयतन से 'n' गुना हो तो '' का मान होगा:
(a) 8
(b) 4
(c) 2
(d) 0.125
उत्तर:
(d) 0.125

प्रश्न 41. 
दो गोलीय साबुन के बुलबुलों की त्रिज्याएँ क्रमश: तथा 172 हैं। यह दोनों समतापीय दशा में निर्वात में मिलते हैं, तो परिणामी बुलबुले की त्रिज्या R होगी:
(a) R = (F1 + 12)/2 
(b) R = r1(r1r2 + r2)
(c) R2 = r 2 + r22
(d) R = r1 + r2
उत्तर:
(c) R2 = r 2 + r22

प्रश्न 42. 
जेगर विधि (jager's method) में बुलबुले के फूटने के समय:
(a) बुलबुले का आन्तरिक दाब बाह्य दाब से हमेशा अधिक होता है। 
(b) बुलबुले का आन्तरिक दाब बाह्य दाब के बराबर होता है। 
(c) बुलबुले का आन्तरिक दाब हमेशा बाह्य दाब से कम होता है। 
(d) बुलबुले का आन्तरिक दाब बाह्य दाब से हमेशा थोड़ा सा अधिक होता है।
उत्तर: 
(a) बुलबुले का आन्तरिक दाब बाह्य दाब से हमेशा अधिक होता है। 

प्रश्न 43. 
केशिकत्व के कारण द्रव नली में ऊपर चढ़ जाता है, यदि स्पर्श कोण है:
(a) न्यून कोण
(b) अधिक कोण
(c) 90°
(d) शून्य
उत्तर: 
(a) न्यून कोण

प्रश्न 44. 
एक द्रव्य एक काँच की केशिकानली में 18 सेमी. की ऊँचाई तक चढ़ता है। एक अन्य काँच की केशिकानली B जिसका व्यास केशनली A का 90% है, को भी समान द्रव्य में डुबोया जाता है, तब केशिकानली B में द्रव्य कितनी ऊँचाई तक चढ़ेगा-
(a) 1.4 सेमी.
(b) 18 सेमी.
(c) 2.0 सेमी.
(d) 2.2 सेमी
उत्तर: 
(c) 2.0 सेमी.

प्रश्न 45. 
एक केशनली की त्रिज्या 2 x 10^-3m है। एक द्रव, जिसका भार 6.28 x 10^-4 N है, केशनली में स्थिर रह सकता है। द्रव का पृष्ठ तनाव है:
(a) 5 x 10^-3 N/m
(b) 5 x 10^-2 N/m
(c) 5 N/m
(d) 50N/m
उत्तर: 
(b) 5 x 10^-2 N/m

प्रश्न 46. 
किसी केशनली को जल में डुबोने पर जल 0.015 मी. की ऊँचाई तक चढ़ता है। यदि जल का पृष्ठ तनाव 75 x 10^-3 न्यूटन / मी. हो, तब केशनली की त्रिज्या होगी:
(a) 0.1 मिमी.
(b) 05 मिमी.
(c) 1 मिमी.
(d) 2 मिमी.
उत्तर: 
(c) 1 मिमी.

प्रश्न 47. 
निम्न प्रेक्षणों को केशिका विधि से पानी का पृष्ठ तनाव T नापमे के लिए किया जाता है:
केशिका का व्यास D = 1.25 x 10^-2 m 
पानी का चढ़ाव = 1.45 x 10^-2 m
g = 9.80 m/s² तथा सरलीकृत सम्बन्ध T = \(\frac{r h g}{2} \times 10^3\) को उपयोग करते हुए पृष्ठ तनाव में सम्भावित त्रुटि का
निकटतम मान होगा:
(a) 10%
(b) 0.15%
(c) 1.5%
(d) 2.4%
उत्तर: 
(c) 1.5%

प्रश्न 48. 
एक कोष्ठ में, साबुन के पानी के दो बुलबुले A तथा B बन्द हैं, जिनकी त्रिज्याएँ क्रमश: 2 cm तथा 4 cm हैं। इस कोष्ठ के अन्दर वायु को 8 N/m2 दाब पर रखा गया है। बुलबुले बनाने के लिए उपयोग किये गये पानी का पृष्ठ तनाव 0.04 N/m है। अनुपात  nb/na की गणना करें, na जहाँ nb बुलबुलों में वायु के मोलों की प्रभावों को नगण्य मानें 
(a) 2
(b) 9
(c) 8
(d) 6
उत्तर: 
(d) 6

प्रश्न 49. 
पृष्ठीय तनाव 2.5 x 10^-2 N/m के किसी डिटरजेन्ट विलयन से 1 mm त्रिज्या का कोई साबुन का बुलबुला फुलाया गया है। इस बुलबुले के भीतर का दाब किसी पात्र में भरे जल के मुक्त पृष्ठ से नीचे किसी बिन्दु Z पर दाब के बराबर है। 8 = 10 m/s² तथा जल का घनत्व 10³ kg/m³ लेते हुए Zo का मान है:
(a) 100cm
(b) 10 cm
(c) 1 cm
(d) 0.5 cm
उत्तर: 
(c) 1 cm

प्रश्न 50. 
यदि एक '' त्रिज्या की केशिका द्रव्यमान 'M' है तो '2r' त्रिज्या की केशिका नली में चढ़ने वाले पानी का द्रव्यमान होगा:
(a) 4M
(b) M
(c) 2M
(d) M/2
उत्तर: 
(c) 2M

प्रश्न 51. 
पारा तथा पानी के पृष्ठ तनाव का अनुपात 75 है जबकि उनके घनत्व का अनुपात 13 : 6 है। उनके काँच के साथ सम्पर्क कोण के लगभग मान क्रमश: 135° तथा 0° हैं यह पाया जाता है कि पारा एक त्रिज्या की केशिका नली में ऊँचाई से अवनत होता है जबकि पानी त्रिज्या, की केशिका नली में उसी ऊँचाई / से उन्नत होता है। अनुपात 71/72 का निकट मान होगा:
(a) 2/3
(b) 3/5
(c) 2/5
(d) 4/5
उत्तर: 
(c) 2/5

प्रश्न 52. 
समान आयतन परन्तु असमान घनत्वों तथा d वाले दो ठोस गोले dA व dB एक धागे से जोड़े गये हैं। ये दोनों dF घनत्व के एक द्रव में डूबे हुए हैं। साम्य अवस्था में वे दोनों चित्र में दिखाये अनुसार हैं और धागे में तनाव है। गेंदों को इस अवस्था में रहने के लिए जरूरी है कि:

(a) dA < dF
(b) dB > dF
(c) dA> dF
(d) dA + dB = 2dF
उत्तर: 
(a) dA < dF

प्रश्न 53. 
एक त्रिज्या R तथा घनत्व वाले ठोस गोलक को एक द्रव्यमान रहित स्प्रिंग के एक सिरे से जोड़ा गया है। इस स्प्रिंग का बल नियतांक & है। स्प्रिंग के दूसरे सिरे को दूसरे ठोस गोलक से जोड़ा गया है जिसकी त्रिज्या R व घनत्व 3p है। पूर्ण विन्यास को 20 घनत्व के द्रव में रखा जाता है और इसको साम्यावस्था में पहुँचने दिया जाता है। सही प्रकथन है/हैं:
(a) स्प्रिंग की नेट दैर्घ्यवृद्धि \(\frac{4 \pi \mathrm{R}^3 \rho g}{3 k}\) है
(b) स्प्रिंग की नेट दैर्घ्यवृद्धि \(\frac{8 \pi R^3 \rho g}{3 k}\) है
(c) हल्का गोलक आंशिक पूर्ण रूप से डूबा हुआ है। 
(d) हल्का गोलक पूर्ण रूप से डूबा हुआ है।
Passage-I
जब आँख में p घनत्व की एक तरल दवाई डालनी होती है, तो एक ड्रापर की सहायता ली जाती है। ड्रापर के ऊपर लगे बल्ब को दबाने पर ड्रापर के नीचे बने छेद पर एक बूंद बनती है। हम इस बूँद के आकार का आकलन करना चाहते हैं। इसके लिए हम यह मान रहे हैं कि बनने वाली बूँद का आकार गोलीय है, क्योंकि इस आकार में पृष्ठ ऊर्जा में न्यूनतम वृद्धि होती है। बूंद के आकार का निर्धारण करने के लिए हम R त्रिज्या की बूँद पर पृष्ठ तनाव T के कारण कुल ऊर्ध्वाधर बल का आकलन करते हैं। जब यह बल बूँद के भार से कम हो जाता है, बूंद ड्रापर से अलग हो जाती है।
उत्तर: 
(a) स्प्रिंग की नेट दैर्घ्यवृद्धि \(\frac{4 \pi \mathrm{R}^3 \rho g}{3 k}\) है

प्रश्न 54. 
यदि ड्रापर के छेद की त्रिज्या है, तब R त्रिज्या की बूँद पर पृष्ठ तनाव के कारण ऊपर की ओर लगने वाला ऊर्ध्वाधर बल (r << R मानते हुए) नीचे दिये गये विकल्पों में से कौनसा होगा:
(a) 2πrT
(b) 2πrRT
\(\text { (c) } \frac{2 \pi r^2 \mathrm{~T}}{\mathrm{R}}\)
\(\text { (d) } \frac{2 \pi \mathrm{R}^2 \mathrm{~T}}{r}\)
उत्तर: 
\(\text { (c) } \frac{2 \pi r^2 \mathrm{~T}}{\mathrm{R}}\)

प्रश्न 55. 
r = 5 x 10^-4 m, p = 10³ kg m^-3, g= 10 ms^-2, T = 0.11 Nm^-1, तो जब बूँद ड्रापर से अलग होती है, उसकी त्रिज्या (लगभग) कितनी होगी, नीचे दिये विकल्पों में से चुनें:
(a) 1.4 x 10^-3 m
(b) 3.3 x 10^-3 m
(c) 2.0 x 10^-3 m
(d) 4.1 x 10^-3 m
उत्तर: 
(a) 1.4 x 10^-3 m

प्रश्न 56. 
ड्रापर से अलग होने के बाद बूँद की पृष्ठ ऊर्जा निम्न में से कौनसी है:
(a) 1.4 × 10^-6 J
(b) 2.7 x 10^-6 J
(c) 5.4 x 10^-6 J
(d) 8.1 x 10^-6 J
उत्तर: 
(b) 2.7 x 10^-6 J

प्रश्न 57. 
एक आन्तरिक त्रिज्या वाली एकसमान केशनली (uniform capillary tube) को ऊर्ध्वाधर तरीके से (vertically) पानी से भरे एक बीकर (beaker) में डुबोया जाता है। केशनली में पानी, बीकर के पानी के पृष्ठ (water surface) से ऊँचाई तक उठता है। पानी का पृष्ठ तनाव (surface tension) ० है पानी और केशनली की दीवार के बीच का सम्पर्क कोण (angle of contact) σ है। मेनिस्कस (meniscus ) में उपस्थित पानी के द्रव्यमान ( mass) की उपेक्षा कीजिए। निम्नलिखित कथनों में से कौनसा (से) सही है ( हैं ) 
(a) एक दिए गये पदार्थ से बनी केशनली का बढ़ाने से / कम होता है 
b) एक दिए गये पदार्थ से बनी केशनली में h पृष्ठ तनाव σ पर निर्भर नहीं करता है
(c) यदि यह प्रयोग एक नियत त्वरण (constant acceleration) से ऊपर जाने वाली लिफ्ट (lift) में किया जाता है, तो /i कम होता है।
(d) h सम्पर्क कोण θ के समानुपातिक (proportional) है
उत्तर: 
(a) एक दिए गये पदार्थ से बनी केशनली का बढ़ाने से / कम होता है