RBSE Class 11 Physics Important Questions Chapter 10 Mechanical Properties of Fluids

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 10 Mechanical Properties of Fluids Important Questions and Answers.

RBSE Class 11 Physics Chapter 10 Important Questions Mechanical Properties of Fluids

Multiple Choice Questions

Question 1.
If there were no gravity, which of the following will not be there for a fluid?
(a) Viscosity
(b) Surface tension
(c) Pressure
(d) Archimedes upward thrust
Answer:
(d) Archimedes upward thrust

Question 2.
An object is moving through the liquid. The viscous damping force acting on it is proportional to the velocity. Then dimensions of constant of proportionality are:
(a) [ML^-1T^-1]
(b) [MLT^-1]
(c) [M⁰LT^-1]
(d) [ML⁰T^-1]
Answer:
(d) [ML⁰T^-1]

Question 3.
Motion of a liquid in a tube is best described by:
(a) Bernoulli’s theorem
(b) Poiseuille’s equation
(c) Stokes law
(d) Archimedes principle
Answer:
(b) Poiseuille’s equation

Question 4.
Which one is not a dimensional number?
(a) Acceleation due to gravity
(b) Surface tension of water
(c) Velocity of light
(d) Reynold’s number
Answer:
(d) Reynold’s number

Question 5.
Critical velocity of the liquid:
(a) Decreases when radius decreases
(b) Increases when radius increases
(c) Decreases when density increases
(d) Increases when density increases
Answer:
(c) Decreases when density increases

Question 6.
An areoplane gets its upward lift due to a phenomenon described by the:
(a) Archimedes principle
(b) Bernoulli’s principle
(c) Buoyancy principle
(d) Pascal law
Answer:
(b) Bernoulli’s principle

Question 7.
The water droplets in free fall are spherical due to:
(a) gravity
(b) viscosity
(c) surface tension
(d) intermolcular attraction
Answer:
(c) surface tension

Question 8.
Two drops of equal radius coalesce to form a bigger drop. What is ratio of surface energy of bigger drop to smaller one?
(a) 2^1/2 : 1
(b) 1 : 1
(c) 2^2/3 : 1
(d) None of these
Answer:
(d) None of these

Question 9.
If a liquid does not wet glass, its angle of contact is:
(a) zero
(b) acute
(c) obtuse
(d) right angle
Answer:
(b) acute

Question 10.
If a mercury drop is divided into 8 equal parts, its total energy:
(a) remains same
(b) becomes twice
(c) becomes half
(d) becomes 4 times
Answer:
(b) becomes twice

Question 11.
A sphere of mass m and radius r is falling in the column of viscous fluid. Terminal velocity attained by falling object implies that:
(a) The ball attains constnat velocity after some time
(b) The ball stops
(c) The speed of ball will keep on increasing
(d) None of the above
Answer:
(a) The ball attains constnat velocity after some time

Question 12.
The velocity of efflux of a liquid through an orifice in the bottom of the tank does not depend upon:
(a) size of orifice
(b) height of liquid
(c) acceleration due to gravity
(d) none of the above
Answer:
(a) size of orifice

Question 13.
The ratio of the terminal velocities of two drops of radii R and R/2 is:
(a) 2
(b) 1
(c) 1/2
(d) 4
Answer:
(d) 4

Question 14.
Dynamic lift is related to:
(a) Bernoulli’s theorem
(b) Archimedes principle
(c) Equation of continuity
(d) Pascal’s law
Answer:
(a) Bernoulli’s theorem

Question 15.
A body of mass 15 kg is dropped into the water. If the apparent weight of the body is 10⁷ N, then the applied thrust will be:
(a) 40 N
(b) 80 N
(c) 60 N
(d) 100 N
Answer:
(a) 40 N

Question 16.
Work done in increasing the size of a soap bubble from a radius of 3 cm to 5 cm is nearly (surface tension of soap solution = 0.03 N/m):
(a) 4π mJ
(b) 0.2 π mJ
(c) 2π mJ
(d) 0.4 π mJ
Answer:
(d) 0.4 π mJ

Question 17.
When the temperature is increased, the angle of contact of a liquid:
(a) increases
(b) decreases
(c) remains the same
(d) first increases and then decreases
Answer:
(a) increases

Question 18.
The surface tension of soap solution is 25 x 10^-3 N/m. The excess pressure inside a soap bubble of diameter 1 cm is:
(a) 10 Pa
(b) 20 Pa
(c) 5 Pa
(d) None of these
Answer:
(b) 20 Pa

Question 19.
Calculate the force required to separate the glass plate of area 10^-2 m² with a film of water 0.05 mm thick (surface tension of water is 70 x 10^-3 N/m):
(a) 25 N
(b) 20 N
(c) 14 N
(d) 28 N
Answer:
(d) 28 N

Question 20.
The unit of coefficient of viscosity is:
(a) Nm/s
(b) Nm²/s
(c) N/(m²s^-1)
(d) Nms^-2
Answer:
(c) N/(m²s^-1)

Fill in the blanks

Question 1.
Surface energy per unit area of liquid surface is called ................................... ?
Answer:
Surface tension of liquid.

Question 2.
Pressure is a ................................... quantity.
Answer:
Scalar

Question 3.
The upward force acting on the body immersed in fluid is called ................................... force.
Answer:
Buoyant

Question 4.
A device used for measuring the rate of flow of liquid through pipes is called ...................................
Answer:
Venturimeter

Question 5.
The reciprocal of viscosity is called ...................................
Answer:
fluidity

Very Short Answer Questions

Question 1.
Why do clouds float in the sky?
Answer:
The final velocity of water drops is zero, so they appear to be floating in the sky.

Question 2.
What is critical velocity?
Answer:
Critical velocity is the limiting velocity above which the fluid flow is turbulent and below which the fluid flow is streamlined.

Question 3.
What is meant by Reynold’s number?
Answer:
It is a pure number that tells about the nature of fluid flow inside the pipe.

Question 4.
What is the effect of temperature on the viscosity of the liquid?
Answer:
Viscosity decreases on increasing the temperature.

Question 5.
At which temperature, the surface tension of liquid is zero?
Answer:
At critical temperature, the surface tension of liquid is zero.

Question 6.
At what temperature, the surface tension of water is maximum?
Answer:
Surface tension of water is maximum at 4°C because the density of water is maximum at 4°C.

Question 7.
What is the effect on the angle of contact on mixing soap solution in water? 
Answer:
The angle of contact decreases.

Question 8.
What is the advantage of ploughing the field?
Answer:
By ploughing the soil, the small capillaries in the soil break down, hence the water does not evaporate through them. This keeps the field moisturised for a long time which helps in germination of seeds.

Question 9.
What is an ideal liquid?
Answer:
A liquid which is non-compressible and non-viscous is called an ideal liquid. In real no liquid is ideal as viscosity and compressibility is not zero for any liquid.

Question 10.
What is the angle of contact for pure water and glass?
Answer:
The angle of contact for pure water and glass is zero.

Question 11.
Name the force responsible for surface tension.
Answer:
Cohesive force.

Question 12.
The bags and suitcases are provided with broad handles. Why?
Answer:
So that the small pressure is exerted while carrying them.

Question 13.
What is pressure? Give the S.I. unit and dimensional formula.
Answer:
The force applied to any surface per unit area is called pressure. Its S.I. unit is N/m or Pascal. Its dimensional formula is [ML^-1T^-2].

Question 14.
What is 1 torr?
Answer:
One torr is the unit of atmospheric pressure where 1 torr = weight of one mm column of mercury.

Question 15.
What is 1 bar?
Answer:
1 bar is the unit of atmospheric pressure used for meterological purposes where 1 bar = 10⁵ Pa.

Question 16.
A body is just floating in a liquid (their densities are equal). What will happen to the body if it is slightly pressed and released?
Answer:
The body will sink to the bottom.

Question 17. 
A beaker containing a liquid is kept inside a big closed jar. If the air inside the jar is continuously pumped out, what will be the pressure in the liquid near the bottom of the liquid?
Answer:
The pressure near the bottom of the liquid will decrease. It is so because the total pressure at a point near the bottom of the liquid is equal to the sum of the pressures due to the column of the liquid and due to air inside the jar. When the air inside the jar is pumped out, the pressure due to air inside the jar decreases inside the jar.

Question 18.
Why are the walls of a water reservoir thick at the bottom?
Answer:
It is so because the pressure of the water in the reservoir increases with the depth.

Question 19.
A block of ice is floating in a liquid of specific gravity 1.2 contained in the, beaker. What will be the effect on the level of the liquid in the beaker when the whole ice melts?
Answer:
The level of water in the beaker will rise. It is so because the density of water formed by melting of ice is less than the density of liquid in the beaker.

Question 20.
A square framed wire of side L is dipped in a liquid. On taking out, a membrane is formed. What will be the force acting on the frame if the surface tension of liquid is T?
Answer:
The membrane has two surfaces. Force on the frame due to surface tension.
= Surface tension x total length = T x (4L x 2) = 8TL

Question 21.
What is the value of surface tension of a liquid at critical temperature?
Answer:
Zero.

Question 22.
When a drop is split into large number of drops, the change in the total potential energy of small drops and the potential energy of the bigger drop is zero, positive or negative?
Answer:
Positive, because on splitting a big drop into small drops, the surface area increases and hence the work is to be done in doing so, which appears as potential energy of small drops.

Question 23.
A number of small drops of mercury coalesce isothermally to form a single drop. What will be the effect on temperature of the drop?
Answer:
Temperature of the drop remains unchanged.

Question 24.
What is the work done in blowing a soap bubble of radius r and surface tension T?
Answer:
Work done = Surface tension x Area of soap bubble
= T x 4πr² x 2 = 8πTr²

Question 25.
What will be the effect on the angle of contact of a liquid if the temperature increases?
Answer:
With the increase in temperature, the surface tension of the liquid decreases. Due to which the liquid surface on the solid surface becomes more flat, consequently the angle of contact of a liquid increases with the increase in temperature.

Question 26.
What will be the effect on the temperature, if the number of small drops of mercury coalesce adiabatically to form a single drop?
Answer:
When a large number of drops coalesce, the surface area will decrease, the energy will be liberated. Due to adiabatic conditions, its temperature will increase.

Question 27. 
When a shaving brush is taken out of water its hair cling together, Why?
Answer:
Due to surface tension, the water film formed between the hair will tend too make the surface area minimum. As a result of which the hair of shaving brush come closer to each other.

Question 28.
When a greased iron needle is placed gently on the surface of water at rest, it floats on the surface of water, why?
Answer:
Due to surface tension, the free surface of water at rest behaves like a stretched membrane. When the upward components of the force of surface tension acting on the iron needle balances its weight on a stretched membrane of water surface, the needle floats on the surface of water at rest.

Question 29.
Surface tension of all lubricating oils and paints is kept low, why?
Answer:
In order to have low value of surface tension so that it can spread over large area.

Question 30.
In soldering, addition of flux makes soldering easy. Why?
Answer:
The addition of flux reduces the surface tension of molten tin, hence it spreads.

Question 31.
Name the material in whose capillary, water will descend instead of rising.
Answer:
Paraffin wax.

Question 32.
Why does the cotton wick in an oil-filled lamp keep on burning?
Answer:
In the cotton wick there are very large number of capillaries in which oil continues to rise.

Question 33.
At what temperature the surface tension of a liquid is zero?
Answer:
At critical temperature.

Question 34.
Water can rise up to a height of 10 cm in a capillary tube. If a capillary of same water but of length 6 cm is held vertically in water, will the water come out in the form of a fountain? Explain.
Answer:
No, when the size of the capillary is less than the height to which the water can rise, the radius of curvature of water meniscus adjusts itself so that there is no over flowing of water but the product of height of liquid and radius of curvature of the meniscus remains a finite constant.

Question 35.
The soap bubble formed at the end of the tube is blown very slowly. Draw the graph between excess of pressure inside the bubble with time.
Answer:
As excess of pressure inside the soap bubble of radius r is

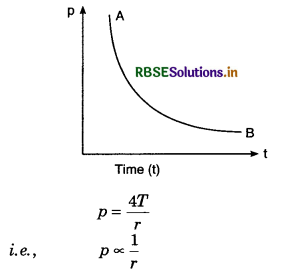
i.e., as r increase with time, p decrease.
So, the variation of p with time (t) will be parabolic curve AB as shown in figure.

Question 36.
A liquid of density p and surface tension T rises to a height h in a capillary tube of diameter D. What is the weight of the liquid in the capillary tube? Angle of contact is 0°.
Answer:
Weight of liquid in the capillary tube is
W = mg = πr² hρg
We know that, h = \(\frac{2 T \cos \theta}{r \rho g}=\frac{2 T}{r \rho g}\)
W = πr²ρg x \(\frac{2 T}{r \rho g}\) = π x 2r x T = πDT

Short Answer Questions

Question 1.
A block of wood floats in a bucket of water in a lift, will the block sink more or less if the lift starts accelerating up?
Answer:
When the lift starts accelerating up, the block of wood will float at the same level in the bucket of water in a lift. It is so, because the equilibrum of floating body is unaffected by variation in acceleration due to gravity. However, thrust of liquid and weight of body both depend on g and will increase.

Question 2.
When bits of camphor are dropped on water, they move helter-skelter. Why?
Answer:
When bits of camphor are dropped on water, they lower the surface tension where they are dipping. Since, the shape of camphor bits is irregular, unequal forces of surface tension act on them. That is why they move helter-skelter or errotically on the surface of water.

Question 3.
Why does oil spreads over the surface of water?
Answer:
Surface tension of oil is less than that of water, when oil is dropped on the surface of water, the force of surface tension of water being larger than that of oil, stretches the oil drops on all sides. Hence the oil spreads over the surface of water.

Question 4.
Why the tip of the nib of a pen is splitted?
Answer:
The tip of the nib of a pen is splitted in order to provide a capillary which helps the ink to rise to the end of the nib and enables it to write continuously.

Question 5.
Why does an iron needle float on clean water but sink when some detergent is added to this water?
Answer:
Due to surface tension, the free surface of liquid at rest behaves like a stretched membrane. When an iron needle floats on the surface of clean water, its weight is supported by the stretched membrane. When some detergent is added to this water, its surface tension decreases. As a result of this thd stretched membrane on the surface of water is weakened and is not able to support the weight of needle. Hence, needle sinks in such water.

Question 6.
Explain why some oil spreads uniformly on water, when others float as drops?
Answer:
The force of surface tension of some oils is less than surface tension of water. When such oils are dropped on the surface of water, they are pulled in all directions due to higher forces of surface tension of water and as such they spread uniformly on water.
In the case of other oils, whose surface tension is equal to or greater than that of water, they float as drops on water.

Question 7.
Water is coming out of a hole made in the wall of a fresh water tank. If the size of the hole is increased, (i) Will the velocity of efflux of water change? (ii) Will the volume of the water coming out per second change?
Answer:
(i) Velocity of'efflux will remain same as it only depends upon the depth of orifice below the free surface of water.
(ii) Volume will change, since volume of the liquid flowing out per second is equal to product of area of hole and velocity of liquid flowing out.

Question 8.
One flask contains glycerine and the other contains water. Both are stirred vigorously and placed on the table. In which flask will the liquid come to rest earlier and why?
Answer:
Since, viscosity of glycerine is large than the water, therefore glycerine will destroy the relative motion between its layers quickly than that of water. This is why glycerine will come to rest earlier than water.

Question 9.
A rain drop of radius r falls in air with a terminal velocity v. What is the terminal velocity of a rain drop of radius 2r?
Answer:
Terminal velocity v = \(\frac{2}{9} \frac{r^2(\rho-\sigma) g}{\eta}\)
i.e., v ∝ r²
∴ \(\frac{v_2}{v_1}=\left(\frac{r_2}{r_1}\right)^2\)
or v² = \(v_1\left(\frac{r_2}{r_1}\right)^2=v\left(\frac{2 r}{r}\right)^2\) = 4r

Question 10.
The cylindrical tube of a spray pump has a radius R, one end of which has n fire holes, each of radius r. If the spread of the liquid in the tube is V, find out the speed of the ejection of the liquid through the holes.
Answer:
Area of cross section of tube, A = πR²
Area of cross section of each hole = πr²
Let v be the speed of ejection of the liquid through each hole. Using equation of continuity, we have
πR²V = (πr²v) n or v = \(\frac{V}{n} \frac{R^2}{r^2}\)

Question 11.
Explain why an air bubble in water rises from bottom to top and grows in size.
Answer:
We know that fluid moves from a region of higher pressure to a region of lower pressure and the fluid pressure increases with depth.
The pressure at the top of the water surface is P₀ (= atmospheric pressure) and the pressure at the bottom of water of depth h = P₀ + hpg, which is greater than that at the top of the water surface. As a result of which an air bubble moves from bottom to top. It can not move side ways as the pressure at same level in a liquid is same. While coming from bottom to top, the pressure decreases. In accordance with Boyle’s law i.e., PV = a constant so volume of the air bubble increases i.e., the bubble will grow in size while coming from bottom to top of water.

Question 12.
Why is the pressure of water reduced when it comes to narrow pipe from wide pipe while flowing?
Answer:
According to principle of continuity, av = constant or v ∝ \(\frac{1}{a}\) i.e., as the water flows from wider tube to narrow tube, its velocity increases. According to Bernoulli’s principle (P + \(\frac{1}{2}\) ρv² = a constant), where velocity is large, the pressure is less.

Question 13.
What is the effect of temperature on the viscosity of gases? Explain it.
Answer:
Viscosity of gases increases with increase in temperature because the velocity of gas molecules increases with temperature and hence collision of molecules increases which decreases the ability of the molecules as a whole to engage in the coordinated move.

Question 14.
A tiny liquid drop is spherical but a larger drop has an oval shape?
Answer:
Each free surface of a liquid behaves as a stretched membrane under the effect of surface tension and its nature is to bring the surface area to the minimum. Hence, the tiny drop is spherical but a large drop becomes oval under the effect of gravity.

Question 15. 
Name the forces which are responsible for shape of liquid surface in a capillary tube.
Answer:
The adhesive force and cohesive force are responsible for shape of liquid surface in a capillary tube.
(i) When the adhesive force > the cohesive force, the shape of the liquid surface is concave.
(ii) If the adhesive force < the cohesive force, the shape of liquid surface is convex.
(iii) If the adhesive force = the cohesive force, the shape of liquid surface is flat.

Long Answer Questions

Question 1.
Explain fluid pressure. Find the value of pressure in a liquid at some depth, derive its formula.
Answer:
When we press a sharp needle against our skin, it pierces our skin. However, when our skin is pressed against a wider contact area like the back of a spoon, it remains intact. Let us assume that an elephant has step on a man’s chest, than it would surely crack his ribs. A circus performer is saved in such a performance by keeping a light but strong plank on his chest. Such daily life experiences convince us that both the force and its area covered are important. When an object is submerged in a fluid (at rest), then a force is exerted by the fluid on its surface. This force is always normal to the surface of the object. If F is the magnitude of this force, then the average pressure Pav is defined as the normal force acting per unit area (Fig. 10.1).

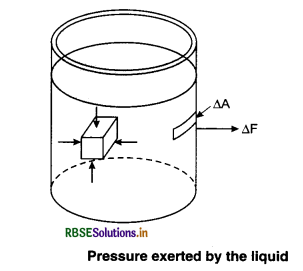
Therefore, P_av = \(\frac{F}{A}\)
In principle, the covered area can be made arbitrarily small, then, the pressure is defined in limiting sense as:
P = \(\lim _{\Delta A \rightarrow 0} \frac{F}{A}\)
Pressure is a scalar quantity. Its dimensions are [ML^-1T^-2]. The SI unit of pressure is named as Pascal (Pa) in honour of the French Scientist Biaise Pascal. Another unit of pressure is the atmosphere (atm), it is the pressure exerted by the atmosphere at sea level (1 atm = 1.013 x 10⁵ Pa).

Consequences of Pressure
1. A camel walks easily on the sandy surface than a man inspite of the fact that a camel is much heavier than a man.
This is because the area of camel’s feet is large as compared to the area of man’s feet. So the pressure exerted by camel on the sand surface is very small as compared to the pressure exerted by man. Hence, camel can walk and run easily on the sandy surface.

2. A sharp knife is more effective in cutting the objects than a blunt knife.
A sharp knife cuts objects better because of its very thin edge and the force of our hand falls over a very small area of the object producing a large pressure. Due to this large pressure it cuts the object easily. In the case of a blunt knife it has thicker edge. Due to its thicker edge, the force of our hand falls over a larger area of the obejct and produces lesser pressure. Due to this lesser pressure it cuts the object with difficulty.


3. Railway tracks are laid on large sized wooden or iron sleepers.
∵ P = \(\frac{T}{A}\) or Pressure = \(\frac{\text { Thrust }}{\text { Area }}\)
The weight (thrust) of the train is spread over a large area of the sleepers. So the pressure acting on the ground under the sleepers is reduced. This prevents the sinking of the ground under the weight of the train.

4. It is painful to hold a heavy bag having strap made of a strong and thin string.
When we hold a heavy bag having strap made of a strong and thin string, then the area under the strap is small. Hence, large .pressure is exerted by the strap on our figures. Due to this large pressure, the strap tends to cut the skin and hence pain is caused.

Question 2.
Explain Pascal’s law taking into consideration the effect of gravity. Explain the working of a hydraulic lift.
Answer:
Now, we know that pressure in a fluid depends only upon depth, and any increase in pressure at the surface must be transmitted to every point in the field. This is known as Pascal’s law as it was first recoginsed by the French Scientist Blaise Pascal.

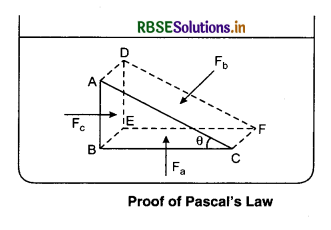
According to this law, pressure exerted on any fluid at any place is transmitted equally in all directions and is always normal to the container. This law is also called the law of transmission of pressure.
Proof of Pascal’s law: We can prove Pascal’s law by using two principles:
(i) The force on any layer of a fluid at rest is normal to the layer, and
(ii) Newton’s 1st law of motion.
We consider a small element ABCDEF in the form of a right angled prism inside a vessel containing fluid at rest.
The effect of gravity is same for all points in the element. We consider that fluid exerts pressure P_a, P_b and P_c on the forces BEFC, ADFC and ADEB respectively of this element and corresponding normal forces on these faces are F_a, F_b and F_c.
Let A_a, A_b and A_c be the respective areas of the three faces. In right angled  ∆ABC, let ∠ACB = θ
Now we consider different forces in equilibrium,
Horizontally, F_b sinθ = F_c .......................(1)
Vertically F_b cosθ = F_a ......................(2)
Also, from the geometry of the figure, we get
A_b sinθ = A_c ....................(3)
and A_b cosθ = A_a .......................(4)
From equations (1), (2), (3) and (4)

This proves Pascal's law

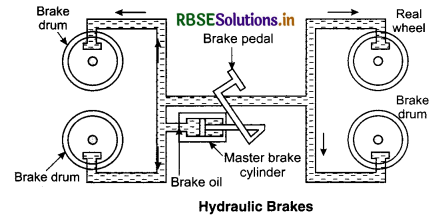
1. Hydraulic Brakes: In hydraulic brakes, when a little force with the foot is applied on the pedal (see fig. 10.8), the pressure so applied gets transmitted through brake oil to act on a larger area where pistons move the brake-shoes against the brake-drums. So on applying a little pressure on the pedal a large force is exerted on the wheel which produces deceleration.

2. Hydraulic Lift: One can see at motor service station that the cars and large trucks being raised to convenient heights so that mechanic can work under them. Here, a slight pressure is transmitted through the liquid to act on a large surface, thus, producing sufficient force to raise up the vehicle. If F₁ is the force acting on the piston of area A₁, then the pressure below that piston is
P = \(\frac{F_1}{A_1}\)

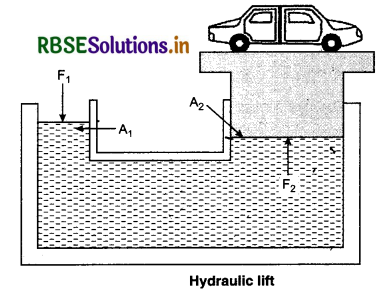
According to the Pascal’s law, the pressure on any area element in the large piston will be same. If the cross-sectional area of this cylinder is A₂, then the total force acting on the larger piston will be
F₂ = P A₂ or P = \(\frac{F_2}{A_2}\)
So, \(\frac{F_1}{A_1}=\frac{F_2}{A_2}\)
The gain in force will be,
\(\frac{F_2}{F_1}=\frac{A_2}{A_1}\)
This ratio is also called mechanical advantage.

Question 3.
What do you mean by atmospheric pressure? Give the principle of Torricelli’s barometer.
Answer:
The pressure exerted by the gaseous cover present around the Earth is called atmospheric pressure. The atmospheric pressure at any point is equal to the weight of that air column, which has a unit cross sectional area and its length starts from that point and goes to the end of the atmosphere.

In most of the circumstances, atmospheric pressure is closely approximated by the hydrostatic pressure caused by the weight of air above the measurement point. The areas with low-pressure have less atmospheric mass above their locations. The high pressure areas have more atmospheric mass above their locations. Likewise, as height increases, there is less atmospheric mass, so the atmospheric pressure decreases with increasing height.

At sea level, the atmospheric pressure is 1.013 x 10⁵ Pa. It is also represented as 1 atm. Barometer is a device with which the pressure of atmosphere is measured. To measure atmospheric pressure water, air or mercury is used. The height of mercury column at sea level is about 76 cm.

Another unit of pressure is bar.
1 bar = 10⁵ Newton/m²
= 10⁵ Pa
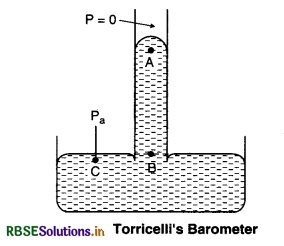
Itallian Scientist E. Torricelli (1608 - 1647) devised for the first time a method for measuring atmosphere pressure. It is called a simple barometer. In this a long glass tube closed at one end and filled with mercury is inverted into a dish of mercury. The space above the mercury column in the tube contains only mercury vapour whose pressure is so small.
∴ P_a = 0
The pressure inside the column at point B and at point C are equal which is equal to atomsphere pressure
P_B = P_C = P_a
If h is the height of mercury column and ρ is the density of mercury, then P_B = P_a  + hρg
or P_a = 0 + hρg
or P_a = hρg
For a mercury barometer, h = 76 cm = 0.76 m, ρ = 13.6 x 10³ kg/m³, g = 9.8 m/s².
∴ Atmospheric pressure
P_a = 0.76 x 13.6 x 10³ x 9.8
= 1.013 x 10⁵ Pa

Question 4.
What do you mean by viscosity of the liquid? Explain velocity gradient.
Answer:
The property of liquid due to which it opposes the relative motion between its layers is called viscosity. Viscosity is not found in solids because relative motion is not present between their layers. In gases also viscosity is very less. Viscosity in liquids is due to the cohesive forces between the molecules. Viscosity is the property that describes a fluid’s resistance to flow. It is a measure of a fluid’s resistance to gradual deformation by shear stress or tensile stress for liquids, it is related to the informal concept of thickness. Thicker the liquid, more is its viscosity. For example, honey is more viscous than water. When the fluid is made to move through a tube, the particles in the fluid move more quickly near the axis of tube and moves more slowly near its wall. So, stress is required to overcome the friction between the layers of the particles to keep the fluid moving. A fluid is called an ideal fluid if it is non viscous and non-compressible. A liquid is called viscous if its viscosity is greater than that of water. A fluid is called mobile if its viscosity is lesser than that of water.

Question 5.
Give a formula to determine viscous force between two layers of a liquid. Explain viscous coefficient.
Answer:
The property of liquid due to which it opposes the relative motion between its layers is called viscosity. Viscosity is not found in solids because relative motion is not present between their layers. In gases also viscosity is very less. Viscosity in liquids is due to the cohesive forces between the molecules. Viscosity is the property that describes a fluid’s resistance to flow. It is a measure of a fluid’s resistance to gradual deformation by shear stress or tensile stress for liquids, it is related to the informal concept of thickness. Thicker the liquid, more is its viscosity. For example, honey is more viscous than water. When the fluid is made to move through a tube, the particles in the fluid move more quickly near the axis of tube and moves more slowly near its wall. So, stress is required to overcome the friction between the layers of the particles to keep the fluid moving. A fluid is called an ideal fluid if it is non viscous and non-compressible. A liquid is called viscous if its viscosity is greater than that of water. A fluid is called mobile if its viscosity is lesser than that of water.

Question 6.
State and explain Stoke’s law. Explain its applications.
Answer:
When a body falls in a viscous medium, it carries layers of fluid which are in body’s contact whereas the layers of fluid in contact with the stationary surface remain almost at rest. The layers of fluid destroys the relative motion and motion of the body is thus opposed. The viscous drag increases with velocity of the body till viscous drag and upthrust of the body are together equal to the weight of the body which acts downwards. When there is no net force, the body moves with the uniform velocity. This velocity is called terminal velocity. Stoke showed that the retarding force F due to viscous drag for a spherical body of radius r that moves with a velocity u in a fluid, with coefficient of viscosity η, is given as:
F = 6πηrv
This expression is known as Stoke's Law.
Derivation with help of dimensions
F ∝ v, velocity;
F ∝ r, radius of the body;
F ∝ η, coefficient of viscosity of the fluid.
⇒ F = A η^a r^b v^c
where A is a constant with no dimensions. Putting the dimensions,
[MLT^-2] = [ML^-1T^-1]^a [L]^b [LT^-1]^c
OR [MLT^-2] = [M^aL^-a+b+c T^-a-c]
Comparing the two sides, we get
a = 1, b = 1 and c = 1
∴ F = k ηr v
As per experiemented results, k = 6π
∴ F = 6π ηr v
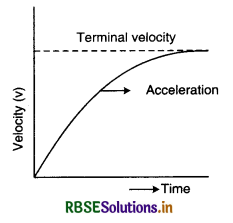
Terminal Velocity
The constant speed that afrelly object eventually reaches when the resistance of medium thorugh which it is falling prevent further acceleration expression for teminal velocity.
Let ρ be the density of the body and σ be the density of the medium, then,
Weight of body = \(\frac{4}{3}\) πr³ ρg ....................(1)

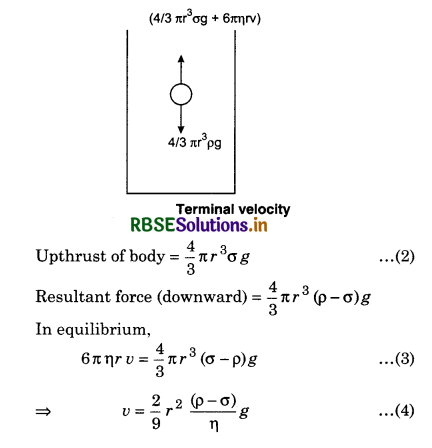
This is the formula for terminal velocity.
It is apparent from the above expression that the terminal velocity is:
(a) Directly proportional to the square of the radius of body.
(b) Directly proportinal t the densities of the body and the medium.
(c) Inversely proportional to the coefficient of viscosity of the medium.
Graph between velocity vs time:
Variation of viscosity with temperature and pressure: (i) Effect of temperature on viscosity:

(i) When a liquid is heated then the kinetic energy of it’s molecules increases and the intermolecular force between them decreases. Hence the viscosity of a liquid decreases with the increase in it’s temperature.
(ii) Viscosity of gases is due to the diffusion of molecules from one moving layer to another. But the rate of diffusion of a gas is directly proportional to the square root of the temperature. So the viscosity of a gas increases with its temperature.
(ii) Effect of pressure:
(i) Except the water, the viscosity of liquid increases with the increase in pressure. In case of water, the viscosity decreases with increase in pressure.
(ii) The viscosity of gas is independent of pressure.

Question 7.
What do you mean by streamline and turbulent flow? How they are decided by Reynold’s number?
Answer:
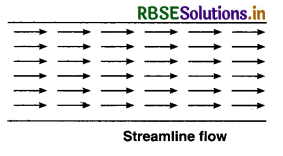
Streamline flow (also called Laminar flow) is a type of flow of fluid in which fluid travels in regular paths. In streamline flow, the velocity, pressure and other such properties remain constant in fluid at each point. When the flow of a liquid is such that the direction (or route) of every particle of the fluid passing through a point is the same as that of first particle that passed through that point then the flow is called streamline flow. The streamline flow over a horizontal surface may be considered as made up of thin layers parallel to each other. The fluid in contact with the horizontal surface is at rest while other layers slide over each other. A streamline may be defined as the path, the tangent to which any point gives the direction of the flow of liquid at that point.

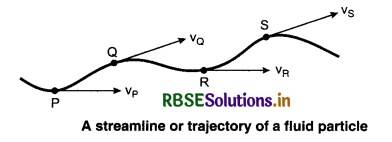
A bundle of many streamlines is called as tube of flow, The boundary of such a tube is always parallel to the velocity of fluid particles. In this no fluid can cross the boundary of the tube.

Turbulent Flow
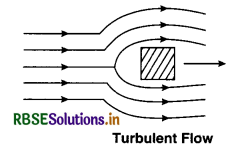
Turbulent flow is a type of flow of fluid in which the fluid travels in irregular path. In this type of flow, the speed of the fluid at a point undergoes changes continuously in both magnitude and direction. Most kinds of fluid flow are turbulent. For example, the flow of air and water. Other examples of this kind of flow are flow of blood in arteries, flow of lava, ocean currents, etc.

Reynold's Number
The flow of a fluid to be steady, streamlined or ratio called the Reynold's number. Reynold number is equivalent to ratio of internal force and viscous force exerted between the layers of the fluid on unit area i.e.;
Reynold's number R = \(\frac{\text { Inertial force on unit area }}{\text { Viscous force on unit area }}\)
Let the mass of fluid ∆m = volume x density
= Av∆tρ
Inertial force acting per unit of area of the fluid

If the Reynold’s number R is:
(i) Between 0 and 2000. then the flow of fluid will be streamlined.
(ii) Between 2000 and 3000, then the flow of liquid will be unstable i.e., it will change from streamline to turbulent flow.
(iii) More than 3000 then the flow of liquid will definitely be turbulent.
Reynold’s number depends upon the velocity of the fluid.
When the value of Reynold’s number is 2000 then the velocity of the fluid is called critical velocity. The critical velocity is that maximum velocity of
the flow of a fluid, at a velocity below which the flow of fluid is streamline and at a velocity above which the flow of fluid is turbulent. Reynold concluded on the basis of the experiments that the value of critical velocity v, depends upon the following factors:
Diameter D of the tube, density of liquid ρ and coefficient of viscosity η.
∴ v_c = \(\frac{R \eta}{\rho D}\)

Question 8.
What are the various forms of energies of a liquid in motion? Prove that in streamline flow the total energy remains constant at each place.
Answer:
A flowing liquid has three types of energies:
1. Pressure Energy-Consider a piston of cross-sectional area A, P is the pressure at the level of the liquid If on displacing the liquid to distance x, F is the external force applied, then, work done is
W = F x = PAx = PV
∴ Pressure energy per unit mass = \(\frac{P A x}{A x \rho}=\frac{P}{\rho}\)
∴ Pressure energy per unit volume = \(\frac{P A x}{A x}\) = P
2. Kinetic Energy: If the mass of liquid is m and volume is V and it flows with velocity v, then, the kinetic energy of liquid = \(\frac{1}{2}\)mv².

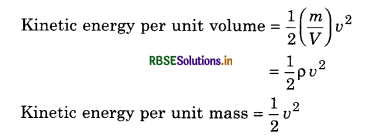
3. Potential Energy: A liquid posseses potential energy by virtue of its position.
Potential energy of liqiud = m g h
where m → mass of liquid
and h → height of liquid
P.E.Volume = \(\frac{m g h}{V}\) = ρ g h
P.E.mass = \(\frac{m g h}{m}\) = gh

Question 9.
On the basis of Bernoulli’s theorem explain the working of aerofoil and Magnus effect.
Answer:
1. Venturimeter: This device is used to measure velocities and mass rate of flow of liquid at the different cross-sections of a pipe. it consists of a constriction inserted in a pipe line and have tapers at the in let and outlet, so that turbulence is avoided. (See fig. 10.18.)

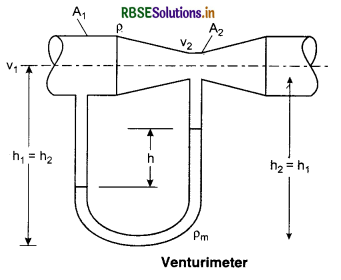
Let at the cross-sectional areas A₁ and A₂, the velocities are v₁ and v₂ respectively.
From the equation of continuity,
A₁v₁ = A₂v₂
From Bernoulli's theorem,


2. Blood flow and heart attack: When on the inner walls of any artery, layer of cholesterol and calcium salt if deposited, its inner diameter decreases i.e.; the artery becomes narrower. To maintain the blood flow in this narrow pact the pressure on the blood should be increased. To increase this pressure the cardiac muscles apply more than normal pressure to push the blood out of the heart. As a result the blood flow in this narrow part increases and from Bernoulli’s principle the pressure in the artery decreases. Thus, in this condition the pressure on the wall of the artery from inside is lesser than the pressure from the outside. So the artery contracts and closes. In this condition Bernoulli’s principle does not apply. Due to pressure applied by the heart on the blood the artery opens again, when blood flows in this constricted part then velocity being more, pressure reduces further and the artery closes again. Now if the deposited layer moves from its place and goes to a smaller blood vessel carrying blood to the heart and blocks it then it leads to heart attack.

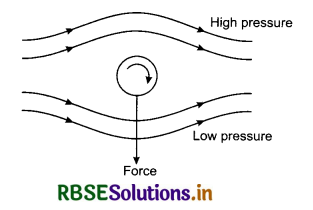
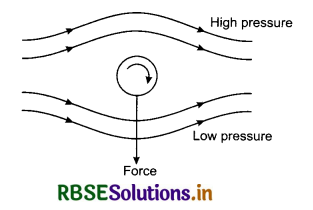
3. Magnus Effect: When a cricket ball is thrown spinning, the air velocity below it becomes more than that on the above. The pressure above it becomes more than that below it. So a resultant force acts on it and hence, the path becomes curved. This effect is called Magnus effect. In other words, Magnus effect is the difference in lateral pressure that causes a ball to take a curved path which is convex towards the greater pressure side.


4. Still water runs deep: The static pressure of deep water is more. So, from the Bernoulli’s principle, the speed of water is less due to more pressure and hence, the water is still.

5. During the arrival of train on the platform, the person standing on the platform bends forward because the velocity of air increases and air pressure decreases due to the fast speed of the train. The air pressure behind the person is more.

6. Atomizer: An atomizer consists of a vessel A containing the liquid which is to be sprayed. Vessel A is connected to a rubber bulb through a tube B.

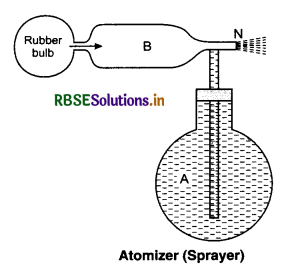
When we press the rubber bulb, air rushes at N. According to Bernoulli’s theorem, low pressure is created near N. The liquid from A rises to B, to compensate the loss of pressure. If we further push the rubber bulb, the liquid comes out from N in the form of fine drops.

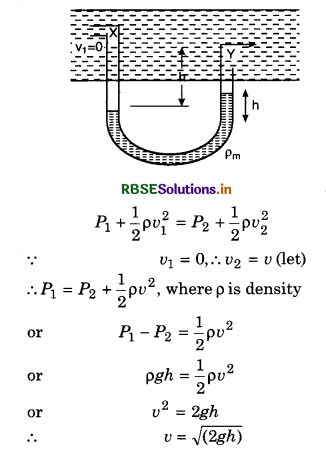
7. Pitot Tube: It is based on Bernoulli’s theorem, it is used to determine the velocity of the fluid. It is basically a U-tube which is shown in the figure. Its X-end is narrow and here velocity of the fluid is zero. It is called as stagnation point. From Bernoulli’s principle, for point X and Y


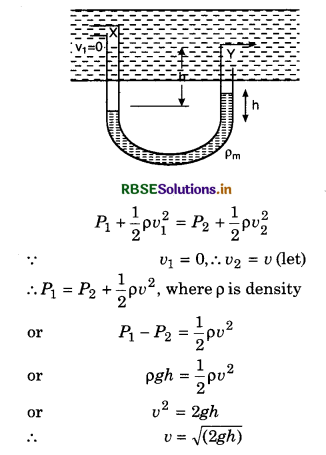
8. Bunsen Burner: In a Bunsen burner, the gas goes out with a great velocity from a fine nozzle. The pressure falls sufficiently below the nozzle and to compensate this decrease, air rushes out from the hole made at the side of the tube. So, air gets mixed with gas and burns.

9. Aerofoil Shape: Bernoulli’s principle is used in designing the shape of wings of aircraft. The curvature on the upper side of the wings is more than that on its lower side and its portion on the back is flat while the portion on the front is round.

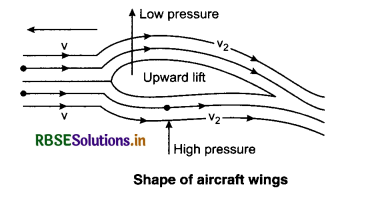
Due to this type of shape of the wings, the velocity of the layers of air on its upper side is more than that on its lower side. Also, the pressure below is more which helps in lifting the plane up and simultaneously pushes it in the forward direction.

Question 10.
What is pitot tube? Explain its working.
Answer:
1. Venturimeter: This device is used to measure velocities and mass rate of flow of liquid at the different cross-sections of a pipe. it consists of a constriction inserted in a pipe line and have tapers at the in let and outlet, so that turbulence is avoided. (See fig. 10.18.)

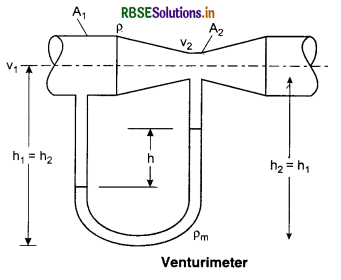
Let at the cross-sectional areas A₁ and A₂, the velocities are v₁ and v₂ respectively.
From the equation of continuity,
A₁v₁ = A2v₂
From Bernoulli's theorem,

2. Blood flow and heart attack: When on the inner walls of any artery, layer of cholesterol and calcium salt if deposited, its inner diameter decreases i.e.; the artery becomes narrower. To maintain the blood flow in this narrow pact the pressure on the blood should be increased. To increase this pressure the cardiac muscles apply more than normal pressure to push the blood out of the heart. As a result the blood flow in this narrow part increases and from Bernoulli’s principle the pressure in the artery decreases. Thus, in this condition the pressure on the wall of the artery from inside is lesser than the pressure from the outside. So the artery contracts and closes. In this condition Bernoulli’s principle does not apply. Due to pressure applied by the heart on the blood the artery opens again, when blood flows in this constricted part then velocity being more, pressure reduces further and the artery closes again. Now if the deposited layer moves from its place and goes to a smaller blood vessel carrying blood to the heart and blocks it then it leads to heart attack.

3. Magnus Effect: When a cricket ball is thrown spinning, the air velocity below it becomes more than that on the above. The
pressure above it becomes more than that below it. So a resultant force acts on it and hence, the path becomes curved. This effect is called Magnus effect. In other words, Magnus effect is the difference in lateral pressure that causes a ball to take a curved path which is convex towards the greater pressure side.


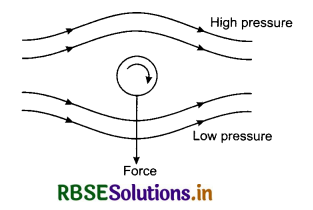
4. Still water runs deep: The static pressure of deep water is more. So, from the Bernoulli’s principle, the speed of water is less due to more pressure and hence, the water is still.

5. During the arrival of train on the platform, the person standing on the platform bends forward because the velocity of air increases and air pressure decreases due to the fast speed of the train. The air pressure behind the person is more.

6. Atomizer: An atomizer consists of a vessel A containing the liquid which is to be sprayed. Vessel A is connected to a rubber bulb through a tube B.

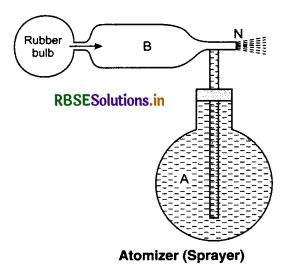
When we press the rubber bulb, air rushes at N. According to Bernoulli’s theorem, low pressure is created near N. The liquid from A rises to B, to compensate the loss of pressure. If we further push the rubber bulb, the liquid comes out from N in the form of fine drops.

7. Pitot Tube: It is based on Bernoulli’s theorem, it is used to determine the velocity of the fluid. It is basically a U-tube which is shown in the figure. Its X-end is narrow and here velocity of the fluid is zero. It is called as stagnation point. From Bernoulli’s principle, for point X and Y


8. Bunsen Burner: In a Bunsen burner, the gas goes out with a great velocity from a fine nozzle. The pressure falls sufficiently below the nozzle and to compensate this decrease, air rushes out from the hole made at the side of the tube. So, air gets mixed with gas and burns.

9. Aerofoil Shape: Bernoulli’s principle is used in designing the shape of wings of aircraft. The curvature on the upper side of the wings is more than that on its lower side and its portion on the back is flat while the portion on the front is round.

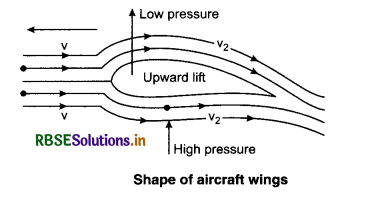
Due to this type of shape of the wings, the velocity of the layers of air on its upper side is more than that on its lower side. Also, the pressure below is more which helps in lifting the plane up and simultaneously pushes it in the forward direction.

Question 11.
Explain cohesive and adhesive forces.
Answer:
Every material is made up of molecules. Molecules exert forces on each other which is called inter-molecular force.
There are two kinds of molecular forces:
1. Adhesive Forces: The force of attraction between the molecules of different substances is called adhesive force. It is different for different pair of substances. For e.g., gum is more adhesive than water.

2. Cohesive Forces: The force of attraction between the molecules of same substances is called cohesive force. It varies as r^-7, where r is the intermolecular separation. So, force of cohesion is more when distance is small and it is negligible when distance is large.

Examples of cohesive and adhesive forces:
1. Water wets the glass but mercury does not: Cohesive force acts between the molecules of a liquid and adhesive force acts between the molecule of a solid and a liquid. The adhesive force between the molecules of water-glass is more the cohesive force between the molecules of water. So the water molecules stick with the molecules of glass and the surface of glass becomes wet. The adhesive force between the molecules of mercury and glass is lesser than the cohesive force between the molecules of mercury. So, the molecules of mercury does not wet the glass.

2. Due to the adhesive forces between the molecules of ink and paper, the ink sticks on the paper. While writing on the block board, due to the adhesive forces between the molecules of chalk and black board,the letters are written on the board.

Question 12.
Explain a formula for excess pressure in a bubble.
Answer:
(i) Mosquitoes sitting on water: Mosquitoes do not sink in water due to surface tension. The liquid surface becomes concave at the points where the legs of the mosquito touch the surface, due to weight of the mosquito. The surface tension acts at a certain angle to the horizontal. Its vertical component acts upwards. The total force acts vertically upwards all along the line of contact, which balances the weight of the mosquito acting downward.

(ii) Excess pressure on concave side of a spherical surface: Consider a small surface element of unit length. If the surface is plane then, the surface tension on the two sides tangential to the surface balances and the resultant force (tangential) is zero. If the surface is convex or concave, the forces due to surface tension acting across the sides of the element will have resultant force R towards the centre of curvature of the surface.

For a curved surface, the surface tension gives rise to a pressure directed towards the centre of curvature of the surface. This pressure balances the opposite pressure acting on the surface. So, there is always an excess pressure on the concave side of the liquid surface.

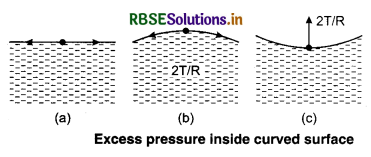
(iii) Hot soup tastes bettter than cold soup: The surface tension in hot soup is less than cold soup. It taster good because it spread out more surface area on tongue.

Question 13.
Derive an expression for the height to which a liquid rises in a capillary tube of radius r.
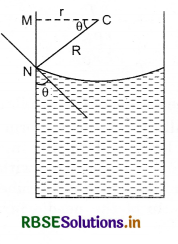
Answer:
Let r be the radius of a capillary tube and θ be the angle of contact. From fig. 10.38,

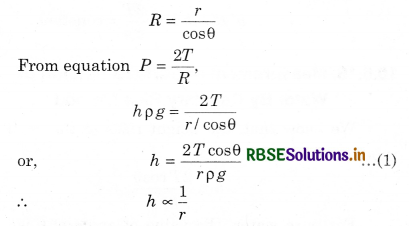
It is apparent that if the radius of the capillary tube is less, then the liquid rises higher.

Question 14.
Explain the method of determination of surface tension by capillary rise method.
Answer:
We know that, the height rises in the capillary tube,
h = \(\frac{2 T \cos \theta}{r \rho g}\)
For pure water, the value of angle of θ is very small.
∴ cosθ ≈ 1
⇒ h = \(\frac{2 T}{r \rho g}\)
or, h = \(\frac{h r \rho g}{2}\)
where r is the radius of the capillary tube.
A clean capillary tube of uniform bore is fixed vertically with its lower end dipping into water taken in a beaker. A needle N is also fixed with the capillary tube as shown in the figure. The tube is raised or lowered until the tip of the needle just touches the water surface.

A travelling microscope M is focused on the meniscus of the water in the capillary tube. The reading R₁ corresponding to the lower meniscus is noted. The microscope is lowered and focused on the tip of the needle and the corresponding reading is taken as R₂. The difference between R₁ and R₂ gives the capillary rise h.

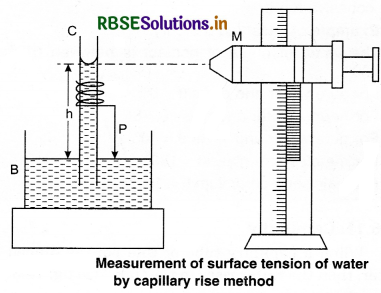
The radius of the capillary tube is determined using the travelling microscope. If ρ is the density of water then the surface tension of water is given by
T = \(\frac{r h \rho g}{2}\)
where g is the acceleration due to gravity.
When a liquid rises in a capillary tube, the weight of the liquid column of density ρ inside the tube is supported by the surface tension (upward) acting around the circumference of the points of contact.
T = \(\frac{r\left(h+\frac{r}{3}\right) \rho g}{2 \cos \theta}\)
where h → height of the liquid column above the liquid meniscus
ρ → density of the liquid
r → inner radius of the capillary tube
θ → angle of contact.

Question 15. 
State and prove Bernoulli’s theorem.
Answer:
Principle: Based on conservation of energy
Statement: According to Bernoulli’s theorem, the sum of the energies possessed by a flowing ideal liquid at a point is constant provided that the liquid is incompressible and non-viscous and flows is streamline.
Potential energy + Kinetic energy + Pressure energy = Constant
P + \(\frac{1}{2}\)ρv² + ρgh = Constant
gh + \(\frac{1}{2}\)v² + \(\frac{P}{\rho}\) = C .....................(1)
where C is a constant.
This is relation is called Bernoulli's theorem.
Dividing equation (1) by g, we get
h + \(\frac{P}{\rho g}+\frac{1}{2} \frac{v^2}{g}\) = C' ......................(2)
where C' is another constant.
For horizontal flow, h remains same thought.
So,
\(\frac{P}{\rho g}+\frac{v^2}{2 g}\) = constant
or, P + \(\frac{1}{2} \rho v^2\) = constant
P is static pressure of the liquid and \(\frac{1}{2} \rho v^2\) is the dynamic and velocity pressure.
Thus, for horizontal motion, the sum of static and dynamic pressure is constant. If P₁, v₁ and P₂, v₂ represent pressures and velocities at two points, then,
P₁ + \(\frac{1}{2} \rho v_1^2\) = P₂ + \(\frac{1}{2} \rho v_2^2\)
Concepts: 1. In Bernoulli's theorem, P + ρgh + \(\frac{1}{2}\)ρv² = constant. The term (P + ρgh) is called static pressure and the term \(\frac{1}{2}\)ρv² is the dynamic pressure of the fluid.
2. Bernoulli theorem is a fundamental principle of the energy.
3. The equation \(\frac{P}{\rho g}+\frac{1}{2} \frac{v^2}{g}\) + h = constant.
the term \(\frac{P}{\rho g}\) = pressure head
the term \(\frac{v^2}{2 g}\) = velocity head
h = gravitational head

Derivation of Bernoulli's Theorem
The energies possessed by a flowing liquid are mutuallly convertiable. When one type of energy increases, the other type of energy decreases and vice-versa. Now, we will derive the Bernoulli's theorem using the work-energy theorem.

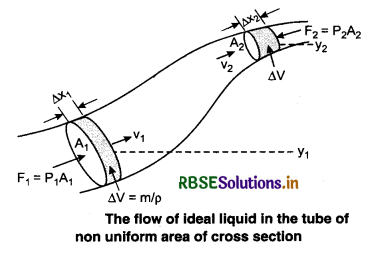
Consider the flow of liquid. Let at any time, the liquid lies between two areas of flowing liquid A₁ and A₂. In time interval ∆t, the liquid displaces from A₁ by ∆x₁ = v₁ ∆t and displaces from A₂ by ∆x₂ = v₂ ∆t. Here v₁ and v₂ are the velocities of the liquid at A₁ and A₂.
The work done on the liquid is P₁ A₁ ∆x₁ by the force and P₂A₂ ∆x₂ against the force respectively.
Net work done,
W = P₁A₁ ∆x₁ - P₂A₂ ∆x₂
⇒ W = P₁A₁ v₁∆t - P₂A₂ v₂ ∆t
= (P₁ - P₂) ∆V .....................(3)
Here, ∆V → the volume of liquid that flows through a cross-section is same (from equation of continuity).
But, the work done is equal to net change in energy (K.E. + P.E.) of the liquid, and

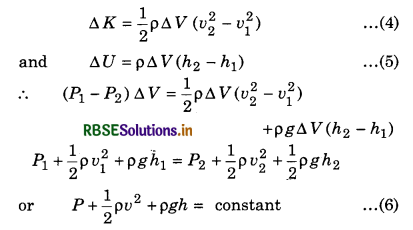
This is the required relation for Bernoulli's theorem.
∵ A₁v₁ = A₂v₂
So, more the cross-sectional area, lesser is the velocity and vice-versa.
So, from Bernoulli's theorem,
P₁ + \(\frac{1}{2}\)ρ₁v₁² = P₂ + \(\frac{1}{2}\)ρ₂v₂²
or P + \(\frac{1}{2}\)ρv² = constant

Question 16. 
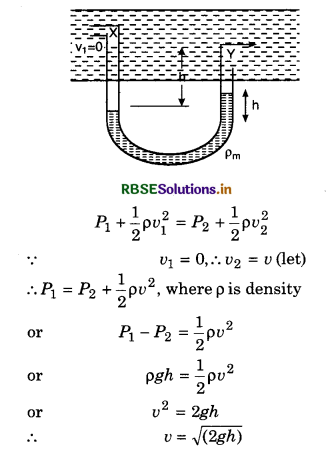
Find out the speed of efflux at a height h from the side of a container both when its top is closed and open. Hence derive Torricelli’s law.
Answer:
Principle: Based on conservation of energy
Statement: According to Bernoulli’s theorem, the sum of the energies possessed by a flowing ideal liquid at a point is constant provided that the liquid is incompressible and non-viscous and flows is streamline.
Potential energy + Kinetic energy + Pressure energy = Constant
P + \(\frac{1}{2}\)ρv² + ρgh = Constant
gh + \(\frac{1}{2}\)v² + \(\frac{P}{\rho}\) = C .....................(1)
where C is a constant.
This is relation is called Bernoulli's theorem.
Dividing equation (1) by g, we get
h + \(\frac{P}{\rho g}+\frac{1}{2} \frac{v^2}{g}\) = C' ......................(2)
where C' is another constant.
For horizontal flow, h remains same through.
So,
\(\frac{P}{\rho g}+\frac{v^2}{2 g}\) = constant
or, P + \(\frac{1}{2} \rho v^2\) = constant
P is static pressure of the liquid and \(\frac{1}{2} \rho v^2\) is the dynamic and velocity pressure.
Thus, for horizontal motion, the sum of static and dynamic pressure is constant. If P₁, v₁ and P₂, v₂ represent pressures and velocities at two points, then,
P₁ + \(\frac{1}{2} \rho v_1^2\) = P₂ + \(\frac{1}{2} \rho v_2^2\)
Concepts: 1. In Bernoulli's theorem, P + ρgh + \(\frac{1}{2}\)ρv² = constant. The term (P + ρgh) is called static pressure and the term \(\frac{1}{2}\)ρv² is the dynamic pressure of the fluid.
2. Bernoulli theorem is a fundamental principle of the energy.
3. The equation \(\frac{P}{\rho g}+\frac{1}{2} \frac{v^2}{g}\) + h = constant.
the term \(\frac{P}{\rho g}\) = pressure head
the term \(\frac{v^2}{2 g}\) = velocity head
h = gravitational head

Question 17.
Derive a formula to measure the rate of flow of a liquid through venturimeter.
Answer:
1. Venturimeter: This device is used to measure velocities and mass rate of flow of liquid at the different cross-sections of a pipe. it consists of a constriction inserted in a pipe line and have tapers at the in let and outlet, so that turbulence is avoided. (See fig. 10.18.)

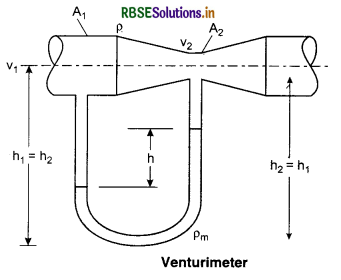
Let at the cross-sectional areas A₁ and A₂, the velocities are v₁ and v₂ respectively.
From the equation of continuity,
A₁v₁ = A₂v₂
From Bernoulli's theorem,

2. Blood flow and heart attack: When on the inner walls of any artery, layer of cholesterol and calcium salt if deposited, its inner diameter decreases i.e.; the artery becomes narrower. To maintain the blood flow in this narrow pact the pressure on the blood should be increased. To increase this pressure the cardiac muscles apply more than normal pressure to push the blood out of the heart. As a result the blood flow in this narrow part increases and from Bernoulli’s principle the pressure in the artery decreases. Thus, in this condition the pressure on the wall of the artery from inside is lesser than the pressure from the outside. So the artery contracts and closes. In this condition Bernoulli’s principle does not apply. Due to pressure applied by the heart on the blood the artery opens again, when blood flows in this constricted part then velocity being more, pressure reduces further and the artery closes again. Now if the deposited layer moves from its place and goes to a smaller blood vessel carrying blood to the heart and blocks it then it leads to heart attack.

3. Magnus Effect: When a cricket ball is thrown spinning, the air velocity below it becomes more than that on the above. The pressure above it becomes more than that below it. So a resultant force acts on it and hence, the path becomes curved. This effect is called Magnus effect. In other words, Magnus effect is the difference in lateral pressure that causes a ball to take a curved path which is convex towards the greater pressure side.


4. Still water runs deep: The static pressure of deep water is more. So, from the Bernoulli’s principle, the speed of water is less due to more pressure and hence, the water is still.

5. During the arrival of train on the platform, the person standing on the platform bends forward because the velocity of air increases and air pressure decreases due to the fast speed of the train. The air pressure behind the person is more.

6. Atomizer: An atomizer consists of a vessel A containing the liquid which is to be sprayed. Vessel A is connected to a rubber bulb through a tube B.

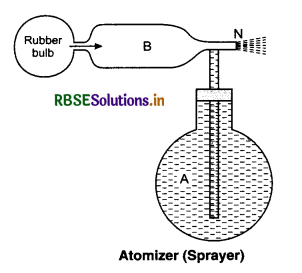
When we press the rubber bulb, air rushes at N. According to Bernoulli’s theorem, low pressure is created near N. The liquid from A rises to B, to compensate the loss of pressure. If we further push the rubber bulb, the liquid comes out from N in the form of fine drops.

7. Pitot Tube: It is based on Bernoulli’s theorem, it is used to determine the velocity of the fluid. It is basically a U-tube which is shown in the figure. Its X-end is narrow and here velocity of the fluid is zero. It is called as stagnation point. From Bernoulli’s principle, for point X and Y


8. Bunsen Burner: In a Bunsen burner, the gas goes out with a great velocity from a fine nozzle. The pressure falls sufficiently below the nozzle and to compensate this decrease, air rushes out from the hole made at the side of the tube. So, air gets mixed with gas and burns.

9. Aerofoil Shape: Bernoulli’s principle is used in designing the shape of wings of aircraft. The curvature on the upper side of the wings is more than that on its lower side and its portion on the back is flat while the portion on the front is round.

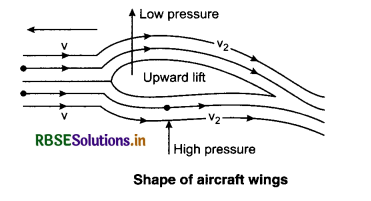
Due to this type of shape of the wings, the velocity of the layers of air on its upper side is more than that on its lower side. Also, the pressure below is more which helps in lifting the plane up and simultaneously pushes it in the forward direction.

Question 18.
Derive an expression for the terminal velocity of a small body falling through a viscous liquid.
Answer:
When a body falls in a viscous medium, it carries layers of fluid which are in body’s contact whereas the layers of fluid in contact with the stationary surface remain almost at rest. The layers of fluid destroys the relative motion and motion of the body is thus opposed. The viscous drag increases with velocity of the body till viscous drag and upthrust of the body are together equal to the weight of the body which acts downwards. When there is no net force, the body moves with the uniform velocity. This velocity is called terminal velocity. Stoke showed that the retarding force F due to viscous drag for a spherical body of radius r that moves with a velocity u in a fluid, with coefficient of viscosity η, is given as:
F = 6πηrv
This expression is known as Stoke's Law.
Derivation with help of dimensions
F ∝ v, velocity;
F ∝ r, radius of the body;
F ∝ η, coefficient of viscosity of the fluid.
⇒ F = A η^a r^b v^c
where A is a constant with no dimensions. Putting the dimensions,
[MLT^-2] = [ML^-1T^-1]^a [L]^b [LT^-1]^c
OR [MLT^-2] = [M^aL^-a+b+c T^-a-c]
Comparing the two sides, we get
a = 1, b = 1 and c = 1
∴ F = k ηr v
As per experiemented results, k = 6π
∴ F = 6π ηr v
Terminal Velocity
The constant speed that afrelly object eventually reaches when the resistance of medium thorugh which it is falling prevent further acceleration expression for teminal velocity.
Let ρ be the density of the body and σ be the density of the medium, then,
Weight of body = \(\frac{4}{3}\) πr³ ρ_g ....................(1)

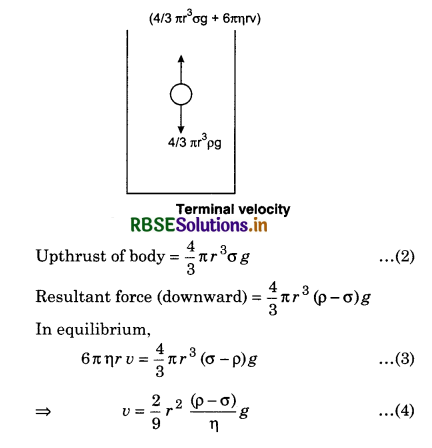
This is the formula for terminal velocity.
It is apparent from the above expression that the terminal velocity is:
(a) Directly proportional to the square of the radius of body.
(b) Directly proportinal t the densities of the body and the medium.
(c) Inversely proportional to the coefficient of viscosity of the medium.
Graph between velocity vs time:
Variation of viscosity with temperature and pressure:
1. Effect of temperature on viscosity:

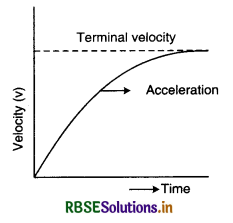
• When a liquid is heated then the kinetic energy of it’s molecules increases and the intermolecular force between them decreases. Hence the viscosity of a liquid decreases with the increase in it’s temperature.
• Viscosity of gases is due to the diffusion of molecules from one moving layer to another. But the rate of diffusion of a gas is directly proportional to the square root of the temperature. So the viscosity of a gas increases with its temperature.

2. Effect of pressure:

• Except the water, the viscosity of liquid increases with the increase in pressure. In case of water, the viscosity decreases with increase in pressure.
• The viscosity of gas is independent of pressure.

Question 19.
Explain surface tension on the basis of molecular forces.
Answer:
It is commonly experienced that drops of a liquid are spherical in shape in the absence of external forces. If a small amount of mercury is dropped from a small height, it is spread out in small spherical globules. The water drops falling from a tap are also spherical. Thus, it is clear that for a given volume the surface area of sphere is minimum. So, on the liquid other than the gravitational force another force acts that tries to minimise its surface area. This force is called the surface tension of the liquid.

Question 20.
Explain some examples which illustrate the existence of surface tension.
Answer:
"The property of the surface of a liquid that allows it to resist an external force, due to the cohesive nature of its molecules."
Walking on water: Small insects such as the water strider can walk on water because their weight is not enough to penetrate the surface.
Floating a needle: A carefully placed small needle can be made to float on the surface of water even though it is several times as dense as water. If the surface is agitated to break up the surface tension, then needle will quickly sink.

Question 21.
Derive a relation between surface tension and surface energy.
Answer:
Consider a rectangular frame (see fig. 10.28), having a sliding wire on one of its arms. Dip the frame in a soap solution and take it out. A soap film is formed on the frame and have two surfaces. Both the surfaces are in contact with the sliding wire. So, surface tension acts on the wire due to both the surface.

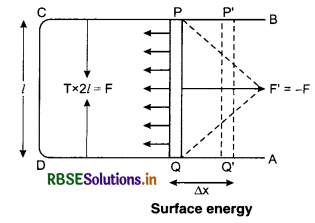
Let T be the surface tension of the soap solution and L be the length of the wire.
The force exerted by each surface on the wire = T x L
So, total force on the wire = 2 T L .................(1)
Let the surfaces contract by ∆x.
Work done on the film, W = F x ∆x
= 2 T L ∆x ......................(2)
Here 2 L x ∆x → total increase in the area of both of the surfaces of film.
Let 2L x ∆x = ∆A
∴ W = T x ∆A
or T = \(\frac{W}{\Delta A}\) ........................(3)
So, surface tension of a liquid is equal to the work done in increasing the surface area of its free surface by one unit. In other words, surface tension is equal to surface energy per unit area.
E_s = T ∆A
The unit of T is J/m^-2 and its dimensional formula is [M¹L⁰T^-2].

Question 22.
Explain some daily life examples based on capillarity.
Answer:
1. As pen nib is split at the tip to provide the narrow capillary and the ink is drawn upto the point continuously.
2. In oil lamps, the oil is drawn up through the capillary of the wick.
3. Clay soils are damped as the water rises quickly to the surface through the capillaries.
4. Water and minerals rise in the plants through the fine capillaries.
5. Blotting paper absorbs ink through the pores.

Question 23.
Explain shape of meniscus for different liquids in capillary.
Answer:
The angle between the tangent drawn on the surface of a liquid from a point of contact of a liquid or solid and on the surface of the solid inside the liquid is called the angle of contact of that liquid or solid. Its value depends on the nature of solid or liquid.

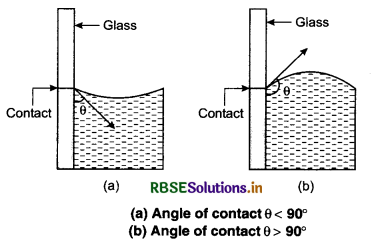
When a glass plate is dipped in water, the molecules of water cling to the glass surface and these molecules rise along the plate. So, the angle of contact between glass and water as less than π/2 (= \(\frac{180^{\circ}}{2}\)) near about 18°.
When the glass plate is dipped in mercury, the liquid is depressed along the plate and angle of contact is greater than \(\frac{\pi}{2}\) near about 1400.

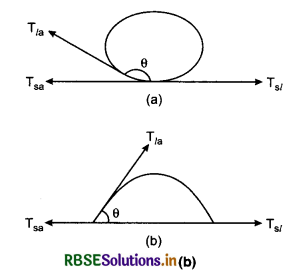
Water forms droplets on lotus leaf as shown in figure 10.31 (a) while water spreads over a clean plastic plate as shown in figure 10.31 (b). Here are three interfacial tensions at all the three interfaces, liquid-air, solid-air and solid-liquid denoted by T_la,T_sa and T_sl respectively.
At the line of contact, the surface forces between the three media must be in equilibrium, from fig. 10.31 (b).
T_la cosθ + T_sl = T_sa
The angle of contact is an angle if T_sl > T_la as in the of water-leaf interface while it is an acute angle if T_sl < T_la as in the case of water-plastic interface,
Cases (i) When θ is an obtuse angle: Here molecules of liquids are attracted strongly to themselves and weakly to those of solid, it costs a lot of energy to create a liquid-solid surface and liquid then does not wet the solid. This is what happens with water on a waxy or oily surface, and with mercury on any surface.
(ii) When θ is an acute angle: If the molecules of the liquid are strongly attracted to those of the solid, this will reduce T_sl and therefore, cosθ may increase or θ may decrease. This is case of water on glass or on plastic and for kerosene oil.
Factors affecting the angle of contact
1. Nature of the solid and liquid in contact.
2. Cleanliness of the surface in contact.
3. Temperature of liquid.
4. Medium above the free surface of liquid.

Question 24.
What do you understand by the term capillarity? Derive an expression for the rise of liquid in a capillary tube.
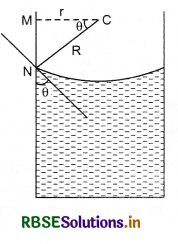
Answer:
When a capillary tube of fine bore is dipped in water, then the water rises in the tube (see fig. 10.36). If the tube is dipped in mercury, there is a
depression of mercury level in the tube. The property of rise or depression of a liquid inside the capillary tube is called capillarity.

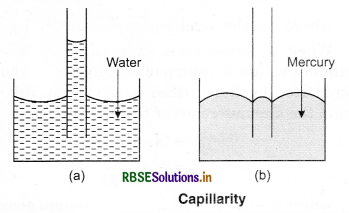
Generally, these liquids which wet the glass rise in the tube while those which do not wet the glass gets depressed.

Let r be the radius of a capillary tube and θ be the angle of contact. From fig. 10.38,

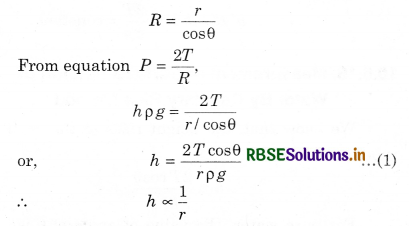
It is apparent that if the radius of the capillary tube is less, then the liquid rises higher.

Conceptual Questions

Question 1.
Why are the droplets of mercury when brought in contact pulled together to form a bigger drop? Also state the reasons whether the temperature of this bigger drop will be the same, or more, or less than the temperature of the smaller drop.
Answer:
It is due to large cohesive forces acting between the molecules of mercury that the droplets of mercury when brought in contact are pulled together to form a bigger drop. The temperature of this bigger drop increases since the surface area decreases.

Question 2.
Explain why a small iron needle sinks in water while a large iron ship floats?
Answer:
A body will float in a liquid if the weight of the liquid displaced by the immersed part of the body in liquid is equal to weight of the body. In case of iron needle, the weight of water displaced by needle is much less than the weight of the needle, hence the iron needle sinks in the water. In case of a large iron ship, the weight of water displaced by the ship is higher than the weight of the ship, hence the ship floats in water.

Question 3.
It is better to wash the clothes in hot soap solution. Why?
Answer:
The soap solution has less surface tension as compared to ordinary water and its surface tension decreases further on heating, the hot soap solution can therefore, spread over large surface area and as such it has more wetting power. It is on account of this property that hot soap solution can penetrate and clean the clothes better than the ordinary water.

Question 4.
When air is blown in between two balls suspended close to each other, they are attracted towards each other. Why?
Answer:
On blowing air in between the two balls, the air velocity is increased and hence pressure is decreased there. Now the pressure on the outer side of the balls being more will exert the force on the balls so that they move towards each other, resulting a collision between them.

Question 5.
A bigger rain drop falls faster than the smaller one. Why?
Answer:
When the rain drops of different sizes fall under gravity, they ultimately move with their terminal velocities due to viscous drag of air. As terminal velocity of a drop varies as the square of its radius, therefore a bigger drop will have greater terminal velocity and hence fall faster than a smaller rain drop.

Question 6.
Machine parts are jammed in winter. Why?
Answer:
A lubricating oil is generally used between the various parts of a machine to reduce the friction. In winter, since the temperature is low, the viscosity of oil between the machine parts increases considerably, resulting in jamming of the machine parts.

Question 7.
The shapes of cars and planes are streamlined, why?
Answer:
When a body moves through a liquid, its motion is opposed by the force of fluid friction, which increases with the speed of the body. When cars and planes, move through air, their motion is opposed by the air friction, which in turn, depends upon the shape of the body. It is due to this reason that cars or planes are given such shapes (known as streamlined shapes) so that air friction is minimum. Rather the movement of air layers on the upper and lower side of streamlined shaped body provides a lift which helps in increasing the speed of the car.

Question 8. 
Two row boats moving parallel to each other and nearby, are pulled towards each other. Explain.
Answer:
According to Bernoulli’s theorem, when velocity of liquid flow increases, the pressure decreases and vice-versa. When two boats move in parallel directions close to each other, the stream of water between the boats is set into vigorous motion. As a result, the pressure exerted by water in between the boats becomes less than the pressure of water outside the boats. Due to this difference of pressures, the boats are pulled towards each other.

Question 9.
According to Bernoulli’s theorem the pressure of water should remain uniform in a pipe of uniform radius. But actually its goes on decreasing, why is it so?
Answer:
When water flows through a pipe, work is done against the viscous force. This work done is taken from the pressure energy. As a result of which the pressure of the water falls, with onward movement of water in pipe. It is due to this reason that a house located at a large distance from a water tank receives water at lower pressure than those houses located closer to water tank.

Question 10.
There is high pressure on the bottom of sea, then how animals survive?
Answer:
There is high pressure at the bottom of the sea. To balance out this pressure, the fishes and other sea animals have extra air dissolved in their blood. This internal fluid pressure balances the high pressure and animals are able to survive. This is the reason why fishes die when they are brought out of water because outside water the internal fluid pressure exceeds the external atmospheric pressure and their veins burst.

Question 11.
Oil is sprinkled on sea waves to calm them. Why?
Answer:
Sprinkling oil reduces the surface tension of sea water due to which a net force acts from lesser surface tension to more surface area and then it calms the sea waves.

Question 12.
Why is it difficult to fill mercury in a glass tube of mercury thermometer?
Answer:
The inner radius of glass tube is very small and due to capillarity the, mercury falls in the tube. Hence it is difficult to fill mercury in glass tube of the thermometer.

Matrix Matching Questions

(A) Match the column I with column II.

Column I	Column II
A. Excess pressure in a liquid drop	P. F = 6πηrv
B. Excess pressure in a soap bubble	Q. \(\frac{\rho v_c D}{\eta}\)
C. Stoke’s law	R. \(\frac{2 T}{r}\)
D. Reynold’s number	S. \(\frac{4 T}{r}\)

Answer:

Column I	Column II
A. Excess pressure in a liquid drop	R. \(\frac{2 T}{r}\)
B. Excess pressure in a soap bubble	S. \(\frac{4 T}{r}\)
C. Stoke’s law	P. F = 6πηrv
D. Reynold’s number	Q. \(\frac{\rho v_c D}{\eta}\)

Numerical Questions

Based on Liquid Pressure

Question 1.
The weight of a man is 60 kg and the area of his each foot is 30 cm². Find out how much pressure he exerts on the earth when (i) he is standing on one foot, (ii) standing on second foot.
Solution:
Given: M = 60 kg; A = 30 x 10^-4 m² = 3 x 10^-3 m²;
g = 9.8 m/s²
(i) When man is standing on one feet,
Pressure P = \(\frac{F}{A}=\frac{M g}{A}=\frac{60 \times 9.8}{3 \times 10^{-3}}\)
= 2 x 9.8 x 10⁴
= 19.6 x 10⁴ N/m²
(ii) When man is standing on both foot, then pressure,
P' = \(\frac{M g}{2 A}=\frac{1}{2} P=\frac{1}{2} \times 19.6 \times 10^4\)
= 9.8 x 10⁴ N/m²

Question 2.
The volume of an air bubble is 1 cm³ at the bottom of a 10 m deep lake. When the bubble reaches at the surface then what will be its volume? The reading of the barometer is 74 cm.
Solution:
Given: h = 10 m; ρ_w = 10³ kg/m³;
V₁ = 1 cm³; V₂ = ?
P_a = 74 cm (mercury)
= 0.74 x 13.6 x 10³ x 9.8 N/m²
Pressure at the bottom of water column
p = hρ_wg = 10 x 10³ x 9.8
= 9.8 x 10⁴ N/m²
From Boyle's law
P₂V₂ = P₁V₁
or P_a.V₂ = (P_a + p) V₁

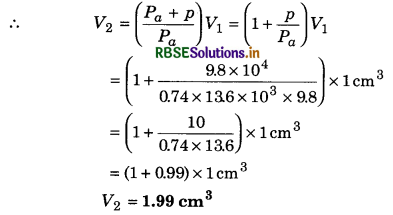
Based on Viscosity

Question 3.
A metal plate 10 cm x 10 cm rests on a layer of glycerine 1 mm thick whose coefficient of viscosity is 1.0 kg m^-1s^-1. Find out the horizontal force required to move the plate with a speed of 1 m/s.
Solution:
Given: A = (10 x 10)cm² = 100 cm²
= 100 x 10^-4 m² = 1 x 10^-2 m²;
∆Z = 1 mm = 1 x 10^-3 m; η = 1.0 kg/ms
∆v = 1.0 cm/s = 10^-2 m/s; F = ?

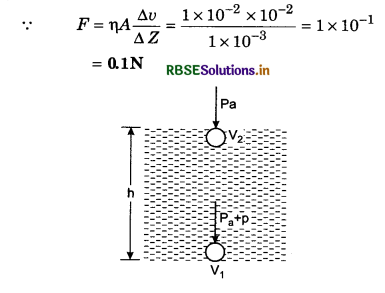
Question 4.
A metal plate of area 100 cm² rests on a layer of glycerine 1 mm thick. If coefficient of viscosity is 1 kg m^-1s^-1, find out the horizontal force required to move the plate with a speed of 7 cm/s.
Solution:
A = 100 cm² = 1 x 10^-2 m²;
∆Z = 1.0 mm = 1 x 10^-3 m;
η = 1.0 kg/m¹s^-1; ∆v = 7.0 cm/s = 7 x 10^-2 m/s; F = ?
F = \(\eta A \frac{\Delta v}{\Delta Z}=\frac{1.0 \times 1 \times 10^{-2} \times 7 \times 10^{-2}}{1 \times 10^{-3}}=0.7 \mathrm{~N}\)

Question 5.
The relative velocity between two parallel layers of water is 8 cm/s and the perpendicular distance between them is 0.1 cm, calculate the velocity gradient.
Solution:
∆v = 8.0 cm/s; ∆x = 0.1 cm
∴ Velocity gradient = \(\frac{\Delta v}{\Delta x}=\frac{8.0}{0.1}\) = 80 s^-1

Based on Terminal Velocity

Question 6.
The diameter of a water drop is 0.003 mm. It is falling in air. Find out the terminal velocity of air. The coefficient of viscosity is 1.8 x 10^-5 kg m^-1s^-1. The density of air is negligible.
Solution:
r = \(\frac{0.003}{2} \mathrm{~mm}=\frac{3 \times 10^{-6}}{2} \mathrm{~m}\) = 1.5 x 10^-6 m; σ = 0; ρ = 10³ kg/m³
η = 1.8 x 10^-5 kg/ms; v_t = ?

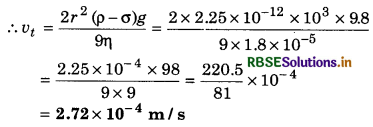
Question 7.
If the terminal velocity of a drop is 12 cm/s, then find out the radius of falling drops in air. The coefficient of viscosity is 1.8 x 10^-4 Poise and density of air is 1.21 x 10^-3 g/cm³.
Solution:
Given: v_t = 12 cm/s = 0.12 m/s; r = ?
η = 1.8 x 10^-4 Poise = 1.8 x 10^-5 kg/ms;
ρ = 1 x 10³ kg/m³
σ = 1.21 x 10^-3 g/cm³ = 1.21 kg/m³

= 0.993052 x 10^-9 = 9.93357 x 10^-10
∴ r = 3.15 x 10^-5 m
= 3.1 x 10^-3 cm

Question 8.
The diameter of sphere A is half that of B. Find out the ratio of their terminal velocity in air.
Solution:
Diameter of A = \(\frac{1}{2}\) x Diameter of B

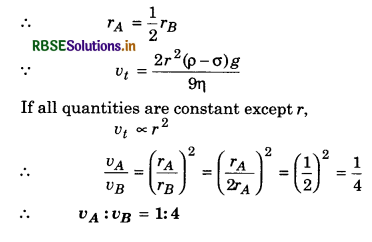
Question 9.
If 2 equal rain drops falling through air the with equal steady velocity of 5 cm/s coalesce. Find out the new terminal velocity of a big drop.
Solution:
∵ v_t ∝ r²
∴ \(\frac{v_2}{v_1}=\frac{R^2}{r^2}=\left(\frac{R}{r}\right)^2\) ...................(1)
∵ Volume of big drop = 2 x Volume of small drop
or \(\frac{4}{3}\)πR³ = 2 x \(\frac{4}{3}\)πr³
or R = 2^1/3 r
∴ From equation (1), \(\frac{v_2}{v_1}=\left(\frac{2^{1 / 3} r}{r}\right)=2^{2 / 3}\)
∴ v₂ = v₁(2)^2/3 = 5(2)^2/3 cm/s

Based on Equation of Continuity

Question 10.
Water flows through a horizontal tap, whose internal diameter is 8 x 10^-3 m, at a speed of 4 x 10^-1 m / s. What should be the diameter of the nozzle if the water is to emerge at a distance 2 x 10^-1 from tap?
Solution:
D₁ = 8 x 10^-3 m, ∴ r₁ = 4 x 10^-3 m
v₁ = 4 x 10^-1 m/s¹ = 0.4 m/s;
h = 2 x 10^-1 m = 0.2 m; D₂ = ?
∵ v² = u² + 2gh
∴ v₂² = v₁² + 2gh = (0.4)² + 2 x 9.8 x 0.2
= 0.16 + 3.92
= 4.08
∴ v₂ = 2.0199 = 2.02 m/s
From equation of continuity
A₂v₂ = A₁v₁ ⇒ πr₂²v₂ = πr₁²v₁

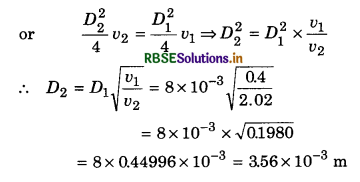
Question 11.
Water flows through a horizontal pipe, whose internal diameter is 2.1 cm, at a speed of 1.1 m/s. What should be the diameter of the nozzle, if the water is to emerge at a speed of 4 m/s?
Solution:
D₁ = 2.1 cm; v₁ = 1.1 m/s, D₂ = ?; v₂ = 4 m/s
From equation of continuity
A₂v₂ = A₁v₁ ⇒ πr₂²v₂ = πr₁²v₁

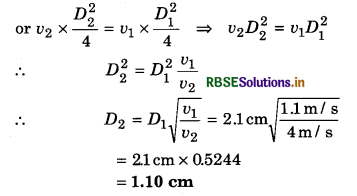
Based on Bernoulli’s Theorem and its Applications

Question 12.
Water of pressure 4 x 10⁴ N/m² is flowing through a pipe of cross sectional area 0.02 m² with velocity 2m/s, the emerging cross-sectional area of the pipe is 0.01 m². What is pressure in the pipe of low cross-sectional area?
Solution:
P₁ = 4 x 104 N/m²; v₁ = 2 m/s; A₁ = 0.02 m²;
A₂ = 0.01 m²; P₂ = ?; ρ = 10³ kg/m³
From equation of continuity

Question 13.
Calculate the minimum pressure required to force the blood from the heart to the top of the head (vertical distance = 50 cm). Assume that the density of blood is 1.04 g/cm. Friction is to be neglected.
Solution:
h = 50 cm = 0.50 m; ρ = 1.04 x 10³ kg/m³;
P = ?
∵ P = ρgh
∴ P = 1.04 x 10³ x 9.8 x 0.5
= 5.096 x 10³ N/m²
= 5.096 x 10³\(\frac{10^5 \text { dyne }}{10^4 \mathrm{~cm}^2}\)
= 5.096 x 10⁴ dyne/m²

Question 14.
The pressure difference between two points along a horizontal pipe, through which water is flowing is 1.4 cm of mercury. If due to non-uniform cross-section, the speed of flow of water at the point of greater cross-section is 60 cm/s, calculate the speed at the other point.
Solution:
P₁ - P₂ = 1.4 cm mercury
= 1.4 x 10^-2 x 13.6 x 10³ x 9.8
= 186.592 x 10
= 1.86 x 10³ N/m²
v₁ = 60 cm/s = 0.6 m/s; v₂ = ?; g = 9.8 m/s²
From Bernoulli's Theorem

Question 15.
The velocity head of water of a horizontal pipe is 1.25 m. Find out the velocity of the flow of water, (g = 10 m/s²)
Solution:
Velocity head = 1.25 m; g = 10 m/s²; v = ?
∵ Velocity head = \(\frac{v^2}{2 g}\)
∴ 1.25 = \(\frac{v^2}{2 \times 10}\)
v₂ = 1.25 x 2 x 10 = 25
∴ v = 5 m/s

Question 16.
The lifting force required to lift an aeroplane is 1000 N/m². If velocity of air flow is 100 m/s inside its wing, then what Will be the velocity from the upper surface of the wing so that the aeroplane receive required lifting force?
(d = 1 kg/m³)
Solution:
Given: P₁ - P₂ = 1000 N/m²; v₁ = 100 m/s; v₂ = ?; P = 1 kg m^-3
From Bernoulli's theorem:

Based on Surface Tension and Surface Energy

Question 17.
The work required by a big drop of water of radius R to break up into 8000 tiny drops of equal volume of water is 5.582 KR Joule. Find out the surface tension of water.
Solution:
∵ Volume of big drop = 8000 x Volume of small drops

Given: ∆W = 5.582πR²
∴ T = \(\frac{\Delta W}{\Delta A}=\frac{5.582 \pi R^2}{4 \pi \times 19 R^2}\)
= \(\frac{5.582}{4 \times 19}\) = 0.0734
T = 7.3 x 10^-2 N/m

Question 18.
The 1000 tiny drops of water, each has radius 10^-7 m coalesce to form a bigger drop. Calculate the surface energy of the bigger drop. Surface tension of water = 7 x 10^-2 N/m.
Solution:

r = 10^-7 m; ∆E = ∆W = ?;
T = 7 x 10^-2 N.m^-1
∵ Volume of big drop = 1000 x Volume small drops
\(\frac{4}{3}\)πR³ = 1000 x \(\frac{4}{3}\)πr³
∴ R = 10r
or R = 10 x 10^-7 = 10^-6 m
∴ Decrease in area
∆A = 1000 x 4πr² - 4πR²
= 4π(1000r² - R²)
= 4π [1000 x (10^-7)² - (10^-6)²]
= 4π [1000 x 10^-14 - 10^-12]
= 4π x 10^-12 [10 - 1]
= 36π x 10^-12 m²
∴ Free energy ∆E = ∆W = T∆A
∆E = 7 x 10^-2 x 36π x 10^-12
= 7 x 36 x \(\frac{22}{7}\) x 10^-14
= 792 x 10^-14
∆E = 7.92 x 10^-12 J

Question 19.
A soap film is on a rectangular wire ring of size 3 cm x 3 cm. If the size of the film is changed to 3 cm x 4 cm, then calculate the work done is this process. The surface tension of soap film is 3 x 10^-2 N/m.
Solution:
A₁ = 3 cm x 3 cm = 9 cm²;
A₂ = 3 cm x 4 cm = 12 cm²;
W = ?; T = 3 x 10^-2 N/m²
∴ ∆A = 2 [A₂ - A₁] = 2 [12 - 9] = 2 x 3 = 6cm²
= 6 x 10-4 m2
∴ W = T∆A = 3 x 10^-2 x 6 x 10^-4 = 18 x 10^-6 J
or W = 1.8 x 10^-5 J

Based on Excess Pressure and Capillarity

Question 20.
Two soap bubbles have radius 0.5 cm and 1.0 cm. The difference in pressure inside the them is 14 N/m². Calculate the surface tension of the soap solution.
Solution:
R₁ = 0.5cm = 0.5 x 10^-2 m;
R₂ = 1.0 cm = 1.0 x 10^-2 m;
∆P = 14 N/m²; T = ?
∆P = ∆P₁ - ∆P₂ = \(\frac{4 T}{R_1}-\frac{4 T}{R_2}\)

Question 21.
The diameter of a U-tube in vertical position are 5.0 mm and 2.0 mm. It is filled with water. What is the difference between water column in the tube? Surface tension of water is 7.3 x 10^-2 N/m.
Solution:
r₁ = \(\frac{5.0}{2}\) = 25 mm = 2.5 x 10^-3 m
r₂ = \(\frac{2.0}{2}\) = 1 mm = 1 x 10^-3 m
T = 7.3 x 10^-2 N/m; d_w = 10³ kg/m³

∴ Difference in water column of both tubes
∆h = h₂ - h₁ = 1.49 - 0.59
= 0.90 cm = 9 mm

Question 22.
Find out excess pressure inside a water drop of radius 2 mm. The surface tension of water is 0.075 N/m.
Solution:
R = 2 mm = 2 x 10^-3 m; P_ex = ?; T = 0.075 N/m
∵ Excess pressure of the drop
P_ex = \(\frac{2 T}{R}=\frac{2 \times 0.075}{2 \times 10^{-3}}\)
= 0.075 x 10³ = 75 N/m²

Question 23.
In a capillary tube water rises upto a height of 3.2 cm. If the diameter of second capillary is twice, then to how much height the liquid will rise?
Solution:
h₁ = 3.2 cm; r₂ = 2r₁; h₂ = ?
∵ r₁h₁ = r₂h₂ ⇒ h₂ = \(\frac{r_1}{r_2}\) h₁
∴ h₂ = \(\frac{r_1}{2 r_1}\) x 3.2 = 1.6 cm
or h₂ = 1.6 cm

Question 24.
Calculate the height to which water will rise in a capillary tube of 0.4 mm radius. If the capillary is inclined at an angle of 60° with the vertical, then what will be the position of the water in the tube? Surface tension of water = 7 x 10^-2 N/m.
Solution:
r = 0.4 mm = 0.4 x 10^-3 m; h = ?; d = 10³ kg/m³; g = 9.8 m/s²; T = 7 x 10^-2 N/m
∵ T = \(\frac{r h d g}{2}\) ⇒ h = \(\frac{2 T}{r d g}\)
∴ h = \(\frac{2 \times 7 \times 10^{-2}}{0.4 \times 10^{-3} \times 10^3 \times 9.8}=\frac{14 \times 10^{-2}}{0.4 \times 9.8}\)
= 3.57 x 10^-2 m
h = 3.57 cm
If capillary tube is inclined to ß angle from vertical, then
l = \(\frac{h}{\cos \beta}\)
Here ß = 60° ∴ cosß = cos 60° = \(\frac{1}{2}\)
∴ l = \(\frac{3.57}{1 / 2}\) = 2 x 3.57
or l = 7.14 cm

Question 25.
Water rises in a capillary tube to a height of 2.0 cm. In another capillary whose radius is one third of it, how much the water will rise? If the first capillary is inclined at an angle of 60° with the vertical, then what will be the position of water in the tube?
Solution:
h₁ = 2 cm, r₂ = \(\frac{r_1}{3}\) then h₂ = ?
∵ r₂h₂ = r₁h₁ ⇒ h₂ = \(\frac{r_1 h_1}{r_2}=\frac{r_1 \times 2}{\frac{r_1}{3}}\) = 2 x 3
h₂ = 6cm
In capillary tube is inclined to ß angle from vertical, then
l = \(\frac{h}{\cos \beta}=\frac{2 \mathrm{~cm}}{\cos 60^{\circ}}=\frac{2 \mathrm{~cm}}{1 / 2}\) = 4 cm
l = 4 cm

Questions for Competitive Examinations

Question 1.
A soap bubble, having radius of 1 mm, is blown from a detergent solution having a surface tension of 2.5 10^-2 N/m. The pressure inside the bubble equals at a point Z₀ below the free surface of water in a container. Taking g = 10 m/s², density of water = 10³ kg/m³, the value of Z₀ is:
(a) 100 cm
(b) 10 cm
(c) 1 cm
(d) 0.5 cm
Solution:
Excess pressure = \(\frac{4 T}{R}\), gauge pressure = ρgz₀
P₀ + \(\frac{4 T}{R}\) = ρ₀ + ρgz₀
z₀ = \(\frac{4 T}{R \times \rho g}\)
z₀ = \(\frac{4 \times 2.5 \times 10^{-2}}{10^{-3} \times 100 \times 10} m\)
z₀ = 1 cm

Question 2.
A small hole of area of cross-section 2 mm is present near the bottom of a fully filled open tank of height 2 m. Taking g = 10 m/s², the rate of flow of water through the open hole would be nearly:
(a) 12.6 x 10^-6 m³/s
(b) 8.9 x 10^-6 m³/s
(c) 2.23 x 10^-6 m³/s
(d) 6.4 x 10^-6 m³/s
Solution:
Rate of flow of liqiud
Q = Av = A\(\sqrt{2gh}\)
= 2 x 10^-6 m² x \(\sqrt{2 \times 10 \times 2} \)m/s
= 2 x 2 x 3.14 x 10^-6 m³/s
= 12.6 x 10^-6 m³/s

Question 3.
Water from a pipe is coming at a rate of 100 litres per minute. If the radius of the pipe is 5 cm, the radius of the pipe is 5 cm, the Reynolds number for the flow is of the order of (density of water = 1000 kg/m³, coefficient of viscosity of water = 1 Pa-s:
(a) 10³
(b) 10⁶
(c) 10²
(d) 10⁴
Solution:
Reynolds number = \(\frac{\rho v d}{\eta}\)
Volume flow rate = v x πr²

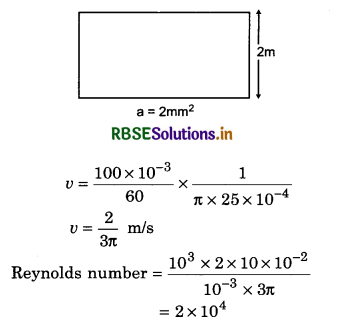
Order = 10⁴

Question 4.
If ''M is the mass of water that rises in a capillary tube of radius V, then mass of water which will rise in a capillary tube of radius ‘2r’ is:
(a) 4 M
(b) M/2
(c) M
(d) 2 M
Solution:
Height of liquid rise in the capillary tube
h = \(\frac{2 T \cos \theta}{r \rho g}\) ⇒ h ∝ \(\frac{1}{r}\)
When raidus becomes double, height becomes half
∴ h' = h/2
Now, M = πr²h x ρ and M' = π (2r)² (h/2) x ρ
= 2M

Question 5.
A small sphere of radius 'r' falls from rest in a viscous liquid. As a result, heat is produced due to viscous force. The rate of production of heat when the sphere attains its terminal velocity is proportional to:
(a) r⁵
(b) r²
(c) r³
(d) r⁴
Solution:
Power = 6πηrv_T. v_T
= 6πηrv_T²
∴ v_T ∝ r²
⇒ Power ∝ r⁵

Question 6.
A small soap bubble of radius 4 cm is trapped inside another bubble of radius 6 cm without any contact. Let P₂ be the pressure inside the inner bubble and P₀, the pressure outside the outer bubble. Radius of another bubble with pressure difference P₂ - P₀ between its inside and outside would be:
(a) 12 cm
(b) 4.8 cm
(c) 2.4 cm
(d) 6 cm
Solution:
Option (c) is correct, fact based question.

Question 7.
A U tube with both the ends open to the atmosphere, is partially filled with water. Oil which is immiscible with water is poured into one side until it stands at a distance of 10 mm above the water level on the other side. Meanwhile the water rises by 65 mm from its original level (see diagram). The density of the oil is:

(a) 425 kg/m³
(b) 800 kg/m³
(c) 928 kg/m³
(d) 650 kg/m³
Solution:
ρ₀g x 140 x 10^-3 = ρ_wg x 130 x 10^-3
ρ₀ = \(\frac{130}{140}\) x 10³ ≈ 928 kg/m³

Question 8.
Water rises to a height ‘h’ in a capillary tube. If the length of capillary tube above the surface of water is made less than 'h', then:
(a) Water rises upto the tip of the capillary tube and then starts overflowing like a fountain.
(b) Water rises upto the top of the capillary tube and stays there without overflowing.
(c) Water rises upto a point a little below the top and stays there.
(d) Water does not rise at all
Solution:
It is given that water rises to a height ‘h’ in the capillary tube, so, the length of the capillary tube above the surface water is made less than ‘h’, then height of water column > length of the capillary tube.
So the liquid will be staying there.

Question 9.
The approximate length of an ocean is 2700 m. The compressibility of water is 45.4 10^-11 Pa^-1 and density of water is 10³ kg/m³. What fractional compression of water will be obtained at the bottom of the ocean?
(a) 0.8 x 10^-2
(b) 1.0 x 10^-2
(c) 1.2 x 10^-2
(d) 1.4 x 10^-2
Solution:
Given, d = 2700 m, ρ = 10³ kg/m³
Compressibility = 45.4 x 10^-11 per pascal
The pressure at the bottom of the ocean is given by
p = ρgd
= 10³ x 10 x 2700
= 27 x 10⁶ Pa
So, fractional compressibility x pressure
= 45.4 x 10^-11 x 27 x 10⁶
= 1.2 x 10^-2

Question 10.
A wind with speed 40 m/s blows parallel to the roof of a house. The area of the roof is 250 m². Assuming that the pressure inside the house is atmospheric pressure, the force exerted by the wind on the roof and the direction of the force will be: (Pair = 1.2kg/m³)
(a) 4.8 x 10⁵ N, downwards
(b) 4.8 x 10⁵ N, upwards
(c) 2.4 x 10⁵ N, upwards
(d) 2.4 x 10⁵ N, downwards
Solution:
From Bernoulli's theorem,
p₁ + \(\frac{1}{2}\)ρv₁² = p₂ + \(\frac{1}{2}\)ρv₂²
where, p₁, p₂ are pressure inside and outside the roof and v₁, v₂ are velocities of wind inside and outside the roof. Neglect the width of the roof.
Pressure difference is
p₁ - p₂ = \(\frac{1}{2}\)ρ(v₂² - v₁²)
= \(\frac{1}{2}\) x 1.2(402 - 0)
= 960 N/m²
Force acting on the roof is given by,
F = (p₁ - p₂)A = 960 x 250
= 24 x 10⁴ N = 2.4 x 10⁵ N
As the pressure inside the roof is more than outside to it. So the force will act in the upward direction. i.e.,
F = 2.4 x 10⁵ N upwards.

Question 11.
A certain number of spherical drops of a liquid of radius r coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then:

Solution:
As energy released = (A_f - A_i)T

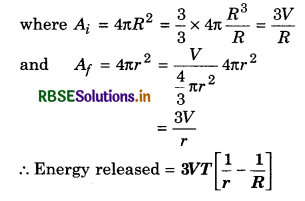
Question 12.
The wettability of a surface by a liquid depends, primarily on:
(a) Viscosity
(b) Surface tension
(c) density
(d) Angle of contact between the surface and the liquid.
Solution:
The wettabiity of a surface by a liquid depends primarily on the angle of contact between the surface and the liquid.

Question 13.
Consider two solid spheres P and Q each of density 8gm cm^-3 and diameters 1 cm and 0.5 cm, respectively. Sphere P is dropped into a liquid of density 0.8 gm cm^-3 and viscosity η = 3 Poiseuilles. Sphere Q is dropped into a liquid of density 1.6 gm cm-3 and viscosity η = 2 Poiseuilles. The ratio of the terminal velocities of P and Q is:
(a) 3
(b) 4
(c) 5
(d) 6
Solution:
6πηrv + ρ_LV_g = ρ₀V_g

Question 14.
There is a circular tube in a vertical plane.Two liquids which do not mix and of densities d₁ and d₂ are filled in the tube. Each liquid subtends 90° angle at the centre. Radius joining their inter face makes an angle a with the vertical. Ratio d₁/d₂ is

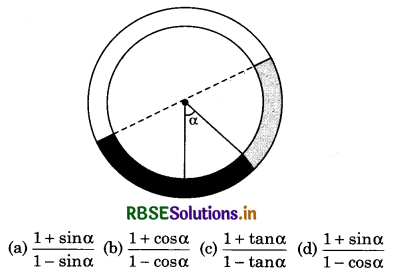
Solution:
Equating pressure at A, we get
R sinαd₂ + R cosαd₂ + R(1 - cosα)d₁ = R(1 - sinα)d₁
(sinα + cosα)d₂ = d₁ (cosα - sinα)

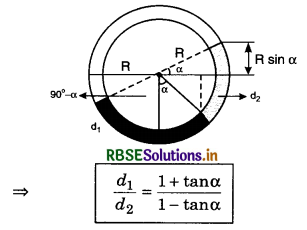
Question 15.
A glass capillary tube is of the shape of truncated cone with an apex angle α so that its two ends have cross-sections of different radii. When dipped in water vertically, water rises in it to a height h, where the radius of its cross-section is b. If the surface tension of water is S, its density is ρ, and its contact angle with glass is θ, the value of h will be (g is the acceleration due to gravity)

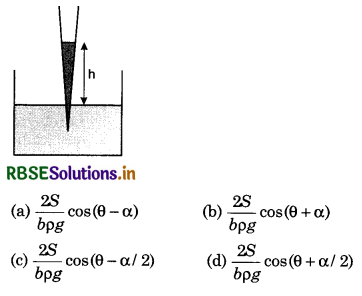
Solution:
Using geometry,

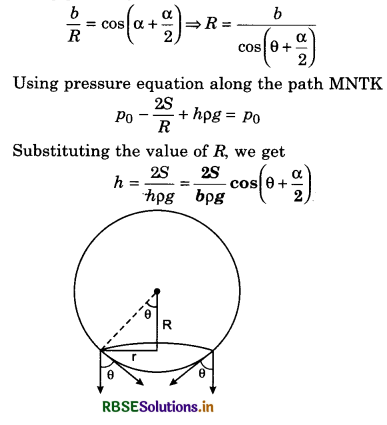
Question 16.
On heating water, bubbles beings formed at the bottom of the vessel detach and rise. Take the bubbles to be spheres of radius R and making a circular contact of radius r with the bottom of the vessel. If r << R and the surface tension of water is T, Value of r just before bubbles detach is (density of water is ρ):

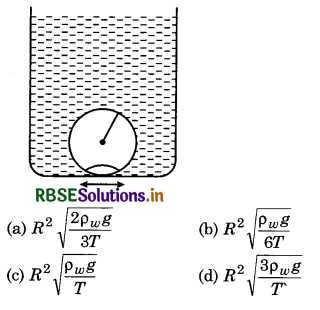
Solution:
The bubble will detach if
∫ sinθT x dl = T(2πr)sinθ
Buoyant force ≥ surface tension force

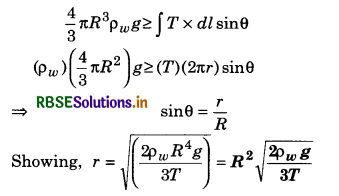
Question 17.
Assume that a drop of liquid evaporates by decrease in its surface energy, so that its temperature remains unchanged. What should be the minimum radius of the drop for this to be possible? The surface tension is T, density of liquid is ρ and L is its latent heat of vaporization.

Solution:
Decrease in surface energy = Heat required in vaporization
∴ (T) (ds) = L (dm)
∴ (T) (2) (4πr) dr = L (4πr² dr)ρ
∴ r = \(\frac{2 T}{\rho L}\)

Question 18.
A thin liquid film formed between a U-shaped wire and a light slider supports a weight of 1 x 10^-2 N (See figure). The length of the slider is 30 cm and its weight is negligible. The surface tension of the liquid film is:

(a) 0.0125 N/m
(b) 0.1 N/m
(c) 0.05 N/m
(d) 0.025 N/m
Solution:
The force of surface tension acting on the slider balances the force due to the weight.

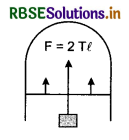
⇒ F = 2Tl = W
⇒ 2T (0.3) = 1.5 x 10^-2
⇒ T = 2.5 x 10^-2 N/m

Question 19.
Water is flowing continuously from a tap having an internal diameter 8 x 10^-3 m. The water velocity as it leaves the tap is 0.4 mis. The diameter of the water stream at a distance 2 x 10^-1 m below the tap is close to:
(a) 7.5 x 10^-3 m
(b) 9.6 x 10^-3 m
(c) 3.6 x 10^-3 m
(d) 5.0 x 10^-3 m
Solution:
By equation of continuity.
(a x v)_top = (a x v)_bottom
vb² - (0.4)² = 2 x 9.8 x 0.2 (∵ v² = u² + 2gh)
∴ vb = 2m/s nearly
π(8 x 10^-3) x 0.4 = πd² x 4
∴ d = 3.6 x 10^-3 m