RBSE Class 11 Physics Important Questions 14 दोलन

Rajasthan Board RBSE Class 11 Physics Important Questions Chapter 14 दोलन Important Questions and Answers.

RBSE Class 11 Physics Chapter 14 Important Questions दोलन

बहुचयनात्मक प्रश्न:

प्रश्न 1. 
सरल आवर्त गति में प्रत्यानयन बल किसके अनुक्रमानुपाती होता है?
(अ) वेग
(ब) माध्य स्थिति से विस्थापन
(स) द्रव्यमान
(द) कोणीय त्वरण 
उत्तर:
(ब) माध्य स्थिति से विस्थापन

प्रश्न 2. 
एक लड़की झूले पर बैठी झूल रही है। यदि लड़की झूले पर खड़ी हो जाये तो झूले के दोलनकाल पर क्या प्रभाव पड़ेगा?
(अ) दोलनकाल अधिक होगा
(ब) दोलनकाल कम होगा
(स) दोलनकाल बदलेगा नहीं
(द) दोलनकाल लड़की के भार पर निर्भर करेगा।
उत्तर:
(ब) दोलनकाल कम होगा

 

प्रश्न 3. 
दो स्थानों पर सेकण्ड लोलक की लम्बाइयां क्रमशः l₁ तथा l₂ हैं, उन स्थानों पर गुरुत्वीय त्वरण की निष्पत्ति (g₁ : g₂) होगी:
(अ) l₂/l₁
(ब) l₁/l₂
(स) l₂²/l₁²
(द) l₁²/l₂²
उत्तर:
(ब) l₁/l₂

प्रश्न 4. 
सरल आवर्त गति करते हुए कण की कला π /2  -है, जबकि उसका
(अ) ऊर्जा का मान अधिकतम हो
(ब) विस्थापन अधिकतम हो
(स) वेग अधिकतम हो
(द) त्वरण का मान अधिकतम हो।
उत्तर:
(ब) विस्थापन अधिकतम हो

प्रश्न 5. 
m द्रव्यमान का एक पिण्ड एक स्प्रिंग से बँधा हुआ है और दोलन करता है। यदि स्प्रिंग का बल नियतांक K हो तो पिण्ड का दोलनकाल होगा: 

उत्तर:
\(\text { (ब) } 2 \pi \sqrt{\frac{m}{\mathrm{~K}}}\)

प्रश्न 6. 
एक सरल लोलक जब दोलन करता है तो:
(अ) मध्यमान स्थिति में इसकी स्थितिज ऊर्जा अधिकतम होती है 
(ब) अधिकतम विस्थापन की स्थिति में इसकी गतिज ऊर्जा अधिकतम होती है।
(स) अधिकतम विस्थापन की स्थिति में इसकी गतिज तथा स्थितिज ऊर्जा न्यूनतम होती है।
(द) मध्यमान स्थिति में इसकी गतिज ऊर्जा अधिकतम होती है।
उत्तर:
(द) मध्यमान स्थिति में इसकी गतिज ऊर्जा अधिकतम होती है।

प्रश्न 7. 
स्थिर गाड़ी की छत से लटके हुए लोलक का आवर्तकाल T है। जब गाड़ी एक समान त्वरण a से त्वरित होती है तब आवर्तकाल:
(अ) बढ़ जायेगा बढ़
(ब) घट जायेगा
(स) अप्रभावित रहेगा
(द) अनन्त हो जायेगा। 
उत्तर:
(ब) घट जायेगा

प्रश्न 8. 
साम्य स्थिति से प्रारम्भ होने वाली सरल आवर्त गति का आयाम 1.0 सेमी. तथा आवर्तकाल 0.1 सेकण्ड है तो तात्कालिक विस्थापन (सेमी.) होग:
(a) y = 0.1 sin 2π/1.0t
(b) y = 0.1 sin 2π/0.1t
(c) y = 0.1 sin 2π/1.0t
(d) y = 0.1 sin 2π x 0.1t
संकेत y = A sin ωt = A sin 2π/Tt
प्रश्नानुसार दिया है A = 1.0 सेमी. तथा T = 0.1 सेकण्ड
 ∴ y = 1.0 sin 2π/0.1t  सेमी.
 उत्तर:
(b) y = 0.1 sin 2π/0.1t
 
प्रश्न 9. 
एक दोलनी स्प्रिंग का तात्कालिक विस्थापन y = 5sin (0.2πt + π/2) मीटर है। इसका दोलनकाल है:
(अ) 1.57 सेकण्ड
(ब) 5 सेकण्ड
(स) 0.2 सेकण्ड
(द) 10 सेकण्ड
संकेत दिया है: y = 5sin (0.2πt + π/2)मीटर
तात्कालिक विस्थापन के सामान्य समीकरण से तुलना करने पर
\(\begin{aligned} y & =A \sin \left(\frac{2 \pi}{T} t+\phi\right) \\ \frac{2 \pi}{T} & =0.2 \pi \end{aligned}\)
= 10 सेकण्ड
उत्तर:
(द) 10 सेकण्ड

प्रश्न 10. 
सरल आवर्त गति की माध्य स्थिति में होगी:
(अ) गतिज ऊर्जा अधिकतम तथा स्थितिज ऊर्जा न्यूनतम 
(ब) गतिज ऊर्जा न्यूनतम तथा स्थितिज ऊर्जा अधिकतम 
(स) गतिज ऊर्जा तथा स्थितिज ऊर्जा दोनों अधिकतम 
(द) गतिज ऊर्जा तथा स्थितिज ऊर्जा दोनों न्यूनतम 
उत्तर:
(अ) गतिज ऊर्जा अधिकतम तथा स्थितिज ऊर्जा न्यूनतम 

प्रश्न 11. 
पिण्ड लोलक में पिण्ड को गुरुत्व केन्द्र से निलम्बन करने पर पिण्ड लोलक का आवर्तकाल होगा:
(अ) शून्य
(ब) अनन्त
(स) शून्य से थोड़ा अधिक
(द) 9.8 सेकण्ड
संकेत: पिण्ड लोलक का आवर्तकाल
\(T=2 \pi \sqrt{\frac{\frac{\mathrm{k}^2}{l}+\mathrm{e}}{\mathrm{g}}}\)
पिण्ड लोलक को गुरुत्व केन्द्र से लटकाने पर t = 0
\(\therefore T=2 \pi \sqrt{\frac{\frac{\mathrm{k}^2}{0}+0}{\mathrm{~g}}}=\infty\)
उत्तर:
(ब) अनन्त

प्रश्न 12. 
सरल आवर्त गति में तात्कालिक विस्थापन कण के तात्कालिक वेग से होता है:
(अ) π/2 कला कोण से पीछे
(ब) π/2 कला कोण से आगे
(स) π कला कोण से पीछे
(द) π कला कोण से आगे
संकेत: तात्कालिक विस्थापन
y = A sin ωt
तात्कालिक वेग
v = dy/dt  = A cos ωt
v = A sin (ωt + π/2)
अतः तात्कालिक विस्थापन कण के तात्कालिक वेग से π/2 कोण से पीछे होता है।
उत्तर:
(अ) π/2 कला कोण से पीछे

प्रश्न 13. 
एक स्प्रिंग में लटके 11 द्रव्यमान का दोलनकाल T है स्प्रिंग को काटकर आधा करके, उस पर दुगुना द्रव्यमान लटकाकर दोलन कराये जाते हैं। अब दोलनकाल होगा:
(अ) T
(ब) 4T
(स) T/2
(द) 8T
संकेत स्प्रिंग का आवर्तकाल
\(\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\)
स्प्रिंग को काट कर आधा करने पर प्रत्येक टुकड़े का बल नियतांक
K = 2k.
अतः आधे टुकड़े से 2m द्रव्यमान लटका कर दोलन कराने पर

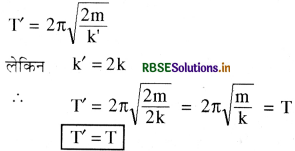
उत्तर:
(अ) T

प्रश्न 14. 
यदि A अनुप्रस्थ काट की यू-नली में द्रव h  ऊँचाई तक चढ़ता है, तब द्रव की दोलनी गति का आवर्तकाल T है। A/4  अनुप्रस्थ काट ऊँचाई तक भर कर दोलन करायें तो वाली यू- नली में द्रव को आवर्तकाल होगा :
(अ) T
(ब) T/2
(स) 2T
(द) T/4
उत्तर:
(अ) T

प्रश्न 15. 
द्रव में तैरते गट्टे को अल्पविस्थापित करने पर यह A आयाम व T आवर्तकाल के दोलन करता है। गति की माध्य स्थिति में इसका वेग होगा:
(अ) 4A/T
(ब) 2A/T
(स) 2A/T
\(\text { (द) } 2 \pi \sqrt{\frac{\mathrm{A}}{\mathrm{T}}}\)
उत्तर:
(स) 2A/T

प्रश्न 16. 
दो सरल आवर्त गतियों की कोणीय आवृत्तियाँ 100 तथा 1000 रेडियन प्रति सेकण्ड हैं। यदि इनका विस्थापन (आयाम) समान हो तो इनके अधिकतम त्वरणों का अनुपात होगा:
(अ) 1 : 10
(ब) 1 : 10²
(स) 1 : 10³
(द) 1 : 10⁴
संकेत:
त्वरण amax =  ω²A
आयाम दोनों के लिये समान है
amax α ω² A
\(\begin{aligned} \frac{\left(\mathrm{a}_{\max }\right)_1}{\left(\mathrm{a}_{\max }\right)_2} & =\frac{\omega_1^2}{\omega_2^2}=\left(\frac{\omega_1}{\omega_2}\right)^2=\left(\frac{100}{1000}\right)^2 \\ & =\frac{1}{10^2} \Rightarrow 1: 10^2 \end{aligned}\)
उत्तर:
(ब) 1 : 10²

प्रश्न 17. 
सरल आवर्त गति एक ऐसी F अनुक्रमानुपाती होता है:
(अ) आयाम के
(ब) विस्थापन के
(स) वेग के
(द) विस्थापन के वर्ग के 
उत्तर:
(ब) विस्थापन के

प्रश्न 18. 
सरल आवर्त गति में:
(अ) कला का मान नियत होता है।
(ब) गतिज ऊर्जा का मान नियत होता है। 
(स) स्थितिज ऊर्जा का मान नियत होता है। 
(द) आयाम का मान नियत होता है।
उत्तर:
(द) आयाम का मान नियत होता है।

प्रश्न 19. 
एक सरल लोलक का आयाम दुगुना करने पर उसके वेग का अधिकतम मान कितना गुना हो जायेगा:
(अ) आधा
(ब) एक-चौथाई
(स) दुगुना
(द) चार गुना
उत्तर:
(स) दुगुना

प्रश्न 20. 
ऋजु रेखा के अनुदिश एक कण आयाम A से सरल आवर्त गति करता है । कण की स्थितिज ऊर्जा तब अधिकतम होगी जब उसका विस्थापन है:
(अ) +A
(ब) शून्य
(स) ±A/3
(द) ± \(\pm \frac{\mathrm{A}}{\sqrt{2}}\)
उत्तर:
(अ) +A

प्रश्न 21. 
एक पिण्ड की गति के समीकरण निम्नलिखित हैं। इनमें सरल आवर्त गति के लिये कौनसा सम्बन्ध सही होगा:
(अ) परिणामी बल = kx
(ब) वेग = k (A² - x²)
(स) त्वरण = kx²
(द) स्थितिज ऊर्जा = 1/2 KA² sin² ωt
उत्तर:
(द) स्थितिज ऊर्जा = 1/2 KA² sin² ωt

प्रश्न 22. 
सरल आवर्त गति करते हुए कण की साम्य स्थिति से दूरी पर स्थितिज ऊर्जा होती है:
(अ) 1⁄2mω²x²
(ब) 1/2mω²A²
(स) 1/2mω²(A² - x²)
(द) शून्य
उत्तर:
(अ) 1⁄2mω²x²

प्रश्न 23. 
सरल आवर्त गति करते समय लोलक की माध्य स्थिति पर गतिज ऊर्जा तथा अधिकतम विस्थापन पर स्थितिज ऊर्जा का अनुपात होता हैं:
(अ) 1 से अधिक
(ब) 1 से कम
(स) 1 के बराबर
(द) इसकी लम्बाई तथा गुरुत्वीय त्वरण के अनुपात के बराबर
उत्तर:
(स) 1 के बराबर

प्रश्न 24. 
सरल आवर्त गति में कण के अधिकतम त्वरण तथा अधिकतम वेग का अनुपात होता है:
(अ) 2π/T
(ब) T/2π
(स) a
(द) aω
उत्तर:
(अ) 2π/T

प्रश्न 25. 
सरल आवर्त गति कर रहे कण की औसत गतिज ऊर्जा होगी:
(अ) 1/4kA²
(ब)  1/2kA²
(स) KA²
(द) इनमें से कोई नहीं 
उत्तर:
(अ) 1/4kA²

प्रश्न 26.
यदि पृथ्वी के व्यास के अनुदिश एक सुरंग बनाई जाये और उसमें एक पत्थर छोड़ दिया तो:
(अ) पत्थर पृथ्वी के केन्द्र पर जाकर रुक जायेगा। 
(ब) पत्थर पृथ्वी के दूसरे सिरे तक पहुँच कर रुक जायेगा।
(स) पत्थर पृथ्वी के केन्द्र पर सरल आवर्त गति करेगा।
(द) पत्थर पृथ्वी के दूसरे सिरे पर पहुँच कर अन्तरिक्ष में चला जायेगा।
उत्तर:
(स) पत्थर पृथ्वी के केन्द्र पर सरल आवर्त गति करेगा।

प्रश्न 27. 
द्रव्यमान m के एक कण की गति है। इसकी कोणीय आवृत्ति होगी-

उत्तर:
\(\text { (अ) } \sqrt{\alpha}\)

प्रश्न 28. 
सरल आवर्त गति कर रहे कण का माध्य स्थिति से x₁ तथा x₂ दूरी पर क्रमश: वेग V₁ तथा V₂ , है तो कण का आवर्तकाल है:

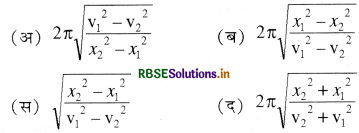
उत्तर:
\(\text { (स) } \sqrt{\frac{x_2^2-x_1^2}{\mathrm{v}_1^2-\mathrm{v}_2{ }^2}}\)

प्रश्न 29. 
यदि सरल लोलक को पानी में दोलन कराया जाये तो आवर्तकाल:
(अ) थोड़ा-सा घटेगा।
(ब) समान रहेगा।
(स) थोड़ा-सा बढ़ेगा।
(द) दुगुना हो जायेगा। 
उत्तर:
(स) थोड़ा-सा बढ़ेगा।

प्रश्न 30. 
धातु से बने एक खोखले गोले में पानी भर कर एक लम्बे धागे से लटकाया गया है। उसमें एक सूक्ष्म छिद्र पेंदे में किया गया है जिससे पानी धीरे-धीरे रिसता है। यदि अब गोले को दोलन कराया जाये तो उसका आवर्तकाल:
(अ) लगातार घटता रहेगा।
(ब) लगातार बढ़ेगा।
(स) पहले बढ़ेगा फिर घटेगा। 
(द) निश्चित रहेगा। 
उत्तर:
(स) पहले बढ़ेगा फिर घटेगा। 

प्रश्न 31. 
सरल आवर्त गति कर रहे कण की यांत्रिक ऊर्जा होती है:
(अ) त्वरण के अनुक्रमानुपाती 
(ब) आयाम के अनुक्रमानुपाती। 
(स) आयाम के वर्ग के अनुक्रमानुपाती।
(द) दोलनकाल के अनुक्रमानुपाती।
उत्तर:
(स) आयाम के वर्ग के अनुक्रमानुपाती।

रिक्त स्थानों की पूर्ति कीजिए:

प्रश्न 1.
धनुष पर प्रत्यंचा चढ़ाकर बाण छोड़ना ................... कहलाती है।
उत्तर:
अनावर्त गति

प्रश्न 2. 
दोलनी या कम्पनिक गति करते कण का माध्य स्थिति से अधिकतम विस्थापन, .................... कहलाता है। 
उत्तर:
आयाम

प्रश्न 3.
सरल आवर्त गति में प्रत्यानयन बल, साम्य स्थिति से विस्थापन के समानुपाती तथा विपरीत दिशा में होता है अर्थात् F = ..................
उत्तर:
-ky

प्रश्न 4. 
समीकरण \(\frac{d^2 y}{d t^2}+\omega^2 y=0\) को रैखिक सरल आवर्त गति का ...................... कहते हैं।
उत्तर:
अवकल समीकरण

प्रश्न 5.
सरल आवर्त गति में विस्थापन से वेग, कला कोण .......................  से सदैव आगे रहता है।
उत्तर:
π /2

प्रश्न 6.
सरल आवर्त गति कर रहे कण का जब विस्थापन शून्य (माध्य स्थिति) होता है, तब कण का वेग ................................  व कण का त्वरण होता है।
उत्तर:
अधिकतम, शून्य

प्रश्न 7.
सरल आवर्त गति में कण की कुल ऊर्जा .....................  रहती है।
उत्तर:
नियत

प्रश्न 8.
यदि किसी स्प्रिंग को काटकर उसके बराबर टुकड़े कर दिये जायें तो प्रत्येक टुकड़े का बल नियतांक ...................... हो जायेगा।
उत्तर:
गुना

प्रश्न 9. 
लोलक का आवर्तकाल गोलक के द्रव्यमान पर ..................... करता है। 
उत्तर:
निर्भर नहीं

प्रश्न 10.
U-नली में द्रव के दोलन का आवर्तकाल T = ........................ होता है।
उत्तर:
\(2 \pi \sqrt{\frac{h}{g}}\)

नीचे दिये गये वाक्यों में सत्य / असत्य कथन का चयन कीजिए:

प्रश्न 1.
एक लड़की झूले पर बैठी झूल रही है। यदि लड़की झूले पर खड़ी हो जाए तो झूले का दोलनकाल कम होगा।
उत्तर:
सत्य

प्रश्न 2.
स्थिर गाड़ी की छत से लटके हुए लोलक का आवर्तकाल T है। जब गाड़ी एक समान त्वरण a से त्वरित होती है तब आवर्तकाल बढ़ जायेगा। 
उत्तर:
असत्य

प्रश्न 3.
दो स्थानों पर सेकण्ड लोलक की लम्बाइयाँ क्रमशः l₁, तथा l₂ हैं, उन स्थानों पर गुरुत्वीय त्वरण की निष्पत्ति g₁ : g₂ का मान l₁ : l₂ होगा। 
उत्तर:
सत्य

प्रश्न 4.
सरल आवर्त गति में तात्कालिक विस्थापन कण के तात्कालिक वेग से π/2 कला कोण से आगे होता है।
उत्तर:
असत्य

प्रश्न 5. 
दो सरल आवर्त गतियों की कोणीय आवृत्तियाँ 10 तथा 100 रेडियन प्रति सेकण्ड हैं। यदि इनका विस्थापन (आयाम) समान हो तो इनके अधिकतम त्वरणों का अनुपात (1 : 10² ) होगा।
उत्तर:
सत्य

प्रश्न 6.
सरल आवर्त गति कर रहे कण की औसत गतिज ऊर्जा 1/2 KA² होगी।
उत्तर:
असत्य

प्रश्न 7.
द्रव्यमान m के एक कण की गति d²x/dt² + ox = 0 द्वारा निरूपित है। इसकी कोणीय आवृत्ति का मान 0 होगा।
उत्तर:
असत्य

प्रश्न 8.
सरल आवर्त गति करते समय लोलक की माध्य स्थिति पर गतिज ऊर्जा तथा अधिकतम विस्थापन पर स्थितिज ऊर्जा का अनुपात 1 के बराबर होता है।
उत्तर:
सत्य

प्रश्न 9.
सरल आवर्त गति में विस्थापन व त्वरण के मध्य कालान्तर का मान 180° होता है।
उत्तर:
सत्य

प्रश्न 10.
यदि एक स्प्रिंग पर 11 द्रव्यमान लटकाने पर उसमें x दूरी का विस्तरण होता है, उस स्प्रिंग का बल नियतांक का परिमाण mg/X होगा।
उत्तर:
सत्य

कॉलम - A से कॉलम B का सही मिलान कीजिए:

प्रश्न 1.

कॉलम-A	कॉलम-B
1. अनावर्त गति का उदाहरण है	(A) रैखिक सरल आवर्त गति का अवकल समीकरण
2. आवर्त गति का उदाहरण है	(B) आयाम के वर्ग तथा आवृत्ति के वर्ग के
3. आवृत्ति तथा आवर्त काल में सम्बन्ध होता है।	\(\text { (C) } K=\frac{K_1 K_2}{K_1+K_2}\)
4. d2y/dt2 + ω2y = 0 है।	(D) nT = 1
5. आवर्तकाल T =	(E) गेंद् को फेंकना
6. कोणीय आवृत्ति ω का मान बराबर होता है।	(F) परमाणु के कक्ष में इलेक्ट्रॉनों की गति
7. अधिकतम विस्थापन \(y  = \pm \mathrm{A}\) लेने पर गतिज ऊर्जा कितनी होगी?	(G) 1/T
8. \(\int_0^T \cos ^2 \omega t d t\) का मान होगा।	(H) शून्य
9. सरल आवर्त गति में कण की सम्पूर्ण ऊर्जा समानुपाती होती है।	\(\text { (I) } \frac{2 \pi}{2}\)
10. श्रेणी क्रम स्प्रिंग संयोजन होता है।	\(\text { (J) } \sqrt{\frac{k}{m}}\)

उत्तर:
 

कॉलम-A	कॉलम-B
1. अनावर्त गति का उदाहरण है	(E) गेंद् को फेंकना
2. आवर्त गति का उदाहरण है	(F) परमाणु के कक्ष में इलेक्ट्रॉनों की गति
3. आवृत्ति तथा आवर्त काल में सम्बन्ध होता है।	(D) nT = 1
4. d2y/dt2 + ω2y = 0 है।	(A) रैखिक सरल आवर्त गति का अवकल समीकरण
5. आवर्तकाल T =	\(\text { (I) } \frac{2 \pi}{2}\)
6. कोणीय आवृत्ति ω का मान बराबर होता है।	\(\text { (J) } \sqrt{\frac{k}{m}}\)
7. अधिकतम विस्थापन \(y  = \pm \mathrm{A}\) लेने पर गतिज ऊर्जा कितनी होगी?	(H) शून्य
8. \(\int_0^T \cos ^2 \omega t d t\) का मान होगा।	(G) 1/T
9. सरल आवर्त गति में कण की सम्पूर्ण ऊर्जा समानुपाती होती है।	(B) आयाम के वर्ग तथा आवृत्ति के वर्ग के
10. श्रेणी क्रम स्प्रिंग संयोजन होता है।	\(\text { (C) } K=\frac{K_1 K_2}{K_1+K_2}\)

 

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1. 
सरल आवर्त गति के लिये त्वरण तथा विस्थापन में क्या सम्बन्ध है?
उत्तर:
त्वरण a α विस्थापन।

प्रश्न 2. 
सीमांत सिरे से सरल आवर्त गति प्रारम्भ करने वाले पिण्ड का प्रारम्भिक कला कोण कितना होता है?
उत्तर:
π/2

प्रश्न 3. 
एक आवर्त गति में प्रारम्भिक कला Φ  = 3π/16 है। इसे आवर्तकाल T में व्यक्त कीजिये।
उत्तर:
प्रारम्भिक कला कोण Φ = 3/32 : T : T = 27 होता है।

प्रश्न 4. 
सरल आवर्त गति में विस्थापन का मान इसके त्वरण मान से कितने कला कोण से आगे होता है?
उत्तर:
अर्थात् सरल आवर्त गति में विस्थापन का मान इसके त्वरण से कला कोण से आगे होते हैं।

प्रश्न 5. 
सरल आवर्त गति में कौनसी भौतिक राशि संरक्षित रहती है? 
उत्तर:
कुल यांत्रिक ऊर्जा।

प्रश्न 6. 
सरल लोलक की कुल ऊर्जा तथा दोलन आवृत्ति में क्या सम्बन्ध है?
उत्तर:
कुल ऊर्जा = 1/2mω²A²
लेकिन ω = 2πn
∴ कुल ऊर्जा = 1/2m(2πn)² A²
= 2π²mn²A ²

प्रश्न 7. 
यदि 0.1 किग्रा. के पिण्ड का आयाम 3 सेमी. तथा दोलनकाल 2 सेकण्ड हो तो कुल यांत्रिक ऊर्जा का मान क्या होगा?
उत्तर:
कुल ऊर्जा = 1/2mω²A²

प्रश्न 8. 
कठोर स्प्रिंग के स्थान पर उतनी ही लम्बाई की मुलायम स्प्रिंग का उपयोग करने पर दोलनकाल पर क्या प्रभाव पड़ेगा?
उत्तर:
बढ़ जायेगा। चूँकि आवर्तकाल \(\mathrm{T}=2 \pi \sqrt{\frac{m}{k}}\)
मुलायम स्प्रिंग के लिये का मान कठोर स्प्रिंग से कम होता है।

प्रश्न 9. 
स्प्रिंग की लम्बाई करने पर उसका स्प्रिंग नियतांक क्या होगा?
उत्तर:
गुना बढ़ जायेगा।

प्रश्न 10. 
सरल लोलक प्रयोग को माउण्ट आबू पर करने पर गुरुत्वीय त्वरण 1% कम हो जाता है। लोलक घड़ी से सही समय प्राप्त करने के लिये लोलक लम्बाई में क्या परिवर्तन होना चाहिये?
उत्तर:
लोलक लम्बाई में 1% कमी होगी।

प्रश्न 11. 
एक लड़की झूला झूल रही है। लड़की झूलते-झूलते खड़ी हो जाती है तो आवर्तकाल पर क्या प्रभाव पड़ेगा?
उत्तर:
आवर्तकाल घटेगा। चूँकि खड़े होने पर उसका द्रव्यमान केन्द्र ऊपर उठ जायेगा, इस कारण से प्रभावकारी लम्बाई कम हो जायेगी जिस कारण से आवर्तकाल घटेगा।

प्रश्न 12. 
सरल लोलक में लोहे के गोलक के स्थान पर उसी आकार का सोने का गोलक लटकाकर प्रयोग करने पर आवर्तकाल में क्या प्रभाव पड़ेगा?
उत्तर:
अपरिवर्तित रहेगा। चूँकि प्रभावकारी लम्बाई में किसी भी प्रकार का परिवर्तन नहीं होता है। इस कारण से आवर्तकाल अपरिवर्तित रहेगा।

प्रश्न 13. 
सरल आवर्त गति करते हुए किसी कण के त्वरण, विस्थापन तथा आवृत्ति के बीच सम्बन्ध लिखिये।
उत्तर:
a = -4π²n²y = -ω²y

प्रश्न 14. 
एक सरल लोलक के दोलन आयाम को उसके वर्तमान मान का आधा कर दिया जाये तो उसके आवर्तकाल का मान कितना हो जायेगा?
उत्तर:
अपरिवर्तित रहेगा। चूँकि आवर्तकाल आयाम पर निर्भर नहीं करता है।

प्रश्न 15 
सरल आवर्त गति में विस्थापन व त्वरण के मध्य कितना कालान्तर होता है?
उत्तर:
π या 180°

प्रश्न 16. 
सरल आवर्त गति कर रहे कण का त्वरण a=(-p/q)x दिया गया है तब इस कण का आवर्तकाल क्या होगा?
उत्तर:
आवर्तकाल \(\mathrm{T}=2 \pi \sqrt{\frac{q}{p}}\)

प्रश्न 17. 
सरल आवर्त गति कर रहे कण की किसी स्थिति पर स्थितिज ऊर्जा कुल ऊर्जा की आधी है, तब उस स्थिति पर विस्थापन क्या होगा?
उत्तर:
0.707 आयाम।

प्रश्न 18. 
एक सरल लोलक की कुल ऊर्जा E है। जिस क्षण पर लोलक का विस्थापन आयाम का आधा होता है उस क्षण लोलक की गतिज ऊर्जा और स्थितिज ऊर्जा क्या होगी?
उत्तर:
गतिज ऊर्जा = 3E/4 स्थितिज ऊर्जा =E/4

प्रश्न 19. 
सरल आवर्त गतिमान कण पर न्यूनतम प्रत्यानयन बल किस स्थिति में होता है?
उत्तर:
साम्यावस्था की स्थिति में।

प्रश्न 20. 
एक हल्के स्प्रिंग से 1 किलोग्राम का बाट लटकाने पर वह 1 सेकण्ड में 4 दोलन करता है, उसी स्प्रिंग से 4 किलोग्राम का बाट लटकाने पर वह प्रति सेकण्ड कितने दोलन करेगा?
उत्तर:
प्रति सेकण्ड दो दोलन करेगा।

प्रश्न 21. 
एक स्प्रिंग से लटके द्रव्यमान m के दोलनों की आवृत्ति है। स्प्रिंग की लम्बाई को काटकर n₁ आधा कर देने पर पुन: वही द्रव्यमान n₂ आवृत्ति से दोलन करता है  n₁/n₂ का मान ज्ञात कीजिये।
उत्तर:
n₁/n₂ = √2

प्रश्न 22. 
यदि एक स्प्रिंग पर m द्रव्यमान लटकाने पर उसमें x दूरी का विस्तरण होता है, उस स्प्रिंग का बल नियतांक का परिमाण क्या होगा।
उत्तर:
स्प्रिंग का बल नियतांक का परिमाण mg/x होगा।

प्रश्न 23. 
सरल लोलक में प्रत्यानयन बल का मान लिखिये, जबकि विस्थापन कोण θ कम हो।
उत्तर:
प्रत्यानयन बल F = mg sinθ
θ बहुत कम है
∴ प्रत्यानयन बल
 sinθ = θ
F = mgθ

प्रश्न 24. 
सरल आवर्त गति में कण की कुल ऊर्जा रहती है।
उत्तर:
कुल ऊर्जा E = 1/2mw² A² स्थिर रहती हैं।

प्रश्न 25. 
सरल लोलक की आवृत्ति का सूत्र लिखिये।
उत्तर:
\(n=\frac{1}{2 \pi} \sqrt{\frac{g}{l}}\)

प्रश्न 26. 
सरल लोलक में लोहे के ठोस गोलक के स्थान पर उसी आकार का खोखला गोलक लटका कर प्रयोग करने पर आवर्तकाल में क्या प्रभाव पड़ेगा?
उत्तर:
अपरिवर्तित रहेगा। चूंकि आवर्तकाल गोलक के द्रव्यमान पर निर्भर नहीं करता है।

प्रश्न 27. 
सरल आवर्त गति कर रहे कण द्वारा एक सम्पूर्ण दोलन में सम्पन्न कार्य कितना होता है?
उत्तर:
शून्य।

प्रश्न 28. 
सरल आवर्त गति कर रहे कण के त्वरण, विस्थापन तथा आवृत्ति को आपस में लिखिये। 
उत्तर:
त्वरण a = ω²y
या
a = (2πn)²y = 4π ²n²y 

प्रश्न 29. 
एक कृत्रिम भू-उपग्रह में लोलक घड़ी क्यों काम नहीं करती?
उत्तर:
भारहीनता के कारण दोलन नहीं होते।

प्रश्न 30. 
सरल आवर्त गति कर रहे कण पर प्रत्यानयन बल किस स्थिति पर अधिकतम होता है?
उत्तर:
चरम स्थिति पर
F = -kr = -KA

प्रश्न 31. 
एक लोलक के दोलक को ऋण आवेशित कर दिया जाता है तथा इसके नीचे धन आवेशित चालक प्लेट रख दी जाती है। लोलक को दोलन कराये जाते हैं। लोलक के आवर्तकाल पर क्या प्रभाव पड़ेगा?
उत्तर:
दोलक और प्लेट के मध्य विद्युत क्षेत्र के कारण आकर्षण बल लगेगा अतः g का प्रभावी मान बढ़ जायेगा, इस कारण आवर्तकाल घट जायेगा।

प्रश्न 32. 
एक केबिन में लटके लोलक की आवृत्ति क्या होगी, जब स्वतंत्रतापूर्वक गिर रहा हो?
उत्तर:
स्वतंत्रतापूर्वक गिरती वस्तुओं पर त्वरण का मान शून्य होता है। अतः आवृत्ति भी शून्य होगी।

प्रश्न 33. 
स्प्रिंग में सरल आवर्त दोलन के लिए प्रत्यानयन बल कहाँ से प्राप्त होता है?
उत्तर:
प्रत्यानयन बल प्राप्त होता है।
सरल लोलक - गुरुत्वीय त्वरण
स्प्रिंग - प्रत्यास्थता

प्रश्न 34. 
एक मनुष्य घड़ी पहने एक मीनार से नीचे गिर रहा है, क्या घड़ी सही समय प्रदर्शित करेगी?
उत्तर:
हाँ, क्योंकि हाथ की घड़ी स्प्रिंग की कार्यप्रणाली पर निर्भर करती है तथा g का कोई प्रभाव नहीं होता है।

प्रश्न 35. 
सरल आवर्त गति कर रहे किसी लोलक के लिए यह आवश्यक क्यों है कि उसका आयाम लम्बाई की तुलना में कम हो?
उत्तर:
चूँकि \(\mathrm{T}=2 \pi \sqrt{\frac{l}{g}}\), के सूत्र में माना गया है कि (sinθ = 0) अतः यह तभी सत्य होती है जब 6 बहुत कम हो अर्थात् लम्बाई की तुलना में आयाम कम हो 
θ =

लघूत्तरात्मक प्रश्न:

प्रश्न 1. 
दर्शाइये कि परवलयिक विभव कूप में कण सरल आवर्त गति करता है।
उत्तर:
जब कोई पिण्ड सरल आवर्त गति करता है तो उसकी माध्य स्थिति से x दूरी पर स्थितिज ऊर्जा PE. = U = 1/2kx² होती है। जब हम स्थितिज ऊर्जा U और विस्थापन x में ग्राफ खींचते हैं तो एक परवलय प्राप्त होता है। इस प्रकार के विभव फलन को परवलयिक विभव कूप कहते हैं क्योंकि इसका आकार कुएं के समान होता है। सरल आवर्त गति इस प्रकार के विभव कूप में पायी जाती है।
स्थितिज ऊर्जा U =1/2kx²
कण पर लगने वाला नैज बल
F = -d/dx(U)
F = -d/dx(1/2kx²) = 1/2k.2x
F = -kx
स्पष्ट है कि प्रत्यावस्थान बल विस्थापन के समानुपाती होता है और उसकी दिशा माध्य स्थितिज की ओर होती है।
अतः पिण्ड सरल आवर्त गति करेगा
कण का त्वरण a = -k/mx = -ω2x
या
\(\frac{d^2 x}{d t^2}=-\omega^2 x\)
तथा इसका हल x = A sin (ωt + Φ ) होगा। अतः यदि किसी वस्तु का विभव फलन U = 1/2kx² हो तो वस्तु सरल आवर्त गति करेगी।

प्रश्न 2. 
कमानी स्प्रिंग से लटके पिण्ड के दोलन में यांत्रिक ऊर्जा संरक्षण को समझाइये
उत्तर:
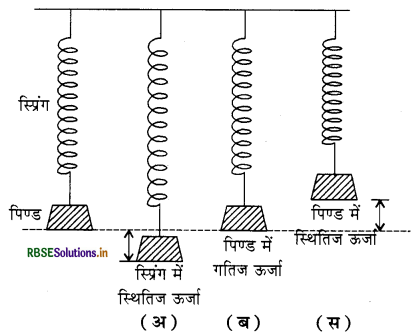
स्प्रिंग से लटके पिण्ड की गति में ऊर्जा रूपांतरण - आगे चित्र दिया है जिसमें एक स्प्रिंग लटकी है, जिसके निचले सिरे पर एक पिण्ड बंधा है। पिण्ड अपनी साम्य स्थिति में है। जब पिण्ड को थोड़ा नीचे खींचकर छोड़ देते हैं तो यह ऊपर-नीचे दोलन करने लगता है। दोलन की विभिन्न स्थितियों को चित्र में दर्शाया गया है। जब पिण्ड को नीचे खींचते हैं तो स्प्रिंग खिंचती है। जैसा चित्र 'अ' में दर्शाया गया है। स्प्रिंग को खींचने में किया गया कार्य इनमें स्थितिज ऊर्जा के रूप में संचित हो जाता है। अतः पिण्ड की निम्नतम स्थिति में कुल ऊर्जा स्प्रिंग में स्थितिज ऊर्जा के रूप में विद्यमान रहती है। जब पिण्ड को छोड़ देते हैं तो स्प्रिंग अपनी सामान्य अवस्था में आने लगती है तथा इसके साथ ही पिण्ड अपनी साम्य स्थिति की ओर लौटने लगता है। अतः स्प्रिंग की स्थितिज ऊर्जा पिण्ड की गतिज ऊर्जा में बदलने लगती है। पिण्ड के साम्य स्थिति में आने पर कुल ऊर्जा पिण्ड की गतिज ऊर्जा के रूप में होती है। जैसा चित्र 'ब' में दर्शाया है।

पिण्ड साम्य स्थिति में ठहरता नहीं है बल्कि जड़त्व के कारण ऊपर की ओर जाता है जिससे कि स्प्रिंग दबने लगती है । पुनः पिण्ड की गतिज ऊर्जा स्प्रिंग की स्थितिज ऊर्जा में बदलने लगती है। पिण्ड की उच्चतम स्थिति में इसकी गतिज ऊर्जा शून्य हो जाती है। तथा कुल ऊर्जा स्प्रिंग की स्थितिज ऊर्जा के रूप में संचित हो जाती है। जैसा चित्र 'स' में दर्शाया गया है। इस प्रकार गतिज तथा स्थितिज ऊर्जाओं का परस्पर रूपान्तरण होता रहता है परन्तु कुल ऊर्जा का मान प्रत्येक स्थिति में उतना ही रहता है । अत: दोलन में यांत्रिक ऊर्जा संरक्षित रहती है।

प्रश्न 3. 
सरल लोलक का आवर्तकाल सूत्र लिखिये। आवर्तकाल किन-किन कारकों से प्रभावित होता है?
उत्तर:
दोलनकाल \(\mathrm{T}=2 \pi \sqrt{\frac{l}{g}}\)
स्पष्ट है कि सरल लोलक का दोलनकाल इसकी प्रभावी लम्बाई (/) के वर्गमूल के समानुपाती तथा गुरुत्वीय त्वरण g के वर्गमूल के व्युत्क्रमानुपाती होता है। गुरुत्वीय त्वरण g के मान में परिवर्तन के कारण दोलन काल भी प्रभावित होता है। दोलन काल, गोलक की द्रव्यमान पर निर्भर नहीं करता है। सरल लोलक की लम्बाई बदलने पर दोलन काल भी प्रभावित होता है। 

प्रश्न 4. 
यदि सरल लोलक (आधार सहित) मुक्त रूप से नीचे गिरने लगे तो दोलन काल कितना होगा? सकारण बताइये।
उत्तर:
यदि सरल लोलक मुक्त रूप से नीचे गिरने लगे तब g = 0 हो जायेगा।
आवर्तकाल का सूत्र
\(\mathrm{T}=2 \pi \sqrt{\frac{l}{g}}\)
g के स्थान मान शून्य रखने पर सरल लोलक का आवर्तकाल अनन्त हो जायेगा जिससे वह दोलन नहीं करेगा।

प्रश्न 5. 
स्प्रिंग का बल नियतांक किन-किन कारकों पर निर्भर करता है?
उत्तर:
स्प्रिंग नियतांक ( प्रत्यानयन गुणांक) k का मान स्प्रिंग के प्रत्यास्थ गुण के अतिरिक्त स्प्रिंग की मूल लम्बाई पर भी निर्भर करता है। मुलायम स्प्रिंग के लिये k का मान कम और कठोर स्प्रिंग के लिये k का मान अधिक होता है। इसी प्रकार अधिक लम्बाई वाली स्प्रिंग के लिये k कम और छोटी स्प्रिंग के लिये k अधिक होता है।

प्रश्न 6. 
पानी में तैरते हुये गट्टे का आवर्तकाल T है। नमकीन पानी में तैरते हुये उसी गट्टे का आवर्तकाल किस प्रकार प्रभावित होगा? 
उत्तर:
तैरते हुये लकड़ी के आयताकार गट्टे का दोलन काल
\(\mathrm{T}=2 \pi \sqrt{\frac{h}{g}}\)
हम जानते हैं कि नमकीन पानी में गद्य कम डूबेगा। इस कारण से h का मान पहले की तुलना में कम प्राप्त होगा, यहाँ g (Constant) है। इस कारण से आवर्तकाल T का मान पहले की तुलना में कम लगेगा।

प्रश्न 7. 
छोटी-छोटी एक जैसी कई स्प्रिंगों को (i) श्रेणी क्रम तथा (ii) समान्तर क्रम में संयोजित करने पर स्प्रिंग नियतांक का मान किस प्रकार प्रभावित होता है?
उत्तर:
छोटी-छोटी एक जैसी कई स्प्रिंगों को जब हम श्रेणीक्रम में संयोजित करते हैं तब संयोजन का प्रभावी स्प्रिंग नियतांक k का मान प्रत्येक छोटी स्प्रिंग के नियतांक का 1/n  गुना हो जाता है। यहाँ n पर छोटी-छोटी एक जैसी स्प्रिंगों की संख्या है। अर्थात् पहले की तुलना में 1/n गुना हो जाता है। समान्तर क्रम में संयोजित स्प्रिंगों के लिये प्रभावी बल नियतांक प्रत्येक स्प्रिंग के बल नियतांक के योग के बराबर होता है।
k = k₁ + k₂

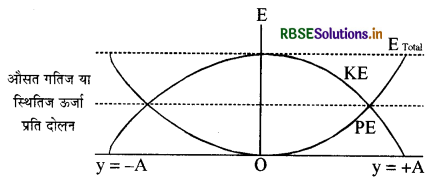
प्रश्न 8. 
औसत गतिज या स्थितिज ऊर्जा प्रति दोलन का ग्राफीय निरूपण कीजिये।
उत्तर:
ग्राफीय निरूपण (Graphical Representation):

प्रश्न 9. 
S.H.M. में एक कण का विस्थापन x = Asin (ωt + Φ) द्वारा दिया जाता है। यदि समय t को 2π/ω  से बढ़ा दिया जाये तो दिखाइये कि x का मान वही रहता है।
उत्तर:
S. H.M. में कण का विस्थापन समय पर 
x = Asin (ωt + Φ) होता है। .................... (1)
यदि समय t + 2π/ω  पर कण का विस्थापन X है तब
x1 = Asin(ω(t + 2π/ω)+Φ)
x1 = Asin[(ωt + 2π) + Φ] = Asin[2π + (ωt + Φ)]
अर्थात् S. H.M. में समय t या [t + 2π/ω] के लिये कण का विस्थापन वही रहता है।

प्रश्न 10. 
एक लड़की बैठी हुई स्थिति में झूल रही है। यदि वह खड़ी हो जाये तो झूले का आवर्तकाल किस प्रकार परिवर्तित होगा? 
उत्तर:
सरल लोलक का दोलन समय
\(\mathrm{T}=2 \pi \sqrt{\frac{1}{g}}\) अर्थात् \(\mathrm{T} \propto \sqrt{l}\)
द्वारा दिया जाता है। जब लड़की खड़ी हो जाती है तो लटकन बिन्दु और झूलते शरीर के द्रव्यमान केन्द्र की दूरी कम हो जाती है। अर्थात् / कम हो जाता है। यही कारण है कि T का मान कम हो जायेगा।

प्रश्न 11. 
पुल पार करते समय कदम मिलाकर चलते सैनिकों से कदम तोड़कर चलने (सामान्य व्यक्ति की तरह चलने) को क्यों कहा जाता है?
उत्तर:
यदि सैनिक कदम से कदम मिलाकर चलेंगे तो उनकी कदम ताल के कारण उत्पन्न आवृत्ति पुल की नैसर्गिक दोलन आवृत्ति के तुल्य हो सकती है। अतएव यह उच्च आयाम से दोलित होकर अनुनाद की घटना उत्पन्न कर सकता है, जिससे पुल को नुकसान हो सकता है।

प्रश्न 12. 
S. H.M. के लिये एक प्रत्यानयन बल क्यों अनिवार्य है?
उत्तर:
प्रत्यानयन बल वह बल है जो पिण्ड को पुनर्स्थापित करता है। या करने का प्रयत्न करता है या उसे अपनी संकलन अवस्था में वापस लाता है। जब एक पिण्ड S. H.M. करता है यह अपनी गतिज ऊर्जा के कारण माध्य स्थिति को पार कर जाता है, प्रत्यानयन बल संतुलन स्थिति की ओर कार्य करके लोलक को उसके सिरे की स्थिति से माध्य स्थिति की ओर लाता है। जब पिण्ड अपनी संतुलन अवस्था के दूसरी ओर होता है, फिर यही प्रक्रिया दोहराई जाती है। इसलिये दोलनी गति में S. H.M. सहित में प्रत्यानयन बल अनिवार्य है।

प्रश्न 13. 
प्रणोदित दोलन और समर्पित दोलनों में विभेद कीजिये।
उत्तर:
बाह्य आयतित बल के प्रभाव में जो पिण्ड अपनी नैसर्गिक आवर्ती से अलग दूसरी आवर्ती से दोलन करता है उस दोलन को प्रणोदित दोलन कहते हैं। जिस दर से दोलक की ऊर्जा में क्षति होती है यदि ऊर्जा की पूर्ति उसी दर से की जाये तो दोलन का आयाम अपरिवर्तित रहता है। ऐसे दोलनों को समर्थित दोलन कहते हैं। उदाहरणार्थ एक पेन्डुलम घड़ी के दोलन या कलाई घड़ी का संतोलक चक्र की गति समर्थित दोलनों के उदाहरण हैं।

प्रश्न 14. 
अनुनादी दोलन से आप क्या समझते हैं?
उत्तर:
जब किसी पिण्ड पर आवर्ती बल लगाया जाये और पिण्ड की आवृत्ति उसकी नैसर्गिक आवर्ती के तुल्य हो अर्थात् प्रणोदी दोलनों की आवृत्ति पिण्ड की नैसर्गिक आवर्ती के तुल्य हो तो दोलन आयाम अधिकतम होगा। ऐसे दोलनों को पिण्ड के अनुनादी दोलन कहते हैं। यदि दोलनों द्वारा ध्वनि उत्पन्न होती है तो यह अधिकतम तीव्रता की होगी।

प्रश्न 15. 
अवमंदित दोलन से आप क्या समझते हैं?
उत्तर:
किसी पिण्ड के वह दोलन जो प्रतिरोधी बल की उपस्थिति में होते हैं जैसे द्रव श्यानता घर्षण वायु घर्षण इत्यादि की उपस्थिति में होने वाले दोलनों का आयाम निरन्तर घटता रहता है। इन दोलनों को अवमंदित दोलन कहते हैं।

प्रश्न 16. 
अवमंदित आवर्त गति की कोणीय आवृत्ति imm है जहाँ b को अवमंदन स्थिरांक कहते हैं। ऐसी गति में विस्थापन x = Ae cos (cot + Q) होता है और मंदन बल F = by जहाँ v कण की चाल है। दिये गये समीकरणों से आप क्या अनुमान लगा सकते हैं:
(a) दोलन आयाम कैसे परिवर्तित होता है?
(b) क्या विस्थापन के साथ दोलनकाल भी बदलता है?
उत्तर:
(a) दोलन आयाम अवमंदन बल के कारण घटता है जैसा कि विस्थापन समीकरण से स्पष्ट है कि दोलन आयाम घातांकी रूप से कम होता जाता है। चूँकि अवमंदन बल वेग पर निर्भर करता है।
(b) अवमंदित दोलन में दोलनकाल नहीं बदलता है।

प्रश्न 17. 
यू-नली में भरे हुए पानी के स्थान पर उतना ही मीठा शर्बत भर कर दोलन कराने पर आवर्तकाल किस प्रकार प्रभावित होता है?
उत्तर:
यू- नली में भरे द्रव का आवर्तकाल
\(\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{h}}{\mathrm{g}}}\)
यदि पानी के स्थान पर उतना ही मीठा शर्बत भरा गया है तो दोलन का आवर्तकाल अपरिवर्तित रहेगा।

प्रश्न 18. 
दोलक द्वारा नियंत्रित घड़ी मैदान से पहाड़ पर ले जाने से सुस्त हो जाती है। परन्तु कमानी द्वारा नियंत्रित कलाई घड़ी अप्रभावित रहती है। घड़ियों के व्यवहार में इस अन्तर का कारण स्पष्ट कीजिये।
उत्तर:
मैदान से पहाड़ पर ले जाने से 'g' के मान कम हो जाता है। 'g' में परिवर्तन के कारण दोलक घड़ी के पेन्डुलम का आवर्तकाल बढ़ जाता है जिससे घड़ी सुस्त हो जाती है। परन्तु कमानी 'g' के परिवर्तन से अप्रभावित रहती है, फलस्वरूप घड़ी भी ठीक समय देती है।

प्रश्न 19. 
रैखिक तथा कोणीय सरल आवर्त गति में अवकल समीकरण और आवर्तकाल के दो अन्तर लिखिये।
उत्तर:
रैखिक सरल आवर्त गति
गति का अवकल समीकरण
\(\frac{\mathrm{d}^2 y}{d t^2}+\omega^2 \mathrm{y}=0\)
जहाँ
\(\omega=\sqrt{\frac{k}{m}}\)
गति का आवर्तकाल \(\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\)
कोणीय सरल आवर्त गति 
गति का अवकल समीकरण

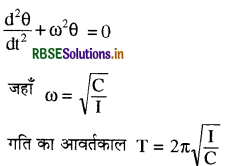
प्रश्न 20. 
दो कण एक ही सरल रेखा में आवर्त गति करते हैं, उनके आयाम व आवृत्ति एक ही हैं। जिस समय उनका विस्थापन आयाम से आधा होता है, एक-दूसरे की विपरीत दिशा में जाते हुए पार करते हैं, उनमें कलान्तर क्या है?
उत्तर:
सरल आवर्त गति का व्यापक समीकरण लेने पर
जहाँ (ωt + Φ) कण की कुल कला कहलाती है।
y = A sin(ωt + Φ)
जब y = 1/2 तब 1/2 A = A sin(ωt + Φ)
⇒ 1/2sin(ωt + Φ)
⇒ ωt + Φ = 30° या 150°
चूँकि जिस क्षण दोनों कण विपरीत दिशाओं में गतिमान हैं, उनमें एक की कला 30° तो दूसरे की कला 180° - 30° = 150° होगी। यदि एक की 150° तो दूसरे की 180° - 150° = 30°
अतः कलान्तर उस क्षण = 150° - 30° = 120° 

प्रश्न 21. 
किसी सरल लोलक का गोलक (Bob) खोखला है जिसे पानी से भर दिया गया है। इसके नीचे एक छोटा-सा छिद्र है। यदि यह गोलक लगातार सरल आवर्त गति करे और छिद्र से पानी बाहर गिरता रहे तो दोलनों का आवर्त काल किस प्रकार परिवर्तित होगा?
उत्तर:
जब गोलक पानी से पूरा भरा होता है तो इसका द्रव्यमान केन्द्र गोले के केन्द्र पर स्थित होता है। माना इसका आवर्तकाल T है। ज्यों-ज्यों पानी गोलक की ओर निकलता है, इसका द्रव्यमान केन्द्र नीचे होता जाता है। इससे लम्बाई बढ़ती जाती है। अतः प्रारम्भ में आवर्तकाल का मान बढ़ता जाता है। जब सारा पानी बाहर आ जाता है तो द्रव्यमान केन्द्र पुनः केन्द्र पर आ जाता है और इस कारण आवर्तकाल का मान पुनः पूर्व मान के बराबर हो जाता है।

प्रश्न 22. 
सरल लोलक बनाने के लिए गोलक को गोलाकार ही क्यों लिया जाता है?
उत्तर:
इसके मुख्य दो कारण हैं:

1. गोलाकार वस्तुओं का गुरुत्व केन्द्र उनके केन्द्र पर स्थित होता है। अतः गुरुत्व केन्द्र की स्थिति शुद्धता से ज्ञात की जा सकती है। अतः लोलक की प्रभावी लम्बाई का मान भी शुद्धता से ज्ञात हो जाता है।
2. दिये गये आयतन के लिए गोलाकार वस्तु की सतह का क्षेत्रफल न्यूनतम होता है, अतः उस पर वायु का घर्षण बल भी न्यूनतम लगता है, इससे दोलन अधिक समय तक चलते रहते हैं।

प्रश्न 23. 
एक सरल लोलक एक छोर से दूसरे छोर तक सेकण्ड में गति करता है, उसकी आवृत्ति क्या होगी?
उत्तर:
आवर्तकाल T = 2 x 1/2 सेकण्ड = 1 सेकण्ड
आवृत्ति n = 1/T = 1 सेकण्ड^-1

प्रश्न 24. 
एक कण सरल आवर्त गति कर रहा है। यदि माध्य x₁ तथा x₂ दूरियों पर कण का वेग क्रमशः v₁ तथा v₂  तो सिद्ध कीजिये कि इसका आवर्तकाल \(T=2 \pi \sqrt{\frac{x_2^2-x_1^2}{v_1^2-v_2^2}}\) होगा।
उत्तर:
वेग V = \(\omega \sqrt{A^2-y^2}\)
जब y = x1 तो v = V1 तथा y = तो v = V2
∴  \(v_1=\omega \sqrt{\mathrm{A}^2-x_1^2}\)
या
v² = ω² (A² - x²) ....(1)
तथा
V² = \(\omega \sqrt{\mathrm{A}^2-x_2^2}\)
या
v² = ω² (A² – x² ) ................ (2)
समीकरण (1) में समीकरण (2) को घटाने पर
v² - v² = ω²(x₂² - x₁²)
या
\(\omega=\sqrt{\frac{v_1^2-v_2^2}{x_2^2-x_1^2}}\)
∴ आवर्तकाल \(\mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{x_2^2-x_1^2}{\mathrm{v}_1^2-\mathrm{v}_2^2}}\)

प्रश्न 25. 
पृथ्वी की सतह पर एक सरल लोलक का आवर्तकाल T1 है और जब उसे पृथ्वी की सतह से 1⁄2R ऊँचाई पर ले जाते हैं तो आवर्तकाल T2 हो जाता है। R पृथ्वी की त्रिज्या है। T1/T2 का मान ज्ञात कीजिये।
उत्तर:

आंकिक प्रश्न:

प्रश्न 1. 
एक सरल आवर्त दोलक का आवर्तकाल 6 सेकण्ड है । साम्य स्थिति से गति प्रारम्भ करने वाले दोलक के लिये कितने समय पश्चात् उसका विस्थापन उसके आयाम का आधा होगा?
उत्तर:
साम्य स्थिति से सरल आवर्त गति प्रारम्भ करने वाले कण
के लिये तात्क्षणिक विस्थापन
x = A sin 2π/T t
यहाँ पर T = 6 सेकण्ड तथा x = 1/2A
मान रखने पर
= A sin 2π/6t

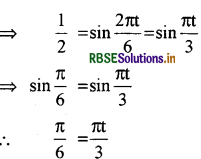
अर्थात् t = 3π/6π = 1/2 सेकण्ड

प्रश्न 2. 
विस्थापन के किस मान के लिये सरल आवर्त गति में स्थितिज एवं गतिज ऊर्जा, मान में बराबर होती है?
उत्तर: 
यदि सरल आवर्त गति में साम्य स्थिति में x विस्थापन दर
स्थितिज ऊर्जा = गतिज ऊर्जा
1/2kx² = 1/2k(A² - x²)
या
x² = A2 - x²
या
\(x= \pm \frac{\mathrm{A}}{\sqrt{2}}= \pm 0.707 \mathrm{~A}\)
x = ± 0.707A 

प्रश्न 3. 
किस समय किसी सरल आवर्त दोलक की स्थितिज और गतिज ऊर्जा बराबर होती है?
उत्तर: 
सरल आवर्त दोलक की स्थितिज ऊर्जा
Ut = 1/2kA²sin² ωt
तथा गतिज ऊर्जा Kt = 1/2kA² cos² ωt
यहां पर 1/2 kA² sin² ωt = 1/2kA²cos² ωt
⇒ sin² ωt = cos² ωt
या
sin² ωt = 1 - sin² ωt
या
2sin² ωt  = 1
sin² ωt = 1/2
∴  \(\sin \omega t= \pm \frac{1}{\sqrt{2}}=\sin \frac{\pi}{4} \text { } \sin \frac{3 \pi}{4}\)
अतः ωt = π/4 या 3π/4 
अभीष्ट समय = \(t=\frac{\pi}{4 \omega}=\frac{\pi}{4 \times \frac{2 \pi}{T}}\)
\(t=\frac{\mathrm{T}}{8}\)
\(t=\frac{3 \pi}{4 \omega}=\frac{3 \pi}{4 \times \frac{2 \pi}{T}}=\frac{3 T}{8}\)

प्रश्न 4. 
एक पिण्ड निम्न समीकरण के अनुसार सरल आवर्त गति करता है:
x = 6sin(3πt + π/3)
ज्ञात कीजिये - (i) आयाम, (ii) आवर्तकाल (iii) प्रारम्भिक कला एवं (iv) विस्थापन, वेग और त्वरण। समय t = 2 पर
उत्तर:  
दिया गया समीकरण
x = 6sin(3πt + π/3)
सरल आवर्त गति का व्यापक समीकरण निम्न होता है:
x = Asin (ωt + Φ)
इसकी तुलना दी गई समीकरण से करने पर 
(i) आयाम A = 6 मीटर उत्तर 
(ii) ω = 3π
लेकिन
ω = 2π/T
T = 2π/ω = 2π/3π = 2/3 सेकण्ड
T = 0.666 सेकण्ड उत्तर

(iii) प्रारम्भिक कला = π/3 रेडियन उत्तर
(iv) समीकरण
x = 6sin (3πt + π/3) में
t = 2 रखने पर
x = 6sin (3π × 2 + π/3)
= 6sinπ/3 = 6 x \(\frac{\sqrt{3}}{2}\)  = 3√3
विस्थापन = 3√3 मी. 
A = 6 व ω = 3π इन मानों को वेग के समीकरण में रखने पर
\(\begin{aligned} & \mathrm{v}=3 \pi\left\{(6)^2-(3 \sqrt{3})^2\right\}^{\frac{1}{2}} \\ & {\left[\because \mathrm{v}=\omega \sqrt{A^2-x^2}\right] } \end{aligned}\)
∴ त्वरण a = ω² x  = (3π)² = 3π x 3√3
= 9π² x 3√3 = 27√3π²
अतः
आयाम = 6, आवर्तकाल = 0.666 सेकण्ड
प्रारम्भिक कला = π/3 विस्थापन = 3√3 मी/से.
वेग = 9π मी/से. व त्वरण
= 27√3π² मी./से²

प्रश्न 5. 
सरल आवर्त गति करते हुए पिण्ड की किस स्थिति में अधिकतम वेग का आधा होता है?
उत्तर:
दिया गया है:
v = 1/2vmax

प्रश्न 6. 
यदि साम्य स्थिति से प्रारम्भ कर सरल आवर्त गति करने वाले 0.8 किग्रा. द्रव्यमान के पिण्ड का आयाम 10 मी. तथा आवर्तकाल 11/7 सेकण्ड हो तो 0.6 मी. विस्थापन पर कण का वेग ज्ञात कर, गति का समीकरण भी लिखिये।
उत्तर: 
दिया गया है:
m = 0.8 kg.
A = 1.0 मीटर
आवर्तकाल T = 11/7 सेकण्ड ∴ आवृत्ति (n) = 7/11प्रति से
विस्थापन
(x) = 0.6 मीटर
v = ?
गति का समीकरण = ?
सरल आवर्त गति में वेग (v) और विस्थापन x में सम्बन्ध
\(\mathrm{v}=\omega \sqrt{\mathrm{A}^2-x^2}\) ............ (1)
लेकिन ω = 2πn
= 2 × 22/7 × 7/11 =  4 रेडियन / से.
समीकरण (1) में का मान रखने पर
\(\begin{aligned} v & =4 \sqrt{(1)^2-(0.6)^2} \\ & =4 \sqrt{1-0.36}=4 \sqrt{0.64} \end{aligned}\)
= 4 × 083.2 मी./से. 
विस्थापन y = Asin ωt
अतः
=1.0sin(4t) ∵ ω = 4 रेडियन / से.
y = 1.0sin ( 4t) मी. 

प्रश्न 7. 
सरल आवर्त गति करने वाले कण का माध्य स्थिति से 3 सेमी. दूर त्वरण π2/3 सेमी./से² है। कण का आवर्तकाल ज्ञात कीजिये।
उत्तर:  
सरल आवर्त गति के लिये त्वरण और विस्थापन y में सम्बन्ध
a = - ω²y
यहाँ पर
a = π²/3 और y = 3 सेमी.
∴  \(\omega=\sqrt{\frac{a}{y}}=\sqrt{\frac{\pi^2}{3 \times 3}}=\frac{\pi}{3}\)
लेकिन
\(\begin{aligned} 2 \pi n & =\frac{\pi}{3} \\ n & =\frac{1}{6} \quad \therefore n=\frac{1}{T} \end{aligned}\)
T = 6 सेकण्ड 

प्रश्न 8. 
सरल आवर्त गति में दोलन का आवर्तकाल 0.5 सेकण्ड तथा आयाम 0.1 मी. है। दोलक का अधिकतम वेग तथा अधिकतम त्वरण ज्ञात करो।
उत्तर:  
सरल आवर्त गति का आवर्तकाल (T) = 0.5 सेकण्ड
A = 0.1 मीटर
V_max = ?
a_max = ?
सरल आवर्त गति में अधिकतम वेग v_max = Aω ∵ अधिकतम वेग के लिये विस्थापन शून्य होता है। 
यहाँ पर A आयाम है।
V_max  = A x 2πn
\(\mathrm{v}_{\max }=\frac{\mathrm{A} \times 2 \pi}{\mathrm{T}} \quad \because n=\frac{1}{\mathrm{~T}}\)
मान रखने पर
\(\mathrm{v}_{\max }=\frac{0.1 \times 2 \pi}{0.5}=0.4 \pi\)
= 0.4 मीटर / से. 
सरल आवर्त गति में अधिकतम त्वरण (amax) = - Aω²
\(=-0.1\left(\frac{2 \pi}{T}\right)^2=-\frac{0.1 \times 4 \pi^2}{0.5 \times 0.5}\)
= - 4π²/2.5 = -  1.6 मी./से. 

प्रश्न 9. 
सरल आवर्त गति करते एक 20 ग्राम द्रव्यमान के पिण्ड का आयाम 5 सेमी. है तथा आवर्तकाल 2π सेकण्ड है। कण की कुल ऊर्जा ज्ञात करो।
उत्तर:   
सरल आवर्त गति का आवर्तकाल T = 2π सेकण्ड
∴ आवर्त गति
ω = 2π/T
ω = 2π/ω = 1 रेडियन /सेकण्ड
और अधिकतम वेग V_max = Aω
यहाँ पर (a) सरल आवर्त गति का आयाम है।
V_max = 5 x 1 = 5 सेमी./से.
सरल आवर्त गति की कुल ऊर्जा = सरल आवर्त गति की अधिकतम गतिज ऊर्जा
सरल आवर्त गति की कुल ऊर्जा = 1/2mv_max²
= 1/2 x 20 x (5)²
= 10 x 25 = 250 अर्ग = 250 x 10^-7 जूल
∵ 1 अर्ग = 10 जूल
= 2.50 × 10^-5 जूल 

प्रश्न 10. 
एक 10 ग्राम द्रव्यमान का पिण्ड 6 सेमी. लम्बी रेखा पर सरल आवर्त गति करता है। इसकी अधिकतम चाल 12 सेमी./सेकण्ड है। इसका आवर्तकाल तथा अधिकतम स्थितिज ऊर्जा ज्ञात करो।
उत्तर:  
दिया गया है:
A = 3 सेमी., ω = v_max/A = 12/3
ω = 4 रेडियन/से.
∴  \(\mathrm{T}=\frac{2 \pi}{\omega}=\frac{2 \pi}{4}=\frac{2 \times 3.14}{4}\)
T = 1.57 सेकण्ड उत्तर
अधिकतम स्थितिज ऊर्जा
U = 1/2mω²A²
U = 1/2 x 10 x 10^-3 x 4 x 4 × 3 × 3 × 10
U = 720 × 10^-7 जूल 

प्रश्न 11. 
एक सरल लोलक प्रति मिनट 60 दोलन करता है। इसकी प्रभावी लम्बाई ज्ञात करो।
उत्तर:  
60 दोलन का समय = 1 मिनट = 60 से.
∴ 1 दोलन का समय = 60/60 = 1 सेकण्ड
∴ दोलन काल (T) = 1 सेकण्ड
हम जानते हैं
\(l=\frac{\mathrm{gT}^2}{4 \pi^2}=\frac{9.8 \times(1)^2}{4 \times 9.86}\left[\because \pi^2=9.86\right]\)
= 0.2485 मीटर
अतः प्रभावी लम्बाई = 0.2485 मीटर

प्रश्न 12. 
एक आदर्श स्प्रिंग से 0.5 किग्रा. द्रव्यमान के एक पिण्ड को लटकाकर ऊर्ध्व दोलन कराये जाते हैं। दोलन काल π/2 है तो स्प्रिंग नियतांक ज्ञात करो।
उत्तर: 
दिया गया है:
m = 0.5 किग्रा. और T = π/2 सेकण्ड

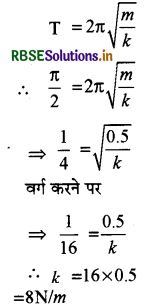
प्रश्न 13. 
किसी एक स्प्रिंग से लटकाये गये पिण्ड की सरल आवर्त गति का आवर्तकाल T है। स्प्रिंग को दो बराबर भागों में काटकर 
(अ) किसी एक स्प्रिंग से उसी पिण्ड को लटकाकर दोलन करायें तो आवर्तकाल ज्ञात कीजिये।'
(ब) दोनों टुकड़ों को समान्तर क्रम में संयोजित कर दोलन कराने पर दोलन काल क्या होगा?
उत्तर: 
(अ) माना स्प्रिंग का बल नियतांक है और पिण्ड का द्रव्यमान है। तब आवर्तकाल
\(T=2 \pi \sqrt{\frac{m}{k}}\) होगा। ....(1)
अब स्प्रिंग को दो बराबर भागों में बाँटा गया है। इस कारण से
स्प्रिंग का बल नियतांक 2k होगा और आवर्तकाल को T-1 माना है।
\(T^1=2 \pi \sqrt{\frac{m}{2 k}}\) ............ (2)
समीकरण (1) में समी. (2) का भाग देने पर

(ख) किसी k नियतांक की स्प्रिंग को 2 बराबर भागों में विभाजित करने पर प्रत्येक टुकड़े का स्प्रिंग नियतांक 2k हो जाता है। इन 2k नियतांक के 2 टुकड़ों को समान्तर क्रम में संयोजित करने पर प्रभावी नियतांक
k = 2k + 2k = 4k

प्रश्न 14. 
एक पिण्डकी स्थितिज ऊर्जा Uy = U0 (1 - cosαy) है। पिण्ड की गति के अभिलक्षण बताइये।
उत्तर: 
दिया गया है: Uy = U ( 1 - cosαy)
फलन का y के सापेक्ष अवकलन करने पर 

यहाँ पर sinαy = αy लेने पर चूँकि acy का मान बहुत ही
∴F = -Uoα²y
=> F = -Ky
यहाँ K = U0α² एक नियतांक है।
अतः पिण्ड की गति सरल आवर्त गति है। चूँकि ऊपर प्राप्त समीकरण सरल आवर्त गति की बल समीकरण है।

प्रश्न 15. 
सरल आवर्त गति करता हुआ एक कण प्रति मिनट 1200 दोलन करता है तथा माध्य स्थिति से गुजरते समय उसका वेग 3. 14 मी./से. रहता है। कण का विस्थापन समीकरण भी प्राप्त कीजिये यदि क्षण t = 0 पर विस्थापन शून्य हो।
उत्तर: 
हम जानते हैं कि माध्य स्थिति में कण का वेग अधिकतम होता है। यदि कण का आयाम A व कोणीय वेग 0 हो, तो अधिकतम वेग, V_max  = ωA
∴ आयाम A = v_max/ω = v_max/2πn
∴ ω = 2πn यहाँ पर n आवृत्ति है।
प्रश्नानुसार = v_max = 3.1मी./से.
n = 1200 प्रति मिनट = 1200/60 प्रति सेकण्ड
n = 20 प्रति सेकण्ड
∴ आयाम  \(A=\frac{3.1}{2 \times 3.14 \times 20}=\frac{1}{40}\)
= 0.025 मीटर
यदि t = 0 पर कण का विस्थापन शून्य है अर्थात् कण अपनी साम्यावस्था में है, तो सरल आवर्त गति का समीकरण है
y = A sin ωt = A sin 2πnt
A तथा n के मान रखने पर
y = 0.025 sin 2π x 20t
या
y = 0.025 sin 40 πt

प्रश्न 16. 
चन्द्रमा पर एक सेकण्ड लोलक की लम्बाई ज्ञात कीजिये जहाँ गुरुत्वीय त्वरण का मान पृथ्वी के गुरुत्वीय त्वरण का 1/6 गुना है। पृथ्वी पर g = 9.8 मी./से.² 
उत्तर: 
हम जानते हैं सेकण्ड लोलक का आवर्त काल 2 सेकण्ड होता है।

प्रश्न 17. 
एक स्प्रिंग से 0.60 किग्रा. का एक पिण्ड लटकाने से उसकी लम्बाई 0.25 मीटर बढ़ जाती है। यदि स्प्रिंग से 0.24 किग्रा. का एक पिण्ड लटकाकर कुछ नीचे छोड़ दिया जाये, तो स्प्रिंग का आवर्तकाल कितना होगा? (g = 10 मी./से.²)
उत्तर:
स्प्रिंग का बल नियतांक k =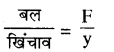
बल F = Mg = 0.60 × 10 = 6.0 म्यूटन
खिंचाव y = 0.25 मीटर
∴ \(\mathrm{k}=\frac{6.0}{0.25}=\frac{600}{25}\)
k = 24 न्यूटन / मीटर
स्प्रिंग से लटके m = 0.24 किग्रा के पिण्ड के दोलनों का दोलन काल
\(\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}}=2 \times 3.14 \sqrt{\frac{0.24}{24}}\)
T = 0.628 सेकण्ड

प्रश्न 18. 
एक सरल लोलक का आवर्त काल 4 सेकण्ड तथा प्रभावी लम्बाई 4 मीटर है। इसकी लम्बाई कितनी कर दी जाये कि वह 30 सेकण्ड में 15 दोलन करने लगे?
उत्तर:
हम जानते हैं कि

प्रश्न 19.
1.00 तथा 1.1025 मीटर लम्बाई के दो लोलक एक साथ कम्पन प्रारम्भ करते हैं। कितने दोलनों के पश्चात् वह पुनः एक साथ दोलन करने लगेंगे?
उत्तर:
माना दोनों लम्बाइयों के आवर्तकाल T₁ तथा T₂  हैं। पुनः एक साथ दोलन करने के लिए दोनों के दोलनों में 1 का अन्तर होना चाहिए। यदि इतने समय अन्तराल में बड़ा लोलक 1 दोलन करता है तो छोटे लोलक के दोलन (n+1) होंगे अर्थात्
nT₂ =  (n + 1)T₁ 
∴ \(\frac{T_1}{T_2}=\frac{n}{n+1}\) ....(1)
प्रश्नानुसार

समीकरण ( 1 ) तथा (2) से
n/n+1 = 1/1.05
1.05n =  n + 1
या
1.05n - n = 1
या
0.05n = 1 ⇒ n = 1/0.05
अतः n = 20
अर्थात् बड़े लोलक के 20 तथा छोटे लोलक के 21 दोलनों के पश्चात् वे पुनः एक साथ दोलन करेंगे।

प्रश्न 20. 
निम्न स्थितियों में सरल लोलक के आवर्त काल में प्रतिशत परिवर्तन का मान ज्ञात कीजिये:
(i) लोलक की लम्बाई 5% बढ़ाने पर
(ii) लोलक का द्रव्यमान 5% बढ़ाने पर 
(iii) लोलक का आयाम 5% घटाने पर। 
उत्तर:
हम जानते हैं:

अतः आवर्तकाल में प्रतिशत वृद्धि = 2.5% 
(ii) आवर्तकाल लोलक के द्रव्यमान पर निर्भर नहीं करता, द्रव्यमान बढ़ाने पर आवर्तकाल वही रहेगा।
अतः
(iii) आवर्तकाल गति के आयाम पर भी निर्भर नहीं करता, अतः आयाम घटाने पर आवर्त काल वही रहेगा।
इसलिए प्रतिशत परिवर्तन शून्य

प्रश्न 21. 
एक आदर्श स्प्रिंग से लटके द्रव्यमान m का आवर्तकाल 2 सेकण्ड है। यदि इसके साथ 2 किग्रा. द्रव्यमान और लटका दें तो आवर्तकाल 3 सेकण्ड हो जाता है। m का मान ज्ञात कीजिये।
उत्तर:
यदि m द्रव्यमान का पिण्ड लटकाने पर आवर्तकाल T हो, तो

गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न:

प्रश्न 1. 
दो विस्थापनों y₁ = a sin (ωt) तथा y₂ = b cos (ωt) के अध्यारोपण से प्राप्त परिणामी गति:
(a) a/b आयाम की सरल आवर्त गति होती है।
(b) \(\sqrt{a^2+b^2}\) आयाम की सरल आवर्त गति होती है।
(c) (a+b)/2 आयाम की सरल आवर्त गति होती है।
(d) सरल आवर्त गति नहीं होती है।
उत्तर:
(b) \(\sqrt{a^2+b^2} \)आयाम की सरल आवर्त गति होती है।

प्रश्न 2. 
एक कण A आयाम से सरल आवर्त दोलन कर रहा है। जब यह अपने मूल स्थान से 2A/3 पर पहुँचता है, तब अचानक इसकी गति तिगुनी कर दी जाती है। तब इसका नया आयाम है:
(a) 3A
(b) A√3
(c) 7A/3
(d) A/3√41
उत्तर:
(c) 7A/3

प्रश्न 3. 
यदि किसी सरल रेखा के अनुदिश सरल आवर्त गति करते हुए किसी कण की मूल बिन्दु से दूरी x1 तथा x2 होने पर उसका वेग क्रमश: V1 तथा V2 है, तो इस कण का आवर्तकाल है:

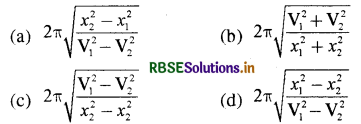
उत्तर:
\(\text { (a) } 2 \pi \sqrt{\frac{x_2^2-x_1^2}{\mathrm{~V}_1^2-\mathrm{V}_2^2}}\)

प्रश्न 4. 
सरल आवर्त गति करते हुए किसी कण का अधिकतम त्वरण α तथा अधिकतम वेग β है, तो कम्पन्न का आवर्तकाल होगा:
(a) α/β
(b) β²/α²
(c) 2πβ/α
(d) β²/α²
उत्तर:
(c) 2πβ/α

प्रश्न 5. 
कोई कण इस प्रकार गति करता है कि उसका त्वरण समीकरण a = - bx द्वारा प्रदर्शित किया जाता है, जिसमें x सन्तुलन स्थिति से विस्थापन तथा b कोई नियतांक है। दोलनकाल होगा:
(a) 2π√b
(b) 2π/√b
(c) 2π/b
(d) \(2 \sqrt{\frac{\pi}{b}}\)
उत्तर:
(b) 2π/√b

प्रश्न 6. 
एक कण एक सरल रेखा में सरल आवर्त गति से गतिशील है। यह विरामावस्था से प्रारम्भ कर प्रथम सेकण्ड में दूरी a और अगले सेकण्ड में दूरी 2a उसी दिशा में तय करता है। तब:
(a) गति का आयाम 30 है। 
(b) दोलनों का आवर्तकाल 87 है।
(c) गति का आयाम 4a है।
(d) दोलनों का आवर्तकाल 6τ है।
उत्तर:
(d) दोलनों का आवर्तकाल 6τ है।

प्रश्न 7. 
धनात्मक (+ve) x-दिशा में चलती हुई किसी तरंग की y-दिशा में विस्थापन 1 m, तरंगदैर्घ्य 2πm है तथा इसकी आवृत्ति 1/πHz है। इस तरंग के लिए सही समीकरण होगा:
(a) y = sin(2πx + 2πt) 
(b) y = sin(x - 2t) 
(c) y = sin (2πx - 2πt )
(d) y = sin (10πx  - 20πt)
उत्तर:
(b) y = sin(x - 2t) 

प्रश्न 8. 
किसी एक समान तार के अनुप्रस्थ काट का क्षेत्रफल A है। इससे बनाये गये एक लोलक का आवर्तकाल T है । इस लोलक के गोलक से एक अतिरिक्त M द्रव्यमान जोड़ देने से लोलक का आवर्तकाल परिवर्तित होकर TM हो जाता है। यदि इस तार के  पदार्थ का यंग गुणांक Y हो, तो 1/Y का मान होगा
(g = गुरुत्वीय त्वरण):

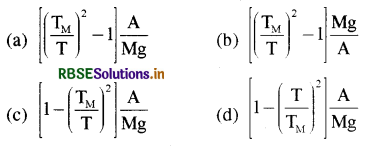
उत्तर:
\(\text { (a) }\left[\left(\frac{\mathrm{T}_{\mathrm{M}}}{\mathrm{T}}\right)^2-1\right] \frac{\mathrm{A}}{\mathrm{Mg}}\)

प्रश्न 9. 
कोई लोलक एक काफी ऊँचे भवन की छत से लटका है और सरल आवर्त दोलक की भाँति मुक्त रूप से आगे-पीछे गति कर रहा है। माध्य स्थिति से 5 m की दूरी पर इसके गोलक का त्वरण 20 m/s² है । दोलन का आवर्तकाल है:
(a) 2πs
(b) πs
(c) 2s
(d) 1s
उत्तर:
(b) πs

प्रश्न 10. 
एक क्षैतिज कमानी से बंधा एक द्रव्यमान M आयाम A1 से सरल आवर्त गति कर रहा है। जब द्रव्यमान M अपनी माध्य अवस्था से गुजर रहा है, तब एक छोटा द्रव्यमान m इसके ऊपर रख दिया जाता है और अब दोनों आयाम A2 से गति करते हैं। (A1/A2) का अनुपात है:

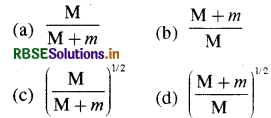
उत्तर:
\(\text { (d) }\left(\frac{\mathrm{M}+m}{\mathrm{M}}\right)^{1 / 2}\)

प्रश्न 11. 
किसी कमानी का ऊपरी सिरा स्थिर है तथा निचले सिरे से द्रव्यमान का एक पिण्ड लटका है। कमानी का अपना द्रव्यमान नगण्य है। कमानी के निचले सिरे को थोड़ा-सा खींचकर छोड़ देने पर द्रव्यमान 12 को पिण्ड दोलन करने लगता है और इसके दोलनों का आवर्तकाल 33 होता है। 71 के मान में 1 kg बढ़ाने पर दोलनों का आवर्तकाल 55 हो जाता है। m का kg में मान है:
(a) 9/16
(b) 3/4
(c) 4/3
(d) 16/9
उत्तर:
(a) 9/16

प्रश्न 12. 
एक स्प्रिंग ( कमानी) का कमानी स्थिरांक & है। इसको तीन भागों में काट दिया गया है जिनकी लम्बाइयों का अनुपात 1 : 2 : 3 है इन तीनों भागों को श्रेणीक्रम में जोड़ने पर संयोजन का कमानी स्थिरांक ४ तथा समान्तर क्रम में जोड़ने पर " है, तो अनुपात K : K" होगा:
(a) 1 : 6
(b) 1 : 9
(c) 1 : 11 
(d) 1 : 14
उत्तर:
(c) 1 : 11 

प्रश्न 13. 
लम्बाई L व द्रव्यमान M की एकसमान छड़ अपने केन्द्र पर कीलित है। इस छड़ के सिरों पर स्प्रिंग नियतांक के एक जैसे स्प्रिंग लगे हैं जिनके दूसरे सिरे दृढ़ आलम्बों से जुड़े हैं। छड़ क्षैतिज तल में स्वतन्त्र रूप से दोलन कर सकती है। छड़ को एक छोटे कोण θ से घुमाकर छोड़ दिया जाता है। छड़ के दोलन की आवृत्ति होगी:

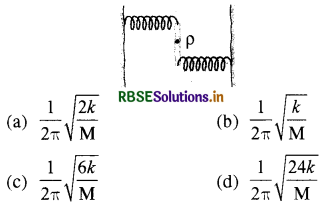
उत्तर:
\(\text { (c) } \frac{1}{2 \pi} \sqrt{\frac{6 k}{\mathrm{M}}}\)

प्रश्न 14. 
सरल आवर्त गति करते किसी कण का विस्थापन y = A0 + A sin ωt + B cos ωt द्वारा निरूपित किया गया है। तब इसके दोलन का आयाम होगा:
(a) \(A_0+\sqrt{A^2+B^2}\)
(b) \(\sqrt{A^2+B^2}\)
(c) \(\sqrt{\mathrm{A}_0^2+(\mathrm{A}+\mathrm{B})^2}\)
(d) A + B
उत्तर:
\(\sqrt{A^2+B^2}\)

प्रश्न 15. 
एक पूर्ण दोलन में सरल आवर्त गति करते किसी कण का औसत वेग होता है:
(a) Aω/2
(b) Aω
(c) Aω²/2
(d) शून्य
उत्तर:
(d) शून्य

प्रश्न 16. 
3 kg द्रव्यमान का एक ठोस सिलिण्डर (बेलन) किसी क्षैतिज समतल पर 4 ms^-1 के वेग से लुढ़क रहा है। यह 200 Nm 1 के बल नियतांक के एक क्षैतिज स्प्रिंग (कमानी) से टकराता है, तो स्प्रिंग से उत्पन्न अधिकतम संपीड़न होगा:
(a) 0.5m
(b) 0.6m
(c) 0.7m
(d) 0.2m
उत्तर:
(b) 0.6m

प्रश्न 17. 
एक ऊर्ध्वाधर बेलनाकार पात्र में रखी एक आदर्श गैस एक द्रव्यमान M के स्वतंत्र रूप से गतिशील पिस्टन को आधार देती है। पिस्टन और बेलन के अनुप्रस्थ परिच्छेद क्षेत्रफल एकसमान A हैं। जब पिस्टन साम्यावस्था में है, तब गैस का आयतन Vo है और इसका  दाब p0 है। पिस्टन को इसी साम्यावस्था स्थिति से थोड़ा-सा विस्थापित किया जाता है और फिर छोड़ दिया जाता है। यह मान लें कि निकाय अपने परिवेश से पूर्णत: रोधी है तब पिस्टन इस आवृत्ति की सरल आवर्त गति करेगा:

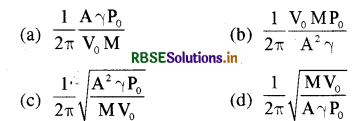
उत्तर:

\(\text { (c) } \frac{1}{2 \pi} \sqrt{\frac{\mathrm{A}^2 \gamma \mathrm{P}_0}{\mathrm{MV}}}\)

प्रश्न 18. 
एक द्रव्यमान रहित स्प्रिंग की तनाव रहित लम्बाई 4.9m है। उसका एक सिरा बंधित है और दूसरे पर एक छोटा गुटका लगा है ( चित्र देखिये) । यह निकाय एक घर्षण रहित क्षैतिज (horizontal) सतह पर रखा है। समय t = 0 पर गुटके को 0.2m खींचकर स्थिर अवस्था से छोड़ा जाता तब वह गुटका ω = -π/3 rod/s आवृत्ति का सरल आवर्त-दोलन करता है। ठीक उसी समय (1 = 0) पर छोटा कंकड़ v चाल से क्षैतिज से 45° कोण पर बिन्दु P से प्रक्षेपित किया जाता है। बिन्दु P की बिन्दु O से दूरी ( क्षैतिज ) 10m है। यदि = 1s पर कंकड़ गुटके पर गिरता है, तब का मान है (g = 10 m/s2 लें ):

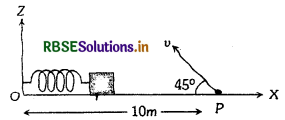
(a) √50m/s
(b) √ 51m/s
(c) √52 m/s
(d) √53m/s
उत्तर:
(a) √50m/s

प्रश्न 19. 
किसी ठोस में चाँदी की एक परमाणु 10¹² / sec की आवृत्ति से किसी दिशा में सरल आवर्त गति करता है। एक परमाणु को दूसरे परमाणु से जोड़ने वाले बंध का बल नियतांक कितना होगा? (चाँदी का आण्विक भार = 10⁸ और अवागाद्रो (Avagadro) संख्या = 6.02 x 10²³ gm mole^-1)
(a) 7.1N/m
(b) 2.2 N/m
(c) 5.5N/m
(d) 6.4 N/m
उत्तर:
(a) 7.1N/m

प्रश्न 20. 
चिकनी सतह पर रखे m द्रव्यमान के एक गुटके को स्प्रिंग नियतांक की एक कमानी (जिसका द्रव्यमान नगण्य है) से जोड़ा गया है। कमानी का दूसरा सिरा चित्रानुसार, अचल है। आरम्भ में गुटका अपनी साम्यावस्था में स्थायी है। यदि गुटके को एक नियत बल F से खींचा जाये तो गुटके की अधिकतम चाल होगी:

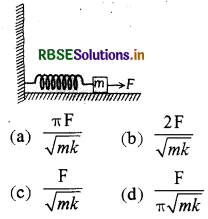
उत्तर:
\(\text { (c) } \frac{F}{\sqrt{m k}}\)

प्रश्न 21. 
एक कण 5cm आयाम से सरल आवते गति कर रहा है। जब कण अपनी मध्य स्थिति से 4cm दूरी पर है तब इसके वेग से परिमाण SI मानकों में इसके त्वरण में परिमाण के बराबर है तो कण का सेकण्ड में आवर्तकाल होगा:
(a) 7/3π
(b) 3/8π
(c) 4π/3
(d) 8π/3
उत्तर:
(d) 8π/3

प्रश्न 22. 
एक प्रगामी आवर्ती तरंग को समीकरण y(x, y) = 10-3 sin (501 + 2x ) से निरूपित किया जाता है, जहाँ x तथा y मीटर में तथा t सेकण्ड में हैं। निम्न में से तरंग के लिए कौनसा कथन सत्य है:
(a) तरंग 25 ms^-1 की वेग से ऋणात्मक x-दिशा में चल रही है।
(b) तरंग 25ms^-1 की वेग से धनात्मक x - दिशा में चल रही है।
(c) तरंग 100ms^-1 की वेग से धनात्मक x-दिशा में चल रही है।
(d) तरंग 100ms^-1 की वेग से ऋणात्मक x-दिशा में चल रही है।
उत्तर:
(a) तरंग 25 ms^-1 की वेग से ऋणात्मक x-दिशा में चल रही है।

प्रश्न 23. 
एक सरल दोलक, जो कि l लम्बाई की डोरी m द्रव्यमान के गोलक से बना है, को एक छोटे कोण θ0 से छोड़ा जाता है । यह गोलक एक द्रव्यमान M के गुटके को, जो कि क्षैतिज समतल पर रखा है, अपने दोलन के न्यूनतम बिन्दु पर प्रत्यास्थ संघट्ट करता है। गोलक संघट्ट कर कोण θ1 तक जाता है, तो M का मान होगा:

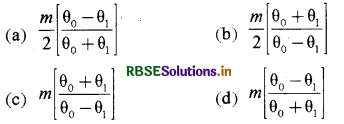
उत्तर:
\(\text { (c) } m\left[\frac{\theta_0+\theta_1}{\theta_0-\theta_1}\right]\)

प्रश्न 24.
एक सरल दोलक का हवा में आवर्तकाल T है। इस दोलक के गोलक को एक श्यानता रहित द्रव, जिसका घनत्व गोलक के 1/16 घनत्व का है, में दोलन करवाते हैं। यदि दोलन के समय यह गोलक पूर्णतया द्रव में रहता है, तो इसका आवर्तकाल होगा:

उत्तर:
\(\text { (a) } 4 \mathrm{~T} \sqrt{\frac{1}{15}}\)

प्रश्न 25. 
एक अवमन्दित आवर्ती दोलक का विस्थापन निम्न है, x(t) = e-0.1t cos[10πt + Φ] यहाँ सेकण्ड में है। इसके दोलन आयाम को अपने आरम्भिक मान से आधा होने में लगे समय का सन्निकट मान होगा:
(a) 13 
(b) 7s
(c) 27s
(d) 4s
उत्तर:
(b) 7s

प्रश्न 26. 
किसी सरल लोलक के लिये, उसके विस्थापन d तथा उसकी गतिज ऊर्जा के बीच और विस्थापन d तथा उसकी स्थितिज ऊर्जा के बीच ग्राफ खींचे गये हैं। निम्नांकित में से कौनसा ग्राफ (आलेख) सही है:
(यहाँ ग्राफ केवल व्यवस्था आरेख है और स्केल के अनुसार नहीं

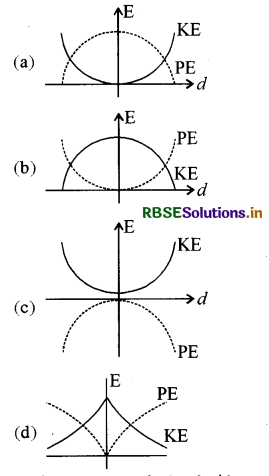
उत्तर:

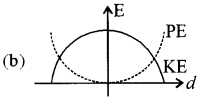
प्रश्न 27. 
किसी पिण्ड (वस्तु) के चिकने क्षैतिज पृष्ठ ( सतह) पर दोलनों
के समीकरण को
X = A cos (ωt) द्वारा
निरूपित किया जाता है, जहाँ
X =t समय पर विस्थापन
ω = दोलनों की आवृत्ति
तो t के साथ a के विचलन (परिवर्तन) को कौनसा ग्राफ (आलेख) सही रूप में दर्शाता है:

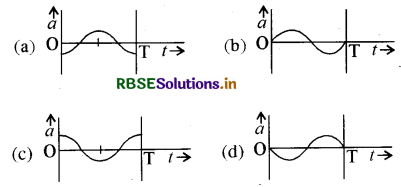
यहाँ a = समय पर त्वरण, T = आवर्तकाल
उत्तर:

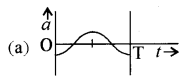
प्रश्न 28. 
दो स्वतंत्र समान द्रव्यमान के आवर्त दोलन मूल बिन्दु से परितः कोणीय आवृत्तियों ω₁ एवं ω₂ तथा कुल ऊर्जाओं क्रमश: E तथा E से दोलन कर रहे हैं। उनके संवेगों (p) का स्थिति के साथ परिवर्तन सम्बन्ध चित्रों में दर्शाये गये हैं। यदि
a/b = n2 तथा a/R = n है, तब सही कथन है (हैं):

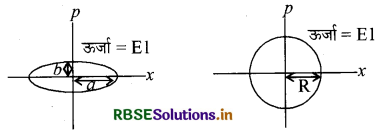
(a) E₁ω₁ = E₂ω₂
(b) ω₂/ω₁ = n₂
(c) ω₁ω₂ = n₂
(d) E₁/ω₁ = E₂/ω₂
Passage-I
जब m द्रव्यमान का एक कण x अक्ष पर V(x) = kx², स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवर्तकाल \(\sqrt{\frac{m}{k}}\) के समानुपाती होता है, जो कि विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालाँकि, यदि किसी एक कण की स्थितिज ऊर्जा x = 0 के दोनों तरफ kx² से भिन्न तरह से बढ़े तथा कण की कुल ऊर्जा इतनी हो कि वह अनन्त तक पलायन न कर सके, तब भी कण की गति आवर्ती हो सकती है। द्रव्यमान का एक कण x अक्ष पर गति करता है। जहाँ \(|x|\) के केन्द्र के पास होने पर स्थितिज ऊर्जा V (x) = ax4, (a > 0) है तथा \(|x| \geq X_0\) के लिए स्थितिज ऊर्जा V(x) = Vo है है (चित्र देखें)

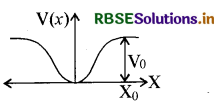
उत्तर:
(b) ω₂/ω₁ = n₂

प्रश्न 29. 
यदि एक कण की समग्र ऊर्जा E है, तो वह आवर्ती गति करेगा केवल जबकि:
(a ) E < 0
(b) E > 0
(c) Vo > E > 0
(d) E > Vo
उत्तर:
(c) Vo > E > 0

प्रश्न 30.
कम आयाम A के दोलन के लिए, कण का आवर्तकाल T निम्न में से किसके समानुपाती है:

उत्तर:
\(\text { (b) } \frac{1}{\mathrm{~A}} \sqrt{\frac{m}{\alpha}}\)

प्रश्न 31. 
\(|x|>\mathrm{X}_0\) के लिए कण का त्वरण:
(a) Vo के समानुपाती है।
(b) \(\frac{\mathrm{V}_0}{m \mathrm{X}_0}\) के समानुपाती है।
(c) \(\sqrt{\frac{\mathrm{V}_0}{m \mathrm{X}_0}}\) के समानुपाती है।
(d) शून्य है
उत्तर:
(d) शून्य है