RBSE Class 11 Economics Notes Chapter 8 सूचकांक

These comprehensive RBSE Class 11 Economics Studies Notes Chapter 8 सूचकांक will give a brief overview of all the concepts.

RBSE Class 11 Economics Chapter 8 Notes सूचकांक

→ प्रस्तावना:
जब चरों में समय-समय पर परिवर्तन होता है तो उन चरों का विश्लेषण करने हेतु सूचकांकों का उपयोग किया जाता है। उदाहरण के लिए जब हम काफी समय बाद बाजार जाते हैं तो कुछ वस्तुओं की कीमतें बढी हुई होती हैं तो कुछ वस्तुओं की कीमतें घटती हुई रहती हैं अतः जब हम उन वस्तुओं की पूर्व कीमतों से विश्लेषण करते हैं तो इस कार्य में सूचकांक हमारी मदद करता है।

→ सूचकांक क्या है?:
सूचकांक संबंधित चरों के समूह के परिमाण में परिवर्तनों को मापने का एक सांख्यिकीय साधन है। यह अपसारित (भिन्न-भिन्न दशाओं में) होने वाले अनुपातों की सामान्य प्रवृत्ति का प्रतिनिधित्व करता है, जिनसे इसको परिकलित किया जाता है। अतः सूचकांक वह अंक है जो दो समय के परिवर्तनों को मापता है। प्रारम्भ में इसका प्रयोग मूल्यों में होने वाले परिवर्तनों को मापने के लिए किया जाता था । वर्तमान युग में सूचकांक का प्रयोग सभी क्षेत्रों (जैसे उत्पादन, मात्रा, बिक्री आदि) में किया जाता है। कीमत सूचकांक कुछ वस्तुओं की कीमतों की माप करता है जिससे उनकी तुलना संभव हो पाती है। परिमाणात्मक सूचकांक उत्पादन की भौतिक मात्रा, निर्माण तथा रोजगार के परिवर्तन को मापता है यद्यपि कीमत सूचकांक का प्रयोग अधिकांश रूप से किया जाता है। उत्पादन सूचकांक भी अर्थव्यवस्था में उत्पादन के स्तर का महत्त्वपूर्ण सूचक होता है।

→ सूचकांक की रचना:
सकल समूहित कीमत सूचकांक का परिकलन विभिन्न वस्तुओं के कीमत परिवर्तन के प्रतिशत के आधार पर किया जाता है। यदि विभिन्न वस्तुओं के लिए प्रतिशत परिवर्तन एक समान रहे तो परिवर्तनों की व्याख्या करने के लिए केवल एक ही मान पर्याप्त रहता तथापि प्रतिशत परिवर्तनों में भिन्नता होती है तथा प्रत्येक मद के लिए प्रतिशत परिवर्तन को रिपोर्ट करना भ्रामक होगा। ऐसा तब होता है जब वस्तुओं की संख्या बहुत अधिक होती है, जो किसी भी वास्तविक बाजार स्थिति में सामान्य है। कीमत सूचकांक इन परिवर्तनों को एकल संख्यात्मक माप के द्वारा प्रस्तुत करता है । सूचकांक रचना की दो विधियाँ हैं
(1) समूहित विधि-एक सरल समूहित कीमत सूचकांक के लिए अग्र सूत्र का प्रयोग किया जाता है
P₀₁ = \(\frac{\Sigma \mathrm{p}_{1}}{\Sigma \mathrm{p}_{0}}\) × 100
यहाँ p₁ = वर्तमान अवधि की कीमत है।
p₀ = आधार अवधि की कीमत है। यह अभारित सूचकांक है, क्योंकि इसमें मदों का सापेक्षिक महत्त्व उपयुक्त रूप से प्रतिबिम्बित नहीं होता है। भारित कीमत सूचकांक को निम्न सूत्र द्वारा ज्ञात किया जा सकता है

(i) लेस्पेयर कीमत सूचकांक-भारित समूहित कीमत सूचकांक जब आधार अवधि की मात्रा को भार के रूप में प्रयोग करता है तो उसे लेस्पेयर कीमत सूचकांक कहा जाता है। इसे निम्न सूत्र द्वारा ज्ञात किया जाता है
P₀₁ = \(\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}}\)
यहाँ p₁ = चालू वर्ष का मूल्य
p₀ = आधार वर्ष का मूल्य
q₀ = आधार वर्ष की मात्रा
Σp₁q₀ = चालू वर्ष का समूही व्यय
Σp₀q₀ = आधार वर्ष का समूही व्यय

(ii) पाशे का मूल्य सूचकांक-जब भारित समूहित कीमत सूचकांक वर्तमान अवधि परिमाण को भार के रूप में प्रयोग करता है तो यह 'पाशे का मूल्य सूचकांक' के नाम से जाना जाता है। इसे अग्र सूत्र द्वारा ज्ञात किया जा सकता है
Σ P₀₁ = \(\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{1}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{1}}\) × 100
यहाँ p₀ = आधार वर्ष की कीमत
p₁ = चालू वर्ष की कीमत
q₁ = चालू वर्ष की मात्रा
Σp₁q₁ = चालू वर्ष के मूल्य व चालू वर्ष की मात्रा के गुणनफल का योग
Σp₀q₁ = आधार वर्ष के मूल्य व चालू वर्ष की मात्रा के गुणनफल का योग है।
कोई सूचकांक तब भारित सूचकांक बन जाता है जब मदों के सापेक्षिक महत्त्व को ध्यान में रखा जाता है। यहाँ भार परिमाणात्मक भार है। भारित समूहित सूचकांक की रचना में कुछ विशेष वस्तुओं को लिया जाता है तथा इनके मूल्य को प्रतिवर्ष परिकलित किया जाता है। इस प्रकार, यह वस्तुओं के एक निश्चित समूह के मूल्यों में होने वाले परिवर्तनों को मापता है।

(2) मूल्यानुपातों की माध्य विधि-जब केवल एक वस्तु हो, तब कीमत सूचकांक वस्तु की वर्तमान अवधि की कीमत तथा आधार अवधि की कीमत का अनुपात होता है। मूल्यानुपातों की माध्य परिकलन विधि इन मूल्यानुपातों के औसत या माध्य का प्रयोग तब करती है, जब वस्तुएँ अधिक होती हैं । मूल्यानुपातों का प्रयोग करने वाले सूचकांक को निम्न प्रकार से व्यक्त किया जा सकता है
p₀₁ = \(\frac{1}{n} \Sigma \frac{p_{1}}{p_{0}}\) × 100

यहाँ p₁ तथा p₀ क्रमशः वर्तमान अवधि और आधार अवधि में वस्तु की कीमतों को इंगित करते हैं। अनुपात \(\frac{\mathrm{p}_{1}}{\mathrm{p}_{0}}\) × 100 को वस्तु का मूल्यानुपात कहा जाता है।

n = वस्तुओं की संख्या है। मूल्यानुपातों का भारित सूचकांक भारित समान्तर माध्य होता है जिसे निम्न प्रकार परिभाषित किया जा सकता है

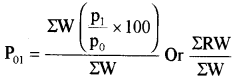
यहाँ w = भार
ΣW = भारों का योग
p₁ = चालू वर्ष की कीमत
p₀ = आधार वर्ष की कीमत
R = \(\frac{\mathrm{p}_{1}}{\mathrm{p}_{0}}\) × 100 है।

→ कुछ महत्त्वपूर्ण सूचकांक: कुछ महत्त्वपूर्ण सूचकांक निम्न प्रकार हैं
(i) उपभोक्ता कीमत सूचकांक:
उपभोक्ता कीमत सूचकांक को निर्वाह सूचकांक के नाम से भी जाना जाता है । यह खुदरा कीमतों में औसत परिवर्तन को मापता है। उपभोक्ता कीमत सूचकांक को अग्र सूत्र द्वारा ज्ञात किया जा सकता है
CPI = \(\frac{\Sigma \mathrm{RW}}{\Sigma \mathrm{W}}\)
यहाँ R = मूल्यानुपात है अर्थात् R = \(\frac{\mathrm{p}_{1}}{\mathrm{p}_{0}}\) × 100 है।
w = भार
ΣRW = मूल्यानुपातों व भार के गुणनफल का योग है।
अतः उपभोक्ता कीमत सूचकांक द्वारा उपभोक्ताओं द्वारा दैनिक जीवन निर्वाह में प्रयोग की जाने वाली विभिन्न वस्तुओं में होने वाले मूल्य परिवर्तनों का अध्ययन किया जाता है।

(ii) थोक कीमत सूचकांक:
थोक कीमत सूचकांक सामान्य कीमत स्तर में परिवर्तन का संकेत देता है। उपभोक्ता कीमत सूचकांक के विपरीत इसके लिए कोई संदर्भ उपभोक्ता श्रेणी नहीं होती है। इसके अन्तर्गत ऐसी मद शामिल नहीं होती है जो किसी सेवा से सम्बन्धित हो।

(iii) औद्योगिक उत्पाद सूचकांक:
औद्योगिक उत्पादन सूचकांक अनेक उद्योगों के औद्योगिक उत्पादन के स्तर में परिवर्तन को मापता है। इसके अन्तर्गत सार्वजनिक तथा निजी क्षेत्रक के उत्पादन शामिल होते हैं । यह परिमाण मूल्यानुपातों का भारित औसत है। सूचकांक के लिए सूत्र है
IIP₀₁ = \(\frac{\Sigma_{q_{1}} \times W}{\Sigma W}\) × 100

(iv) मानव विकास सूचकांक:
मानव विकास सूचकांक का उपयोग एक देश के विकास के अध्ययन के लिए किया जाता है।

(v) संवेदी सूचकांक:
संवेदी सूचकांक का सम्बन्ध शेयर बाजार अथवा अंशों के सूचकांक से है। जैसे-जैसे शेयर की कीमत में वृद्धि होती है, जो संवेदी सूचकांक में वृद्धि द्वारा प्रतिबिम्बित होती है, शेयर धारकों की सम्पत्ति का मान भी बढ़ता है। सूचकांक में अर्थव्यवस्था की स्थिति का पता चलता है। सेंसेक्स मुम्बई स्टॉक एक्सचेंज संवेदी सूचकांक का संक्षिप्त रूप है जिसका आधार वर्ष 1978-79 है।

→ सूचकांक की रचना में मुद्दे:
सूचकांक की रचना करते समय निम्न महत्त्वपूर्ण मुद्दों को ध्यान में रखा जाना चाहिए

• सूचकांक के उद्देश्य के बारे में स्पष्ट जानकारी होनी चाहिए।
• किसी भी सूचकांक के लिए मदों का चयन सावधानीपूर्वक किया जाना चाहिए ताकि जहाँ तक संभव हो | सके ये मदों का प्रतिनिधित्व कर सकें।
• प्रत्येक सूचकांक का एक आधार होना चाहिए तथा जहाँ तक संभव हो यह आधार सामान्य होना चाहिए।
• अध्ययन किए जाने वाले प्रश्न की प्रकृति के आधार पर सूत्र का चुनाव किया जाना चाहिए।
• आँकड़ों के संग्रह में उचित सावधानी बरतनी चाहिए। यदि प्राथमिक आँकड़ों को प्रयुक्त नहीं किया जाता है तो फिर सर्वाधिक विश्वसनीय द्वितीयक आँकड़ों के स्रोत का चुनाव किया जाना चाहिए।

→ अर्थशास्त्र में सूचकांक:
अर्थशास्त्र में थोक कीमत सूचकांक (WPI), उपभोक्ता कीमत सूचकांक (CPI) तथा औद्योगिक उत्पादन सूचकांक (IIP) का नीति निर्धारण में व्यापक रूप से प्रयोग किया जाता है। इन सूचकांकों के आधार पर कई प्रकार की नीतियों का निर्माण किया जाता है। अर्थशास्त्र में सूचकांकों की निम्न उपयोगिता है

• उपभोक्ता कीमत सूचकांक अथवा निर्वाह सूचकांक का प्रयोग मजदूरी समझौते, आय नीति, कीमत नीति, किराया नियन्त्रण, कराधान तथा सामान्य आर्थिक नीतियों के निर्माण में किया जाता है।
• थोक कीमत सूचकांक का उपयोग समुच्चयों की कीमतों में परिवर्तन जैसे कि राष्ट्रीय आय, पूँजी निर्माण आदि के परिवर्तनों के प्रभावों को समाप्त करने के लिए किया जाता है।
• थोक कीमत सूचकांक का उपयोग सामान्य रूप से मुद्रा स्फीति दर को मापने में किया जाता है।
• उपभोक्ता कीमत सूचकांक का मुद्रा की क्रय शक्ति व वास्तविक मजदूरी के परिकलन के लिए प्रयोग किया जाता है।
• औद्योगिक उत्पादन सूचकांक हमें औद्योगिक क्षेत्र में उत्पादन में परिवर्तन के बारे में परिमाणात्मक अंक प्रदान करता है।
• कृषि उत्पादन सूचकांक हमें कृषि क्षेत्र में निष्पादन का तत्काल परिकलन प्रदान करता है।
• संवेदी सूचकांक स्टॉक मार्केट में निवेशकों के लिए उपयोगी मार्गदर्शक का काम करता है।

→ हमें ये सूचकांक कहाँ से मिल सकते हैं?:
सामान्य रूप से प्रयोग में लिए जाने वाले कुछ सूचकांक नियमित रूप से भारत सरकार के वार्षिक प्रकाशन 'आर्थिक समीक्षा' में प्रकाशित किए जाते हैं।