RBSE Class 11 Economics Notes Chapter 7 सहसंबंध

These comprehensive RBSE Class 11 Economics Studies Notes Chapter 7 सहसंबंध will give a brief overview of all the concepts.

RBSE Class 11 Economics Chapter 7 Notes सहसंबंध

→ प्रस्तावना:
गर्मियों में तापमान बढ़ने पर पर्वतीय स्थलों पर सैलानियों की संख्या में वृद्धि हो जाती है तथा गर्मी बढ़ने पर आइसक्रीम की बिक्री बढ़ जाती है। इस प्रकार तापमान एवं सैलानियों की संख्या में एक सम्बन्ध है तथा तापमान एवं आइसक्रीम की बिक्री में भी सम्बन्ध है। इस प्रकार के सम्बन्धों का अध्ययन सहसम्बन्ध में किया जाता है। सहसम्बन्ध एक सांख्यिकीय माप है जो दो चरों के मध्य पाए जाने वाले सम्बन्ध की मात्रा को दर्शाता है।

→ सम्बन्धों के प्रकार:
सम्बन्ध कई प्रकार के होते हैं। जैसे-माँगी गई मात्रा तथा किसी वस्तु की कीमत में परिवर्तन का सम्बन्ध माँग के सिद्धान्त का अभिन्न अंग है, सम्बन्धों के इस प्रकार के उदाहरण को कारण और परिणाम के रूप में समझा जा सकता है। कई अन्य सम्बन्ध संयोग मात्र भी हो सकते हैं जैसे-जूते की माप तथा जेब में पैसों का सम्बन्ध संयोग सम्बन्ध का एक उदाहरण है। कुछ सम्बन्धों में दो चरों पर तीसरे चर के प्रभाव से, दोनों चरों के बीच के सम्बन्ध प्रभावित हो सकते हैं।

→ सहसम्बन्ध किसका माप करता है?:
सहसम्बन्ध चरों के बीच सम्बन्धों की गहनता एवं दिशा का अध्ययन एवं मापन करता है। सहसम्बन्ध सह-प्रसरण का मापन करता है न कि कार्य-कारण सम्बन्ध का। दो चरों X तथा Yके बीच सहसम्बन्ध की उपस्थिति का अर्थ है कि जब एक चर का माप किसी दिशा में बदलता है तो दूसरे चर का मान या तो उसी दिशा में बदलता है या फिर विपरीत दिशा में।

→ सहसम्बन्ध के प्रकार:
सहसम्बन्ध को मुख्य रूप से दो भागों में विभाजित किया जा सकता है-पहला. धनात्मक सहसम्बन्ध तथा दूसरा, ऋणात्मक सहसम्बन्ध । जब चरों की गति एक ही दिशा में एक-साथ होती है तो सहसम्बन्ध को धनात्मक कहा जाता है जैसे-आय में वृद्धि होने से उपभोग में वृद्धि होती है। जब चर विपरीत दिशा में गतिमान हों तो सहसम्बन्ध ऋणात्मक कहलाता है जैसे-सेब की कीमतों में गिरावट आती है तो उसकी माँग बढ़ जाती है।

→ सहसम्बन्ध को मापने की प्रविधियाँ:
सहसम्बन्ध के अध्ययन के लिए अधिकांश रूप से प्रयुक्त होने वाली प्रविधियाँ निम्न प्रकार हैं : प्रकीर्ण आरेख, कार्ल पियरसन का सहसम्बन्ध गुणांक तथा स्पीयरमैन का कोटि सहसम्बन्ध ।

→ प्रकीर्ण आरेख:
प्रकीर्ण आरेख, किसी संख्यात्मक मान के बिना सम्बन्धों के स्वरूप की जाँच दृश्य रूप में प्रस्तुत करने की एक उपयोगी प्रविधि है। इस प्रविधि में, दो चरों के मान को ग्राफ पेपर पर बिन्दुओं के रूप में आलेखित किया जाता है। आलेखित बिन्दुओं के इस गुच्छ को प्रकीर्ण आरेख कहा जाता है। प्रकीर्ण आरेख के द्वारा सम्बन्धों के स्वरूप को काफी सही रूप में जाना जा सकता है। प्रकीर्ण आरेख में प्रकीर्ण बिन्दुओं के समीप्य की कोटि और उसकी व्यापक दिशा के आधार पर उसके आपसी सम्बन्धों की जानकारी प्राप्त की जा सकती है।

→ कार्ल पियरसन का सहसम्बन्ध गुणांक:
कार्ल पियरसन सहसम्बन्ध गुणांक को गुणन आघूर्ण सहसम्बन्ध तथा सरल सहसम्बन्ध गुणांक के नामों से भी जाना जाता है। यह दो चरों X एवं Y के बीच रेखीय सम्बन्धों के सही संख्यात्मक मान की कोटि दर्शाता है।
कार्ल पीयरसन के सहसम्बन्ध गुणांक को तभी उपयोग में लाना चाहिए जब चरों के बीच रेखीय सम्बन्ध हो। चरों के बीच गैर-रेखीय सम्बन्ध होने पर कार्ल पीयरसन सहसम्बन्ध की गणना भ्रामक हो सकती है।
सहसम्बन्ध गुणांक ज्ञात करने हेतु x तथा y चरों के समान्तर माध्य, प्रसरण तथा सह-प्रसरण की आवश्यकता होती है, जो निम्न प्रकार है

→ समान्तर माध्य की गणना
x तथा y का समान्तर माध्य निम्न प्रकार ज्ञात करेंगे
X̄ = \(\frac{\Sigma X}{N}\), Ȳ = \(\frac{\Sigma Y}{N}\)

x तथा y का प्रसरण निम्न प्रकार ज्ञात करेंगे

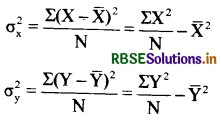
यहाँ x एवं y के मानक विचलन क्रमशः उनके प्रसरण के धनात्मक वर्गमूल हैं। x तथा y के सह-प्रसरण निम्नलिखित हैं
Co-variance (X, Y)
= \(\frac{\Sigma(\mathrm{X}-\overline{\mathrm{X}})(\mathrm{Y}-\overline{\mathrm{Y}})}{\mathrm{N}}=\frac{\Sigma \mathrm{xy}}{{N}}\)
यहाँ x = X - X̄ तथा y = Y - Ȳ। ये X तथा Y के माध्य मानों से उनके id के मान के विचलन हैं।

X तथा Y के बीच सह-प्रसरण का चिह्न सहसम्बन्ध गुणांक के चिह्न का निर्धारण करता है। गुणन आघूर्ण सहसम्बन्ध या कार्ल पीयरसन का सहसम्बन्ध मापन नीचे दिये जा रहा है

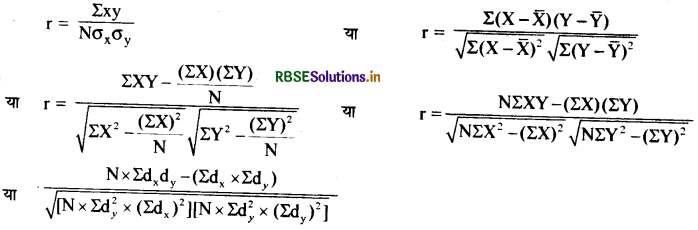
संकेताक्षर- r = सहसम्बन्ध गुणांक
σ_x = x श्रेणी का मानक विचलन
σ_y = y श्रेणी का मानक विचलन
N = पद-युग्मों की संख्या
X̄ = x श्रेणी का समान्तर माध्य
Ȳ = y श्रेणी का समान्तर माध्य

→ सहसम्बन्ध गुणांक के गुण
सहसम्बन्ध गुणांक के गुण निम्नलिखित हैं :

• r की कोई इकाई नहीं होती। यह एक संख्या मात्र है।
• r का ऋणात्मक मान प्रतिलोम सम्बन्ध दर्शाता है। किसी चर में बदलाव, दूसरे चर में विपरीत दिशा में बदलाव के साथ सम्बद्ध रहता है।
• यदि r धनात्मक होता है तो दोनों चर एक ही दिशा में गतिमान होते हैं।
• r = 0 हो तो चर असम्बन्धित होते हैं, इनके बीच कोई रेखीय सम्बन्ध नहीं होता है।
• यदि r = + 1 या r = - 1 है तो सहसम्बन्ध पूर्ण है।
• r का उच्च मान सुदृढ़ रेखीय सम्बन्ध दर्शाता है जब यह मान +1 या -1 के निकट हो तो वह उच्च कहलाता है।
• r का निम्न मान दुर्बल रेखीय सम्बन्ध दर्शाता है। जब यह शून्य के निकट हो तो इसका मान निम्न कहलाता
• सहसम्बन्ध गुणांक का मान -1 तथा +1 के बीच स्थित होता है। यदि किसी भी अभ्यास में r का मान इस परास के बाहर होता है तो इससे परिकलन में त्रुटि का संकेत मिलता है।
• r का मान उद्गम परिवर्तन या पैमाने के परिवर्तन से प्रभावित नहीं होता है।

→ स्पीयरमैन का कोटि सहसम्बन्ध:
स्पीयरमैन कोटि सहसम्बन्ध का विकास ब्रिटिश मनोवैज्ञानिक सी.ई. स्पीयरमैन द्वारा किया गया था। इस विधि का प्रयोग तब किया जाता है, जब चरों का सार्थक रूप से मापन नहीं किया जा सकता है। दूसरे शब्दों में इस रीति का प्रयोग उस स्थिति में किया जाता है, जबकि तथ्यों को प्रत्यक्ष रूप से संख्या में मापना सम्भव न हो परन्तु उन्हें एक निश्चित क्रम में रखा जा सकता हो, जैसे-कुशलता, सुन्दरता, स्वास्थ्य, योग्यता आदि।

इस विधि में सहसम्बन्ध की गणना करने हेतु सर्वप्रथम दोनों श्रेणियों के मूल्यों को क्रम प्रदान किया जाता है। सबसे बड़े मूल्य को 1, उससे छोटे मूल्य को 2 तथा आगे इसी प्रकार क्रम प्रदान किये जायेंगे। x-श्रेणी के क्रमों को R, से तथा Y-श्रेणी के क्रमों को R₂, से दर्शाया जायेगा। दोनों श्रेणियों के क्रमों का अन्तर ज्ञात किया जाता है। क्रमान्तर का योग सदैव शून्य होता है। क्रमान्तरों का वर्ग ज्ञात कर उनका योग (ΣD²) किया जाता है तथा निम्न सूत्र द्वारा सहसम्बन्ध गुणांक ज्ञात किया जाता है

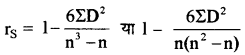
जब कोटियों को दोहराया जाता है, तो निम्नलिखित सूत्र का प्रयोग किया जाता है

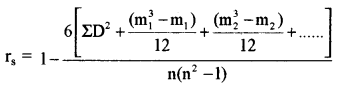
यहाँ m₁, m₂, ............, कोटियों की दोहराई गई संख्याएँ हैं तथा \(\frac{\mathrm{m}_{1}^{3}-\mathrm{m}_{1}}{12}\) ........... उनके संगत संशोधन M गुणांक हैं।

कोटि सहसम्बन्ध का परिकलन निम्न तीन स्थितियों में किया जा सकता है

• जब कोटियाँ दी गई हों।
• जब कोटियाँ नहीं दी गई हों। उन्हें आँकड़ों से प्राप्त किया जाना हो।
• जब कोटियों की पुनरावृत्ति की गई हो।