RBSE Class 11 Economics Important Questions Chapter 8 सूचकांक

Rajasthan Board RBSE Class 11 Economics Important Questions Chapter 8 सूचकांक Important Questions and Answers.

RBSE Class 11 Economics Important Questions Chapter 8 सूचकांक

वस्तुनिष्ठ प्रश्न:

प्रश्न 1. 
सूचकांक की विशेषता है।
(अ) लाभ प्राप्ति का आधार 
(ब) विशेष प्रकार का माध्य नहीं है।
(स) तुलना का आधार 
(द) अव्यापक 
उत्तर:
(स) तुलना का आधार 

 

प्रश्न 2. 
उपभोक्ता मूल्य सूचकांक है।
(अ) सामान्य मूल्य स्तर का सूचकांक 
(ब) एक स्थान पर रहने वाले उपभोक्ताओं के मूल्य का सूचकांक 
(स) किसी विशेष वर्ग के लोगों को निर्वाह लागत में होने वाले परिवर्तनों की दिशा तथा मात्रा को प्रकट करने वाला सूचकांक 
(द) एक स्थान पर रहने वाले उपभोक्ताओं की आय का सूचकांक 
उत्तर:
(स) किसी विशेष वर्ग के लोगों को निर्वाह लागत में होने वाले परिवर्तनों की दिशा तथा मात्रा को प्रकट करने वाला सूचकांक 

प्रश्न  3.
\(\frac{\Sigma \mathrm{RW}}{\Sigma \mathrm{W}}\) में R का अर्थ है।
(अ) \(\frac{\mathrm{p}_{0}}{\mathrm{p}_{1}} \times 100\)
(ब) \(\frac{\mathrm{p}_{1}}{\mathrm{~W}} \times 100\)
(स) \(\frac{p_{1}}{p_{0}} \times 100\)
(द) \(\frac{\mathrm{p}_{1}}{\mathrm{~W}} \times 100\)
उत्तर:
 (स) \(\frac{p_{1}}{p_{0}} \times 100\)

प्रश्न 4. 
लेस्पेयर विधि के अन्तर्गत भार दिया जाता है।
(अ) चालू वर्ष की मात्रा के आधार पर 
(ब) आधार वर्ष की मात्रा के आधार पर 
(स) चालू वर्ष व आधार वर्ष दोनों की मात्राओं के आधार पर
(द) उपर्युक्त में से कोई नहीं 
उत्तर:
(ब) आधार वर्ष की मात्रा के आधार पर 

प्रश्न 5. 
पारिवारिक बजट रीति के अन्तर्गत सूचकांक निर्माण का सूत्र है।
(अ) \(\mathrm{P}_{01}=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}} \times 100\)
(ब) \(\mathrm{P}_{01}=\frac{\Sigma \mathrm{RW}}{\Sigma \mathrm{W}} \times 100\)
(स) \(\mathbf{P}_{01}=\frac{\Sigma \mathbf{R W}}{\Sigma \mathbf{W}}\)
(द) \(\mathrm{P}_{01}=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{1}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{1}} \times 100\)
उत्तर:
 (अ) \(\mathrm{P}_{01}=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}} \times 100\)

प्रश्न 6. 
पाशे विधि के अन्तर्गत भार दिए जाते हैं।
(अ) चालू वर्ष की मात्रा के आधार पर 
(ब) आधार वर्ष की मात्रा के आधार पर 
(स) चालू तथा आधार वर्ष दोनों की मात्राओं के आधार पर
(द) उपर्युक्त में से कोई नहीं 
उत्तर:
(स) चालू तथा आधार वर्ष दोनों की मात्राओं के आधार पर

प्रश्न 7. 
पाशे विधि के अनुसार सूचकांक ज्ञात करने का।
(अ) \(\mathbf{P}_{01}=\frac{\sum \mathbf{R W}}{\sum \mathbf{W}}\)
(ब) \(P_{01}=\frac{2 p_{1} q_{0}}{\Sigma p_{0} q_{0}} \times 100\)
(स) \(\mathrm{P}_{01}=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{1}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{1}} \times 100\)
(द) \(\mathrm{P}_{01}=\frac{\Sigma \mathrm{p}_{0} \mathrm{q}_{1}}{\Sigma \mathrm{p}_{1} \mathrm{q}_{1}} \times 100\)
उत्तर:
 (ब) \(P_{01}=\frac{2 p_{1} q_{0}}{\Sigma p_{0} q_{0}} \times 100\)

प्रश्न 8. 
लेस्पेयर विधि के अनुसार सूचकांक का सूत्र है।
(अ) \(\mathrm{P}_{01}=\frac{\Sigma \mathrm{RW}}{\Sigma \mathrm{W}}\)
(ब) \(\mathrm{P}_{01}=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}} \times 100\)
(स) \(\mathrm{P}_{01}=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{1}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{1}} \times 100\)
(द) \(\mathrm{P}_{01}=\frac{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}}{\Sigma \mathrm{p}_{1} \mathrm{q}_{0}} \times 100\)
उत्तर:
 (अ) \(\mathrm{P}_{01}=\frac{\Sigma \mathrm{RW}}{\Sigma \mathrm{W}}\)

प्रश्न 9. 
उपभोक्ता कीमत सूचकांक मापता है।
(अ) खुदरा कीमतों में औसत परिवर्तन को 
(ब) आय में औसत परिवर्तन को 
(स) वस्तुओं की माँग में औसत परिवर्तन को
(द) वस्तुओं की पूर्ति में औसत परिवर्तन को 
उत्तर:
(स) वस्तुओं की माँग में औसत परिवर्तन को

प्रश्न 10. 
निम्न में से किस सूचकांक की सहायता से मुद्रास्फीति का माप किया जाता है।
(अ) उपभोक्ता कीमत सूचकांक 
(ब) थोक कीमत सूचकांक 
(स) कृषि उत्पादन सूचकांक 
(द) संवेदी सूचकांक
उत्तर:
(ब) थोक कीमत सूचकांक 

रिक्त स्थान वाले प्रश्ननीचे दिए गए वाक्यों में रिक्त स्थानों की पूर्ति करें:

प्रश्न 1. 
.............. सम्बन्धित चरों के समूह के परिमाण में परिवर्तनों को मापने का एक सांख्यिकीय साधन है।
उत्तर:
सूचकांक

प्रश्न 2. 
भारित समूहित कीमत सूचकांक जब आधार अवधि की मात्रा को भार के रूप में प्रयोग करता है तो इसे .............. कीमत सूचकांक कहा जाता है।
उत्तर:
लेस्पेयर

प्रश्न 3. 
जब भारित समूहित कीमत सूचकांक वर्तमान अवधि की मात्रा को भार के रूप में प्रयोग करता है तो इसे .............. कीमत सूचकांक कहा जाता है।
उत्तर:
पाशे 

प्रश्न 4. 
.............. सूचकांक का उपयोग सामान्य रूप से मृदा स्फीति दर को मापने में किया जाता है।
उत्तर:
थोक कीमत 

प्रश्न 5. 
सेंसेक्स मुम्बई स्टॉक एक्सचेंज संवेदी सूचकांक का संक्षिप्त रूप है जिसका आधार वर्ष .............. है।
उत्तर:
1978-79

सत्य / असत्य वाले प्रश्ननीचे दिए गए कथनों में सत्य / असत्य कथन छाँटिए:

प्रश्न 1. 
संवेदी सूचकांक स्टॉक मार्केट में निवेशकों के लिए उपयोगी मार्गदर्शक का काम करता है। 
उत्तर:
 सत्य

प्रश्न 2. 
थोक कीमत सूचकांक का मुद्रा की क्रय शक्ति एवं वास्तविक मजदूरी के परिकलन के लिए प्रयोग किया जाता है।
उत्तर:
असत्य

प्रश्न 3. 
औद्योगिक श्रमिकों के लिए उपभोक्ता कीमत सूचकांक का आधार वर्ष 2001 है। 
उत्तर:
 सत्य

प्रश्न 4. 
मदों के सापेक्षिक महत्व को बताने वाले सूचकांक को सरल समूहित सूचकांक कहते हैं। 
उत्तर:
सत्य

प्रश्न 5. 
अखिल भारतीय संयुक्त उपभोक्ता कीमत सूचकांक का आधार वर्ष 2001 है। 
उत्तर:
असत्य

मिलान करने वाले प्रश्ननिम्न को सुमेलित कीजिए:

प्रश्न 1. 

(1) उपभोक्ता कीमत सूचकांक का आधार वर्ष	(अ) 1986 - 87
(2) सेंसेक्स का आधार वर्ष	(ब) 2011-12
(3) औद्योगिक उत्पादन सूचकांक का आधार वर्ष	(स) 2012
(4) अखिल भारतीय ग्रामीण उपभोक्ता सूचकांक का आधार वर्ष	(द) 2001
(5) कृषि श्रमिकों के लिए अखिल भारतीय उपभोक्ता कीमत	(य) 1978 - 79

उत्तर:

(1) उपभोक्ता कीमत सूचकांक का आधार वर्ष	(द) 2001
(2) सेंसेक्स का आधार वर्ष	(य) 1978 - 79
(3) औद्योगिक उत्पादन सूचकांक का आधार वर्ष	(ब) 2011-12
(4) अखिल भारतीय ग्रामीण उपभोक्ता सूचकांक का आधार वर्ष	(स) 2012
(5) कृषि श्रमिकों के लिए अखिल भारतीय उपभोक्ता कीमत	(अ) 1986 - 87

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1. 
सूचकांक क्या है?
उत्तर:
सूचकांक संबंधित चरों के समूह के परिमाण में परिवर्तनों को मापने का एक सांख्यिकीय साधन है।

प्रश्न 2. 
आधार वर्ष का अर्थ लिखिए।
उत्तर:
सूचकांकों में दिए गए अंक किसी अवधि (वर्ष) के एक निश्चित अवधि (वर्ष) में अनुपात को दर्शाते हैं, इस निश्चित अवधि (वर्ष) को आधार वर्ष कहते हैं।

प्रश्न 3. 
सूचकांकों की कोई एक विशेषता बतलाइये।
उत्तर:
सूचकांकों की सहायता से पूरे समूह के सापेक्ष परिवर्तनों का माप किया जा सकता है।

प्रश्न 4. 
सूचकांकों का कोई एक महत्त्व बतलाइये।
उत्तर:
मुद्रा की क्रय शक्ति मापने के लिए सूचकांकों का प्रयोग किया जाता है।

प्रश्न 5. 
उपभोक्ता कीमत सूचकांक से आपका क्या आशय है?
उत्तर:
यह वह सूचकांक है जो उपभोक्ताओं द्वारा उपभोग की जाने वाली वस्तुओं तथा सेवाओं की कीमतों में होने वाले परिवर्तनों को मापता है।

प्रश्न 6. 
थोक मूल्य सूचकांक से क्या आशय है?
उत्तर:
यह वह सूचकांक है जो थोक बाजार में विक्रय की जाने वाली वस्तुओं की थोक कीमतों में होने वाले परिवर्तनों को मापते हैं।

प्रश्न 7. 
किन्हीं चार प्रकार के सूचकांकों के नाम बताइए।
उत्तर:

1. उपभोक्ता कीमत सूचकांक 
2. थोक कीमत सूचकांक 
3. कृषि उत्पादन सूचकांक 
4. औद्योगिक उत्पादन सूचकांक।

प्रश्न 8. 
सरल समूहित विधि के अन्तर्गत कीमत सूचकांक ज्ञात करने का सूत्र बताइए। 
उत्तर:
\(P_{01}=\frac{\Sigma p_{1}}{\Sigma p_{0}} \times 100\)
यहाँ Po₁ = वर्तमान वर्ष का मूल्य सूचकांक
P₁ = वर्तमान वर्ष का मूल्य
p₀ = आधार वर्ष का मूल्य 

प्रश्न 9. 
यदि ∑p₁q₀ = 450, ∑p₀q₀ = 461, ∑p₁q₁ = 560 तथा  ∑p₀q₁ = 567 हो तो पाशे विधि से सूचकांक की गणना कीजिए।
उत्तर:
 पाशे का कीमत सूचकांक
\(=\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}} \times 100\)
\(\mathrm{P}_{01}=\frac{560}{567} \times 100\)
= 98.77 

प्रश्न 10. 
यदि ∑p₁q₀ = 23400, ∑p₀q₀ = 19000. ∑p₁q₁ = 33400 तथा ∑p₀q₁ = 26800 हो तो लेस्पेयर विधि द्वारा कीमत सूचकांक की गणना कीजिए।
उत्तर:
 लेस्पेयर का कीमत सूचकांक
\(=\frac{\sum \mathrm{p}_{1} q_{0}}{\sum \mathrm{p}_{0} \mathrm{q}_{0}} \times 100\)
\(\mathrm{P}_{01}=\frac{23400}{19000} \times 100\)
= 123.16 

प्रश्न 11. 
निम्न समंकों से दो अवधियों के उपभोक्ता मूल्य सूचकांक की गणना कीजिए
∑RW = 104500, ∑pq = 148300, ∑W = 800
उत्तर:
'उपभोक्ता कीमत अथवा मूल्य सूचकांक
\(\begin{aligned} &=\frac{\Sigma R W}{\Sigma W} \times 100 \\ &=\frac{104500}{800} \end{aligned}\)
= 130.62 

प्रश्न 12. 
परम्परागत रूप से सूचकांकों को किस - रूप में व्यक्त किया जाता है?
उत्तर:
परम्परागत रूप से सूचकांकों को प्रतिशत के रूप में व्यक्त किया जाता है।

प्रश्न 13. 
परिमाणात्मक सूचकांक द्वारा किसका मापन किया जाता है?
उत्तर:
परिमाणात्मक सूचकांक उत्पादन की भौतिक मात्रा, निर्माण तथा रोजगार में परिवर्तनों को मापता है।

प्रश्न 14. 
लेस्पेयर कीमत सूचकांक ज्ञात करने का सूत्र लिखिए।
उत्तर:
लेस्पेयर कीमत सूचकांक
\(=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}} \times 100\)
यहाँ p₀ = आधार वर्ष की कीमत, P₁ = वर्तमान वर्ष की कीमत, q₀ = आधार वर्ष की मात्रा तथा q₁ = वर्तमान वर्ष की मात्रा है।

प्रश्न 15. 
पाशे के कीमत सूचकांक का सूत्र लिखिए।
उत्तर:
पाशे का कीमत सूचकांक
\(=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{1}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{1}} \times 100\)
यहाँ p_o = आधार वर्ष की कीमत, P₁ =  चालू वर्ष की कीमत, q₀ = आधार वर्ष की मात्रा तथा q₁ = चालू वर्ष की मात्रा है।

प्रश्न 16. 
सूचकांक की रचना करने की दो विधियों के नाम बताइए।
उत्तर:

1. समूहित विधि 
2. मूल्यानुपातों की माध्य विधि।

प्रश्न 17. 
उपभोक्ता कीमत सूचकांक का महत्त्व बताइए।
उत्तर:
यह मजदूरी समझौता, आय नीति, कीमत नीति, किराया नियन्त्रण, कराधान तथा सामान्य आर्थिक नीतियों के निर्माण में सहायक है।

प्रश्न 18. 
सामान्यतः मुद्रास्फीति को मापने हेतु किस सूचकांक का प्रयोग किया जाता है?
उत्तर:
सामान्यतः मुद्रास्फीति को मापने हेतु थोक कीमत सूचकांक का प्रयोग किया जाता है।

प्रश्न 19. 
कृषि उत्पादन सूचकांक का क्या महत्त्व
उत्तर:
कृषि उत्पादन सूचकांक हमें कृषि क्षेत्र के निष्पादन का तत्काल परिकलन प्रदान करता है।

प्रश्न 20. 
संवेदी सूचकांक का कोई एक महत्त्व बताइए।
उत्तर:
संवेदी सूचकांक स्टॉक मार्केट में निवेशकों के लिए उपयोगी मार्गदर्शक का काम करता है। 

लघूत्तरात्मक प्रश्न:

प्रश्न 1. 
उपभोक्ता कीमत सूचकांक को समझाइए।
उत्तर:
उपभोक्ता कीमत अथवा मूल्य सूचकांक-उपभोक्ता कीमत सूचकांक वह सूचकांक है जो उपभोक्ताओं द्वारा उपभोग की जाने वाली वस्तुओं तथा सेवाओं की कीमतों से आधार वर्ष की तुलना में चालू वर्ष में होने वाले परिवर्तन को मापता है। उपभोक्ता कीमत सूचकांक को निर्वाह सूचकांक के नाम से भी जाना जाता है। यह खुदरा कीमतों में औसत परिवर्तन को मापता है। भारत में औद्योगिक श्रमिकों, शहरी गैर शारीरिक कर्मचारियों तथा कृषि श्रमिकों हेतु उपभोक्ता कीमत सूचकांक की गणना की जाती है।

प्रश्न 2. 
सूचकांक क्या है?
उत्तर:
सूचकांक संबंधित चरों के समूह के परिमाण में परिवर्तनों को मापने का एक सांख्यिकीय साधन है। यह अपसारित (भिन्न-भिन्न दिशाओं में) होने वाले अनुपातों की सामान्य प्रवृत्ति का प्रतिनिधित्व करता है, जिनसे इसको परिकलित किया जाता है। यह दो भिन्न स्थितियों में सम्बन्धित चरों के किसी समूह में औसत परिवर्तन का माप है। अन्य शब्दों में सूचकांक ऐसे विशिष्ट माध्य हैं जिन्हें प्रतिशतों में व्यक्त किया जाता है, जिनके आधार पर तुलना की जा सकती है।

प्रश्न 3. 
आधार अवधि से आपका क्या अभिप्राय है?
उत्तर:
आधार अवधि: दो अवधियों में से, जिस अवधि के साथ तुलना की जाती है, उसे आधार अवधि के रूप में जाना जाता है। आधार अवधि में सूचकांक का मान 100 होता है। यदि हम यह जानना चाहें कि 1990 के स्तर से वर्ष 2005 में कीमतों में कितना परिवर्तन हुआ है? तब 1990 आधार अवधि मानी जाएगी। किसी भी अवधि का सूचकांक इसके अनुपात में होता है।

प्रश्न 4. 
थोक मूल्य सूचकांक क्या है?
उत्तर:
थोक मूल्य सूचकांक:  यह वह सूचकांक है जो थोक बाजार में विक्रय की जाने वाली वस्तुओं की थोक कीमतों में होने वाले परिवर्तनों को मापते हैं। इन सूचकांकों में उपभोक्ता कीमत सूचकांक के विपरीत इसके लिए कोई संदर्भ उपभोक्ता श्रेणी नहीं होती है । इसके अन्तर्गत ऐसे मद शामिल नहीं होते हैं जो सेवा से सम्बन्धित हों जैसे नाई के व्यय, मरम्मत आदि। ये सूचकांक व्यापार व उद्योग जगत में अत्यन्त उपयोगी

प्रश्न 5. 
सूचकांक की कोई चार विशेषताएँ बतलाइये।
उत्तर:
सूचकांकों की चार विशेषताएँ निम्नलिखित हैं

1. सूचकांक एक विशेष प्रकार के माध्य हैं।
2. सूचकांकों की सहायता से पूरे समूह का सापेक्ष परिवर्तनों का माप करना सम्भव है।
3. सूचकांक की सहायता से समय या स्थान के आधार पर तुलनात्मक अध्ययन किया जाता है।
4. सूचकांक मूल्यों में होने वाले परिवर्तनों को मापने के अलावा किसी भी ऐसी घटना के सापेक्ष माप के लिए प्रयोग किये जा सकते हैं जिसका प्रत्यक्ष या अप्रत्यक्ष अध्ययन न किया जा सके।

प्रश्न 6. 
सूचकांकों के उपयोग को संक्षेप में स्पष्ट कीजिए।
उत्तर:

1. ये नीति निर्धारण में सहायक हैं।
2. इनसे आर्थिक क्रियाओं के सम्बन्ध में पूर्वानुमान लगाया जा सकता है।
3. सूचकांकों से भविष्य की प्रवृत्तियों की जानकारी मिलती है।
4. सूचकांकों से वास्तविक स्थिति की जानकारी मिलती है।
5. ये आँकड़ों के सरलीकरण एवं तुलना में सहायक हैं।
6. चकांक सरकारी नीतियों के निर्धारण में उपयोगी हैं।

प्रश्न 7. 
सूचकांकों के कोई तीन महत्त्व बताइए।
उत्तर:

1. उपभोक्ता कीमत सूचकांक अथवा निर्वाह सूचकांक, मजदूरी समझौता, आय नीति, कीमत नीति, किराया नियन्त्रण, कराधान तथा सामान्य आर्थिक नीतियों के निर्माण में सहायक होते हैं।
2. थोक कीमत सूचकांक का प्रयोग समुच्चयों की कीमतों में परिवर्तन जैसे कि राष्ट्रीय आय, पूँजी निर्माण आदि के परिवर्तनों के प्रभाव को समाप्त करने के लिए किया जाता है।
3. थोक कीमत सूचकांक का प्रयोग सामान्य रूप से मुद्रा स्फीति दर को मापने में किया जाता है।

प्रश्न 8. 
औद्योगिक उत्पादन सूचकांक क्या है?
उत्तर:
औद्योगिक उत्पादन सूचकांक वह सूचकांक है जो एक देश के औद्योगिक उत्पादन की मात्रा के आधार वर्ष की तुलना में चालू वर्ष में होने वाले परिवर्तनों की माप करता है। इसके अन्तर्गत सार्वजनिक एवं निजी क्षेत्रक के उत्पादन को शामिल किया जाता है। भारत में औद्योगिक उत्पादन सूचकांक का आधार वर्ष 2011 - 12 है। इन सूचकांकों की सहायता से केवल औद्योगिक उत्पादन में होने वाले परिवर्तनों की जानकारी मिलती है, न कि औद्योगिक उत्पादन के मूल्यों में होने वाले परिवर्तनों की जानकारी।

प्रश्न 9. 
सूचकांकों की रचना में आने वाली प्रमुख समस्याएँ क्या हैं?
उत्तर:
सूचकांकों की रचना में निम्न प्रमुख समस्याएँ आती हैं।

1. सूचकांकों के उद्देश्य का निर्धारण करना
2. आधार अवधि का चुनाव करना
3. प्रतिनिधि वस्तुओं का चयन करना
4. मूल्यों को ज्ञात करना
5. माध्य का चुनाव करना
6. उचित भार का चुनाव करना
7. उचित विधि का चुनाव करना।

प्रश्न 10. 
उपभोक्ता मूल्य सूचकांक अथवा 1 उपभोक्ता कीमत सूचकांक की गणना करने की प्रक्रिया को स्पष्ट कीजिए।
उत्तर:

(1) सर्वप्रथम हम चालू वर्ष के मूल्य (P₁) में आधार वर्ष के मूल्य (p₀) का भाग देकर 100 से गुणा करके मूल्यानुपात (R) ज्ञात करेंगे।

\(\mathrm{R}=\frac{\mathrm{p}_{1}}{\mathrm{p}_{0}} \times 100\)

(2) प्रत्येक वस्तु पर किये गये व्यय को भार (Weight - W) कहते हैं। प्रश्न में भार स्पष्ट न दिया होने पर आधार वर्ष का मूल्य (p₀) तथा आधार वर्ष की मात्रा (q₀) को गुणा किया जाता है।

W = P_o x q₀

(3) मूल्यानुपात (R) को भार (W) से गुणा करके उनका योग ज्ञात करेंगे। (∑RW)

(4) इसके पश्चात् भारों का योग ज्ञात करेंगे। (∑W)

सूत्र-उपभोक्ता मूल्य सूचकांक = \(\frac{\Sigma W R}{\Sigma W}\)

प्रश्न 11. 
एक सांख्यिकी अधिकारी होने के नाते आपको सूचकांक तैयार करने हेतु विभिन्न मदों को उनके महत्त्व के अनुसार भार देना है। इस हेतु आप कौनसे समान्तर माध्य की गणना करेंगे? इसकी गणना विधि एवं कोई दो विशेषताएँ बताइए।
उत्तर:
यदि हमें सूचकांक तैयार करने हेतु विभिन्न मदों को उनके महत्त्व के अनुसार भार देना हो तो हम भारित समान्तर माध्य की गणना करेंगे। भारित समान्तर माध्य की गणना निम्न सूत्र द्वारा करेंगेभारित समान्तर माध्य
\(=\frac{w_{1} x_{1}+w_{2} x_{2}+\ldots \ldots+w_{n} x_{n}}{w_{1}+w_{2}+\ldots \ldots+w n}\)
\(=\frac{\Sigma \mathbf{W X}}{\Sigma \mathbf{W}}\)
 यहाँ w = पदों का भार, x = पदों का मूल्य है।
भारित समान्तर माध्य की विशेषताएँ:

1. इसप्ने विभिन्न मदों को उनके महत्त्व के अनुसार भार दिया जाता है।
2. भारित समान्तर माध्य अधिक वास्तविक माध्य है।

प्रश्न 12. 
सरल समूहित कीमत सूचकांक का उपयोग सीमित क्यों होता है? ।
उत्तर:
एक सरल समूहित कीमत सूचकांक का उपयोग सीमित होता है। इसका कारण यह है कि विभिन्न वस्तुओं की कीमतों के माप की इकाइयाँ समान नहीं होती हैं। यह अभारित सूचकांक है क्योंकि इसमें मदों का सापेक्षिक महत्त्व उपयुक्त रूप से प्रतिबिंबित नहीं होता है। लेकिन वास्तव में, क्रय की गई मदों के महत्त्व में क्रम में भिन्नता होती है। हमारे व्यय में खाद्य पदार्थों का अनुपात काफी अधिक होता है। ऐसी स्थिति में अधिक भार वाली मद की कीमत में तथा कम भार वाली मद की कीमत में समान वृद्धि के द्वारा कीमत सूचकांक में होने वाले कुल परिवर्तन के आशय भिन्न-भिन्न होंगे। अतः सरल समूहित कीमत सूचकांक का उपयोग सीमित होता है।

प्रश्न 13. 
अभारित सूचकांक की अपेक्षा भारित समूहित सूचकांक अधिक श्रेष्ठ क्यों है?
उत्तर:
अभारित समूहित सूचकांक में मदों का सापेक्षिक महत्त्व उपयुक्त रूप से प्रतिबिंबित नहीं होता है। कोई सूचकांक तब भारित सूचकांक बन जाता है, जब मदों के सापेक्षिक महत्त्व को ध्यान में रखा जाता है। यहाँ भार परिमाणात्मक भार है। भारित समूहित सूचकांक की रचना में कुछ विशेष वस्तुओं को लिया जाता है तथा इनके मूल्य को प्रतिवर्ष परिकल्पित किया जाता है। इस प्रकार यह वस्तुओं के एक निश्चित समूह के मूल्यों में होने वाले परिवर्तनों को मापता है। क्योंकि वस्तुओं में निश्चित समूह के कुल मूल्य में परिवर्तन होता है, यह परिवर्तन कीमत में परिवर्तन के कारण होता है। भारित समूहित सूचकांक परिकलन की विभिन्न विधियों में भिन्न - भिन्न समय में वस्तुओं के भिन्न-भिन्न समूहों का प्रयोग किया जाता है। अतः भारित समूहित सूचकांक अधिक श्रेष्ठ है।

प्रश्न 14. 
सूचकांकों की मुख्य विशेषताएँ बताइए।
उत्तर:

1. सूचकांकों के द्वारा सामूहिक परिवर्तनों का सापेक्ष माप किया जाता है।
2. सूचकांक विशेष प्रकार के माध्य हैं।
3. सूचकांक द्वारा परिवर्तनों को संख्यात्मक रूप में व्यक्त किया जाता है।
4. सूचकांकों की गणना प्रतिशत में की जाती
5. सूचकांकों का मूलभूत उद्देश्य तुलना करना होता है।
6. सूचकांकों का उपयोग व्यापक क्षेत्र में किया जाता है।

प्रश्न 15. 
सूचकांकों की मूल्यानुपातों की माध्य परिकलन विधि को स्पष्ट कीजिए।
उत्तर:
जब केवल एक वस्तु हो, तब कीमत सूचकांक वस्तु की वर्तमान अवधि की कीमत तथा आधार अवधि की कीमत का अनुपात होता है। सामान्यतः इसे प्रतिशत में व्यक्त किया जाता है। मूल्यानुपातों की माध्य परिकलन विधि इन मूल्यानुपातों के औसत या माध्य का प्रयोग तब करती है, जब वस्तुएँ अधिक होती हैं। मूल्यानुपातों का प्रयोग करने वाले सूचकांक को इस प्रकार व्यक्त किया जाता है
\(\mathrm{P}_{01}=\frac{1}{\mathrm{n}} \Sigma \frac{\mathrm{p}_{1}}{\mathrm{p}_{0}} \times 100\)
यहाँ n= वस्तुओं की संख्या
P₁ = वर्तमान समय में वस्तु की कीमत
P_o = आधार अवधि में वस्तु की कीमत है।

प्रश्न 16. 
भारित मूल्यानुपात सूचकांक में भारों का निर्धारण किस अवधि के आधार पर किया जाता
उत्तर:
भारित मूल्यानुपात सूचकांक में भारों का निर्धारण आधार वर्ष में कुल व्यय में उन पर किए गए व्यय के अनुपात अथवा प्रतिशत द्वारा किया जा सकता है। यह वर्तमान अवधि के लिए भी हो सकता है, जो प्रयोग किए गए सूत्र पर निर्भर करता है। अनिवार्यतः ये कुल व्यय में विभिन्न वस्तुओं पर किए गए व्यय के मूल्यांश होते हैं। सामान्यतः आधार अवधि भार को वर्तमान अवधि भार की अपेक्षा अधिक वरीयता दी जाती है। ऐसा इसलिए होता है क्योंकि प्रतिवर्ष भार का परिकलन असुविधाजनक होता है।

प्रश्न 17. 
भारत में उपभोक्ता कीमत सुचकांक (CPI) पर संक्षिप्त टिप्पणी लिखिए।
उत्तर:
उपभोक्ता कीमत सूचकांक (CPI) को निर्वाह सूचकांक भी कहा जाता है। यह सूचकांक खुदरा कीमतों में औसत परिवर्तन को मापता है। भारत में राजकीय संस्थाओं/एजेन्सीश द्वारा बड़ी संख्या में उपभोक्ता कीमत सूचकांकों की रचना की जाती है जिनमें कुछ निम्न प्रकार हैं-औद्योगिक श्रमिकों के लिए उपभोक्ता कीमत सूचकांक, कृषि श्रमिकों के लिए अखिल भारतीय उपभोक्ता कीमत सूचकांक, ग्रामीण श्रमिकों के लिए अखिल भारतीय उपभोक्ता कीमत सूचकांक, अखिल भारतीय ग्रामीण उपभोक्ता सूचकांक, अखिल भारतीय शहरी उपभोक्ता कीमत सूचकांक, अखिल भारतीय संयुक्त उपभोक्ता कीमत सूचकांक।

प्रश्न 18. 
संवेदी सूचकांक से आप क्या समझते
उत्तर:
संवेदी सूचकांक का सम्बन्ध शेयर बाजार अथवा अंशों के सूचकांक से होता है। जैसे-जैसे शेयर की कीमत में वृद्धि होती है, जो संवेदी सूचकांक में वृद्धि द्वारा प्रतिबिम्बित होती है, शेयर धारकों की सम्पत्ति का मान भी बढ़ता है। सूचकांक से अर्थव्यवस्था की स्थिति का भी पता चलता है। सेन्सेक्स मुम्बई स्टॉक एक्सचेंज संवेदी सूचकांक का संक्षिप्त रूप है जिसका आधार वर्ष 1978 - 79 है। संवेदी सूचकांक स्टॉक मार्केट में निवेशकों के लिए उपयोगी मार्गदर्शक का काम करता है। यदि सूचकांक चढ़ता है तो निवेशक भावी अर्थव्यवस्था के निष्पादन की दिशा में आशावादी होते हैं।

प्रश्न 19. 
सूचकांक की रचना करते समय ध्यान रखने योग्य किन्हीं चार बातों का उल्लेख कीजिए।
उत्तर:

1. सूचकांक की रचना करते समय उसके उद्देश्य की स्पष्ट जानकारी होनी चाहिए।
2. किसी भी सूचकांक के लिए मदों का चयन सावधानीपूर्वक किया जाना चाहिए ताकि जहाँ तक संभव हो सके ये मदों का प्रतिनिधित्व कर सकें।
3. प्रत्येक सूचकांक का एक आधार होना चाहिए तथा जहाँ तक संभव हो सके यह आधार सामान्य होना चाहिए।
4. अध्ययन किए जाने वाले प्रश्न की प्रकृति के आधार पर सूचकांक के सूत्र का प्रयोग किया जाना चाहिए।

प्रश्न 20. 
थोक कीमत सूचकांक (WPI) द्वारा मुद्रा स्फीति की गणना किस प्रकार की जाती है?
उत्तर:
थोक कीमत सूचकांक (WPI) का प्रयोग सामान्य रूप से मुद्रा स्फीति दर को मानने के लिए किया जाता है। मुद्रा स्फीति कीमतों में सामान्य तथा निरन्तर वृद्धि को कहते हैं। यदि मुद्रा स्फीति बहुत बढ़ जाती है, तो मुद्रा अपने पारम्परिक गुणों जैसे विनिमय का साधन एवं लेखे की इकाई आदि को खो सकती है। इसका मुख्य प्रभाव मुद्रा के मूल्य में कमी का होता है।
 साप्ताहिक मुद्रा स्फीति दर निम्न सूत्र द्वारा प्राप्त होती
\(\frac{X_{t}-X_{t-1}}{X_{t-1}} \times 100\)
यहाँ x_t एवं X_t-1, t वे तथा t -1 वे सप्ताहों के थोक कीमत सूचकांकों को दर्शाते हैं।

प्रश्न 21. 
सूचकांकों के कोई दो लाभ तथा सीमाओं का उल्लेख कीजिए।
उत्तर:
सूचकांकों के लाभ:

1. सूचकांक जटिल तथ्यों को सरल बनाकर प्रस्तुत करने में सहायता करते हैं जिससे उन्हें समझने में मदद मिलती है।
2. सूचकांक सामान्य मूल्य में परिवर्तन का अध्ययन करते हैं।

सूचकांकों की सीमाएँ अथवा दोष

1. सूचकांकों के निर्माण में प्रयुक्त माध्यों की सीमाएँ सूचकांकों पर भी लागू होती हैं।
2. सूचकांक संकेत मात्र होते हैं, ये वास्तविक स्थिति का सही ज्ञान नहीं करवाते हैं।

प्रश्न 22. 
उपभोक्ता कीमत सूचकांक (CPI) के कोई दो महत्त्व बताइए।
उत्तर:

1. उपभोक्ता कीमत सूचकांक अथवा निर्वाह सूचकांक, मजदूरी समझौता, आय नीति, कीमत नीति, किराया नियन्त्रण, कराधान तथा सामान्य आर्थिक नीतियों के निर्माण में सहायक होते हैं।
2. उपभोक्ता कीमत सूचकांक का मुद्रा की क्रय शक्ति एवं वास्तविक मजदूरी के परिकलन के लिए प्रयोग किया जाता है। इसकी सहायता से वर्ग विशेष के व्यक्तियों के रहन-सहन के व्यय में हो रहे या होने वाले परिवर्तनों का ज्ञान होता है।

प्रश्न 23. 
थोक कीमत सूचकांक का महत्त्व स्पष्ट कीजिए।
उत्तर:
थोक कीमत सूचकांक का प्रयोग अर्थव्यवस्था में भाग तथा पूर्ति सम्बन्धी अनुमान लगाने के लिए किया जा सकता है। थोक कीमत सूचकांक में वृद्धि अत्यधिक माँग का सूचक है, इसके विपरीत कमी. कम माँग का सूचक है। थोक कीमत सूचकांक का उपयोग राष्ट्रीय आय, राष्ट्रीय व्यय आदि समुच्चयों के मौद्रिक तथा वास्तविक मूल्यों का निर्धारण करने के लिए हो सकता है। इस सूचकांक को किसी भी देश में मुद्रा स्फीति की दर का अनुमान लगाने हेतु प्रयोग किया जा सकता है। मुद्रा स्फीति की दर का अनुमान लगाने हेतु प्रयोग किया जा सकता है।

प्रश्न 24. 
निम्न समंकों की सहायता से लेस्पेयर तथा पाशे के कीमत सूचकांकों की गणना कीजिए
∑p_oq_o = 136, ∑p_oq₁ = 182, ∑p₁q_o = 183, ∑p₁q₁ = 243
उत्तर:
लेस्पेयर का कीमत सूचकांकलेस्पेयर का कीमत सूचकांक निम्न सूत्र द्वारा ज्ञात किया जा सकता है
\(\mathrm{P}_{01}=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}} \times 100\)
\(=\frac{183}{136} \times 100\)
= 134.56
पाशे का कीमत सूचकांक: पाशे का कीमत सूचकांक निम्न सूत्र द्वारा ज्ञात किया जा सकता है
\(P_{01}=\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}} \times 100\)
\(=\frac{243}{182} \times 100\)
= 133.52 

प्रश्न 25. 
यदि ∑p_oq_o = 600, ∑p_oq₁ = 900, ∑p₁q_o = 800 तथा 141% 1200 हो तो भारित कीमत सूचकांक ज्ञात कीजिए।
उत्तर:
भारित कीमत सूचकांक ज्ञात करने का सूत्र निम्न प्रकार है
\(\mathrm{P}_{01}=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{1}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{1}} \times 100\)
अतः भारित कीमत सूचकांक
\(=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{1}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{1}} \times 100\)
\(=\frac{1200}{800} \times 100\)
= 150

निबन्धात्मक प्रश्न:

(क) सैद्धान्तिक प्रश्न:

प्रश्न 1. 
सूचकांक से आप क्या समझते हैं? सूचकांक की रचना करते समय किन-किन बातों को ध्यान में रखने की आवश्यकता है?
उत्तर:
सूचकांक का अर्थ-सूचकांक संबंधित चरों के समूह के परिमाण में परिवर्तनों को मापने का एक सांख्यिकीय साधन है। यह अपसारित (भिन्न-भिन्न दिशाओं में) होने वाले अनुपातों को सामान्य प्रवृत्ति का प्रतिनिधित्व करता है, जिससे इनको परिकलित किया जाता है। यह दो भिन्न स्थितियों में सम्बन्धित चरों के किसी समूह में औसत परिवर्तन का माप है। अन्य शब्दों में, सूचकांक ऐसे विशिष्ट माध्य हैं जिन्हें प्रतिशतों में व्यक्त किया जाता है, जिनके आधार पर तुलना की जा सकती है। तुलना समान वर्गों में की जा सकती है, जैसे व्यक्तियों, स्कूलों, अस्पतालों आदि में। सूचकांक उल्लेखित वस्तुओं की सूची में कीमतों, उद्योग के विभिन्न क्षेत्रकों में उत्पादन की मात्रा, विभिन्न कृषि फसलों का उत्पादन, निर्वाह खर्च आदि चरों के मूल्य में परिवर्तन को भी मापता है।

सूचकांक की रचना करते समय ध्यान रखी जाने वाली बातें-सूचकांक की रचना करते समय निम्न महत्त्वपूर्ण मुद्दों को ध्यान में रखा जाना चाहिए।

1. सूचकांक की रचना करते समय यह आवश्यक है कि सूचकांक के उद्देश्य के बारे में स्पष्ट जानकारी होनी चाहिए।
2. किसी भी सूचकांक के लिए मदों का चयन सावधानीपूर्वक किया जाना चाहिए ताकि जहाँ तक संभव हो सके ये मदों का प्रतिनिधित्व कर सकें।
3. प्रत्येक सूचकांक का एक आधार होना चाहिए तथा जहाँ तक संभव हो सके यह आधार सामान्य होना चाहिए। आधार अवधि के लिए चरम मानों को नहीं चुना जाना चाहिए।
4. सूचकांक की रचना करते समय प्रश्न की प्रकृति के आधार पर सूत्र का प्रयोग किया जाना चाहिए।
5. आँकड़ों के संग्रह में उचित सावधानी बरती जानी चाहिए। यदि प्राथमिक आँकड़ों को प्रयुक्त नहीं किया जाता है तो फिर सर्वाधिक विश्वसनीय द्वितीयक आँकड़ों के स्रोत का चुनाव किया जाना चाहिए।

प्रश्न 2. 
सूचकांक की विभिन्न विधियों का सविस्तार वर्णन कीजिये।
उत्तर:
सूचकांक की रचना करने की दो प्रमुख विधियाँ हैं जिनका विस्तृत विवेचन निम्न प्रकार है।
(1) सरल समूहित विधि या समूही व्यय विधि या भारित समूही विधि - इस रीति में आधार वर्ष के समूही व्यय तथा चालू वर्ष के समूही व्यय (आधार वर्ष की मात्रा के आधार पर) की सापेक्षिक तुलना करके सूचकांकों का निर्माण किया जाता है। सूचकांक निर्माण प्रक्रिया निम्नलिखित है।

(अ) आधार वर्ष के मूल्य (p_o) तथा आधार वर्ष की उपभोग मात्रा (q_o) को गुणा करके आधार वर्ष का समूही व्यय ज्ञात करते हैं तथा उनका योग लगाते हैं। ∑p_oq_o

(ब) चालू वर्ष के मूल्य (p₁) को आधार वर्ष की उपभोग मात्रा (q_o) से गुणा करके चालू वर्ष का समूही व्यय ज्ञात करते हैं तथा उनका योग लगाते हैं । ∑p₁q_o

(स) निम्न सूत्र द्वारा मूल्य सूचकांक की रचना करते हैंमूल्य सूचकांक (समूही व्यय रीति) चालू वर्ष का समूही व्यय आधार वर्ष का समूही व्यय

लेस्पेयर कीमत सूचकांक का सूत्र 

\(\mathrm{P}_{01}=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}} \times 100\)

(2) भारित मूल्यानुपात विधि या पारिवारिक बजट रीति-इस विधि द्वारा सूचकांक निर्माण की प्रक्रिया निम्नलिखित है
(अ) प्रत्येक मद या वस्तु के चालू वर्ष के मूल्य (p₁) तथा आधार वर्ष के मूल्य (p_o) के आधार पर मूल्यानुपात (R) ज्ञात किया जाता है।
\(\mathrm{R}=\frac{\mathrm{p}_{1}}{\mathrm{p}_{0}} \times 100\)
या
Price Relative 

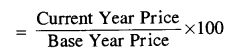
(ब) प्रत्येक पद या वस्तु पर किये गये कुल व्यय को भार (W) कहते हैं। यदि प्रश्न में भार स्पष्ट रूप से नहीं दिया हो तो प्रत्येक मद पर किये गये कुल व्यय की गणना हेतु आधार वर्ष के मूल्य (p_o) व आधार वर्ष की मात्रा (q_o) को गुणा करके p_oq_o ज्ञात किया जाता है तथा इसे ही भार (W) के रूप में प्रयोग किया जाता है।

(स) प्रत्येक वस्तु के मूल्यानुपात (R) को भार (W) से गुणा करके उनका योग (∑RW) लगाया जाता

(द) निम्न सूत्र द्वारा भारित कीमत सूचकांक की रचना की जाती है।
\(\mathrm{P}_{01}=\frac{\Sigma \mathrm{RW}}{\Sigma \mathrm{W}}\)

(ख) व्यावहारिक / क्रियात्मक प्रश्न:

प्रश्न 1. 
निम्नलिखित समंकों से 2018 के आधार पर 2019 के लिए सरल समूहित विधि से सूचकांक की रचना कीजिए।

वस्तुएँ	1	2	3	4	5	6	7	8	9
2018 के मूल्य	165	189	205	208	173	196	110	140	150
2019 के मूल्य	176	190	216	212	142	206	123	265	132

उत्तर:

वस्तु	2018 का मूल्य (po)	2019 का मूल्य (p1)
1	162	176
2	189	196
3	205	216
4	208	212
5	173	142
6	196	206
7	110	123
8	140	165
9	150	132
10	160	182
	∑po = 196	∑p1 = 1744

 सरल समूहित विधि द्वारा सूचकांक निम्न सूत्र की सहायता से ज्ञात किया जाता है

\(\begin{aligned} \mathrm{P}_{01} &=\frac{\Sigma \mathrm{p}_{1}}{\Sigma \mathrm{p}_{0}} \times 100 \\ \mathrm{P}_{01} &=\frac{1744}{1696} \times 100 \end{aligned}\)
\(=\frac{174400}{1696}\)

= 102.83

प्रश्न 2. 
निम्न से भारित समूहित रीति के अनुसार 2018 के मूल्यों के आधार पर 2019 के लिए उपभोक्ता मूल्य सूचकांक की गणना कीजिये। 

मद	2018 में मात्रा	इकाई	2018 में कीमत	2019 में कीमत
गेहूँ	2 Q	Per Q	100.00	200.00
चावल	1 Q	Per Q	160.00	220.00
अरहर	20 Kg	Per Kg	1.20	2.80
चीनी	50 Kg	Per kg	2.00	3.00
नमक	10 Kg	Per kg	0.40	0.60
तेल	10 Kg	Per kg	4.00	8.00
कपडे	20 Metre	Per Metre	3.00	5.00
पेट्रोल	4 Q	Per Q	16.00	20.00
मकान किराया	1	Per House	20.00	30.00

उत्तर:

मद	2018 में मात्रा	इकाई	2018 में कीमत	2019 में कीमत	P1qo	poqo
गेहूँ	2 Q	Per Q	100.00	200.00	400	200
चावल	1 Q	Per Q	160.00	220.00	220	16
अरहर	20 Kg	Per Kg	1.20	2.80	56	24
चीनी	50 Kg	Per kg	2.00	3.00	150	100
नमक	10 Kg	Per kg	0.40	0.60	6	4
तेल	10 Kg	Per kg	4.00	8.00	80	40
कपडे	20 Metre	Per Metre	3.00	5.00	100	60
पेट्रोल	4 Q	Per Q	16.00	20.00	80	64
मकान किराया	1	Per House	20.00	30.00	30	20
					1122 ∑p1qo	672 ∑poqo

सूत्र-उपभोक्ता कीमत सूचकांक
\(=\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}} \times 100\)

\(=\frac{1122}{672} \times 100\)
= 166.96

टिप्पणियाँ:
1.p₁q_o ज्ञात करने हेतु चालू वर्ष के मूल्य (p₁) तथा आधार वर्ष की उपभोग मात्रा (q_o) को गुणा किया जाता
2. p_oq_o ज्ञात करने हेतु आधार वर्ष के मूल्य (p_o) तथा आधार वर्ष की मात्रा (q_o) को गणा किया गया है। 

प्रश्न 3. 
निम्न आँकड़ों से लेस्पेयर तथा पाशे विधि से कीमत सूचकांकों की गणना कीजिए। 

मात्रा	आधार वर्ष		चाल वर्ष
	कीमत	मात्रा	कीमत	मात्रा
A B C D	8 2 1 1	20 6 2 5	50 15 20 10	60 10 15 3

उत्तर:
लेस्पेयर विधि द्वारा कीमत सूचकांकलेस्पेयर विधि द्वारा सूचकांक की गणना निम्न स्त्र द्वारा की जाएगी। 
\(\mathrm{P}_{01}=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}} \times 100\)
\(=\frac{1180}{184} \times 100\)
= 641.39

पाशे विधि द्वारा कीमत सूचकांकपाशे विधि द्वारा कीमत सूचकांक निम्न सूत्र द्वारा ज्ञात किया जाएगा। 
\(P_{01}=\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}} \times 100\)
\(=\frac{3730}{541} \times 100\)
= 689.46

प्रश्न 4.
निम्नांकित समंकों से लेस्पेयर एवं पाशे विधि के द्वारा कीमत सूचकांकों की गणना कीजिए। 

वस्तु	आधार वर्ष		चाल वर्ष
	कीमत	मात्रा	कीमत	मात्रा
A B C D	8 2 1 1	20 6 2 5	50 15 20 10	60 10 15 3

उत्तर:

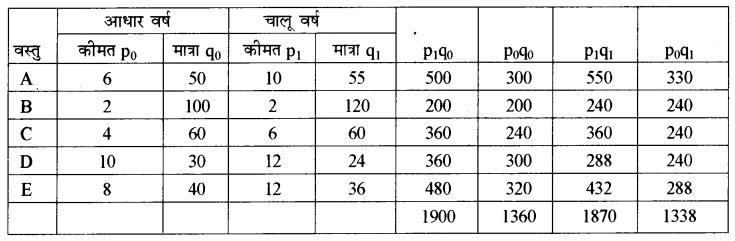
लेस्पेयर विधि द्वारा कीमत सूचकांक की गणना का सूत्र
\(\mathrm{P}_{01}=\frac{\sum \mathrm{p}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}} \times 100\)

\(=\frac{1900}{1360} \times 100\)
 = 139.71

पाशे विधि द्वारा कीमत सूचकांक की गणना का सूत्र
\(\mathrm{P}_{01}=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{1}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{1}} \times 100\)
\(=\frac{1870}{1338} \times 100\)
= 139.76

प्रश्न 5. 
निम्न समंकों से भारित समूहित विधि 2003 को आधार वर्ष मानकर सूचकांक ज्ञात कीजिए। 

वस्तु	उपभोग की कीमत	इकाई	कीमत प्रति इकाई
गेहूँ चावल चना दालें	4Qtl 1Qtl 1Qtl 2Qtl	क्विं क्विं क्विं क्विं	80 120 100 200

उत्तर:

वस्तु	(Q) उपभोग मात्रा (qo)	इकाई	आधार की कीमत 2003 (po)	चालू वर्ष (p1)	poqo	P1qo
गेहूँ	4Qlt	क्विं	80	200	320	800
चावल	1Qlt	क्विं	120	250	120	250
चना	1Qlt	क्विं	100	150	100	150
दालें	2Qlt	क्विं	200	300	400	600
					∑poqo	∑p1qo = 1800

भारित समूहित विधि:
उपभोक्ता कीमत सूचकांक =  \(\frac{\sum \mathrm{p}_{1} \mathrm{q}_{0}}{\sum \mathrm{p}_{0} \mathrm{q}_{0}} \times 100\)
\(=\frac{1800}{940} \times 100\) = 191.49

प्रश्न 6. 
नीचे तालिका में विभिन्न वर्षों के थोक कीमत सूचकांक दिए गए हैं तथा वर्ष 1993 - 94 को आधार वर्ष मानते हुए मुद्रास्फीति की दर की गणना कीजिए। 

वर्ष	थोक कीमत सूचकांक (1993-94-100)
1995-96 1996-97 1997-98 1998-99 1999-2000 2000-01 2001-02 2002-03 2003-04 2004-05	121 127 132 140 145 155 161 166 175 184

उत्तर:
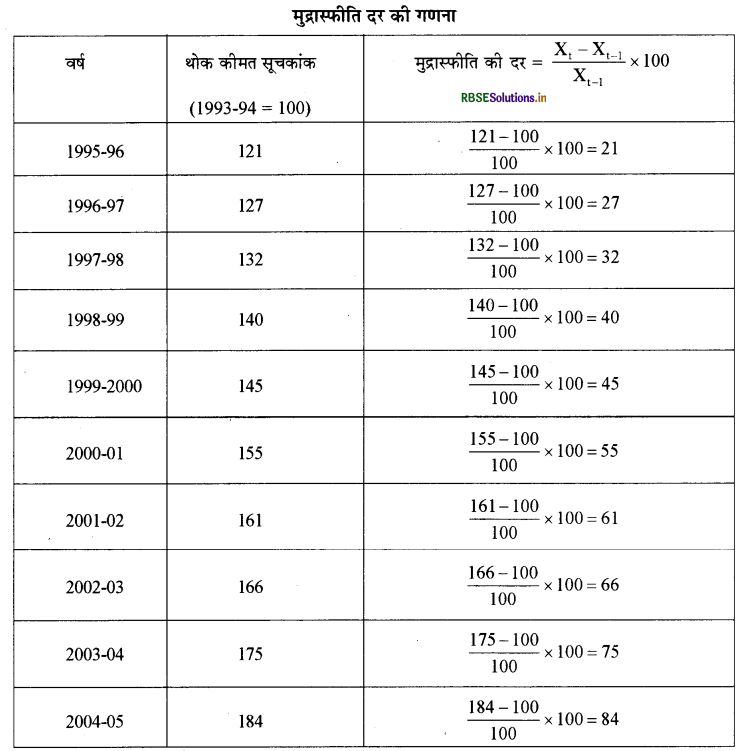
थोक मूल्य अथवा कीमत सूचकांक से मुद्रास्फीति की दर निम्न सूत्र द्वारा निकाली जाएगीमुद्रास्फीति
= \(\frac{X_{t}-X_{t-1}}{X_{t-1}} \times 100\)
यहाँ xt = वर्तमान अथवा चालू वर्ष का थोक कीमत सूचकांक
Xt -1 = आधार वर्ष का थोक कीमत सूचकांक

प्रश्न 7.
मूल्यानुपात विधि द्वारा 2018 को आधार वर्ष मानकर 2019 का सूचकांक तैयार कीजिए:

वस्तु	A	B	C	D	E	F
2018 का मूल्य	100	100	2	6	2	8
2019 का मूल्य	200	300	5	12	5	12

उत्तर:
मूल्यानुपात विधि द्वारा सूचकांक की गणना:

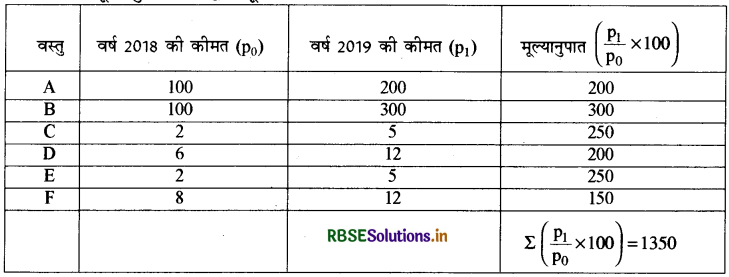
\(\begin{aligned} \mathbf{P}_{01} &=\frac{\sum\left(\frac{\mathrm{p}_{1}}{\mathrm{p}_{0}} \times 100\right)}{\mathrm{N}} \\ &=\frac{1350}{6} \end{aligned}\)

= 225

प्रश्न 8.
निम्न समंकों से लेस्पेयर तथा पाशे विधि से सचकांकों की गणना कीजिए:

मद	P0	Q0	P1	Q1
A	4	2	6	3
B	3	5	2	1
C	8	2	4	6

उत्तर:
लेस्पेयर तथा पाशे विधि द्वारा सूचकांकों की गणना:

मद	P0	Q0	P1	Q1	P0q0	P1q0	P0q1	P1q1
A	4	2	6	3	8	12	12	18
B	3	5	2	1	15	10	3	2
C	8	2	4	6	16	8	48	24
					39	30	63	44

लेस्पेयर विधि द्वारा सूचकांक गणना:
\(​​​​​​​\begin{aligned} \mathrm{P}_{01} &=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}} \times 100 \\ &=\frac{30}{39} \times 100 \\ &=\frac{3000}{39}=76.92 \end{aligned}\)
पाशे विधि द्वारा सूचकांक गणना:
\(\mathrm{P}_{01}=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{1}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{1}} \times 100\)
\(\begin{aligned} &=\frac{44}{63} \times 100 \\ &=\frac{4400}{63}=69.84 \end{aligned}\)

प्रश्न  9.
निम्नांकित समंकों से वर्ष 2018 का भारित कीमत सूचकांक ज्ञात कीजिए:

कीमत (2018)	कीमत (2018)	कीमत (2018)	कीमत (2018)	कीमत (2018)
190	190	190	190	190
210	210	210	210	210
1200	1200	1200	1200	1200
24	24	24	24	24
700	700	700	700	700

उत्तर:
भारित कीमत सचकांक की गणना:

कीमत (2018)	कीमत (2018)	qo	po	P1	P1 q0	P0q0
190	190	80	175	190	15200	14000
210	210	75	190	210	15750	14250
1200	1200	250	1000	1200	300000	250000
24	24	40	20	24	960	800
700	700	60	250	700	42000	15000

भारित कीमत सूचकांक \(=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}} \times 100\)
\(=\frac{373910}{294050} \times 100\)=
= 127.16

प्रश्न 10.
निम्न आँकड़ों की सहायता से 2017 को आधार वर्ष मानकर 2018 के जीवन निर्वाह सूचकांक ज्ञात कीजिए:

मद	भार	कीमत (2017) रु.	कीमत (2018) रु.
खाद्य पदार्थ	3	32.00	36.00
कपड़े	2	4.00	3.60
तेल	1	2.00	10.00
बिजली	1	0.40	0.50
मकान किराया	2	20.00	24.00
विविध	1	1.00	1.20

उत्तर:
जीवन निर्वाह सूचकांक की गणना:

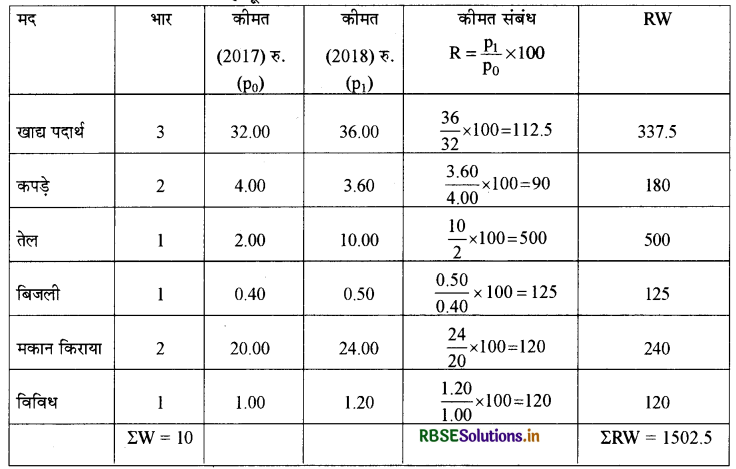
उपभोक्ता कीमत सूचकांक \(\left(\mathrm{P}_{01}\right)=\frac{\Sigma \mathrm{RW}}{\Sigma \mathrm{W}}\)
अथवा जीवन निर्वाह सूचकांक
\( \begin{aligned} &=\frac{1502.5}{10} \\ &=150.25 \end{aligned} \)

प्रश्न 11.
निम्नांकित समंकों से (I) भारित समूहित रीति एवं (II) मूल्यानुपात विधि से मार्च, 2019 के आधार पर मार्च, 2020 के लिए उपभोक्ता मूल्य सूचकांक की गणना कीजिए:
उत्तर:

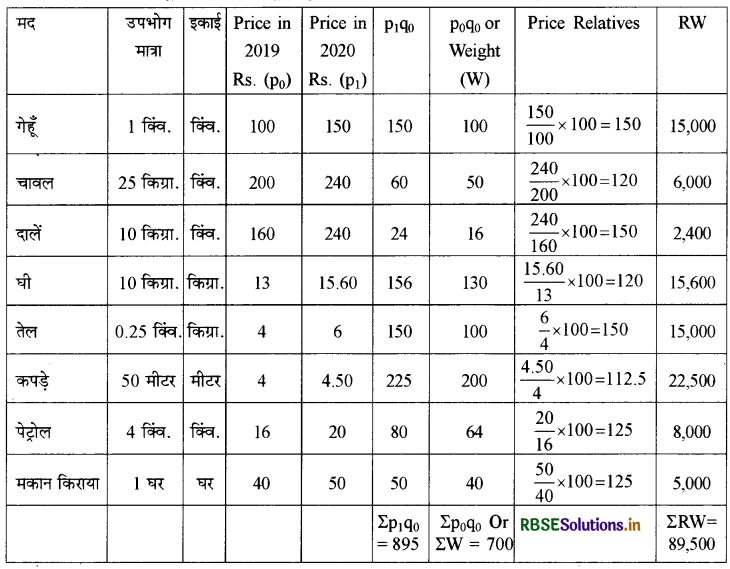
(i) भारित समूहित विधि
\( \begin{aligned} \left(\mathrm{P}_{01}\right) &=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}} \times 100 \\ &=\frac{895}{700} \times 100=127.86 \end{aligned} \)

(ii) मूल्यानुपात विधि उपभोक्ता कीमत सूचकांक:
\(​​​​​​​ \left(\mathrm{P}_{01}\right)=\frac{\Sigma \mathrm{RW}}{\Sigma \mathrm{W}}=\frac{89500}{700}\)
=127.86

टिप्पणियाँ:

1. चावल व दालों की उपभोग मात्रा किग्रा. में दी है जबकि कीमत की इकाई प्रति क्विण्टल है। अतः सर्वप्रथम कीमतों में 100 का भाग देकर कीमत प्रति किग्रा. ज्ञात की गई है। इसके पश्चात् कीमत प्रति किग्रा. को आधार वर्ष की उपभोग मात्रा से गुणा किया गया है। इसे निम्न प्रकार समझा जा सकता है:
2. तेल की उपभोग मात्रा क्विण्टल में दी गई है जबकि कीमत प्रति किग्रा. दी गई है। अतः उपभोग मात्रा को किग्रा. में परिवर्तित करके कीमत प्रति किग्रा. से गुणा किया जायेगा। इसकी गणना अग्र प्रकार समझी जा सकती है:

प्रश्न 12.
निम्नांकित समंकों से 2017 के लिए 2015 को आधार मानकर भारित समूहित विधि एवं मूल्यानुपात विधि से जीवन-निर्वाह सूचकांक ज्ञात कीजिये:
उत्तर:

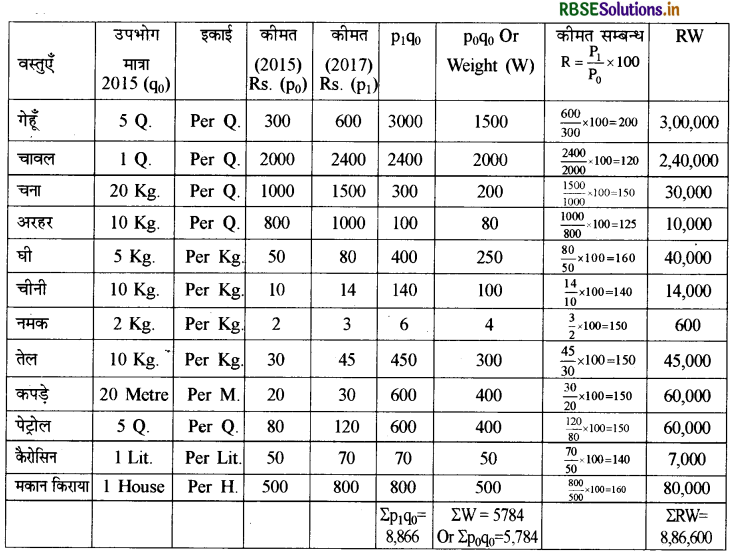
(i) भारित समूहित विधि
जीवन निर्वाह सूचकांक
\(\left(\mathrm{P}_{01}\right)=\frac{\Sigma \mathrm{p}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}} \times 100 =\frac{8,866}{5,784} \times 100=153.28 \)

(ii) मूल्यानुपात विधि
जीवन निर्वाह सूचकांक
\(​​​​​​​\left(\mathrm{P}_{01}\right)=\frac{\Sigma \mathrm{RW}}{\Sigma \mathrm{W}} \)
\(=\frac{8,86,600}{5,784}=153.28 \)

टिप्पणी:चना एवं अरहर की उपभोग मात्रा किग्रा. में दी है, जबकि मूल्य की इकाई प्रति क्विण्टल है। अतः सर्वप्रथम मूल्यों में 100 का भाग देकर मूल्य प्रति किग्रा. ज्ञात किये गये हैं। इसके पश्चात् मूल्य प्रति किग्रा. को आधार वर्ष की उपभोग मात्रा से गुणा किया गया है।

प्रश्न 13. 
2015 को आधार वर्ष मानते हुए 2020 के लिए पारिवारिक बजट विधि से उपभोक्ता मृल्य सूचकांक ज्ञात कीजिए।
उत्तर:
उपभोक्ता मूल्य सूचकांक की गणना ( पारिवारिक बजट विधि )

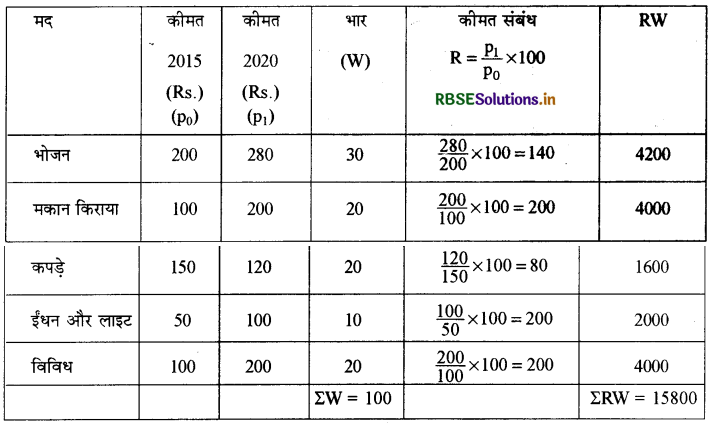
उपभोक्ता मूल्य सूचकांक:
\(\begin{aligned} \left(\mathrm{P}_{01}\right) &=\frac{\Sigma \mathrm{RW}}{\Sigma W} \\ &=\frac{15800}{100}=158 \end{aligned}\)

प्रश्न 14. 
निम्न आँकड़ों से भारित कीमत सूचकांक ज्ञात कीजिए:
उत्तर:
भारित कीमत सूचकांक की गणना:

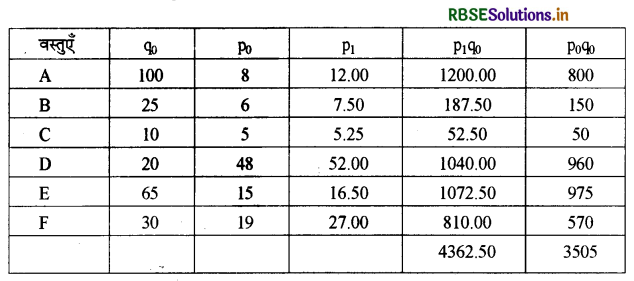
भारित कीमत सूचकांक:
\(​​​​​​​\begin{aligned} \text { } &=\frac{\Sigma \mathrm{p}_{1} q_{0}}{\Sigma \mathrm{p}_{0} \mathrm{q}_{0}} \times 100 \\ &=\frac{4362.50}{3505} \times 100 \\ &=124.5 \end{aligned}\)