RBSE Class 11 Economics Important Questions Chapter 7 सहसंबंध

Rajasthan Board RBSE Class 11 Economics Important Questions Chapter 7 सहसंबंध Important Questions and Answers.

RBSE Class 11 Economics Important Questions Chapter 7 सहसंबंध

वस्तुनिष्ठ प्रश्न:

प्रश्न 1. 
जब दो सम्बद्ध श्रेणियों के पद मूल्य एक ही दिशा में परिवर्तन होते हैं, तो उनमें सहसम्बन्ध पाया जाता है। 
(अ) ऋणात्मक 
(ब) धनात्मक
(स) शून्य 
(द) उपर्युक्त में से कोई नहीं। 
उत्तर:
(ब) धनात्मक

 

प्रश्न 2. 
उच्चस्तरीय धनात्मक सहसम्बन्ध है। 
(अ) - 75 से -1 के बीच
(ब) + 75 से +1 के बीच 
(स) -25 से - 75 के बीच
(द) + 25 से + 75 के बीच। 
उत्तर:
(ब) + 75 से + 1 के बीच 

प्रश्न 3. 
सीमित धनात्मक सहसम्बन्ध है। 
(अ) + 1
(ब) -1 
(स) 0 से + 0.25 
(द) शून्य। 
उत्तर:
(स) 0 से + 0.25 

प्रश्न 4. 
निम्नस्तरीय ऋणात्मक सहसम्बन्ध कहलाता है। 
(अ) 0 से 0.25 के बीच 
(ब) + 0.25 से 0.50 के बीच 
(स) -0.25 से 0 के बीच
(द) - 0.75 से - 0.50 के बीच। 
उत्तर:
(स) -0.25 से 0 के बीच

प्रश्न 5. 
जब दो सह सम्बन्धित श्रेणियों के पद-मूल्यों के विपरीत दिशा में परिवर्तन पाया जाता है, तो उनमें सहसम्बन्ध होगा। 
(अ) निरर्थक 
(ब) धनात्मक 
(स) शुन्य
(द) ऋणात्मक। 
उत्तर:
(अ) निरर्थक 

प्रश्न 6. 
दो समंक श्रेणियों के मध्य पारस्परिक निर्भरता नहीं हो अथवा उनके परिवर्तनों में आपस में कोई सम्बन्ध न हो तो सहसम्बन्ध का परिमाण होगा। 
(अ) सहसम्बन्ध का अभाव 
(ब) पूर्ण सहसम्बन्ध 
(स) सीमित सहसम्बन्ध
(द) उपर्युक्त में से कोई नहीं। 
उत्तर:
(ब) पूर्ण सहसम्बन्ध 

प्रश्न 7. 
स्पीयरमैन कोटि सहसम्बन्ध का सूत्र है। 
(अ) \(\mathrm{r}_{\mathrm{S}}=1-\frac{6 \Sigma \mathrm{D}^{2}}{\mathrm{~N}^{2}-\mathrm{N}}\) 
(ब) \(\mathrm{r}_{\mathrm{S}}=1-\frac{6 \Sigma \mathrm{D}^{2}}{\mathrm{~N}^{3}-\mathrm{N}}\)
(स)  \(r_{S}=1-\frac{4 \Sigma D^{2}}{N^{3}-N}\)
(द)  \(r_{S}=1-\frac{8 \Sigma D^{2}}{N^{3}-N}\)
उत्तर:
(ब) \(\mathrm{r}_{\mathrm{S}}=1-\frac{6 \Sigma \mathrm{D}^{2}}{\mathrm{~N}^{3}-\mathrm{N}}\)

प्रश्न 8. 
किसी संख्यात्मक माप के बिना, सम्बन्धों के स्वरूप की जाँच दृश्य रूप में प्रस्तुत करने की विधि को कहा जाता है। 
(अ) प्रकीर्ण आरेख विधि 
(ब) कार्ल पियरसन का सहसम्बन्ध गुणांक 
(स) स्पीयरमैन का कोटि सहसम्बन्ध 
(द) उपर्युक्त में से कोई नहीं।
उत्तर:
(अ) प्रकीर्ण आरेख विधि 

रिक्त स्थान वाले प्रश्ननीचे दिए गए वाक्यों में रिक्त स्थानों की पूर्ति करें:

प्रश्न 1. 
............... एक सांख्यिकीय माप है जो दो चरों के मध्य पाए जाने वाले सम्बन्ध की मात्रा को दर्शाता। 
उत्तर:
सहसम्बन्ध

प्रश्न 2. 
जब चर विपरीत दिशा में गतिमान हों तो सहसम्बन्ध .............. कहलाता है।
उत्तर:
ऋणात्मक

प्रश्न 3. 
यदि सहसम्बन्ध .............. होता है तो दोनों चर एक ही दिशा में गतिमान होते हैं।
उत्तर:
धनात्मक

प्रश्न 4. 
सहसम्बन्ध गुणांक मान 0 से अधिक किन्तु .............. से कम हो तो यह निम्नस्तरीय सहसम्बन्ध कहलाता है।
उत्तर:
425

प्रश्न 5. 
स्पीयरमैन कोटि सहसम्बन्ध का विकास ब्रिटिश मनोवैज्ञानिक .............. द्वारा किया गया।
उत्तर:
सी.ई. स्पीयरमैन

प्रश्न 6. 
कार्ल पियरसन सहसम्बन्ध गुणांक समंक माला के .............. पद मूल्यों पर आधारित होता है।
उत्तर:
सभी

सत्य / असत्य वाले प्रश्ननीचे दिए गए कथनों में सत्य / असत्य कथन छाँटिए:

प्रश्न 1. 
सहसम्बन्ध गुणांक का मान -1 से +1 के बीच स्थित होता है।
उत्तर:
सत्य

प्रश्न 2. 
सहसम्बन्ध के द्वारा दो या दो से अधिक श्रेणियों का तुलनात्मक अध्ययन किया जा सकता है।
उत्तर:
सत्य

प्रश्न 3. 
जब सहसम्बन्ध गुणांक का मान + 0.25 या उससे अधिक हो परन्तु + 0.50 से कम हो तो इसे मध्यमस्तरीय सहसम्बन्ध कहा जाता है। 
उत्तर:
असत्य

प्रश्न 4. 
सहसम्बन्ध अनुपस्थिति की दशा में सहसम्बन्ध गुणांक -1 होता है।
उत्तर:
असत्य

प्रश्न 5. 
सहसम्बन्ध कोई इकाई नहीं होती है, यह एक संख्या मात्र है।
उत्तर:
सत्य

प्रश्न 6. 
r = 0 हो तो चर असम्बन्धित होते हैं। इनके बीच कोई रेखीय सम्बन्ध नहीं होता है। 
उत्तर:
सत्य

मिलान करने वाले प्रश्ननिम्न को सुमेलित कीजिए:

प्रश्न 1.

(1) पूर्ण सहसम्बन्ध गुणांक	(अ) 0 तथा +0.25 के मध्य
(2) धनात्मक उच्च सहसम्बन्ध गुणांक	(ब) 0 से तथा -.25 के मध्य
(3) धनात्मक मध्यम सहसम्बन्ध गुणांक	(स) -1 व +1
(4) ऋणात्मक न्यून सहसम्बन्ध गुणांक	(द) + 5 या अधिक किन्तु +1 से कम
(5) धनात्मक न्यून सहसम्बन्ध गुणांक	(य) + 25 से अधिक परन्तु + 75 से कम

उत्तर:

(1) पूर्ण सहसम्बन्ध गुणांक	(स) -1 व +1
(2) धनात्मक उच्च सहसम्बन्ध गुणांक	(द) + 5 या अधिक किन्तु +1 से कम
(3) धनात्मक मध्यम सहसम्बन्ध गुणांक	(य) + 25 से अधिक परन्तु + 75 से कम
(4) ऋणात्मक न्यून सहसम्बन्ध गुणांक	(अ) 0 तथा +0.25 के मध्य
(5) धनात्मक न्यून सहसम्बन्ध गुणांक	(ब) 0 से तथा -.25 के मध्य

 

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1. 
अनुपस्थित सहसम्बन्ध से आप क्या समझते हैं?
उत्तर:
जब दो श्रेणियों के मध्य पारस्परिक निर्भरता न हो या उनके परिवर्तनों में कोई सम्बन्ध न हो।

प्रश्न 2. 
सहसम्बन्ध मापने की किन्हीं तीन विधियों के नाम बताइए।
उत्तर:

1. प्रकीर्ण आरेख विधि 
2. कार्ल पियरसन का सहसम्बन्ध गुणांक 
3. स्पीयरमैन का कोटि सहसम्बन्ध।

प्रश्न 3. 
कार्ल पियरसन सहसम्बन्ध गुणांक की परिभाषा लिखिए।
उत्तर:
कार्ल पियरसन का सहसम्बन्ध गुणांक दो चरों के सह-विचरण के माप का ही गुणांक है।

प्रश्न 4. 
स्पीयरमैन के कोटि सहसम्बन्ध का उपयोग कब किया जाता है?
उत्तर:
जब तथ्यों की प्रत्यक्ष रूप से संख्यात्मक माप सम्भव न हो परन्तु उन्हें एक निश्चित क्रम प्रदान किया जा सकता है।

प्रश्न 5. 
निम्नस्तरीय सहसम्बन्ध कब कहलाता है?
उत्तर:
सहसम्बन्ध गुणांक मान 0 से अधिक किन्तु + .25 से कम हो, तो यह निम्नस्तरीय सहसम्बन्ध कहलाता है।

प्रश्न 6. 
उच्चस्तरीय सहसम्बन्ध कब कहलाता
उत्तर:
जब सहसम्बन्ध गुणांक का मान + .75 से +1 के मध्य होता है तो उच्चस्तरीय सहसम्बन्ध कहलाता

प्रश्न 7. 
सहसम्बन्ध विश्लेषण से आप क्या समझते हैं?
उत्तर:
सहसम्बन्ध विश्लेषण के अन्तर्गत दो चरों के बीच के सम्बन्धों का अध्ययन किया जाता है।

प्रश्न 8. 
स्पीयरमैन कोटि सहसंबंध का विकास किसने किया?
उत्तर:
स्पीयरमैन कोटि सहसंबंध का विकास ब्रिटिश मनोवैज्ञानिक सी.ई. स्पीयरमैन द्वारा किया गया।

प्रश्न 9. 
मध्यम स्तरीय सहसम्बन्ध कौनसा कहलाता है?
उत्तर:
जब सहसम्बन्ध गुणांक (1) का मान + 0.25 या उससे अधिक हो परन्तु + 0.75 से कम हो तो इसे मध्यम स्तरीय सहसम्बन्ध कहा जाता है।

प्रश्न 10. 
स्पीयरमैन कोटि सहसम्बन्ध गुणांक का सूत्र लिखिए।
उत्तर:
स्पीयरमैन कोटि सहसम्बन्ध गुणांक =
\(1-\frac{6 \Sigma \mathrm{D}^{2}}{\mathrm{~N}^{3}-\mathrm{N}} \text { } 1-\frac{6 \Sigma \mathrm{D}^{2}}{n\left(n^{2}-1\right)}\)

प्रश्न 11. 
धनात्मक सहसम्बन्ध का अर्थ लिखिए।
उत्तर:
यदि दो चर-मूल्यों में परिवर्तन एक ही दिशा में हो, तो उनमें धनात्मक सहसम्बन्ध होता है।

प्रश्न 12. 
मूल्य तथा माँग में किस प्रकार का सहसम्बन्ध होता है?
उत्तर:
मूल्य तथा माँग में ऋणात्मक सहसम्बन्ध होता है।

प्रश्न 13. 
ऋणात्मक सहसम्बन्ध को परिभाषित कीजिए।
उत्तर:
जब दो चरों में परिवर्तन विपरीत दिशा में हो तो ऐसे सहसम्बन्ध को ऋणात्मक सहसम्बन्ध कहते

प्रश्न 14. 
सहसम्बन्ध का कोई एक महत्त्व लिखिए।
उत्तर:
सहसम्बन्ध के द्वारा दो या दो से अधिक श्रेणियों का तुलनात्मक अध्ययन किया जा सकता है।

प्रश्न 15. 
काल पियरसन सहसम्बन्ध गुणांक की कोई एक विशेषता बताइए।
उत्तर:
कार्ल पियरसन सहसम्बन्ध गुणांक समंकमाला के सभी पद-मूल्यों पर आधारित होता है।

प्रश्न 16. 
सहसम्बन्ध गुणांक का मान किन मानों के बीच स्थित होता है?
उत्तर:
सहसम्बन्ध गुणांक का मान -1 से +1 के बीच स्थित होता है। 

लघूत्तरात्मक प्रश्न:

प्रश्न 1. 
सहसम्बन्ध से आप क्या समझते हैं?
उत्तर:
व्यावहारिक क्षेत्र में बहुत: सी दशाओं में घटनाएँ अथवा चर एक-दूसरे से सम्बन्धित होकर परिवर्तित होते रहते हैं। अत: कभी - कभी दो तथ्यों में होने वाले परिवर्तन एक - दूसरे पर आश्रित रहते हैं अर्थात् एक श्रेणी में होने वाले परिवर्तन दूसरी श्रेणी में परिवर्तन उत्पन्न करते हैं, जैसे-किसी वस्तु की माँग में वृद्धि होने पर उस वस्तु की कीमत में भी वृद्धि होती है। अतः यह कहा जा सकता है कि जब दो समंक श्रेणियों में इस प्रकार का सम्बन्ध हो कि एक समंक श्रेणी में परिवर्तन होने पर दूसरी समंक श्रेणी में भी उसी दिशा में या विपरीत दिशा में परिवर्तन हो तो इस परिवर्तन के गणितीय माप को सहसम्बन्ध कहा जाता है।

प्रश्न 2. 
धनात्मक सहसम्बन्ध का क्या तात्पर्य
उत्तर:
धनात्मक सहसम्बन्ध: जब दो चर मूल्यों या समंकमालाओं में परिवर्तन एक ही दिशा में हो अर्थात् एक चर - मूल्य या श्रेणी में वृद्धि होने पर दूसरे चर - मूल्य या श्रेणी में वृद्धि हो अथवा एक चर-मूल्य या श्रेणी में कमी होने पर दूसरे चर - मूल्य या श्रेणी में कमी आए तो ऐसे सहसम्बन्ध को धनात्मक सहसम्बन्ध कहते हैं। जैसे वस्तु की मांग में वृद्धि होने पर मूल्यों में वृद्धि होना या वस्तु की मांग में कमी होने पर मूल्यों में कमी होना।

प्रश्न 3. 
ऋणात्मक सहसम्बन्ध से आप क्या समझते हैं?
उत्तर:
जब दो चरों में परिवर्तन विपरीत दिशा में हो अर्थात् एक चर में वृद्धि होने पर दूसरे चर में कमी हो अथवा एक चर में कमी होने पर दूसरे चर में वृद्धि हो, तो ऐसे सहसम्बन्ध को 'ऋणात्मक सहसम्बन्ध' कहा जाता है। उदाहरण के लिए, मूल्य में वृद्धि होने पर माँग में कमी होना या मूल्य कम होने पर माँग में वृद्धि होना। अतः यह कहा जाता है कि मूल्य तथा माँग में ऋणात्मक सहसम्बन्ध है।

प्रश्न 4. 
सम्बन्धों के प्रकारों को स्पष्ट कीजिए। 
उत्तर:
सम्बन्धों के कई प्रकार हैं। एक सम्बन्ध वे होते हैं, जिनमें कारण परिणामों की व्याख्या की जा सकती है। उदाहरण के लिए, मांगी गई मात्रा तथा किसी वस्तु की कीमत के मध्य पाए जाने वाला सम्बन्ध। कुछ सम्बन्ध केवल संयोग मात्र होते हैं, जैसे - किसी पक्षी विहार में पक्षियों के आने तथा उस क्षेत्र में जन्म - दर के मध्य सम्बन्ध मात्र संयोग होता है। तीसरे प्रकार का सम्बन्ध वह होता है जिसमें दो चरों पर तीसरे चर के प्रभाव से, दोनों चरों के बीच सम्बन्ध प्रभावित हो जाते हैं। उदाहरण के लिए गर्मियों में आइसक्रीम की बिक्री में तेजी डूबकर मरने वालों की संख्या से जोड़ी जा सकती है, यद्यपि मरने वाले आइसक्रीम खाकर नहीं डूबते हैं। किन्तु गर्मियों में लोग आइसक्रीम भी ज्यादा खाते हैं तथा तरणतालों में भी अधिक जाते हैं।

प्रश्न 5. 
सहसम्बन्ध किसका मापन करता है?
उत्तर:
सहसम्बन्ध चरों के बीच सम्बन्धों की गहनता एवं दिशा का अध्ययन एवं मापन करता है। सहसम्बन्ध सह-प्रसरण का मापन करता है न कि कार्यकारण सम्बन्ध का। सहसम्बन्ध को कार्य-कारण सम्बन्ध के रूप में नहीं समझा जाना चाहिए। दो चरों x और y के बीच सहसम्बन्ध की उपस्थिति का अर्थ है कि जब एक चर का मान किसी दिशा में बदलता है तो दूसरे चर का मान या तो उसी दिशा में बदलता है या उसकी विपरीत दिशा में बदलता है।

प्रश्न 6. 
सहसम्बन्ध को मापने की विभिन्न प्रविधियों पर संक्षिप्त टिप्पणी लिखिए।
उत्तर:
सहसम्बन्ध को मापने हेतु मुख्य रूप से निम्न प्रविधियों का प्रयोग किया जाता है-प्रकीर्ण आरेख विधि, कार्ल पियरसन का सहसम्बन्ध गुणांक तथा स्पीयरमैन का कोटि सहसम्बन्ध । प्रकीर्ण आरेख साहचर्य के स्वरूप को कोई विशिष्ट संख्यात्मक मान दिए बिना दृश्य रूप में प्रस्तुत करता है। कार्ल पियरसन का सहसम्बन्ध गुणांक दो चरों के बीच के रेखीय सम्बन्धों का संख्यात्मक मापन करता है। स्पीयरमैन का सहसम्बन्ध गुणांक एक अन्य मापन प्रविधि है जिसमें व्यष्टिगत मदों के बीच उनके गुणों के आधार पर निर्धारित कोटियों के द्वारा रेखीय सहसम्बन्ध को मापा जाता है।

प्रश्न 7. 
सहसम्बन्ध को मापने की प्रकीर्ण आरेख विधि को स्पष्ट कीजिए।
उत्तर:
प्रकीर्ण आरेख विधि: प्रकीर्ण आरेख किसी संख्यात्मक माप के बिना सम्बन्धों के स्वरूप की जाँच दृश्य रूप में प्रस्तुत करने की एक उपयोगी प्रविधि है। इस प्रविधि में दो चरों के मान को ग्राफ पेपर पर बिन्दुओं के रूप में आलेखित किया जाता है। आलेखित . बिन्दुओं के इस गुच्छ को प्रकीर्ण आरेख कहा जाता है। प्रकीर्ण आरेख द्वारा सम्बन्धों के स्वरूप को काफी सही रूप में जाना जा सकता है। प्रकीर्ण आरेख में प्रकीर्ण बिन्दुओं के सामीप्य की कोटि और उसकी व्यापक दिशा के आधार पर उसके आपसी सम्बन्धों की जानकारी प्राप्त की जाती है।

प्रश्न 8. 
सहसम्बन्ध गुणांक के कोई चार गुण बताइए।
उत्तर:

1. सहसम्बन्ध की कोई इकाई नहीं होती है, यह एक संख्या मात्र है।
2. सहसम्बन्ध का ऋणात्मक मान प्रतिलोम सम्बन्ध दर्शाता है। किसी चर में बदलाव दूसरे चर में विपरीत दिशा में बदलाव के साथ सम्बद्ध रहता है।
3. यदि सहसम्बन्ध धनात्मक रहता है तो दोनों चर एक ही दिशा में गतिमान रहते हैं।
4. r = 0 हो तो चर असम्बन्धित होते हैं, इनके बीच कोई रेखीय सम्बन्ध नहीं होता है।
    

प्रश्न 9. 
सहसम्बन्ध के कोई चार महत्त्व बताइए।
उत्तर:

1. सहसम्बन्ध दो या दो से अधिक श्रेणियों का तुलनात्मक अध्ययन करने में सहायक होता।
2. सहसम्बन्ध दो या दो से अधिक श्रेणियों में सहसम्बन्ध की मात्रा व सहसम्बन्ध की दिशा बताने में सहायक है।
3. सहसम्बन्ध के आधार पर पूर्वानुमान अधिक विश्वसनीय व यथार्थता के नजदीक होते हैं।
4. सहसम्बन्ध की सहायता से एक चर के दिए गए निश्चित मूल्य के आधार पर दूसरे चर के सम्भावित मूल्य का अनुमान लगाया जा सकता है।

प्रश्न 10. 
सहसम्बन्ध की कोई तीन सीमाएँ बताइए।
उत्तर:

1. एक श्रेणी के मूल्य के आधार पर दूसरी श्रेणी के तत्सम्बन्धी मूल्य का सर्वोत्तम अनुमान नहीं लगाया जा सकता है।।
2. दो श्रेणियों में उच्च सम्बन्ध होने पर यह ज्ञात करना कठिन होता है कि कौनसी श्रेणी कारण है तथा कौनसा परिणाम है।
3. सहसम्बन्ध गुणांक में मूल तथा अनुमाप परिवर्तन का कोई प्रभाव नहीं पड़ता है।

प्रश्न 11. 
सहसम्बन्ध के परिमाण (Degree of Correlation) को स्पष्ट कीजिए।
उत्तर:
सहसम्बन्ध का परिमाण (Degree of Correlation): सहसम्बन्ध गुणांक ज्ञात करने के बाद सहसम्बन्ध का परिमाण या निर्वचन ज्ञात किया जाता है। इसे निम्नलिखित तालिका से समझा जा सकता है।

प्रश्न 12. 
स्पीयरमैन कोटि सहसम्बन्ध गुणांक कैसे ज्ञात किया जाता है?
उत्तर:
स्पीयरमैन कोटि सहसम्बन्ध गुणांक ज्ञात करने हेतु सर्वप्रथम दोनों श्रेणियों के मूल्यों को क्रम प्रदान किया जाता है। सबसे बड़े मूल्य को 1, उससे छोटे मूल्य को 2 तथा आगे इसी प्रकार क्रम प्रदान किया जाता है। X श्रेणी के क्रमों को R₁ से तथा y श्रेणी के क्रमों को R₂ से दर्शाया जाता है। इसके पश्चात् निम्न सूत्र द्वारा दोनों श्रेणियों के क्रमों का अन्तर ज्ञात किया जाता है। \(\mathrm{D}=\mathrm{R}_{1}-\mathrm{R}_{2}\) क्रमान्तरों का वर्ग ज्ञात कर ∑D² ज्ञात किया जाता।
\(\mathrm{r}_{\mathrm{S}}=1-\frac{6 \Sigma \mathrm{D}^{2}}{\mathrm{n}^{3}-\mathrm{n}} \text { } 1-\frac{6 \Sigma \mathrm{D}^{2}}{\mathrm{n}\left(\mathrm{n}^{2}-1\right)}\)

प्रश्न 13. 
निम्न समंकों से। और y के बीच सहसम्बन्ध गुणांक की गणना कीजिए ∑xy = 122, ∑x² = 136, ∑y² = 138,
N = 15, \(\overline{\mathbf{X}} \) =25, \(\overline{\mathbf{Y}}\) = 18
उत्तर:
सहसम्बन्ध गुणांक (r) को निम्न सूत्र द्वारा ज्ञात किया जा सकता है।
\(\begin{aligned} r &=\frac{\Sigma x y}{\sqrt{\Sigma x^{2} \times \Sigma y^{2}}} \\ &=\frac{122}{\sqrt{136 \times 138}} \\ r &=\frac{122}{\sqrt{18768}} \\ &=\frac{122}{136.996} \end{aligned}\)
=89 अतः यह उच्चस्तरीय धनात्मक सहसम्बन्ध है।

प्रश्न 14. 
दो समंक श्रेणियों के मध्य सहसम्बन्ध कब सार्थक होता है? कोई दो उदाहरण दीजिए।
उत्तर:
सहसम्बन्ध सार्थक तभी माना जाता है जब दोनों श्रेणियों में कारण-परिणाम सम्बन्ध हो अर्थात् एक श्रेणी में होने वाले परिवर्तन का प्रभाव दूसरी श्रेणी पर होता हो, जैसे-मूल्य वृद्धि होने पर माँग कम होना, वाहनों की संख्या में वृद्धि के कारण दुर्घटनाएँ बढ़ना आदि। सहसम्बन्ध की मात्रा के आधार पर यह निष्कर्ष नहीं निकाला जा सकता है कि दोनों श्रेणियों में प्रत्यक्ष कारण - परिणाम सम्बन्ध भी है। कारण-परिणाम सम्बन्ध के अभाव में सहसम्बन्ध केवल सह-विचरण को ही दर्शाता है, जो अर्थहीन या निरर्थक या भ्रामक सहसम्बन्ध को दर्शाता है।

प्रश्न 15. 
निम्न समंकों से सहसम्बन्ध गुणांक का परिकलन कीजिए।
x तथा y श्रेणियों के तदनुरूपी विचलनों के गुणनफल का योग 4,800 है।
उत्तर:
प्रश्नानुसार, N = 1,000
σ_x = 4.5 σ_y = 3.6 ∑xy = 4,800
\(r=\frac{\Sigma x y}{N \sigma_{x} \sigma_{y}}\)
\(=\frac{4800}{1000 \times 4.5 \times 3.6}\)
\(=\frac{4800}{16200}\)
= 0.296 अत: यह मध्यम स्तरीय धनात्मक सहसम्बन्ध है।

प्रश्न 16.
1 तथा y श्रेणी में निम्नलिखित आँकड़ों से सहसम्बन्ध गुणांक की गणना कीजिए।
उत्तर:
x तथा y श्रेणी के मध्य सहसम्बन्ध गुणांक : की गणना निम्न सूत्र द्वारा की जा सकती है।
\(r=\frac{\Sigma(X-\bar{X})(Y-\bar{Y})}{\sqrt{\Sigma(X-\bar{X})^{2} \times \Sigma(Y-\bar{Y})^{2}}}\)
प्रश्नानुसार दिया हुआ है
\(\Sigma(\mathbf{X}-\overline{\mathrm{X}})(\mathbf{Y}-\overline{\mathbf{Y}})=120\)
\(\begin{array}{r} \Sigma(X-\bar{X})^{2}=210 \\ \Sigma(Y-\bar{Y})^{2}=148 \end{array}\)
N = 0
\(r=\frac{120}{\sqrt{210 \times 148}}\)

\(=\frac{120}{\sqrt{31080}}\)
\(=\frac{120}{176.30}\)
= 176.30 अतः श्रेणी x श्रेणी y में मध्यम स्तर का धनात्मक सहसम्बन्ध है।

प्रश्न 17. 
यदि N = 8, ∑\((\mathbf{X}-\overline{\mathbf{X}})^{2}\) = 36, ∑\((\mathbf{Y}-\overline{\mathbf{Y}})^{2}\) = 44 तथा ∑\((\mathbf{X}-\overline{\mathbf{X}})(\mathbf{Y}-\overline{\mathbf{Y}})\) = 24 हो तो सहसम्बन्ध गुणांक (r) ज्ञात कीजिए।
उत्तर:
\(r=\frac{\Sigma(X-X)(Y-Y)}{\sqrt{\Sigma(X-\bar{X})^{2} \times \Sigma(Y-\bar{Y})^{2}}}\)
\(r=\frac{24}{\sqrt{36 \times 44}}\)
\(\begin{aligned} &=\frac{24}{\sqrt{1584}} \\ &=\frac{24}{39.80} \end{aligned}\)
r = 60 अत: x तथा y में मध्यम स्तर का धनात्मक सहसम्बन्ध है।

प्रश्न 18. 
सहसम्बन्ध गुणांक ज्ञात करने की सर्वश्रेष्ठ विधि कौनसी है एवं क्यों?
उत्तर:
सहसम्बन्ध गुणांक ज्ञात करने की कार्ल पियरसन की विधि सर्वश्रेष्ठ है। इस विधि में सहसम्बन्ध की दिशा तथा मात्रा के साथ-साथ संख्यात्मक माप भी किया जाता है। यह सहसम्बन्ध गुणांक, माध्य एवं प्रमाप विचलन पर आधारित है। इस कारण यह विधि गणितीय दृष्टि से पूर्णरूपेण शुद्ध एवं सही है। अत: कार्ल पियरसन की विधि सहसम्बन्ध गुणांक ज्ञात करने की सर्वश्रेष्ठ विधि है।

प्रश्न 19. 
सांख्यिकीय विश्लेषण में सहसम्बन्ध तकनीक किस प्रकार महत्त्वपूर्ण है? स्पष्ट कीजिए।
उत्तर:
सांख्यिकीय विश्लेषण में सहसम्बन्ध तकनीक निम्न प्रकार से महत्त्वपूर्ण है।

1. दो या दो से अधिक श्रेणियों में तुलनात्मक अध्ययन करने हेतु।
2. दो या दो से अधिक श्रेणियों में सहसम्बन्ध की मात्रा तथा दिशा (धनात्मक अथवा ऋणात्मक) जानकारी हेतु।
3. सहसम्बन्ध के आधार पर पूर्वानुमान अधिक विश्वसनीय व यथार्थता के निकट होते हैं। 
4. सहसम्बन्ध की सहायता से एक चर के दिए गए निश्चित मूल्य के आधार पर दूसरे चर के सम्भावित मूल्य का अनुमान लगाया जा सकता है। यह प्रतीपगमन विश्लेषण का आधार है।
5. सहसम्बन्ध आन्तरगणन तथा बाह्य-गणन में सहायक होता है।

प्रश्न 20. 
सहसम्बन्ध गुणांक ज्ञात करने की कार्ल पियरसन विधि की कोई दो विशेषताओं का उल्लेख कीजिए।
उत्तर:

1. आदर्श माप: यह सहसम्बन्ध गुणांक समंकमाला के सभी पद मूल्यों पर आधारित होता हैं तथा समान्तर माध्य एवं प्रमाप विचलन के आधार पर ज्ञात किए जाने के कारण यह एक आदर्श माप समझा जाता है।
2. दिशाओं का ज्ञान: यह सहसम्बन्ध गुणांक पद - मूल्यों में परिवर्तनों की दिशाओं की जानकारी प्रदान करता है अर्थात् यदि सहसम्बन्ध गुणांक (+) में होता है तो धनात्मक सहसम्बन्ध होगा और यदि वह (-) है, तो ऋणात्मक सहसम्बन्ध होगा।

प्रश्न 21. 
पूर्ण सहसम्बन्ध से आप क्या समझते हैं?
उत्तर:
यह वह स्थिति है जब दो मद मूल्यों का परिवर्तन समान अनुपात में होता है। यह परिवर्तन ऋणात्मक भी हो सकता है, धनात्मक भी। यदि परिवर्तन समान अनुपात में एक ही दिशा में हो तो सहसम्बन्ध पूर्ण धनात्मक होगा तथा सहसम्बन्ध गुणांक +1 होगा। अगर परिवर्तन समान अनुपात में विपरीत दिशा में हो तो सहसम्बन्ध पूर्ण ऋणात्मक व सहसम्बन्ध गुणांक -1 होगा।

प्रश्न 22. 
बहुगुणी सहसम्बन्ध से आप क्या समझते हैं?
उत्तर:
बहुगुणी सहसम्बन्ध: जब दो या दो से अधिक स्वतन्त्र चर-मूल्यों या आश्रित समंक श्रेणियों के सम्मिलित प्रभाव का अध्ययन करते हैं तो सहसम्बन्ध को बहुगुणी सहसम्बन्ध कहते हैं। इसमें स्वतन्त्र श्रेणी एक से अधिक हो सकती हैं, जबकि आश्रित समंक श्रेणी केवल एक ही होती है। उदाहरण हेतु वर्षा , खाद, तापक्रम, मिट्टी का स्वभाव तथा गेहूं के उत्पादन के मध्य सहसम्बन्ध का निर्धारण करना। यहाँ वर्षा, खाद, तापक्रम, मिट्टी का स्वभाव स्वतन्त्र श्रेणी है, जबकि गेहूँ का उत्पादन आश्रित श्रेणी है। इन दोनों के मध्य सहसम्बन्ध बहुगुणी सहसम्बन्ध कहलाएगा।

प्रश्न 23. 
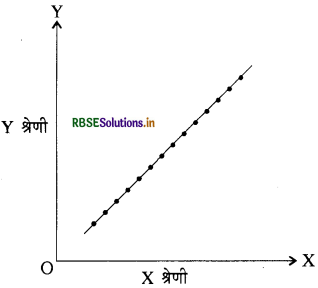
पूर्णतया धनात्मक सहसम्बन्ध को रेखाचित्र द्वारा स्पष्ट कीजिए।
उत्तर:
यदि श्रेणी x तथा श्रेणी y को रेखाचित्र पर अंकित करें तथा यदि सभी बिन्दु बायीं ओर से निचले कोने से दायीं ओर ऊपर की ओर एक सीधी रेखा अथवा सरल रेखा में हों तो वह पूर्णतया धनात्मक सहसम्बन्ध होगा। इसे  अग्रांकित रेखाचित्र द्वारा दर्शाया जा सकता है।

प्रश्न 24. 
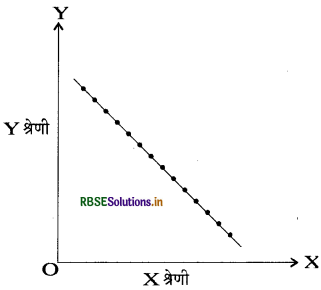
पूर्णतया ऋणात्मक सहसम्बन्ध को रेखाचित्र द्वारा दर्शाइए।
उत्तर:
यदि श्रेणी x तथा श्रेणी y को रेखाचित्र पर अंकित किया जाए तथा इन सभी बिन्दुओं को मिलाने वाली रेखा एक सरल रेखा हो तथा वह ऊपर से नीचे की ओर एक सीधी रेखा में हो तो वह पूर्णतया ऋणात्मक सहसम्बन्ध को दर्शाएगी। इसे अन रेखाचित्र द्वारा दर्शाया जा सकता है।

प्रश्न 25. 
सरल सहसम्बन्ध तथा आंशिक सहसम्बन्ध से आप क्या समझते हैं?
उत्तर:
सरल सहसम्बन्ध-किन्हीं दो समक श्रेणियों के सहसम्बन्ध को सरल सहसम्बन्ध कहते हैं। इनमें से एक श्रेणी कारण या स्वतन्त्र चर होती है तथा दुसरी श्रेणी परिणाम या आश्रित चर होती है। उदाहरण हेतु आयु एवं वजन के सहसम्बन्ध का माप सरल सहसम्बन्ध है। आंशिक सहसम्बन्ध-जब दो से अधिक समंक श्रेणियों के मूल्यों का अध्ययन करते हैं तो अन्य समंक श्रेणियों के मूल्यों के प्रभाव को स्थिर रखकर केवल दो श्रेणियों के मूल्यों में ही सहसम्बन्ध ज्ञात करना आंशिक सहसम्बन्ध कहलाता है।

निबन्धात्मक प्रश्न:

(क) सैद्धान्तिक प्रश्न:

प्रश्न 1. 
सहसम्बन्ध से आप क्या समझते हैं? चरों की संख्या के आधार पर सहसम्बन्ध के प्रकारों | को स्पष्ट कीजिए।
अथवा 
सहसम्बन्ध से आप क्या समझते हैं? सरल सहसम्बन्ध, बहुगुणी सहसम्बन्ध तथा आंशिक सहसम्बन्ध का अर्थ स्पष्ट कीजिए।
उत्तर:
सहसम्बन्ध का अर्थ: जब दो समंक श्रेणियों में इस प्रकार का सम्बन्ध हो कि एक समंक श्रेणी में परिवर्तन होने पर दूसरी समंक श्रेणी में भी उसी दिशा या विपरीत दिशा में परिवर्तन हो जाए तो इस सहपरिवर्तन के गणितीय माप को ही सहसम्बन्ध कहा जाता है। दोनों श्रेणियों में समान दिशा में परिवर्तन होने पर सहसम्बन्ध धनात्मक होता है तथा विपरीत दिशा में परिवर्तन होने पर सहसम्बन्ध ऋणात्मक सहसम्बन्ध होता है। सहसम्बन्ध दो श्रेणियों में पारस्परिक सम्बन्ध की दिशा व मात्रा का विश्लेषण करता है; परन्तु सहसम्बन्ध की मात्रा के आधार पर यह नहीं कहा जा सकता है कि दोनों सम्बन्धित श्रेणियों में आवश्यक रूप से प्रत्यक्ष कार्य - कारण सम्बन्ध भी है। चरों की संख्या के आधार पर सहसम्बन्ध के प्रकार
1. सरल सहसम्बन्ध: किन्हीं दो समंक श्रेणियों के सहसम्बन्ध को सरल सहसम्बन्ध कहते हैं। इनमें से एक श्रेणी कारण या स्वतन्त्र चर होती है तथा दूसरी श्रेणी परिणाम या आश्रित चर होती है। उदाहरण हेतु आयु एवं वजन के सहसम्बन्ध का माप सरल सहसम्बन्ध है।

2. बहुगुणी सहसम्बन्ध: जब दो या दो से अधिक स्वतन्त्र चर मूल्यों या आश्रित समंक श्रेणियों के सम्मिलित प्रभाव का अध्ययन करते हैं तो ऐसे सहसम्बन्ध को बहुगुणी सह-सम्बन्ध कहते हैं। इसमें स्वतन्त्र श्रेणी एक से अधिक हो सकती हैं, जबकि
आश्रित-समंक श्रेणी केवल एक ही होती है। उदाहरण हेतु वर्षा, खाद, तापक्रम, मिट्टी का स्वभाव स्वतन्त्र श्रेणी है, जबकि इनका गेहूं के उत्पादन (आश्रित श्रेणी) से सम्बन्ध बहुगुणी सहसम्बन्ध होता है।

3. आंशिक सहसम्बन्ध: जब दो से अधिक समंक श्रेणियों के मूल्यों का अध्ययन करते हैं तो अन्य समंक श्रेणियों के मूल्यों के प्रभाव को स्थिर रखकर केवल दो श्रेणियों के मूल्यों में ही सहसम्बन्ध ज्ञात करना आंशिक सहसम्बन्ध कहलाता है।

प्रश्न 2. 
सहसम्बन्ध से आप क्या समझते हैं? सहसम्बन्ध को मापने की विभिन्न विधियों को स्पष्ट कीजिए।
उत्तर:
सहसम्बन्ध का अर्थ-जब दो समंक श्रेणियों में इस प्रकार का सम्बन्ध हो कि एक समंक श्रेणी में परिवर्तन होने पर दूसरी समंक श्रेणी में भी उसी दिशा या विपरीत दिशा में परिवर्तन हो जाए तो इस सहपरिवर्तन के गणितीय माप को सहसम्बन्ध कहा जाता है।
सहसम्बन्ध को मापने की विधियाँ: मुख्य रूप से सहसम्बन्ध को मापने की निम्न तीन विधियाँ हैं।
1. प्रकीर्ण आरेख विधि
2. कार्ल पियरसन का सहसम्बन्ध गुणांक
3. स्पीयरमैन का कोटि सहसम्बन्ध इन सभी विधियों का विस्तृत विवरण निम्न प्रकार

1. प्रकीर्ण आरेख विधि: प्रकीर्ण आरेख, किसी संख्यात्मक माप के बिना सम्बन्धों के स्वरूप की जांच दृश्य रूप में प्रस्तुत करने की एक उपयोगी प्रविधि है। इस प्रविधि में, दो चरों के मान को ग्राफ पेपर पर बिन्दुओं के रूप में आलेखित किया जाता है। आलेखित बिन्दुओं के इस गुच्छ को प्रकीर्ण आरेख कहा जाता है। प्रकीर्ण आरेख के द्वारा सम्बन्धों के स्वरूप को काफी सही रूप में जाना जा सकता है। प्रकीर्ण आरेख में प्रकीर्ण बिन्दुओं के सामीप्य की कोटि और उसकी व्यापक दिशा के आधार पर उसके आपसी सम्बन्धों की जानकारी प्राप्त की जा सकती है।

2. कार्ल पियरसन का सहसम्बन्ध गुणांककार्ल पियरसन सहसम्बन्ध गुणांक को गुणन आघूर्ण सहसम्बन्ध तथा सरल सहसम्बन्ध गुणांक के नाम से भी जाना जाता है। यह दो चरों x एवं y के बीच रेखीय सम्बन्धों के सही संख्यात्मक मान की कोटि दर्शाता है। काल पियरसन के सहसम्बन्ध गुणांक को तभी उपयोग में लाना चाहिए जब चरों के बीच रेखीय सम्बन्ध हों। सहसम्बन्ध गुणांक ज्ञात करने हेतु सर्वप्रथम x तथा y समंक श्रेणियों का समान्तर माध्य ज्ञात किया जाता है, जो निम्न प्रकार है।
x श्रेणी का समान्तर माध्य \((\bar{X})=\frac{\Sigma X}{N}\)  
y श्रेणी का समान्तर माध्य \((\bar{Y})=\frac{\Sigma Y}{N}\)
x तथा y के प्रसरण की गणना भी ज्ञात की जाती है।
जो निम्न प्रकार है।
\(\begin{aligned} \sigma_{\mathrm{x}}^{2} &=\frac{\Sigma(\mathrm{X}-\overline{\mathrm{X}})^{2}}{\mathrm{~N}}=\frac{\Sigma \mathrm{X}^{2}}{\mathrm{~N}}-\overline{\mathrm{X}}^{2} \\ \sigma_{\mathrm{y}}^{2} &=\frac{\Sigma(\mathrm{Y}-\overline{\mathrm{Y}})^{2}}{\mathrm{~N}}=\frac{\Sigma \mathrm{Y}^{2}}{\mathrm{~N}}-\overline{\mathrm{Y}}^{2} \end{aligned}\)
यहाँ x एवं y के मानक विचलन क्रमशः उनके प्रसरण के धनात्मक वर्गमूल हैं। x तथा y के सहप्रसरण निम्नलिखित हैं
Co-variance (x, y) 
\(=\frac{\Sigma(\mathrm{X}-\overline{\mathrm{X}})(\mathrm{Y}-\overline{\mathrm{Y}})}{\mathrm{N}}=\frac{\Sigma \mathrm{xy}}{\mathrm{N}}\)

x तथा y के बीच सह-प्रसरण का चिह्न सहसम्बन्ध गुणांक के चिह्न का निर्धारण करता है। इसके पश्चात् निम्न सूत्रों की सहायता से कार्ल पियरसन का सहसम्बन्ध गुणांक ज्ञात किया जाएगा
\(r=\frac{\Sigma x y}{N \cdot \sigma_{x} \sigma_{y}}\)
अधवा 
\(r=\frac{\Sigma(X-\bar{X})(Y-\bar{Y})}{\sqrt{\Sigma(X-\bar{X})^{2}} \sqrt{\Sigma(Y-\bar{Y})^{2}}}\)
अथवा
\(r=\frac{\Sigma X Y-\frac{(\Sigma X)(\Sigma Y)}{N}}{\sqrt{\Sigma X^{2}-\frac{(\Sigma X)^{2}}{N}} \sqrt{\Sigma Y^{2}-\frac{(\Sigma Y)^{2}}{N}}}\)
अथवा
\(r=\frac{N \Sigma X Y-(\Sigma X)(\Sigma Y)}{\sqrt{N^{2}-(\Sigma X)^{2}} \sqrt{N \Sigma Y^{2}-(\Sigma Y)^{2}}}\)
अथवा
\(r=\frac{N \times \Sigma d_{x} d_{y}-\left(\Sigma d_{x} \times \Sigma d_{y}\right)}{\sqrt{\left[N \times \Sigma d^{2} x \times(\Sigma d x)^{2}\right]\left[N \times \Sigma d^{2} y-(\Sigma d y)^{2}\right]}}\)
संकेताक्षर: r = सहसम्बन्ध गुणांक
σ_x   = X श्रेणी का प्रमाप विचलन
σ_y  = Y श्रेणी का प्रमाप विचलन
N = पद - युग्मों की संख्या
\(\overline{\mathbf{X}}\) = X श्रेणी का समान्तर माध्य
\(\overline{\mathbf{Y}}\) = Y श्रेणी का समान्तर माध्य

3. स्पीयरमैन का कोटि सहसम्बन्ध-स्पीयरमैन कोटि सहसम्बन्ध का विकास ब्रिटिश मनोवैज्ञानिक सी.ई. स्पीयरमैन द्वारा किया गया था। इस विधि का प्रयोग तब किया जाता है जब चरों का सार्थक रूप से मापन नहीं किया जा सकता हो। दूसरे शब्दों में इस रीति का प्रयोग उस स्थिति में किया जाता है जबकि तथ्यों को प्रत्यक्ष रूप से संख्या में मापना सम्भव न हो किन्तु उन्हें एक निश्चित क्रम में रखा जा सकता हो, जैसे - कुशलता, सुन्दरता, स्वास्थ्य, योग्यता आदि। इस विधि में सहसम्बन्ध की गणना करने हेतु सर्वप्रथम दोनों श्रेणियों के मूल्यों को क्रम प्रदान किया जाता है। सबसे बड़े मूल्य को 1 तथा उससे छोटे मूल्य को 2 तथा आगे इसी प्रकार क्रम प्रदान । किया जाता है। x श्रेणी के क्रमों को R, से तथा y श्रेणी के क्रमों को R, से दर्शाया जायेगा। दोनों श्रेणियों के क्रमों का अन्तर ज्ञात किया जाता है, क्रमान्तरों का योग सदैव शून्य होता है। क्रमान्तरों का वर्ग ज्ञात कर उनका योग (∑D²) ज्ञात किया जाता है तथा निम्न सूत्र के द्वारा सहसम्बन्ध गुणांक ज्ञात किया जाता है।
\(\mathrm{r}_{\mathrm{S}}=1-\frac{6 \Sigma \mathrm{D}^{2}}{\mathrm{n}^{3}-\mathrm{n}} \text { } 1-\frac{6 \Sigma \mathrm{D}^{2}}{\mathrm{n}\left(\mathrm{n}^{2}-1\right)}\)
जब कोटियों को दोहराया जाता है तो निम्न सूत्र का प्रयोग किया जाएगा
\(\mathbf{r}_{\mathrm{S}}=1-\frac{6\left[\Sigma \mathrm{D}^{2}+\left(\frac{m_{1}^{3}-m_{1}}{12}\right)+\left(\frac{m_{2}^{3}-m_{2}}{12}\right)+\ldots .+\right]}{\mathrm{n}\left(\mathrm{n}^{2}-1\right)}\)

यहाँ m1, m2 = कोटियों की दोहराई गई संख्याएँ हैं।
\(\frac{m_{1}^{3}-m_{1}}{12}, \ldots \ldots,=\) यह दोहराई गई संख्याओं के संगत संशोधन गुणांक हैं।

(ख) व्यावहारिक अथवा क्रियात्मक प्रश्न:

प्रश्न 1. 
निम्न समंकों से कार्ल पियरसन का सहसम्बन्ध गुणांक ज्ञात कीजिए।

X	3	4	6	7	10	12	14
Y	9	11	14	15	16	18	22

उत्तर:

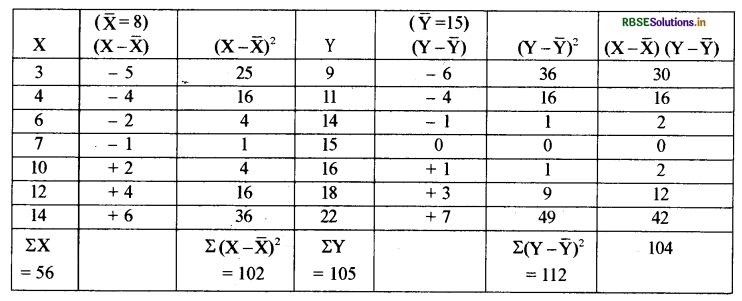
सहसम्बन्ध गुणांक की गणना:
\(​​​​​​​\overline{\mathrm{X}}=\frac{\Sigma \mathrm{X}}{\mathrm{N}}\)
= \(\frac{56}{7}\)
= 8

\(\overline{\mathrm{Y}}=\frac{\Sigma Y}{\mathrm{~N}}\)
= 105/7
= 15
समान्तर माध्य की गणना:
\(r=\frac{\Sigma(X-\bar{X})(Y-\bar{Y})}{\sqrt{\Sigma(X-\bar{X})^{2}} \sqrt{\Sigma(Y-\bar{Y})^{2}}}\)
\(=\frac{104}{\sqrt{102} \sqrt{112}}=\frac{104}{10.1 \times 10.58}\)
\(r=\frac{104}{106.858}\)
r = 0.97
अतःX तथा Y समंक श्रेणियों में उच्चस्तरीय धनात्मक सहसम्बन्ध है। 

प्रश्न 2. 
निम्न समंक श्रेणियों का सहसम्बन्ध गुणांक ज्ञात कीजिए। 

X	78	36	98	25	75	82	90	62	65	39
Y	84	51	41	60	68	62	70	58	53	47

उत्तर:

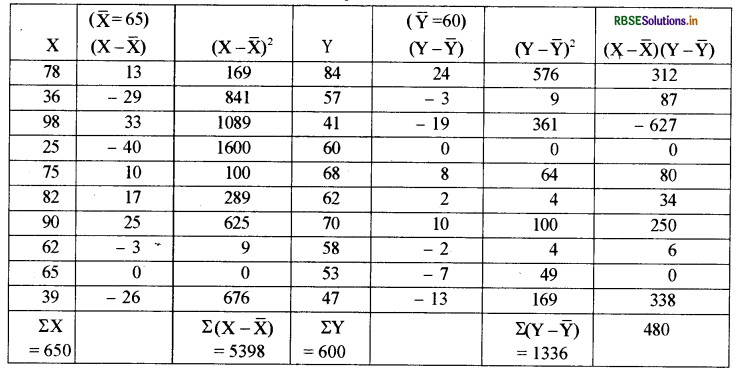
समान्तर माध्य की गणना:
\(\overline{\mathbf{X}}=\frac{\Sigma \mathbf{X}}{\mathbf{N}}\)

= 650/10
= 65

\(\overline{\mathbf{Y}}=\frac{\Sigma Y}{N}\)
= 600/100
= 60

सहसम्बन्ध गुणांक की गणना:

\(\begin{aligned} r &=\frac{\Sigma(X-\bar{X})(Y-\bar{Y})}{\sqrt{\Sigma(X-\bar{X})^{2}} \sqrt{\Sigma(Y-\bar{Y})^{2}}} \\ &=\frac{480}{\sqrt{5398} \sqrt{1336}} \\ &=\frac{480}{73.47 \times 36.55} \\ r &=\frac{480}{2685.33} \end{aligned}\)

r = 0.18

प्रश्न 3. 
निम्न समंकों के आधार पर प्रत्यक्ष विधि द्वारा कार्ल पियरसन का सहसम्बन्ध गुणांक ज्ञात कीजिए

X	10	20	30	40	50	60	90	70	80	90	100
Y	2	4	8	5	10	14	15	58	20	22	30

उत्तर:

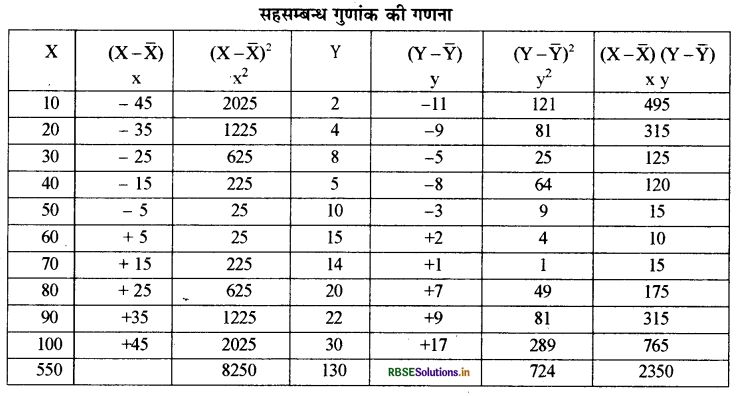
समान्तर माध्य की गणना:
\(\bar{X}=\frac{\Sigma X}{N}\)
= 550/10 = 55
\(\bar{Y}=\frac{\Sigma Y}{N}\)

= 130/10 = 13

प्रमाप विचलन का गणना:
\(\sigma_{\mathrm{x}}=\sqrt{\frac{\sum(\mathrm{X}-\overline{\mathrm{X}})^{2}}{\mathrm{~N}}}\)

\(\begin{aligned} &=\sqrt{\frac{8250}{10}} \\ &=\sqrt{825} \end{aligned}\)

σ_x  = 28.72

\(\sigma_{\mathrm{y}}=\sqrt{\frac{\Sigma(\mathrm{Y}-\overline{\mathrm{Y}})^{2}}{\mathrm{~N}}}\)

\(\begin{aligned} &=\sqrt{\frac{724}{10}} \\ &=\sqrt{72.4} \end{aligned}\)

σ _y = 8.51

 सहसम्बन्ध गुणांक की गणना:
\(r=\frac{\Sigma x y}{N \cdot \sigma_{x} \cdot \sigma_{y}}\)

\(=\frac{2350}{10 \times 28.72 \times 8.51}=\frac{2350}{2444.1}\)

r = 0.96

अतः X तथा Y में उच्चस्तरीय धनात्मक सहसम्बन्ध पाया जाता है।
अन्य सूत्र द्वारा गणना:

\(\begin{aligned} \mathrm{r} &=\frac{\Sigma(\mathrm{X}-\overline{\mathrm{X}})(\mathrm{Y}-\overline{\mathrm{Y}})}{\sqrt{\Sigma(\mathrm{X}-\overline{\mathrm{X}})^{2}} \sqrt{\Sigma(\mathrm{Y}-\overline{\mathrm{Y}})^{2}}} \\ &=\frac{2350}{\sqrt{8250} \sqrt{724}} \\ &=\frac{2350}{90.83 \times 26.91} \\ &=\frac{2350}{2444.24} \end{aligned}\)

= 0.96

अत: X तथा Y में उच्चस्तरीय धनात्मक सम्बन्ध पाया जाता है।

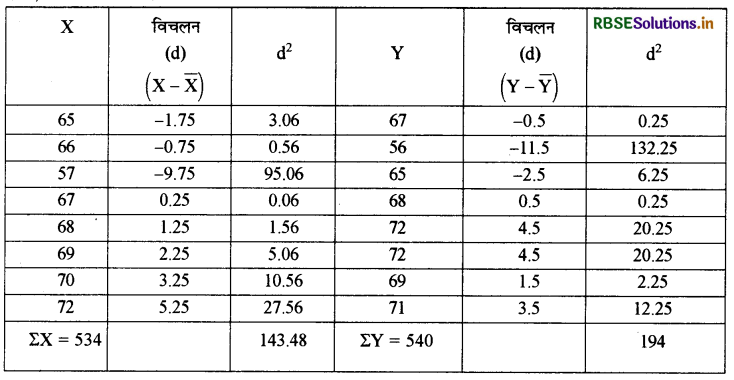
प्रश्न 4. 
निम्नलिखित समंकों से कार्ल पियरसन का सहसम्बन्ध गुणांक ज्ञात कीजिए।

X	50	54	56	60	62	61	65	67	71	71	75
Y	22	25	34	28	26	30	32	30	28	34	40

उत्तर:

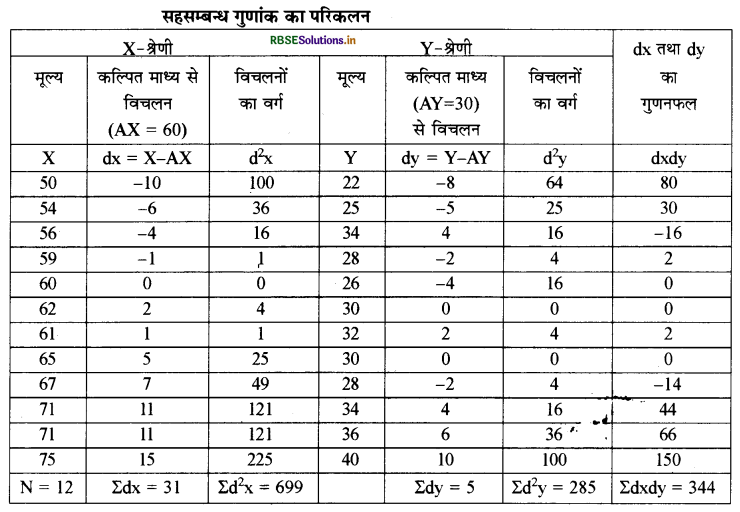
\(r=\frac{N \times \Sigma d x d y-(\Sigma d x \times \Sigma d y)}{\sqrt{\left[N \times \Sigma d^{2} x-(\Sigma d x)^{2}\right]\left[N \times \Sigma d^{2} y-(\Sigma d y)^{2}\right]}}\)

\(\begin{aligned} &=\frac{12 \times 344-(31 \times 5)}{\sqrt{\left[12 \times 699-(31)^{2}\right]\left[12 \times 285-(5)^{2}\right]}} \\ &=\frac{4128-155}{\sqrt{[8388-961][3420-25]}} \\ &=\frac{3973}{\sqrt{7427 \times 3395}} \\ &=\frac{3973}{5021.42} \end{aligned}\)

= 0.79
अत: x एवं y श्रेणी के मूल्यों में उच्च स्तर का धनात्मक सहसम्बन्ध है।

प्रश्न 5. 
निम्न सारणी से कालं पियरसन के सहसम्बन्ध गुणांक की गणना कीजिए।

x-श्रेणी	10.5	11.5	12.5	13.5	14.5	15.5
Y-श्रेणी	75	60	50	50	45	40

उत्तर:

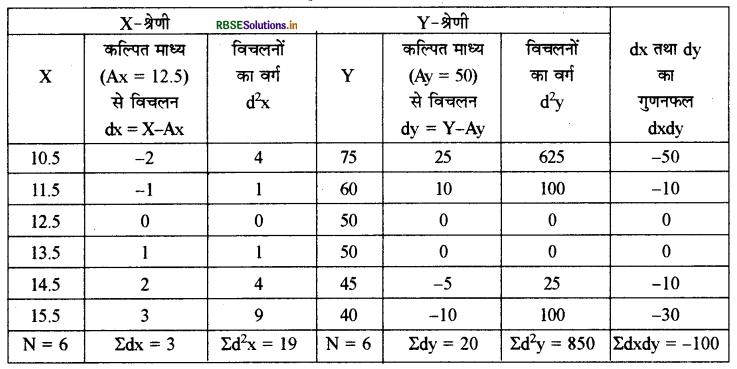
\(\begin{aligned} r &=\frac{N \times \Sigma d x d y-(\Sigma d x \times \Sigma d y)}{\sqrt{\left[N \times \Sigma d^{2} x-(\Sigma d x)^{2}\right]\left[N \times \Sigma d^{2} y-(\Sigma d y)^{2}\right]}} \\ r &=\frac{6 \times-100-(3 \times 20)}{\sqrt{\left[6 \times 19-(3)^{2}\right]\left[6 \times 850-(20)^{2}\right]}} \\ r &=\frac{-600-60}{\sqrt{[114-9][5100-400]}} \\ r &=\frac{-660}{\sqrt{105 \times 4700}} \\ r &=\frac{-660}{\sqrt{493500}} \\ r &=\frac{-660}{702.5} \end{aligned}\)

r = -0.94
 अतःX तथा Y श्रेणियों में उच्च स्तर का ऋणात्मक सम्बन्ध है। 

प्रश्न 6. 
निम्न समंकों से कार्ल पियरसन के सहसम्बन्ध गुणांक की गणना कीजिए।

X	5	7	9	11	13	15
Y	4	6	8	9	11	14

उत्तर:

मूल्य	मूल्य वर्ग	मूल्य	मूल्य वर्ग	x तथा y का गुणनफल
X	Y	X2	Y2	XY
5	25	4	16	20
7	49	6	36	42
9	81	8	64	72
11	121	9	81	99
13	169	11	122	143
15	225	14	196	210
∑X = 60	∑X2 = 670	∑Y = 52	∑Y2 = 514	∑XY = 586

\(\begin{aligned} &r=\frac{N \cdot \Sigma x y-(\Sigma x)(\Sigma y)}{\sqrt{N \cdot \Sigma x^{2}-(\Sigma x)^{2}} \sqrt{N \cdot \Sigma y^{2}-(\Sigma y)^{2}}} \\ &r=\frac{6 \times 586-(60)(52)}{\sqrt{6 \times 670-(60)^{2}} \sqrt{6 \times 514-(52)^{2}}} \end{aligned}\)

\(\begin{aligned} &=\frac{3516-3120}{\sqrt{4020-3600} \sqrt{3084-2704}} \\ &=\frac{396}{\sqrt{420} \sqrt{380}} \\ &=\frac{396}{20.49 \times 19.49} \\ &=\frac{396}{399.35} \end{aligned}\)

r = 0.99
अतः इतिहास एवं भूगोल में निम्न स्तर का धनात्मक सहसम्बन्ध है।

प्रश्न 7. 
गणित और विज्ञान विषय के निम्न प्राप्तांकों से कार्ल पियरसन के सहसम्बन्ध गुणांक ज्ञात कीजिए।

X	1	2	3	4	5	6	7
y	2	3	5	6	8	9	12

उत्तर:
माना गणित के अंक = x
माना विज्ञान के अंक = y
कार्ल पियरसन के सहसम्बन्ध गुणांक की गणना

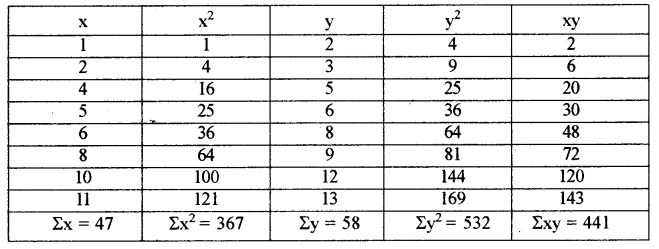
\(r=\frac{N \cdot \Sigma x y-(\Sigma x)(\Sigma y)}{\sqrt{N \cdot \Sigma x^{2}-(\Sigma x)^{2}} \sqrt{N \cdot \Sigma y^{2}-(\Sigma y)^{2}}}\)

\(=\frac{8 \times 441-(47)(58)}{\sqrt{8 \times 367-(47)^{2}} \sqrt{8 \times 532-(58)^{2}}}\)

\(r=\frac{3528-2726}{\sqrt{2936-2209} \sqrt{4256-3364}}\)

\(=\frac{802}{\sqrt{727} \sqrt{892}}=\frac{802}{26.96 \times 29.87}=\frac{802}{805.30}\)

= 0.9959

प्रश्न 8.
निम्नलिखित समंकों से कोटि क्रमान्तर रीति द्वारा सहसम्बन्ध गणांक की गणना कीजिए:

उत्तर:
कोटि क्रमान्तर रीति द्वारा सहसम्बन्ध गणांक की गणना:

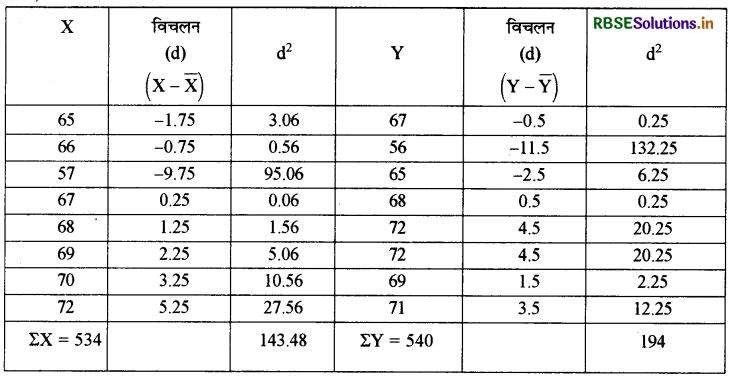
\(\begin{aligned} r_{\mathrm{S}} &=1-\frac{6 \times \sum D^{2}}{\mathrm{~N}\left(\mathrm{~N}^{2}-1\right)} \\ &=1-\frac{6 \times 6}{8\left(8^{2}-1\right)} \\ &=1-\frac{36}{8(64-1)} \\ &=1-\frac{36}{8 \times 63} \\ &=1-\frac{36}{504}=1-.07 \end{aligned}\)

r_s = 93

प्रश्न 9.
इतिहास तथा भूगोल में सात विद्यार्थियों द्वारा प्राप्त कोटि क्रम निम्न प्रकार है। इनमें कोटि क्रमान्तर सहसम्बन्ध ज्ञात कीजिए:

इतिहास में कोटि क्रम (Rank in History)	7	1	4	6	5	3	2
भूगोल में कोटि क्रम (Rank in Geography)	5	1	2	3	4	7	6

उत्तर:
कोटि क्रमान्तर रीति द्वारा सहसम्बन्ध गुणांक की गणना:

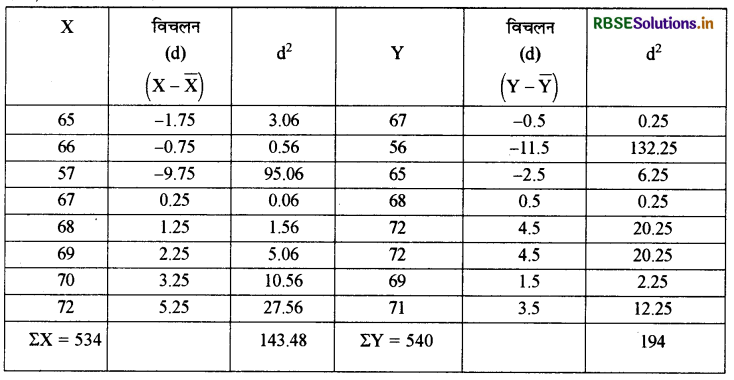
\(\begin{aligned} \mathrm{r}_{\mathrm{S}} &=1-\frac{6 \times \Sigma \mathrm{D}^{2}}{\mathrm{~N}\left(\mathrm{~N}^{2}-1\right)} \\ &=1-\frac{6 \times 50}{7\left(7^{2}-1\right)} \\ &=1-\frac{300}{7(49-1)} \\ &=1-\frac{300}{7 \times 48} \\ &=1-\frac{300}{336} \end{aligned}\)

अत: इतिहास एवं भूगोल में निम्न स्तर का धनात्मक सहसम्बन्ध है।
[नोट: प्रश्न में मूल्य को पहले से ही क्रम (Rank) दिये हुए हैं, अतः इन्हें क्रम प्रदान करने की आवश्यकता नहीं है।

प्रश्न 10.
निम्न तथ्यों की सहायता से कोटि क्रमान्तर सहसम्बन्ध गुणांक का परिकलन कीजिए:

क्रम संख्या (S. No.)	1	2	3	4	5	6	7	8	9	10
कोटि अन्तर (Rank Difference)	-4	-2	+3	-1	0	2	?	3	-2	3

उत्तर:
नोट-कोटि क्रमान्तरों का योग हमेशा शून्य होता है। दिए गए कोटि क्रमान्तरों के अन्तरों का योग 2 होने के कारण अज्ञात (-2) होगा।

क्रम संख्या (S. No.)	कोटि अन्तर (D) (R1 - R2)	कोटि अन्तरों के वर्ग D2
1	-4	16
2	-2	4
3	3	9
4	1	1
5	0	0
6	2	4
7	-2	4
8	3	9
9	-2	4
10	3	9
N = 10	∑ D = 10	∑ D2 = 10

\(\begin{aligned} \mathrm{r}_{\mathrm{S}} &=1-\frac{6 \Sigma \mathrm{D}^{2}}{\mathrm{~N}\left(\mathrm{~N}^{2}-1\right)} \\ &=1-\frac{6 \times 60}{10\left(10^{2}-1\right)} \\ &=1-\frac{360}{990} \\ &=1-0.36 \end{aligned}\)

अतः यहाँ मध्य-स्तर का धनात्मक सहसम्बन्ध है।

प्रश्न 11.
निम्न समंकों से कोटि क्रमान्तर सहसम्बन्ध गुणांक का परिकलन कीजिए:

X -श्रेणी	48	33	40	9	16	16	85	24	16	57
y -श्रेणी	13	13	24	6	15	4	20	9	6	19

उत्तर:
क्रमान्तर सहसम्बन्ध गुणांक का परिकलन:

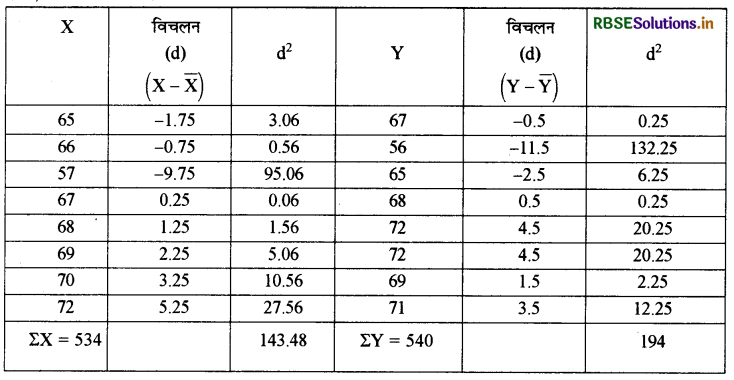
\(\begin{aligned} \mathrm{r}_{\mathrm{S}} &=1-\frac{6\left[\Sigma \mathrm{D}^{2}+\frac{\left(\mathrm{m}_{1}^{3}-\mathrm{m}_{1}\right)}{12}+\frac{\left(\mathrm{m}_{2}^{3}-\mathrm{m}_{2}\right)}{12}+\frac{\left(\mathrm{m}_{3}^{3}-\mathrm{m}_{3}\right)}{12}\right]}{\mathrm{n}\left(\mathrm{n}^{2}-1\right)} \\ &=1-\frac{6\left[41+\frac{\left(3^{3}-3\right)}{12}+\frac{\left(2^{3}-2\right)}{12}+\frac{\left(2^{3}-2\right)}{12}\right]}{10\left(10^{2}-1\right)} \\ &=1-\frac{6\left[41+\frac{(27-3)}{12}+\frac{(8-2)}{12}+\frac{(8-2)}{12}\right]}{10(100-1)} \\ &=1-\frac{6[41+2+.5+.5]}{10 \times 99} \\ &=1-\frac{6 \times 44}{990} \\ &=1-\frac{264}{990} \end{aligned}\)

rs = 0.73
अतः X एवं  Y श्रेणी में मध्यम स्तरीय धनात्मक सहसम्बन्ध है।
नोट : 1. x  श्रेणी में मूल्य 16 तीन बार आया है जिसे औसत क्रम संख्या \(\left(\frac{7+8+9}{3}\right)=8\) देंगे।
2. y श्रेणी में मूल्य 13 दो बार आया है जिसे औसत क्रम संख्या \(\left(\frac{5+6}{2}\right)=5.5\) देंगे।
3. y श्रेणी में मूल्य 6 दो बार आया है जिसे औसत क्रम संख्या \(\left(\frac{8+9}{2}\right)=8.5\) देंगे।
4. श्रेणी में तीन मूल्यों की पुनरावृत्ति हुई है अतः मूल सूत्र में तीन बार संशोधन कारक \(\left(\frac{\mathrm{m}^{3}-\mathrm{m}}{12}\right)\) जोड़ा जाएगा। यहाँ m से तात्पर्य यह है कि वह मूल्य जिसकी पुनरावृत्ति हुई है वह कितनी बार आया है।

प्रश्न 12.
x तथा y श्रेणी से क्रमान्तर सहसम्बन्ध गुणांक (Rank Coefficient of Correlation) की गणना कीजिए:

X -श्रेणी	70	85	67	99	55	85	115	90	125	73
y -श्रेणी	87	93	73	49	66	93	100	93	90	80

उत्तर:
कोटि क्रमान्तर सहसम्बन्ध गुणांक की गणना:

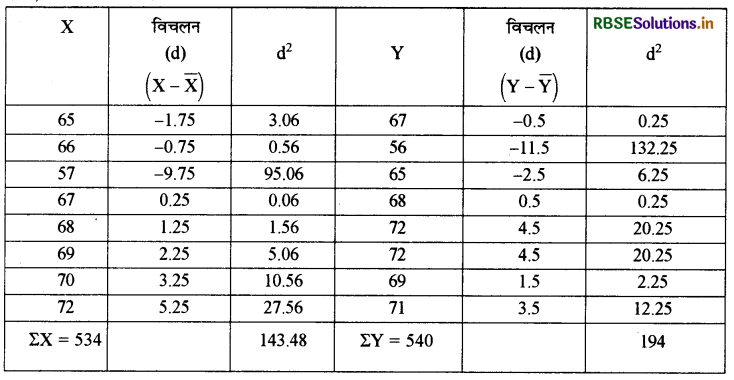
\(\begin{aligned} r_{\mathrm{S}} &=1-\frac{6\left[\Sigma \mathrm{D}^{2}+\frac{\left(\mathrm{m}_{1}^{3}-\mathrm{m}_{1}\right)}{12}+\frac{\left(\mathrm{m}_{2}^{3}-\mathrm{m}_{2}\right.}{12}\right.}{\mathrm{n}\left(\mathrm{n}^{2}-1\right)} \\ &=1-\frac{6\left[85.5+\frac{\left(2^{3}-2\right)}{12}+\frac{\left(3^{3}-3\right)}{12}\right]}{10\left(10^{2}-1\right)} \\ &=1-\frac{6\left[85.5+\frac{(8-2)}{12}+\frac{(27-3)}{12}\right]}{10(100-1)} \\ &=1-\frac{6[85.5+0.5+2]}{10 \times 99} \\ &=1-\frac{6 \times 88}{10 \times 99}=1-\frac{528}{990} \end{aligned}\)

= 1- 0.53
= 0.47
अत: X एवं Y श्रेणी में मध्यम स्तरीय धनात्मक सहसम्बन्ध है।

प्रश्न 13.
निम्न समंकों की सहायता से स्पीयरमैन की कोटि अन्तर रीति से सहसम्बन्ध गुणांक की गणना कीजिए:

X -श्रेणी	2	3	5	7	6	3
y -श्रेणी	1	2	4	6	3	3

उत्तर:
स्पीयरमैन के कोटि सहसम्बन्ध गुणांक की गणना:

( नोट: श्रेणी x में 3 दो बार आया है जिसकी क्रम संख्या \(\left(\frac{4+5}{2}\right) 4.5\) दी गई है।)
\(\begin{aligned} r_{\mathrm{S}} &=1-\frac{6\left[\Sigma \mathrm{D}^{2}+\frac{\left(\mathrm{m}_{1}^{3}-\mathrm{m}_{1}\right)}{12}\right]}{\mathrm{n}\left(\mathrm{n}^{2}-1\right)} \\ &=1-\frac{6\left[10.5+\frac{\left(2^{3}-2\right)}{12}\right]}{6\left(6^{2}-1\right)} \\ &=1-\frac{6\left[10.5+\frac{(8-2)}{12}\right]}{6(36-1)} \\ &=1-\frac{6[10.5+0.5]}{6 \times 35} \\ &=1-\frac{66}{210} \end{aligned}\)
= 1 - 0.31
r_s = 0.69
अतः दोनों श्रेणियों में मध्यम स्तरीय धनात्मक सहसम्बन्ध है।