RBSE Class 11 Economics Important Questions Chapter 6 परिक्षेपण के माप

Rajasthan Board RBSE Class 11 Economics Important Questions Chapter 6 परिक्षेपण के माप Important Questions and Answers.

RBSE Class 11 Economics Important Questions Chapter 6 परिक्षेपण के माप

वस्तुनिष्ठ प्रश्न:

प्रश्न 1. 
किसी वितरण में अधिकतम एवं न्यूनतम मानों के बीच का अन्तर कहलाता है।
(अ) परास 
(ब) बहुलक
(स) माध्य विचलन 
(द) मानक विचलन 
उत्तर:
(ब) बहुलक

 

प्रश्न 2. 
चतुर्थक विचलन का सूत्र है।
(अ) Q₃ + Q₁ 
(ब) Q₃ - Q₁
(स) \(\frac{Q_{3}-Q_{1}}{2}\)
(द) \(\frac{Q_{3}+Q_{1}}{2}\)
उत्तर:
 (स) \(\frac{Q_{3}-Q_{1}}{2}\)

प्रश्न 3. 
पांच छात्रों के सांख्यिकी में प्राप्त अंक 20, 35, 25, 30 तथा 15 हैं तो इनका परास होगा।
(अ) 15 
(ब) 20
(स) 25 
(द) 30 
उत्तर:
(स) 25 

प्रश्न 4. 
अन्तर चतुर्थक विस्तार का सूत्र है।
(अ) Q₃ + Q₁
(ब) Q₃ - Q₂
(स) Q₃ - Q₁ 
(द) Q₃ + Q₂ 
उत्तर:
(अ) Q₃ + Q₁

प्रश्न 5. 
चतुर्थक विचलन गुणांक का सूत्र है।
(अ)  \(\frac{Q_{3}+Q_{1}}{Q_{3}-Q_{1}}\)
(ब)   \(\frac{Q_{3}-Q_{1}}{Q_{3}+Q_{1}}\)
(स) \(\frac{Q_{3}-Q_{1}}{2}\)
(द)  \(\frac{Q_{3}+Q_{1}}{2}\)
उत्तर:
 (द)  \(\frac{Q_{3}+Q_{1}}{2}\)

प्रश्न 6. 
यदि समान्तर माध्य से लिए गये विचलनों का योग \(\Sigma|d|=3220\) एवं पदों की संख्या 5 है तो माध्य विचलन का मान होगा।
(अ) 1610 
(ब) 644
(स) 6440 
(द) 322 
उत्तर:
(द) 322 

प्रश्न 7. 
व्यक्तिगत श्रेणी में प्रत्यक्ष रीति में समान्तर माध्य की सहायता से माध्य विचलन ज्ञात करने का सूत्र बताइए।
(अ) \(\text { M.D. }=\frac{\Sigma|d|}{N}\)
(ब) \(\text { M. D. }=\frac{\mathbf{N}}{\Sigma|\mathrm{d}|}\)
(स) \(\text { M. D. }=\frac{\Sigma \mathbf{X}}{\mathrm{N}}\)
(द) \(\text { M.D. }=\frac{\bar{X}}{N}\) 
उत्तर:
 (स) \(\text { M. D. }=\frac{\Sigma \mathbf{X}}{\mathrm{N}}\)

प्रश्न 8. 
अपकिरण को मापने की सर्वोत्तम विधि है।
(अ) माध्य विचलन 
(ब) मानक विचलन
(स) विस्तार 
(द) चतुर्थक विचलन 
उत्तर:
(ब) मानक विचलन

प्रश्न 9. 
विचरण का बिन्दु रेखाचित्र द्वारा जो प्रदर्शन किया जाता है, उसे कहा जाता है।
(अ) सरल रेखीय वक्र 
(ब) वृत्ताकार चित्र 
(स) लॉरेंज वक्र 
(द) आयत चित्र
उत्तर:
(द) आयत चित्र

प्रश्न 10. 
मानक विचलन की गणना हेतु विचलन लिए जाते।
(अ) समान्तर माध्य से 
(ब) मध्यिका से 
(स) बहुलक से 
(द) सहसम्बन्ध से
उत्तर:
(अ) समान्तर माध्य से 

रिक्त स्थान वाले प्रश्ननीचे दिए गए वाक्यों में रिक्त स्थानों की पूर्ति करें:

प्रश्न 1. 
परिक्षेपण की माप हमें आय की के बारे में बता सकता है।
उत्तर:
असमानताओं

प्रश्न 2.
............. किसी वितरण के अधिकतम (L) एवं न्यूनतम (S) मानों के बीच का अन्तर है।
उत्तर:
परास

प्रश्न  3. 
किसी समंक श्रेणी के तृतीय चतुर्थक व प्रथम चतुर्थक के अन्तर का आधा ............. होता है।
उत्तर:
परास

प्रश्न 4. 
मानक विचलन माध्य से विचलनों के वर्गों के माध्य का वर्गमूल है।
उत्तर:
धनात्मक

प्रश्न  5. 
अपकिरण को मापने की सर्वोत्तम विधि
उत्तर:
ऋणात्मक

 सत्य / असत्य वाले प्रश्ननीचे दिए गए कथनों में सत्य / असत्य कथन छाँटिए:

प्रश्न  1. 
विचरण का बिन्दु रेखाचित्र द्वारा जो प्रदर्शन किया जाता है उसे लॉरेंज वक्र कहते हैं। 
उत्तर:
सत्य

प्रश्न  2. 
मध्यिका से लिए गए पदों के विचलनों का योग समान्तर माध्य से निकाले गए विचलनों के योग से अधिक होता है।
उत्तर:
असत्य

प्रश्न  3. 
मानक विचलम की गणना केवल समान्तर माध्य की सहायता से की जाती है। 
उत्तर:
सत्य

प्रश्न  4. 
मानक विचलन एक सापेक्ष माप है जबकि विचरण गुणांक एक सापेक्ष माप है। 
उत्तर:
असत्य

प्रश्न  5. 
प्रमाप विचलन विभिन्न पद मूल्यों के समान्तर, माध्य से प्राप्त विचलनों के वर्गों के समान्तर माध्य का वर्गमूल होता है।
उत्तर:
सत्य

मिलान करने वाले प्रश्ननिम्न को सुमेलित कीजिए:

प्रश्न 1. 

(1) मानक विचलन गुणांक का सूत्र	(अ) \(\frac{\sigma}{(\bar{X})} \times 100\)
(2) चतुर्थक विचलन ज्ञात करने का सूत्र	(ब) \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{\mathrm{Q}_{3}+\mathrm{Q}_{1}}\)
(3) चतुर्थक विचलन गुणांक ज्ञात करने का सूत्र	(स) \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
(4) परास गुणांक का सूत्र	(द) L - S
(5) परास ज्ञात करने का सूत्र	(य) \(\frac{L-S}{L+S}\)

उत्तर:

(1) मानक विचलन गुणांक का सूत्र	(अ) \(\frac{\sigma}{(\bar{X})} \times 100\)
(2) चतुर्थक विचलन ज्ञात करने का सूत्र	(स) \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
(3) चतुर्थक विचलन गुणांक ज्ञात करने का सूत्र	(ब) \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{\mathrm{Q}_{3}+\mathrm{Q}_{1}}\)
(4) परास गुणांक का सूत्र	(य) \(\frac{L-S}{L+S}\)
(5) परास ज्ञात करने का सूत्र	(द) L - S

​
अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1. 
परास किसे कहते हैं?
उत्तर:
किसी समंक श्रेणी के अधिकतम मूल्य तथा न्यूनतम मूल्य के अन्तर को परास कहा जाता है।

प्रश्न 2. 
परास ज्ञात करने का सूत्र लिखिए। 
उत्तर:
परास ज्ञात करने का सूत्र = L - S
यहाँ L = वितरण में अधिकतम मान
S = वितरण में न्यूनतम मान। 

प्रश्न 3. 
मुक्तांत वितरण क्या है?
उत्तर;
मुक्तांत वितरण वे हैं जिनमें या तो निम्नतम वर्ग की निम्न सीमा या उच्चतम वर्ग की उच्च सीमा या दोनों ही नहीं दी होती हैं।

प्रश्न 4. 
चतुर्थक विचलन कैसे ज्ञात किया जाता
उत्तर:
किसी समंक श्रेणी के तृतीय चतुर्थक व प्रथम चतुर्थक के अन्तर का आधा चतुर्थक विचलन होता है अर्थात् चतुर्थक विचलन = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\) होता है।

प्रश्न 5. 
पाँच छात्रों के अर्थशास्त्र में 15, 16, 19, 21, 36 अंक प्राप्त हुए हैं, इनका परास अथवा विस्तार ज्ञात कीजिए।
उत्तर:
परास = L - S
यहाँ L = अधिकतम मूल्य,
S = न्यूनतम मूल्य
= 36 - 15
= 21 

प्रश्न 6. 
एक समंक श्रेणी में प्रथम चतुर्थक (Q₁) का मूल्य 4.12 है तथा तृतीय चतुर्थक (Q₃) का मूल्य 7.11 है। चतुर्थक विचलन ज्ञात कीजिए। 
उत्तर:
चतुर्थक विचलन = \(\frac{Q_{3}-Q_{1}}{2}\)
\(=\frac{7.11-4.12}{2}=\frac{2.99}{2}\)
= 14.5 

प्रश्न 7. 
माध्य विचलन की गणना में मध्यिका का प्रयोग सर्वोत्तम क्यों माना जाता है?
उत्तर:
मध्यिका से लिये गये पदों के विचलनों का योग समान्तर माध्य से निकाले गये विचलनों के योग से कम होता है। इसी कारण मध्यिका का प्रयोग सर्वोत्तम माना जाता है।

प्रश्न 8. 
माध्य विचलन किसे कहते हैं?
उत्तर:
एक श्रृंखला के किसी सांख्यिकी माध्य से निकाले गये मूल्यों के विचलनों के समान्तर माध्य को इस श्रृंखला का माध्य विचलन कहा जाता है।

प्रश्न 9. 
एक व्यक्तिगत श्रेणी में मध्यिका मूल्य 21 व माध्य विचलन 44 है, माध्य विचलन गुणांक ज्ञात कीजिए।
उत्तर:
माध्य विचलन गुणांक = \(\frac{\mathrm{M} . \mathbf{D} \cdot(\mathrm{M})}{\mathbf{M}}\)
= 4.4/21 = 0.21 

प्रश्न 10. 
किसी वितरण का समान्तर माध्य 14.53 व माध्य विचलन गुणांक 0.46 हो तो माध्य विचलन ज्ञात कीजिये।
उत्तर:
माध्य विचलन गुणांक
\(=\frac{\mathrm{M} \cdot \mathrm{D} \cdot(\overline{\mathrm{X}})}{(\overline{\mathrm{X}})}\)
\(0.46=\frac{\mathrm{M} \cdot \mathrm{D} \cdot(\overline{\mathrm{X}})}{14.53}\)
\(\mathbf{M} \cdot \mathbf{D} \cdot(\overline{\mathrm{x}})\) = 1453 x 0.46
= 6.68

प्रश्न 11. 
मानक विचलन की गणना किस सांख्यिकीय माध्य की सहायता से की जाती है?
उत्तर:
मानक विचलन की गणना केवल समान्तर माध्य की सहायता से की जाती है।

प्रश्न 12. 
मानक विचलन गुणांक का सूत्र लिखिए। 
उत्तर:
मानक विचलन गुणांक = \(\frac{\sigma}{(\overline{\mathbf{X}})} \times 100\)
यहाँ  σ  = मानक विचलन
(x) = समान्तर माध्य

प्रश्न 13. 
प्रमाप अथवा मानक विचलन से आप क्या समझते हैं?
उत्तर:
प्रमाप विचलन विभिन्न पद: मूल्यों के समान्तर माध्य से प्राप्त विचलनों के वर्गों के समान्तर माध्य का वर्गमूल होता है।

प्रश्न 14. 
निम्न सूचनाओं से मानक विचलन की गणना कीजिए
∑d² = 1000, ∑X = 60, N = 10 
उत्तर:
मानक विचलन (6)
\(=\sqrt{\frac{\Sigma \mathrm{d}^{2}}{\mathrm{~N}}}\)
\(=\sqrt{\frac{1000}{10}}=\sqrt{100}=10\)

प्रश्न 15. 
निम्न समंकों से विचरण गुणांक ज्ञात कीजिए
N = 100, ∑fx = 1650,  σ  = 3.25
उत्तर:
सर्वप्रथम समान्तर माध्य की गणना की जाएगी
\(\bar{X}=\frac{\Sigma \mathrm{fx}}{\mathrm{N}}\)
= 1650/100
= 16.50
विचरण गुणांक (C.v)  \(=\frac{\sigma}{\overline{\mathbf{X}}} \times 100\)
3.25/165 x100
= 19.70% 

प्रश्न 16. 
मानक विचलन तथा विचरण गुणांक में एक अन्तर बताइए।
उत्तर:
मानक विचलन एक निरपेक्ष माप है जबकि विचरण गुणांक एक सापेक्ष माप है।

लघूत्तरात्मक प्रश्न:

प्रश्न 1. 
परास किसे कहते हैं? परास की गणना किस प्रकार की जाती है?
उत्तर:
किसी समंक श्रेणी के अधिकतम मूल्य तथा न्यूनतम मूल्य के अन्तर को परास कहा जाता है। इसे निम्न सूत्र से ज्ञात करते हैं
R = L - S
R = परास या विस्तार, L = अधिकतम मूल्य, S = न्यूनतम मूल्य परास अथवा विस्तार की गणना करते समय व्यक्तिगत, विविक्त तथा संतत श्रेणी में उपर्युक्त सूत्र का ही प्रयोग किया जाता है। विविक्त तथा संतत श्रेणी में विस्तार अथवा परास की गणना में आवृत्तियों का ध्यान नहीं रखा जाता है। संतत श्रेणी में प्रथम वर्ग की निचली सीमा तथा अन्तिम वर्ग की ऊपरी सीमा लेकर विस्तार ज्ञात किया जाता है।

प्रश्न 2. 
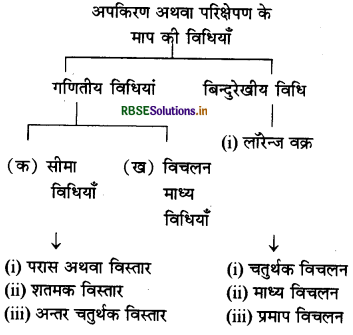
अपकिरण से आप क्या समझते हैं? इसके विभिन्न मापों के नाम लिखिए।
अथवा 
परिक्षेपण से आप क्या समझते हैं? परिक्षेपण का माप करने की कौन - कौनसी विधियाँ हैं?
उत्तर:
अपकिरण अथवा परिक्षेपण का अर्थअपकिरण श्रेणी के मूल्यों के बिखराव या प्रसार या विचरण का माप है।

प्रश्न 3. 
परास अथवा विस्तार के कोई चार दोष बताइए।
उत्तर:

1. परास से किसी भी श्रृंखला की बनावट की जानकारी प्राप्त नहीं होती है, यह केवल अधिकतम एवं न्यूनतम मान को ही लेता है।
2. परास की गणना में श्रेणी के सभी मूल्यों को महत्व नहीं दिया जाता है। केवल न्यूनतम व अधिकतम मूल्य के आधार पर परास की गणना की जाती है।
3. न्यायदर्श में परिवर्तन होने पर परास भी परिवर्तित हो जाता है, इस प्रकार परास या विस्तार पर न्यायदर्श का प्रभाव पड़ता है।
4. खुले सिरे वाली श्रेणी में परास की गणना करना संभव नहीं है।

प्रश्न 4. 
चतुर्थक विचलन एवं चतुर्थक विचलन गुणांक का सूत्र लिखिए।
उत्तर:
चतुर्थक विचलन: किसी श्रेणी के तृतीय चतुर्थक (Q₃) व प्रथम चतुर्थक (Q₁) के अन्तर का आधा चतुर्थक विचलन होता है। चतुर्थक विचलन की गणना निम्न सूत्र द्वारा की जाती है।
चतुर्थक विचलन = \(\frac{Q_{3}-Q_{1}}{2}\)

चतुर्थक विचलन गुणांक: दो श्रेणियों के तुलनात्मक अध्ययन हेतु चतुर्थक विचलन गुणांक ज्ञात किया जाता है क्योंकि यह एक सापेक्ष माप है। इसकी गणना निम्न सूत्र द्वारा की जाती है।
चतुर्थक विचलन गुणांक = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{\mathrm{Q}_{3}+\mathrm{Q}_{1}}\)

प्रश्न 5. 
अन्तर चतुर्थक परास से आप क्या समझते
उत्तर:
अन्तर चतुर्थक परास अथवा विस्तार: समंक श्रेणी के तृतीय चतुर्थक (Q₃) तथा प्रथम चतुर्थक (Q₁) के अन्तर को अन्तर चतुर्थक परास कहते हैं। इसे मध्यवर्ती 50 प्रतिशत मूल्यों का परास या विस्तार भी कहते हैं। अन्तर चतुर्थक विस्तार की गणना में आवृत्तियों को भी महत्व दिया जाता है तथा यह अपकिरण के माप के साथ स्थिति का माप भी है। अन्तर चतुर्थक परास को निम्न सूत्र द्वारा मापा जाता है।
= Q₃ - Q₄
यहाँ Q₃ = तृतीय चतुर्थक।
Q₁ = प्रथम चतुर्थक है। 

प्रश्न 6. 
निरपेक्ष माप एवं सापेक्ष माप से आप क्या समझते हैं?
अथवा 
निरपेक्ष अपकिरण तथा सापेक्ष अपकिरण से आप क्या समझते हैं?
उत्तर:

1. निरपेक्ष अपकिरण: यह माप श्रेणी के फैलाव को निरपेक्ष रूप में व्यक्त करता है। इसमें अपकिरण को उसी इकाई में व्यक्त किया जाता है जिसमें समंक श्रेणी दी गई है। इसके द्वारा दो श्रेणियों का तुलनात्मक अध्ययन संभव नहीं है।
2. सापेक्ष अपकिरण: समीकरण के विभिन्न मापों को तुलनात्मक बनाने हेतु इन्हें सापेक्ष रूप में परिवर्तित किया जाता है। निरपेक्ष माप में सम्बन्धित माध्य से भाग देने पर जो अनुपात प्राप्त होता है, उसे ही सापेक्ष अपकिरण कहते हैं। इसे अपकिरण का गुणांक भी कहते हैं।

प्रश्न 7. 
व्यक्तिगत श्रेणी में चतुर्थकों की गणना कैसे की जाती है?
उत्तर:
व्यक्तिगत श्रेणी में चतुर्थकों की गणना अर्थात् Q₁ व Q₃ की गणना हेतु सर्वप्रथम श्रेणी के मूल्यों को आरोही अर्थात् बढ़ते हुए क्रम में व्यवस्थित किया जाता है तथा निम्न सूत्रों द्वारा चतुर्थक संख्या ज्ञात की जाती हैप्रथम चतुर्थक संख्या
= Size of 1 x \(\left(\frac{N+1}{4}\right)^{\text {th }}\) item तृतीय चतुर्थक संख्या
= Size of 3 x \(\left(\frac{N+1}{4}\right)^{\text {th }}\) item तथा इन चतुर्थक संख्याओं का मूल्य ही चतुर्थकों का मान होगा।

प्रश्न 8. 
विविक्त अथवा खण्डित श्रेणी में चतुर्थकों की गणना कैसे की जाती है?
उत्तर:
विविक्त अथवा खण्डित श्रेणी में चतुर्थकों की गणना हेतु सर्वप्रथम श्रेणी को आरोही या बढ़ते हुए क्रम में व्यवस्थित किया जाता है। एक आवृत्ति से दूसरी आवृत्ति जोड़कर संचयी आवृत्ति ज्ञात की जाती है। इसके पश्चात् निम्न सूत्रों द्वारा चतुर्थक संख्या ज्ञात की जाती हैं।
प्रथम चतुर्थक संख्या
= Size of 1 x \(\left(\frac{N+1}{4}\right)^{\text {th }}\) item तृतीय चतुर्थक संख्या
= Size of 3 x \(\left(\frac{N+1}{4}\right)^{\text {th }}\) item जिस संचयी आवृत्ति में चतुर्थक संख्या होगी उसके सामने वाला मूल्य ही Q₁ व Q₃ का मूल्य होगा।

प्रश्न 9. 
माध्य विचलन का अर्थ बताइए।
उत्तर:
एक श्रृंखला या श्रेणी के किसी सांख्यिकी माध्य (समान्तर माध्य या मध्यिका या बहुलक) से निकाले गए मूल्यों के विचलनों के समान्तर माध्य को उस श्रेणी का माध्य विचलन कहते हैं। मूल्यों के विचलन ज्ञात करते समय इसमें बीजगणितीय चिह्नों (धनात्मक या ऋणात्मक) को ध्यान नहीं रखा जाता है अर्थात् ऋणात्मक विचलनों को भी धनात्मक मान सकते हैं।

प्रश्न 10. 
माध्य विचलन की कोई तीन विशेषताएँ बताइए।
उत्तर:

1. माध्य विचलन श्रेणी के सभी मूल्यों पर आधारित होते हैं तथा इसकी गणना किसी भी माध्य से की जा सकती है। अत: यह श्रेणी की आकृति पर पूर्ण प्रकाश डालता है।
2. अपकिरण के अन्य मापों की तुलना में माध्य विचलन की गणना आसान है तथा इसे शीघ्रता से समझा जा सकता है।
3. यह समान्तर माध्य तथा बहुलक मध्यिका में से किसी भी माध्य को आधार मानकर ज्ञात किया जा सकता है।

प्रश्न 11. 
व्यक्तिगत श्रेणी में प्रत्यक्ष विधि द्वारा समान्तर माध्य एवं मध्यिका द्वारा माध्य विचलन ज्ञात करने की विधि को स्पष्ट कीजिए।
उत्तर:
समान्तर माध्य द्वारा माध्य विचलन (प्रत्यक्ष विधि)-इस हेतु सर्वप्रथम समान्तर माध्य ज्ञात किया जाता है। समान्तर माध्य से पदों के विचलन ज्ञात किए जाते हैं जिसमें बीजगणितीय चिह्नों की उपेक्षा की जाती है। इन विचलनों का योग कर उसे पदों की संख्या (n) द्वारा विभाजित कर माध्य विचलन ज्ञात किया जा सकता है।
सूत्र \(\text { M.D. }(\overline{\mathrm{X}})=\frac{\Sigma|d|}{\mathrm{n}}\)

मध्यिका द्वारा माध्य विचलन (प्रत्यक्ष विधि)व्यक्तिगत श्रेणी का माध्य विचलन मध्यिका द्वारा ज्ञात करने हेतु सर्वप्रथम मध्यिका ज्ञात की जाती है। इसके पश्चात् बीजगणितीय चिह्नों की उपेक्षा करते हुए मध्यिका से पदों के विचलन ज्ञात कर उनका योग किया जाता है। इसके पश्चात् इसमें पदों की संख्या का भाग देकर माध्य विचलन ज्ञात किया जाता है।
सूत्र \(\text { M.D. }(\mathrm{M})=\frac{\Sigma|\mathrm{d}|}{\mathrm{n}}\)

प्रश्न 12. 
व्यवहार में माध्य विचलन की गणना हेतु आप किस माध्य का चुनाव करेंगे एवं क्यों?
उत्तर:
सैद्धान्तिक रूप से माध्य विचलन की गणना में किसी भी माध्य का प्रयोग किया जा सकता है परन्तु व्यवहार में समान्तर माध्य या मध्यिका का ही प्रयोग किया जाता है क्योंकि अनेक परिस्थितियों में बहुलक मूल्य अनिश्चित होता है। अतः इसके प्रयोग से भ्रामक परिणाम प्राप्त हो सकते हैं। समान्तर माध्य एवं मध्यिका में से भी मध्यिका का प्रयोग अधिक उपयुक्त माना जाता है क्योंकि मध्यिका के लिए गये पदों के विचलनों का योग समान्तर माध्य से लिए गए विचलनों से कम होता है।

प्रश्न 13. 
मानक विचलन अथवा प्रमाप विचलन से आप क्या समझते हैं?
उत्तर:
किसी श्रेणी के मूल्यों का समान्तर माध्य से ज्ञात किए गए विचलनों के वर्गों के माध्य का वर्गमूल मानक अथवा प्रमाप विचलन होता है। मानक विचलन अथवा प्रमाप विचलन की गणना करते समय ऋणात्मक विचलनों को भी धनात्मक माना जाता है अर्थात् बीजगणितीय नियमों को ध्यान में नहीं रखा जाता है। इस अशुद्धि को दूर करने हेतु प्रमाप अथवा मानक विचलन की गणना की जाती है। मानक विचलन की गणना केवल समान्तर माध्य की सहायता से की जाती है।

प्रश्न 14. 
प्रमाप अथवा मानक विचलन गुणांक का सूत्र लिखिए।
उत्तर:
प्रमाप अथवा मानक विचलन एक निरपेक्ष माप है, किन्तु इससे दो श्रेणियों का तुलनात्मक अध्ययन नहीं किया जा सकता। अतः दो श्रेणियों का तुलनात्मक अध्ययन हेतु मानक विचलन गुणांक ज्ञात किया जाता है। इसे निम्न सूत्र द्वारा ज्ञात किया जा सकता है
मानक विचलन गुणांक = \(\frac{\sigma}{\overline{\bar{X}}}\) x 100
यहाँ  σ  = मानक अथवा प्रपाप विचलन है।
\(\overline{\mathbf{X}}\)  = समान्तर माध्य है। 

प्रश्न 15. 
व्यक्तिगत श्रेणी में मानक विचलन ज्ञात करने की वास्तविक माध्य विधि को स्पष्ट कीजिए।
उत्तर:
जब समान्तर माध्य पूर्ण अंक में आता है तो यह विधि अधिक उपयुक्त रहती है। इस विधि में मानक विचलन ज्ञात करने हेतु सर्वप्रथम श्रेणी का समान्तर माध्य (X) ज्ञात किया जाता है। श्रेणी के प्रत्येक मूल्य में से समान्तर माध्य घटाकर विचलन (d) ज्ञात किया जाता है। इसके पश्चात् प्रत्येक विचलन का वर्ग (d) करके उसका योग किया जाता है। वर्गों के योग में मदों की संख्या का भाग देकर निम्न सूत्र द्वारा प्रमाप अथवा माध्य विचलन ( σ ) ज्ञात किया जाता है।
\(\sigma=\sqrt{\frac{\Sigma \mathrm{d}^{2}}{n}}\)

प्रश्न 16. 
व्यक्तिगत श्रेणी में मानक विचलन ज्ञात करने की कल्पित माध्य विधि अथवा लघु विधि को स्पष्ट कीजिए।
उत्तर:
यह विधि समान्तर माध्य पूर्ण अंक में न आने पर उपयुक्त रहती है। इस विधि में मानक विचलन ज्ञात करने हेतु श्रेणी में दिये गये मूल्यों में से किसी एक को कल्पित माध्य मानते हैं। कल्पित माध्य से श्रेणी के सभी मूल्यों के विचलन (d = x - A) निकालकर उसका योग ∑d किया जाता है। इसके पश्चात् विचलनों का वर्ग निकालकर उनका योग (∑d²) किया जाता है। उसके पश्चात् निम्न सूत्र की सहायता से मानक विचलन ज्ञात किया जाता है।
\(\sigma=\sqrt{\frac{\Sigma d^{2}}{n}-\left(\frac{\Sigma d}{n}\right)^{2}}\)

प्रश्न 17. 
माध्य विचलन तथा मानक विचलन में कोई दो अन्तर बताइए।
उत्तर:

अन्तर का माध्य	मानक विचलन (M.D)	मानक विचलन (σ)
1. विचलन	इसकी गणना में विचलन समान्तर माध्य या मध्यिका या बहुलक में किसी एक के द्वारा लिए जाते हैं।	मानक विचलन की गणना में विचलन ह मेशा समान्तर माध्य से लिए जाते हैं।
2. चिह	माध्य विचलन ज्ञात करते समय बीजगणितीय चिह्नों को छोड़ देते हैं अर्थात् ऋणात्मक चिह्न को भी धनात्मक मानते हैं।	मानक विचलन ज्ञात करते समय बीजगणितीय चिह्रों को ध्यान में रखा जाता है।

प्रश्न 18. 
लॉरेंज वक्र से आप क्या समझते हैं?
उत्तर:
'लॉरेंज वक्र: अपकिरण का माप ज्ञात करने की यह एक बिन्दुरेखीय विधि है। यह एक संचयी प्रतिशत वक्र है। इस रीति का प्रयोग लाभ, मजदूरी, क्रय - विक्रय आदि के वितरण का अध्ययन करने के लिए किया जाता. है। इसमें यदि लॉरेंज वक्र समान वितरण की रेखा के अधिक पास है तो विचरण कम होगा और यदि वक्र इस रेखा से दूर है तो विचरण अधिक होगा। इस वक्र की सबसे बड़ी कमी यह है कि इसके द्वारा वितरण का संख्यात्मक माप ज्ञात नहीं किया जा सकता है।

प्रश्न 19. 
मानक विचलन के कोई तीन गुण बताइए।
उत्तर-:

1. मानक विचलन श्रेणी की सभी मदें, सभी मूल्यों पर आधारित होती हैं, मानक विचलन में किसी भी मूल्य को छोड़ा नहीं जाता है।
2. मानक विचलन का उच्चतर बीजगणितीय अध्ययन में प्रयोग किया जाता है। मानक विचलन की गणना के लिए विचलनों के वर्ग बनाए जाते हैं। फलस्वरूप सभी मदें धनात्मक हो जाती हैं अतः इनका अग्रिम विवेचन भी किया जा सकता है।
3. मानक विचलनों पर अन्य अपकिरण मापों की अपेक्षा निदर्शन परिवर्तनों का सबसे कम प्रभाव पड़ता है।

प्रश्न 20. 
एक कक्षा के 10 विद्यार्थियों द्वारा अर्थशास्त्र में प्राप्तांक निम्न प्रकार हैं। इससे परास तथा परास गुणांक ज्ञात कीजिएरोल नम्बर।

निम्न	1	2	3	4	5	6
प्राप्तांक	34	16	28	26	18	6
	7	8	9	10
	18	19	35	40

उत्तर:
परास की गणना निम्न सूत्र द्वारा की जाएगी।
R = L - S
यहाँ L = अधिकतम मूल्य,
S = न्यूनतम मूल्य
R = 40 - 6 = 34
परास गुणांक = \(\frac{L-S}{L+S}=\frac{40-6}{40+6}=\frac{34}{46}\) = 0.74

प्रश्न 21. 
निम्नलिखित समंकों से विस्तार अथवा परास और परास गुणांक ज्ञात कीजिए।

आकार	4.5	5.5	6.5	7.5	8.5
	9.5	10.5	11.5
आवृत्ति	4	5	6	3	2
	1	3	2

उत्तर:
परास निम्न सूत्र द्वारा ज्ञात किया जाएगा
R = L - S
यहाँ L = अधिकतम मूल्य है तथा
S = न्यूनतम मूल्य है।
[नोट - विविक्त अथवा खण्डित श्रेणी में परास अथवा विस्तार की गणना करते समय आवृत्तियों का ध्यान नहीं रखा जाता है।
R = 11.5 - 4.5 = 7
परास गुणांक = \(=\frac{L-S}{L+S}=\frac{11.5-4.5}{11.5+4.5}=\frac{7}{16}\) = 0.44

प्रश्न 22. 
निम्नलिखित विवरण में विस्तार अथवा परास तथा उसका गुणांक ज्ञात कीजिए।

अंक	विद्यार्थियों की संख्या
10 – 20	4
20 – 30	10
30 – 40	16
40 – 50	22
50 – 60	20
60 – 70	18
70 – 80	8
80 – 90	2
90 - 100	5

उत्तर:
परास निम्न सूत्र द्वारा ज्ञात किया जाता है।
R = L - S
यहाँ L= अधिकतम मूल्य,
S= न्यूनतम मूल्य है।
[नोट-संतत अथवा अखण्डित श्रेणी में परास अथवा विस्तार करते समय आवृत्तियों का ध्यान नहीं रखा जाता है।]
R = 100 - 10
=90
परास गुणांक  \(=\frac{L-S}{L+S}\)
\(=\frac{100-10}{100+10}=\frac{90}{110}\) = 0.82

प्रश्न 23. 
निम्न समंकों से चतुर्थक विचलन एवं चतुर्थक विचलन गुणांक की गणना कीजिए।
25, 34, 21, 27, 30, 32, 36
उत्तर:
सर्वप्रथम श्रेणी के मूल्यों को बढ़ते हुए क्रम में व्यवस्थित करेंगे।
21, 25, 27, 30, 32, 34, 36
प्रथम चतुर्थक (Q₁)
= Size of \(\left(\frac{N+1}{4}\right)^{\text {th }}\) item
= Size of \(\left(\frac{7+1}{4}\right)^{\text {th }}\) item
= Size of 2nd item
= 25

तृतीय चतुर्थक (Q₃)
= Size of 3\(\left(\frac{N+1}{4}\right)^{\text {th }}\) item
= Size of 3\(\left(\frac{7+1}{4}\right)^{\text {th }}\) item
= Size of 6th item
=34

चतुर्थक विचलन (Q.D.)
\(=\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
\(=\frac{34-25}{2}\) 
= 9/2 = 4.5

चतुर्थक विचलन गुणांक
\(\begin{aligned} &=\frac{Q_{3}-Q_{1}}{Q_{3}+Q_{1}} \\ &=\frac{34-25}{34+25} \end{aligned}\)
= 39/2 = 0.153 

प्रश्न 24. 
एक श्रेणी के परास का सापेक्ष माप 0.29 है और अधिकतम मूल्य 64.5 है। न्यूनतम मूल्य बताइये। 
उत्तर:
प्रश्नानुसार परास गुणांक = 0.29
= 64.5
S = ?
परास गुणांक = \(\frac{L-S}{L+S}\)
0.29 \(=\frac{64.5-S}{64.5-S}\)
वज्र गुणनफल करने पर
18.705 + 0.29S = 64.5 - S
0.29s + S = 64.5 - 18.705
1.29S = D45.795
S = 45.795/1.29
s=35.5 

प्रश्न 25. 
एक श्रेणी में चतुर्थक विचलन 1.5 और तृतीय चतुर्थक 8 हो तो उसका प्रथम चतुर्थक ज्ञात कीजिये।
उत्तर:
चतुर्थक विचलन = \(\frac{Q_{3}-Q_{1}}{2}\)
1.5 = \(\frac{8-Q_{1}}{2}\)
वज्र गुणा करने पर
3 = 8 - Q₁
Q1 = 8 - 3
Q₁ = 5

प्रश्न 26. 
निम्न समावेशी सतत श्रृंखला का परास एवं परास गुणांक ज्ञात कीजिए

अंक	20 -29	30 -39	40 -49
विद्यार्थियों की संख्या	16	24	40
	50 -59	60 -69
	14	6

उत्तर:
यहाँ पर प्रश्न में समावेशी श्रेणी दी गई है अतः पहले उसे अपवर्जी श्रेणी में परिवर्तित करके परास ज्ञात किया जाएगा

अंक	विद्यार्थियों की संख्या	X
20 -29	16	19.5 – 29.5
30 - 39	24	29.5 – 39.5
40 - 49	40	39.5 – 49.5
50 - 59	16	49.5 – 59.5
60 - 69	4	59.5 – 69.5

उपर्युक्त अपवर्जी श्रेणी में
L (अधिकतम मूल्य) = 69.5
S = (न्यूनतम मूल्य) = 19.5
परास = L - S
= 69.5 - 19.5 = 350
परास गुणांक = \(\frac{L-S}{L+S}\)
\(=\frac{69.5-19.5}{69.5+19.5}\)
\(=\frac{50}{89}\) = 0.56

प्रश्न 27. 
निम्नलिखित मूल्य से मध्यिका द्वारा माध्य विचलन ज्ञात कीजिए

क्रमांक	1	2	3	4	5	6
मल्य	30	27	23	45	10	15
	7	8	9	10
	20	20	18	12

उत्तर:
सर्वप्रथम मूल्यों को आरोही क्रम में व्यवस्थित करना होगा

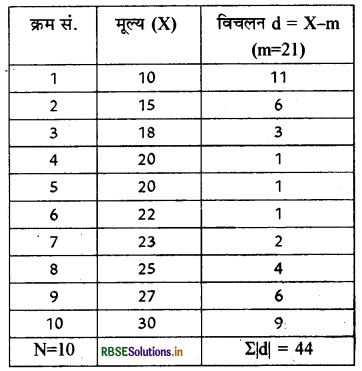
मध्यिका संख्या की गणना
= Size of \(\left(\frac{\mathbf{N}+1}{2}\right)^{\text {th }}\) item
= Size of \(\left(\frac{10+1}{2}\right)^{\text {th }}\) item
= Size of 55th item
Value of 5.5th item 
\(=\frac{\text { Value of } 5^{\text {th }} \text { item }+\text { Value of } 6^{\text {th }} \text { item }}{2}\)
मध्यिका मूल्य  \(=\frac{20+22}{2}\)
= 21
माध्य विचलन की गणना \(=\frac{\Sigma|\mathrm{d}|}{\mathbf{n}}\)
= 44/10 = 4.4

प्रश्न 28. 
आय सम्बन्धी निम्न समंकों से मध्यिका, माध्य विचलन तथा उसके गुणांक का परिकलन कीजिए
4000, 4200, 4400, 4600, 4800
उत्तर:
मध्यिका संख्या = Size of \(\left(\frac{\mathrm{N}+1}{2}\right)^{\mathrm{th}}\) item
= Size of \(\left(\frac{5+1}{2}\right)^{\text {th }}\) item
= Size of 3rd item
पद संख्या 3 का मूल्य 4400 है अत: M= 4400
माध्य विचलन:
\(\begin{aligned} &=\frac{\Sigma|d|}{n} \\ &=\frac{1200}{5} \end{aligned}\) 
माध्य विचलन गुणांक 
\(=\frac{M \cdot D \cdot(M)}{M}\)

\(=\frac{240}{4400}\) = 0.055

प्रश्न 29. 
छ: व्यक्तियों की निम्नलिखित मासिक आय से समान्तर माध्य का उपयोग करते हुए, माध्य विचलन ज्ञात कीजिए
852, 635, 792, 836, 995, 750
उत्तर:
माध्य विचलन की गणना

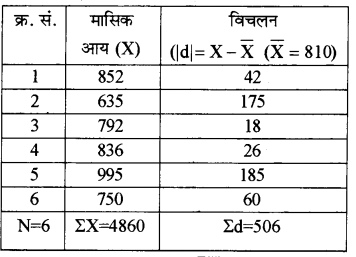
समान्तर माध्य \((\bar{X})=\frac{\Sigma X}{N}=\frac{4860}{6}\)

\(=\frac{\Sigma|\mathbf{d}|}{\mathbf{N}}\) = 506/6 = 84.33 

प्रश्न 30. 
एक समान उद्योग क और ख दो कारखानों की औसत साप्ताहिक मजदूरी (रुपयों में) तथा मानक विचलन निम्न प्रकार है

कारखाना	समान्तर माध्य	प्रमाप	मजदूरों की संख्या
क	34.5	5.0	476
ख	28.5	4.5	524

क तथा ख में से किस कारखाने की व्यक्तिगत मजदूरी में अधिक परिवर्तनशीलता है?
उत्तर:
व्यक्तिगत मजदूरी में परिवर्तनशीलता की जाँच हेतु विचरण गुणांक ज्ञात किया जायेगा।
कारखाना 'क' 
\(\text { C.V. }=\frac{\sigma}{\overline{\mathbf{X}}} \times 100\)
\(=\frac{5}{34.5} \times 100\)
= 14.49%

कारखाना 'ख' 
\(\text { C.V. }=\frac{\sigma}{\bar{X}} \times 100\)

\(=\frac{4.5}{28.5} \times 100\)
= 15.79%
कारखाना ख के श्रमिकों की व्यक्तिगत मजदूरी में अधिक परिवर्तनशीलता है क्योंकि इसका विचरण गुणांक अधिक है।

प्रश्न 31. 
दो श्रेणियों का विचरण गुणांक क्रमशः 30% और 40% है तथा मानक विचलन क्रमश: 15 और 12 है। उनके समान्तर माध्य ज्ञात कीजिए।
उत्तर:
श्रेणि 1:
c.v = 30%
 σ   = 15
\(\begin{aligned} \text { C.V. } &=\frac{\sigma}{\bar{X}} \times 100 \\ \frac{30}{1} &=\frac{15}{\bar{X}} \times 100 \end{aligned}\)
\(\begin{aligned} 30 \cdot \overline{\mathbf{X}} &=1500 \\ \overline{\mathbf{X}} &=\frac{1500}{30} \\ \overline{\mathbf{X}} &=50 \end{aligned}\)

प्रश्न 32. 
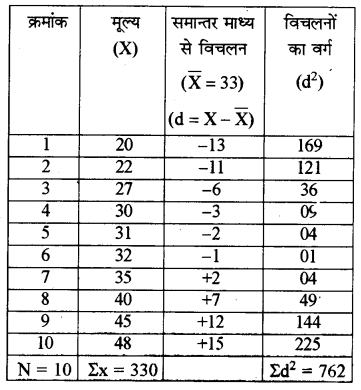
निम्न समंकों का मानक अथवा प्रमाप विचलन ज्ञात कीजिए
20, 22, 27, 30, 31, 32, 35, 40, 45, 48, 
उत्तर:
 मानक / प्रमाप विचलन की गणना

प्रश्न 33. 
दो श्रेणी A व B का समान्तर माध्य क्रमशः 100 तथा 81 है, प्रमाप विचलन क्रमशः 10 तथा १ है तथा पद युग्मों की संख्या क्रमश: 600 व 500 है तो बताइये किस श्रेणी में विचरण अधिक है?
उत्तर:
विचरण गुणांक का सूत्र = \(\frac{\sigma}{\overline{\bar{X}}}\) x 100
A श्रेणी का विचरण गुणांक
= 10/100 x 100 = 10%
B श्रेणी का विचरण गुणांक
= 9/81  x100 = 1111%
अतः श्रेणी B का विचरण अधिक है क्योंकि इसका विचरण गुणांक अधिक है। 

निबन्धात्मक प्रश्न:

(क) सैद्धान्तिक प्रश्न:

प्रश्न 1. 
चतुर्थक विचलन किसे कहते हैं? चतुर्थक विचलन की गणना करने की विधियों को स्पष्ट कीजिए।
उत्तर:
चतुर्थंक विचलन (Quartile Deviation): किसी श्रेणी के तृतीय चतुर्थक व प्रथम चतुर्थक के अन्तर का आधा चतुर्थक विचलन होता है। चतुर्थक विचलन की गणना निम्न सूत्र द्वारा की जाती है।
चतुर्थक विचलन \((\text { Q.D. })=\frac{Q_{3}-Q_{1}}{2}\)
दो श्रेणियों के तुलनात्मक अध्ययन हेतु चतुर्थक विचलन गुणांक ज्ञात किया जाता है क्योंकि यह एक सापेक्ष माप है। इसकी गणना निम्न सूत्र द्वारा की जाती
चतर्थक विचलन गुणांक = \(\frac{Q_{3}-Q_{1}}{Q_{3}+Q_{1}}\)
चतुर्थक विचलन तथा चतुर्थक विचलन गुणांक की गणना के उपर्युक्त सूत्र व्यक्तिगत, खण्डित तथा अखण्डित श्रेणी में समान हैं।

चतुर्थकों की गणना: चतुर्थकों की गणना मध्यिका की तरह ही की जाती है।
व्यक्तिगत श्रेणी में चतुर्थकों की गणनाप्रक्रिया:
1. श्रेणी के मूल्यों को आरोही या बढ़ते हुए क्रम में व्यवस्थित करेंगे।
2. चतुर्थक संख्या ज्ञात करेंगे। प्रथम चतुर्थक संख्या (q₁)
= Size of 1 x \(\left(\frac{N+1}{4}\right)^{\text {th }}\) item

तृतीय चतुर्थक संख्या (q₃)
= Size of 3 x \(\left(\frac{\mathrm{N}+1}{4}\right)^{\text {th }}\) item
3. n^th item (चतुर्थक संख्या) का मूल्य ही Q₁ व Q₃ का मान होगा।
संकेताक्षर:
Q₁ = प्रथम चतुर्थक; Q₃ = तृतीय
N = प्रथम चतुर्थक संख्या, q₁ तृतीय चतुर्थक संख्या विविक्त अथवा खण्डित श्रेणी में चतुर्थकों की गणना

प्रक्रिया:
1. श्रेणी के मूल्यों को आरोही क्रम में व्यवस्थित करेंगे।
2. एक आवृत्ति में दूसरी आवृत्ति जोड़कर संचयी आवृत्ति ज्ञात करेंगे।
3. निम्न सूत्र द्वारा चतुर्थक संख्या ज्ञात कीजियेप्रथम चतुर्थक संख्या (q₁)
= Size of 1 x \(\left(\frac{N+1}{4}\right)^{\text {th }}\) item
तृतीय चतुर्थक संख्या (q₃) = Size of 3 \(\left(\frac{N+1}{4}\right)^{\text {th }}\) item
4. जिस संचयी आवृत्ति में n^th item (चतुर्थक संख्या) होगा, उसके सामने वाला मूल्य ही Q₁ तथा Q₃ का मान होगा।
संकेताक्षर: Q₁ = प्रथम चतुर्थक; Q₃ = तृतीय चतुर्थक; N = आवृत्तियों का योग, q₁ = प्रथम चतुर्थक संख्या, q₃ = तृतीय चतुर्थक संख्या

संतत अथवा अखण्डित श्रेणी में चतुर्थकों की गणना
प्रक्रिया:
1. श्रेणी के वर्गान्तरों को आरोही क्रम में व्यवस्थित करेंगे।
2. संचयी आवृत्ति ज्ञात करेंगे।
3. निम्न सूत्र द्वारा चतुर्थक संख्या ज्ञात कीजियेप्रथम चतुर्थक संख्या (q₁)
= Size of I x \(\left(\frac{\mathrm{N}}{4}\right)^{\text {th }}\) item
तृतीय चतुर्थक संख्या (q₃) 
= Size of 3 x \(\left(\frac{N}{4}\right)^{\text {th }}\) item
4. n^th item (चतुर्थक संख्या) जिस संचयी आवृत्ति में होगा, उसके सामने वाला वर्ग ही चतुर्थक वर्ग होगा।
चतुर्थक वर्ग की सहायता से प्रथम एवं तृतीय चतुर्थक निम्न सूत्र द्वारा ज्ञात किया जाएगा
\(\begin{aligned} &Q_{1}=L+\frac{\frac{n}{4}-c . f .}{f} \times i \\ &Q_{3}=L+\frac{\frac{3 n}{4}-c . f .}{f} \times i \end{aligned}\)

संकेताक्षर:
Q₁ =  प्रथम चतुर्थक
q₁ = प्रथम चतुर्थक संख्या
Q₃ = तृतीय चतुर्थक
q₃ = तृतीय चतुर्थक संख्या
L = चतुर्थक वर्ग की निचली सीमा
i =  चतुर्थक वर्ग का वर्ग विस्तार
N = आवृत्तियों का योग
f = चतुर्थक वर्ग की आवृत्ति।

प्रश्न 2. 
निरपेक्ष तथा सापेक्ष माप का अर्थ उदाहरण सहित लिखिए।
उत्तर:
अपकिरण के विभिन्न मापों को दो रूपों में व्यक्त किया जाता है।

1. निरपेक्ष माप
2. सापेक्ष माप

(i) निरपेक्ष माप: जब किसी श्रेणी के विचरण का माप उस श्रेणी में स्थित इकाइयों के माप से किया जाता है तब वह अपकिरण का निरपेक्ष माप कहलाता है। जैसे - विद्यार्थियों की आयु व भार, रुपए, लीटर, मीटर, किग्रा. आदि। निरपेक्ष माप द्वारा दो श्रेणियों का तुलनात्मक अध्ययन नहीं किया जा सकता है क्योंकि दो श्रेणियों के निरपेक्ष अपकिरण माप अलग - अलग इकाइयों में हो सकते हैं।

(ii) सापेक्ष माप: जब दो श्रेणियों के समंक भिन्न इकाइयों में हों (जैसे चीनी क्विंटल में तथा गेहूँ टनों में) तो निरपेक्ष माप द्वारा तुलनात्मक अध्ययन सम्भव नहीं हो पाता है। अतः तुलनात्मक अध्ययन हेतु निरपेक्ष माप को सम्बन्धित माध्य से भाग देने पर जो अनुपात प्राप्त होता है उसे ही अपकिरण का सापेक्ष माप कहते हैं। इसे अनुपात या प्रतिशत में व्यक्त किया जाता है। इसे अपकिरण का गुणांक (Coefficient of Dispersion) भी कहते हैं। इसके द्वारा दो श्रेणियों के मूल्यों का तुलनात्मक अध्ययन सम्भव हो जाता है।

उदाहरण:

1. परास एक निरपेक्ष माप है जबकि परास गुणांक सापेक्ष माप है।
2. चतुर्थक विचलन एक निरपेक्ष माप है जबकि चतुर्थक विचलन गुणांक एक सापेक्ष माप है।

प्रश्न 3. 
माध्य विचलन किसे कहते हैं? माध्य विचलन ज्ञात करने की विभिन्न विधियों को स्पष्ट कीजिए।
उत्तर:
माध्य विचलन (Mean Deviation): एक श्रेणी के किसी सांख्यिकीय माध्य (समान्तर माध्य या मध्यिका या बहुलक) से ज्ञात किए गये मूल्य के विचलनों के समान्तर माध्य को उस श्रेणी का माध्य विचलन कहते।
(क) असमूहित आँकड़ों अथवा व्यक्तिगत श्रेणी के लिए समान्तर माध्य से माध्य विचलन का परिकलन निम्न प्रकार किया जा सकता है
(i) प्रत्यक्ष विधि: सर्वप्रथम समान्तर माध्य \((\bar{X})\) ज्ञात किया जाता है। समान्तर माध्य से मूल्यों के विचलन ज्ञात करने के पश्चात् उनका योग \((\Sigma|\mathrm{d}|)\) लगाया जाता है। तथा विचलन लेते समय बीजगणितीय चिह्नों का ध्यान नहीं रखा जाता है। इसके पश्चात् निम्न सूत्र की सहायता से माध्य विचलन ज्ञात किया जाएगा
\(\text { M.D. }(\bar{X})=\frac{\Sigma|\mathrm{d}|}{\mathbf{n}}\)
मध्यिका की सहायता से भी माध्य विचलन की गणना की जा सकती है।

(ii) कल्पित माध्य विधि: माध्य विचलन, कल्पित है। यह विधि विशेष रूप से तब अपनाई जाती है, जब वास्तविक माध्य भिन्नात्मक संख्या में होता है। इस हेतु निम्न सूत्र का प्रयोग किया जाएगा
\(\text { M.D. }(\overline{\mathrm{X}})=\frac{\Sigma|\mathrm{d}|+\left(\overline{\mathrm{X}}-\mathrm{A} \overline{\mathrm{X}}^{-}\right)\left(\Sigma \mathrm{f}_{\mathrm{B}}-\Sigma \mathrm{f}_{\mathrm{A}}\right)}{\mathrm{n}}\)
यहाँ \(\Sigma|\mathrm{d}|\) = कल्पित माध्य से लिए गए निरपेक्ष विचलनों का योग है।
\((\overline{\mathbf{X}})\)  = वास्तविक माध्य है
\(A_{\bar{x}}\) = कल्पित माध्य है
\(\Sigma f_{B}\) =  वास्तविक माध्य तथा उससे नीचे के मानों की संख्या है।
\(\Sigma \mathrm{f}_{\mathrm{A}}\) = वास्तविक माध्य से ऊपर के मानों की संख्या है।
असमूहित आँकड़ों अथवा व्यक्तिगत श्रेणी के लिए मध्यिका से माध्य विचलन की गणना

(i) प्रत्यक्ष विधि: सर्वप्रथम उस श्रेणी की मध्यिका ज्ञात की जाती है। इसके पश्चात् बीजगणितीय चिह्नों को छोड़कर मध्यिका से मूल्यों का विचलन ज्ञात किया जाता है तथा उनका योग \((\Sigma|\mathrm{d}|)\) लगाया जाता है तथा निम्न सूत्र की सहायता से माध्य विचलन ज्ञात किया जाता है।
\(\text { M.D.(Median) }=\frac{\Sigma|\mathrm{d}|}{\mathrm{n}}\)

(ii) कल्पित माध्य विधि अथवा संक्षिप्त विधिसंक्षिप्त विधि द्वारा माध्य विचलन को परिकलित करने हेतु किसी मान (A) को विचलनों के परिकलन के लिए प्रयुक्त किया जाता है तथा इसके लिए निम्न सूत्र है।
\(\text { M.D. (Median) }=\frac{\Sigma|\mathrm{d}|+(\operatorname{Median}-\mathbf{A})\left(\Sigma \mathrm{f}_{\mathrm{B}}-\mathbf{\Sigma \mathrm { f } _ { \mathrm { A } }}\right)}{\mathrm{n}}\)

यहाँ पर A एक स्थिरांक है, जिससे विचलनों को परिकलित करते हैं।

(ख) संतत वितरण अथवा अखण्डित श्रेणी के लिए समान्तर माध्य से माध्य विचलन: (प्रत्यक्ष विधि से) - समान्तर माध्य से माध्य विचलन ज्ञात करने हेतु सर्वप्रथम वितरण का समान्तर माध्य ज्ञात किया जाता है। माध्य से वर्गों के मध्य बिन्दुओं का निरपेक्ष विचलन d की गणना की जाती है। इसके पश्चात् प्रत्येक |d| के | मान को इसकी संगत बारम्बारता से गुणा किया जाता है
तथा इन्हें जोड़कर \(\Sigma \mathrm{f}|\mathrm{d}|\) प्राप्त किया जाता है तथा निम्न सूत्र की सहायता से माध्य विचलन ज्ञात किया जाता
\(\mathrm{M} \cdot \mathrm{D}_{\cdot(\overline{\mathrm{X}})}=\frac{\Sigma \mathrm{f}|\mathrm{d}|}{\Sigma \mathrm{f}}\)

संतत वितरण अथवा अखण्डित श्रेणी के लिए मध्यिका से माध्य विचलन: (प्रत्यक्ष विधि)मध्यिका से माध्य विचलन ज्ञात करने हेतु सर्वप्रथम मध्यिका की गणना की जाती है। उसके पश्चात् मध्यिका से मूल्यों का विचलन ज्ञात किया जाता है अर्थात् |d| ज्ञात किया जाता है। इसके पश्चात् प्रत्येक |d| के मान को इसकी संगत बारम्बारता से गुणा किया जाता है तथा इन्हें जोड़कर  प्राप्त किया जाता है तथा अग्र सूत्र की सहायता से माध्य विचलन ज्ञात किया जाता है।
\(\text { M.D. }(\text { Median })=\frac{\sum f|d|}{\Sigma f}\)

[नोट  -विविक्त अथवा खण्डित श्रेणी एवं संतत अथवा अखण्डित श्रेणी में माध्य विचलन ज्ञात करने की विधियाँ समान हैं। अन्तर यह है कि अखण्डित श्रेणी में माध्य विचलन हेतु पहले मध्य मूल्य ज्ञात किया जाता है उसके पश्चात् खण्डित श्रेणी की भाँति माध्य विचलन ज्ञात किया जाता है, अर्थात् दोनों श्रेणियों में समान सूत्रों से मानक विचलन ज्ञात किया जाता है।]

प्रश्न 4. 
मानक विचलन अथवा प्रमाप विचलन किसे कहते हैं? मानक विचलन ज्ञात करने की विभिन्न विधियों को स्पष्ट कीजिए।
उत्तर:
मानक विचलन (Standard Deviation): किसी श्रेणी के मूल्यों का समान्तर माध्य से ज्ञात किए गये विचलनों के वर्गों के माध्य का वर्गमूल मानक अथवा प्रमाप विचलन होता है। माध्य विचलन की गणना करते समय ऋणात्मक विचलनों को भी धनात्मक माना जाता है अर्थात् बीजगणितीय नियमों को ध्यान में नहीं रखा जाता है। इस अशुद्धि को दूर करने हेतु मानक विचलन अथवा प्रमाप विचलन की गणना की जाती है प्रमाप अथवा मानक विचलन की गणना केवल समान्तर माध्य की सहायता से की जाती है।

(A) असमूहित आँकड़ों के लिए मानक विचलन का परिकलन: व्यक्तिगत श्रेणी के मानक विचलन के परिकलन के लिए चार वैकल्पिक विधियाँ उपलब्ध हैं। इन सभी विधियों के द्वारा मानक विचलन का मान एक ही प्राप्त होता है। ये विधियाँ निम्न प्रकार हैं
(क) वास्तविक माध्य विधि
(ख) कल्पित माध्य विधि
(ग) प्रत्यक्ष विधि
(घ) पद - विचलन विधि 
(क) वास्तविक माध्य विधि अथवा प्रत्यक्ष विधि: इस विधि में श्रेणी का समान्तर माध्य (X) ज्ञात किया जाता है तथा श्रेणी के प्रत्येक मूल्य में से समान्तर माध्य घटाकर विचलन (d) ज्ञात किया जाता है। इसके पश्चात् प्रत्येक विचलन का वर्ग करके उसका योग (d) ज्ञात किया जाता है। वर्गों के योग में मदों की संख्या का भाग देकर निम्न सूत्र द्वारा प्रमाप विचलन ज्ञात किया जाता

(ख) कल्पित माध्य विधि: यह विधि समान्तर माध्य पूर्ण अंक में न आने पर उपयुक्त रहती है। इसमें श्रेणी में दिए गये मूल्यों में से किसी एक को कल्पित माध्य माना जाता है तथा कल्पित माध्य से श्रेणी के सभी मूल्यों का विचलन निकालकर उसका योग \((\overline{\mathbf{X}})\) निकाला जाता है, विचलनों का वर्ग करके उसका योग \(\left(\Sigma d^{2}\right)\) किया जाता है तथा निम्न सूत्र की सहायता से प्रमाप अथवा मानक विचलन निकाला जाता है।
\(\sigma=\sqrt{\frac{\Sigma d^{2}}{n}-\left(\frac{\Sigma d}{n}\right)^{2}}\)

(ग) प्रत्यक्ष विधि: मानक विचलन के लिए मानों से सीधे भी अर्थात् विचलनों को बिना लिए भी परिकलित किया जा सकता है, इसे निम्न सूत्र द्वारा ज्ञात किया जाता है।
\(\sigma=\sqrt{\frac{\Sigma \mathrm{d}^{2}}{\mathrm{n}}-(\overline{\mathrm{X}})^{2}}\)

(घ) पद - विचलन विधि: यदि मान किसी समापवर्तक से विभाज्य हैं तो उन्हें विभाजित किया जा सकता है तथा उसके पश्चात् मानक विचलन की गणना निम्न सूत्र की सहायता से की जा सकती है
\(\sigma=\sqrt{\frac{\sum \mathrm{d}^{\prime 2}}{n}} \times C\)

यहाँ C = समापवर्तक है। वैकल्पिक तौर पर किसी समापवर्तक द्वारा मानों को विभाजित करने की अपेक्षा, विचलनों को किसी समापवर्तक से विभाजित किया जाता है। इस समय निम्न सूत्र का प्रयोग किया जाएगा
\(\sigma=\sqrt{\frac{\Sigma \mathrm{d}^{\prime 2}}{\mathrm{n}}-\left(\frac{\Sigma \mathrm{d}^{\prime}}{\mathrm{n}}\right)^{2}} \times \mathbf{C}\)

(B) संतत बारम्बारता वितरण अथवा अखण्डित श्रेणी में मानक विचलन का परिकलन-असमूहित आँकड़ों की भाँति समूहित आँकड़ों में अखण्डित श्रेणी में मानक विचलन को निम्नलिखित में से किसी भी विधि द्वारा परिकलित किया जा सकता है
(क) वास्तविक माध्य विधि
(ख) कल्पित माध्य विधि
(ग) पद - विचलन विधि
(क) वास्तविक माध्य विधि अथवा प्रत्यक्ष विधि: इस हेतु सर्वप्रथम श्रेणी के सभी वर्गों के मध्य  \((\overline{\mathbf{X}})\) मूल्य जात किए जाते हैं। इन मध्य मूल्यों को सम्बन्धित आवृत्ति से गुणा करके, उनका योग करके  की गणना की जाती है तथा इसके आधार पर समान्तर माध्य की गणना की जाती है। इसके पश्चात् माध्य से मध्य बिन्दु का विचलन (d) की गणना की जाती है। इस विचलन के साथ संगत बारम्बारता को गुणा करके \(\left(\Sigma \mathrm{d}^{2}\right)\) ज्ञात किया जाता है।  मानों को d से गुणा करके की गणना की जाती है तथा निम्न सूत्र द्वारा प्रमाप अथवा मानक विचलन की गणना की जाती है
\(\sigma=\sqrt{\frac{\Sigma \mathrm{d}^{2}}{n}}\)

(ख) कल्पित माध्य विधि: सर्वप्रथम वर्गों के मध्य बिन्दु की गणना की जाती है। किसी कल्पित माध्य से मध्य बिन्दुओं के विचलन (d) की गणना की जाती है। d के मान को संगत बारम्बारता से गुणा करके की गणना की जाती है। d मानों के साथ के मानों को गुणा करके की प्राप्ति की जाती है तथा निम्न सूत्र की सहायता से मानक विचलन का परिकलन किया जाता
\(\sigma=\sqrt{\frac{\Sigma \mathrm{d}^{2}}{\mathrm{n}}-\left(\frac{\Sigma \mathrm{d}}{\mathrm{n}}\right)^{2}}\)

(ग) पद-विचलन विधि: इस विधि में वर्ग के मध्य बिन्दुओं का परिकलन करके किसी भी स्वैच्छिक मूल्य से इसका विचलन निकाला जाता है। इसके पश्चात् विचलनों में समापवर्तक (C) का भाग दिया जाता है तथा d' प्राप्त किया जाता है। d मूल्यों को संगत बारम्बारता (1) से गुणा कर का मूल्य प्राप्त किया जाता है, को पुन: d' से गुणा करके विज्ञात किया जाता है। इसके पश्चात् निम्न सूत्र की सहायता से मानक विचलन की गणना की जाती है
\(\sigma=\sqrt{\frac{\Sigma d^{2}}{n}-(\bar{X})^{2}}\)

[नोट-विविक्त अथवा खण्डित श्रेणी तथा संतत अथवा अखण्डित श्रेणी में मानक विचलन ज्ञात करने की विधियाँ समान हैं। अन्तर यह है कि अखण्डित श्रेणी में माध्य विचलन हेतु पहले मध्य मूल्य ज्ञात किया जाता है, उसके पश्चात् दोनों श्रेणियों में समान सूत्रों से मानक विचलन ज्ञात किया जाता है।]

प्रश्न 5. 
लॉरेन्ज वक्र को बनाने की प्रक्रिया को उदाहरण सहित स्पष्ट कीजिये।
अथवा 
लरिज वक्र क्या है? रेखाचित्र द्वारा इसको स्पष्ट कीजिए।
उत्तर:
लॉरेन्ज वक्र का अर्थ: अपकिरण का माप ज्ञात करने की यह एक बिन्दु-रेखीय रीति है। यह एक संचयी प्रतिशत वक्र है। इस रीति का प्रयोग सर्वप्रथम डॉ. मैक्स लॉरेंज द्वारा धन व आय वितरण के माप के लिए किया गया था। उन्हीं के नाम पर इस वक्र का नाम लॉरेंज वक़ पड़ा। अब इस रीति का प्रयोग लाभ, मजदूरी, क्रयविक्रय आदि के वितरण का अध्ययन करने के लिए किया जाता है।

लॉरेन्ज वक्र बनाने की प्रक्रिया-इस वक्र को बनाने की प्रक्रिया निम्नानुसार है।

1. श्रेणी के मूल्यों या मध्य - बिन्दुओं का संचयी योग ज्ञात करना।
2. अन्तिम संचयी योग को 100 मानकर प्रत्येक संचयी मूल्य को प्रतिशत में बदलना।
3. मूल्यों की भाँति आवृत्तियों को संचयी करके अन्तिम संचयी आवृत्ति को 100 मानते हुए सभी आवृत्तियों को प्रतिशत में बदल लिया जाता है।
4. मूल्यों के प्रतिशत को x अक्ष पर और आवृत्तियों के प्रतिशत को y - अक्ष पर दिखाया जाता है। इसके विपरीत भी दिखाया जा सकता है।
5. y - अक्ष का मापदण्ड 0 से 100 तथा x - अक्ष का मापदण्ड 100 से 0 तक लिखा जाता है।
6. x - अक्ष के 0 तथा y - अक्ष के 100 को एक सीधी रेखा द्वारा मिला दिया जाता है। यह रेखा समान वितरण की रेखा मानी जाती है।
7. संचयी आवृत्तियों के प्रतिशत एवं संचयी मूल्यों के प्रतिशत बिन्दुओं को अंकित करके वक्र द्वारा मिला दिया जाता है। यही लारेंज वक्र कहलाता है।

यदि वक्र समान वितरण की रेखा के अधिक पास है तो विचरण कम होगा और यदि वक्र इस रेखा से दूर है तो विचरण अधिक होगा। इस वक्र की सबसे बड़ी कमी यह है कि इसके द्वारा वितरण का संख्यात्मक माप ज्ञात नहीं किया जा सकता।
उदाहरण द्वारा स्पष्टीकरण: निम्नांकित समंकों से लॉरेन्ज वक्र बनाइये  लॉरेन्ज वक्र की रचना करने से पूर्व संचयी योग तथा उनकी प्रतिशतें अन प्रकार ज्ञात की जायेंगी।

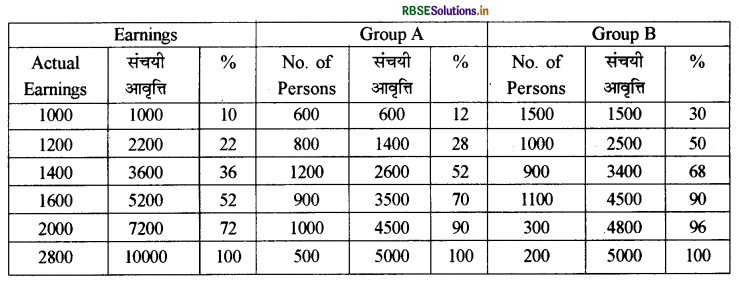
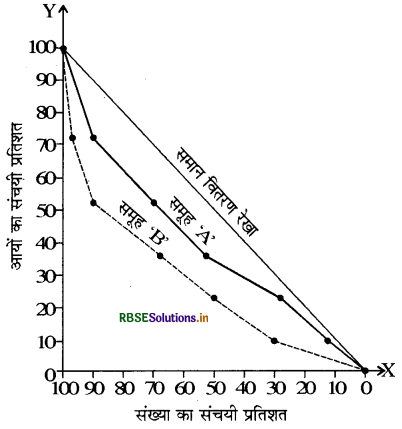
प्रश्न 6. 
माध्य विचलन तथा मानक अथवा प्रमाप विचलन में अन्तर बताइए।
उत्तर:
माध्य विचलन व मानक विचलन में अन्तर अन्तर का आधार माध्य विचलन

अन्तर का आधार	माध्य विचलन	मानक विचलन
1. विचलन	माध्य विचलन में विचलन समान्तर माध्य, मध्यिका या बहुलक किसी से भी लिया जा सकता है।	मानक विचलन में विचलन केवल समान्तर माध्य से लिया जा सकता है।
2. चिह्न	माध्य विचलन में विचलनों के बीजगणितीय चिन्हों को ध्यान में नहीं रखा जाता है अर्थात् ऋणात्मक चिह्न को भी धनात्मक माना जा सकता है।	मानक विचलन में विचलनों के बीजगणितीय चिन्ह्रों को ध्यान में रखा जाता है।
3. वर्ग करना	माध्य विचलन निरपेक्ष विचलनों का औसत होते हैं।	यह विचलनों के वर्गों के माध्य \((\bar{X})\) का वर्गमूल होता है।
4. गणितीय	माध्य विचलन गणितीय दृष्टि से एक अशुद्ध माप है।	यह गणितीय दृष्टि से शुद्ध माप है।
5. वैज्ञनिक माप	यह एक वैज्ञानिक माप नहीं है।	मानक विचलन एक वैज्ञानिक माप है।

(ख ) व्यावहारिक क्रियात्मक प्रश्न:

प्रश्न 1. 
निम्नलिखित आँकड़ों से अपकिरण का चतुर्थक माप एवं उसका गुणांक ज्ञात कीजिए
उत्तर:
अपकिरण के चतुर्थक माप से तात्पर्य चतुर्थक विचलन से है। चतुर्थक विचलन की गणना हेतु सर्वप्रथम प्रथम चतुर्थक व तृतीय चतुर्थक के मूल्य की गणना करनी होगी। 
प्रथम चतुर्थक की गणना

आकार	4	6	8	10	14	12	16
आवृत्ति	2	4	5	6	7	8	9

q₁ = Size of 1 x \(\left(\frac{\mathrm{N}+1}{4}\right)^{\mathrm{th}}\)Item
= Size of 1 x \(\left(\frac{21+1}{4}\right)^{\text {th }}\)
= Size of 5.5th Item

चतुर्थक संख्या 5.5 ऊपर से C.F 6 में है। अत: इसके सामने वाला मूल्य 6 ही प्रथम चतुर्थक का मूल्य होगा। अत: Q₁ = 6
तृतीय चतुर्थक की गणना
q₃ = Size of 3 x \(\left(\frac{N+1}{4}\right)^{\text {th }}\) Item
= Size of 3 x \(\left(\frac{21+1}{4}\right)^{\text {th }}\)  tem
= Size of 66^th/4 Item
= Size of 16.5^th Item
चतुर्थक संख्या 16.5 ऊपर से C.F 17 में है। अत: उसके सामने वाला मूल्य 14 ही तृतीय चतुर्थक का मूल्य होगा। अत: Q₃ = 14

चतुर्थक विचलन की गणना (Calculation of Quartile Deviation):
\(\text { Q.D. }=\frac{Q_{3}-Q_{1}}{2}\)
\(=\frac{14-6}{2}\)
Q D = 4
चतुर्थक संख्या 5.5 ऊपर से C.F 6 में है। अत: इसके सामने वाला मूल्य 6 ही प्रथम चतुर्थक का मूल्य होगा। अत: Q = 6
तृतीय चतुर्थक की गणना
q₃ = Size of 3 x \(\left(\frac{N+1}{4}\right)^{\text {th }}\) Item
= Size of 3 x \(\left(\frac{21+1}{4}\right)^{\text {th }}\)  Item
= Size of 66^th Item
= Size of 16.5^th Item
चतुर्थक संख्या 16.5 ऊपर से C.F. 17 में है। अत: उसके सामने वाला मूल्य 14 ही तृतीय चतुर्थक का मूल्य होगा। अत: Q₃ = 14
चतुर्थक विचलन की गणना (Calculation of Quartile Deviation):
\(\mathrm{Q} . \mathrm{D} .=\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
\(=\frac{14-6}{14+6}\)
= 8/20 = 0.40

प्रश्न 2. 
निम्नलिखित आँकड़ों से चतुर्थक विचलन गुणांक ज्ञात करें :
15,20,23,23,25,25,27 और 40 
उत्तर:
चतुर्थक विचलन गुणांक की गणना

क्रमांक मल्य	मल्य (X)
1	15
2	20
3	23
4	23
5	25
6	25
7	27
8	40
N = 8

प्रथम चतुर्थक (q₁)
= Size of \(\left(\frac{N+1}{4}\right)^{\text {th }}\)  item
= Size of  \(\left(\frac{8+1}{4}\right)^{\text {th }}\) item
= Size of 2.25 item
size of 2.25^th item = size of 2nd item + o.25 (3rd item - 2nd item)
= 20 + 0.25 (23 - 20)
= 20 + 0.75

Size of 2.25^th item = 2.075  है। अतः प्रथम चतुर्थक का मान 20.75 होगा।
Q₁ = 2.075
तृतीय चतुर्थक (q₃):
= Size of 3 x  item
= Size of 3 x   item
= Size of  item
= Size of 6.75^th item
= Size of 6th item + 0.75 (7th item - 6th item)
= 25 + 0.75 (27 - 25)
= 25 + 1.5
Size of 6.75th item = 6.25 है। अतः तृतीय चतुर्थक का मान 265 होगा।

Q₃ = 26.5

चतुर्थक

\(\begin{aligned} &=\frac{Q_{3}-Q_{1}}{Q_{3}+Q_{1}} \\ &=\frac{26.5-20.75}{26.5+20.75} \\ &=\frac{5.75}{47.25} \end{aligned}\)

= 0.122

प्रश्न 3. 
निम्नलिखित से चतुर्थक विचलन गुणांक ज्ञात कीजिए:

मजदूर का नाम	11	13	15	17	19	21	23
मजदूरी (रुपए में)	2	9	20	25	24	15	5

उत्तर:
प्रश्न में मध्य मूल्य दिये हुए हैं। अतः यह प्रश्न अखण्डित श्रेणी का है। मध्य मूल्यों से सर्वप्रथम वर्ग बनाये जायेंगे तथा उसके पश्चात् प्रथम व तृतीय चतुर्थक का मूल्य ज्ञात कर चतुर्थक विचलन गुणांक ज्ञात किया जायेगा। मध्य मूल्यों में अन्तर 2 का है। इस अन्तर का आधा (1) प्रत्येक मध्य मूल्य में से घटाने पर वर्ग की निचली सीमा तथा प्रत्येक मध्य मूल्य में जोड़ने पर ऊपरी सीमा ज्ञात हो जायेगी। आवृत्तियों में परिवर्तन नहीं होगा।

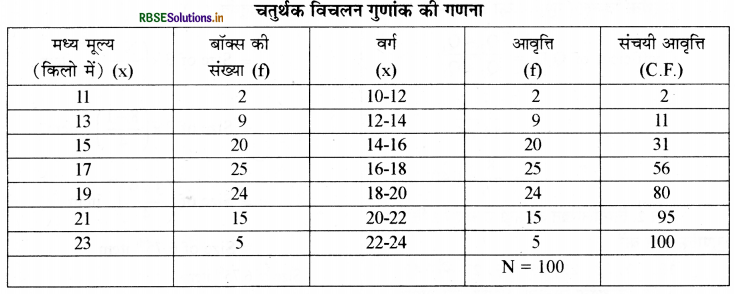
प्रथम चतुर्थक की गणना:
q1 = Size of 1 x  item
= Size of 1 x  item
= Size of 25th item
चतुर्थक संख्या 25 ऊपर से C.F. 31 में है। अतः उसके सामने वाला वर्ग 14-16 चतुर्थक वर्ग होगा। इस वर्ग की सहायता से प्रथम चतुर्थक का मूल्य निम्न सूत्र द्वारा ज्ञात किया जायेगा
\(\begin{aligned} Q_{1} &=L+\frac{\frac{n}{4}-c . f}{f} \times i \\ &=14+\left(\frac{25-11}{20}\right) \times 2 \\ &=14+\frac{14 \times 2}{20} \end{aligned}\)

= 14 + 14  
Q₁ = 15.4

तृतीय चतुर्थक की गणना:
Size of 3 x  item
= Size of 3 x  item
= Size of 75th item

चतुर्थक की गणना उसके सामने वाला वर्ग 18 - 20 चतुर्थक वर्ग होगा। इस वर्ग की सहायता से तृतीय चतुर्थक का मूल्य निम्न सूत्र द्वारा ज्ञात किया जायेगा
\(Q_{3}=L+\frac{\frac{3 n}{4}-c . f .}{f} \times i\)
\(\begin{aligned} &=18+\frac{75-56}{24} \times 2 \\ &=18+\frac{19 \times 2}{24} \\ &=18+\frac{38}{24} \end{aligned}\)

= 18 + 1.58
Q₃ = 19.58

चतुर्थक विचलन गुणांक की गणना:

\(\begin{aligned} &=\frac{Q_{3}-Q_{1}}{Q_{3}+Q_{1}} \\ &=\frac{19.58-15}{19.58+15} \\ &=\frac{4.18}{34.98} \end{aligned}\)

= 0.12

प्रश्न 4. 
निम्नलिखित समकों से चतुर्थक विचलन एवं चतुर्थक विचलन गुणांक ज्ञात कीजिए
उत्तर:
चतुर्थक विचलन की गणना करने से पूर्व प्रश्न में दी गई समावेशी श्रेणी को अपवर्जी श्रेणी में परिवर्तित करना होगा। प्रत्येक वर्ग की ऊपरी सीमा तथा अगले वर्ग की निचली सीमा का अन्तर 1 है। इस अंतर का आधा (5) प्रत्येक वर्ग की निचली सीमा में से घटाने पर तथा ऊपरी सीमा में जोड़ने पर अपवर्जी श्रेणी बन जायेगी। आवृत्तियों में कोई परिवर्तन नहीं होगा। 
चतुर्थक विचलन की गणना
प्रथम चतुर्थक की गणना
q₁ = Size of \(\left(\frac{N}{4}\right)^{\text {th }}\) item
= Size of \(\left(\frac{184}{4}\right)^{\text {th }}\) item
= Size of 46th item
46वें पद का मान ऊपर से C.F 62 में है।
अत: उसके सामने वाला वर्ग 24.5 - 28.5 चतुर्थक वर्ग होगा। इसकी सहायता से प्रथम चतुर्थक निम्नलिखित सूत्र द्वारा ज्ञात किया जायेगा
\(\begin{aligned} Q_{1} &=L+\frac{\frac{n}{4}-c . f .}{f} \times \mathrm{i} \\ &=24.5+\frac{46-10}{52} \times 4 \\ &=24.5+\frac{36 \times 4}{52} \\ &=24.5+\frac{144}{52} \end{aligned}\)
= 24.5 + 2.77 
Q₁ = 27.27

तृतीय चतुर्थक की गणना
q₃ = Size of 3 \(\left(\frac{\mathrm{N}}{4}\right)^{\text {th }}\) item
= Size of 3 \(\left(\frac{184}{4}\right)^{\text {th }}\) item
= Size of 3 46th item
= Size of 138t" item 138वें पद का मान ऊपर से C.F. 162 में है अतः उसके सामने वाला वर्ग 28.5-32.5 चतुर्थक वर्ग होगा।
\(Q_{3}=L+\frac{\frac{3 n}{4}-c . f}{f} \times i\)
\(\begin{aligned} &=28.5+\frac{138-62}{100} \times 4 \\ &=28.5+\frac{76 \times 4}{100} \\ &=28.5+\frac{304}{100} \end{aligned}\)
= 28.5 + 3.04
Q₃ = 31.54

चतुर्थक विचलन की गणना

चतुर्थक विचलन (Q.D) = \(\frac{Q_{3}-Q_{1}}{2}\)
\(\begin{aligned} &=\frac{31.54-27.27}{2} \\ &=\frac{4.27}{2} \end{aligned}\)
चतुर्थक विचलन = 2.135
चतुर्थक विचलन गुणांक की गणना
चतुर्थक विचलन गुणांक = \(\frac{Q_{3}-Q_{1}}{Q_{3}+Q_{1}}\)
\(=\frac{31.54-27.27}{31.54+27.27}\)
\(=\frac{4.27}{58.81}\)
= 0.073 

प्रश्न 5. 
निम्न श्रेणी से मध्यिका द्वारा माध्य विचलन एवं उसके गुणांक की गणना कीजिए
उत्तर:

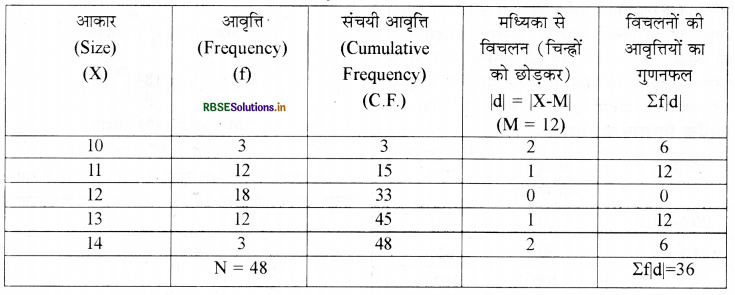
मध्यिका की गणना
M = Size of \(\left(\frac{\mathrm{N}+1}{2}\right)^{\text {th }}\) Item
= Size of \(\left(\frac{48+1}{2}\right)^{\text {th }}\) Item
= Size of 24.5th Item
24.5वां पद ऊपर से C. F. 33 में है, अत: उसके सामने वाला मूल्य 12 ही मध्यिका मूल्य होगा। M = 12
माध्य विचलन की गणना
\(M . D \cdot(M)=\frac{\sum f|d|}{n}\)
\(=\frac{36}{48}\)
\(\text { M.D. }(\mathrm{M})=\mathbf{0 . 7 5}\)

 माध्य विचलन गुणांक = \(\frac{\text { M. D. }(\mathrm{M})}{\mathrm{M}}\)
\(=\frac{0.75}{12}=0.0625\)

प्रश्न 6. 
निम्न समंकों से समान्तर माध्य द्वारा माध्य विचलन एवं उसके गुणांक ज्ञात कीजिए

मल्य	0 -15	5 -10	10 - 20	20 - 25	25 - 30	30 - 35	35 - 40
आवृत्ति	2	9	20	25	24	15	5

उत्तर:

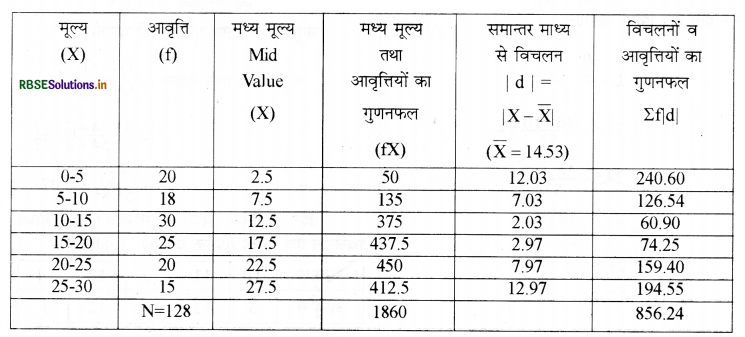
समान्तर माध्य की गणना
\(\begin{aligned} \bar{X} &=\frac{\Sigma f X}{N} \\ &=\frac{1860}{128} \\ \bar{X} &=\mathbf{1 4 . 5 3} \end{aligned}\)

माध्य विचलन की गणना
\(\text { M. D. }(\overline{\mathrm{X}})=\frac{\sum \mathrm{fd} \mid}{\mathrm{n}}\)
\(=\frac{856.24}{128}\)

\(\text { M. } D_{\cdot(\bar{X})}=6.69\)

माध्य विचलन गुणांक की गणना
\(\begin{aligned} &=\frac{M \cdot D \cdot(\bar{X})}{\bar{X}} \\ &=\frac{6.69}{14.53}=0.46 \end{aligned}\)

प्रश्न 7. 
निम्न समंकों का प्रमाप अथवा मानक विचलन ज्ञात कीजिए
47, 48, 65, 57, 31, 60, 37, 48, 78, 59
उत्तर:
मानक अथवा प्रमाप विचलन की गणना

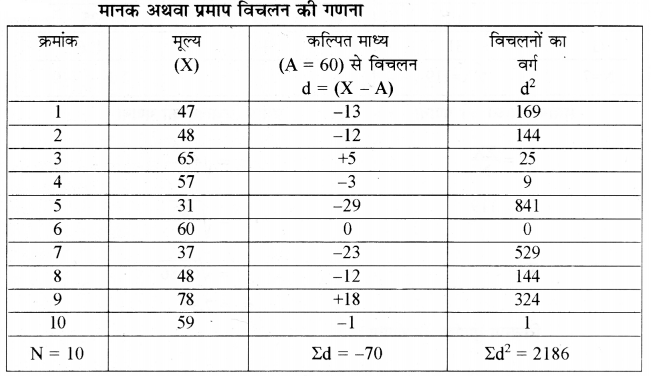
\(\begin{aligned} \sigma &=\sqrt{\frac{\Sigma \mathrm{d}^{2}}{\mathrm{n}}-\left(\frac{\Sigma \mathrm{d}}{\mathrm{n}}\right)^{2}} \\ &=\sqrt{\frac{2186}{10}-\left(\frac{-70}{10}\right)^{2}} \\ &=\sqrt{218.6-(-7)^{2}} \\ &=\sqrt{218.6-(+49)} \\ &=\sqrt{218.6-49} \\ &=\sqrt{169.6} \end{aligned}\)
= 13.02

प्रश्न 8. 
निम्न आँकड़ों से वास्तविक माध्य विधि से मानक विचलन एवं विचरण गुणांक ज्ञात कीजिए
उत्तर:
प्रमाप विचलन एवं विचरण गणांक की गणना

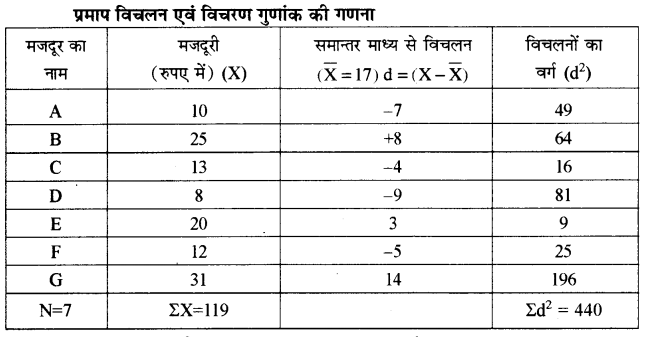
समान्तर माध्य की गणना
\(\begin{aligned} \bar{X} &=\frac{\Sigma X}{N} \\ &=\frac{119}{7} \end{aligned}\)
\(\overline{\mathbf{X}}=17\)

प्रमाप विचलन की गणना
\(\begin{aligned} \sigma &=\sqrt{\frac{\Sigma \mathrm{d}^{2}}{n}} \\ &=\sqrt{\frac{440}{7}} \\ &=\sqrt{62.86} \end{aligned}\)
 σ  = 7.93

विचरण गुणांक की गणना
\(\text { C.V. }=\frac{\sigma}{\overline{\mathrm{X}}} \times 100\)
\(=\frac{7.93}{17} \times 100\)
= 46.655%

प्रश्न 9. 
एक फैक्ट्री में कार्यरत श्रमिकों सम्बन्धी आवृत्ति वितरण से समान्तर माध्य, प्रमाप विचलन एवं विचरण गुणांक की गणना कीजिए
उत्तर:
समान्तर माध्य व प्रमाप विचलन की गणना 

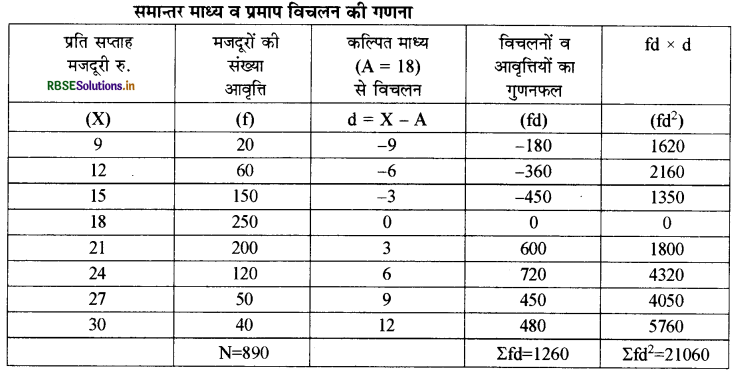
समान्तर माध्य की गणना
\(\bar{X}=A+\frac{\Sigma \mathrm{fd}}{\mathrm{N}}=18+\frac{1260}{890}\)
= 18+ 1.42
= 19.42

मानक / प्रमाप विचलन की गणना
\(\sigma=\sqrt{\frac{\Sigma \mathrm{fd}^{2}}{\mathrm{n}}-\left(\frac{\Sigma \mathrm{fd}}{\mathrm{n}}\right)^{2}}\)

\(\begin{aligned} &=\sqrt{\frac{21060}{890}-\left(\frac{1260}{890}\right)^{2}} \\ &=\sqrt{23.66-2}=\sqrt{21.66}=4.65 \end{aligned}\)

विचरण गुणांक की गणना
\(\text { C.V. }=\frac{\sigma}{\bar{X}} \times 100\)
\(=\frac{4.65}{19.42} \times 100=23.94 \%\)

प्रश्न 10.
निम्न समंकों से समान्तर माध्य एवं प्रमाप विचलन ज्ञात कीजिए:

X	5 -10	10 - 15	15 – 20	20 - 25	25 - 30	30 - 35	35 - 40
Frequency (f)	1	10	20	8	6	3	1

उत्तर:

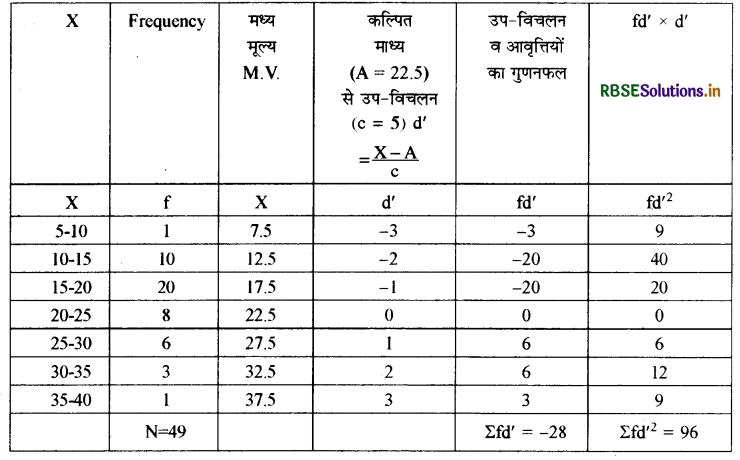
समान्तर माध्य की गणना:
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma \mathrm{fd}^{\prime}}{\mathrm{N}} \times \mathrm{c}\)
= 22.50 + \(\left(\frac{-28 \times 5}{49}\right) \\\)
= 22.50 + \(\left(-\frac{140}{49}\right) \\\)
= 22.50 - 2.86 
=19.64

प्रमाप विचलन की गणना:
\(\begin{aligned} \sigma &=\sqrt{\frac{\sum \mathrm{fd}^{\prime 2}}{\mathrm{n}}-\left(\frac{\sum \mathrm{fd}^{\prime}}{\mathrm{n}}\right)^{2}} \times \mathrm{c} \\ &=\sqrt{\frac{96}{49}-\left(\frac{-28}{49}\right)^{2}} \times 5 \\ &=\sqrt{1.9591-(-0.57)^{2}} \times 5 \end{aligned}\)
\(\begin{aligned} &=\sqrt{1.9591-(+0.3249)} \times 5 \\ &=\sqrt{1.9591-0.3249} \times 5 \\ &=\sqrt{1.6342} \times 5 \end{aligned}\)
= 1.28 x 5
= 6.40

प्रश्न 11.
निम्न समंकों से प्रमाप विचलन एवं विचरण गुणांक ज्ञात कीजिए:

आयु ( वर्षों में )	व्यक्तियों की संख्या
10 से कम	15
20 से कम	30
30 से कम	53
40 से कम	75
50 से कम	100
60 से कम	110
70 से कम	110
80 से कम	120

उत्तर:

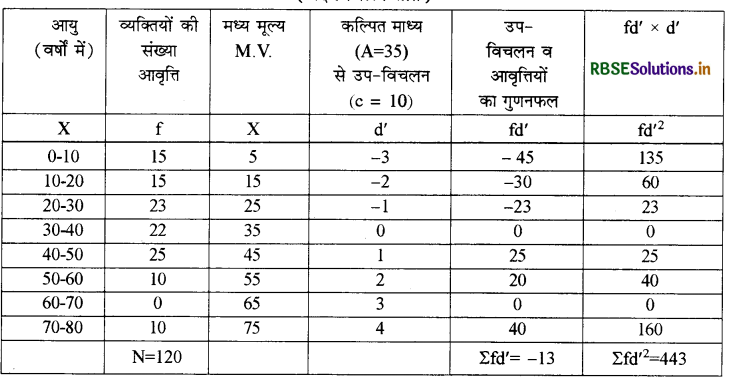
\(\begin{aligned} \overline{\mathrm{X}}=\mathrm{A} &+\frac{\Sigma \mathrm{fd}^{\prime}}{\mathrm{N}} \times \mathrm{c}=35+\left(\frac{-13 \times 10}{120}\right) \\ &=35-1.08=33.92 \text { } \\ \sigma &=\sqrt{\frac{\Sigma \mathrm{fd}^{\prime 2}}{\mathrm{n}}-\left(\frac{\Sigma \mathrm{fd}^{\prime}}{\mathrm{n}}\right)^{2}} \times \mathrm{c}=\sqrt{\frac{443}{120}-\left(\frac{-13}{120}\right)^{2}} \times 10 \\ &=\sqrt{3.6916-0.0116} \times 10 \\ &=\sqrt{3.6800} \times 10 \end{aligned}\)
= 19.8 x100
σ = 19.8

विचरण गुणांक की गणना:
 C.V = \(\frac{\sigma}{\bar{X}} \times 100 \\\)
= \(\frac{19.18}{33.92} \times 100 \\\)
C.V.  = 56.54
( नोट: प्रश्न में Less than series दी गई है अत: दिये गये मूल्यों से वर्ग बनाये जायेंगे तथा आवृत्तियों को भी संशोधित किया जायेगा। दिये गये मूल्य में से वर्गन्तर 10 घटाने पर प्रत्येक वर्ग की निचली सीमा ज्ञात हो जायेगी तथा संशोधित आवृत्ति ज्ञात करने हेतु बड़ी आवृत्ति में से छोटी आवृत्ति घटा दी जायेगी।)

प्रश्न 12.
किसी क्रिकेट टीम के लिए एक बल्लेबाज का चयन करना है। यह चयन X और Y के बीच पूर्ववर्ती टेस्टों के स्कोर के आधार पर करना है, जो अग्रवत् हैं:
X - 65,66,57,67,68,69,70,72 
Y - 67,56,65,68,72,72,69,71
किस बल्लेबाज को टीम में चुना जाना चाहिये:
(अ) अधिक रन स्कोर करने वाले बल्लेबाज को या
(ब) अधिक भरोसेमन्द बल्लेबाज को।
उत्तर:
इस प्रश्न के उत्तर हेतु हमें समान्तर माध्य तथा मानक विचलन से विचरण गुणांक की गणना करनी होगी, जो निम्न प्रकार है:

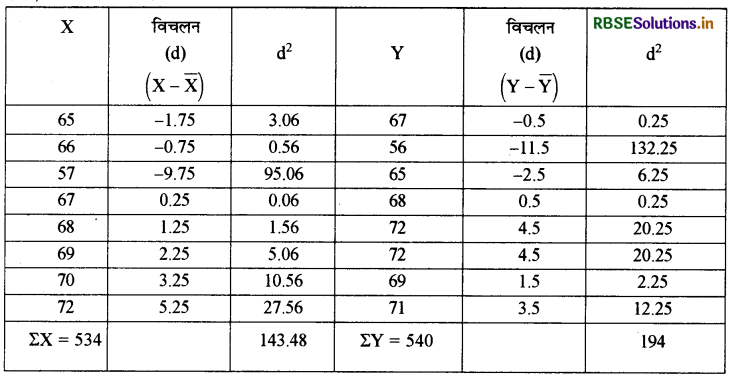
X श्रेणी का समान्तर माध्य
N = 8
\(\Sigma \mathrm{X}=534\)
\(\overline{\mathrm{X}}=\frac{\Sigma \mathrm{X}}{\mathrm{N}} \)
= 534/8 = 66.75

मानक विचलन की गणना:

\(\begin{aligned} \sigma_{\mathrm{x}} &=\sqrt{\frac{\Sigma \mathrm{d}^{2}}{\mathrm{n}}} \\ &=\sqrt{\frac{143.48}{8}} \end{aligned}\)
\(=\sqrt{17.935}\)
= 4.23
विचलन की गणना:
\( \begin{aligned} &=\frac{\sigma}{\overline{\mathrm{X}}} \times 100 \\ &=\frac{4.23}{66.75} \times 100 \\ &=6.34 \% \end{aligned} \)

Y श्रेणी का समान्तर माध्य:
N = 8 
\(\begin{aligned} &\Sigma Y=540 \\ &\bar{Y}=\frac{\Sigma Y}{N} \end{aligned}\)
= 540/8 = 67.5

मानक विचलन की गणना:
\(\begin{aligned} \sigma_{\mathrm{y}} &=\sqrt{\frac{\Sigma \mathrm{d}^{2}}{\mathrm{n}}} \\ &=\sqrt{\frac{194}{8}} \end{aligned}\)
विचलन की गणना:
\(\begin{aligned} \frac{\sigma}{\overline{\mathrm{Y}}} & \times 100 \\ &=\frac{4.92}{67.5} \times 100 \end{aligned}\)
= 7.29%

(अ) यदि अधिक रन बनाने वाले बल्लेबाज का चुनाव करना हो तो हमें Y का चुनाव करना होगा क्योंकि इसका समान्तर माध्य X से अधिक है।
(ब) यदि हमें अधिक भरोसेमंद बल्लेबाज का चुनाव करना हो तो हम X बल्लेबाज का चुनाव करेंगे क्योंकि उसका विचरण गुणांक Y से कम है जो अधिक संगतता को दर्शाता है।