RBSE Class 11 Economics Important Questions Chapter 5 केंद्रीय प्रवृत्ति की माप

Rajasthan Board RBSE Class 11 Economics Important Questions Chapter 5 केंद्रीय प्रवृत्ति की माप Important Questions and Answers.

RBSE Class 11 Economics Important Questions Chapter 5 केंद्रीय प्रवृत्ति की माप 

वस्तुनिष्ठ प्रश्न:

प्रश्न 1. 
केन्द्रीय प्रवृत्ति अथवा औसतों के सांख्यिकीय माप में सम्मिलित है।
(अ) समान्तर माध्य 
(ब) मध्यिका
(स) बहुलक 
(द) उपर्युक्त सभी। 
उत्तर:
(द) उपर्युक्त सभी। 

 

प्रश्न 2. 
सामान्यतः श्रेणी के विभिन्न पद-मूल्यों के समान्तर माध्य से ज्ञात विचलनों का योग होता है।
(अ) 0 
(ब) +1 
(स) + 2 
(द) - 1 
उत्तर:
(ब) +1 

प्रश्न 3. 
किसी श्रेणी का बहुलक मूल्य होता है।
(अ) मध्यवर्ती मूल्य 
(ब) सर्वाधिक आवृत्ति वाला मूल्य
(स) प्रथम मूल्य
(द) न्यूनतम आवृत्ति वाला मूल्य 
उत्तर:
(द) न्यूनतम आवृत्ति वाला मूल्य 

प्रश्न 4. 
निम्न श्रेणी का बहुलक मूल्य होगा:
7,5,7,10, 13, 7, 10, 18, 19,7 
(अ) 10 
(ब) 13
(स) 19
(द) 18 
उत्तर:
(ब) 13

प्रश्न  5. 
निम्न में से कौनसा सही है। 
(अ) ∑(x - x̅) = 0
(ब) ∑(x - x̅) = 1
(स) ∑(x - x̅) = 2
(द) ∑(x - x̅) = 3
उत्तर:
(ब) ∑(x - x̅) = 1

प्रश्न 6. 
चतुर्थक, मानों के कुल समुच्चय को कितने बराबर भागों में बाँटते हैं। 
(अ) दो भागों में 
(ब) चार भागों में
(स) छ: भागों में 
(द) आठ भागों में। 
उत्तर:
(स) छ: भागों में 

प्रश्न 7. 
द्वितीय चतुर्थक (Q₂) बराबर होता है। 
(अ) समान्तर माध्य के 
(ब) मध्यिका के
(स) बहुलक के 
(द) हरात्मक माध्य के। 
उत्तर:
(अ) समान्तर माध्य के 

प्रश्न 8. 
निम्न में से निम्न चतुर्थक है। 
(अ) Q₁
(ब) Q₂
(स) Q₃
(द) उपर्युक्त में से कोई नहीं। 
उत्तर:
(द) उपर्युक्त में से कोई नहीं। 

प्रश्न 9. 
एक श्रेणी में कितने दशमक होते हैं?
(अ) 14
(ब) 10 
(स) 11
(द) 12 
उत्तर:
(स) 11

प्रश्न 10. 
एक श्रृंखला में कितने शतमक होते हैं? 
(अ) 50
(ब) 100 
(स) 150
(द) 200
उत्तर:
(अ) 50

रिक्त स्थान वाले प्रश्ननीचे दिए गए वाक्यों में रिक्त स्थानों की पूर्ति करें:

प्रश्न 1. 
किसी समंक श्रेणी की लगभग समस्त इकाइयों का प्रतिनिधित्व करने वाली एक सरल संख्या को ................. कहते हैं। 
उत्तर:
सांख्यिकीय माध्य

प्रश्न 2.
............... केन्द्रीय प्रवृत्ति का सबसे अधिक प्रयोग किया जाने वाला माप है।
उत्तर:
समान्तर माध्य

प्रश्न 3. 
................. को प्रेक्षणों के मान के योग का प्रेक्षणों की संख्या से विभाजन के भागफल के रूप में परिभाषित करते हैं। 
उत्तर:
मध्यिका

प्रश्न 4. 
समान्तर माध्य से मदों के विचलनों का योग सदैव ................. के बराबर होता है।
उत्तर:
शून्य

प्रश्न 5. 
चतुर्थक मानों के कुल समुच्चय को ................. बराबर भागों में बाँटते हैं।
उत्तर:
चार

प्रश्न 6. 
................. वह मान है जो सबसे अधिक बार प्रकट होता है।
उत्तर:
बहुलक 

सत्य / असत्य वाले प्रश्ननीचे दिए गए कथनों में सत्य / असत्य कथन छौंटए:

प्रश्न 1. 
मध्यिका वितरण का केन्द्रीय मान है अर्थात् मध्यिका से कम मानों की संख्या, इससे अधिक मानों की संख्या के बराबर होती है।
उत्तर:
सत्य 

प्रश्न 2. 
कोई भी चरम मूल्य, किसी भी तरह, औसत माध्य को ऊपर या नीचे धकेल सकता है। 
उत्तर:
सत्य 

प्रश्न 3. 
मध्यिका उस चर का स्थितिक मान है जो वितरण को चार समान भागों में बाँट देता है। 
उत्तर:
असत्य 

प्रश्न 4. 
शतमक वितरण को सौ बराबर भागों में विभाजित करता है।
उत्तर:
सत्य 

प्रश्न 5. 
बहुलक सर्वाधिक प्रेक्षित आँकड़ा मान है।
उत्तर:
सत्य 

प्रश्न 6. 
बहुलक सदैव समान्तर माध्य एवं मध्यिका के बीच रहता है।
उत्तर:
असत्य 

मिलान करने वाले प्रश्ननिम्न को सुमेलित कीजिए:

प्रश्न 1. 

(1) गुणात्मक मापन के लिए उपयुक्त माप	(अ) शतमक
(2) विध्यालय में छात्रों की औसत लम्बाई हेतु माप	(ब) चतुर्थक
(3) सर्वाधिक माँग वाले जूतों के आकार हेतु माप	(स) बहुलक
(4) आँकड़ों को चार बराबर भागों में बाँटने वाला माप	(द) समान्तर माध्य
(5) आँकड़ों को 100 बराबर भागों में बाँटने वाला माप	(य) मध्यिका

उत्तर:

(1) गुणात्मक मापन के लिए उपयुक्त माप	(य) मध्यिका
(2) विध्यालय में छात्रों की औसत लम्बाई हेतु माप	(द) समान्तर माध्य
(3) सर्वाधिक माँग वाले जूतों के आकार हेतु माप	(स) बहुलक
(4) आँकड़ों को चार बराबर भागों में बाँटने वाला माप	(ब) चतुर्थक
(5) आँकड़ों को 100 बराबर भागों में बाँटने वाला माप	(अ) शतमक

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1. 
केन्द्रीय प्रवृत्ति के मापों से आप क्या समझते हैं?
उत्तर:
केन्द्रीय प्रवृत्ति के माप आँकड़ों को संक्षिप्त रूप में व्याख्या करने की संख्यात्मक विधि है।

प्रश्न 2. 
केन्द्रीय प्रवृत्ति का सबसे अधिक प्रयोग किया जाने वाला माप कौनसा है?
उत्तर:
केन्द्रीय प्रवृत्ति का सबसे अधिक प्रयोग किया जाने वाला माप समान्तर माध्य है।

प्रश्न 3. 
वर्गान्तरों की संख्या अधिक हो एवं वर्ग विस्तार समान होने पर समान्तर माध्य ज्ञात करने की कौनसी विधि सर्वोत्तम होगी?
उत्तर:
पद विचलन रीति।

प्रश्न 4. 
केन्द्रीय प्रवृत्ति को मापने के प्रमुख माध्यों के नाम लिखिए।
उत्तर:
केन्द्रीय प्रवृत्ति को मापने के प्रमुख माध्य निम्न हैं:

1. समान्तर माध्य, 
2. मध्यिका, 
3. बहुलक, 
4. गुणोत्तर माध्य, 
5. हरात्मक माध्य।

प्रश्न 5. 
विभिन्न मदों के मूल्यों का समान्तर माध्य के लिए, लिए गए विचलनों का योग क्या होता है?
उत्तर:
विभिन्न मदों के मूल्यों का समान्तर माध्य के लिए, लिए गए विचलनों का योग शून्य होता है। अर्थात्
\(\Sigma(X-\bar{X})=0\)

प्रश्न 6. 
मध्यिका का अर्थ लिखिए।
उत्तर:
किसी श्रेणी को आरोही तथा अवरोही क्रम में व्यवस्थित करने पर उसके मध्य में जो मूल्य आता है उसे ही मध्यिका मूल्य कहते हैं।

प्रश्न 7. 
बहुलक का अर्थ लिखिए।
उत्तर:
बहुलक वह मूल्य है जो श्रेणी के मूल्यों में सबसे अधिक बार आता है।

प्रश्न 8.
चतुर्थक किसे कहते हैं?
उत्तर:
चतुर्थक वे माप हैं जो आँकड़ों को चार बराबर भागों में विभाजित करते हैं और प्रत्येक भाग में बराबर संख्या में प्रेक्षण दिए होते हैं।

प्रश्न 9. 
यदि किसी श्रेणी का समान्तर माध्य 13 एवं मध्यिका 12 है तो बहुलक का मान ज्ञात कीजिए।
उत्तर:
Z = 3M - 2x
यहाँ Z = बहुलक,
M = मध्यिका एवं
X = समान्तर माध्य है
अतः
Z = 3 x 12 - 2 x 13
Z = 36 - 26 = 10 

प्रश्न 10. 
शतमक किसे कहते हैं?
उत्तर:
शतमक वह मान है जो वितरण को 100 बराबर भागों में विभाजित करता है।

प्रश्न 11. 
बहुलक की समूहीकरण विधि कब प्रयोग में ली जाती है?
उत्तर:
जब आवृत्तियाँ अनियमित हों तथा अधिकतम आवृत्ति ज्ञात करना कठिन हो तो समूहीकरण विधि का प्रयोग किया जाता है।

प्रश्न 12. 
शर्ट की कॉलर माप का औसत आकार जानने हेतु कौनसा माध्य उपयुक्त रहेगा?
उत्तर:
शर्ट की कॉलर माप का औसत आकार जानने हेतु बहुलक उपयुक्त रहेगा।

प्रश्न 13. 
समान्तर माध्य का कोई एक गुण बताइए।
उत्तर:
समान्तर माध्य श्रेणी के सभी मदों पर आधारित होता है।

प्रश्न 14. 
किसी कक्षा में छात्रों के अर्थशास्त्र विषय में प्राप्तांक निम्न प्रकार थे 
40,50,55,78,58 इनका समान्तर माध्य ज्ञात कीजिए। 
उत्तर:
समान्तर माध्य
\(=\frac{\Sigma X}{N}=\frac{40+50+55+78+58}{5}=56.2\)

प्रश्न 15. 
व्यक्तिगत श्रेणी में समान्तर माध्य ज्ञात करने का सूत्र लिखिए।
उत्तर:
व्यक्तिगत श्रेणी में समान्तर माध्य (X)
यहाँ Ex = सभी प्रेक्षणों का योग है।
N = प्रेक्षणों की संख्याएँ हैं। 

प्रश्न 16. 
कल्पित माध्य विधि का प्रयोग क्यों किया जाता है?
उत्तर:
जहाँ आँकड़ों में प्रेक्षणों की संख्या अधिक एवं बड़ी हो, इस विधि द्वारा गणना को सरल बनाया जाता है। 

लघूत्तरात्मक प्रश्न:

प्रश्न 1. 
केन्द्रीय प्रवृत्ति की माप से आप क्या समझते हैं?
उत्तर:
सांख्यिकीय माध्यों को केन्द्रीय प्रवृत्ति का माप कहा जाता है। प्रत्येक समंक श्रेणी में एक ऐसा बिन्दु है जिसके आस पास अन्य समंकों के केन्द्रित होने की प्रवृत्ति पाई जाती है। सम्पूर्ण सर्मक श्रेणी की केन्द्रीय प्रवृत्ति को सरल व सारांश रूप में अभिव्यक्त करने वाला प्रतिनिधि मूल्य केन्द्रीय प्रवृत्ति का माप या माध्य कहलाता है। केन्द्रीय प्रवृत्ति या औसतों के कई सांख्यिकीय माप हैं, जैसे-समान्तर माध्य, मध्यिका, बहुलक, ज्यामितीय माध्य, हरात्मक माध्य इत्यादि।

प्रश्न 2. 
समान्तर माध्य का अर्थ बताइए।
उत्तर:
समान्तर माध्य गणितीय माध्यमों में सबसे सरल और सबसे अधिक लोकप्रिय माप है। समान्तर माध्य को 'अंकगणितीय माध्य' या 'औसत' भी कहा जा सकता है। समान्तर माध्य औसत की भाँति है, इसे ज्ञात करने हेतु किसी श्रेणी के सभी मदों के मूल्यों का योग कर उसमें उन मदों की संख्या का भाग देना पड़ता है। दूसरे शब्दों में, वह मूल्य जो किसी श्रेणी के समस्त पदमूल्यों के योग में पदों की कुल संख्या का भाग देने पर प्राप्त होता है, समान्तर माध्य कहलाता है।

प्रश्न 3. 
माध्य को केन्द्रीय प्रवृत्ति का माप क्यों कहा जाता है?
उत्तर:
प्रत्येक समंक श्रेणी में एक ऐसा बिन्दु होता है जिसके आस-पास अन्य सर्मकों के केन्द्रित होने की प्रवृत्ति पाई जाती है। सम्पूर्ण समंक श्रेणी की केन्द्रीय प्रवृत्ति को सरल एवं सारांश रूप में अभिव्यक्त करने वाला प्रतिनिधि मूल्य केन्द्रीय प्रवृत्ति का माप या माध्य कहलाता है। माध्य को केन्द्रीय प्रवृत्ति का माप इसलिए कहा जाता है क्योंकि व्यक्तिगत चर-मूल्यों का जमाव अधिकतर उसी के आस-पास होता है।

प्रश्न 4. 
व्यक्तिगत श्रेणी में समान्तर माध्य ज्ञात करने की कल्पित माध्य विधि को स्पष्ट कीजिए।
उत्तर:
व्यक्तिगत श्रेणी में कल्पित माध्य विधि से समान्तर माध्य ज्ञात करने हेतु सर्वप्रथम श्रेणी के किसी मूल्य या अन्य किसी मूल्य को कल्पित माध्य (A) मान लिया जाता है। इसके पश्चात् प्रत्येक मद (X) में से कल्पित माध्य (A) को घटाकर विचलन (d) ज्ञात किया जाता है। इसके पश्चात् सभी विचलनों का योग (∑d) कर निम्न सूत्र की सहायता से समान्तर माध्य ज्ञात किया जाता है
\(\bar{X}=A+\frac{\Sigma d}{N}\)

प्रश्न 5. 
समंकों के केन्द्रीय प्रवृत्ति के माप के किन्हीं तीन उद्देश्यों का विवेचन कीजिए।
उत्तर:

1. केन्द्रीय प्रवृत्ति के माप अथवा माध्य द्वारा जटिल समंकों का सरल, स्पष्ट तथा संक्षिप्त चित्र प्रस्तुत होता है जिसे याद रखना तथा समझना आसान होता है।
2. केन्द्रीय प्रवृत्ति के माप अथवा माध्यों का अध्ययन करके पूरे समय के बारे में निष्कर्ष प्राप्त किए जा सकते हैं।
3. केन्द्रीय प्रवृत्ति की माप अथवा माध्यों की सहायता से दो या दो से अधिक समंक समूहों का तुलनात्मक अध्ययन आसानी से किया जा सकता है।

प्रश्न 6. 
पद-विचलन विधि द्वारा समान्तर माध्य ज्ञात करने की प्रक्रिया को स्पष्ट कीजिए।
उत्तर:
पद - विचलन विधि द्वारा समान्तर माध्य ज्ञात करने हेतु सर्वप्रथम मध्य मूल्यों में से किसी एक को कल्पित माध्य (A) माना जाता है। प्रत्येक मध्य मूल्य में से कल्पित माध्य को घटाकर अन्तर को वर्ग-विस्तार से भाग दे दिया जाता है। इस प्रकार पद-विचलन ज्ञात हो जाते
\(\mathrm{d}^{\prime}=\frac{\mathrm{X}-\mathrm{A}}{\mathrm{c}}\)
इसके पश्चात् पद - विचलन (d') को आवृत्तियों से गुणा करके गुणनफलों का योग (∑fd') निकाला जाता है तथा निम्न सूत्र द्वारा समान्तर माध्य की गणना की जाती
\(\bar{X}=A+\frac{\Sigma f^{\prime}}{N} \times c\)
यहाँ ∑fd' = पद - विचलनों व आवृत्तियों के गुणनफल का योग है।
c = समापवर्तक वर्ग विस्तार
A = कल्पित माध्य
N= आवृत्तियों का योग है। 

प्रश्न 7. 
निम्नलिखित आठ छात्रों के अर्थशास्त्र विषय में प्राप्त किये गए अंकों का समान्तर माध्य एवं बहुलक ज्ञात कीजिए
6,7,5,6,3,8,6,7 
उत्तर:
समान्तर माध्य की गणना
समान्तर माध्य = \(\frac{\Sigma \mathrm{X}}{\mathrm{N}}\)
\(=\frac{6+7+5+6+3+8+6+7}{8}\)
= 48/6 = 6
बहुलक की गणना: उपयुक्त श्रेणी में हम अवलोकन विधि द्वारा बहुलक ज्ञात कर सकते हैं, उपयुक्त श्रेणी में 6 की बारम्बारता सबसे अधिक है अर्थात् 6 सबसे ज्यादा बार आया है अत: 6 ही बहुलक

प्रश्न 8.
दिये गये आँकड़ों से समान्तर माध्य ज्ञात कीजिए
10, 15, 25, 10, 5, 8, 7, 15
उत्तर:
समान्तर माध्य की गणना:

क्रम संख्य	मूल्य (X)
1	10
2	15
3	25
4	10
5	5
6	8
7	7
8	15
N = 8	∑ X = 95

\( \begin{aligned} \overline{\mathrm{X}} &=\frac{\Sigma \mathrm{X}}{\mathrm{N}} \\ \frac{95}{8} &=11.88 \end{aligned}\)

प्रश्न 9. 
मध्यिका की तीन प्रमुख विशेषताएँ बताइए।
उत्तर:

1. मध्यिका एक स्थिति सम्बन्धी माध्य है, जिसका मूल्य समंक माला के किसी मूल्य के बराबर होना आवश्यक नहीं है।
2. अति सीमान्त मूल्यों का मध्यिका मूल्य पर बहुत कम प्रभाव पड़ता है। यह पदों की संख्या से प्रभावित होता है।
3. मध्यिका की गणना उस दशा में की जा सकती है, जब श्रेणी की मदों को संख्यात्मक रूप नहीं दिया जा सकता हो अर्थात् गुणात्मक तथ्यों के अध्ययन के लिए मध्यिका उपयुक्त रहती है।

प्रश्न 10. 
बहुलक की कोई तीन प्रमुख विशेषताएँ लिखिए।
उत्तर:

1. बहुलक मूल्य पर असाधारण मूल्यों का प्रभाव नहीं पड़ता है अर्थात् श्रेणी के उच्चतम एवं निम्नतम मूल्यों का बहुत कम प्रभाव पड़ता है।
2. यदि आवृत्ति वितरण अनियमित है तो बहुलक मूल्य निर्धारण के लिए पर्याप्त गणना की आवश्यकता होती है तथा बहुलक का निर्धारण करना भी कठिन होता
3. बहुलक सर्वाधिक घनत्व वाला बिन्दु होता है, अतः श्रेणी के वितरण का अनुमान सरलता से लगाया जा सकता है।

प्रश्न 11. 
व्यक्तिगत श्रेणी में मध्यिका का मूल्य ज्ञात करने की प्रक्रिया को स्पष्ट कीजिए।
उत्तर:
मध्यिका का मूल्य ज्ञात करने हेतु सर्वप्रथम समंक माला के समस्त मूल्यों को आरोही (बढ़ते हुए) या अवरोही (घटते हुए) क्रम में व्यवस्थित कर लिया जाता है। श्रेणी के मूल्यों की क्रम संख्या भी साथ - साथ लिखनी चाहिए। एक व्यवस्थित क्रम में क्रमबद्ध करने के बाद निम्न सूत्र द्वारा मध्यिका मूल्य ज्ञात किया जाता है। 
\(M=\left(\frac{N+1}{2}\right)\) वाँ मद
उपर्युक्त सूत्र से पद की क्रम संख्या ज्ञात हो जाती है। इस क्रम संख्या का मूल्य ही मध्यिका मूल्य कहलाता है।

प्रश्न 12. 
निम्न समंकों के आधार पर कल्पित माध्य विधि से समान्तर माध्य ज्ञात कीजिए।

व्यक्त	A	B	C	D	E	F
मासिक आय	500	650	400	750	450	550

उत्तर:
समान्तर माध्य की गणना:

परिवार	मासिक माध् (X)	कल्पित माध् (A = 500) विचलन (d = x - A)
A	500	500 – 500 = 0
B	650	650 – 500 = 150
C	400	400 – 500 = - 100
D	750	750 – 500 = 250
E	450	450 – 500 = -50
F	550	550 – 500 = 50
N = 6		∑ d = 300

\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma \mathrm{d}}{\mathrm{N}}\)

\(=500+\frac{300}{6}\)

= 500 + 50 = 550

प्रश्न 13. 
निम्न सारणी से मध्यिका का मूल्य ज्ञात कीजिए
18, 12, 10, 5, 6, 20, 23, 23, 37, 28, 24, 50, 55, 57, 60
उत्तर:
सर्वप्रथम हम मूल्यों को आरोही (बढ़ते हुए) क्रम में व्यवस्थित करेंगे

क्र. सं.	1	2	3	4	5	6	7	8
मूल्	5	6	10	2	18	20	23	23
	9	10	11	12	13	7	15	N = 15
	24	28	37	50	55	14	60

 मध्यिका वर्ग = \(\left(\frac{N+1}{2}\right)\) वाँ मद
\(=\frac{15+1}{2}\)वाँ मद
= 8वाँ मद 8वीं मद का आकार अथवा मूल्य 23 है अत: मध्यिका मूल्य 23 होगा।

प्रश्न 14. 
निम्नलिखित समंकों से मध्यिका ज्ञात कीजिए
84,91, 72, 87, 68, 78, 95,65
उत्तर:
सर्वप्रथम सर्मकों को आरोही (बढ़ते हुए) क्रम में व्यवस्थित करेंगे

क्रम संख्य	मूल्य (X)
1	65
2	68
3	72
4	78
5	84
6	67
7	91
8	95
N = 8

मध्यिका = \(\left(\frac{N+1}{2}\right)\) वाँ मद
= \(=\left(\frac{8+1}{2}\right)\) वाँ मद
= 4.5वाँ मद
4.5वें मद का मूल्य ज्ञात करने हेतु 4वें मद तथा 5वें मद का मूल्य जोड़ कर 2 का भाग दिया जाएगा।
\(=\frac{78+84}{2}\)
= 162/2 = 81 अत: मध्यिका का मूल्य 81 होगा।

प्रश्न 15. 
निम्न आँकड़ों से निम्न एवं उच्च चतुर्थक के मान ज्ञात कीजिए
26, 22, 14, 30, 18, 11, 35, 41, 12, 32, 34,  41
उत्तर:
सर्वप्रथम आँकड़ों को आरोही क्रम में व्यवस्थित करेंगे
11, 12, 14, 18, 22, 26, 30, 32, 34, 35, निम्न चतुर्थक (Q₁) की गणना
Q₁ = \(\left(\frac{N+1}{2}\right)\) वें मद का आकार
= \(\left(\frac{11+1}{4}\right)\) = 12/3 = 3 वाँ मद का आकार
Q = 14
उच्च चतुर्थक (Q₃) की गणना
\(\left(\frac{N+1}{2}\right)\)वें मद का आकार
\(\begin{aligned} &=\frac{3(11+1)}{4} \\ &=\frac{3(12)}{4}=\frac{36}{4} \end{aligned}\)
 = 9 वाँ मद का आकार Q = 34 

प्रश्न 16. 
दस श्रमिकों की मासिक मजदूरी निम्नांकित है:
मजदूरी (रुपये में) : 400, 415, 405, 417, 415, 425, 415, 417, 432
उपर्युक्त समंकों के आधार पर बहुलक का मूल्य ज्ञात कीजिए।
उत्तर:
बहुलक का मूल्य (निरीक्षण विधि द्वारा गणना)-श्रेणी का निरीक्षण करने से यह ज्ञात होता है कि इस श्रेणी में 415 रुपये की मजदूरी सबसे अधिक तीन बार आई है अत: बहुलक का मूल्य 415 रुपये होगा।

प्रश्न 17. 
विविक्त श्रृंखला में मध्यिका मूल्य ज्ञात करने की प्रक्रिया को स्पष्ट कीजिए।
उत्तर:
विविक्त शृंखला अथवा खण्डित श्रेणी में मध्यिका ज्ञात करने हेतु सर्वप्रथम यदि समंक अव्यवस्थित है तो उन्हें बढ़ते या घटते क्रम में व्यवस्थित करेंगे तथा उसके पश्चात् एक आवृत्ति में दूसरी आवृत्ति को जोड़कर संचयी आवृत्ति (c.f.) ज्ञात की जाती है। इसके पश्चात् अग्न सूत्र द्वारा मध्यिका की क्रम संख्या अथवा मध्यिका संख्या ज्ञात की जाती है
मध्यिका = \(\left(\frac{\mathrm{N}+1}{2}\right)\)वाँ मद
मध्यिका की क्रम संख्या ऊपर से जिस संचयी आवृत्ति में आती है उसके सामने वाले मूल्य को ही मध्यिका मूल्य कहते हैं।

प्रश्न 18. 
निम्न बारम्बारता वितरण से माध्यिका आय का परिकलन कीजिए

आय (रुपये में)	लोगों की संख्या
10	5
20	7
30	14
40	4

उत्तर:
माध्यिका मूल्य ज्ञात करने हेतु सर्वप्रथम संचयी आवृत्ति ज्ञात की जाएगी

आय रुपये में	लोगों की संख्या	संचयी आवृत्ति
X	f	c.f
10	5	5
20	7	12
30	14	26
40	4	30
	N = 30

मध्यिका = \(\left(\frac{\mathrm{N}+1}{2}\right)\)
\(=\left(\frac{30+1}{2}\right)\) वाँ मद
वाँ मद - 155 वाँ मद माध्यिका संख्या 15.5 ऊपर से संचयी आवृत्ति 26 के अन्तर्गत आती है अत: इसके सामने वाला पद 30 ही मध्यिका का मूल्य है।

प्रश्न 19. 
निम्नलिखित समंकों से मध्यिका का

प्राप्तांक	5	10	30	20	35	15
विद्यार्थियों की संख्या	4	16	8	11	9	5

उत्तर:
मध्यिका मूल्य ज्ञात करने हेतु सबसे पहले समंकों को बढ़ते क्रम में रखेंगे तथा संचयी आवृत्ति (c.f.) ज्ञात की जाएगी

X	f	c.f
5	5	5
10	7	12
15	14	26
20	4	30
25	12	23
30	7	13
35	3	22
	N = 30

मध्यिका = \(\left(\frac{\mathrm{N}+1}{2}\right)\)
\(=\left(\frac{53+1}{2}\right)\) वाँ मद
= 27वाँ मद
मध्यिका संख्या 27 ऊपर से संचयी आवृत्ति में 36 के अन्तर्गत आती है अतः उसके सामने वाला मद मूल्य 20 ही मध्यिका का मूल्य है।

प्रश्न 20. 
निम्न सारणी से बहुलक वर्ग का निर्धारण कीजिए

वर्ग	20 -30	30 - 40	40 - 50	50 - 60	60 - 70	70 - 80
आवृत्ति	3	23	0	42	11	9

उत्तर:
उपर्युक्त प्रश्न में समूहीकरण विधि द्वारा बहुलक वर्ग की गणना करेंगे

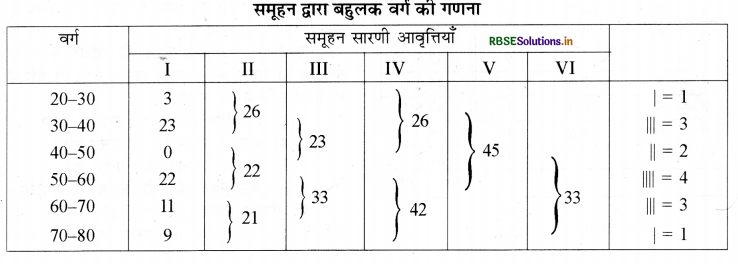
प्रश्न 21. 
निम्न समंकों के आधार पर भारित समान्तर माध्य ज्ञात कीजिए

विषय	अंक (x)	भार (w)
हिन्दी	68	4
अंग्रेजी	67	3
भूगोल	58	2
अर्थशास्त्र	65	1

उत्तर:

विषय	अंक (x)	भार (w)	XW
हिन्दी	68	4	252
अंग्रेजी	67	3	192
भूगोल	58	2	116
अर्थशास्त्र	65	1	97

भारित समान्तर माध्य  \(=\frac{\Sigma \mathrm{XW}}{\Sigma \mathrm{W}}=\frac{630}{10}=63\)                                     

निबन्धात्मक प्रश्न:

(क) सैद्धान्तिक प्रश्न

प्रश्न 1. 
समान्तर माध्य से आप क्या समझते हैं? समान्तर माध्य ज्ञात करने की विभिन्न विधियों को स्पष्ट कीजिए।
उत्तर:
समान्तर माध्य: समान्तर माध्य गणितीय माध्यों में सबसे सरल और सबसे अधिक लोकप्रिय माप माना जा सकता है। इसे गणितीय माध्य अथवा औसत अथवा माध्य भी कहा जाता है। किसी समंक श्रेणी का समान्तर माध्य, उस श्रेणी के मूल्यों को जोड़कर उसकी कुल संख्या का भाग देने से प्राप्त होता है। दूसरे शब्दों में, वह मूल्य जो किसी श्रेणी के समस्त पद मूल्यों के योग में पदों की कुल संख्या का भाग देने पर प्राप्त होता है, समान्तर माध्य कहलाता है।

समान्तर माध्य ज्ञात करने की विधियाँ: समान्तर माध्य के परिकलन का अध्ययन मोटे तौर पर दो श्रेणियों के अन्तर्गत किया जा सकता है।
(क) असमूहित आँकड़ों का समान्तर माध्य 
(ख) समूहित आँकड़ों का समान्तर माध्य इनका विस्तृत विवेचन निम्न प्रकार है।
(क) असमूहित आँकड़ों का समान्तर माध्य
(i) प्रत्यक्ष विधि: यह विधि उस समय उपयुक्त रहती है जब चर मूल्यों की संख्या कम हो तथा वे।
दशमलव में हों। समान्तर माध्य ज्ञात करने हेतु श्रेणी के सभी मूल्यों का योग ज्ञात कर निम्न सूत्र का प्रयोग किया जाता है।
\(\bar{X}=\frac{\Sigma X}{N}\)

(ii) कल्पित माध्य विधि: इस रीति में श्रेणी के मूल्यों में से किसी भी मूल्य को कल्पित माध्य (A) माना जाता है। श्रेणी के प्रत्येक मूल्य (x) में से कल्पित माध्य (A) को घटाकर विचलन (d) ज्ञात किये जाते हैं तथा उनका योग ज्ञात करते हैं। समान्तर माध्य की गणना निम्न सूत्र द्वारा की जाती है
\(\bar{X}=A+\frac{\Sigma d}{N}\)
संकेताक्षर:
\(\bar{X}\) = समान्तर माध्य
N = प्रेक्षणों की कुल संख्या
∑d = विचलनों का योग
A = कल्पित माध्य।

(iii) पद - विचलन विधि: इसमें कल्पित माध्य से लिए गए सभी विचलनों को समापवर्तक 'C' से विभाजित करके और भी सरल बनाया जा सकता है। इसका उद्देश्य बड़ी संख्याओं से बचना है। इसे d = x - A के स्थान पर d' अर्थात् \(\mathrm{d}^{\prime}=\frac{\mathrm{X}-\mathrm{A}}{\mathrm{C}}\) ज्ञात किया जाता है तथा समान्तर माध्य अग्र सूत्र द्वारा ज्ञात किया जाता है
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma \mathrm{d}^{\prime}}{\mathrm{N}} \times \mathrm{C}\)
यहाँ C = समापवर्तक,
N = प्रेक्षणों की कुल संख्या तथा
A = कल्पित माध्य है।

(ख) समूहित आँकड़ों के लिए समान्तर माध्य का परिकलन:

1. विविक्त श्रृंखला अथवा खण्डित श्रेणी में गणना: विविक्त श्रृंखला अथवा खण्डित श्रेणी में निम्न तीन विधियों द्वारा समान्तर माध्य ज्ञात किया जाता है।

(i) प्रत्यक्ष विधि: विविक्त श्रृंखला में प्रत्यक्ष विधि में निम्न सूत्र की सहायता से समान्तर माध्य ज्ञात किया जाता है।
\(\bar{X}=\frac{\Sigma f x}{\Sigma f}\)
यहाँ ∑fK = चरों के उत्पाद तथा बारम्बारता के गुणनफल का योग है,
∑f = बारम्बारताओं का योग है,
\(\overline{\mathrm{X}}=\) समान्तर माध्य है।

(ii) कल्पित माध्य विधि: विविक्त श्रृंखला में इस विधि में श्रेणी के मूल्यों में से किसी भी मूल्य को कल्पित माध्य (A) माना जाता है तथा श्रेणी के प्रत्येक मूल्य (X) में से कल्पित माध्य (A) घटाकर विचलन d = x - A ज्ञात किया जाता है। विचलनों (d) को आवृत्तियों (1) से गुणा करके उनका योग (∑d) ज्ञात किया जाता है। इसके पश्चात् निम्न सूत्र द्वारा समान्तर माध्य ज्ञात किया जाता है
\(\overline{\mathbf{X}}=\mathrm{A}+\frac{\Sigma \mathrm{fd}}{\Sigma \mathrm{f}}\)

(iii) पद-विचलन विधि: इस विधि में विचलनों को समापवर्तक 'C' द्वारा विभाजित किया जाता है जो कि परिकलन को सरल बना देता है। यह संख्यात्मक अंकों के आकार को घटाकर परिकलन को सरल बनाने के लिए \(\mathrm{d}^{\prime}=\frac{\mathrm{d}}{\mathrm{c}}=\frac{\mathrm{X}-\mathrm{A}}{\mathrm{C}}\) का आकलन किया जाता है। इस विधि के अनुसार समान्तर माध्य ज्ञात करने का निम्न सूत्र है
\(\bar{X}=A+\frac{\Sigma f^{\prime}}{\Sigma f} \times C\)

2. संतत श्रृंखला अथवा अखण्डित श्रेणी में समान्तर माध्य की गणना:
(i) प्रत्यक्ष विधि: इस विधि में श्रेणी के प्रत्येक वर्ग की दोनों सीमाओं का योग कर दो का भाग देकर मध्य मूल्य (m) ज्ञात किया जाता है। इसके पश्चात् विविक्त अथवा खण्डित श्रेणी की भाँति ही समान्तर माध्य की गणना की जाती है। इसमें निम्न सूत्र का प्रयोग किया जाता है।
\(\overline{\mathbf{X}}=\frac{\sum \mathrm{fm}}{\sum f}\)

(ii) कल्पित माध्य विधि: इस विधि में श्रेणी के प्रत्येक वर्ग के मध्य मूल्य ज्ञात करने के पश्चात् समान्तर माध्य की गणना, प्रक्रिया व सूत्र विविक्त अथवा खण्डित श्रेणी के समान ही है। इसमें समान्तर माध्य को निम्न सूत्र द्वारा ज्ञात किया जाएगा।
\(\bar{X}=A+\frac{\Sigma f d}{\Sigma f}\)

(iii) पद-विचलन विधि: पद - विचलन की विधि में श्रेणी के प्रत्येक वर्ग के मध्य मूल्य ज्ञात करने के पश्चात् समान्तर माध्य की गणना, प्रक्रिया व सूत्र विविक्त अथवा खण्डित श्रेणी के समान ही है। इसे निम्न सूत्र द्वारा ज्ञात किया जा सकता है
\(\bar{X}=A+\frac{\Sigma f^{\prime}}{\Sigma f} \times C\)

प्रश्न 2. 
उदाहरण द्वारा सिद्ध कीजिए कि समान्तर माध्य से विभिन्न मदों के विचलनों का योग शून्य होता है।
उत्तर:
समान्तर माध्य की अत्यन्त महत्त्वपूर्ण बीजगणितीय विशेषता यह है कि वास्तविक समान्तर माध्य से लिए गए विभिन्न पद-मूल्यों के विचलनों का योग सदैव शून्य होता है, अर्थात् \(\Sigma(\mathbf{X}-\overline{\mathbf{X}})\) = 0 होता है। इसके लिए निम्नानुसार गणना प्रक्रिया अपनायी जाती

1. सर्वप्रथम श्रेणी का समान्तर माध्य \((\bar{X})\) ज्ञात किया जाता है।
2. इसके पश्चात् इसके विभिन्न पद - मूल्यों का विचलन ज्ञात करते हैं अर्थात् \((X-\bar{X})=d\)
3. इन विचलनों का योग (2d) सदैव शून्य होता है।

उदाहरण द्वारा सत्यापन :
निम्न सर्मकों से समान्तर माध्य से विचलन ज्ञात कीजिए :

दिन	1	2	3	4	5	6	7
आय (रुपयों में)	18	15	16	17	16	25	19

उत्तर:
हल - समान्तर माध्य से विचलन:

 
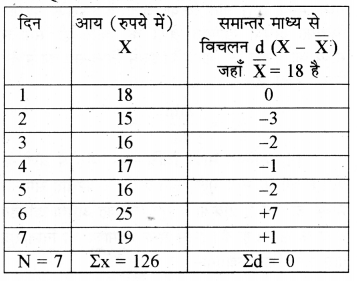
\(\bar{X}=\frac{\Sigma \mathbf{X}}{N}\)
\(=\frac{126}{7}\)
18 रुपये
उपर्युक्त उदाहरण से सिद्ध होता है कि समान्तर माध्य से विचलनों का योग सदैव शून्य होता है।

प्रश्न 3. 
मध्यिका से आप क्या समझते हैं? मध्यिका को मापने की विभिन्न विधियों का विस्तार से विवेचन कीजिए।
उत्तर:
मध्यिका का अर्थ: मध्यिका उस चर का स्थितिक मान है, जो वितरण को दो समान भागों में बाँट देता है। एक भाग के अन्तर्गत सभी मान मध्यिका मान से अधिक या उसके बराबर होते हैं तथा दूसरे भाग के सभी मान उससे कम या उसके बराबर होते हैं। दूसरे शब्दों में किसी समंक मात्रा को आरोही या अवरोही क्रम में व्यवस्थित करने पर, उस श्रेणी के मध्य में जो मूल्य आता है, वही मध्यिका कहलाता है।

मध्यिका की गणना अथवा अभिकलन:  मध्यिका की गणना करने हेतु आँकड़ों को आरोही अथवा अवरोही क्रम में व्यवस्थित करते हुए मध्यिका को मध्यमान द्वारा आसानी से अभिकलित किया जा सकता है। विभिन्न प्रकार की श्रेणियों में मध्यिका की गणना निम्न प्रकार की जा सकती है।

(i) व्यक्तिगत श्रेणी में मध्यिका की गणनाइसमें सर्वप्रथम श्रेणी को मूल्य के आरोही या अवरोही क्रम में लिखा जाता है तथा मूल्यों के साथ क्रम संख्या भी लिखी जाती है। इसके पश्चात् निम्न सूत्र द्वारा मध्यिका संख्या की गणना की जाती है
मध्यिका संख्या = \(\left(\frac{\mathrm{N}+1}{2}\right)\)मद का आकार
यहाँ N= मदों की संख्या है तथा इस सूत्र से जो मध्यिका संख्या आती है उसके सामने का मूल्य ही मध्यिका का मूल्य होगा।

(ii) विविक्त श्रृंखला अथवा खण्डित श्रेणी में मध्यिका की गणना-इस श्रेणी में भी सर्वप्रथम संचयी आवृत्ति ज्ञात की जाती है। इसके पश्चात् निम्न सूत्र की सहायता से मध्यिका संख्या की गणना की जाती है।
मध्यिका संख्या = \(\left(\frac{\mathrm{N}+1}{2}\right)\) वीं इकाई
मध्यिका की यह इकाई ऊपर से जिस संचयी आवृत्ति में आती है उसके सामने वाला मूल्य ही मध्यिका मूल्य कहलाता है। यहाँ पर N = आवृत्तियों का योग होता है।

(iii) संतत श्रृंखला अथवा अखण्डित श्रेणी में मध्यिका की गणन: इस श्रृंखला में भी सर्वप्रथम संचयी आवृत्ति ज्ञात की जाती है। इसके पश्चात् अग्र सूत्र द्वारा मध्यिका संख्या ज्ञात की जाती है।
मध्यिका संख्या = \(\left(\frac{\mathrm{N}+1}{2}\right)\)वाँ मद।

मध्यिका संख्या ऊपर से जिस संचयी आवृत्ति में आती है उसके सामने वाला वर्ग ही मध्यिका वर्ग होता है। मध्यिका वर्ग की सहायता से मध्यिका मूल्य की गणना निम्न सूत्र की सहायता से की जाएगी।
यहाँ L = मध्यिका वर्ग की निचली सीमा है, c.f. = मध्यिका वर्ग के पूर्ववर्ती वर्ग की संचयी बारम्बारता है, f = मध्यिका वर्ग की बारम्बारता है, h = मध्यिका वर्ग के अन्तराल का परिमाण है।

प्रश्न 4. 
बहुलक से आप क्या समझते हैं? बहुलक की गणना करने वाली विभिन्न विधियों को स्पष्ट कीजिए।
उत्तर:
बहुलक-बहुलक शब्द फ्रेंच भाषा के शब्द 'ला मोड' से व्युत्पन्न है, जो वितरण के सर्वाधिक प्रचलित मानों का द्योतक है क्योंकि यह श्रृंखला में सबसे अधिक बार दोहराया जाता है। बहुलक सर्वाधिक प्रेक्षित आँकड़ा मान है, इसे M, के द्वारा दर्शाया जाता है। अत: बहुलक मूल्य वह मूल्य है जो श्रेणी में सबसे अधिक बार आता है।

बहुलक की गणना करने की विधियाँ: विभिन्न श्रेणियों में बहुलक की गणना करने की प्रमुख विधियाँ निम्न प्रकार हैं।
1. व्यक्तिगत श्रेणी में बहुलक की गणनाव्यक्तिगत श्रेणी में बहुलक को निरीक्षण विधि द्वारा, व्यक्तिगत श्रेणी को खण्डित श्रेणी या अखण्डित श्रेणी में बदलकर तथा माध्यों के अन्तर्सम्बन्धों द्वारा ज्ञात किया जा सकता है। सामान्यतः व्यक्तिगत श्रेणी में समंक माला के विभिन्न मूल्यों में जो मूल्य सबसे अधिक बार आता है, वह बहुलक मूल्य माना जाता है।

2. विविक्त श्रृंखला अथवा खण्डित श्रेणी में बहुलक की गणना:
(i) निरीक्षण रीति: इस रीति का उपयोग तब किया जाता है जब किसी श्रेणी में आवृत्ति वितरण नियमित हो अर्थात् प्रारम्भ में आवृत्तियाँ बढ़ रही हों तथा अधिकतम आवृत्ति श्रेणी के लगभग बीच में हो, तत्पश्चात् पुनः आवृत्तियाँ घट रही हों। ऐसी श्रेणी में अधिकतम आवृत्ति वाला मूल्य ही बहुलक मूल्य होता।

(ii) समूहन रीति: जब किसी खण्डित श्रेणी में आवृत्ति वितरण अनियमित हो तो उसमें बहुलक मूल्य ज्ञात करने के लिए समूहन रीति का उपयोग किया जाता है। इसमें निम्नानुसार आवृत्तियों की सहायता से 6 समूह बनाये जाते हैं।
(अ) प्रथम समूह: दी गयी आवृत्तियाँ 
(ब) दूसरा समूह: दो - दो आवृत्तियों का योग।
(स) तीसरा समूह: प्रथम आवृत्ति को छोड़कर, आगामी आवृत्तियों से पुनः दो - दो आवृत्तियों का योग।
(द) चौथा समूह: प्रथम से तीन-तीन आवृत्तियों का योग।
(य) पाँचवाँ समूह: प्रथम आवृत्ति को छोड़कर आगामी आवृत्ति से पुनः तीन - तीन आवृत्तियों का योग।
(र) छठा समूह: प्रथम दो आवृत्तियों को छोड़कर आगामी आवृत्ति से पुन: तीन - तीन आवृत्तियों का योग।
तत्पश्चात् प्रत्येक समूह की अधिकतम आवृत्ति योग को रेखांकित कर दिया जाता है। समूहीकरण के बाद विश्लेषण सारणी तैयार करके बहुलक मूल्य ज्ञात कर लिया जाता है।

3. अखण्डित या सतत श्रेणी में बहुलक की गणना-सर्वप्रथम निरीक्षण द्वारा बहुलक वर्ग निश्चित कर लिया जाता है। यदि आवृत्तियाँ नियमित हों तो निरीक्षण विधि तथा अनियमित हों तो समूहीकरण द्वारा बहुलक वर्ग का निर्धारण करना चाहिए। तत्पश्चात् निम्न सूत्र द्वारा बहुलक मूल्य ज्ञात किया जाता है
\(\mathrm{M}_{0}=\mathrm{L}+\frac{\mathrm{D}_{1}}{\mathrm{D}_{1}+\mathrm{D}_{2}} \times \mathrm{h} \text { }\)
\(\mathrm{L}+\frac{\mathrm{f}_{1}-\mathrm{f}_{0}}{2 \mathrm{f}_{1}-\mathrm{f}_{0}-\mathrm{f}_{2}} \times i\)
यहाँ L = बहुलक की निम्न सीमा, D₁ = बहुलक वर्ग की बारम्बारता और बहुलक वर्ग के पूर्ववर्ती वर्ग की बारम्बारता के बीच का अन्तर, D₂ = बहुलक वर्ग की बारम्बारता और बहुलक वर्ग के परवर्ती वर्ग की बारम्बारता के बीच अन्तर, h = वितरण का वर्ग अन्तराल, f₁ = बहुलक वर्ग की आवृत्ति, f₂ = बहुलक वर्ग से तुरन्त पहले वर्ग की आवृत्ति, f = बहुलक वर्ग से तुरन्त बाद वाले वर्ग की आवृत्ति, i = वर्ग विस्तार। 

(ख) व्यावहारिक प्रश्न / क्रियात्मक प्रश्न:

प्रश्न 1. 
निम्न श्रेणी से प्रत्यक्ष विधि एवं कल्पित माध्य विधि द्वारा समान्तर माध्य की गणना कीजिए।

क्र. सं.	1	2	3	4	5
ऊँचाई (सेमी.)	150	160	140	150	168
	7	8	9	10	11
	165	162	145	180	167

उत्तर:

क्रम संख्या	ऊँचाई ( सेमी. ) (X)
1	150
2	160
3	140
4	150
5	168
6	170
7	165
8	162
9	145
10	180
11	167
12	165
N = 12	∑ x  = 120

 कल्पित माध्य विधि द्वारा समान्तर माध्य:
\(\bar{X}=A+\frac{\Sigma d}{N}\)

\(=150+\frac{120}{12}\)
= 160

प्रश्न 2.
निम्नलिखित से समान्तर माध्य ज्ञात कीजिए:

कॉल की संख्या	1	2	3	4	5	6	7
आवृत्ति	14	21	25	43	51	39	12

उत्तर:

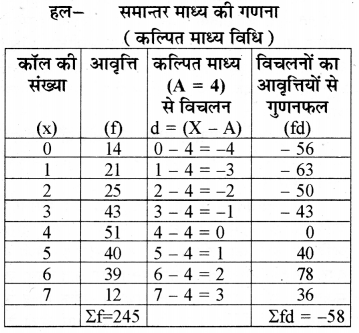
सूत्र: 
\(\begin{aligned} &\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma \mathrm{fd}}{\sum \mathrm{f}} \\ &\overline{\mathrm{X}}=4+\frac{-58}{245} \end{aligned}\)

= 4 - 0.24
= 3.76
संकेताक्षर: 
\(\overline{\mathrm{X}}\) =  समान्तर माध्य
A = कल्पत माध्य
f = आवृत्तियाँ
∑fd = आवृत्तियों एवं विचलनों के
गुणनफलों का योग

प्रश्न 3.
निम्न श्रेणी का प्रत्यक्ष विधि द्वारा समान्तर माध्य ज्ञात कीजिए:

कॉल की संख्या	10	20	25	40	60	80
आवृत्ति	5	25	30	40	15	5

उत्तर:
समान्तर माध्य की गणना ( प्रत्यक्ष विधि द्वारा ):

आकार (x)	आवृत्ति (f)	fx
10	5	50
20	25	500
25	20	500
40	30	1200
60	15	900
80	5	400
	∑f =100	∑fx = 3550

प्रत्यक्ष विधि द्वारा समान्तर माध्य \(\bar{x}=\frac{\Sigma f x}{\Sigma f}\)
\(=\frac{3550}{100}\)
= 35.50

प्रश्न 4. 
निम्न श्रेणी का प्रत्यक्ष विधि द्वारा समान्तर माध्य ज्ञात कीजिए:

लाभांश ( रुपये में )	अंशों की संख्या
0 – 10 10 – 20 20 – 30 30 – 40 40 – 50 50 - 60	10 12 20 15 5 3

उत्तर: 
विधि द्वारा समान्तर माध्य:

लाभांश ( रुपये में )	अंशों की संख्या	माध्य	f x m
0 – 10 10 – 20 20 – 30 30 – 40 40 – 50 50 - 60	10 12 20 15 5 3	5 15 25 35 45 55	50 180 500 525 225 165

समान्तर माध्य = \(\frac{\Sigma \mathrm{fm}}{\Sigma \mathrm{f}}\)

\(=\frac{1970}{70}\)
= 28 .14

प्रश्न 5.
निम्नलिखित से समान्तर माध्य ज्ञात कीजिए:

प्राप्तांक	0 -5	6 – 10	11 – 15	16 – 20
विद्यार्थियों की संख्या	5	7	12	19
	21 – 25	26 – 30	31 – 35	36 – 40
	17	19	15	6

उत्तर: 
हल - प्रश्न में समावेशी श्रेणी दी गयी है; किन्तु समान्तर माध्य ज्ञात करने के लिए इसे अपवर्जी श्रेणी में परिवर्तित करने की आवश्यकता नहीं है; क्योंक दोनों ही स्थितियों में मध्यमान समान होते हैं।

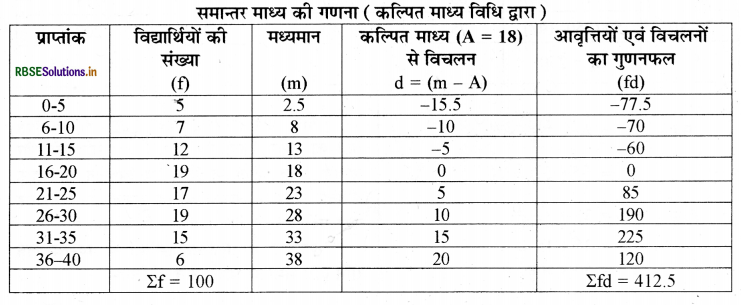
\(\begin{aligned} &\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma \mathrm{fd}}{\Sigma \mathrm{f}} \\ &\overline{\mathrm{X}}=18+\frac{412.5}{100} \end{aligned}\)

= 18 + 41.3
= 22.13

प्रश्न 6. 
निम्नलिखित समंकों से समान्तर माध्य का परिकलन कीजिए:

प्राप्तांक ( से कम )	10	20	30	40	50	60	70	80
विद्यार्थियों की संख्या	15	35	60	84	96	127	198	250

उत्तर:
प्रश्न में संचयी आवृत्तियाँ दी गई हैं। अतः उन्हें सतत श्रेणी में परिवर्तित कर समान्तर माध्य की गणना की जायेगी:
समान्तर माध्य की गणना ( पद - विचलन रीति द्वारा )

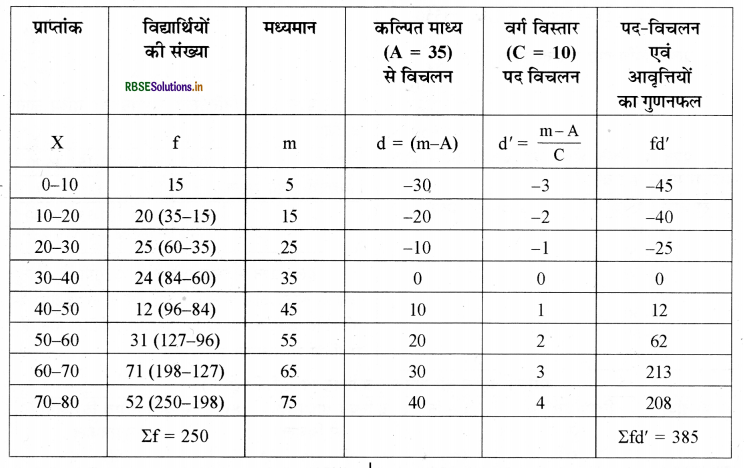
सूत्र: 
\(\begin{aligned} &\bar{X}=A+\frac{\Sigma f^{\prime}}{\Sigma f} \times C \\ &\bar{X}=35+\frac{385}{250} \times 10 \end{aligned}\)
\(=35+\frac{3850}{250}\)

= 35 + 15.4
= 50 .4

प्रश्न 7. 
अग्रलिखित समंकों से पद-विचलन रीति द्वारा समान्तर माध्य ज्ञात कीजिए:

वर्ग	0 - 4	5 - 9	10 - 14	15 - 19	20 - 24	25 - 29	30 - 34
आवृत्ति	2	4	6	10	7	6	3

उत्तर:
प्रश्न में समावेशी श्रेणी दी गई है। अतः समान्तर माध्य की गणना से पूर्व इसे अपवर्जी श्रेणी में परिवर्तित किया जायेगा।

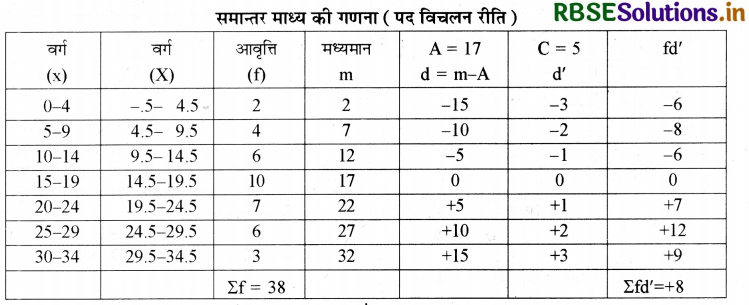
\(\begin{aligned} \overline{\mathrm{X}} &=\mathrm{A}+\frac{\Sigma \mathrm{fd}^{\prime}}{\Sigma \mathrm{f}} \times \mathrm{C} \\ &=17+\frac{8}{38} \times 5 \\ &=17+\frac{40}{38} \\ &=17+1.05 \end{aligned}\)
\(\overline{\mathrm{X}}\) = 18.05

प्रश्न 8.
निम्न आवृत्ति वितरण से मध्यिका ज्ञात कीजिए:

वर्ग	10 - 15	15 - 20	20 - 25	25 - 30
आवृत्ति	3	7	16	12
	30 - 35	35 - 40	40 - 45
	9	5	3

उत्तर:

वर्ग (x)	आवृत्ति ( f)	संचयी  आवृत्ति ( c.f)
10 - 15	3	3
15 - 20	7	10
20 - 25	16	26 (c.f)
(L) 25 - 30	12 (f)	38
30 - 35	9	47
35 - 40	5	52
40 - 45	3	55
	N = 55

m = Size of (N/2)th item
= Size of (55/2)th item = 27.5 th item
वाँ मध्यिका पद ऊपर से 38 c.f. में है। अतः उसके सामने वाला वर्ग 25 - 30 मध्यिका वर्ग है। वर्ग अन्तराल h = 5 है।

मध्यिका \(\begin{aligned} (\mathrm{M}) &=\mathrm{L}+\frac{\left(\frac{\mathrm{N}}{2}-\mathrm{c} . f\right)}{\mathrm{f}} \times \mathrm{h} \\ &=25+\frac{27.5-26}{12} \times 5 \end{aligned}\)
M = 25 + 0.625 = 25.625

प्रश्न 9.
निम्नलिखित श्रेणी से मध्यिका ज्ञात कीजिए:

आकार (Size)	1	2	3	4	5
आवृत्ति (Frequency)	2	7	17	29	38
	6	7	8	9	10
	41	40	30	17	6

उत्तर:

आकार (Size)	आवृत्ति (Frequency)	संचयी  आवृत्ति ( c.f)
1	2	2
2	7	9
3	17	26 (c.f)
4	29	55
5	38	93
6	41	134
7	40	174
8	30	204
9	17	221
10	6	227
	N = 227

 
m = Size of  \(\left(\frac{\mathrm{N}+1}{2}\right)^{\text {th }}\) item
= Size of \(\left(\frac{227+1}{2}\right)^{\text {th }}\) item
m = Size of 114th item
मध्यिका संख्या 114 ऊपर से C.F. 134 में है, अतः उसके सामने वाला मूल्य 6 मध्यिका मूल्य होगा। अतः M = 6 होगा।

प्रश्न 10. 
निम्नलिखित समंकों से मध्यिका ज्ञात कीजिए:

आयु वर्षों में	कमचारियां की सख्या
25 से कम	8
30 से कम	23
35 से कम	51
40 से कम	81
45 से कम	103
50 से कम	113
55 से कम	117
60 से कम	120

उत्तर:
इस प्रश्न में संचयी आवृत्ति दी गई है, अतः इसे सरल आवृत्ति में बदलना पड़ेगा।

आयु वर्षों में	कमचारियां की सख्या	संच्यी आवृत्ति (c.f.)
20 - 25	8	8
25 - 30	15	23
35 - 40	28	51 (c.f)
40  - 45	30(f)	81
45 - 50	22	103
50  - 55	10	113
55  - 60	4	117
60 - 65	3	120
	N = 120

M = Size of (N/2)th item

= Size of (120)th item
= Size of 60th item
यह संचयी आवृत्ति 81 में आ रहा है जिसके सामने मध्यिका वर्ग 35 - 40 है तथा यहाँ पर वर्ग अन्तराल h = 5 है। अब मध्यिका का मूल्य निम्न सूत्र द्वारा जात किया जायेगा:

\(\begin{aligned} (\mathrm{M}) &=\mathrm{L}+\frac{\left(\frac{\mathrm{N}}{2}-\mathrm{c.f}\right)}{\mathrm{f}} \times \mathrm{h} \\ &=35+\frac{60-51}{30} \times 5 \\ &=35+\frac{9}{30} \times 5 \\ &=35+\frac{45}{30}=35+1.5=36.5 \end{aligned}\)

अतः M = 65

प्रश्न 11.
निम्नांकित तालिका के आधार पर मध्यिका की गणना कीजिए:

पद मूल्य X	11 - 15	16 - 20	21 - 25	26 - 30
आवृत्ति (F)	7	10	13	26
	31 - 35	36 - 40	41 - 45	46 - 50
	35	22	11	5

उत्तर:
मध्धियका ज्ञात करने हेतु सर्वप्रथम श्रेणी को अपवर्जी विधि में बदलना आवश्यक है।

पद मूल्य (x)	आवृत्ति ( f)	संचयी  आवृत्ति ( c.f)
10.5 – 15.5	7	7
15.5 – 20.5	10	17
20.5 – 25.5	13	30
(L) 25.5 – 30.5	26	56(c.f)
30.5 – 35.5	35(f)	91
35.5 – 40.5	22	113
40.5 – 45.5	11	124
45.5 – 50.5	5	129
	N = 129

M = Size of (N/2)th item

= Size of (129/2)th item
= Size of 64.5th item

64.5 वाँ मध्यिका पद ऊपर से c.f. 91 में है। अतः उसके सामने वाला वर्ग 30.5 - 35.5 मध्यिका वर्ग होगा। वर्ग अन्तराल h(5) है।
अतः मध्यिका का मूल्य निम्न सूत्र द्वारा ज्ञात किया जाएगा:
\(\begin{aligned} (\mathrm{M}) &=\mathrm{L}+\frac{\left(\frac{\mathrm{N}}{2}-\text { c.f. }\right)}{\mathrm{f}} \times \mathrm{h} \\ &=30.5+\frac{64.5-56}{35} \times 5 \\ &=30.5+\frac{8.5}{35} \times 5 \\ &=30.5+\frac{42.5}{35} \\ &=30.5+1.21 \end{aligned}\)
M = 31.71
नोट : प्रश्न में समावेशी श्रेणी दी गई है। अतः उसे अपवर्जी श्रेणी में परिवर्तित करने के बाद ही मध्यिका ज्ञात किया जायेगा। प्रत्येक वर्ग की ऊपरी सीमा व उससे अंगले वर्ग की निचली सीमा का अन्तर 1 है। इस अन्तर का आधा करके (.5) उसे प्रत्येक वर्ग की निचली सीमा में से घटाने पर तथा ऊपरी सीमा में जोड़ने पर अपवर्जी श्रेणी तैयार हो जाती है।

प्रश्न 12.
निम्नांकित समंकों से मध्यिका ज्ञात कीजिए:

आकार	0 – 2.5	2.5 - 5	5 - 10	10 - 15
आवृत्ति (f)	6	8	7	9
	15 - 20	20 - 30	30 - 40	40 - 50
	26	28	14	12

उत्तर:
प्रश्न में असमान वर्गान्तर है, अतः सर्वप्रथम वर्गान्तरों को समान बनाया जायेगा तथा उसके पश्चात् ही मध्यिका की गणना की जायेगी। प्रश्न में सर्वाधिक वर्गान्तर 10 का है। अतः सभी वर्गों का अन्तर 10 रखा जायेगा।

आकार	आवृत्ति (f)	आवृत्ति (C.f)
0 – 10	21(6+ 8+7)	21(C.F)
10 – 20	35(9+ 26) (f)	56
20 – 30	28	84
30 – 40	14	98
40 -50	12	110
	N = 110

मध्यिका पद 55 ऊपर से 56 में है अतः उसके सामने वाला वर्ग 10 - 20 मध्यिका वर्ग होगा। वर्ग अन्तराल (h) 10 है।
अब निम्न सूत्र की सहायता से मध्यिका का मूल्य ज्ञात किया जाएगा: 
मध्यिका \((M)=L+\frac{\left(\frac{N}{2}-c . f\right)}{f} \times h\)
\(\begin{aligned} &=10+\frac{55-21}{35} \times 10 \\ &=10+\frac{34}{35} \times 10 \\ &=10+\frac{340}{35} \\ &=10+9.71 \end{aligned}\)
M = 19.71

प्रश्न 13.
निम्न सारणी में प्रस्तुत समंकों से बहुलक की गणना कीजिए:

जूतों का आकार	0	1	2	3
बेचे गये जूतों की संख्या	4	5	7	6
	4	5	6	7
	8	7	8	5

उत्तर:
प्रश्न में अधिकतम आवृत्ति 8 दो मूल्यों 4 व 6 की है तथा आवृत्तियाँ अनियमित हैं। अतः समूहीकरण द्वारा बहुलक मूल्य का निर्धारण किया जायेगा।

उपर्युक्त तालिका से यह स्पष्ट है कि मूल्य 4 की आवृत्ति सबसे अधिक 5 बार प्राप्त हुई है। अतः बहुलक मल्य 4 होगा।

प्रश्न 14.
निम्नलिखित आवृत्ति सारणी से बहलक ज्ञात कीजिए:

मासिक किराया	परिवार की संख्या
20 – 40	6
40 – 60	9
60 – 80	11
80 – 100	14
100 – 120	20
120 – 140	15
140 – 160	10
160 – 180	8
180 - 200	7

उत्तर:
श्रेणी में नियमित आवृत्ति बंटन है इसलिए निरीक्षण विधि द्वारा बहुलक की गणना की जा सकती है।
निरीक्षण से यह स्पष्ट है कि सबसे अधिक आवृत्ति 20 वर्ग 100 - 120 की है। अतः बहुलक वर्ग 100 - 120 होगा।
अतः L₁ = 100 ; i = 20 ; f₁ = 20 ; f₀ = 14,
f₂ = 15
\(\begin{aligned} \mathbf{M}_0 &=\mathrm{L}_1+\frac{\mathrm{f}_1-\mathrm{f}_0}{2 \mathrm{f}_1-\mathrm{f}_0-\mathrm{f}_2} \times i \\ &=100+\frac{20-14}{2 \times 20-14-15} \times 20 \end{aligned}\)
\(\begin{aligned} &=100+\frac{6 \times 20}{40-29} \\ &=100+\frac{120}{11} \end{aligned}\)
= 100 + 10.9
M₀ = 110.9 

संके ताक्षर:
L₁ =  बहुलक वर्ग की निचली सीमा
f₁ = बहुलक वर्ग की आवृत्ति
f₀ = बहुलक वर्ग के तुरन्त पूर्व
वाले वर्ग की आवृत्ति
f₂ = बहुलक वर्ग के तुरन्त बाद
वाले वर्ग की आवृत्ति
i =  बहुलक वर्ग का वर्ग विस्तार
M₀ =  बहुलक मूल्य।

प्रश्न 15.
निम्न श्रेणी से बहुलक ज्ञात कीजिए:

वर्गान्तर	आवृत्ति
5 – 10	10
10 – 15	12
15 – 20	16
20 – 25	14
25 – 30	10
30 – 35	8
35 – 40	17
40 – 45	5
45 - 50	4

उत्तर:
श्रेणी में आवृत्तियाँ अनियमित होने के कारण बहुलक वर्ग जानने हेतु समूहन रीति का प्रयोग किया जायेगा।

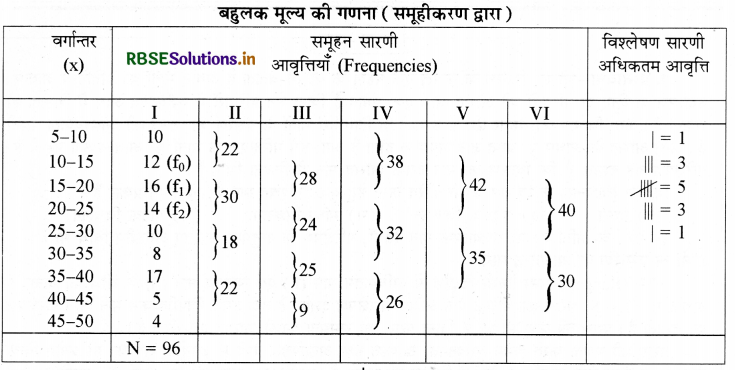
उपर्युक्त तालिका से स्पष्ट है कि वर्ग 15 - 20 की आवृत्ति सबसे अधिक 5 बार आई है, अतः बहुलक वर्ग 15 - 20 होगा।
\(\begin{aligned} \mathrm{M}_0 &=\mathrm{L}_1+\frac{\mathrm{f}_1-\mathrm{f}_0}{2 \mathrm{f}_1-\mathrm{f}_0-\mathrm{f}_2} \times i \\ &=15+\frac{16-12}{2 \times 16-12-14} \times 5 \\ &=15+\frac{4 \times 5}{32-26} \\ &=15+\frac{20}{6} \end{aligned}\)
= 15  + 3.33
M₀ =  18.33

प्रश्न 16.
निम्न समंकों से बहुलक ज्ञात कीजिए:

वर्ग	2	3	4	5-7
आवृत्ति	1	2	2	3
	7 - 10	10 - 15	15 - 20	20 - 25
	5	10	8	4

उत्तर:
प्रश्न में असमान वर्ग विस्तार है, अतः समान वर्ग विस्तार बनाकर प्रश्न को हल किया जायेगा।

वर्ग	आवृत्ति
0 - 5	5(1+2+2)
5 – 10	8(3+5)(f0)
10 – 15	10(f1)
15 – 20	8(f2)
20 – 25	4

निरीक्षण द्वारा यह स्पष्ट है कि सबसे अधिक आवृत्ति 10 वर्ग 10 - 15 की है तथा उसके आस-पास भी आवृत्तियों का जमाव अधिक है। अतः बहुलक वर्ग 10 - 15 होगा।
\(\mathbf{M}_0=\mathrm{L}_1+\frac{\mathrm{f}_1-\mathrm{f}_0}{2 \mathrm{f}_1-\mathrm{f}_0-\mathrm{f}_2} \times i\)
\(\begin{aligned} &=10+\frac{10-8}{2 \times 10-8-8} \times 5 \\ &=10+\frac{2 \times 5}{20-16} \\ &=10+\frac{10}{4} \end{aligned}\)
= 10 + 2.5
M_{0 = 12.5}