RBSE Solutions for Class 12 Maths Chapter 9 Differential Equations Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 9 Differential Equations Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 9 Differential Equations Miscellaneous Exercise

Question 1.
For each of the differential equations given below, indicate its order and degree (if defined):
(i) \(\frac{d^2 y}{d x^2}+5 x\left(\frac{d y}{d x}\right)^2\) - 6y = log x
Answer:
The order of differential equation is 2 and degree is 1, because highest differential coefficient is \(\frac{d^2 y}{d x^2}\) whose degree is 1

(ii) \(\left(\frac{d y}{d x}\right)^3-4\left(\frac{d y}{d x}\right)^2\) + 7y = sin x
Answer:
The order of differential equation is 1 and degree is 3, because highest differential coefficient is \(\frac{d y}{d x}\) whose degree is 3.

(iii) \(\frac{d^4 y}{d x^4}-\sin \left(\frac{d^3 y}{d x^3}\right)\) = 0
Answer:
The order of differential equation is 4, because highest differential coefficient is \(\frac{d^4 y}{d x^4}\) but its degree is not defined.

Question 2.
For each of the exercises given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
(i) y = ae^x + be^-x + x²: x\(\frac{d^2 y}{d x^2}\) + 2\(\frac{d y}{d x}\) - 2xy + x² - 2 = 0
Answer:

= x(ae^x + be^{- x} + 2) + 2(ae^x - be^{- x} + 2x) - 2x(ae^x + be^{- x} + x²) + x² - 2
= axe^x + bx.e^{- x} + 2x + 2ae^x - 2be^{- x} + 4x - 2axe^x - 2bxe^{- x} - 2x³ + x² - 2
= 2(ae^x - be^{- x}) + 6x - 2x³ + x² - 2 - axe^x - bxe^{- x} ≠ 0
Hence, y = ae^x + be^-x + x² is not solution of differential equation, x\(\frac{d^2 y}{d x^2}\) + 2\(\frac{d y}{d x}\) - 2xy + x² - 2 = 0

(ii) y = e^x(a cos x + b sin x): \(\frac{d^2 y}{d x^2}\) - 2\(\frac{d y}{d x}\) + 2y = 0
Answer:
y = e^x(a cos x + b sin x): \(\frac{d^2 y}{d x^2}\) - 2\(\frac{d y}{d x}\) + 2y = 0
Differentiating, y = e^x (a cos x + b sin x) w.r.t. "x", we get
\(\frac{d y}{d x}\) = e^x (a cos x + b sin x) + e^x (- a sin x+ b cos x)
and \(\frac{d^2 y}{d x^2}\) = e^x (a cos x + b sin x) + e^x (- a sin x + b cos x) + e^x (- a sin x + b cos x) + e^x (- a cos x - b sin x)
= e^x (a cos x + b sin x) - e^x (a cos x + b sin x) + 2e^x (- a sin x + b cos x)
= 2e^x (- a sin x + b cos x)
Now \(\frac{d^2 y}{d x^2}\)-2 \(\frac{d y}{d x}\)+2 y
= 2e^x (- a sin x + b cos x) - 2[e^x (a cos x + b sin x) + e^x(- a sin x + b cos x)] + 2e^x (a cos x + b sin x)
= 2e^x [- a sin x + b cos x - a cos x - b sin x + a sin x - b cos x + a cos x + b sin x]
= 2e^x (0) = 0
Hence, y = e^x (a cos x + b sin x) is the solution of differential equation \(\frac{d^2 y}{d x^2}\) - 2\(\frac{d y}{d x}\) + 2y = 0

(iii) y = x sin 3x: \(\frac{d^2 y}{d x^2}\) + 9y - 6 cos 3x = 0
Answer:
y = x sin 3x: \(\frac{d^2 y}{d x^2}\) + 9y - 6 cos 3x = 0
Differentiating y = x sin 3x, w.r.t. "x", we get

= 6 cos 3x - 9x sin 3x + 9x sin 3x - 6 cos 3x
= 0
Hence, y = x sin 3x is the solution of differential equation \(\frac{d^2 y}{d x^2}\) + 9y - 6 cos 3x = 0

(iv) x² = 2y² log y: (x² + y²)\(\frac{d y}{d x}\) - xy = 0
Answer:
x² = 2y² log y: (x² + y²)\(\frac{d y}{d x}\) - xy = 0
Differentiating x² = 2y² log y, w.r.t. "x", we get

= 0 = R.H.S (∵ x² = 2y² log y)
Hence, equation x² = 2y² log y is the solution of the differential equation (x² + y²) \(\frac{d y}{d x}\) - xy = 0

Question 3.
Form the differential equation re1presenting the family of curves given by(x - a)² + 2y² = a², where a is an arbitrary constant.
Answer:
Given equation is
(x - a)² + 2y² = a²
or x² - 2ax + a² + 2y² = a²
or x² - 2ax + 2y² = 0 ..... (1)
Differentiating equation (1) w.r.t. “x, we get

This is the required differential equation.

Question 4.
Prove that x² - y² = C(x² + y²)² is the general solution of differential equation
(x³ - 3xy²) dx = (y³ - 3x²y) dy,
where C is a parameter.
Answer:
Given equation is
x² - y² = c(x² + y²)² ......... (1)
and given differential equation is
(x³ - 3xy²) dx = (y³ - 3x²y) dy ...... (2)
From differential equation (2), we get

Clearly, differential equation (2) is homogeneous.
Thus, putting y = vx in equation(3), we get
\(\frac{d y}{d x}\) = v + x \(\frac{d v}{d x}\) ........ (4)
From equations (3) and (4), we get


or \(\sqrt{x^2-y^2}\) = C1 (x² + y²) (∵ x ≠ 0)
or (x² - y²) = C₁² (x² + y²)²
Hence (x² - y²) = C(x² + y²)² (C₁² = C)
is the required solution of given differential equation.
Hence Proved.

Question 5.
Form the differential equation of the family of circles in the first quadrant which touch the coordinate axes.
Answer:
The equation of the family of circles which touch the coordinate axes in the first quadrant is,
(x - a)² + (y - a)² = r² ...... (1)
Differentiate w.r.t.”x”, we get


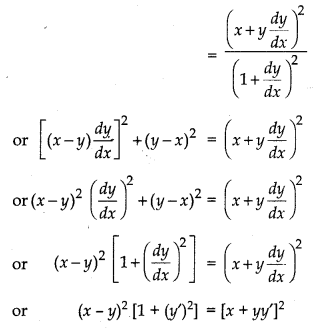
which is the required differential equation.

Question 6.
Find the general solution of the differential equation \(\frac{d y}{d x}+\sqrt{\frac{1-y^2}{1-x^2}}\) = 0
Answer:
Given differential equation is

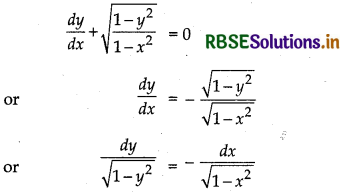
Integrating both sides, we get
∫\(\frac{d y}{\sqrt{1-y^2}}\) = ∫\(\frac{d x}{\sqrt{1-x^2}}\)
or sin^-1 = - sin^-1 x + C
or sin^-1 y + sin^-1 x = C
which is the required solution.
Hence proved.

Question 7.
Show that the general solution of the differential equation.
\(\frac{d y}{d x}+\frac{y^2+y+1}{x^2+x+1}\) = 0
is given by (x + y + 1) = A(1 - x - y - 2xy), where A is parameter.
Answer:
Given differential equation is

or x + y + 1 = A(1 - x - y - 2xy)
which is the required solution of the given differential equation.
Hence Proved.

Question 8.
Find the equation of the curve passing through the point (o, \(\frac{\pi}{4}\)) whose differential equation is
sin x cos y dx + cos x sin y dy = 0
Answer:
Given differential equation is
sin x cos y dx + cos x sin y dy = 0
or \(\frac{\sin x}{\cos x}\) dx + \(\frac{\sin y}{\cos y}\) = 0
or tan x dx + tan y dy = 0
Integrating both sides, we get
∫tan x dx + ∫tan y dy = 0
or log sec x + log sec y = logC
or log (sec x sec y) = log C
or sec x.sec y = C
curve passes through (0, π/4), putting x = 0, y = π/4 in equation (1),

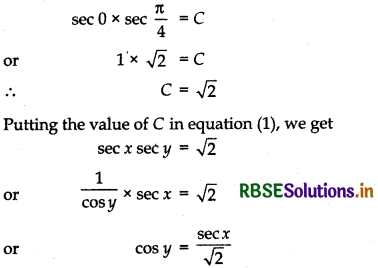
which is the required equation of the curve.

Question 9.
Find the particular solution of the differential equation (1 + e^2x) dy + (1 + y²) e^x dx = 0 given that y = 1, when x = 0.
Answer:
Given differential equation is
(1 + e^2x)dy + (1 + y²)e^x dx = 0

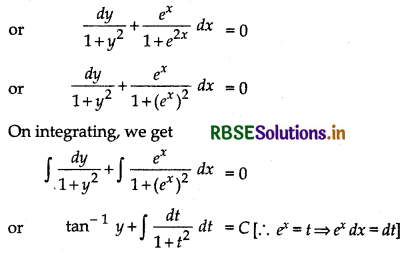
or tan^-1 y + tan^-1 t = C
or tan^-1 y + tan^-1 (e^x) = C ....... (1)
Putting x = 0 and y = 1 in equation (1), we get
tan^-1 1 + tan^-1 e⁰ = C
or tan^-1 1 + tan^-1 1 = C
or \(\frac{\pi}{4}+\frac{\pi}{4}\) = C
or C = \(\frac{\pi}{2}\)
Putting the value of C in equation (1),
tan^-1 y + tan^-1 (e^x) = \(\frac{\pi}{2}\)
which is the particular solution of the given differential equation.

Question 10.
Solve the differential equation
ye^x/y dx = (xe^x/y + y²)dy (y ≠ 0)
Answer:
Given differential equation is
ye^x/y dx = (xe^x/y + y²)dy

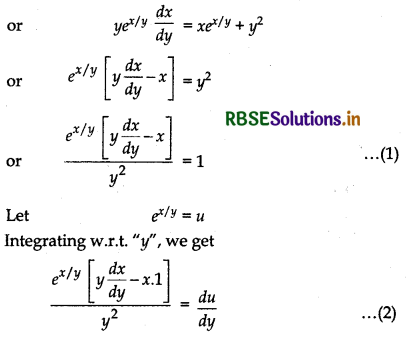
From equation (1) and (2)
\(\frac{d u}{d y}\) = 1
or du = dy
On integrating
∫du = ∫dy + C
or u = y + C
or e^x/y = y + C
which is the required solution.

Question 11.
Find a particular solution of the differential equation (x - y) (dx + dy) = dx - dy given that y = - 1, when x = 0.
Answer:
Given differential equation is
(x - y) (dx + dy) = dx - dy


or 2x = (x - y) + log(x - y) + 2C₁
or log(x - y) = 2x - x + y - 2C₁
or log(x - y) = x + y + C ...... (3)
(∵ C = - 2C₁₎(∵ C = - 2C₁)
Putting x = 0 and y = - 1 in equation (3), we get
log[0 - (- 1)] = 0 - 1 + C
or log 1 = - 1 + C
or 0 = - 1 + C
or c = 1
Putting the value of C in equation (3), we get
log(x - y) = x + y + 1
which is the particular solution.

Question 12.
Solve the differential equation
\(\left[\frac{e^{-2 \sqrt{x}}}{\sqrt{x}}-\frac{y}{\sqrt{x}}\right]\) \(\frac{d x}{d y}\) = 1(x ≠ 0)
Answer:
Given differential equation is

Question 13.
Find a particular solution of the differential equation \(\frac{d y}{d x}\) + y cot x = 4x cosec x(x ≠ 0), given that y = 0 when x = π/2.
Answer:
Given differential equation is
\(\frac{d y}{d x}\) + (cot x)y = 4x cosec x ....... (1)
Comparing equation (1) with \(\frac{d y}{d x}\) + Py = Q, we get
P = cot x. Q = 4x cosec x
∴ IF = e^{∫ cot x dx}
= e^{log sin x} = sin x
∴ I.F. = sin x
On multiplying equation (1) by sin x, we get
sin x \(\frac{d y}{d x}\) + sin x (cot x)y = 4x sin x × cosec x

which is the required particular solution.

Question 14.
Find a particular solution of the differential equation (x + 1)\(\frac{d y}{d x}\) = 2e^-y - 1, given that y = 0 when x = 0.
Answer:
Given differential equation is

or - log(2 - e^y) = log(x + 1) + C₁
or log(x + 1) + log(2 - e^y) = - C₁
or log (x + 1) (2 - e^y) = log C (- C₁ = log C)
or (x + 1) (2 - e^y) = C ......... (1)
Putting x = 0 and y = 0 in equation (1), we get
(0 + 1) (2 - e⁰) = C
or (2 - 1) = C
or C = 1
Putting the value of C in equation (1), we get
(x + 1) (2 - e^y) = 1

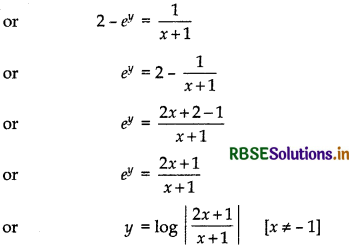
which is the required particular solution.

Question 15.
The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 20,000 in 1999 and 25,000 in the year 2004, what will be the population of the village in 2009?
Answer:
Let population of the village is y at any time t..
Then, according to question

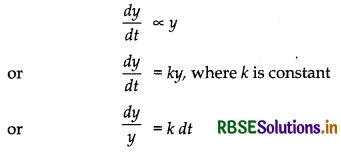
Integrating both sides, we get
∫\(\frac{d y}{y}\) = k∫dt
or log y = kt + C ..... (1)
Let in 1999, t = 0,
Then population = 20,000
Putting t = 0 and y = 20,000 in equation (1)
log 20,000 = k × 0 + C
or C = log 20,000
Putting the value of C in equation (1), we get
log y = kt + log 20,000 ...... (2)
In 2004, t = 5 and y = 25,000 [1999 to 2004 = 5 Years]
Putting t = 5 and y = 25,000
log 25,000 = k × 5 + log 20,000
or 5k = log 25,000 - log 20,000

= 25 × 1,250 = 31,250
Hence, population will be 31, 250 in 2009.

Question 16.
The general solution of the differential equation \(\frac{y d x-x d y}{y}\) = 0
(A) xy = C
(B) x = Cy²
(C) y = Cx
(D) y = Cx²
Answer:
Given differential equation is
\(\frac{y d x-x d y}{y}\) = 0
or y dx - x dy = 0
or \(\frac{d x}{x}-\frac{d y}{y}\) = 0
On integrating we get
\(\int \frac{d x}{x}-\int \frac{d y}{y}\) = log C₁
or log x - log y = log C₁
or log\(\frac{x}{y}\) = log C₁
or \(\frac{x}{y}\) = C₁
or y = \(\frac{x}{C_1}\) = Cx (∵ C = \(\frac{1}{C_1}\))
or y = Cx
Hence, option (C) is correct.

Question 17.
The general solution of a differential equation of the type \(\frac{d x}{d y}\) + P₁x = Q₁ is:
(A) ye^{∫P₁ dy} = ∫(Q₁ e^{∫ P₁ dy}) dy + C
(B) ye^{∫P₁ dx} = ∫(Q₁ e^{∫ P₁ dx}) dx + C
(C) ye^{∫P₁ dy} = ∫(Q₁ e^{∫ P₁ dy}) dy + C
(D) ye^{∫P₁ dx} = ∫(Q₁ e^{∫ P₁ dy}) dx + C
Answer:
Given differential equation is
\(\frac{d x}{d y}\) + P₁x = Q₁
where P₁ and Q₁ either constant or function of y.
∴ I.F. = e^{∫P₁ dy}
Thus, required solution is
xe^{∫P₁ dy} = ∫(Q₁ × e^{∫P₁ dy})dy + C
Hence, option (C) is correct.

Question 18.
The general solution of the differential equation e^x dy + (ye^x 2x) dx = 0 is
(A) xe^x + x² = C
(B) xe^y + y² = C
(C) ye^x + x² = C
(D) ye^x + x² = C
Answer:
Given differential equation is:
e^x dy + (ye^x + 2x)dx = 0