RBSE Class 12 Maths Notes Chapter 9 Differential Equations

These comprehensive RBSE Class 12 Maths Notes Chapter 9 Differential Equations will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 9 Notes Differential Equations

Introduction:
We know that any function defined in any domain is differentiable. We write differential of f as f'(x) or \(\frac{d f(x)}{d x}\) for every x of the domain. Similarly, we have read methods of integration which are used in mathematics to integrate the functions. If differential of any function / is g, then function/can be find out.
i.e., \(\frac{d f(x)}{d x}\) = g(x)
or \(\frac{d y}{d x}\) = g(x) [∵ y = f(x)]
The above equation represents a differential equation.

Differential equation plays a very important role in the solution of many problems of Physics, Chemistry, Biology and Economics. In this chapter we will study some basic concepts related to differential equation, general and particular solutions of a differential equation, formation of differential equations, some methods to solve a first order- first degree differential equation and some applications of differential equations in different areas.

 

Basic Concepts:
Let us consider the equations
x + y = 8 ...(1)
x² - 5x + 4 = 0 ...(2)
sin x - cos x = 0 ...(3)
and x² \(\frac{d y}{d x}\) + 2y = 0 ...(4)

We see that equation (1) involves one independent variable and one dependent variable. Equation (2) involves one independent variable. Equation (3) also involves one independent variable x. But equation (4) involves variables as well as derivative of the dependent variable y with respect to the independent variable x. Such an equation (4) is called a differential equation.

Differential Equations
Definition of Differential Equation
A differential equation is an equation which involves independent variable, dependent variable and derivatives of dependent variable with respect to independent variable, is called a differential equation.

For example:
\(\frac{d y}{d x}\) = \(\frac{x}{x+y}\), x² \(\frac{d^{2} y}{d x^{2}}\) + x\( \frac{d y}{d x}\) + x y = 0
y dx + x dy = 0 etc. are differential equations.

Order of a Differential Equation
The order of the highest order derivative of dependent variable with respect to independent variable involved in the differential equation is called the order of the differential equation.

For example:

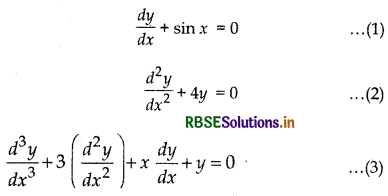
The equations (1), (2), (3) involves the highest derivative of first, second and third order respectively. Therefore, the order of these equations are 1, 2 and 3 respectively.

Remark:
Order of a differential equation is always positive integers.

Degree of a Differential Equation
The degree of a differential equation is the degree of the highest order derivative, when differential coefficients are made free from radicals and fractions.
In other words, the degree of a differential equation is the power of the highest order derivative occurring in a differential equation when it is written as a polynomial in differential coefficients.

For Example:
Degree of the differential equation
\(\frac{d^{3} y}{d x^{3}}+3\left(\frac{d^{2} y}{d x^{2}}\right)+x \frac{d y}{d x}\) + y = 0
is 1, because power of highest order derivative is 1.

Degree of the differential equation
\(\left(\frac{d^{2} y}{d x^{2}}\right)^{2}\) + x\(\left(\frac{d y}{d x}\right)^{3}\) + y³ = 0 is 2, because highest order derivative is \(\frac{d^{2} y}{d x^{2}}\) and its power is 2.
Degree of the differential equation \(\frac{d y}{d x}\) + cos \(\left(\frac{d y}{d x}\right)\) = 0
is not defined because, this differential equation cannot be expressed as a polynomial in differential coefficients. Write the differential equation

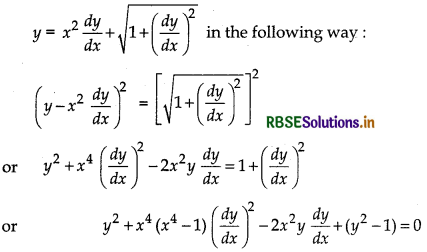
Here, the highest order derivative is \(\frac{d y}{d x}\) and its power is 2. So, degree of the differential equation is 2.

Remark:
Degree of a differential equation (if defined) is always positive integer.

General and Particular Solutions of a Differential Equation:
The solution of a differential equation is a relation between the variables involved, which satisfies the differential equation. Such a relation and the derivatives obtained when substituted in the differential equation, makes L.H.S. and R.H.S. identically equal.

For example:
Solution of the differential equation dy
\(\frac{d y}{d x}\) = cos x is y = sin x
and solution of the differential equation
\(\frac{d y}{d x}\) = y is y = e^x

Now, differentiating y = sin x w.r.t., we get
\(\frac{d y}{d x}\) = cos x

When we put \(\frac{d y}{d x}\) = cos x in L.H.S. of equation (1) then it is equal to R.H.S.
Similarly, differentiating y = e^x w.r.t. 'x', we get
\(\frac{d y}{d x}\) = e^x = y
When we put \(\frac{d y}{d x}\) = e^x = y in L.H.S. of equation (2) then it is equal to R.H.S.

General solution :
The solution which contains many arbitrary constants of the differential equation is said to be the general solution (primitive) of the differential equation.
For example : \(\frac{d^{2} y}{d x^{2}}\) + y = 0 ...(1)
and equation y = a sin x + b cos x where a and b are arbitrary constants. ...(2)

Differentiating equation (2) w.r.t. ‘x’, we get
\(\frac{d y}{d x}\) = a cos x + b(- sin x)
or \(\frac{d y}{d x}\) = a cos x - b sin x ...........(3)

Again, differentiating equation (3) w.r.t ‘x!, we get
\(\frac{d^{2} y}{d x^{2}}\) = - a sin x - b cos x dx
= - (a sin x + b cos x)
= - y [From equation (2)]
∵ \(\frac{d^{2} y}{d x^{2}}\) + y = 0 [which is differential equation (1)]
Hence, equation y = a sin x + b cos x is general solution of equation (1), because order of the differential equation is 2 and number of arbitrary constant is also 2 [Two arbitrary constant a and b].

Particular Solution :
The solution of a differential equation which is free from arbitrary constant is called particular solution, i.e., the solution obtained from the general solution by giving particular values to the arbitrary constant is called a particular solution of the differential arbitrary constant a and b then the equation y = 4 cos x + 5 equation.

For example:
General solution of differential equation \(\frac{d^{2} y}{d x^{2}}\) + y = 0 is y = a cos x + b sin x. If we give the value 4 and 5 to the \(\frac{d^{2} y}{d x^{2}}\) + y = 0 Similarly, we can get different particular solution for different values of a and b

Formation of a Differential Equation whose Solution is given
Let y = Ae^tan-1x is a equation of family of curves with one arbitrary constant A. We can get different equation of the curves by putting different values of A.
Now, differentiating w.r.t. 'x', we get

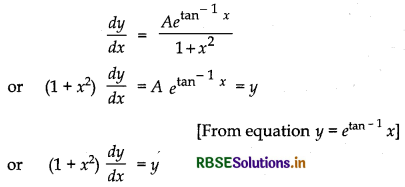
Thus, by eliminating one arbitrary constant A, a differential equation of first order and first degree is obtained. In other words, we can say, one parameter family of curves is represented by a first order and first degree differential equation.
Now, consider a two parameter family of curves given by
y = a cos 3x + b sin 3x ...(1)
where a and b are arbitrary constants.

Differentiating equation (1) w.r.t. x, we get dy
\(\frac{d y}{d x}\) = - 3a sin 3x + 3b cos 3x ...(2)
Again, differentiating equation (2) w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = -9a cos 3x - 9b sin 3x dx
= - 9 (a cos 3x + b sin 3x)
= -9y
[Eliminating constants a and b from equation (1)]
or \(\frac{d^{2} y}{d x^{2}}\) + 9y = 0
Here, we see that by eliminating two arbitrary constants, a differential equation of second order is obtained. In other words, we can say a two parameter family of curves is represented by a second order differential equation.

Similarly, by eliminating three arbitrary constants a differential equation of third order is obtained. In other words, we can say a three parameter family of curves is represented by a third order differential equation.

Thus, from the above examples it can be concluded that if an equation involves n arbitrary constants, a differential equation of nth order can be obtained by eliminating n arbitrary constants. In other words we can say a n parameter family of curves is represented by an nth order of differential equation.

Formulating a differential equation from a given equation representing a family of curves means finding a differential equation whose solution is given equation. Differentiating the given equation with respect to independent variable x as many times of the number of arbitrary constant.

Now, eliminate the arbitrary constants from given equation and the equations obtained by differentiation. The equation so obtained is the differential equation of order x for the family of given curves.

Procedure to Form a Differential Equation that will Represent a Given Family of Curves
To form a differential equation we follow the following steps:

• Step 1. Write the given equation involving independent variable (x), dependent variable (y) and arbitrary constants.
• Step 2. Obtain the number of arbitrary constants.
• Step 3. Differentiate the given equation as many times as the number of arbitrary constants.
• Step 4. Eliminate the arbitrary constants from equation getting from step 3 and equation getting from step 1.

Methods of Solving First Order and First Degree Differential Equations
In this section we shall discuss methods of solving differential equations.

Differential Equations with Variable Separable.
A first order and first degree differential equation is of the form
\(\frac{d y}{d x}\) = F(x, y)

If F(x, y) can be expressed as a product of h(x) and g(y) i.e., if
F(x, y) = h(x) x g(y) then
\(\frac{d y}{d x}\) = h(x) x g(y) ...(2)
or \(\frac{d y}{g(y)}\) = h(x) dx

Integrating both sides of equation (3), we get
∫\(\frac{1}{g(y)}\)dy = ∫h(x)dx
So, (4) provides the Solutions of given differential; equation in the form
or G(y) = H(x) + C ...(4)
Here, G(y) and H(x) are the anti derivatives of \(\frac{1}{g(y)}\) and h(x) respectively and C is the arbitrary constant.

Homogeneous Differential Equations
Any function f(x, y) is said to be homogeneous function of power n, if f(λx, λy) = λⁿ f(x, y), where X is a non-zero constant.

For example,
For f(x, y) = x³ + y³ + x²y + xy²
f(λx, λy) = (λx)³ + {λy)³ + (λx)²(λy) + (λx)(λy)²
= λ³x³ + λ³y³ + λ³x²y + λ³xy²
= λ³ (x³ + y³ + x²y + xy²)
= λ³f(x,y)
Hence, function f(x, y) is a homogeneous function of degree 3.

Similarly, F(x,y) = 3x + 4y
And H(x, y) = tan \(\left(\frac{x}{y}\right)\)
For F(λx, λy) = 3λx + 4(λy)
= λ(3x + 4y) = λ ≠ F(x, y)

Hence, F(x, y) is a homogeneous function of degree 1.
And H(λx, λy) = tan\(\left(\frac{\lambda x}{\lambda y}\right)\) = tan \(\left(\frac{x}{y}\right)\)
= λ° tan\(\left(\frac{x}{y}\right)\) (∵ λ° = 1)
Hence, H(x, y) is a homogenerous function of degree 0.

Now, for the function G(x, y) = sec x + tan y
G(λx, λy) = sec (λx) + tan (λy)
≠ λ(sec x + tan y)
∴ G(λx, λy) ≠ λG(x, y)
Hence, function G(x, y), is not homogeneous function.

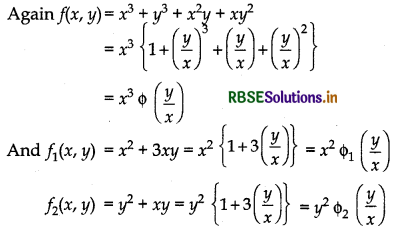
Hence, we can write a homogeneous function of degree in the following way :
f(x, y) = xⁿ f\(\left(\frac{y}{x}\right)\) 1 or f(x, y) = yⁿ\(\left(\frac{x}{y}\right)\)

Definition of Homogeneous Differential Equation
If a differential equation of first order and first degree is:
\(\frac{d y}{d x}=\frac{f(x, y)}{g(x, y)}\)
where f(x, y) and g(x, y) is the homogeneous fimction of same degree [g(x, y) ≠ 0], then differential equation (1) is said to be homogeneous differential equation.
Let \( \frac{d y}{d x}\) = F(x, y) = f\(\left(\frac{y}{x}\right)\).............(1)
is a homogeneous differential equation.

For solving this differential equation,
Putting \(\frac{y}{x}\) = v
or y = vx .......(2)

Differentialing equation (1) w.r.t. 'x',
\( \frac{d y}{d x}\) = v + x \(\frac{d v}{d x}\) ........(3)

Putting the value of from equation (3) in equation (1) we get

Now, putting v = \(\frac{y}{x}\) in equation (5) and we get general solution of differential equation (1).

Remark:
If the homogeneous differential equation is the form of \(\frac{d y}{d x}\) = f(x, y), where, f(x, y) is the homogeneous function of zero degree, then we find \(\frac{d y}{d x}\) by putting x = vy and we find the general differential equation by putting the value of \(\frac{d y}{d x}\)in \(\frac{d y}{d x}\) = f(x, y).

Linear Differential Equations
"If dependent variable (y) and its derivative (differential coefficient) both are of first degree, then differential equation is of first order."

General form of first order differential equation
\(\frac{d y}{d x}\) + Py = Q ...(1)
where P and Q are constants or functions of x.

For example:

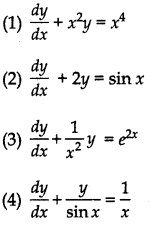
etc. are linear equations.

Remark: Second form of first order linear equation is \(\frac{d y}{d x}\) + P₁x = Q₁ where P₁ and Q₁ are either constant or functions of y.

For example :

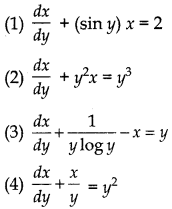
Solution of Linear Differential Equation of First Order
Differential equation of first order
\(\frac{d y}{d x}\) + Py = Q ......(1)
Multiplying both side by f(x) function of x, we get
f(x)\(\frac{d y}{d x}\) + f(x)Py = f(x)Q .....(2)
Here, choosing function/in such a way that R.H.S. of equation (2), will be differential of yf(x).

Hence, multiplying equation (1) by f(x) = e^∫Pdx, L.H.S. will be differential coefficient of any function of x and y.
f(x) = e^∫Pdx is known as integrating factor (I.F.) of given differential equation.
Putting f(x) = e^∫Pdx in equation (2),
e^∫Pdx\(\frac{d y}{d x}\) + Pe^∫Pdxy = Qe^∫Pdx
or \(\frac{d}{d x}\)[e^∫Pdxy] = Qe^∫Pdx

Integrating both sides w.r.t. 'x', we get
∫\(\frac{d y}{d x}\)[e^∫Pdxy]dx = ∫Qe^∫Pdxdx
or ye^∫Pdx = ∫Qe^∫Pdxdx + C
or y = e^-∫Pdx[∫Q(e^∫Pdx)dx + C] ............(4)
Equation (4) is the general solution of differential equation (1).

Step for solving linear differential equation of first order:

• Step I. Write the given differential equation in the form \(\frac{d y}{d x}\) + Py = Q, where P and Q are constants or functions of x.
• Step II. Find the integrating factor (I.F.) = e^∫Pdx
• Step III. The differential equation of step I is multiplied by e^∫Pdx on both sides.
• Step IV. Now, we integrate the differential equation w.r.t. 'x'.
  ye^∫Pdx = ∫Qe^∫Pdx + C
  or y × (I.F.) = ∫Q (I.F.) dx + C
  which is the solution of differential equation.

Similarly, first order differential equation \(\frac{d y}{d x}\) + P₁y = Q₁, where PT and Q1 are constants or functions of y only, then for this
I.F. = e^∫P₁dx
and solution of the equation is
x(I.F.) = ∫(Q₁ x I.F.) dy + C

→ An equation involving derivatives of the independent variable with respect to independent variable (variables) is called a differential equation.

→ Order of a differential equation is defined as the order of the highest order derivative of the dependent variable with respect to the independent variable.

→ Degree of a differential equation is the highest power (positive integer only) of differential coefficient.

→ In the differential equation of first order and first degree independent variable (x), dependent variable (y) and differential coefficient \(\left(\frac{d y}{d x}\right)\) of first order is involved. This type of equation is defined in the following form :
\(\frac{d y}{d x}\) = F(x, y) ...........(1)
or \(\frac{d y}{d x}=\frac{h(x, y)}{g(x, y)} \).......(ii)
where h(x, y) and g(x, y) is the function of x and y.
Simply, the differential equation of first order and first degree are written as :
P(x, y, \(\frac{d y}{d x}\)) = 0

→ Differential equation of first order and first degree of separable variable
\(\frac{d y}{d x}\) = h(x) × g(x)
or solution of \(\frac{d y}{g(y)}\) = h(x) dx
∫\(\frac{1}{g(y)}\)dy = ∫h(x)dx or G(y) = H(x) + C
where G(y) and H(x) are antiderivatives of \(\frac{1}{g(y)}\) h(x).

→ If differential equation of first order and first degree is defined as:
\(\frac{d y}{d x}=\frac{f(x, y)}{g(x, y)}\) ....(i)
where f(x, y) and g(x, y) is the homogeneous equation of same degree then differential equation (1) is called as homogeneous differential equation.
For finding its solution, it is shown in the following way:
im-9
On substituting v = \(\frac{y}{x}\) in equation (iii) the general solution of the differential equation is obtained.

→ A differential equation of the form
\(\frac{d y}{d x}\) + Py = Q
where P and Q are constants or functions of x only is called a first order linear differential equation.

→ Step involved to solve first order linear differential equation:

• Step I. Write the given differential equation in the form
• Step II. Find the integrating factor (IF) = e^∫Pdx
• Step III. Multiply by e^∫Pdx in both sides of differential equation obtained by step I.
• Step IV. Write the solution of the given differential equation as
  ye∫PdX = ∫Qe^∫Pdx + C
  or y × (IF) = ∫Q (IF) dx + C

Similarly, the first order linear differential equation is in
\(\frac{d y}{d x}\) + P₁y = Q₁
where P₁ and Q₁ are constants or functions of y only. Then
I.F. = e∫P₁dy
and the solution of the differential equation is given by
x(I.F.) = ∫Q₁ × (I.F)dy + C