RBSE Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.6

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.6 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 9 Differential Equations Ex 9.6

Question 1.
\(\frac{d y}{d x}\) + 2y = sin x
Answer:
Given differential equation is
\(\frac{d y}{d x}\) + 2y = sin x ........... (1)
Comparing equation (1) with \(\frac{d y}{d x}\) + Py = Q
P = 2, Q = sin x
∴ I.F. = e^{∫2 dx} = e^2x
Multiplying equation (1) by e^2x, we get
e^2x \(\frac{d y}{d x}\) + 2e^2x y = e^2x sin x
or \(\frac{d}{d x}\) (ye^2x) = e^2x sin x
Integrating both sides w.r.t. “x”, we get
ye^2x = ∫e^2x sin x dx ...... (2)
Let I = ∫e^2x sin x dx
= e^2x ∫sin x dx - ∫{\(\frac{d}{d x}\) e^2x ∫ sin x dx} dx
[Integrating by parts taking e^2x as first function]
= e^2x (- cos x) - ∫2e^2x (- cos x) dx
= - cos x e^2x + 2 ∫e^2x cos x dx + C₁
= cos x e^2x + 2 [e^2x ∫ cos x - ∫{\(\frac{d}{d x}\) (e^2x) ∫cos x dx } dx] + C₁
or I = - e^2x cos x + 2[e^2x sin x - ∫2e^2x sin x dx] + C₁
= - e^2x cos x + 2e^2x sin x - 4∫e^2x sin x dx + C₁
= - e^2x cos x + 2e^2x sin x - 4I + C₁
or I + 4I = - e^2x cos x + 2e^2x sin x + C₁
or 5I = - e^2x cos x + 2e^2x sin x + C₁
or I = \(\frac{1}{5}\) [- e^2x cos x + 2e^2x sin x] + \(\frac{1}{5}\)C₁
Putting the value of I in equation (2), we get

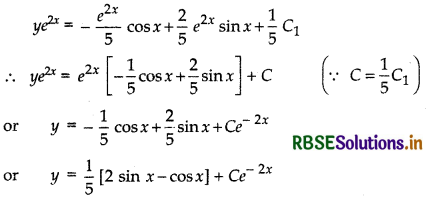
which is the required solution.

Question 2.
\(\frac{d y}{d x}\) + 3y = e^-2x
Answer:
Given differential equation is
\(\frac{d y}{d x}\) + 3y = e^-2x
Comparing equation (1) with \(\frac{d y}{d x}\) + Py = Q
P = 3, Q = e^{- 2x}
∴ I.F. = e^{∫3 dx} = e^3x
Multiplying equation (1) by e^3x, we get
e^3x \(\frac{d y}{d x}\) + 3e^3xy = e^-2x × e^3x
or \(\frac{d}{d x}\)(ye^3x) = e^x
integrating both sides w.r.t. “x”, we get
ye^3x = ∫e^x dx + C
or ye^3x = e^x + C
or y = e^x × e^-3x + Ce^-3x
or y = e^-2x + Ce^-3x
which is the required solution.

Question 3.
\(\frac{d y}{d x}+\frac{y}{x}\) = x²
Answer:
Given differential equation is
\(\frac{d y}{d x}+\frac{y}{x} \) = x² ............ (1)
Comparing equation (1) with \(\frac{d y}{d x}\) + Py = Q

which is the required solution.

Question 4.
\(\frac{d y}{d x}\) + (sec x)y = tan x (0 ≤ x < \(\frac{\pi}{2}\))
Answer:
Given differential equation is
\(\frac{d y}{d x}\) + (sec x)y = tan x
Comparing equation (1) with \(\frac{d y}{d x}\) + Py = Q
P = sec x, Q = tan x
∴ I.F. = e^{∫ sec x dx} = e^{log(sec x + tan x)}
= sec x + tan x
Multiplying equation (1) by (sec x + tan x), we get
(sec x + tan x) \(\frac{d y}{d x}\) + (sec x + tan x) (sec x)y = (sec x + tan x) tan x
or (sec x + tan x)\(\frac{d y}{d x}\) + (sec² x + sec x tan x)y = sec x tan x + tan² x
or \(\frac{d y}{d x}\) {(sec x + tan x)y} = sec x tan x + (sec²x - 1)
Integrating both sides w.r.t. “x”, we get
y(sec x + tan x) = ∫sec x tan x dx + ∫ sec² x dx - ∫dx + C
or y(sec x + tan x) = sec x + tan x - x + C
which is required solution.

Question 5.
cos² x \(\frac{d y}{d x}\) + y = tan x (0 ≤ x < \(\frac{\pi}{2}\))
Answer:
Given differential equation is

Question 6.
x \(\frac{d y}{d x}\) + 2y = x² log x
Answer:
Given differential equation is

Question 7.
x log x \(\frac{d y}{d x}\) + y = \(\frac{2}{x}\) log x
Answer:
Given differential equation is

which is required solution.

Question 8.
(1 + x²) dy + 2xy dx = cot dx (x ≠ 0)
Answer:
Given differential equation is
(1 + x²) dy + 2xy dx = cot x dx
Dividing equation (1) by (1 + x²) dx, we get
or \(\frac{d y}{d x}+\frac{2 x}{1+x^2}\) y = \(\frac{\cot x}{1+x^2}\) ....... (1)
Comparing equation (1) with \(\frac{d y}{d x}\) + Py = Q, we get
P = \(\frac{2 x}{1+x^2}\), Q = \(\frac{\cot x}{1+x^2}\)
∴ I.F. = \(e^{\int \frac{2 x}{1+x^2}}\) dx = e^{log (1 + x2)} = (1 + x²)
Multiplying equation (1) by (1 + x²), we get
(1 + x²)\(\frac{d y}{d x}\) + 2xy = cot x
or \(\frac{d}{d x}\)[y(1 + x²)] = cot x
Integrating both sides w.r.t. “x”, we get
y(1 + x²) = ∫ cot x dx + C.
or y(1 + x²) = log |sin x| + C
or y = (1 + x²)^-1 log |sin x| + C(1 + x²)^-1
which is required solution.

Question 9.
x\(\frac{d y}{d x} \)+ y - x + xy cot x = 0, (x ≠ 0).
Answer:
Given differential equation is

Integrating both sides w.r.t. "x", we get
xy sin x = ∫ x sin x dx + C
(Taking x as first function)
= x ∫sin x dx - ∫ {\(\frac{d}{d x}\) (x) ∫ sin x dx } dx + C
= x (- cos x) - ∫1 (- cos x) dx + C
= - x cos x + ∫ cos x dx + C
= - x cos x + sin x + C
or xy sin x = - x cos x + sin x + C

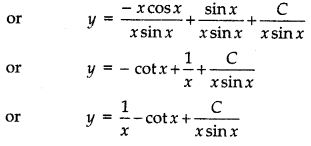
which is required solution.

Question 10.
(x + y)\(\frac{d y}{d x}\) = 1
Answer:
Given differential equation is
(x + y)\(\frac{d y}{d x}\) = 1

Integrating both sides w.r.t. "y", we get
xe^-y = ∫ye^-y dy + C
= - y(e^-y - ∫{\(\frac{d}{d y}\) (y) ∫e^-y dy } dy + C
(Integrating by parts taking y as a first function.)
= - ye^-y - ∫1.(- e^-y) dy + C
= - ye^-y + ∫e^-y dy + C
= - ye^-y - e^-y + C
xe^-y = - ye^-y - e^-y + C
or xe^-y = - e^-y (y + 1) + C
or x = - (y + 1) + Ce^Y
or x + y + 1 = Ce^Y
which is the required solution.

Question 11.
y dx + (x - y²)dy = 0
Answer:
Given differential equation is
y dx + (x - y²)dy = 0

Question 12.
(x + 3y²)\(\frac{d y}{d x}\) = y (x > 0)
Answer:
Given differential equation is

Question 13
\(\frac{d y}{d x}\) + 2y tan x = sin x; y = 0 when x = \(\frac{\pi}{3}\).
Answer:
Given differential equation is
\(\frac{d y}{d x}\) + (2 tan x)y = sin x
Comparing equation (1) with \(\frac{d y}{d x}\) +Py = Q, we get
P = 2 tan x, Q = sin x
∴ I.F. = e^{∫2 tan x dx} = e^{2∫tan x dx}
= e^{2 log sec x} = e^{log (sec2 x)}
or I.F. = sec² x
Multiplying equation (1) by sec² x
sec² x \(\frac{d y}{d x}\) + (2 sec² x tan x)y
= sec² x sin x = \(\frac{\sin x}{\cos ^2 x}\)
or \(\frac{d}{d x}\) (y sec² x) = sec x tan x
Integrating both sides w.r.t. “x”, we get
y sec² x = ∫ sec x tan x dx + C
or y sec² x = sec x + C ...... (2)
Putting x = \(\frac{\pi}{3}\) and y = 0 in equation (2), we get
0 × sec² \(\frac{\pi}{3}\) = sec \(\frac{\pi}{3}\) + C
or 0 = 2 + C
∴ C = - 2
Putting the value of C in equation (2), we get
y sec² x = sec x - 2
or y = \(\frac{\sec x}{\sec ^2 x}-\frac{2}{\sec ^2 x}\)
or y = cos x - 2 cos² x
which is the particular solution.

Question 14.
(1 + x²) \(\frac{d y}{d x}\) + 2xy = \(\frac{1}{1+x^2}\); y = 0 when x = 1
Answer:
Given differential equation is

Integrating both sides w.r.t. "x", we get
y(1 + x²) = ∫\(\frac{1}{1+x^2}\) dx + C
or y(1 + x)² = tan^-1 x + C ........ (2)
Putting x = 1 and y O in equation (2), we get
0(1 + 1)² = tan^-1 1 + C
or 0 = \(\frac{\pi}{4}\) + C
or C = - \(\frac{\pi}{4}\)
Putting the value of C in equation (2), we get
y(1 + x²) = tan^-1 x -\(\frac{\pi}{4}\)
which is the required solution.

Question 15.
\(\frac{d y}{d x}\) - 3y cot x = sin 2x; y = 2 when x = \(\frac{\pi}{2}\).
Answer:
Given differential equation is
\(\frac{d y}{d x}\) - 3y cot x = sin 2x
or \(\frac{d y}{d x}\) - (3 cot x)y = sin 2x ............. (1)
Comparing equation (1) with \(\frac{d y}{d x}\) + Phy = Q, we get
P = - 3 cot x, Q = sin 2x
∴ I.F. = e^{- ∫ 3 cot x dx} = e ^{- 3 log |sin x|}
= e^{log (sin x)-3} = (sin x)^{- 3} = cosec³ x
or I.F. = cosec³ x
On multiplying equation (1) by cosec³ x, we get

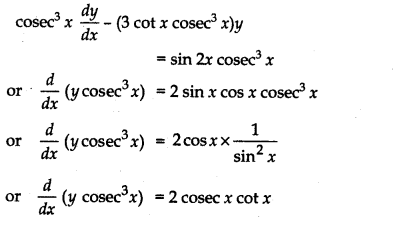
Integrating both sides w.r.t. “x”, we get
y cosec³ x = 2∫cosec x cot x dx + C
or y cosec³ x = - 2 cosec x + C
Putting x = \(\frac{\pi}{2}\) and y = 2 in equation (2), we get
2 × cosec² \(\frac{\pi}{2}\) = - 2 cosec \(\frac{\pi}{2}\) + C
2 × 1 = - 2 × 1 + C
or 2 = - 2 + C
or C = 4
Putting the value of C in equation (2)
y cosec³ x = - 2 cosec x + 4
or y = 4 sin³ x - 2 sin²x
or y = - 2 sin² x(1 - 2 sin x)
which is the required solution.

Question 16.
Find the equation of a curve passing through the origin given that the slope of the tangent to the curve at any point (x, y) is equal to the sum of the co-ordinate of the point.
Answer:
Slope of the tangent at point(x, y) of the curve is \(\frac{d y}{d x}\).
∴ Given \(\frac{d y}{d x}\) = x + y
or \(\frac{d y}{d x}\) - y = x

(Integrating by parts taking x as the first function)
= x(- e^-x) - ∫1.(- e^-x)dx + C
= - xe^-x + ∫e^-x dx + C
or ye^-x = - xe^-x - e^-x + C
or ye^-x = - e^-x (x + 1) + C ........ (2)
∵ Curve passes through origin (0, 0), so, putting x = 0,
y = 0 in equation (2), we get
0 × e^-0 = - e^-0 (0 + 1) + C
or 0 = - 1 (1) + C
or C = 1
Puffing the value of C in equation (2), we get
ye^-x = - e^-x(x + 1) + 1
or y = - (x + 1) + e^x
or y + x + 1 = e^x
or x + y + 1 = e^x
which is the required equation of the curve.

Question 17.
Find the equation of a curve passing through the point (0, 2) given that the sum of the co-ordinates of any point on the curve exceeds the magnitude of the slope of the tangent to the curve at that point by 5.
Answer:
Slope of the tangent at point (x, y) of the given curve is \(\frac{d y}{d x}\).
Given, x + y = \(\left|\frac{d y}{d x}\right|\) + 5
or \(\left|\frac{d y}{d x}\right|\) = x + y - 5
or \(\frac{d y}{d x}\) = ± (x + y - 5)

(i) Taking + ve sign,

= x(- e^-x) - ∫1 (- e^-x)dx + 5e^-x + C
= - xe^-x + ∫e^-x dx + 5e^-x + C
= - xe^-x - e^-x + 5e^-x + C
or ye^-x = - e^-x (x - 4) + C
or y = - (x - 4) + Ce^x
or x + y - 4 = Ce^X ..... (3)
Putting x = 0 and y = 2 in equation (3), we get
0 + 2 - 4 = Ce⁰
or - 2 = C
C = - 2
Putting the value of C in equation (3), we get
x + y - 4 = 2e^x
y = 4 - x - 2e^x
which is the required solution:

(ii) Taking - ve sign,
\(\frac{d y}{d x}\) = - (x + y - 5) = - x - y + 5
or \(\frac{d y}{d x}\) + y = 5 - x ........... (1)
Comparing equation (1) with \(\frac{d y}{d x}\) + Py = Q, we get
p = 1, Q = 5 - x
∴ I.F. = e^{∫1 dx} = e^x

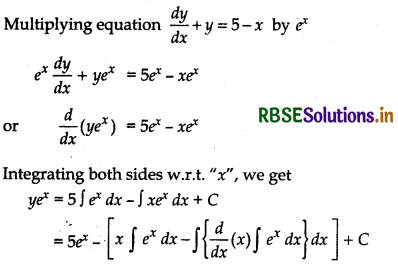
= 5e^x - [xe^x - ∫1 e^x dx] + C
= 5e^x - xe^x + e^x + C
or ye^x = 6e^x - xe^x + C
Putting x = 0 and y = 2 in equation (4), we get
2 × e⁰ = 6e⁰ - 0 × e⁰ + C
or 2 = 6 + C
or C = 2 - 6 = - 4
∴ C = - 4
Putting the value of C in equation (4), we get
ye^x = 6e^x - xe^x - 4
or y = 6 - x - 4e^{- x}
or x + y = 6 - 4e^{- x}
which is the required equation of the curve.

Question 18.
The integrating factor of the differential equation x \(\frac{d y}{d x}\) - y = 2x² is:
(A) e^-x
(B) e^-y
(C) \(\frac{1}{x}\)
(D) x
Answer:
Given differential equation

Hence, option (C) is correct

Question 19.
The integrating factor of the differential equation
(1 - y²)\(\frac{d x}{d y}\) + yx = ay {- 1 < y < 1} is:
(A) \(\frac{1}{y^2-1}\)
(B) \(\frac{1}{\sqrt{y^2-1}}\)
(C) \(\frac{1}{1-y^2}\)
(D) \(\frac{1}{\sqrt{1-y^2}}\)
Answer:
Given differential equation is

Hence, option (D) is correct.