RBSE Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.4

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.4 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 9 Differential Equations Ex 9.4

Question 1.
\(\frac{d y}{d x}=\frac{1-\cos x}{1+\cos x}\)
Answer:
The given differential equation is:

Equation (2) is the general solution of the given differential equation.

Question 2.
\(\frac{d y}{d x} = \sqrt{4-y^2}\); (- 2 < y < 2)
Answer:
The given differential equation is

or y = 2 sin(x + C) ....... (2)
Equation (2) is the general solution of the given differential equation.

Question 3.
\(\frac{d y}{d x}\) + y = 1; (y ≠ 1).
Answer:
The given differential equation is:

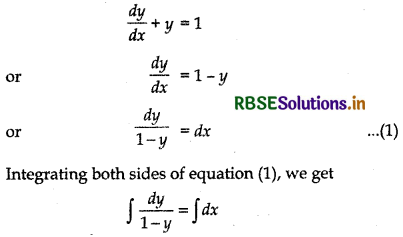
or - log |1 - y| = x + log C
⇒ x = - log C - log (1 - y)
⇒ - x = log C + log(1 - y)
⇒ - x = log C(1 - y)
⇒ C(1 - y) = e^-x
⇒ 1 - y = \(\frac{e^{-x}}{C}\)
⇒ y = 1 - \(\frac{e^{-x}}{C}\)
⇒ y = 1 + Ae^-x [where A = - \(\frac{1}{C}\)]
which is the required general solution of the given differential equation.

Question 4.
sec² x tan y dx + sec² y tan x dy = 0
Answer:
Given differential equation is
sec² x tan y dx + sec² y tan x dy = 0
Dividing equation (1) by tan x tan y
\(\frac{\sec ^2 x}{\tan x}\) dx + \(\frac{\sec ^2 y}{\tan y}\) dy = 0 ......(2)
Integrating equation (2), we get
∫\(\frac{\sec ^2 x}{\tan x}\) dx + ∫\(\frac{\sec ^2 y}{\tan y}\) dy = 0
or log |tan x| + log |tan y| = log C
or log |tan x tan y| = log C
or tan x tan y = C ........ (3)
(x, y ∈ R and x, y is riot the odd multiple of π/2)
Equation (3) is the required solution of given differential equation.

Question 5.
(e^x + e^-x)dy - (e^x - e^-x)dx = 0
Answer:
Given differential equation is
(e^x + e^-x)dy - (e^x - e^-x)dx = 0

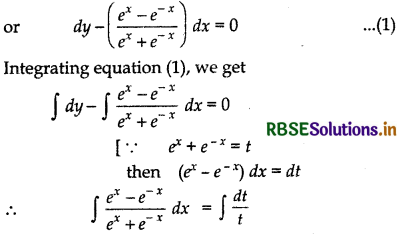
= log |t|
= log (e^x + e^-x)
or y - log(e^x + e^-x) + C = 0
or y = log (e^x + e^-x) + C ....... (2)
Equation (2) is the required solution of given differential equation.

Question 6.
\(\frac{d y}{d x}\) = (1 + x²) (1 + y²)
Answer:
Given differential equation is
\(\frac{d y}{d x} \)= (1 + x²) (1 + y²)
or \(\frac{d y}{1+y^2}\) = (1 + x²) dx ..... (1)
Integrating both sides of equation (1), we get
∫\(\frac{d y}{1+y^2}\) = ∫(1 + x²) dx
or tan^-1 y = x + \(\frac{x^3}{3}\) + C ...... (2)
Equation (2) is the required solution of given differential equation.

Question 7.
y log y dx - x dy = 0
Answer:
Given differential equation can be written as
\(\frac{d x}{x}-\frac{d y}{y \log y}\) = 0
Integrating equation (1), we get

Equation (2) is the required solution of given differential equation.

Question 8.
x⁵\(\frac{d y}{d x}\) = - y⁵
Answer:
Given differential equation is

Equation (2) is the required solution of given differential equation.

Question 9.
\(\frac{d y}{d x}\) = sin^-1 x
Answer:
Given differential equation is
\(\frac{d y}{d x}\) = sin^-1 x
or dy = sin^-1 x dx
or dy = 1.sin^-1 x dx
Integrating both sides of equation (1), we get
∫dy = ∫1.sin^-1 x dx
(Taking 1 as second function and sin^-1 x as first function)

Equation (2) is the required solution of given differential equation.

Question 10.
e^x tan y dx + (1 - e^x) sec² y dy = 0
Answer:
Given differential equation is
e^x tan y dx + (1 - e^x)sec² y dy = 0
Dividing equation (1) by (1 - e^x) tan y, we get
\(\left(\frac{e^x}{1-e^x}\right)\) dx + \(\frac{\sec ^2 y}{\tan y}\) dy = 0 .......... (2)
Integrating equation (2), we get
∫\(\frac{e^x}{1-e^x}\) dx + ∫\(\frac{\sec ^2 y}{\tan y}\) dy = 0
or - log |1 - e^x| + log |tan y| = log C
[Let 1 - e^x = u
or - e^x dx = du
or e^x dx = - du]
∴ ∫\(\frac{e^x}{1-e^x}\) = - ∫\(\frac{d u}{u}\)
= - log |u|
= - log |1 - e^x|
and tan y = V
sec² y dy = dV
∫\(\frac{\sec ^2 y}{\tan y}\) dy = ∫\(\frac{d V}{V}\)
= - log |V|
= log |tan y|
or log |tan y| = log C + log |1 - e^x|
or log |tan y| = log C(1 - e^x)
or tan y = C(1 - e^x) ...... (3)
Equation (3) is the required solution of given differential equation.

Question 11.
(x³ + x² + x + 1)\(\frac{d y}{d x}\) = 2x² + x; if x = 0, y = 1
Answer:
Given differential equation is
(x³ + x² + x + 1)\(\frac{d y}{d x}\) = 2x² + x

or 2x² + x = A(x² + 1) + (Bx + C) (x + 1)
or 2x² + x = Ax² + A + Bx² + Bx + Cx + C
or 2x² + x = (A + B)x² + (B + C)x + A + C
On comparing the coefficients of x, x² and constant terms of both sides, we get
A + B - 2, B + C = 1, A + C = 0
Solving these equations, we get


Equation (5) is the required solution of given differential equation.

Question 12.
x(x² - 1)\(\frac{d y}{d x}\) = 1; y = 0 when x = 2
Answer:
Given differential equation is

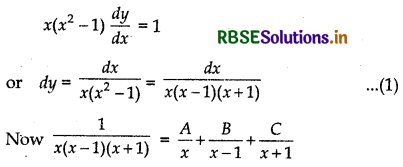
1 = A(x² - 1) + B(x² + x) + C(x² - x)
or 1 = (A + B + C)x² + (B - C)x - A
On comparing the coefficients of x, x² and constant terms of both sides, we get
A + B + C = 0, B - C = 0, A = - 1
Solving, these equations, we get
A = - 1, B = \(\frac{1}{2}\), C = \(\frac{1}{2}\)


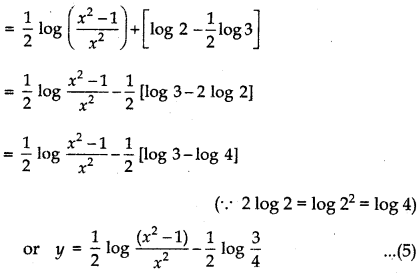
Equation (5) is the required solution of given differential equation.

Question 13.
cos \(\left(\frac{d y}{d x}\right)\) = a (a ∈ R); y = 1 when x = 0
Answer:
Given differential equation is
cos \(\left(\frac{d y}{d x}\right)\) = a
or \(\frac{d y}{d x}\) = cos^-1 a
or dy = cos^-1 a dx
Integrating both sides of equation (1), we get
∫dy = cos^-1 a ∫dx
or y = x cos^-1 a + C ..... (2)
When x = 0, then y = 1,
∴ 1 = 0 × cos^-1 a + C
∴ C = 1
Putting the value C in equation (2), we get
y = x cos^-1 a + 1
or y - 1 = x cos^-1 a
or \(\frac{y-1}{x}\) = cos^-1 a
or a = cos\(\left(\frac{y-1}{x}\right)\)
Equation (3) is the required solution of given differential equation.

Question 14.
\(\frac{d y}{d x}\) = y tan x; y = 1 if x = 0
Answer:
Given differential equations is
\(\frac{d y}{d x }\) = y tan x
or \(\frac{d y}{y}\) = tan x dx
Integrating both sides of equation (1), we get
∫\(\frac{d y}{y}\) = ∫tan x dx
or log y = - log cos x + C ... (2)
Putting x = 0 and y = 1 in equation (2), we get
log1 = - log cos 0 + C
or 0 = - log 1 + C
or 0 = 0 + C
or C = 0
Putting C = 0 in equation (2), we gc t
log y = - log cos x
or log y = - log \(\frac{1}{\sec x}\) = log sec x
or y = sec x ....... (3)
Equation (3) is the required solution of given differential equation.

Question 15.
Find the equation of a curve passing through the point (0, 0) and whose differential equation is y' = e^x sin x
Answer:
Given differential equation is
y' = e^x sin x
or \(\frac{d y}{d x}\) = e^x sin x
or dy = e^x sin x dx .............. (1)
Integrating both sides of equation (1), we get
∫dy = ∫e^x sin x dx
or y = ∫e^x sin x dx + C ........... (2)
Let I = ∫e^x sin x dx
I = sin x ∫e^x dx - ∫{\(\frac{d}{d x}\) sin ∫e^x dx} dx
(Taking sin x as first function and e^x as second function)
I = sin x.e^x - ∫cos x e^x dx
I₁ = ∫ cos x e^x dx
(Taking cos x as first function and e^x as second function)
I = sin x ∫e^x dx - ∫{\(\frac{d}{d x}\) sin ∫e^x dx} dx
or I₁ = cos x e^x + ∫sin x e^x dx ...... (4)
Putting the value of I₁ in equation (3), we get
I = sin x e^x - cos x e^x - ∫sin x e^x dx
or I = sin x e^x - cos x e^x - 1
or 2I = sin x e^x - cos x e^x
or 2I = (sin x - cos x) e^x
or I = \(\frac{e^x}{2}\) (sin x - cos x)
y =\( \frac{e^x}{2}\) (sin x - cos x) + C ... (5)
Putting x = 0 and y = 0 in equation (5), we get

or 2y = e^x (sin x - cos x) + 1
or 2y - 1 = e^x(sin x - cos x)
which is the required equation of curve.

Question 16.
For the differential equation xy\(\frac{d y}{d x}\) = (x + 2) (y + 2), find the solution curve passing through the point (1, - 1).
Answer:
Given differential equation is

or y - 2 log |y + 2| = x + 2 log x + C
Putting x = 1, y = - 1 in equation (2)
or - 1 - 2 log |- 1 + 2| = 1 + 2 log l + C
or - 1 - 2 log 1 = 1 + 2 × 0 + C
or - 1 - 0 = 1 + C
or C = - 1 - 1 = - 2
or C = - 2
Putting the value of C in equation (2)
y - 2 log (y + 2) = x + 2 log x - 2
or y - x + 2 = 2 log x + 2 log(y +2)
or y - x + 2 = log x² + log(y + 2)²
or y - x + 2 = log{x² (y + 2)²}
which is the required equation of the curve.

Question 17.
Find the equation of a curve passing through the point (0, - 2) given that at any point (x, y) on the curve, the product of the slope of its tangent and y co-ordinate of the point is equal to the x co-ordinate of the point.
Answer:
The slope of the tangent of the curve at point (x, y)

or y² = x² + 4
or y² - x² = 4 is the required equation of the curve.

Question 18.
At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (- 4, - 3). Find the equation of the curve given that it passes through point (- 2, 1).
Answer:
The slope of the tangent of the curve at point (x, y).
= \(\frac{d y}{d x}\)
The slope of the line joining the points (x, y) and

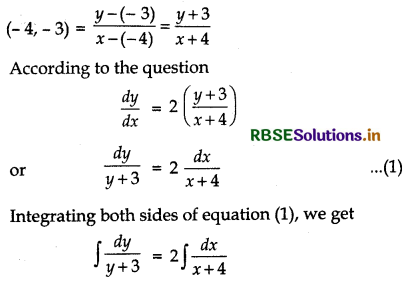
or log |y + 3| = 2 log |x + 4| + C ........ (2)
Putting x = - 2 and y = 1 in equation (2)
log |1 + 3| = 2 log |- 2 + 4| + C
or log 4 = 2 log 2 + C
or log 4 = log 4 + C
(∵ 2 log 2 = log 2² = 4)
∴ C = 0
Putting the value of C in equation (2)
log |y + 3| = 2 log |x + 4| + 0
or log (y + 3) = log (x + 4)²
or y + 3 = (x + 4)²
or (x + 4)² = y + 3
This is the required equation of the curve.

Question 19.
The volume of spherical balloon being inflated changes at a constant rate. if initially its radius is 3 units and after 3 second it is 6 units. Find the radius of balloon after t seconds.
Answer:
Let volume of balloon at any time t is V.
According to the question

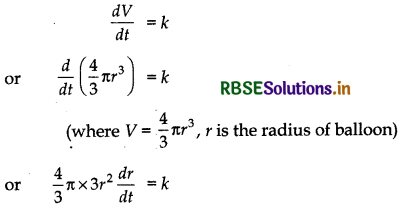
or 4πr² dr = k dt .......... (1)
Integrating both sides of equation (1), we get
4π ∫ r² dr = k ∫ df
or 4π × \(\frac{r^3}{3}\) = kt + C ............ (2)
When t = 0, then r = 3
∴ 4π × \(\frac{3^3}{3}\) = k × 0 + C
or 4π × 9 = C
C = 36π
Putting the value of C in equation (2)
\(\frac{4}{3}\)πr³ = kt + 36π
Again, when t = 3, then r = 6
∴ From equation (3), we get
\(\frac{4}{3}\)π × 6³ = k × 3 + 36π
or \(\frac{4}{3}\)π × 6 × 6 × 6 = 3k + 36π
or 288π = 3k + 36π
or 3k = 288π - 36π
or 3k = 252π
or k = 84π
Puffing the value of k in equation (3), we get
\(\frac{4}{3}\)πr³ = 84πt + 36π
or \(\frac{r^3}{3} = \frac{4 \pi}{4 \pi}\)(21t + 9)
or r³ = 63t + 27
or r³ = 9(7t + 3)
or r = [9(7t + 3)]1/3
Hence, after t second, radius of balloon is [9(7t + 3)]^1/3.

Question 20.
In a bank, principle increases continuously at the rate of r% per year. Find the value of r if ₹ 100 double itself in 10 years. (log_e 2 = 0.6931)
Answer:
Let principle is P.
According to the question

∴ r = 0.6931 × 10 = 6.931
or r = 6.93
Hence, rate of interest = 6.93%.

Question 21.
In a hank, principal increases continuously at the rate of 5% per year. An amount of ₹ 1000 is deposited with this bank, how much will it worth after 10 years. (e^0.5 = 1.648)
Answer:
Let principal is P.
According to the question

or P = Ce^0.05t ..... (2)
When t = 0, then P = 1000
∴ 1000 = Ce^{0.05 × 0} = Ce⁰ = C
∴ C = 1000
∴ From equation (2), p = 100e^0.05t
When t = 10 then P = 1000 ^{0.05 × 0}
= 1000e^0.5
= 1000 × 1.648
∴ P = 1648
Hence, in 10, years ₹ 1,000, will be ₹ 1,648.

Question 22.
In a culture, the bacteria count is 1,00,000. The number is increased by 10% in 2 hours. In how many hours will the count reach 2,00,000, if the rate of growth of bacteria is proportional to the number present?
Answer:
Let the number of bacteria is P.
According to the question

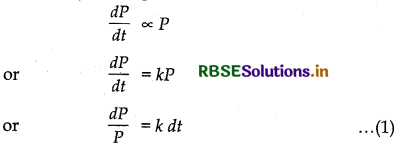
Integrating both sides of equation (1), we have
∫\(\frac{d P}{P}\) = ∫ k dt
or log P = kt + C
When t = 0, then P = P₀
∴ log P₀ = k × 0 + C
[Where P₀ is the initial number of bacteria]
∴ C = log P₀
or log P = kt + log P_o
or log P - log P_o = kt
or log \(\frac{P}{P_0}\) = kt ............... (2)
According to the question, bacteria increases 10% in 2 hours.

Question 23.
The general solution of the differential equation \(\frac{d y}{d x}\) = e^{x + y} is:
(A) e^x + e^-y = C
(B) e^x + e^y = C
(C) e^-x + e^y = C
(D) e^-x + e^-y = C
Answer:
Given differential equation
\(\frac{d y}{d x}\) = e^{x + y} = e^x e^y
or \(\frac{d y}{e^y}\) = e^x dx
or e^-y dy = e^x dx
Integrating both sides of equation (1), we get
∫e^-y dy = ∫e^x dx
or - e^{- y} = e^x + C₁
or e^x + e^-y = - C₁
or e^x + e^-y = C (where - C¹ = C)
Hence, option (A) is correct.