RBSE Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.3

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.3 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 9 Differential Equations Ex 9.3

Question 1.
\(\frac{x}{a}+\frac{y}{b}\) = 1
Answer:
The given equation is:
\(\frac{x}{a}+\frac{y}{b}\) = 1
Differentiating equation (1) w.r.t. 'x', we get

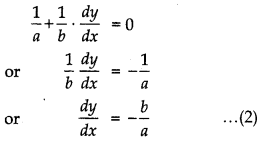
Again, differentiating equation (2) w.r.t. 'x', we get
\(\frac{d^2 y}{d x^2}\) = 0
or y'' = 0
Hence, equation (3) is the required differential equation.
Hence proved.

Question 2.
y² = a(b² - x²)
Answer:
The given equation is
y² = a(b² - x²)
Differentiating equation (1) w.r.t. 'x', we get
2y\(\frac{d y}{d x}\) = a(- 2x)
or y\(\frac{d y}{d x}\) = - ax
Again, differentiating equation (2) w.r.t. 'x', we get
y \(\frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^2\) = - a ...... (3)
Substituting the value of - a from equation (3) in equation (2), we get

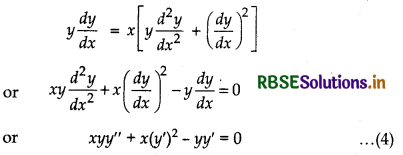
Hence, equation (4) is the required differential equation.

Question 3.
y = ae^3x + be^-2x
Answer:
The given equation is:
y = ae^3x + be^-2x ...... (1)
Differentiating equation (1) w.r.t. ‘x’, we get
\(\frac{d y}{d x}\) = 3ae^3x - 2be^-2x ....... (2)
Again, differentiating equation (2) w.r.t. ‘x’, we get
\(\frac{d^2 y}{d x^2}\) = 9ae^3x + 4be^-2x ..... (3)
Multiplying equation (1) by 2 and then adding in equation (2)
2y + \(\frac{d y}{d x}\) = 2ae^3x + 2be^-2x + 3ae^3x - 2be^{- 2x}
or 2y + \(\frac{d y}{d x}\) = 5ae^3x
or ae^3x = \(\frac{2 y+\frac{d y}{d x}}{5}\)
Now, multiply equation (1) by 3 and subtract from equation (2), we get

Hence, equation (4) is the required differential equation.

Question 4.
y = e^2x (a + bx)
Answer:
The given equation is
y = e^2x (a + bx)
or ye^-2x = a + bx ......... (1)
Differentiating equation (1) w.r.t. ‘x’, we get
\(\frac{d y}{d x}\)e^-2x - 2e^{- 2x} y = b ....... (2)
Again, differentiating equation (2) w.r,t. ‘x’, we get

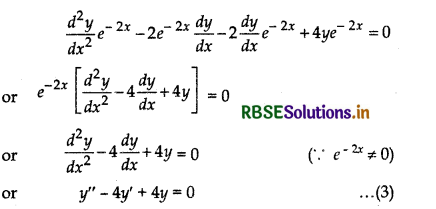
Hence, equation (3) is the required differential equation.

Question 5.
y = e^x (a cos x + b sin x)
Answer:
The given equation is:
y = e^x (a cos x + b sin x)
or ye^-x = a cos x + b sin x ........ (1)
Differentiating equation (1) w.r.t. 'x', we get

Hence, equation (3) is the required differential equation.

Question 6.
Form the differential equation of the family of circles touching the y-axis at origin.
Answer:
Let c denote the family of circles touching y-axis at origin. Let (a, 0) be the co-ordinates of the centre and a be the radius of any member of the family. Therefore, equation of family c is:
(x - a)² + y² = a²
or x² - 2ax + a² + y² = a²
or x² + y² = 2ax ........ (1)

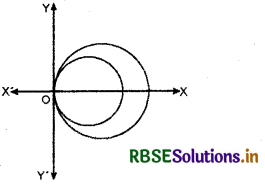
Differentiating equation (1) w.r.t. 'x', we get
2x + 2y\(\frac{d y}{d x}\) = 2a or x + y\(\frac{d y}{d x}\) = a
Putting the value of a in equation (1), we get

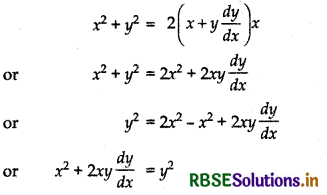
or 2xyy' + x² = y²
Hence, equation (2) is the required differential equation.

Question 7.
Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.
Answer:
Equation of parabola having vertex at the origin and axis along positive y-axis is:
x² = 4ay .......... (1)
Differentiating equation (1) w.r.t. ‘x’, we get


Hence, equation (2) is the required differential equation.

Question 8.
Form the differential equation of the family of ellipses having foci on y-axis and centre at origin.
Answer:
Equation of family of ellipses having foci on y-axis and centre at origin (0, 0).

Hence, equation (3) is the required differential equation.

Question 9.
Form the differential equation of the family of hyperbolas having foci on x-axis and centre at origin.
Answer:
Equation of family of hyperbolas with centre at the origin and foci along x-axis is:
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1


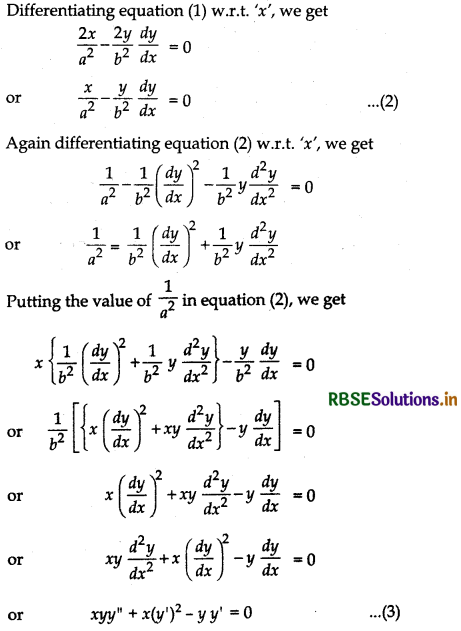
Hence, equation (3) is the required differential equation.

Question 10.
Form the differential equation of the family of circles having centre on y-axis and radius 3 units.
Answer:
Equation of family of circles with centre (0, b) and radius 3 units.
(x - 0)² + (y - b)² = 9
or x² + (y - b)² = 9 ....... (1)

Hence, equation (2) is the required differential equation.

Question 11.
Which of the following differential equations has y = c₁e^x + c₂e^-x as the general solution?
(A) \(\frac{d^2 y}{d x^2}\) + y = 0
(B) \(\frac{d^2 y}{d x^2}\) - y = 0
(C) \(\frac{d^2 y}{d x^2}\) + 1 = 0
(D) \(\frac{d^2 y}{d x^2}\) - 1 = 0
Answer:
The given equation is:
y = c₁e^x - c₂e^-x ....... (1)
Differentiating equation (1) w.r.t. 'x', we get
\(\frac{d y}{d x}\) = c₁e^x - c₂e^-x ............ (2)
Again, differentiating equation (2) w.r.t, 'x', we get

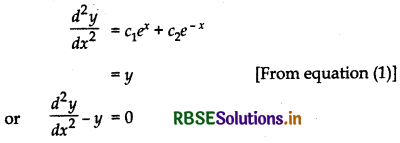
Hence, (B) is the correct answer.

Question 12.
Which of the following differential equations has y = x as one of its particular solution?
(A) \(\frac{d^2 y}{d x^2}\) - x² \(\frac{d y}{d x}\) + xy = x
(B) \(\frac{d^2 y}{d x^2}\) + x \(\frac{d y}{d x}\) + xy = x
(C) \(\frac{d^2 y}{d x^2}\) - x² \(\frac{d y}{d x}\) + xy = 0
(D) \(\frac{d^2 y}{d x^2}\) + x \(\frac{d y}{d x}\) + xy = 0
Answer:
The given equation is:
y = x ............ (1)
Differentiating equation (1) w.r.t. ‘x’, we get
\(\frac{d y}{d x}\) = 1 ....... (2)
Again, differentiating equation (2) w.r.t. ‘x’, we get
\(\frac{d^2 y}{d x^2}\) = 0 ......... (3)
Putting the values of \(\frac{d^2 y}{d x^2}\) = 0 and y = x in equation
\(\frac{d^2 y}{d x^2}\) - x²\(\frac{d y}{d x}\) + xy = 0
L.H.S. = 0 - x² × 1 + x.x
= - x² + x² = 0 = R.H.S.
Hence, (C) is the correct answer.