RBSE Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.2

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.2 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 9 Differential Equations Ex 9.2

Question 1.
y = e^x + 1 : y'' - y' = 0
Answer:
The given function is:
y = e^x + 1 ..... (1)
Differentiating equation (1) w.r.t. ‘x’, we get
\(\frac{d y}{d x}\) = e^x
or y' = e^x ........ (2)
Again, differentiating equation (2) w.r.t, ‘x’, we get
y'' = e^x
or y'' = y' [From equation (2)]
or y'' - y' = 0
Hence, the given function y = e^x + 1 is the solution of the differential equation y'' - y' = 0.
Hence Proved.

Question 2.
y = x² + 2x + C: y' - 2x - 2 = 0
Answer:
The given function is:
y = x² + 2x + C .......... (1)
Differentiating equation (1) w,r.t. ‘x’, we get
y' = 2x + 2
or y' - 2x - 2 = 0
Hence, the given function y = x² + 2x + C is the solution of the differential equation y’ - 2x - 2 = 0.
Hence Proved.

Question 3.
y = cos x + C: y’ + sin x = 0.
Answer:
The given function is:
y = cos x + C ...... (1)
Differentiating equation (1) w.r.t ‘x’, we get
y' = - sin x
or y’+ sin x = 0
Hence, the given function y = cos x + C is the solution of the differential equation y’ + sin x = 0.
Hence Proved.

Question 4.
y = \(\sqrt{1+x^2}\): y' = \(\frac{x y}{1+x^2}\).
Answer:
The given function is:
y = \(\sqrt{1+x^2}\) ....... (1)
Differentiating equation (1) w.r.t. 'x', we get

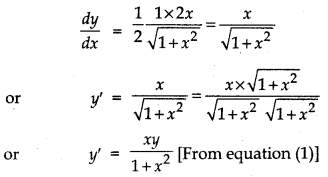
Hence, the given function y = \(\sqrt{1+x^2}\), is the solution of the differential equation y' = \(\frac{x y}{1+x^2}\).
Hence Proved.

Question 5.
y = Ax : xy’ = y(x ≠ 0)
Answer:
The given function is:
y = Ax
Differentiating equation (1) w.r.t. ‘x’, we get
y’ = A
Multiplying by x in both sides of equation (2), we get
xy’ = Ax = y [From equation (1)1
or xy’ = y
Hence, the given function y = Ax, is the solution of the differential equation xy’ = y.
Hence Proved.

Question 6.
y = x sin x : xy' = y + x\(\sqrt{x^2-y^2}\) (x ≠ 0 and x > y or x < - y)
Answer:
The given function is:
y = x sin x ...... (1)
Differentiating equation (1) w.r.t. ‘x, we get
y' = 1 × sin x + x cos x
or y' = sin x + x cos x ........ (2)
Multiplying by x in both sides of equation (2), we get
xy' = x sin x + x² cos x

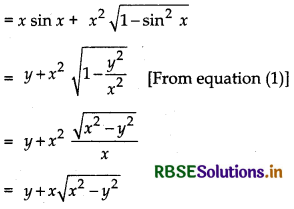
Hence, the given function y = x sin x is the solution of the differential equation xy’ = y + x\(\sqrt{x^2-y^2}\)
Hence Proved.

Question 7.
xy = log y + C : y' = \(\frac{y^2}{1-x y}\) (xy ≠ 1)
Answer:
The given function is:
xy = log y + C ......... (1)
Differentiating equation (1) w.r.t. ‘x’, we get
x\(\frac{d y}{d x}\) + y = \(\frac{1}{y} \cdot \frac{d y}{d x}\)
⇒ xy' + y = \(\frac{1}{y}\) . y' (∵ \(\frac{d y}{d x}\) = y')
⇒ xyy' + y² = y'
⇒ y² = y' - xyy'
⇒ y² = y'(1 - xy)
⇒ y' = \(\frac{y^2}{1-x y}\)
Hence, the given function xy = log y + C is the solution of the differential equation y’ = \(\frac{y^2}{1-x y}\).
Hence Proved.

Question 8.
y - cos y = x : (y sin y + cos y + x)y' = y
Answer:
The given function is:
y - cos y = x ......... (1)
Differentiating equation (1) w.r.t, ‘x’, we get
y' + (sin y)y' = 1
or (1 + sin y)y' = 1 ........ (2)
Multiplying by y in both sides of equation (2), we get
(y + y sin y)y' = y ....... (3)
or (y sin y + cos y + x)y’ = y
[Putting the value of y = cos y + x from equation (1) in L.H.S. of equation (3)]
Hence, the given function y - cos y = x, is the solution of differential equation (y sin y + cos y + x)y’ = y.
Hence Proved.

Question 9.
x + y = tan^-1 y : y²y' + y² + 1 = 0
Answer:
The given function is:
x + y = tan^-1 y
Differentiating equation (1) w.r.t. ‘x’, we get
1 + y' = \(\frac{1}{1+y^2}\) . y'
⇒ (1 + y²) + (1 + y²)y’ = y’
⇒ 1 + y² + y’ + y²y’ = y’
⇒ y²y’+ y² + 1 = 0
Hence, the given function x + y = tan^-1 y is the solution of the differential equation y²y’ + y² + 1 = 0.
Hence Proved.

Question 10.
y = \(\sqrt{a^2-x^2}\), x ∈ (- a, a):x + y \(\frac{d y}{d x}\) = 0, (y ≠ 0).
Answer:
The given function is:
y = \(\sqrt{a^2-x^2}\)
Differentiating equation (1) wr.t. ‘x’, we get

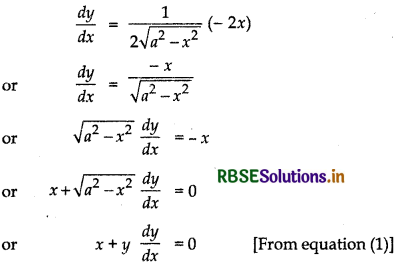
Hence, the given function y = \(\sqrt{\left(a^2-x^2\right)}\) the solution of the differential equation x + y \(\frac{d y}{d x}\) = 0.
Hence Proved.

Question 11.
The number of arbitrary constants in the general solution of a differential equation of fourth order are:
(A) 0
(B) 2
(C) 3
(D) 4
Answer:
Number of constants in the general solution of a differential equation of fourth order is 4.
Here, differential equation is of fourth order.
∴ Number of arbitrary constants 4.
Hence (D) is the correct answer.

Question 12.
The number of arbitrary constant in the particular solution of a differential equation of third order are:
(A) 3
(B) 2
(C) 1
(D) 0
Answer:
In a particular solution of a differential equation, there is no arbitrary constant.
Hence (D) is the correct answer.