RBSE Solutions for Class 12 Maths Chapter 8 समाकलनों के अनुप्रयोग विविध प्रश्नावली

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 8 समाकलनों के अनुप्रयोग विविध प्रश्नावली Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 8 समाकलनों के अनुप्रयोग विविध प्रश्नावली

प्रश्न 1.
दिए हुए वक्रों एवं रेखाओं से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए :
(i) y = x², x = 1, x = 2 एवं x-अक्ष
(ii) y = x⁴, x = 1, x = 5 एवं y-अक्ष
हल:
(i) प्रश्नानुसार परवलय y = x² का शीर्ष (0,0) है और सममित रेखा OY है।
y = x², x = 1, x = 2 एवं x-अक्ष से घिरे क्षेत्र का क्षेत्रफल

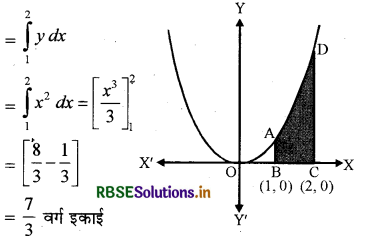
(ii) प्रश्नानुसार वक्र y = x बिन्दु (0, 0) से होकर जाता है। इसकी सममित रेखा OY है।
\(\frac{d y}{d x}\) = 4x³.\(\frac{d y}{d x}\) का चिह्न - ve से +ve में बदलता है जब x, x = 0 से होकर आगे बढ़ता है।
अर्थात् x = 0 निम्नतम बिन्दु है।
∴ y = x⁴, x = 1, x = 5

तथा x-अक्ष से घिरे क्षेत्र का क्षेत्रफल

 

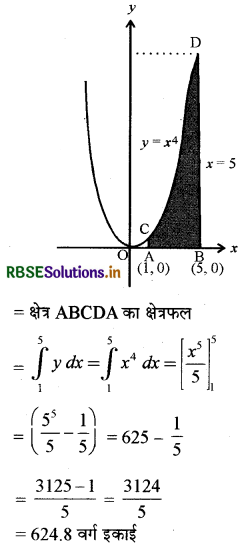
प्रश्न 2.
वक्रों y = x² एवंy=x के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
y = x² एक परवलय है जिसका शीर्ष (0,0) है तथा सममित रेखा OY

प्रश्नानुसार
y = x .....(i)
तथा y = x² ....(ii)
y का मान y = x² में रखने पर
x = x² या x² - x = 0
(x - 1) = 0
x = 0, x = 1
यदि x = 0 तो y = 0 तथा यदि x = 1 तो y = 1
अतः y = x एवं y = x, (0, 0) तथा (1, 1) पर मिलते हैं।

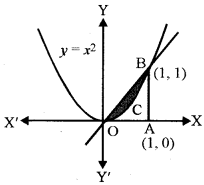
वक्र y = x² एवं y = x से घिरे क्षेत्र का क्षेत्रफल
= क्षेत्र OCBO का क्षेत्रफल
= क्षेत्र OABO का क्षेत्रफल - क्षेत्र OABCO का क्षेत्रफल

प्रश्न 3.
प्रथम चतुर्थांश में सम्मिलित एवं y = 4x², x = 0, y = 1 तथा y = 4 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
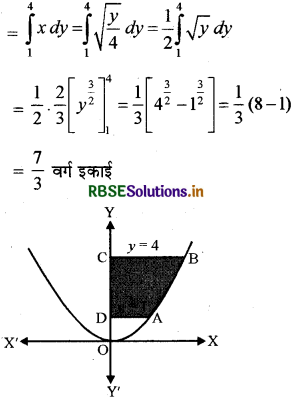
प्रश्नानुसार y = 4x² एक परवलय जिसका शीर्ष (0, 0) है और OY सममित रेखा है।
y = 4x², x = 0,y = 1, y = 4 से घिरा क्षेत्र छायांकित है।

इसका क्षेत्रफल
= क्षेत्र ABCD का क्षेत्रफल

प्रश्न 4.
y = |x + 3| का ग्राफ खींचिए एवं \(\int_{-6}^0\)|x+3|dr का मान ज्ञात कीजिए।
हल:
प्रश्नानुसार y = |x + 3|

इसका आलेख आकृति के अनुसार है।

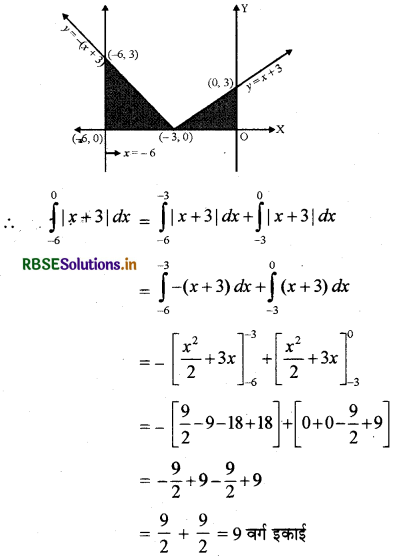
प्रश्न 5.
x = 0 एवं x= 2π तथा वक्र y = sinx से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
y = sin x के ग्राफ पर x के कुछ मानों के संगत' के मान निम्न प्रकार हैं।
इन बिन्दुओं को वक्र द्वारा मिलाने से निम्नानुसार ग्राफ प्राप्त होता है :

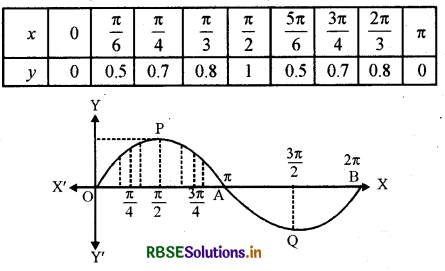
प्रश्न 6.
परवलय y = 4ax एवं रेखा y = mx से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
दिए हुए वक्र और सरल रेखा का समीकरण
y² = 4ax ....(i)
y = mx
y का मान समीकरण (i) में रखने पर
m²x² = 4ax ∴ x = \(\frac{4 a}{m^2}\), और x = 0
इस प्रकार वक्र y² = 4ax और रेखा y = mx बिन्दु 0 (0, 0) तथा P\(\left(\frac{4 a}{m^2}, \frac{4 a}{m}\right)\) पर प्रतिच्छेदन करते हैं। अत: y² = 4ax तथा y = mx से घिरे क्षेत्र का क्षेत्रफल
= क्षेत्र OCBDO का क्षेत्रफल
= क्षेत्र ABCOA का क्षेत्रफल - ΔODBAO का क्षेत्रफल

प्रश्न 7.
परवलय 4y = 3x² एवं रेखा 2y = 3x + 12 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
परवलय तथा रेखा के समीकरण
4y = 3x² ....(i)
2y = 3x + 12 ....(ii)
2y का मान समीकरण (i) में रखने पर
2 (3x + 12) = 3x²
या 3x² - 6x - 24 = 0
या x² - 2x - 8 = 0.
या (x - 4) (x + 2) = 0
या x = 4, -2
यदि x= 4 तो 2y = 12 + 12 = 24
y = 12
तथा यदि x = - 2 तो 2y = - 6 + 12 = 6
या y = 3
इस प्रकार परवलय और रेखा एक-दूसरे को A(- 2, 3) तथा D(4, 12) पर प्रतिच्छेदन करते हैं। वक्र 4y = 3x² तथा रेखा 2y = 3x + 12 द्वारा घिरे क्षेत्र का क्षेत्रफल
= \(\int_{-2}^4\) y₁ dx (रेखा के लिए) - \(\int_{-2}^4\) y₂ dar (परवलय के लिए)

यहाँ y₁, रेखा 2y = 3x + 12, तथा y, परवलय 4y = 3x² के लिए लेने पर

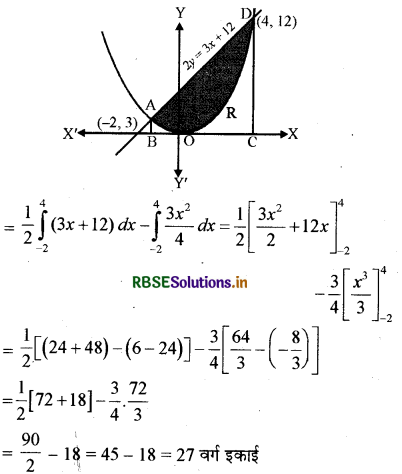
प्रश्न 8.
दीर्घवृत्त \(\frac{x^2}{9}+\frac{y^2}{4}\) = 1 एवं रेखा \(\frac{x}{3}+\frac{y}{2}\) = 1 से घिरे लघु क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
दीर्घवृत्त \(\frac{x^2}{9}+\frac{y^2}{4}\) = 1 को रेखा \(\frac{x}{3}+\frac{y}{2}\) = 1
बिन्दु A(3, 0), B(0, 2) पर काटती है।

प्रश्न 9.
दीर्घवृत्त \(\frac{x}{a}+\frac{y}{b}\) = 1 एवं रेखा \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 से घिरे लघु क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
रेखा \(\frac{x}{a}+\frac{y}{b}\) = 1 दीर्घवृत्त \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 को A(a, 0), B(0, b) पर काटती है।
अभीष्ट क्षेत्रफल = क्षेत्र BCAB का क्षेत्रफल
= क्षेत्र OACBO का क्षेत्रफल - क्षेत्र OABO का क्षेत्रफल

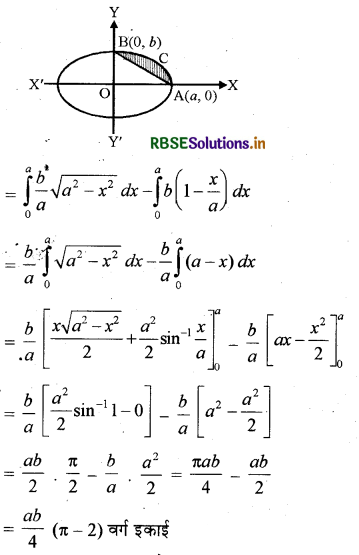
प्रश्न 10.
परवलय x² = y, रेखा y = x + 2 और x-अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
प्रश्नानुसार x² = y ....(i)
और y = x + 2 ....(ii)
(i) व (ii) मिलते हैं जब
x² = x + 2
x² - x - 2 = 0
(x - 2) (x + 1) = 0
x = 2, x = -1
x = 2 तो y = (2)² = 4 और यदि
x = - 1 तो y = (-1)² = 1

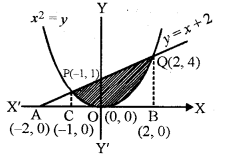
इसलिए दो वक्र x² = y और y = x + 2 बिन्दु (2, 4) और (-1, 1) पर प्रतिच्छेदन करते हैं।

प्रश्न 11.
समाकलन विधि का उपयोग करते हुए वक्र |x| + |y| = 1 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
संकेत—आवश्यक क्षेत्र, रेखाओं x + y = 1, x -y = 1, -x + y = 1 एवं -x - y = 1 से घिरा है।
हल:
प्रश्नानुसार दिए गए समीकरण
x + y = 1, x > 0, y > 0 ....(1)
x - y = 1, x > 0, y < 0 ....(ii)
-x + y = 1, x < 0, y > 0 .....(iii)
x - y = 1, x < 0, y < 0 ....(iv)

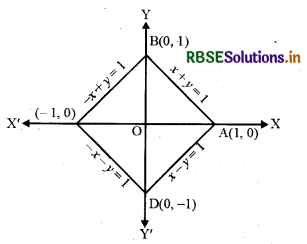
चारों रेखाओं का अनुरेखण करने पर अभीष्ट क्षेत्रफल = 4ΔOAB का क्षेत्रफल
= 4 \(\int_0^1\) y (रेखा (i) के लिए) dx
क्योंकि आकृति x-अक्ष तथा y-अक्ष दोनों के लिए सममित है।
= 4 \(\int_0^1\)(1 - x)dx = 4\(\left[x-\frac{x^2}{2}\right]_0^1\)
= 4[1 - \(\frac{1}{2}\) - 0) = 4.\frac{1}{2} = 2 वर्ग इकाई

प्रश्न 12.
वक्रों {(x, y), y ≥ x². तथा y = |x|} से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
वक्र x =y एक परवलय है जिसका शीर्ष (0, 0) है तथा सममित अक्ष
OY है। समीकरण y = |x| दो रेखाओं को निरूपित करता है।
यदि x > 0 तो y = x
तथा यदि x < 0, y = -x
अर्थात् y = x, x² = y को (0, 0), (1, 1) पर काटती है।
y= -x, x =y को (0,0), (-1, 1) पर काटती है।

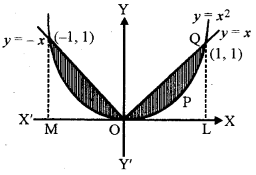
अतः
अभीष्ट क्षेत्रफल = 2 × क्षेत्र OPQO का क्षेत्रफल
= 2 [ΔOLQ का क्षेत्रफल - क्षेत्र OLQPO का क्षेत्रफल]

प्रश्न 13.
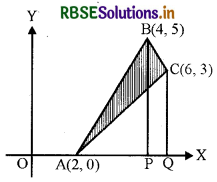
समाकलन विधि का उपयोग करते हुए, एक ऐसे त्रिभुज ABC का क्षेत्रफल ज्ञात कीजिए जिसके शीर्षों के निर्देशांक A(2,0), B(4, 5) एवं C(6, 3) हैं।
हल:
प्रश्नानुसार रेखा AB का समीकरण
y - 0 = \(\frac{5-0}{4-2}\)(x - 2)
अर्थात् y = (x - 2)

इसी प्रकार रेखा BC का समीकरण है
y - 5 = \(\frac{3-5}{6-4}\)(x - 4)
या y = - x + 9

तथा रेखा CA का समीकरण है
y - 3 = \(\frac{0-3}{2-6}\) (x - 2)
अभीष्ट क्षेत्रफल
= ΔABC द्वारा घेरा गया क्षेत्र का क्षेत्रफल = क्षेत्र ΔAPB का क्षेत्रफल + समलम्ब चतुर्भुज BPQC का क्षेत्रफल - क्षेत्र ΔAQC का क्षेत्रफल

प्रश्न 14.
समाकलन विधि का उपयोग करते हुए, रेखाओं 2x + y = 4, 3x - 2y = 6 एवं x - 3y + 5 = 0 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
प्रथम दो रेखाओं के समीकरण
2x + y =4 ..........(i)
3x - 2y = 6 .........(ii)

समीकरण (i) को 2 से गुणा करके (ii) में जोड़ने पर
7x = 14 ∴ x = 2

अब समीकरण (i) से
4 + y = 4 ∴ y = 0

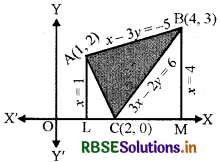
∴ बिन्दु C के निर्देशांक = (2, 0)
तीसरी रेखा का समीकरण x -3y = - 5 ......(iii)

समीकरण (iii) को 2 से गुणा करके समीकरण (i) में से घटाने पर
7y = 14 ∴ y= 2
पुनः समीकरण (i) से 2x + 2 = 4 ∴ x = 1

∴ बिन्दु A के निर्देशांक = (1, 2)
समीकरण 3x - 2y = 6 .......(ii)
x - 3y = -5 .........(iii)
समीकरण (iii) को 3 से गुणा करके समीकरण (ii) में से घटाने पर
7y = 21 ∴ y = 3

अब समीकरण (ii) से 3x - 6 = 6 ∴ x = 4
∴ बिन्दु B के निर्देशांक (4, 3) हैं।

त्रिभुज ABC का क्षेत्रफल= समलम्ब चतुर्भुज ALMB का क्षेत्रफल - ΔALC का क्षेत्रफल - ΔBCM का क्षेत्रफल

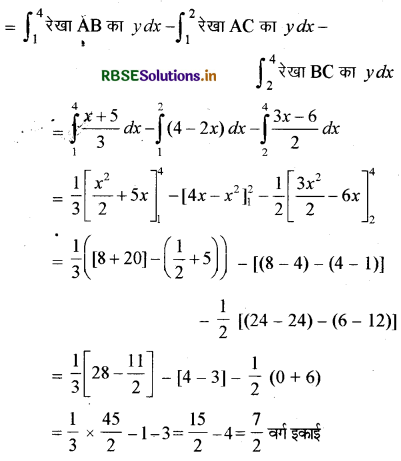
प्रश्न 15.
क्षेत्र {(x,y) :y² ≤ 4x, 4x² +4y² ≤ 9} का क्षेत्रफल ज्ञात कीजिए।
हल:
प्रश्नानुसार y² = 4x एक परवलय है जिसका शीर्ष मूल बिन्दु (0,0) है तथा जिसका अक्ष x-अक्ष है, साथ ही 4x² +4y² = 9 एक वृत्त को निरूपित करता है जिसका केन्द्र (0, 0) और त्रिज्या = \(\frac{3}{2}\) है।

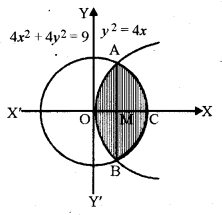
अतः y² = 4x और x² + y² = \(\frac{9}{4}\)
परवलय y² = 4x और वृत्त x² + y² = \(\frac{9}{4}\) के समीकरण को हल करने पर

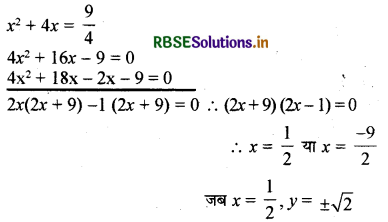
दोनों वक्र x-अक्ष के सापेक्ष सममित हैं, y² < 4x (1, 0) के लिए सत्य, है, अतः (1, 0) अर्ध समतल में स्थित है और प्रतिच्छेदन बिन्दु A(\(\frac{1}{2}\), √2) और B(\(\frac{1}{2}\), -√2)

अतः अभीष्ट क्षेत्रफल = छायांकित भाग का क्षेत्रफल = 2[OACMO का क्षेत्रफल

16 से 19 तक के प्रश्नों में सही उत्तर का चयन कीजिए

प्रश्न 16.
वक्र y = x³, x-अक्ष एवं कोटियों x = - 2, x = 1 से घिरे क्षेत्र का क्षेत्रफल है
(A) -9
(B) -\(\frac{15}{4}\)
(C) \(\frac{15}{4}\)
(D) \(\frac{17}{4}\)
हल:
(D) \(\frac{17}{4}\)

दिया गया है y = x³
तथा x = -2, x = 1

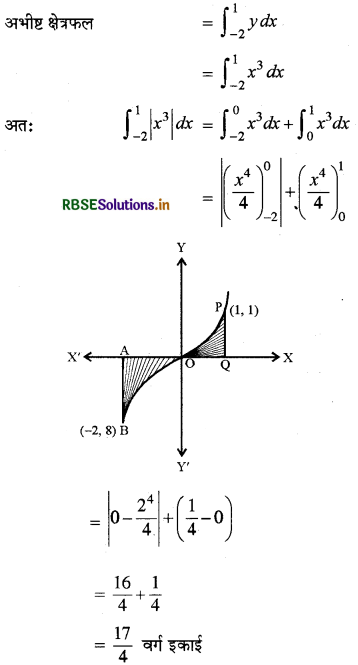
अतः सही विकल्प (D) है।

प्रश्न 17.
वक्र y = x|x|, x-अक्ष एवं कोटियों x = - 1 तथा x = 1 से घिरे क्षेत्र का क्षेत्रफल है
(A) 0
(B) \(\frac{1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{4}{3}\)
[संकेत–y = x² यदि x > 0 एवं y = -x² यदि x <0]
हल:
(C) \(\frac{2}{3}\)

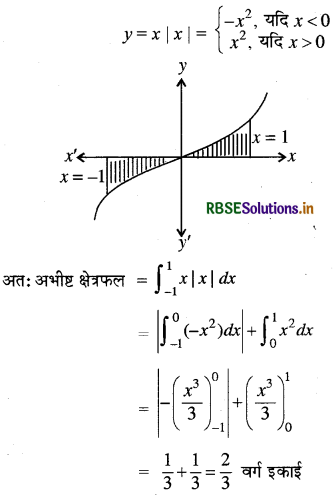
अतः सही विकल्प (C) है।

प्रश्न 18.
क्षेत्र y² > 6x और वृत्त x² + y² = 16 में सम्मिलित क्षेत्र का क्षेत्रफल है
(A) \(\frac{4}{3}\)(4π - √3)
(B) \(\frac{4}{3}\)(4π + √5)
(C) \(\frac{4}{3}\)(8π - √5)
(D) \(\frac{4}{3}\)(8π + √3)
हल:
(C) \(\frac{4}{3}\)(8π - √5)

दिया गया वृत्त x² + y² = 16 ...........(1)
तथा परवलय y² = 6x ...........(2)

समीकरण (1) तथा (2) से
x² + 6x = 16
⇒ x² + 6x - 16 = 0
⇒ (x + 8) (x - 2)= 0
⇒ x = -8,2
∵ x 2 0 अतःx = 2

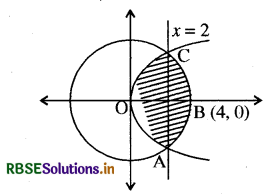
चूँकि क्षेत्रफल x-अक्ष के परितः सममित है, अत: अभीष्ट क्षेत्रफल

अतः सही विकल्प (C) है।

प्रश्न 19.
y-अक्ष, y = cos x एवं y = sin x, 0 ≤ x ≤ \(\frac{\pi}{2}\), से घिरे क्षेत्र का क्षेत्रफल है
(A) 2(√2 -1)
(B) √2 - 1
(C) √2 + 1
(D) √2
हल:
(B) √2 - 1

दिया गया है- y = cos x और y = sin x
अतः sin x = cos x
या tan x = 1
x = \(\frac{\pi}{4}\)

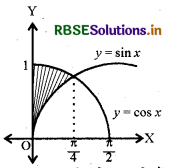
अतः दोनों वक्र x = 4 पर प्रतिच्छेद करते हैं। अभीष्ट क्षेत्रफल

अतः सही विकल्प (B) है।