RBSE Solutions for Class 12 Maths Chapter 8 Application of Integrals Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 8 Application of Integrals Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 8 Application of Integrals Miscellaneous Exercise

Question 1.
Find the area under the given curves and given lines:
(i) y = x², x = 1, x = 2 and x-axis
Answer:
Shaded region enclosed by the curves y = x², lines x = 1, x = 2 and x-axis is the required area shown in the figure.

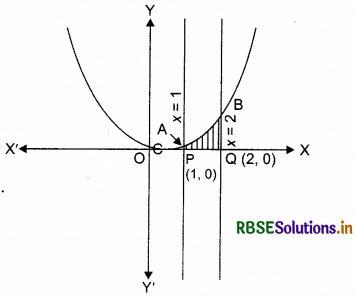
y = x² ....................... (i)
x = 1 ....................... (ii)
x = 2 ....................... (iii)
Solving equations (i) and (ii), we get,
y = 1
Hence, co-ordinate of point A are (1, 1).
Solving equations (2) and (3), we get,
y = 4
∴ co-ordinate of point B are (2,4).
Required area = area of region PQBAP
= \(\int_{1}^{2}\) y dx = \(\int_{1}^{2}\) x² dx
= \(\left[\frac{x^{3}}{3}\right]_{1}^{2}=\left(\frac{2^{3}}{3}-\frac{1}{3}\right)=\frac{8}{3}-\frac{1}{3}\)
= \(\frac{7}{3}\) sq.unit

(ii) y = x⁴, x = 1, x = 5 and x-axis
Answer:
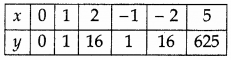
The given curve is y = x⁴. For all values of x, the value of y is positive real number. Some values of x and the corresponding values of y are given below:

Shaded region enclosed by the curve y = x⁴, lines x = 1, x = 5 and x-axis is the required area shown in the figure.

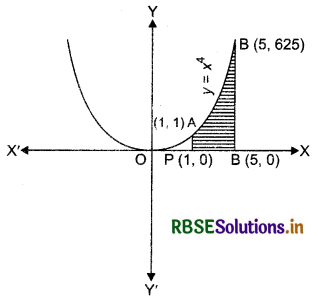
Required area = area of the region PQBAP
= ∫ (y for curve y = x⁴) dx

Question 2.
Find the area between the curves y = x and y = x².
Answer:
y = x is a straight line passing through origin O(0, 0) and y = x² is an upward parabola with its vertex at origin (0,0). On solving i x and y = x² we get x = 0, 1 and y = 0, 1.
Points of intersection are (0, 0) and (1, 1). Shaded region enclosed by the line y = x and parabola y = x² is the required area shown in the figure.

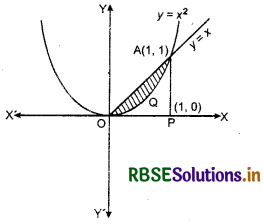
Required area = area of the region OQAO
= area of region OPAO - area of region OPAQO
= ∫ y(for line) dx - ∫ y (for parabola) dx

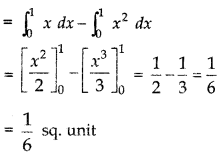
Question 3.
Find the area of the region lying in the first quadrant and bounded by y = 4x², x = 0, y = 1 and y = 4.
Answer:
y = 4x² is an upward parabola with its vertex at origin O(0, 0).

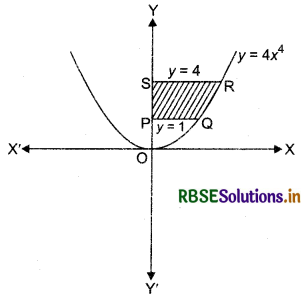
Equations of curves are
y = 4x² ...... (1)
y = 1 ....... (2)
y = 4 ........ (3)
Solving equations (1) and (2), we get x = ±\(\frac{1}{2}\).
So, points of intersection of y = 4x² and y = 1 are \(\left(\frac{1}{2}, 1\right)\) and \(\left(-\frac{1}{2}, 1\right)\).
On solving equations (1) and (3), we get x = ± 1.
So, points of intersection of y = 4x² and y = 4 are (1, 4) and (- 1, 4). Shaded region is the required area as shown in the figure.
Required area = area of region PQRSP
= ∫ x(for parabola y = 4x²)dy

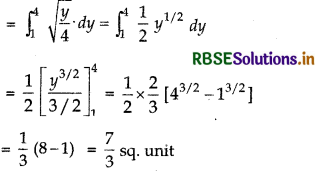
Question 4.
Sketch the graph of y = |x + 3| and evaluate:
\(\int_{-6}^{0}\) |x + 3| dx
Answer:
y = |x + 3|

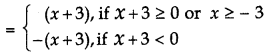
∴ y = |x + 3| represents the lines y = x + 3 and y = - x - 3.
Sketch of these lines are given in the figure below.

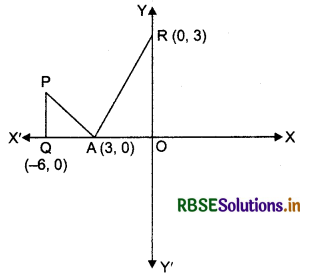
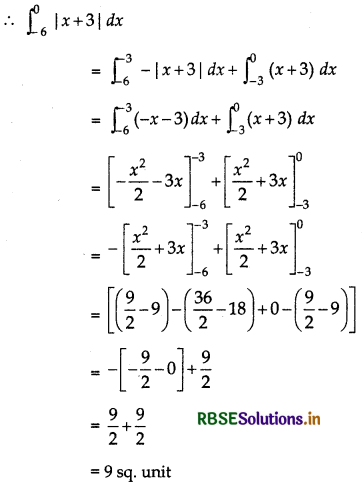
Question 5.
Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
Answer:
The shaded region enclosed by the curve y = sin x, and x = 0 and x = 2π is the required area given in the figure below. Some values of x and the corresponding values of y are given below.


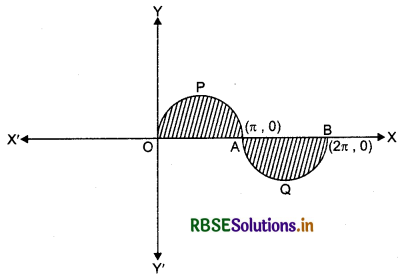
Required area = area of region OPAO + area of region AQBA

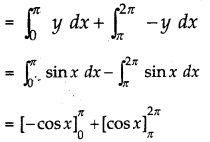
= - [cos π - cos 0] + [cos 2π - cos π]
= - [- 1 - 1] + [- 1(- 1)]
= - (- 2) + (1 + 1) = 2 + 2
= 4 sq.cm

Question 6.
Find the area enclosed between the parabola y² = 4ax and the line y = mx.
Answer:
Vertex of the parabola y² = 4ax is at origin 0(0,0).
Line y = mx passes through origin (0,0).
y² = 4ax ....... (1)
y = mx ........ (2)
Putting y = mx in equation (1), we get
m²x² = 4ax
∴ x(m²x - 4a) = 0
x = 0 or x = \(\frac{4 a}{m^2}\)
When x = 0, then y = o,
When x = \(\frac{4 a}{m^2}\), then y = m × \(\frac{4 a}{m^2}\) = \(\frac{4 a}{m}\)
Points of intersection of parabola y² = 4ax and line y = mx are O(0, 0) and A\(\left(\frac{4 a}{m^2}, \frac{4 a}{m}\right)\). Shaded region is the required area shown in the figure.

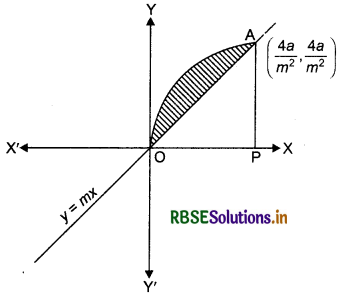
Required area = area of region OAQO
= ∫ y(for parabola) dx - ∫y(for line) dx

Question 7.
Find the area enclosed by the parabola 4y = 3x² and the line 2y = 3x + 12.
Answer:
Vertex of the upward parabola 4y = 3x² is at origin O(0, 0).
Equation of the parabola 4y = 3x² ..... (1)
Equation of line 2y = 3x + 12
On solving equations (1) and (2), we get
3x² = 6x + 24
or 3x² - 6x - 24 = 0
or x² - 2x - 8 = 0
or x² - 4x + 2x - 8 = 0
or x(x - 4) + 2(x - 4) = 0
or (x - 4) (x + 2) = 0
Either (x - 4) = 0 or x + 2 = 0
⇒ x = 4 or x = - 2
∴ When x = 4, then 4y = 3 × 4² or y = 12
When x = - 2, then 4y = 3(- 2)² or y = 3
Hence, points of intersection of parabola 4y = 3x² and
line 2y = 3x + 12 are P(- 2, 3) and A(4, 12).
Shaded region is the required area shown in the figure below.

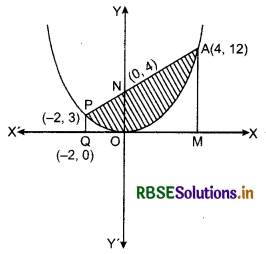
Required area area of region POAP
= area of trapezium PQMA - area of region PQOMA
= ∫ y (for line) dx - ∫ y (for parabola)dx

Question 8.
Find the area of the smaller region bounded by the ellipse \(\frac{x^2}{9}+\frac{y^2}{4}\) = 1 and the line \(\frac{x}{3}+\frac{y}{2}\) = 1.
Answer:
Ellipse \(\frac{x^2}{9}+\frac{y^2}{4}\) = 1 and line \(\frac{x}{a}+\frac{y}{b}\) = 1 intersect each other at points A(0, b) and B(a, 0). Shaded region is the required area shown in the figure.
Required small area APBA = area of region OBPAO - area of ΔAOB

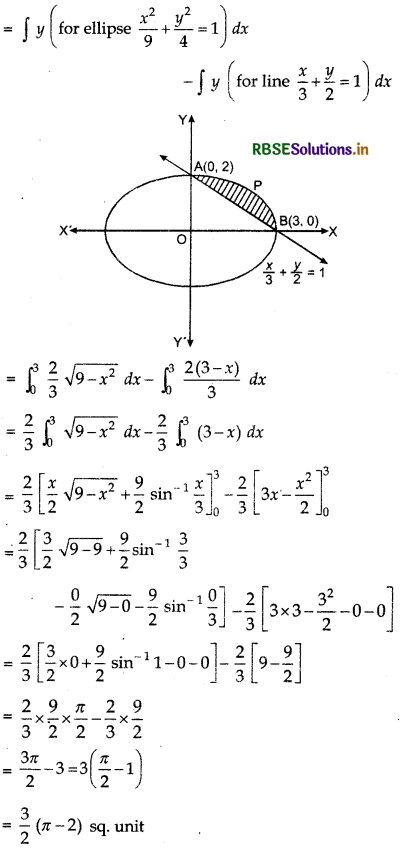
Question 9.
Find the area of the smaller region bounded by the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 and the line \(\frac{x}{a}+\frac{y}{b}\) = 1.
Answer:
Ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 and line \(\frac{x}{a}+\frac{y}{b}\) = 1 intersect each other at points A(0, b) and B(a, 0). Shaded region is the required area shown in the figure.
Required area = area of region APBA
= area of region OAPBO - area of ΔAOB

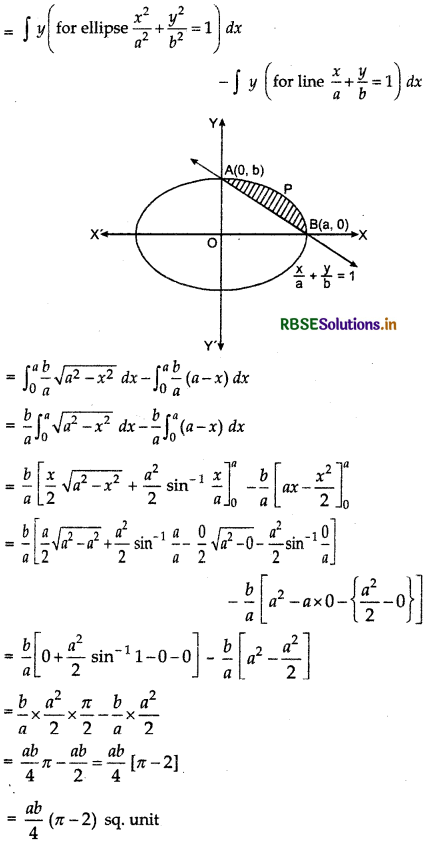
Question 10.
Find the area of the region enclosed by the parabola x² = y, the line y = x + 2 and the x-axis.
Answer:
Vertex of the parabola x² = y is at origin O(0,0) and it is symmetrical about x-axis. It is an upward parabola. Line y x + 2 meets at x-axis at point L(- 2, 0).

Parabola x² = y and line y = x + 2 intersect each other at points A(2, 4) and B(- 1, 1). Shaded region enclosed by parabola x² = y, line y = x +2 and x-axis is the required area shown in the figure below.
Required area = area of region BPOQAB
= area of region POQABP - area of region BOMAB
= ∫y(for line y = x + 2)dx - ∫ y(for parabola x² = y) dx

Question 11.
Using the method of integration, find the area bounded by the curve |x| + |y| = 1.
Answer:
Equation |x| + |y| = 1 represents four lines.
(i) If x > 0, y > 0, then x + y = 1 or y = 1 - x
(ii) If x < 0, y > 0, then - x + y = 1 or y = 1 + x
(iii) If x > 0, y < 0, then x - y = 1 or y = x - 1
(iv) If x < 0, y < 0 then - x - y = 1 or x + y = - 1
Shaded region enclosed by four lines is the required area shown in given figure.

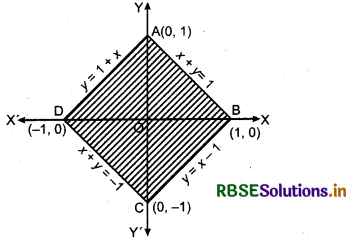
Required area = area of quadrilateral ABCD
= 4 × area of ∆AOB = 4\(\int_0^1\) y dx
= 4 \(\int_0^1\) (1 - x) dx = 4 \(\left[x-\frac{x^2}{2}\right]_0^1\)
= 4[1 - \(\frac{1}{2}\) - (0 - 0)] = 4 × \(\frac{1}{2}\)
= 2 sq. unit

Question 12.
Find the area bounded by curves {(x, y):y ≥ x² and y = |x| }.
Answer:
Curve y = x2 is an upward parabola with its vertex (0, 0) and it is symmetrical about y axis.
Equation y = |x| represent two straight lines.
When x > 0, then y = x
When x <0, then y = - x
Points of intersection of line y = x and parabola y = x² are O(0, 0) and A(1, 1).
Similarly, points of intersection of line y = - x and parabola y = x² are O(0, 0) and B(- 1,1).
Area bounded by lines y = x and y = - x, and parabola y = x² is shown by shaded region in the figure given below.

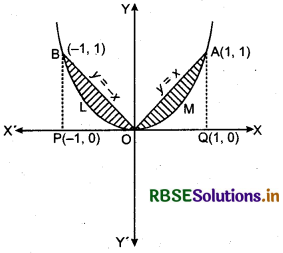
Required area = area of region BLOMA
= 2 × area of OMA
= 2 [area of ∆OQA - area of OMAQO]
= ∫y (for line y = x) dx - ∫ y (for parabola y = x²)dx

Question 13.
Using the method of integration find the area of the triangle ABC, co-ordinates of whose vertices are A(2, 0), B(4, 5) and C(6, 3).
Answer:
Shaded region of triangle is the required area shown in the figure below.

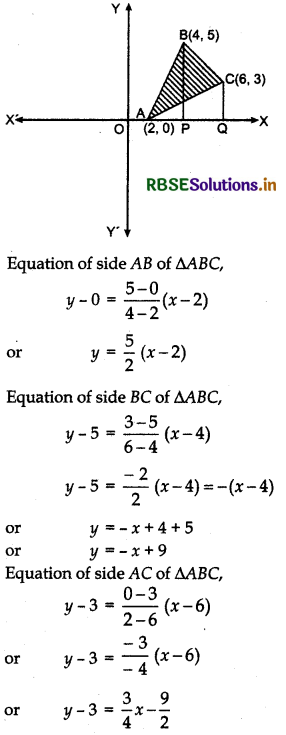
Question 14.
Using the method of integration find the area of the region bounded by lines:
2x + y = 4, 3x - 2y = 6 and x - 3y + 5 = 0
Answer:
Given lines are:
2x + y = 4 .......... (1)
3x - 2y = 6 .......... (2)
x - 3y = - 5 ........... (3)
On solving equations (1) and (2), we get x = 2 and y = 0.
Points intersection of lines (1) and (2) is (2, 0).
On solving equations (2) and (3), we get x = 4, y = 3.
∴ intersection of lines (2) and (3) is (4, 3).
Solving equations (1) and (3), we get x = 1 and y = 2.
Points of intersection of lines (1) and (3) is (1, 2)
Shaded region enclosed with the three lines is the required area shown in the figure below.

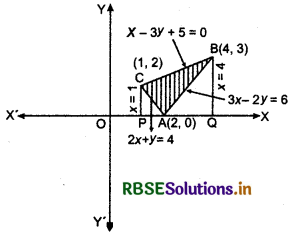
Required area = area of ∆ABC
= Area of trapezium PQBC - area of ∆PAC - area of ∆ABQ
= ∫ y(for line x - 3y + 5 = 0)dx - ∫y(for line 2x + y = 4)dx - ∫ y (for line 3x - 2y = 6) dx

Question 15.
Find the area of the region:
{(x, y) : y² ≤ 4x, 4x² + 4y² ≤ 9}
Answer:
Curve y² = 4x is a parabola with its vertex origin O(0, 0).
Curve 4x² + 4y² = 9 or x² + y² = \(\frac{9}{4}\) is a circle with its centre (0, 0) and radius \(\frac{3}{2}\). Both the curves are symmetrical about x-axis.
On solving y² = 4x and 4x² + 4y² = 9, we get
x = - \(\frac{9}{2}\), x = \(\frac{1}{2}\) and y = ± √2
But, y is not real for x = -\(\frac{9}{2}\).
Hence points of intersection of the curves are A\(\left(\frac{1}{2}, \sqrt{2}\right)\) and B\(\left(\frac{1}{2}, -\sqrt{2}\right)\).
Shaded region enclosed by the given curves is the required area shown in the figure below.

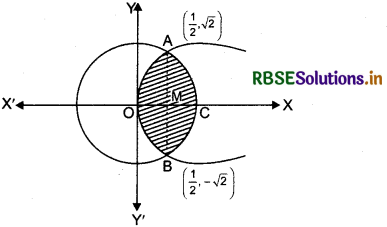
Required area = 2 × area of region AOCA
= 2 [area of region OMAQ + area of region MCAM]
= 2∫y (for parabola) dx + 2∫ y (for circle) dx

Question 16.
Area bounded by the curve y = x3, the x-axis and the ordinates x = - 2, x = 1 is:
(A) - 9
(B) - \(\frac{15}{4}\)
(C) \(\frac{15}{4}\)
(D) \(\frac{17}{4}\)
Answer:
Point of intersection of the curves y = x³ and x = - 2
is A(- 2, - 8) and point of intersection of the curves y = x³ and x = 1 is B(1, 1).
Shaded region enclosed by the curves, is the required area shown in the figure below.

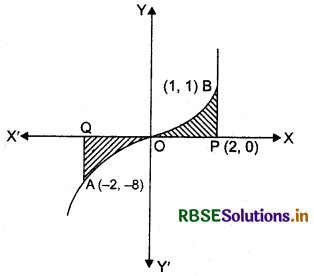
Required area = area of region AOQA + area of region OPBO
= ∫y dx + ∫y dx

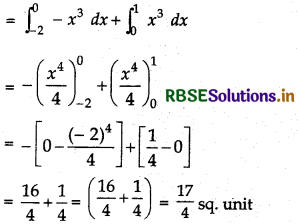
Hence, (D) is the correct answer.

Question 17.
The area bounded by the curve y = x|x|, x-axis and the ordinates x = - 1 and x = 1 is given by:
(A) 0
(B) \(\frac{1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{4}{3}\)
Answer:
Required area = 2 area of region BOQB

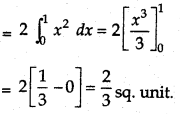
Hence (C) is the correct answer.

Question 18.
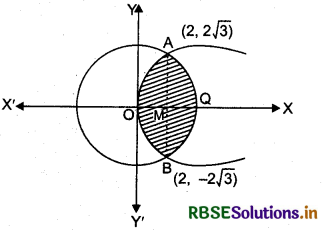
The area of the circle x² + y² = 16 exterior of the parabola y² = 6x is:
(A) \(\frac{4}{3}\) (4π - √3)
(B) \(\frac{4}{3}\) (4π + √3)
(C) \(\frac{4}{3}\) (8π - √3)
(D) \(\frac{4}{3}\) (8π + √3)
Answer:
Points of intersection of curves y² = 6x and x² + y² = 16 are A(2, 2√3) and B(2, - 2√3).
y² = 6x is a parabola with its vertex at origin O(0, 0).
x² + y² = 16 is a circle with its centre at origin O(0, 0) and radius 4 units.
Shaded region enclosed by the curves y² = 6x and x² + y² = 16 is shown in the given figure.

Both the curves are symmetrical about x-axis
Shaded area = area of region OBQAO = 2 × [area of region OMQAO]
2[area of region OAM + area of region AMQI
2[∫ y (for parabola y² = 6x) dx + ∫ y (for circle x² + y² = 16) dx]


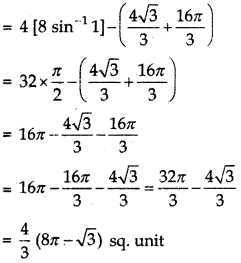
Hence, (C) is the correct answer.

Question 19.
The area bounded by the y-axis, y = cos x and y = sin x when 0 < x < \(\frac{\pi}{2}\) is:
(A) 2(√2 - 1)
(B) √2 - 1
(C) √2 + 1
(D) √2
Answer:
On solving equations y = cos x and y = sin x, we get
tan x = 1 = tan \(\frac{\pi}{4}\)
∴ x = \(\frac{\pi}{4}\)
∴ sin x = cos x = \(\frac{1}{\sqrt{2}}\)
Shaded region enclosed by the y-axis, y = cos x, y = sin x is the required area shown in the figure below.
(0 ≤ x ≤ \(\frac{\pi}{2}\))

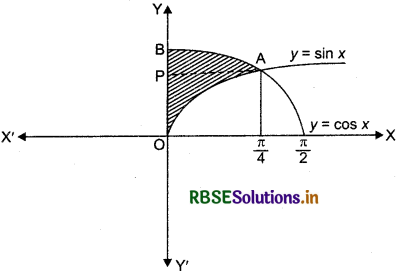
Required area = area of region QABO
= area of region QAP + area of region APO
= ∫x (for y = sin x) dy + ∫x (for y = cos x) dy
= \(\int_0^{1 / \sqrt{2}}\) sin^-1 y dy + \(\int_0^{1 / \sqrt{2}}\) cos^-1 y dy
Using integration by parts in both integrals, taking 1 as the second function

Hence (B) is the correct answer.