RBSE Solutions for Class 12 Maths Chapter 8 Application of Integrals Ex 8.2
Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 8 Application of Integrals Ex 8.2 Textbook Exercise Questions and Answers.
Rajasthan Board RBSE Solutions for Class 12 Maths in Hindi Medium & English Medium are part of RBSE Solutions for Class 12. Students can also read RBSE Class 12 Maths Important Questions for exam preparation. Students can also go through RBSE Class 12 Maths Notes to understand and remember the concepts easily.
RBSE Class 12 Maths Solutions Chapter 8 Application of Integrals Ex 8.2
Question 1.
Find the area of the circle 4x2 + 4y2 = 9 which is interior to the parabola x2 = 4y.
Answer:
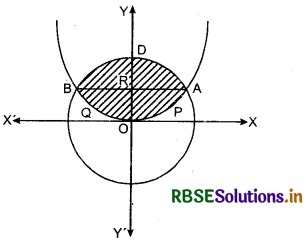
x2 = 4y is upward parabola with its vertex at origin O(0, 0). 4x2 + 4y2 = 9 or x2 + y2 = \(\frac{9}{4}\) is a circle with its centre at O(0, 0) and radius \(\frac{3}{2}\).
Parabola x2 = 4y is symmetrical to y-axis, wherever circle x2 + y2 = \(\frac{9}{4}\) is symmetrical to both axis. Shaded region is the required area common to the parabola and circle as shown in the figure below.
Equation of the parabola
x2 = 4y ....... (1)
Equation.of the circle
x2 + y2 = \(\frac{9}{4}\) ........ (2)
Putting x2 = 4y from equation (1) in equation (2), we get
4y + y2 = \(\frac{9}{4}\)
or 4y2 + 16y - 9 = 0
or 4y2 + 18y - 2y - 9 = 0
or 2y(2y + 9) - 1(2y + 9) = 0
or (2y + 9) (2y - 1) = 0
or 2y + 9 = 0 or 2y - 1 = 0
y = - \(\frac{9}{2}\) or y = \(\frac{1}{2}\)
∴ When y = \(\frac{-9}{2}\), from x2 = 4y]
x2 = 4 × (- 9/2) = - 18
or x = ± √- 18 which is not real.
∴ When y = \(\frac{1}{2}\), then from x2 = 4y
x2 = 4 × \(\frac{1}{2}\) = 2
or x = ±√2
Thus, points of intersection of the curves are A(√2, \(\frac{1}{2}\)) and B (-√2, \(\frac{1}{2}\)). Co-ordinate of D is (0, \(\frac{3}{2}\)).
(∵ radius of circle is \(\frac{3}{2}\) and point D is on circle and y-axis both)
Required area = area of OPADBQQ
= 2 × Area of OPARBQO
2[Area of OPARO + area of RADR]
= 2[∫(x for parabola) di, + ∫(x for circle) dy]
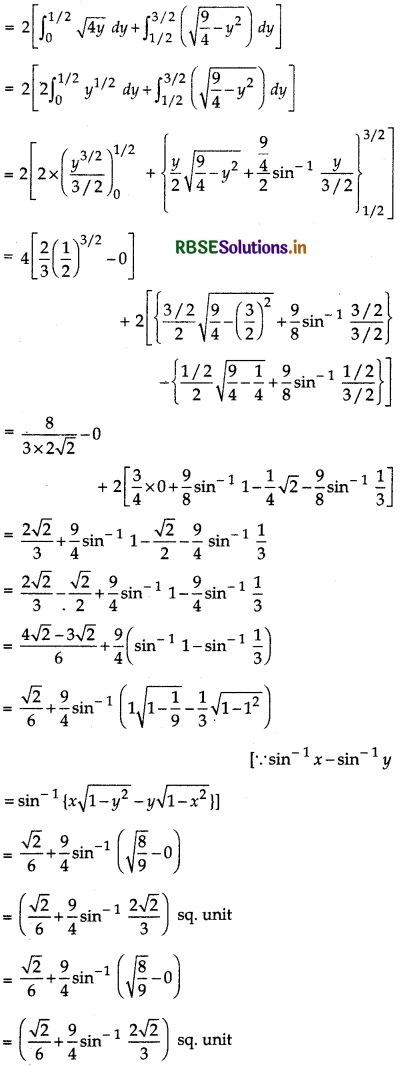

Question 2.
Find the area bounded by curves (x - 1)2 + y2 = 1 and x2 + y2 = 1.
Answer:
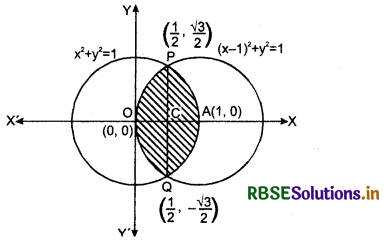
Curve (x - 1)2 + y2 = 1 is a circle with its centre (1, 0) and radius I unit and curve x2 + y2 = 1 is also a circle with its centre origin (0, 0) and radius 1 unit. Shaded region is the required area shown in the given figure.
Equations of the circle are:
(x - 1)2 + y2 = 1 ....... (1)
and x2 + y2 = 1 ......... (2)
Putting y2 = 1 - x2 from (2) in equation (1), we get
(x - 1)2 + 1 - x2 = 1
or x2 - 2x + 1 + 1 - x2 = 1
or - 2x = 1 - 2
or - 2x = - 1
or x = \(\frac{1}{2}\)
∴ y2 = 1 - x2
= 1 - \(\left(\frac{1}{2}\right)^{2}\) = 1 - \(\frac{1}{4}\) = \(\frac{3}{4}\)
or y = ± \(\frac{\sqrt{3}}{2}\)
Hence, both the circle intersect each other, at points P\(\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)\) and Q\(\left(\frac{1}{2},-\frac{\sqrt{3}}{2}\right)\).
Required area = area of OQAPO
= 2 × area of OAPO


Question 3.
Find the area of the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 3.
Answer:
Curve y = x2 + 2 is a parabola with its vertex (0, 2). y = x is a straight line which passes through origin (0, 0). Shaded region is the required area shown in the figure below. Point of intersection of curve y = x2 + 2 and line x 3 is Q (3, 11).
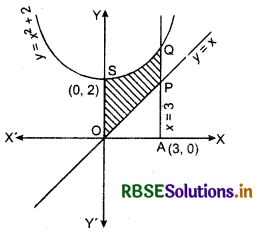
Required area area of PQSOP
= area of OAPQSOA - area of ∆OAP
=∫ y(for parabola) dx + ∫ y(for line) dx

Question 4.
Using integration, find the area of region bounded by the triangle whose vertices are (- 1, 0), (1, 3) and (3, 2).
Answer:
The points A(- 1, 0), B(1, 3) and C(3, 2) are plotted and joined. Shaded region is the required area shown in the figure below.
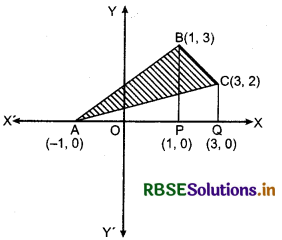
Required area = area of ∆ABC
= area of ∆ABP + area of trapezium BPQC - area of ∆AQC ...... (1)
Equation of line AB
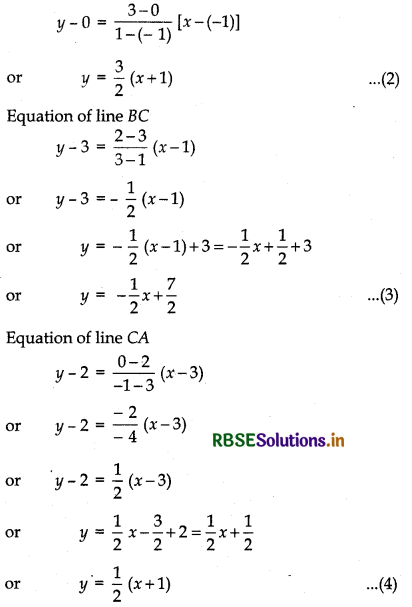

Now, putting the values of area of ∆ABP, area of trapezium BPAQ and area of ∆AQC in equation (1),
we get Required area of ∆ABC
= 3 + 5 - 4 = 4 sq. unit
∴ Area of ∆ABC = 4sq.unit

Question 5.
Using integration, find the area of the triangular region whose sides have the equations y = 2x + 1, y = 3x + 1 and x = 4.
Answer:
Let the sides of the triangle are AB, BC and AC.
Then, equation of AB y = 2x + 1 ...(1)
Equation of BC y = 3x + 1 ......... (2)
and equation of AC x = 4 ......... (3)
From equations (1) and (2), we get
3x + 1 = 2x + 1
∴ 3x - 2x = 0 ⇒ x = 0
Then y = 1
∴ Co-ordinate of point B are (0, 1).
From equations (2) and (3), we get
y = 3 × 4 + 1 = 13
Co-ordinate of point C are (4, 13).
From equations (1) and (3), we get
y = 2 × 4 + 1 = 9
∴ Co-ordinate of point A are (4, 9).
∆ABC is shown in the figure.
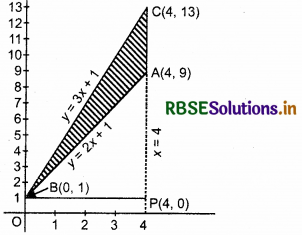
Area of ∆ABC = area of trapezium BOPC - area of trapezium BOPA
= ∫ (y for line BC) dx - ∫ (y for line AB) dx
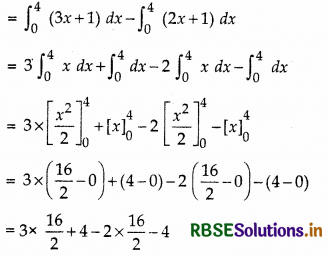
= 24 + 14 - 16 - 4 = 8 sq.unit
Thus, area of ∆ABC = 8 sq.unit
Question 6.
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is:
(A) 2(π - 2)
(B) π - 2
(C) 2π - 1
(D) 2(π + 2)
Answer:
Shaded region enclosed by circle x2 + y2 = 4 and line x + y = 2, is the required area as shown in the figure below.
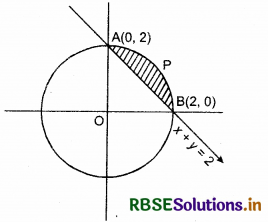
Required area = Area of OBPAO - Area of ∆OAB
= ∫ y(for circle) dx - ∫y (for line) dx
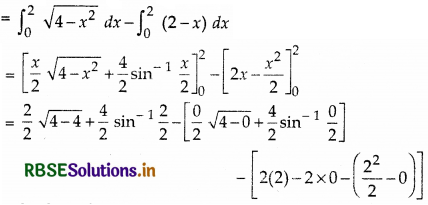
= 0 + 2 sin-1 1 - 0 + 0 - 4 + 2
= 2 × \(\frac{\pi}{2}\) - 2 = (π - 2) sq.units
Hence, (B) is the correct answer.

Question 7.
Area lying between the curves y2 = 4x and y = 2x is:
(A) \(\frac{2}{3}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{1}{4}\)
(D) \(\frac{3}{4}\)
Answer:
Shaded region enclosed by the parabola y2 = 4x and line y = 2x, is the required area shown in the figure below.
Both the curves pass through the origin O and the curve y2 = 4x is symmetrical about x-axis.
Equations of the curves are:
y2 = 4x ..... (1)
y = 2x ....... (2)
Solving the equations, we get,
(2x)2 = 4x
or 4x2 = 4x
or 4x(x - 1) = 0
x = 0 or x = 1
Co-ordinate of point A = (1, 2)
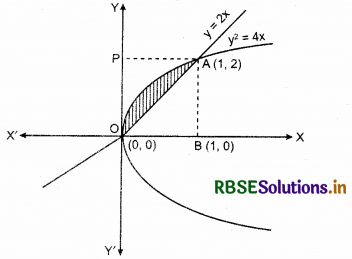
Required area = area of OPAO
= area of OBAPO - area of AOAB
= ∫y (for parabola)dx - ∫(for line) dx
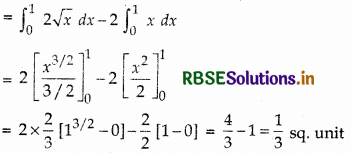
Hence, (B) is the correct answer.
Question 8.
Find the area of the parabola y2 = 4ax bounded by its latus rectum.
Answer:
From figure, the vertex of the parabola y2 = 4ax is at origin (0, 0). The equation of the latus rectum LSL is x = a. Also, parabola is symmetrical about the x-axis.
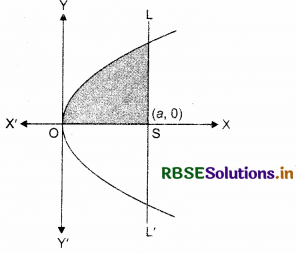
The required area of the region OLL'O
= 2(area of the region OLSO)
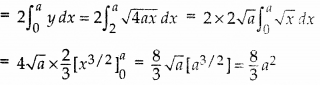

- RBSE Class 12 Maths Notes Chapter 13 Probability
- RBSE Class 12 Maths Notes Chapter 12 Linear Programming
- RBSE Class 12 Maths Notes Chapter 11 Three Dimensional Geometry
- RBSE Class 12 Maths Notes Chapter 10 Vector Algebra
- RBSE Class 12 Maths Notes Chapter 9 Differential Equations
- RBSE Class 12 Maths Notes Chapter 8 Application of Integrals
- RBSE Class 12 Maths Notes Chapter 7 Integrals
- RBSE Class 12 Maths Notes Chapter 6 Application of Derivatives
- RBSE Class 12 Maths Notes Chapter 5 Continuity and Differentiability
- RBSE Class 12 Maths Notes Chapter 4 Determinants
- RBSE Class 12 Maths Notes Chapter 3 Matrices