RBSE Solutions for Class 12 Maths Chapter 8 Application of Integrals Ex 8.1

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 8 Application of Integrals Ex 8.1 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 8 Application of Integrals Ex 8.1

Question 1.
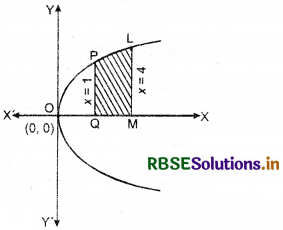
Find the area of the region bounded by the curve y² = x and the lines x = 1, x = 4 and the x-axis in the first quadrant.
Answer:
Parabola y² = x is symmetrical about x-axis whose vertex is origin O(0, 0).
The area of the region bounded by the lines x = 1, x = 4, x-axis and curve y² = x is shown in the figure below.
Required area PQMLP
= \(\int_{1}^{4}\) y dx = \(\int_{1}^{4}\) √x dx (∵ y² = x)

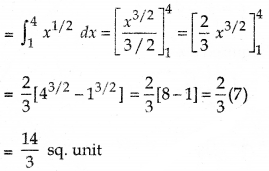
Question 2.
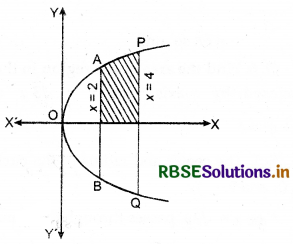
Find the area of the region bounded by y² = 9x, x = 2, x = 4 and the x-axis in the first quadrant.
Answer:
Curve (parabola) y² = 9x, is symmetrical about x-axis with vertex at origin O(0, 0). The area of the region bounded by the lines x = 2, x = 4, x-axis and curve y² = 9x is shown in the figure below.

Question 3.
Find the area of the region bounded by x² = 4y, y = 2, y = 4 and the y-axis ¡n the first quadrant.
Answer:
Curve x² = 4y is a parabola whose vertex is at origin and it is symmetrical about x-axis.
The area of the region bounded by the lines y = 2, y = 4, y-axis and curve x² = 4y is shown in the figure below.

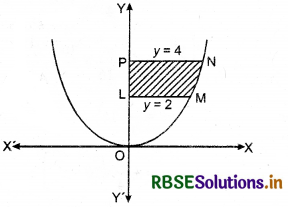
The required area is LMNPL.

Question 4.
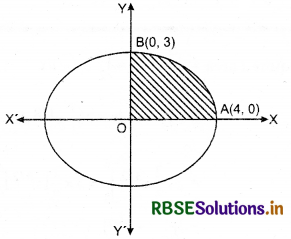
Find the area of the region bounded by the ellipse \(\frac{x^{2}}{16}+\frac{y^{2}}{9}\) = 1.
Answer:
Ellipse \(\frac{x^{2}}{16}+\frac{y^{2}}{9}\) = 1, is symmetrical about both x-axis and y-axis.

Question 5.
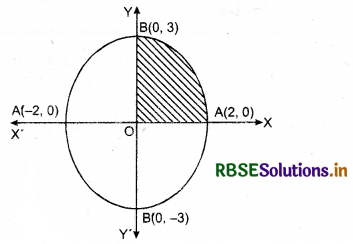
Find the area of the region bounded by the ellipse \(\frac{x^{2}}{4}+\frac{y^{2}}{9}\) = 1.
Answer:
Ellipse \(\frac{x^{2}}{4}+\frac{y^{2}}{9}\) = 1 is symmetrical about both axis. The center of this ellipse is at (0, 0).

Question 6.
Find the area of the region in the st quadrant enclosed by x-axis, line x = √3 y and the circle x² + y² = 4.
Answer:
The centre and radius of the circle x² + y² = 4 is (0, 0) and 2.
Line x = √3y passes through (0, 0) and (√3, 1)

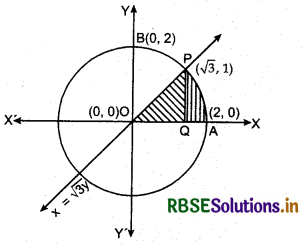
Required area = Shaded region
= Area of OQP + Area of QAP
= ∫ y(for line)dx + ∫ y(for circle)dx

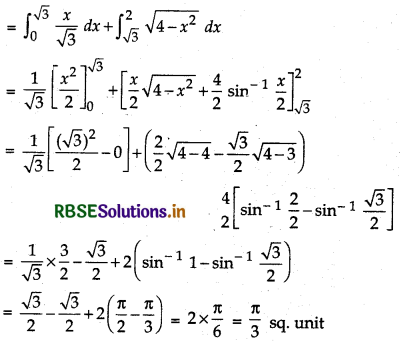
Question 7.
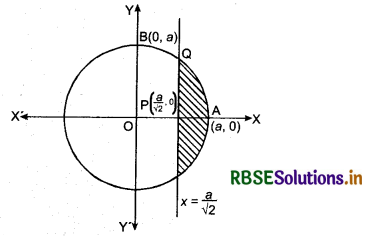
Find the area of the smaller part of the circle x² + y² = a² cut off by the line x = \(\frac{a}{\sqrt{2}}\).
Answer:
x² + y² = a² is a circle with centre 0(0,0) and radius a.
Line x = \(\frac{a}{\sqrt{2}}\) is parallel to y-axis at a distance \(\frac{a}{\sqrt{2}}\) from origin.
Shaded region bounded by the circle x² + y² = a² and y-axis a line x = \(\frac{a}{\sqrt{2}}\) is shown in the figure.
Points of intersection of line x = \(\frac{a}{\sqrt{2}}\) and circle x² + y² = a² are

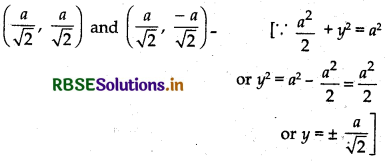
∴ Required area = 2[area of APQA]

Question 8.
The area between x = y² and x = 4 is divided into two equal parts by the line x = a. Find the value of a.
Answer:
Curve x = y² is a parabola whose vertex is at origin and it is symmetrical about x-axis. Line x = 4 is parallel to y-axis at a distance 4 units from origin or y-axis.

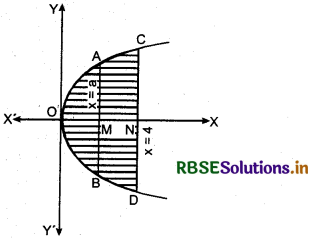
Area bounded by the curve x = y² and line x = 4 is ODCA
Now, area of ODCO = 2 × CONC

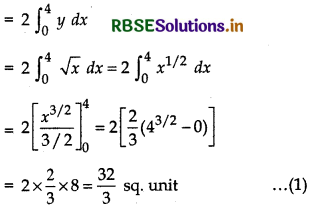
Line x = a is at a distance a units from y-axis.
Area bounded by the curve x = y² and line x = a is AOBA
Now, Area of AOBA = 2 × Area of AOMA

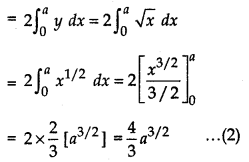
According to the question,
Area of ODCO = 2 × area of AOBA

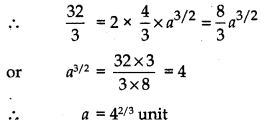
Question 9.
Find the area of the region bounded by the parabola y = x² and y = |x|.
Answer:
Clearly, x² = y represents a parabola with vertex at origin and it opens upwards.
Equation y = |x|, represent two lines y = x passing through the origin and makes an angle as 45° and 135° with the positive direction of the x-axis.

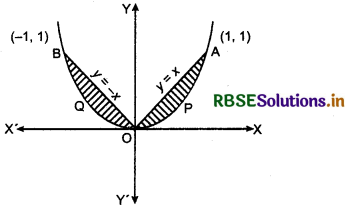
Lines y = x and y = - x cuts the parabola y = x² at points O(0, 0), A (1, 1) and B(- 1, 1).
The required region is the shaded region as shown in
the figure. Both the regions are symmetrical about y-axis.
∴ Required area
= 2(shaded area in the first quadrant)
= 2 × area of APOA

Question 10.
Find the area bounded by the curve x² = 4y and the line x = 4y - 2.
Answer:
Clearly x² = 4y is a parabola with vertex at origin 0(0, 0) and it opens upwards. Parabola x² = 4y is symmetrical about y-axis.
Equation of curve x² = 4y ....... (1)
Equation of line x = 4y - 2 ........ (2)
Solving equations (1) and (2), we get
(4y - 2)² = 4y
or 16y² + 4 - 16y = 4y
or 16y² - 16y - 4y + 4 = 0
or 16y² - 20y + 4 = 0
or 4y² - 5y + 1 = 0
or 4y² - (4 + 1)y + 1 = 0
or 4y² - 4y - y + 1 = 0
or 4y(y - 1) - 1(y - 1) = 0
or (4y - 1) (y - 1) = 0
∴ 4y - 1 = 0 or y - 1 = 0
or y = \(\frac{1}{4}\) or y = 1
∴ From equation (2), we get
When y = \(\frac{1}{4}\), then x = 4 × \(\frac{1}{4}\) - 2 = - 1
When y = 1, then x = 4 × 1 - 2 = 2
∴ Points of intersection of line x = 4y - 2 and curve x² = 4y are A(2, 1) and B\(\left(-1, \frac{1}{4}\right)\).
Clearly, shaded region is the required area AOBA as shown in figure below.

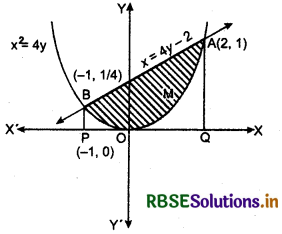
Area of AOBA
= area of AQOPBA - (area of AQO + area of OPB)

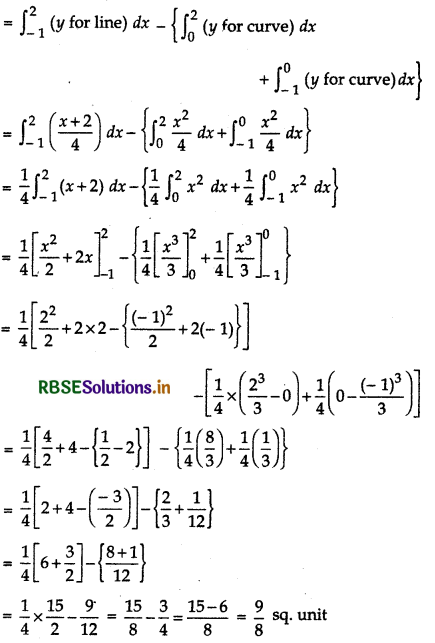
Question 11.
Find the area of the region bounded by the curve y² = 4x and the line x = 3.
Answer:
The curve y² = 4x is a parabola which is symmetrical about x-axis with vertex at origin O.
Line x = 3 is parallel to y-axis at a positive distance of 3 units from it.
Required area is AOBA which is shown in figure.

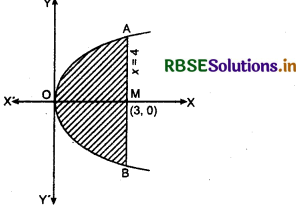
Area of AOBA = 2 × area of AMOA

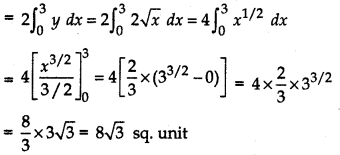
Question 12.
Area lying in the first quadrant and bounded by the circle x² + y² = 4 and the lines x = 0 and x = 2 is:
(A) π
(B) \(\frac{\pi}{2}\)
(C) \(\frac{\pi}{3}\)
(D) \(\frac{\pi}{4}\)
Answer:
Shaded region of first quadrant is shown in figure by the circle x² + y² = 4 and the lines x = 0 and x = 2.

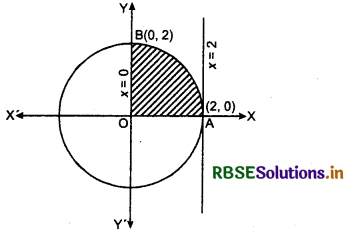
Required area AOBA

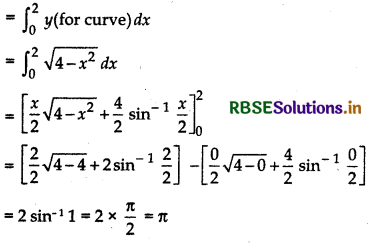
Hence, (A) is the correct answer.

Question 13.
Area lying in the first quadrant and bounded by the curve y² = 4x, and the y-axis and the line y = 3 is:
(A) 2
(B) \(\frac{9}{4}\)
(C) \(\frac{9}{3}\)
(D) \(\frac{9}{2}\)
Answer:
Curve y² = 4x is a parabola with vertex at origin O and it is symmetrical about x-axis.
Shaded area which is AOBA, bounded by the curve y² = 4x, y-axis and line y = 3 is shown in the figure below.

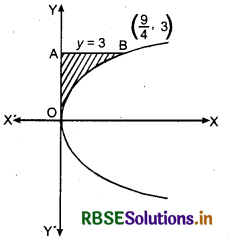
∴ Required area AOBA

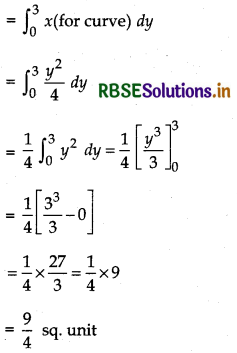
Hence, (B) is the correct answer.