RBSE Solutions for Class 12 Maths Chapter 7 Integrals Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 7 Integrals Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 7 Integrals Miscellaneous Exercise

Question 1.
∫\(\frac{1}{x-x^{3}}\) dx
Answer:
Let \(\frac{1}{x-x^{3}}=\frac{1}{x\left(1-x^{2}\right)}=\frac{1}{x(1+x)(1-x)}\)
= \(\frac{A}{x}+\frac{B}{1+x}+\frac{C}{1-x}\)
⇒ 1 = A(1 + x)(1 - x) + Bx(1 - x) + Cx(1 + x) ...... (1)
Putting x = 0 in (1), we get
1 = A(1 + 0) (1 - 0) ⇒ A = 1
Putting x = - 1 in (1), we get
1 = B(- 1) (1 + 1) ⇒ B = - \(\frac{1}{2}\)
Putting x = 1 in (1), we get
1 = C(1) (1 + 1) ⇒ C = \(\frac{1}{2}\)

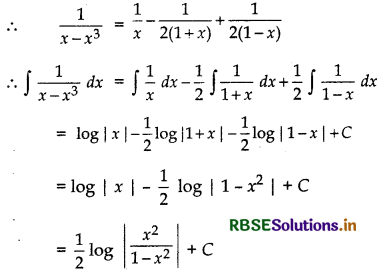
Question 2.
\(\frac{1}{\sqrt{x+a}+\sqrt{x+b}}\)
Answer:

Question 3.
\(\frac{1}{x \sqrt{a x-x^{2}}}\)
Answer:

Question 4.
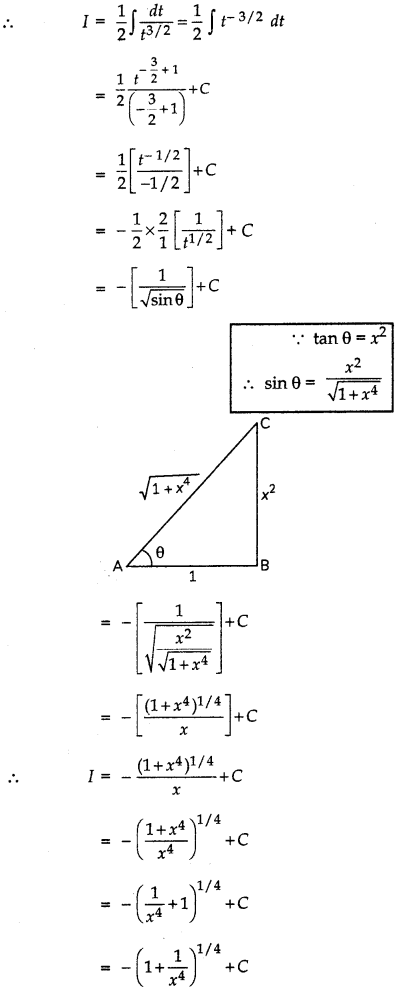
\(\frac{1}{x^{2}\left(x^{4}+1\right)^{3 / 4}}\)
Answer:

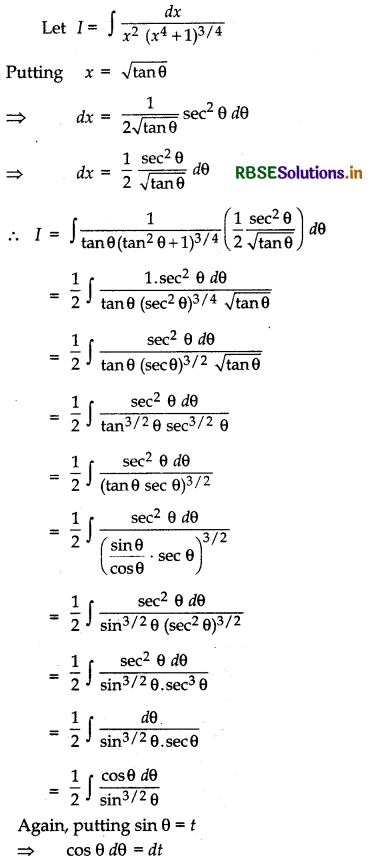
Question 5.
\(\frac{1}{x^{1 / 2}+x^{1 / 3}}\)
Answer:

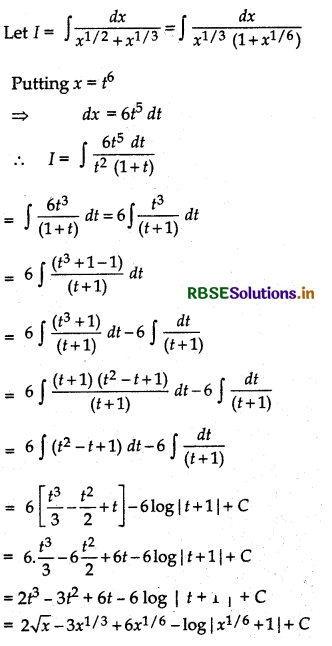
Question 6.
\(\frac{5 x}{(x+1)\left(x^{2}+9\right)}\)
Answer:
Let I = ∫\(\frac{5 x}{(x+1)\left(x^{2}+9\right)}\) ....... (1)
Now \(\frac{5 x}{(x+1)\left(x^{2}+9\right)}=\frac{A}{(x+1)}+\frac{B x+C}{\left(x^{2}+9\right)}\)
5x = A(x² + 9 + (x + 1) (Bx + C)
or 5x = Ax² + 9A + Bx² + Bx + Cx + C
or 5x = (A + B)x² + (B + C)x + 9A + C
Equating the coefficients of x, x² and constant term on both sides, we get
A + B = 0, B + C = 5, 9A + C = 0
Now, solving these equations, we get

Question 7.
\(\frac{\sin x}{\sin (x-a)}\)
Answer:
Let I = ∫\(\frac{\sin x}{\sin (x-a)}\) dx
Putting x - a = t
⇒ dx = dt
and x = t + a

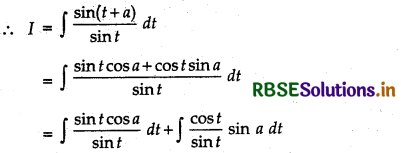
= cos a ∫1 dt + sin a ∫cot t dt
= t cos a + sin a log |sin t| + C₁
= (x - a) cos a + sin a log |sin (x - a)| + C₁
= sin a log |sin (x - a)| + x cos a - a cos a + C₁
∴ I = sin a log |sin (x - a)| + x cos a + C
(∵ C = C₁ - a cos a)

Question 8.
\(\frac{e^{5 \log x}-e^{4 \log x}}{e^{3 \log x}-e^{2} \log x}\)
Answer:

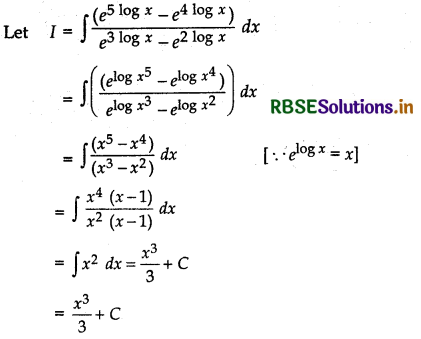
Question 9.
\(\frac{\cos x}{\sqrt{4-\sin ^{2} x}}\)
Answer:
Let I = ∫ \(\frac{\cos x}{\sqrt{4-\sin ^{2} x}}\) dx
Putting sin x = t
⇒ cos x dx = dt
∴ I = ∫ \(\frac{d t}{\sqrt{4-t^{2}}}\) = sin^-1 \(\frac{t}{2}\) + C
∴ I = sin^-1 \(\left(\frac{\sin x}{2}\right)\) + C

Question 10.
\(\frac{\sin ^{8} x-\cos ^{8} x}{1-2 \sin ^{2} x \cos ^{2} x}\)
Answer:

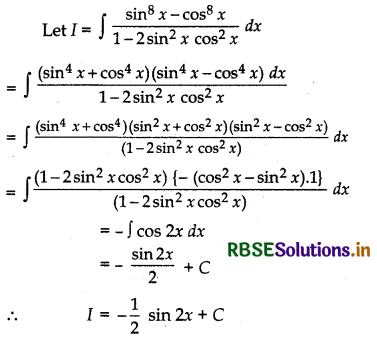
Question 11.
\(\frac{1}{\cos (x+a) \cos (x+b)}\)
Answer:

Question 12.
\(\frac{x^{3}}{\sqrt{1-x^{8}}}\)
Answer:
Let I = ∫\(\frac{x^{3}}{\sqrt{1-\left(x^{4}\right)^{2}}}\) dx
Putting x⁴ = t
⇒ 4x³ dx = dt
or x³.dx = \(\frac{1}{4}\)dt
∴ I = \(\frac{1}{4} \int \frac{d t}{\sqrt{1-t^{2}}}=\frac{1}{4}\) sin^-1 t + C
= \(\frac{1}{4}\) sin^-1 (x⁴) + C

Question 13.
\(\frac{e^{x}}{\left(1+e^{x}\right)\left(2+e^{x}\right)}\)
Answer:
Let I = \(\frac{e^{x} d x}{\left(1+e^{x}\right)\left(2+e^{x}\right)}\)
Putting e^x = t
⇒ e^x dx = dt
∴ I = ∫\(\frac{d t}{(1+t)(2+t)}\)
Now \(\frac{1}{(1+t)(2+t)}=\frac{A}{1+t}+\frac{B}{(2+t)}\)
1 = A(2 + t) + B(1 + t)
= 2A + At + B + Bt
= (A + B)t + 2A + B
Now, equating the coefficients of t and constant term on both sides, we get
A + B = 0 and 2A + B = 1
Solving equations, we get
A = 1, B = - 1
∴ \(\frac{1}{(1+t)(2+t)}=\frac{1}{(1+t)}-\frac{1}{(2+t)}\)
∴ I = ∫\(\frac{d t}{1+t}\) - ∫\(\frac{d t}{2+t}\)
= log |1 + t| - log |2 + t| + C
= log |1 + e^x| - log |2 + e^x| + C
= log \(\left|\frac{1+e^{x}}{2+e^{x}}\right|\) + C

Question 14.
\(\frac{1}{\left(x^{2}+1\right)\left(x^{2}+4\right)}\)
Answer:
Let I = ∫\(\frac{d x}{\left(x^{2}+1\right)\left(x^{2}+4\right)}\)
Putting x² = y
\(\frac{1}{\left(x^{2}+1\right)\left(x^{2}+4\right)} = \frac{1}{(y+1)(y+4)}\)
= \(\frac{A}{(y+1)}+\frac{B}{(y+4)}\)
or 1 = A(y + 4) + B(y + 1)
Putting y = - 1
1 = A(- 1 + 4) + B(- 1 + 1)
or 1 = A(3) + B × 0
∴ A = \(\frac{1}{3}\)
Putting y = - 4
1 = A(- 4 + 4) + B(- 4 + 1)
or 1 = A × 0 + B(- 3)
∴ B = - \(\frac{1}{3}\)

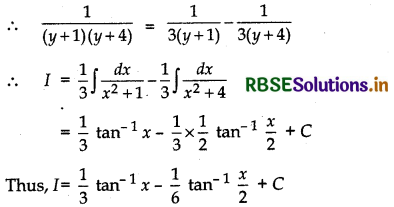
Question 15.
cos³ x e^{log sin x}
Answer:
Let I = ∫cos³ x e^{log sin x}
or I = ∫ cos³ x sin x dx(∵ e^{log x} = x)
Putting cos x = t
⇒ - sin x dx = dt
∴ I = - ∫ t³ dt
= - \(\frac{t^{4}}{4}\) + C
= - \(\frac{(\cos x)^{4}}{4}\) + C = \(\frac{\cos ^{4} x}{4}\) + C
∴ I = - \(\frac{1}{4}\) cos⁴ x + C

Question 16.
e^{3 log x} (x⁴ + 1)^-1
Answer:
Let I = ∫e^{3 log x} (x⁴ + 1)^-1 dx
= ∫e^{log x3} \(\left(\frac{1}{x^{4}+1}\right)\) dx
or I = ∫\(\frac{x^{3}}{x^{4}+1}\) dx (∵ e^{log x} = x)
Putting x⁴ + 1 = t
⇒ 4x³ dx = dt
∴ x³ dx = \(\frac{1}{4}\) dt
or I = \(\frac{1}{4} \int \frac{d t}{t}=\frac{1}{4}\) log|t| + C
= \(\frac{1}{4}\) log |x⁴ + 1| + C

Question 17.
f'(ax + b) [f(ax + b)]ⁿ
Answer:
Let I = ∫f'(ax + b) [f(ax + b)]ⁿ dx
putting f(ax + b) = t
⇒ f'(ax + b) dx = \(\frac{1}{4}\) dt

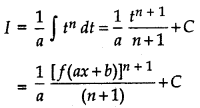
Question 18.
\(\frac{1}{\sqrt{\sin ^{3} x \sin (x+\alpha)}}\)
Answer:
Let I = ∫\(\frac{d x}{\sqrt{\sin ^{3} x \sin (x+\alpha)}}\)
Now, sin³ x sin (x + α)
= sin³ x (sin x cos α + cos x sin α)
= sin⁴ x cos α + sin³ x cos x sin α
= sin⁴ x (cos α + cot x sin α)

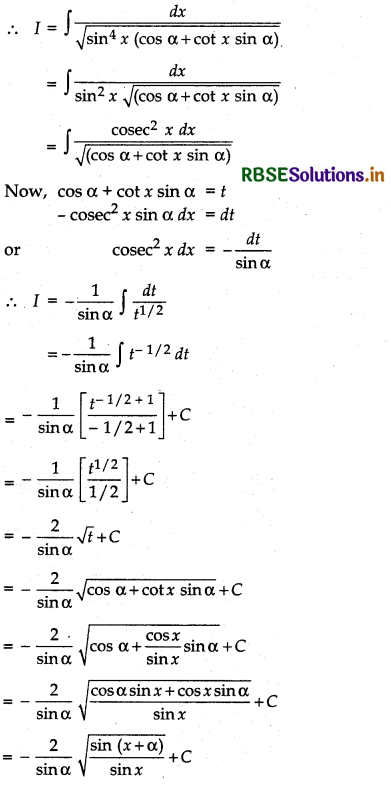
Question 19.
\(\frac{\sin ^{-1} \sqrt{x}-\cos ^{-1} \sqrt{x}}{\sin ^{-1} \sqrt{x}+\cos ^{-1} \sqrt{x}}\), {x ∈ [0, 1]}
Answer:

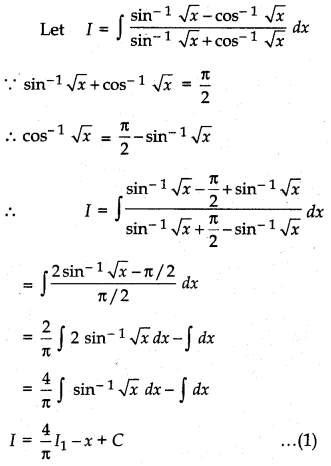
Now, I₁ = ∫sin^-1 √x dx
Let √x = t
∴ x = t²
Then dx = 2t dt
∴ I₁ = 2 ∫sin^-1 (t).dt
= 2∫t sin^-1 (t)

Question 20.
\(\sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}}\)
Answer:
Let I = ∫\(\sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}}\) dx
Putting √x = cos t
⇒ \(\frac{1}{2 \sqrt{x}}\) dx = - sin t dt
⇒ dx = - 2√x sin t dt
= - 2 cos t sin t dt
= - 2 cos t sin t dt
= - sin 2t dt

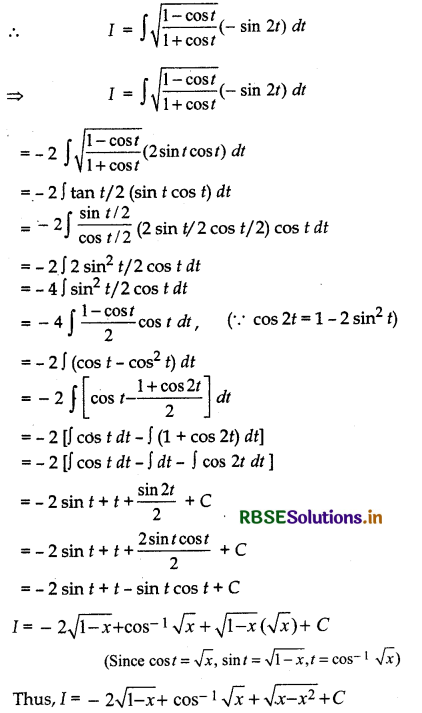
Question 21.
\(\frac{2+\sin 2 x}{1+\cos 2 x}\) e^x
Answer:
Let

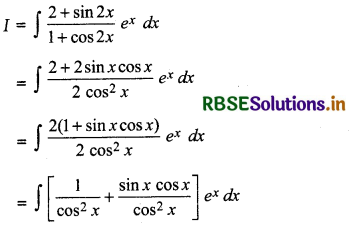
= ∫ (sec² x + tan x) dx = dt
Now, let e^x tan x = t
Then (e^x sec² x + e^x tan x) dx = dt
∴ e^x (sec² x + tan x)dx = dt
∴ I = ∫ dt = t + C
∴ I = e^x tan x + C

Question 22.
\(\frac{x^{2}+x+1}{(x+1)^{2}(x+2)}\)
Answer:
Let I = ∫ \(\frac{x^{2}+x+1}{(x+1)^{2}(x+2)}\) dx
Now,
\(\frac{x^{2}+x+1}{(x+1)^{2}(x+2)}=\frac{A}{x+1}+\frac{B}{(x+1)^{2}}+\frac{C}{(x+2)}\)
or x² + x + 1 = A(x + 1) (x + 2) + B(- 1 + 2) + C(x + 1)²
Putting x = - 1
(- 1)² - 1 + 1 = A(- 1 + 1) (- 1 + 2) + B(- 1 + 2) + C(- 1 + 1)²
⇒ 1 = B × 1= B
∴ B = 1
Putting x = - 2
(- 2)² - 2 + 1 = A(- 2 + 1) (- 2 + 2) + B(- 2 + 2) + C(- 2 + 1)²
or 4 - 2 + 1 = 0 + 0 + C(- 1)²
or 4 - 2 + 1 = C
or 3 = C
∴ C = 3
Now, equating the coefficients of x² on both sides,
we get
1 = A + C
or 1 = A + 3
or A = 1 - 3 = - 2

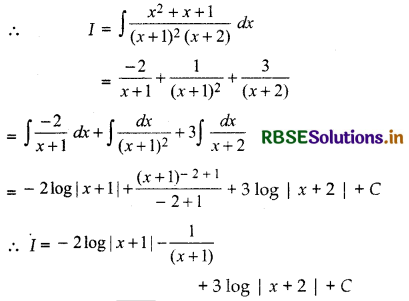
Question 23.
tan^-1 \(\sqrt{\frac{1-x}{1+x}}\)
Answer:
Let I = ∫ tan^-1 \(\sqrt{\frac{1-x}{1+x}}\) dx
Putting x = cos θ
⇒ dx = - sin θ dθ

Question 24.
\(\frac{\sqrt{x^{2}+1}\left[\log \left(x^{2}+1\right)-2 \log x\right]}{x^{4}}\)
Answer:

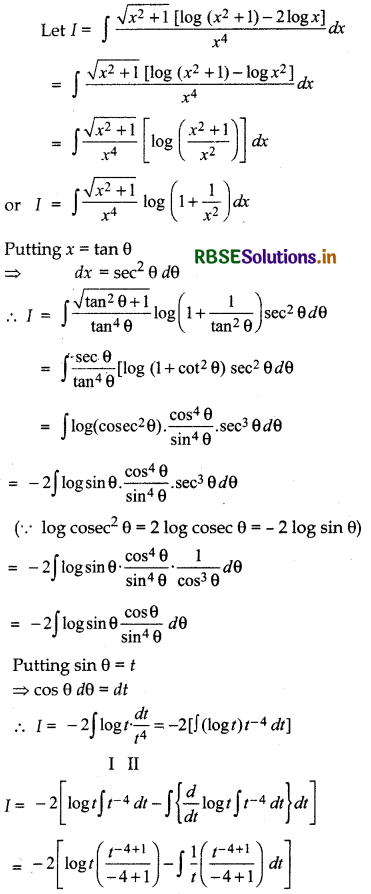
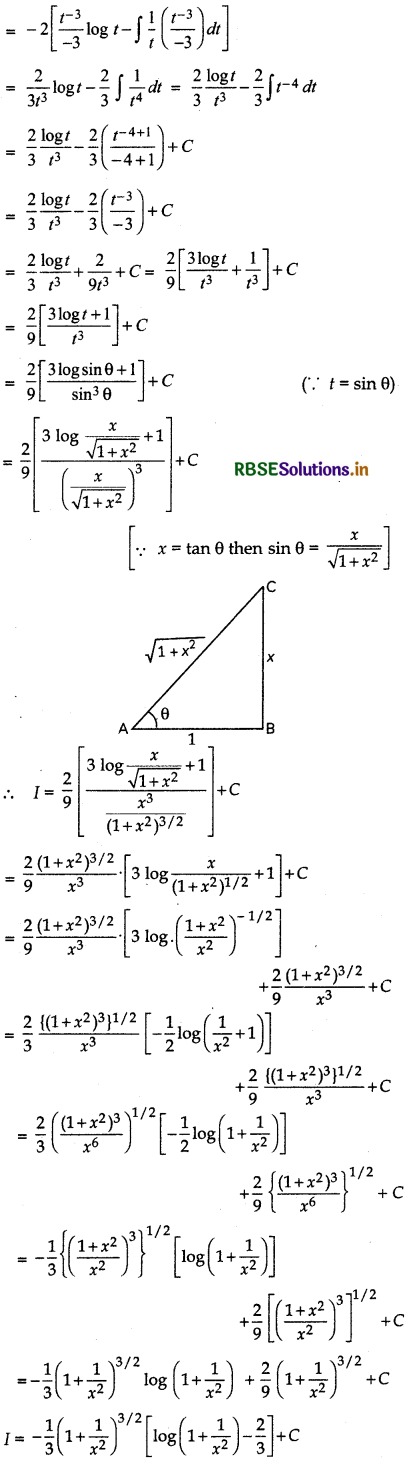
Question 25.
\(\int_{\pi / 2}^{\pi} e^{x}\left(\frac{1-\sin x}{1-\cos x}\right)\) dx
Answer:

Question 26.
\(\int_{0}^{\pi / 4} \frac{\sin x \cos x}{\cos ^{4} x+\sin ^{4} x}\) dx
Answer:
Let I = \(\int_{0}^{\pi / 4} \frac{\sin x \cos x}{\cos ^{4} x+\sin ^{4} x}\) dx
Dividing numerator and denominator by cos⁴ x,
we get

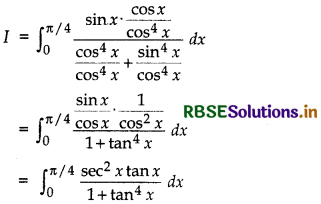
Putting tan² x = t
⇒ 2 tan x sec² x dx = dt
when x = 0, then t = 0
when x = \(\frac{\pi}{4}\), then t = tan² \(\frac{\pi}{4}\) = 1

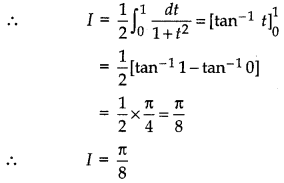
Question 27.
\(\int_{0}^{\pi / 2} \frac{\cos ^{2} x}{\cos ^{2} x+4 \sin ^{2} x}\) dx
Answer:

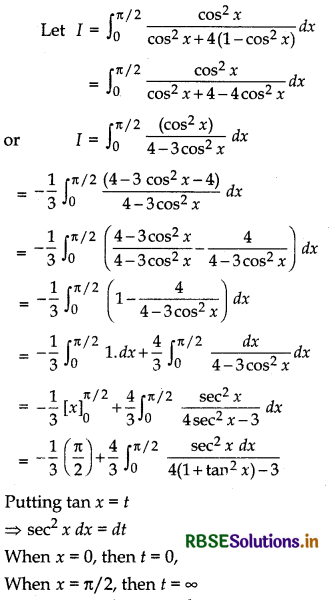
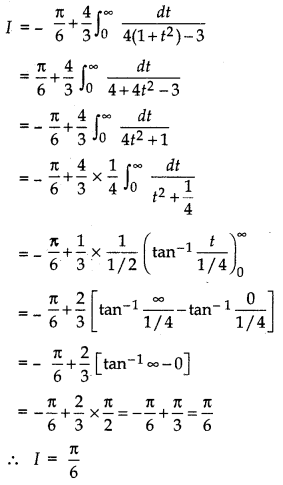
Question 28.
\(\int_{\pi / 6}^{\pi / 3} \frac{\sin x+\cos x}{\sqrt{\sin 2 x}}\) dx
Answer:

Question 29.
\(\int_{0}^{1} \frac{d x}{\sqrt{1+x}-\sqrt{x}}\)
Answer:

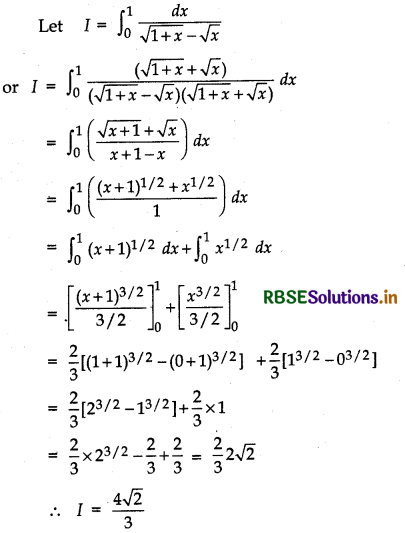
Question 30.
\(\int_{0}^{\pi / 4} \frac{\sin x+\cos x}{9+16 \sin 2 x}\) dx
Answer:
Let I = \(\int_{0}^{\pi / 4} \frac{\sin x+\cos x}{9+16 \sin 2 x}\) dx
Putting sin x - cos x = t
⇒ (cos x + sin x)dx = dt
and (sin x - cos x)² = t²
or sin² x + cos² x - 2 sin x cos x = t²
or 1 - 2 sin x.cos x
or 1 - sin 2x = t²
or sin 2x = 1 - t²
When x = 0, then sin 0 - cos 0 = t
or - 1 = t or t = - 1

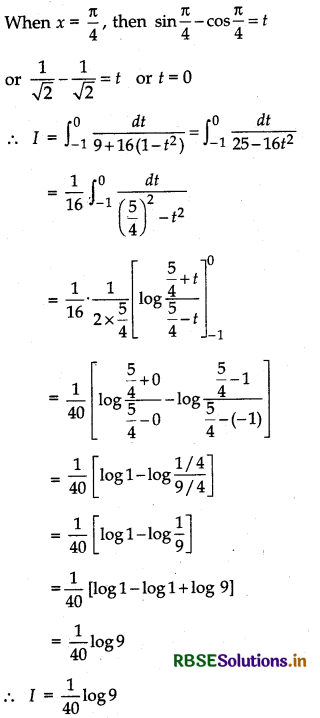
Question 31.
\(\int_{0}^{\pi / 2}\) sin 2x tan^-1 (sin x) dx
Answer:
Let I = \(\int_{0}^{\pi / 2}\) sin 2x tan^-1 (sin x) dx
= \(\int_{0}^{\pi / 2}\) (2 sin x cos x) tan^-1 (sin x) dx
= 2 \(\int_{0}^{\pi / 2}\) sin x cos x tan^-1 (sin x) dx
Putting sin x = t
⇒ cos x dx = dt
When x = 0, then t = 0
When x = \(\frac{\pi}{2}\), then t = 1

Question 32.
\(\int_{0}^{\pi} \frac{x \tan x}{\sec x+\tan x}\) dx
Answer:

Question 33.
\(\int_{1}^{4}\) [|x - 1| + |x - 2| + |x - 3|] dx
Answer:
Let

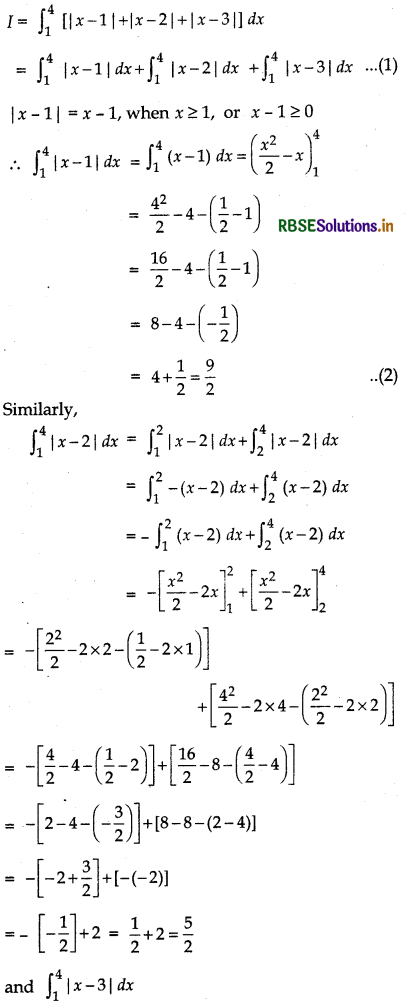
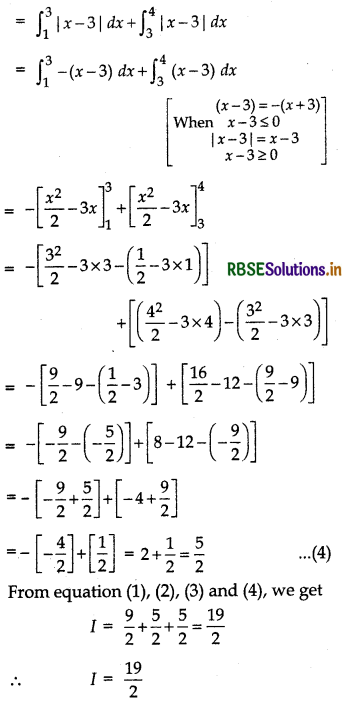
Question 34.
\(\int_{1}^{3} \frac{d x}{x^{2}(x+1)}\) = \(\frac{2}{3}\) + log \(\frac{2}{3}\)
Answer:
Let I = \(\frac{1}{x^{2}(x+1)}\)
Now, \(\frac{1}{x^{2}(x+1)}=\frac{A}{x}+\frac{B}{x^{2}}+\frac{C}{(x+1)}\) (Let)
or 1 = A(x + 1)x + B(x + 1) + Cx²
or 1 = A(x² + x) + Bx + B + Cx²
1 = (A + C)x² + (A + B)x + B
Equating the coefficients of x, x² and constant terms on both sides, we get
A + C = 0, A + B = 0, B = 1
Now, solving these equations, we get
A = - 1, C = 1, B = 1

Question 35.
\(\int_{0}^{1}\) xe^x dx = 1
Answer:

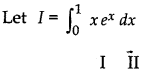
Now, \(\int_{0}^{1}\) xe^x = x∫e^x dx - ∫{\(\frac{d}{d x}\) (x) ∫e^x dx} dx
or ∫xe^x dx = x e^x - ∫1.e^x dx = x e^{x - ex}
∴ I = \(\int_{0}^{1}\) xe^x dx = \(\left[x e^{x}-e^{x}\right]_{0}^{1}\)
= 1 (1e¹ - e¹) - [0e⁰ - e⁰]
= (e - e) - (- 1)
= 1 = R.H.S.
∴ \(\int_{0}^{1}\) xe^x dx = 1

Question 36.
\(\int_{-1}^{1}\) x¹⁷ cos⁴ x dx = 0
Answer:
\(\int_{-1}^{1}\) x¹⁷ cos⁴ x dx = 0
If f(- x) dx = 0, when f is an odd function.
f(- x) = (- x)¹⁷ cos⁴ (- x)
= - x¹⁷ cos⁴ x = - f(x)
∴ x¹⁷ cos⁴ x is an odd function.
∴ \(\int_{-1}^{1}\) x¹⁷ cos⁴ x = 0
Hence Proved.

Question 37.
\(\int_{-1}^{1}\) sin³ dx = \(\frac{2}{3}\)
Answer:
Let I = \(\int_{0}^{\pi / 2}\) sin³ x dx
= \(\int_{0}^{\pi / 2}\) sin² x.sin x dx
= \(\int_{0}^{\pi / 2}\) (1 - cos² x)sin x dx
Putting cos x = t
⇒ - sin x dx = dt or sin x dx = - dt
When x = 0, then t = cos 0 = 1
When x = \(\frac{\pi}{2}\), then t = cos \(\frac{\pi}{2}\) = 0

Question 38.
\(\int_{0}^{\pi / 4} \)2 tan³ x dx = 1 - log 2
Answer:

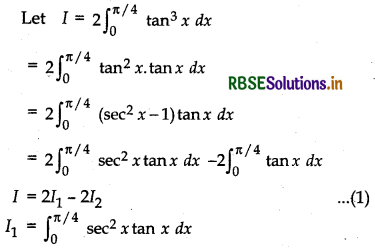
Putting tan x = t
⇒ sec² x dx = dt
When x = 0, then t = 0
When x = \(\frac{\pi}{4}\), then t = tan \(\frac{\pi}{4}\) = 1

Question 39.
\(\int_{0}^{1}\) sin^-1 x dx = \(\frac{\pi}{2}\) - 1
Answer:
Let I = \(\int_{0}^{1}\) sin^-1 x dx
Putting sin^-1 x = t
⇒ x = sin t ∴ dx = cos t dt
When x = 0, then t = 0
When x = 1, then t = sin^-1 1 = \(\frac{\pi}{2}\)
∴ I = \(\int_{0}^{\pi / 2}\) t.cost dt ..... (1)
Now,
∫t cos t dt = t∫cos t dt - ∫{\(\frac{d}{d t}\) t∫cos t dt} dt
= t (sin t) - ∫1.sin t dt
= t sin t - (- cos t)
= t sin t + cos t
∴ I = \([t \sin t+\cos t]_{0}^{\pi / 2}\)
= [\(\frac{\pi}{2}\) sin \(\frac{\pi}{2}\) + cos \(\frac{\pi}{2}\) - 0 × sin 0 - cos 0]
= \(\frac{\pi}{2}\) × 1 + 0 - 0 - 1
Thus, I = \(\frac{\pi}{2}\) - 1
Hence Proved.

Question 40.
Evaluate \(\int_{0}^{1}\) e^{2 - 3x} dx as a limit of a sum.
Answer:
Let I = \(\int_{0}^{1}\) e^{2 - 3x} dx
Here a = 0, b = 1, f(x) = e^{2 - 3x}, nh = (1 - 0) = 1

Question 41.
∫\(\frac{d x}{e^{x}+e^{x}}\) is equal to:
(A) tan^-1 (e^x) + C
(B) tan^-1 (e^-1) + C
(C) log (e^x - e^-x + C
(D) log (e^x + e^-x) + C
Answer:

I = tan^-1 (e^x) + C
Hence, (A) is the correct answer.

Question 42.
∫\(\frac{\cos 2 x}{(\sin x+\cos x)^{2}}\) dx is equal to:
(A) \(\frac{-1}{\sin x+\cos x}\) + C
(B) log |sin x + cos x| + C
(C) log |sin x - cos x| + C
(D) \(\frac{1}{(\sin x+\cos x)^{2}}\) + C
Answer:

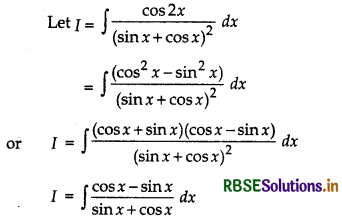
Putting sin x + cos x = t
⇒ (cos x - sin x) dx = dt
∴ I = ∫\(\frac{d t}{t}\) = log |t| + C
or I = log |sin x + cos x| + C
Hence, (B) is the correct answer.

Question 43.
If f(a + b - x) = f(x), then \(\int_{a}^{b}\) xf(x) dx is equal to:
(A) \(\frac{a+b}{2} \int_{a}^{b} f(b-x) d x\)
(B)\( \frac{a+b}{2} \int_{a}^{b} f(b+x)\) d x
(C) \(\left(\frac{b-a}{2}\right) \int_{a}^{b}\) f(x) d x
(D) \(\left(\frac{a+b}{2}\right) \int_{a}^{b}\) f(x) d x
Answer:

Hence, (D) is the correct answer.

Question 44.
The value of \(\int_{0}^{1} \tan ^{-1}\left(\frac{2 x-1}{1-x-x^{2}}\right)\) dx is:
(A) 1
(B ) 0
(C) - 1
(D) \(\frac{\pi}{4}\)
Answer:

Hence, (B) is the correct answer.