RBSE Solutions for Class 12 Maths Chapter 6 Application of Derivatives Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 6 Application of Derivatives Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 6 Application of Derivatives Miscellaneous Exercise

Question 1.
Using differentials, find the approximate value of each of the following:
(a) \(\left(\frac{17}{81}\right)^{1 / 4}\)
Answer:

(b) (33)^-1/5
Answer:

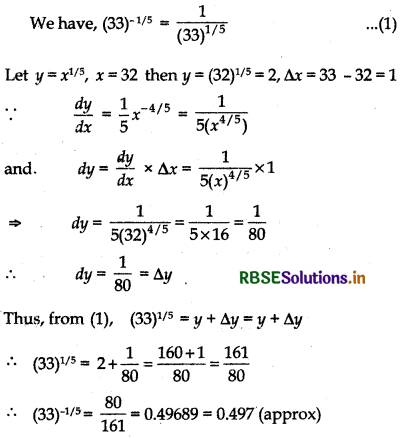
Question 2.
Show that the function given by f (x) = \(\frac{\log x}{x}\) has maximum at x = e.
Answer:

Question 3.
The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base?
Answer:
Let ∆ABC is an isosceles triangle.
In which AB = AC = x, BC = b (given)

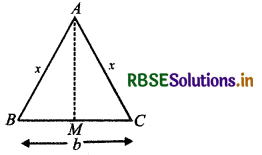
Let M is the mid-point of base BC.

Quesstion 4.
Find the equation of the normal to the curve x² = 4y which passes through the point (1, 2).
Answer:
Equation of curve is x² = 4y
⇒ y = \(\frac{x^{2}}{4}\) ⇒ \(\frac{d y}{d x}=\frac{2 x}{4}=\frac{x}{2}\)
∴ Slope of tangent at point (1, 2) = \(\frac{1}{2}\) = m(say)
∴ Slope of normal at point (1, 2) is
= -\(\frac{1}{m}=-\frac{1}{1 / 2}\) = - 2
∴ At point (1, 2) equation of normal is
y - 2 = (- 2) (x - 1)
⇒ y - 2 = - 2x + 2
⇒ 2x + y - 4 = 0
Thus, 2x + y - 4 = 0 is the required equation of the normal.

Question 5.
Show that the normal at any point θ to the curve x = a cos θ + aθ sin θ, y = a sin θ - a θ cos θ is at a constant distance from the origin.
Answer:
x = a cos θ + aθ sin θ and y = a sin θ - a θ cos θ
Differentiating x and y w. r. t. θ

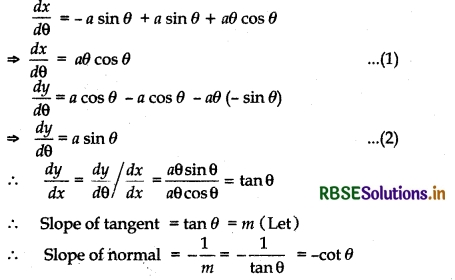
∴ Equation of normal
y - (a sin θ - aθ cos θ) = - cot θ(x -(a cos θ + aθ sin θ)
Multiplying both sides by sin θ
y sin θ - a sin²θ + aθ cos θ sin θ
= sin θ × \(\left(-\frac{\cos \theta}{\sin \theta}\right)\) × [(x - (a cos θ + a θ sin θ)]
= y sin θ - a sin²θ + a θ cos θ sin θ
= - x cos θ + a cos²θ + a θ cos θ sin θ
= x cos θ + y sin θ = a sin²θ + a cos²θ
= x cos θ + y sin θ = a(sin²θ + cos²θ)
= x cos θ + y sin θ = a
Distance of normal from origin
\(\left(\frac{0 \times \cos \theta+0 \times \sin \theta-a}{\sqrt{\cos ^{2} \theta+\sin ^{2} \theta}}\right)\) = |- a| (constant no.)
|- a| = a constant number (distance cannot be negative)
Thus, normal at curve is at a constant distance from origin.
Hence Proved.

Question 6.
Find the intervals in which the function f given by
f(x) = \(\frac{4 \sin x-2 x-x \cos x}{2+\cos x}\), 0 ≤ x ≤ 2π
is (i) increasing, (ii) decreasing.
Answer:

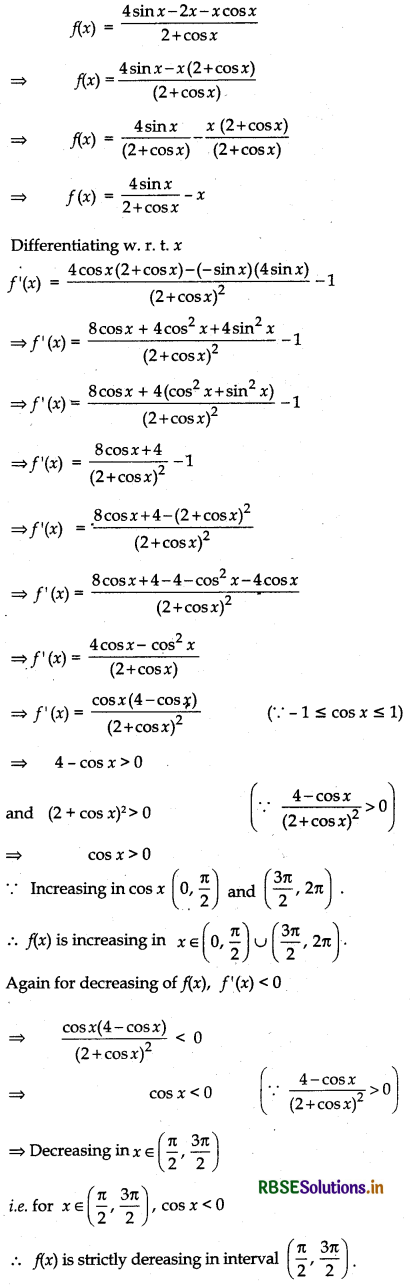
Question 7.
Find the integrals in which the function f is given by:
f(x) = x³ + \(\frac{1}{x^{3}}\), x ≠ 0
(i) increasing,
(ii) decreasing
Answer:
We have, f(x) = x³ + \(\frac{1}{x^{3}}\)
Differentiating w. r. t. x
f(x) = 3x² - \(\frac{3}{x^{4}}\)
For increasing! decreasing f (x) = 0
⇒ 3x² - \(\frac{3}{x^{4}}\) = 0 ⇒ x² = \(\frac{1}{x^{4}}\)
⇒ x⁶ = 1 ⇒ (x²)³ = 1 ⇒ x² = 1
⇒ x = ±1 ∴ x = - 1, x = 1

(i) For interval (- ∞, - 1)

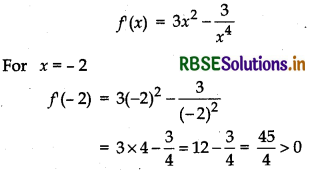
Similarly, we can show for other points.
∴ For x ∈ (- ∞, - 1) function is increasing.

(ii) For (- 1, 0)

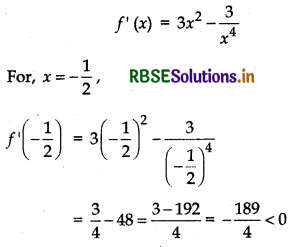
Similarly, we can show for other points.
∴ In (- 1, 0) function is decreasing.

(iii) For (0, 1)

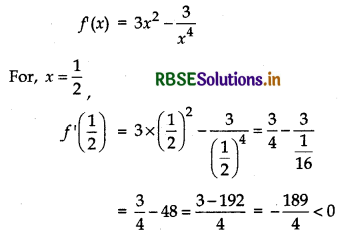
Similarly, we can show for other points.
∴ In (0, 1) function is decreasing.

(iv) For (1, ∞)

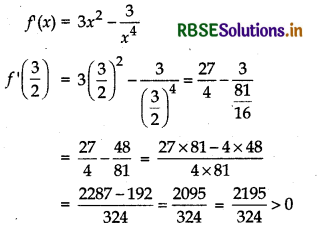
Thus, in (1, ∞) function is increasing.

Question 8.
Find the maximum area of an isosceles triangle inscribed in the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 with its vertex at one end of the major axis.
Answer:
Let P(a cos θ, b sin θ) be any point on ellipse and APQ is an isosceles triangle whose one vertex is one end of major axis.
Side PQ of ∆APQ cuts major axis at point M as shown in the following figure.

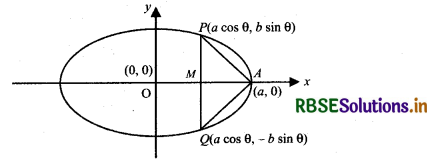
Area of ∆APQ A = \(\frac{1}{2}\) PQ × AM
A = \(\frac{1}{2}\) (2b sin θ) (a - a cos θ)
(∵ PQ = 2PM = 2b sin θ)
and AM = OA - OM = a - a cos θ)
A = \(\frac{1}{2}\) ab × 2 sin θ(1 - cos θ)
A = ab(sin θ - sin θ cos θ) = ab (sin θ - \(\frac{1}{2}\)sin 2θ)
(∵ sin θ cos θ = \(\frac{1}{2}\)sin 2θ)
Differentiating w.r.t θ
\(\frac{d A}{d \theta}\) = ab (cos θ - \(\frac{1}{2}\) × 2 cos 2θ)
= ab (cos θ - cos 2θ) ....... (1)
A will be maximum, when \(\frac{d A}{d \theta}\) = 0
⇒ ab(cos θ - cos 2θ) = 0 ⇒ cos θ - cos 2θ = 0
⇒ cos 2θ = cos θ ⇒ 2θ = 2π - θ
⇒ 3θ = 2π ⇒ θ = \(\frac{2 \pi}{3}\)
Again, differentiating equation (1) w.r.t. θ

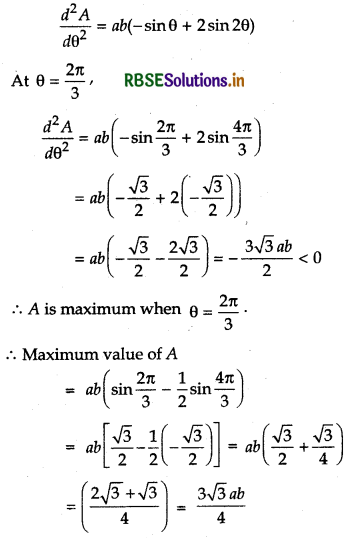
Question 9.
A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m³. If building of tank costs ₹ 70 per square metres for the base and ₹ 45 per square metre for sides, what is the cost of least expensive tank?
Answer:
Let length and breadth of rectangular tank are x metres and y metres.

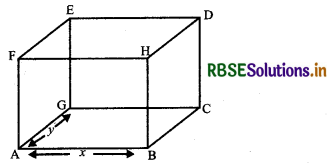
Depth of tank = 2m
Volume of tank = 2 × x × y = 8 (given)
⇒ xy = 4
Area of base = xy
Cost for the base = ₹ 70 per m²
∴ Total expanses for base = ₹ 70xy
Area of four walls = 2(x + y) × 2 = 4(x + y) m²
Rate of expenses on walls = ₹ 45 per m²
Total cost on walls = ₹ [45 × 4 (x + y)]
= ₹ 180 (x + y)
Then total expenses on walls and base
S = ₹ [70 xy + 180(x + y)] ......... (2)
From equation (1), putting y = \(\frac{4}{x}\) in equation (2)


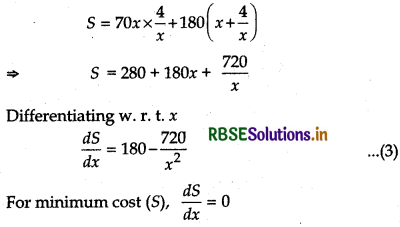
Thus, at x = 2 cost is minimum.
At x = 2, minimum cost S = 280 + 180 × 2 + \(\frac{720}{2}\)
= 280 + 360 + 360 = 1000
Thus, cost of least expensive S = ₹ 1,000

Question 10.
The sum of the perimeter of a circle and square is k, where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
Answer:
Let x be the side of square and r be radius of circle.
Perimeter of square = 4x
Perimeter of circle (circumference) = 2πr
Sum of two perimeters = 4x + 2πr = k ..... (1)
Area of circle A₁ = πr²
Area of square A₂ = x²
∴ Sum of areas A = πr² + x² ............ (2)

Thus, side of square are twice the radius of circle whereas sum of both areas are minimum.
Hence Proved.

Question 11.
A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the windows is 10 m. Find the dimensions of the window to admit maximum light through the whole opening.
Answer:
Let ABCDPA is a window in which APD is semicircular. Centre of semi-circle is O.
∴ AD = 2r, AB = CD = x
Then, APD = \(\frac{1}{2}\) × 2πr = πr

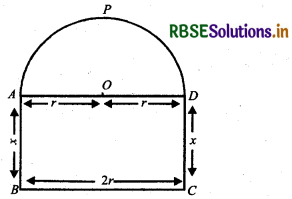
∴ Perimeter of window = 2x + 2r + πr
= 10 m
⇒ 10 = 2x + r(π + 2)
And area of window A = 2rx + \(\frac{1}{2}\) πr²
From equation (1), 2x = 10 - (π + 2)r

Question 12.
A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle. Show that the minimum length of the hypotenuse is \(\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)^{3 / 2}\)
Answer:
Let ∆ABC is a right-angled triangle in which ∠B = 90°, and Pbe any point on hypotenure AC which is a distance from side AB and distance b from side BC.
Side PM is perpendicular to side AB and PN is perpendicular to side BC.
Again, let ∠ACB = θ = ∠APM.

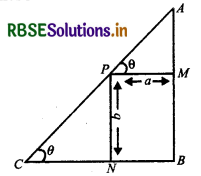
∴ AP = a sec θ
PC = b cosec θ
Let length of hypotenuse is I, then
l = AP + PC
⇒ l = a sec θ + b cosec θ
Differentiating w. r. t. θ
\(\frac{d l}{d \theta}\) = a sec θ tan θ - b cosec θ cot θ
For minimum l, \(\frac{d l}{d \theta}\) = 0
a sec θ tan θ - b cosec θ cot θ = 0

Question 13.
Find the points at which the function f given by f(x) = (x - 2)⁴ (x + 1)³ has
(i) local maxima
(ii) local minima
(iii) point of inflexion
Answer:
Given, f(x) = (x - 2)⁴ (x + 1)³
Differentiating w. r. t. x
⇒ f'(x) = 4(x - 2)³ (x + 1)³ + 3(x - 2)⁴ (x + 1)²
⇒ f’(x) = (x - 2)³ (x + 1)² [4(x + 1) + 3(x - 2)]
⇒ f'(x) = (x - 2)³ (x + 1)² (4x + 4 + 3x - 6)
⇒ f'(x) = (x - 2)³ (x + 1)² (7x - 2)
For local maxima/minima f (x) = 0
f'(x) = 0 = (x - 2)³ (x + 1)² (7x - 2) = 0
⇒ (x - 2)³ = 0 or (x + 1)² = 0 or 7x - 2 = 0
⇒ x = 2 or x = - 1 or x = \(\frac{2}{7}\)

(i) For x = - 1
x = - 1.1 taking (left side of - 1)

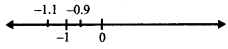
f' (- 1. 1) = (- 1.1 - 2)³ (- 1.1 + 1)² [7(- 1.1) - 2]
⇒ f (x) = (- 3.1)³ (- 0.1)² (- 9.7)
⇒ f (x) = (3.1)³ (- 0.1)² (- 9.7)
⇒ f’ (1.1) = (3.1)³ (0.1)² (9.7) > 0
Taking x = - 0.9 (right side of - 1)
f (- 0.9) = (- 0.9- 2)³ (- 0.9 + 1)² {7(- 0.9) - 2}
f’ (- 0.9) = (- 2.9)³ (0.1)² (- 6.3 - 2)
⇒ f (-0.9) = (- 2.9)³ (0.1)² (- 8.3)
⇒ f (-0.9) = (2.9)³ (0.1) (8.3)
⇒ f (-0.9) = (2.9)³ (0.1) (8.3) > 0
Thus at x = -1 sign of function does not change.
∴ x = - 1 is point of inflection.

(ii) For x = \(\frac{2}{7}\)

∴ Sign of f'(x) changes from +ve to -ve
Thus, x = \(\frac{2}{7}\) is local maximum point of function f.

(iii) For, x = 2 taking x = 1.9 (2 left side of),
[(1.9) = (1.9 - 2)² (1.9 + 1)² {7 × (1.9) - 2}
⇒ f’ (1.9) = (- 0.1)³ (2.9)³ (13.3 - 2)
⇒ f (1.9) = (- 0.1)³ (2.9)² (11 3) < 0
Taking,x=2.1 (right sideof 2),
f (2.1) = (2.1 - 2)³ (2.1 + 1)² (7 × 2.1 - 2)
⇒ f(2.1) = (0.1)³ (3.1)² (14.7 - 2)
⇒ f(2.1) = (0.1)³ (3.1)² (12.7) > 0
Thus, at x =2, sign of f (x) changes from -v to +ve.
∴ x = 2 is local minimum point of function.
(i) x = \(\frac{2}{7}\) local maxima of function
(ii) x = 2 local minima of function
(iii) x = - 1 point of inflection of function

Question 14.
Find the absolute maximum and minimum values of the function f given by
f (x) = cos² x + sin x, x ∈ [0, π]
Answer:
Given, f(x) = cos² x + sin x
Differentiating w. r. t. x
f’(x) = 2 cos x(- sin x) + cos x
f’(x) = - 2 sin x cos x + cos x
f(x) = cos x(1 - 2 sin x)
For maxima/minima f’ (x) = 0
∴ f’(x) = 0 ⇒ cos x(1 - 2 sin x) = 0
cos x = 0 or 1 - 2 sin x = 0
x = π/2 or sin x = \(\frac{1}{2}\) = sin \(\left(\frac{\pi}{6}\right)\)
x = π/2 or x = π/6
Now π/6, π/2 ∈ [0, π]
f(0) = cos² 0 + sin 0 = 1 + 0 = 1
f(π/6) = cos²(π/6) + sin(π/6)
= \(\left(\frac{\sqrt{3}}{2}\right)^{2}+\frac{1}{2}=\frac{5}{4}\)
f(π/2) = cos²(π/2) + sin π/2 = 0 + 1 = 1
f(π) = cos²π + sin π = (- 1)² + 0 = 1
Thus, absolute maximum value = \(\frac{5}{4}\)
Absolute minimum value = 1

Question 15.
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is \(\frac{4 r}{3}\).
Answer:
Let ABC is cone which is inscribed in a circle of radius r. O is the centre of circle.

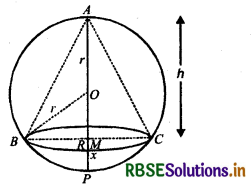
Let radius of cone be R.
Height of cone (h) AM = AP - MP
AM = (2r - x) (∵ MP = x)
In right-angled ∆ 0MB,
OM² + BM² = OB²
(r - x)² + R² = r²
R² = r² - (r - x)²
R² = r² - (r² - 2xr + x²)
R² = r² - r² + 2rx - x² = 2rx - x²

Question 16.
Let f be a function defined on [a, b] such that f(x) > 0 for all x ∈ (a, b). Then prove that f is an increasing function on [a, b].
Answer:
Let x₁, x₂ ∈ (a, b) such that for x₁ < x₂ f(x) is differentiable in interval (a, b) and [x₁, x₂] ∈ (a, b).
∴ f is continuous in internal [x₁, x₂] and differentiable in (x₁, x₂) then by mean value theorem.
∴ c ∈ (x₁, x₂) exists such that
f' (c) = \(\frac{f\left(x_{2}\right)-f\left(x_{1}\right)}{x_{2}-x_{1}}\) ......... (1)
Hence, for (a, b), f' (x) > 0
∵ f (c) > 0 [∵ c ∈ (x₁, x₂) c(a, b)]
⇒ c ∈ (a, b)
And f'(c) > 0 ⇒ \(\frac{f\left(x_{2}\right)-f\left(x_{1}\right)}{x_{2}-x_{1}}\) > 0
⇒ f(x₂) - f(x₁) > 0 (∵ x₂ - x₁ > 0, when x₁ < x₂)
⇒ f(x₂) > f(x₁)
⇒ f(x₁) < f(x₂), If x₁ < x₂
Since x₁, x₂ ∈ (a, b) arbitrary points.
∴ x₁ < x₂ ⇒ f(x₁) < f(x₂) ∀ x₁, x₂ ∈ (a, b)
∴ f(x) is increasing function in interval [a, b].
Hence Proved.

Question 17.
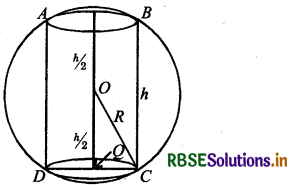
Show that the height of the cylinder of maximum volume that can be inscribed In a sphere of radius R is \(\frac{2 \boldsymbol{R}}{\sqrt{3}}\). Also, find the maximum volume.
Answer:
Let ABCD is a cylinder which be inscribed in a circle of radius R and volume of cylinder be V.
V = πr²h ........ (1)

Question 18.
Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi-vertical angle a is one-third that of the cone and the greatest volume of cylinder is \(\frac{4}{27}\)πh³ tan² α.
Answer:
Let ABC is cone.
Height of cone = h
Semi-vertical angle = α
Cylinder PQRS is inscribed in cone ABC.
Let x be radius of cylinder.

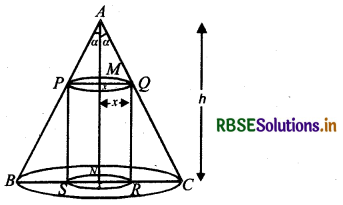
Height of cylinder = MN = AN - AM
= h - x cot α
∵ In ∆ AMQ, cot α = \(\frac{A M}{x}\)
⇒ AM = x cot α
Volume of cylinder, V = πr²h(h - x cot α)
Differentiating w. r. t. x
\(\frac{d V}{d x}\) = 2πx(h - x cot ) + πx²(- 1. cot α)
⇒ \(\frac{d V}{d x}\) = 2πxh - 2πx² cot α - πx²cot α
⇒ \(\frac{d V}{d x}\) = 2πxh - 3πx² cot α
Volume of cylinder will be maximum, if
\(\frac{d V}{d x}\) = 0
⇒ 2πxh - 3πx² cot α = α
⇒ πx(2h - 3x cot α) = 0
⇒ 2h - 3x cot α = 0 (∵ x ≠ 0)
⇒ x = \(\frac{2 h}{3 \cot \alpha}\)
Differentiating equ. (!) w.r.t.x.

∴ Height of cylinder = \(\frac{1}{3}\)h = \(\frac{1}{3}\) (height of cone)
Thus, height of cylinder is one third height of cone.
Maximum volume of cylinder
= πx² (h - x cot α)

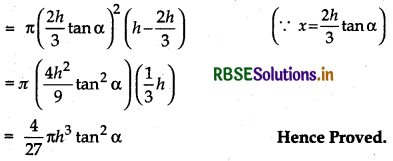
Choose the correct answer in the Q. 19 to Q. 24

Question 19.
A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of:
(A) 1 m/h
(B) 0.1 m/h
(C) 1.1 m/h
(D) 0.5 m/h
Answer:
Let H be height of cylinderical tank and r be radius.
Volume of tank V = πr²H
At, r = 10, V = π × 10 × 10 × H
∴ V = 100πH
Differentiating w. r. t. t

Question 20.
The slope of the tangent to the curve x = t² + 3t - 8, y = 2t² - 2t - 5 at the point (2, - 1) is:
(A) \(\frac{22}{7}\)
(B) \(\frac{6}{7}\)
(C) \(\frac{7}{6}\)
(D) -\(\frac{6}{7}\)
Answer:
Given, x = t² + 3t - 8, y = 2t² - 2t - 5
Differentiating x and y w.r.t t

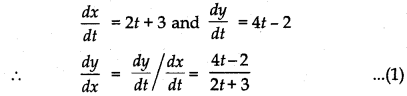
Putting x = 2 in x = t² + 3t - 8
2 = t² + 3t - 8
⇒ t² + 3t - 8 - 2 = 0
⇒ t² + 3t - 10 = 0
⇒ t² + (5 - 2)t - 10 = 0
⇒ t² + 5t - 2t - 10 = 0
⇒ t(t + 5)- 2 (t + 5) = 0
⇒ (t + 5) (t - 2) = 0
⇒ (t + 5) = 0 or (t - 2) = 0
⇒ t = - 5 or t = 2
Similarly, putting y = - 1 y = 2t² - 2t - 5
- 1 = 2t² - 2t - 5
⇒ 2t² - 2t - 5 + 1 = 0
⇒ 2t² - 2t - 4 = 0
⇒ t² - t - 2 = 0
⇒ (t - 2) (t + 1) = 0
⇒ t - 2 = 0 or t + 1 = 0
⇒ t = 2 or t = - 1
t = 2 is common in both.
∴ At t = 2, \(\frac{d y}{d x}=\frac{4 \times 2-2}{2 \times 2+3}=\frac{8-2}{4+3}=\frac{6}{7}\) [From equation (1)]
∴ Slope of tangent = \(\frac{6}{7}\)
Thus, (B) is correct. 

Question 21.
The line y = mx +1 is a tangent to the cuxve y² = 4x if the value of m is:
(A) 1
(B) 2
(C) 3
(D) \(\frac{1}{2}\)
Answer:
Given, Curve y² = 4x
Differentiating w. r. t. x

⇒ y₁ = 0 or y₁ = 2
But y₁ ≠ 0
∴ y₁ = 2
Putting y₁ = 2 im equation my₁ = 2
2m = 2 ⇒ m = 1
Thus, (A) is correct.

Question 22.
The normal at the point (1, 1) on the curve 2y + x² = 3 is:
(A) x + y = 0
(B) x - y = 0
(C) x + y + 1 = 0
(D) x - y = 3
Answer:
Given, curve 2y + x² = 3
Differentiating w. r. t. x

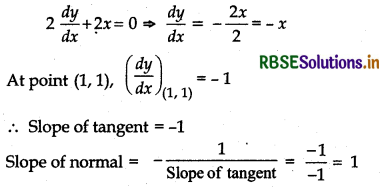
∴ Equation of normal is
y - 1 = 1 (x - 1)
Or y - 1 = x - 1 or x - y = 0
Thus, (B) is correct.

Question 23.
The normal to the curve 4y passing through (1, 2) is:
(A) x + y = 3
(B) x - y = 3
(C) x + y = 1
(D) x - y = 1
Answer:
Equation of curve is x² = 4y
Differentiating w. r. t. x

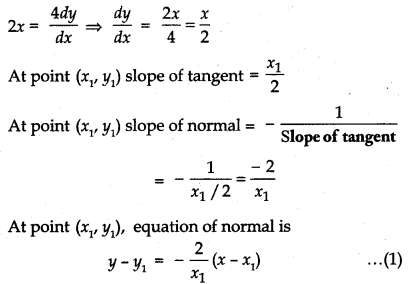
Given, that equation of normal passes through point (1, 2) then, from equation (1)
2 - y1 = - \(\frac{2}{x_{1}}\)(1 - x₁)
⇒ 2x₁ - x₁y₁ = - 2 + 2x₁
⇒ x₁y₁ = 2 ⇒ y₁ = \(\frac{2}{x_{1}}\) ...... (2)
Point (x₁, y₁) thus lies on curve x² = 4y.
x₁² = 4y₁ ........ (3)
From equation (2), putting value of y in equation (1)
x₁² = 4 \(\frac{2}{x_{1}}\) ⇒ x₁³ = 8 ⇒ x₁ = 2
Putting value of x1 in equation (3)
(2)² = 4y₁ ⇒ 4 = 4y₁ ⇒ y₁ = 1
Putting x₁ = 2 and y₁ = 1 in equation (1)
y - 1 = \(\frac{-2}{2}\) (x - 2)
⇒ y - 1 = - x + 2 ⇒ x + y = 3
So, the equation of normal is x + y = 3
Thus, (A) is correct.

Question 24.
The points on the curve 9y² = x³, where the normal to the curve makes equal intercepts with the axes are:
(A) \(\left(4, \pm \frac{8}{3}\right)\)
(B) \(\left(4,-\frac{8}{3}\right)\)
(C) \(\left(4, \pm \frac{3}{8}\right)\)
(D) \(\left(\pm 4, \frac{3}{8}\right)\)
Answer:
Given, curve 9y² = x³
Differentiating w.r.t. x