RBSE Solutions for Class 12 Maths Chapter 6 अवकलज के अनुप्रयोग विविध प्रश्नावली

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 6 अवकलज के अनुप्रयोग विविध प्रश्नावली Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 6 अवकलज के अनुप्रयोग विविध प्रश्नावली

प्रश्न 1.
अवकलज का प्रयोग करके निम्नलिखित में से प्रत्येक का सन्निकट मान ज्ञात कीजिए:
(a) \(\left(\frac{17}{81}\right)^{\frac{1}{4}}\)
हल:

∴ 17^{\(\frac{1}{4}\)} = y + Δy = 2 + 0.03125
= 2.03125
∴ \(\left(\frac{17}{81}\right)^{\frac{1}{4}}\) = \(\frac{2.03125}{3}\) = 0.677083
= 0.677

(b) (33)^{-\(\frac{1}{5}\)}
हल:

प्रश्न 2.
सिद्ध कीजिए कि f(x) = \(\frac{\log x}{x}\) द्वारा प्रदत्त फलन x = e पर उच्चतम है।
हल:
प्रश्नानुसार f(x) = \(\frac{\log x}{x}\)

अर्थात् प्रदत्त फलन x = e पर उच्चतम है।

प्रश्न 3.
किसी निश्चित आधार b के एक समद्विबाहु त्रिभुज की समान भुजाएँ 3 cm./sec. की दर से घट रही हैं। उस समय जब त्रिभुज की समान भुजाएँ आधार के बराबर हैं, उसका क्षेत्रफल कितनी तेजी से घट रहा है ?
हल:
माना कि ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC = x और BC = b


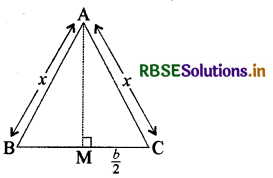
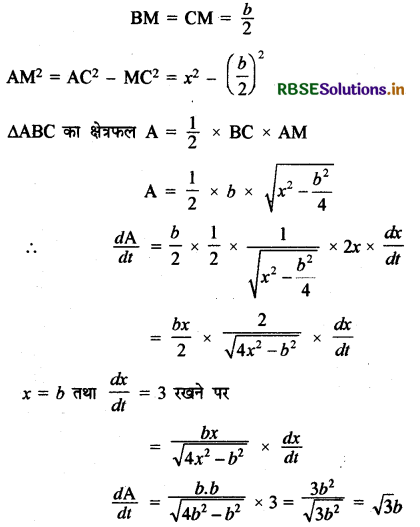
अतः क्षेत्रफल में कमी = √3b cm²/sec.
∆ABC का क्षेत्रफल √3b cm²/sec. की दर से घट रहा है।

प्रश्न 4.
वक्र x² = 4y के बिन्दु (1, 2) पर अभिलम्ब का समीकरण ज्ञात कीजिए।
हल:
वक्र का समीकरण x² = 4y
x के सापेक्ष अवकलन करने पर 2x = 4\(\frac{d y}{d x}\)
∴ \(\frac{d y}{d x}=\frac{2 x}{4}=\frac{x}{2}\)
बिन्दु (x₁, y₁) पर स्पर्श रेखा की प्रवणता = \(\frac{x_1}{2}\) = m
∴ अभिलम्ब का समीकरण
y - y₁ = \(\frac{-2}{x_1}\) (x - x₁) ...... (1)
यह रेखा (1, 2) से होकर जाती है
2 - y₁ = - \(\frac{2}{x_1}\) (1 - x₁)
या 2x₁ - x₁y₁ = - 2 + 2x₁
∴ x₁y₁ = 2 ....... (2)
(x₁, y₁) वक्र पर स्थित है ∴ x₁² = 4y₁ ......... (3)
समीकरण (2) और (3) से, x₁² = 4. \(\frac{2}{x_1}\) या x₁³ = 8, x₁ = 2
⇒ y₁ = 1
∴ बिन्दु (2, 1) पर अभिलम्ब का समीकरण
y - 1 = \(\frac{-2}{2}\) (x - 2) = - (x - 2)
x + y - 2 - 1 = 0 या x + y - 3
= 0

प्रश्न 5.
सिद्ध कीजिए कि वक्र x = a cos θ + aθ sin θ, y = a sin θ - aθ cos θ के किसी बिन्दु θ पर अभिलम्ब मूल बिन्दु से अचर दूरी पर है।
हल:
प्रश्नानुसार x = a cos θ + a θ sin θ
∴ \(\frac{d x}{d \theta}\) = - a sin θ + a[sin θ + θ cos θ]
[(uv)' = u'v + uv']
= - a sin θ + a θ cos θ + a sin θ
= a θ cosθ
तथा y = a sin θ - a θ cos θ
∴ \(\frac{d y}{d \theta}\) = a cos θ - a [cos θ - θ sin θ]
= a cos θ - a cos θ + a θ sin θ
= a θ sin θ
∵ \(\frac{d y}{d x}=\frac{d y}{d \theta} \div \frac{d x}{d \theta}\)
= \(\frac{a \theta \sin \theta}{a \theta \cos \theta}\) = \(\frac{\sin \theta}{\cos \theta}\) = tan θ
∴ स्पर्श रेखा की प्रवणता = tan θ
∴ अभिलम्ब की प्रवणता = -\(\frac{1}{m}\) = \(\frac{-1}{\tan \theta}\) = - cot θ
m अभिलम्ब का समीकरण y - y₁ = - \(\frac{1}{m}\) (x - x₁)
[y - (a cos θ + a θ sin θ)] = - cot θ
[x - (a cos θ + a θ sin θ)]
sin θ से गुणा करने पर
[y sin θ - (a sin² θ - aθ sin θ cos θ)]
- x cos θ + (a cos20 + a θ sin θ cos θ)]
या x cos θ + y sin θ = (a cos² θ + aθ sin θ cos θ) + a sin² θ - a θ sin θ cos θ
= a (cos²θ + sin²θ) = a
या x cos θ + y sin θ = a,
या x cos θ + y sin θ - a = 0
मूल बिन्दु से अभिलम्ब की दूरी \(\left[d=\frac{a x_1+b y_1+c}{\sqrt{a^2+b^2}}\right]\) से
= \(\left|\frac{-a}{\sqrt{\cos ^2 \theta+\sin ^2 \theta}}\right|\) = a
= अचर संख्या

प्रश्न 6.
अन्तराल ज्ञात कीजिए जिन पर f(x) = \(\frac{4 \sin x-2 x-x \cos x}{2+\cos x}\) से प्रदत्त फलन f (i) वर्धमान (ii) ह्रासमान है।
हल:

(i) फलन वृद्धिमान होगा यदि f'(x) > 0
⇒ cos x (4 - cos x)> 0
⇒ cos x > 0 [∵ 4 - cos x > 0]

(ii) फलन f(x) ह्रासमान होगा यदि f(x) < 0
⇒ cos x . (4 - cos x)< 0
⇒ cos x < 0 [∵ 4 - cos x > 0]
⇒ \(\frac{\pi}{2}\) < x < \(\frac{3 \pi}{2}\)
⇒ x ∈ \(\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)\)

प्रश्न 7.
अन्तराल ज्ञात कीजिए जिन पर f(x) = x³ + \(\frac{1}{x^3}\), x ≠ 0 से प्रदत्त फलन (i) वर्धमान (ii) ह्रासमान है।
हल:

फलन वृद्धिमान होगा यदि f'(x) > 0
⇒ (x² - 1) (x⁴ + x² + 1) > 0
⇒ x² - 1 > 0 [∵ x⁴ + x² + ≥ 0, ∀ x]
⇒ (x + 1) (x - 1) > 0
स्थिति I (x - 1) > 0, (x + 1) > 0 ⇒ x > 1, x > - 1
स्थिति II (x - 1) < 0, (x + 1) < 0 ⇒ x < 1, x < - 1
(- ∞, -1) ∪ (1, ∞)
अतः फलन वृद्धिमान होगा ह्रासमान फलन के लिये f'(x) < 0
⇒ (x² - 1) < 0 या (x - 1) (x + 1) < 0
स्थिति I x - 1 < 0 एवं (x + 1) > 0 ⇒ x < 1, x > - 1
स्थिति II x - 1 > 0 एवं x + 1 < 0 ⇒ x > 1, x < - 1
⇒ - 1 < x < 1 ⇒ x ∈ (-1, 1)
अतः x ∈ (-1, 1) में फलन ह्रासमान है।

प्रश्न 8.
दीर्घ वृत्त \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 के अन्तर्गत उस समद्विबाहु त्रिभुज का महत्तम क्षेत्रफल ज्ञात कीजिए जिसका शीर्ष दीर्घ अक्ष का एक सिरा है।
हल:
दीर्घ वृत्त का समीकरण \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
दीर्घ वृत्त पर एक बिन्दु P(a cos θ, b sin θ) मान लिया। शीर्ष A से उतनी ही दूरी पर दूसरा सिरा P(a cos θ, - b sin θ) लिया ताकि त्रिभुज APP' एक समद्विबाहु त्रिभुज बन सके।

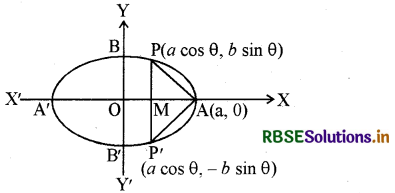
PP' दीर्घ वृत्त के अक्ष AA' को M पर काटती है।
∆APP' का क्षेत्रफल A

प्रश्न 9.
हल:
आयताकार आधार व आयताकार दीवारों की 2m गहरी और 8 m³ आयतन की एक बिना ढक्कन की टंकी का निर्माण करना है। यदि टंकी के निर्माण में आधार के लिए Rs. 70/m² और दीवारों पर Rs. 45/m² व्यय आता है तो निम्नतम खर्च से बनी टंकी की लागत क्या है?
हल:
माना कि आकृति के अनुसार बनाया गया एक टैंक है जिसकी लम्बाई x मीटर और चौड़ाई y मीटर है। इस टैंक की गहराई 2m है।
∴ इसका आयतन
= 2 × x × y
= 2xy = 8 (दिया है)
∴ xy = 4
आधार का क्षेत्रफल = xy
आधार पर खर्च की दर = 70/m²

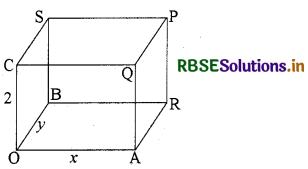
∴ आधार पर किया गया खर्च 70 × xy रु. = 70xy रु.
चारदीवारी का क्षेत्रफल = 2(x + y) × 2m² = 4(x + y) m²
दीवारों पर खर्च की दर = 45 रु./m²
दीवारों पर कुल खर्च = 45 × 4(x + y) = 180(x + y) रु.
आधार व दीवारों पर कुल खर्च
C = Rs. [70 xy + 180(x + y)] ...... (2)
समीकरण (1) से y = \(\frac{4}{x}\), (2) में रखने पर

अर्थात् C निम्नतम है।
या C का x = 2 पर निम्नतम खर्च है।
∴ निम्नतम खर्च = 280 + 180\(\left(2+\frac{4}{2}\right)\)
= 280 + 180 × 4
= 280 + 720
= 1000 रु.

प्रश्न 10.
एक वृत्त और एक वर्ग के परिमापों का योग k है जहाँ k एक अचर है। सिद्ध कीजिए कि उनके क्षेत्रफलों का योग निम्नतम है, जब वर्ग की भुजा वृत्त की त्रिज्या की दुगुनी है।
हल:
माना कि वर्ग की भुजा तथा वृत्त की त्रिज्या । है।
वर्ग का परिमाप = 4x, वृत्त की परिधि = 2πr
दोनों परिमापों का योग = 2πr + 4x = k ...... (1)
वृत्त का क्षेत्रफल = πr²
वर्ग का क्षेत्रफल = x²
दोनों का योग (A) = πr² + x²
∴ A = πr² + x² .......... (2)
(1) से x = \(\frac{k-2 \pi r}{4}\) ........ (3)

प्रश्न 11.
किसी आयत के ऊपर बने अर्द्धवृत्त के आकार वाली खिड़की है। खिड़की का सम्पूर्ण परिमाप 10 m है। पूर्णतया खुली खिड़की से अधिकतम प्रकाश आने के लिए खिड़की की विमाएँ ज्ञात कीजिए।
हल:
'माना कि ABCPD खिड़की है जिसमें CPD अर्द्धवृत्त है।

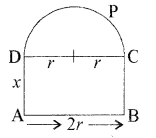
यदि AB = 2r, BC = AD = x तो CPD = \(\frac{1}{2}\) × 2πr = πr
खिड़की का परिमाप = 2x + 2r + πr = 10(दिया है)
या 10 = (π + 2)r + 2x ........ (1)
खिड़की का क्षेत्रफल A = 2rx + \(\frac{1}{2}\)πr²
समीकरण (1) से 2x का मान रखने पर
A = r[10 - (π + 2)r] + \(\frac{1}{2}\)πr²

प्रश्न 12.
त्रिभुज की भुजाओं से a और b दूरी पर त्रिभुज के कर्ण पर स्थित एक बिन्दु है। सिद्ध कीजिए कि कर्ण की न्यूनतम लम्बाई
\(\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)^{\frac{3}{2}}\) है।
हल:
माना कि त्रिभुज ABC के कर्ण पर एक बिन्दु P है। P से AB
पर PL तथा P से CB पर PM लम्ब खींचे गए। मान लिया
∠ACB = θ = ∠APL
AP = a sec θ, PC = b cosec θ
माना l कर्ण की लम्बाई है, तब
l = AP + PC
= a sec θ + b cosec θ, 0 < θ < \(\frac{\pi}{2}\)
∴ \(\frac{d l}{d \theta}\) = a sec θ tan θ - b cosec θ cot θ

प्रश्न 13.
उन बिन्दुओं को ज्ञात कीजिए जिन पर f(x) = (x - 2)⁴ (x + 1)³ द्वारा प्रदत्त फलन fका
(i) स्थानीय उच्चतम बिन्दु है,
(ii) स्थानीय निम्नतम बिन्दु है,
(iii) नति परिवर्तन बिन्दु है।
हल:
प्रश्नानुसार f(x) = (x - 2)⁴ (x + 1)³
∴ f"(x) = (x - 2)⁴. 3(x + 1)² + (x + 1)³ . 4(x - 2)³
= (x - 2)³ (x + 1)² [3(x - 2) + 4(x + 1)]
= (x - 2)³ (x + 1)² (7x - 2)
= 7(x - 2)³ (x + 1)² (x - \(\frac{2}{7}\))
उच्चतम व निम्नतम के लिए f'(x) = 0
अर्थात् 7(x - 2)³ (x + 1)² (x - \(\frac{2}{7}\)) = 0
अतः x = 2, - 1, \(\frac{2}{7}\)

(i) x = 2 पर
x, 2 के निकट और 2 के बायीं ओर हो तो fox) = (-)(+)(+) = ऋणात्मक
x, 2 के निकट और 2 के दायीं ओर हो तो f(x) = (+)(+)(+) = धनात्मक
∴ जब x, x = - 2 से होकर आगे बढ़ता है तो f'(x) का चिह्न ऋण से धन में परिवर्तित हो जाता है।
अर्थात् दिया गया फलन x = 2 पर स्थानीय निम्नतम है।

(ii) x = - 1 पर
x, - 1 के निकट और 1 से कम मान रखने से
f(x) = (-)(+)(-) = धनात्मक
x, - 1 के निकट और - 1 से अधिक मान रखने पर
f(x) = (-)(+)(-) = धनात्मक
अर्थात् x = - 1 पर एक नति परिवर्तन बिन्दु है।

(iii) x = \(\frac{2}{7}\) = 0.28 पर
x का \(\frac{2}{7}\) के निकट \(\frac{2}{7}\) से कम मान रखने पर
f'(x) = (-)(+)(-) = धनात्मक
x का \(\frac{2}{7}\) के निकट और \(\frac{2}{7}\) से अधिक मान रखने पर
f(x) = (-)(+)(+) = ऋणात्मक
अर्थात् x = \(\frac{2}{7}\) पर f(x) धन से ऋण में परिवर्तित हो जाता है जैसे ही x, x = \(\frac{2}{7}\) से होकर आगे बढ़ता है।
अर्थात् दिया गया फलन x = \(\frac{2}{7}\) पर स्थानीय उच्चतम है।

प्रश्न 14.
f(x) = cos²x + sin x, x ∈ [0, π] द्वारा प्रदत्त फलन का निरपेक्ष उच्चतम और निम्नतम मान ज्ञात कीजिए।
हल:
प्रश्नानुसार f(x) = cos² x + sin x, x ∈ [0, π]
f'(x) = 2 cos x (- sin x) + cos x
= cos x (- 2 sin x + 1)
f(x) = 0, 1 - 2 sin x = 0, sin x = \(\frac{1}{2}\) ⇒ x = \(\frac{\pi}{6}\) तथा cos x = 0 ⇒ x = \(\frac{\pi}{2}\)
अन्तराल [0, π], क्रान्तिक बिन्दु x = \(\frac{\pi}{6}\) और x = \(\frac{\pi}{2}\) हैं
∴ f(0) = cos² 0 + sin 0 = 1

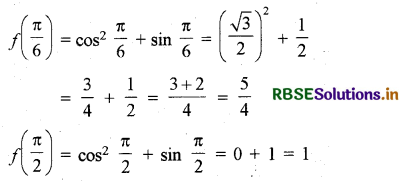
निरपेक्ष उच्चतम मान = \(\frac{5}{4}\), निरपेक्ष निम्नतम मान = 1

प्रश्न 15.
सिद्ध कीजिए कि एक r त्रिज्या के गोले के अन्तर्गत उच्चतम आयतन के लम्ब वृत्तीय शंकु की ऊँचाई का \(\frac{4 r}{3}\) है।
हल:
माना कि । त्रिज्या वाले गोले के अन्तर्गत एक R त्रिज्या वाला शंकु बनाया गया है। मान लिया 0, गोले का केन्द्र है।

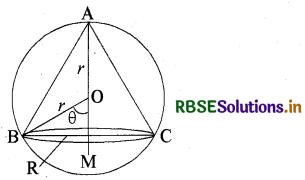
शंकु की ऊँचाई = AM
= AO + OM = r + r cos θ
जबकि ∠BOM = θ
BC = शंकु के आधार का व्यास है
शंकु की ऊँचाई = r + r cos θ = r(1 + cos θ)
शंकु की त्रिज्या = r sin θ

प्रश्न 16.
मान लीजिए [a, b] पर परिभाषित एक फलन । है इस प्रकार कि सभी x ∈ (a, b) के लिए f'(x) > 0, तो सिद्ध कीजिए कि (a, b) पर एक वर्धमान फलन है।
हल:
माना x₁, x₂ ∈ (a, b) इस प्रकार है कि x₁ < x₂
क्योंकि f(x), (a, b) पर अवकलनीय है और [x₁, x₂] ⊂ (a, b)
∴ f(x), [x₁, x₂] पर संतत है और (x₁, x₂) पर अवकलनीय है।
इसलिए माध्यमान प्रमेय के अनुसार, यहाँ C ∈ (x₁, x₂) का अस्तित्व इस प्रकार है कि ।
f'(c) = \(\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}\) ....... (1)
क्योंकि सभी x ∈ (a, b), f'(x) > 0; इसलिए विशेषतया, f'(c) > 0.
अब, f(c) > 0 ⇒ \(\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}\) > 0
[समीकरण (1) का प्रयोग करने पर]
या f(x₂) - f(x₁) > 0 [∵ x₂ - x₁ > 0 जब x₁ < x₂]
या f(x₂) > f(x₂)
या f(x₂) < f(x₂) यदि x₁ < x₂
क्योंकि x₁, x₂, (a, b) में स्वेच्छ बिन्दु है।
∴ x₁ < x₂
अर्थात् f(x₁) < (x₂) सभी x₁, x₂ ∈ (a, b) के लिए
इसलिए f(x), (a, b) में एक वर्धमान फलन है।

प्रश्न 17.
सिद्ध कीजिए कि एक R त्रिज्या के गोले के अन्तर्गत अधिकतम आयतन के बेलन की ऊँचाई \(\frac{2 \mathrm{R}}{\sqrt{3}}\) है। अधिकतम आयतन भी ज्ञात कीजिए।
हल:

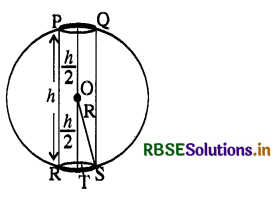
माना
PQRS एक बेलन है जो R त्रिज्या के गोले के अन्तर्गत बना है। जिसमें गोले का केन्द्र O है। बेलन की ऊँचाई और त्रिज्या क्रमशः h और r है और इसका आयतन V है।
∴ बेलन का आयतन V = πr²h .......... (1)
समकोण ∆OTS में
R² = (OT)² + (TS)²

प्रश्न 18.
सिद्ध कीजिए कि अर्द्धशीर्ष कोण α और ऊँचाई h के लम्ब वृत्तीय शंकु के अन्तर्गत अधिकतम आयतन के बेलन की ऊँचाई शंकु की ऊँचाई की एक-तिहाई है और बेलन का अधिकतम आयतन \(\frac{4}{27}\)πh³ tan² α है।
हल:
माना कि शंकु VAB की ऊँचाई h तथा अर्द्धशीर्ष कोण a है। बेलन A'B'DC जो शंकु के अन्तर्गत बनाया गया है, की AD त्रिज्या x है।
OO' बेलन की ऊँचाई = VO - VO' = h - x cot α
बेलन का आयतन (V) = πx² (h - x cot α) .... (1)

19 से 24 तक के प्रश्नों के सही उत्तर चुनिए:

प्रश्न 19.
एक 10 m त्रिज्या के बेलनाकार टंकी में 314 m³/h की दर से गेहूँ भरा जाता है। भरे गए गेहूँ की गहराई की वृद्धि दर है।
(A) 1 m/h
(B) 0.1 m/h
(C) 1.1 m/h
(D) 0.5 m/h
उत्तर:
(A) 1 m/h

हल:
बेलन का आयतन V = πr²h
V = π(10)² h = 100 πh
∴ \(\frac{d \mathrm{~V}}{d t}\) = 100π \(\frac{d h}{d t}\)
314 = 100 × 3.14 \(\frac{d h}{d t}\)
⇒ \(\frac{d h}{d t}\) = 1 m/h
अतः सही विकल्प (A) है।

प्रश्न 20.
वक्र x = t² + 3t - 8, y = 2t² - 2t - 5 के बिन्दु (2, - 1) पर स्पर्श रेखा की प्रवणता है :
(A) \(\frac{22}{7}\)
(B) \(\frac{6}{7}\)
(C) \(\frac{7}{6}\)
(D) \(\frac{-6}{7}\)
उत्तर:
(B) \(\frac{6}{7}\)

हल:
दिये गये वक्रों के समीकरण से
x = t² + 3t - 8, y = 2t² - 2t - 5

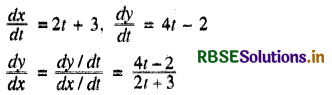
t² + 3t - 8 = 2 ⇒ t² + 3t – 10 = 0
∴ t = 2, - 5
और 2t² - 2t - 5 = - 1 ⇒ 212 - 2t - 4 = 0
∴ t = 2, - 1
अतः t = 2 पर स्पर्श रेखा की प्रवणता का मान
\(\frac{d y}{d x}=\frac{4 \times 2-2}{2 \times 2+3}=\frac{6}{7}\)
अतः सही विकल्प (B) है।

प्रश्न 21.
रेखा y = mx + 1, वक्र y² = 4x की एक स्पर्श रेखा है यदि m का मान है
(A) 1
(B) 2
(C) 3
(D) \(\frac{1}{2}\)
उत्तर:
(A) 1

हल:
y² = 4x

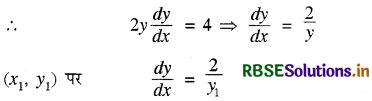
y = mx + 1 परवलय की स्पर्श रेखा है, अतः
m = \(\frac{2}{y_1}, \frac{2 x_1}{y_1}\) = 1
⇒ y₁ = 2x₁
y₁² = 4x₁- ⇒ (2x₁)² = 4x₁
⇒ 4x₁² - 4x₁ = 0
x₁ = 0, 1 ∴ y₁ = 0, 2.
अतः m = \(\frac{2}{2}\) = 1
अतः सही विकल्प (A) है।

प्रश्न 22.
वक्र 2y + x² = 3 के बिन्दु (1, 1) पर अभिलम्ब का समीकरण है :
(A) x + y = 0
(B) x - y = 0
(C) x + y + 1 = 0
(D) x - y = 1
उत्तर:
(B) x - y = 0

हल:
2y + x² = 3

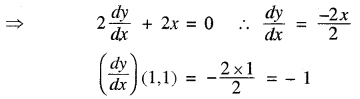
∴ बिन्दु (1, 1) पर अभिलम्ब का समीकरण
y - 1 = 1(x - 1)
x - y = 0
अतः सही विकल्प (B) है।

प्रश्न 23.
वक्र x² = 4y का बिन्दु (1, 2) से होकर जाने वाला अभिलम्ब है :
(A) x + y = 3
(B) x - y = 3
(C) x + y = 1
(D) x - y = 1
उत्तर:
(A) x + y = 3

हल:
x² = 4y
⇒ \(\frac{d y}{d x}=\frac{2 x}{4}=\frac{1}{2}\) x
∴ \(\left(\frac{d y}{d x}\right)_{\left(x_1, y_1\right)}=\frac{1}{2} x_1\)
(x₁, y₁) पर अभिलम्ब का समीकरण
y - y₁ = \(\frac{-2}{x_1}\)(x - x₁)
यह अभिलम्ब (1, 2) से गुजरता है
2 - y₁ = \(\frac{-2}{x_1}\)(1 - x₁)
⇒ 2x₁ - x₁y₁ = - 2 + 2x₁
⇒ x₁y₁ = 2 ∴ y₁ = \(\frac{2}{x_1}\) ........ (1)
बिन्दु (x₁, y₁) वक्र पर स्थित है अतः
x₁² = 4y₁
⇒ x₁² = 4 × \(\frac{2}{x_1}\)
⇒ x₁³ = 8 ⇒ x₁ = 2
समीकरण (1) से है y₁ = \(\frac{2}{2}\) = 1
अतः अभिलम्ब का समीकरण .
y - 1 = -\(\frac{2}{2}\)(x - 2)
y - 1 = - x + 2
∴ x + y = 3
अतः सही विकल्प (A) है।

प्रश्न 24.
वक्र 9y² = x³, पर वे बिन्दु जहाँ पर वक्र का अभिलम्ब अक्षों से समान अन्त:खण्ड बनाता है:
(A) \(\left(4, \pm \frac{8}{3}\right)\)
(B) \(\left(4,-\frac{8}{3}\right)\)
(C) \(\left(4, \pm \frac{3}{8}\right)\)
(D) \(\left(\pm 4, \frac{3}{8}\right)\)
उत्तर:
(A) \(\left(4, \pm \frac{8}{3}\right)\)

हल:
दिये गये वक्र का समीकरण
9y² = x³
x के सापेक्ष अवकलन करने पर,

पुनः अभिलम्ब अक्षों पर समान अन्त:खण्ड बनाता है
∴ अभिलम्ब की प्रवणता = ±1
∴ \(\frac{-6 y_1}{x_1^2}\) = ±1
∴ 6y₁ = ±x₁²
∵ (x₁, y₁) वक्र पर स्थित है।
∴ 9y₁² = x₁³
समीकरण (1) से y का मान समीकरण (2) में रखने पर