RBSE Solutions for Class 12 Maths Chapter 6 अवकलज के अनुप्रयोग Ex 6.5

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 6 अवकलज के अनुप्रयोग Ex 6.5 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 6 अवकलज के अनुप्रयोग Ex 6.5

Class 12 Maths Ncert Solutions Chapter 6 Exercise 6.5 In Hindi प्रश्न 1.
निम्नलिखित दिए गए फलनों के उच्चतम या निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए:
(i) f(x) = (2x - 1)² + 3
हल:
दिया है f(x) = (2x - 1)² + 3
(2x - 1)² का कम से कम मान = 0
∵ (2x - 1)² ≥ 0 अर्थात् इसका कोई भी उच्चतम मान नहीं है।
अतः f(x) का निम्नतम मान = 3

(ii) f(x) = 9x² + 12x + 2
हल:
दिया है f(x) = 9x² + 12x + 2
= 9x² + 12x + 4 - 2
= (3x + 2)² - 2
(3x + 2)² का निम्नतम मान = 0
∵ (3x + 2)² ≥ 0 अर्थात् इसका कोई भी उच्चतम मान नहीं है।
अतः f(x) का निम्नतम मान = - 2

(iii) f(x) = - (x - 1)² + 10
हल:
दिया है f(x) = - (x - 1)² + 10
∵ (x - 1)² ≥ 0
⇒ - (x - 1)² ≤ 0
⇒ - (x - 1)² + 10 ≤ 10
अतः f का उच्चतम मान = 10

(iv) g(x) = x³ + 1
हल:
g(x) = x³ + 1
g'(x) = 3x² जो x ∈ R के लिए सदैव धनात्मक है।
अतः f एक वर्धमान फलन है अर्थात् कोई निम्नतम व उच्चतम मान नहीं है।

Class 12 Math Chapter 6.5 In Hindi प्रश्न 2.
निम्नलिखित दिए गए फलनों के उच्चतम या निम्नतम मान, यदि . कोई हों, तो ज्ञात कीजिए:
(i) f(x) = |x + 2| - 1
हल:
f(x) = x + 2 - 1
|x + 2| का निम्नतम मान 0 है अत: f(x) = |x + 2|
- 1 ≥ - 1 ∀ x ∈ R
∴ f का निम्नतम मान - 1 है एवं उच्चतम मान का अस्तित्व नहीं है।

(ii) g(x) = - |x + 1| + 3
हल:
g(x) = - |x + 1| + 3
|x + 1| ≥ 0 ⇒ - |x + 1| ≤ 0
⇒ - |x + 1 + 3 ≤ 3
∴ g(x) = - |x + 1| + 3 का उच्चतम मान 0 + 3 = 3 है एवं निम्नतम मान का अस्तित्व नहीं है।

(iii) h(x) = sin (2x) + 5
हल:
h(x) = sin (2x) + 5
sin 2x का अधिकतम मान = 1 क्योंकि - 1 ≤ sin 2x ≤ 1
∴ h(x) = sin 2x + 5 का उच्चतम मान 1 + 5 = 6
sin 2x का न्यूनतम मान = - 1
∴ h(x) = sin 2x + 5 का निम्नतम मान
= - 1 + 5 = 4

(iv) f(x) = |sin 4x + 3|
हल:
f(x) = |sin 4x + 3|
sin 4x का अधिकतम मान = 1 क्योंकि - 1 ≤ sin 4x ≤ 1
f(x) = |sin 4x + 3| का उच्चतम मान |1 + 31 = 4 है।
तथा sin 4x का निम्नतम मान - 1
f(x) = |sin 4x + 3| का निम्नतम मान = |- 1 + 3| = 2 है।

(v) h(x) = x + 1, x ∈ (- 1, 1)
हल:
h(x) = x + 1
h'(x) = 1 = धनात्मक
∴ h वर्धमान फलन है।
अर्थात् इसका कोई उच्चतम या निम्नतम मान नहीं है। उत्तर

Exercise 6.5 Class 12 Maths NCERT Solutions In Hindi प्रश्न 3.
निम्नलिखित फलनों के स्थानीय उच्चतम या निम्नतम, यदि कोई हों तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम मान, जैसी स्थिति हो, भी ज्ञात कीजिए:
(i) f(x) = x²
हल:
f(x) = x² ⇒ f'(x) = 2x
उच्चतम एवं निम्नतम के लिये
f'(x) = 0 ⇒ 2x = 0 ⇒ x = 0
f"(x) = 2
क्योंकि [f"(x)]_{at x = 0} = 2 > 0.
इसलिए f(x) का स्थानीय निम्नतम मान x = 0 पर होगा और निम्नतम मान = f(x) = 0

(ii) g(x) = x³ - 3x
हल:
g(x) = x³ - 3x ⇒ g'(x) = 3x² - 3
g(x) = 0 ⇒ 3x² - 3 = 0 ⇒ x² - 1 = 0 ⇒ x = ± 1
g''(x) = 6x
x = 1 पर g''(x) = 6 > 0
इसलिए x = 1 पर, g(x) का स्थानीय निम्नतम मान होगा और स्थानीय निम्नतम मान
= (1)³ - 3(1) = 1 - 3 = - 2
x = - 1 पर g"(x) = - 6 < 0
इसलिए x = - 1 पर g(x) का स्थानीय उच्चतम मान होगा और स्थानीय उच्चतम मान
= (-1)³ - 3(- 1) = 3 - 1 = 2

(iii) h(x) = sin x + cos x, 0 < x < \(\frac{\pi}{2}\),
हल:
h(x) = sin x + cos x, 0 < x < \(\frac{\pi}{2}\)
h'(x) = cos x - sin x
उच्चिष्ठ एवं निम्निष्ठ के लिये
h'(x) = 0 ⇒ cos x - sin x = 0
⇒ cos x = sin x ⇒ tan x = 1 ⇒ x = \(\frac{\pi}{4}\) ∈ \(\left(0, \frac{\pi}{2}\right)\)
अब h''(x) = - sin x - cos x
x = \(\frac{\pi}{4}\) पर h''(x) = -\( \frac{1}{\sqrt{2}}\) - \(\frac{1}{\sqrt{2}}\) < 0
इसलिए h(x) x = \(\frac{\pi}{4}\) पर h(x) का स्थानीय उच्चतम मान होगा और स्थानीय उच्चतम मान
= \(\sin \frac{\pi}{4}+\cos \frac{\pi}{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\)

(iv) f(x) = sin x - cos x, 0 < x < 2π
हल:
f(x) = sin x - cos x, 0 < x < 2π
⇒ f(x) = cos x + sin x
f(x) = 0 ⇒ cos x + sin x = 0 ⇒ tan x = - 1

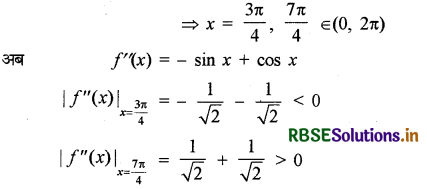
इसलिए f(x) का x = \(\frac{3 \pi}{4}\) पर स्थानीय उच्चतम मान होगा
और x = \(\frac{7 \pi}{4}\) पर स्थानीय निम्नतम मान होगा।
∴ स्थानीय उच्चतम मान = sin \(\frac{3 \pi}{4}\) - cos \(\frac{3 \pi}{4}\)
= \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\) = √2
और स्थानीय निम्नतम मान = sin \(\frac{7 \pi}{4}\) - cos \(\frac{7 \pi}{4}\)
= - \(\frac{1}{\sqrt{2}}\) - \(\frac{1}{\sqrt{2}}\) = - √2

(v) f(x) = x³ - 6x² + 9x + 15
हल:
f(x) = x³ - 6x² + 9x + 15
⇒ f(x) = 3x² - 12x + 9
उच्चिष्ठ एवं निम्निष्ठ के लिये
f'(x) = 0 ⇒ 3x² - 12x + 9 = 0
⇒ x² - 4x + 3 = 0
⇒ (x - 1) (x - 3) = 0 ⇒ x = 1, 3
अब f"(x) = 6x - 12
x = 1 पर f"(x) = 6 - 12 < 0 और x = 3 पर f"(x) = 18 - 12 > 0
इसलिए x = 1 पर, f(x) का स्थानीय उच्चतम मान होगा।
और x = 3 पर f(x) का स्थानीय निम्नतम मान होगा।
स्थानीय उच्चतम मान = 1 - 6 + 9 + 15 = 19
और स्थानीय निम्नतम मान = (3)³ - 6(3)² + 9(3) + 15
= 27 - 54 + 27 + 15 = 15

(vi) g(x) = \(\frac{x}{2}\) + \(\frac{2}{x}\), x > 0
हल:

(vii) g(x) = \(\frac{1}{x^2+2}\)
हल:

(viii) f(x) = x \(\sqrt{1-x}\), x > 0
हल:

इसलिए x = \(\frac{2}{3}\) पर f(x) का स्थानीय उच्चतम मान होगा और स्थानीय उच्चतम मान
= \(\frac{2}{3} \sqrt{1-\frac{2}{3}}=\frac{2}{3} \cdot \frac{1}{\sqrt{3}}=\frac{2}{3 \sqrt{3}}\)
= \(\frac{2 \sqrt{3}}{9}\)

Class 12 Math 6.5 Solution In Hindi प्रश्न 4.
सिद्ध कीजिए कि निम्नलिखित फलनों का उच्चतम या निम्नतम मान नहीं है:
(i) f(x) = e
हल:
f(x) = e^x
∴ f(x) = e^x > 0, x ∈ R
अतः f(x) का चिह्न x के किसी मान के लिये सदैव धनात्मक रहता है।
∴ फलन का न तो उच्चतम मान है और न ही निम्नतम मान है।

(ii) g(x) = log x
हल:
g(x) = log x जहाँ x > 0
g(x) = \(\frac{1}{x}\), > 0 ∀ x > 0
इसलिए g(x) का कोई उच्चतम या निम्नतम मान नहीं है।
[∵ g(x) = log x में x > 0 ही रहेगा, नहीं तो फलन परिभाषित नहीं होगा।]

(iii) h(x) = x³ + x² + x + 1
हल:
h(x) = x³ + x² + x + 1

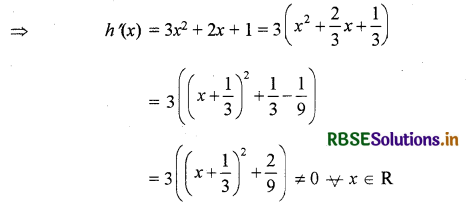
क्योंकि h (x) ≠ 0 ∀ x ∈ R
इसलिए h(x) का कोई उच्चतम या निम्नतम मान नहीं है।

Class 12 Math 6.5 In Hindi प्रश्न 5.
प्रदत्त अन्तरालों में निम्नलिखित फलनों के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए:
(i) (x) = x, x ∈ [- 2, 2]
हल:
दिया है f(x) = x, x ∈ [- 2, 2]
∴ f(x) = 3x²
f'(x) = 0 ⇒ 3x² = 0 ∴ x = 0
f(- 2) = (- 2) = - 8;
f(0) = (0)³ = 0
और f(2) = (2)³ = 8
निरपेक्ष उच्चतम मान = 8
निरपेक्ष निम्नतम मान = - 8

(ii) f(x) = sin x + cos x, x ∈ [0, 2]
हल:
दिया है f(x) = sin x + cos x, x ∈ [0, π]
∴ f'(x) = cos x - sin x
f'(x) = 0
अतः cos x - sin x = 0 ∴ tan x = 1
∴ x = \(\frac{\pi}{4}\)
अतः = sin 0 + cos 0 = 1
f\(\left(\frac{\pi}{4}\right)\) = \(\sin \frac{\pi}{4}+\cos \frac{\pi}{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\)
= √2
f(π) = sin π + cos π = 0 - 1 = - 1
निरपेक्ष उच्चतम मान = √2
निरपेक्ष निम्नतम मान = - 1

(iii) f(x) = 4x - \(\frac{1}{2}\)x², x ∈ [0, π]
हल:

∴ निरपेक्ष उच्चतम मान = 8
तथा निरपेक्ष निम्नतम मान = - 10

(iv) (x) = (x - 1)² + 3, x ∈ [- 3, 1]
हल:
f(x) = (x - 1)² + 3, x ∈ [- 3, 1]
∴ f(x) = 2(x - 1)
∵ f(x) = 0 ⇒ 2(x - 1) = 0, x = 1
∴ f(1) = (1 - 1)² + 3 = 0 + 3 = 3
f(- 3) = (-3 - 1)² + 3 = 16 + 3 = 19
∴ निरपेक्ष उच्चतम मान = 197
तथा निरपेक्ष निम्नतम मान = 3

Class 12 Maths Chapter 6 In Hindi प्रश्न 6.
यदि लाभ फलन p(x) = 41 - 72x - 18x² से प्रदत्त है तो किसी कम्पनी द्वारा अर्जित उच्चतम लाभ ज्ञात कीजिए।
हल:
लाभ फलन p(x) = 41 - 72x - 18x²
∴ p'(x) = - 72 - 36x = - 36 (2 + x)
p"(x) = - 36
p'(x) = 0 ⇒ - 36 (2 + x) = 0
x = - 2
p''(x) = ऋणात्मक
⇒ x = - 2 पर p(x) उच्चतम है।
∴ उच्चतम लाभ = p(- 2)
= 41 - 72(- 2) - 18(- 2)²
= 41 + 144 - 72
= 185 - 72 = 113 इकाई

प्रश्न 7.
अन्तराल [0, 3] पर 3x⁴ - 8x³ + 12x² - 48x + 25 के उच्चतम मान और निम्नतम मान ज्ञात कीजिए।
हल:
प्रश्नानुसार f(x) = 3x⁴ - 8x³ + 12x² - 48x + 25
∴ f(x) = 12x³ - 24x² + 24x - 48
= 12[x²(x - 2) + 2(x - 2)]
= 12(x² + 2) (x - 2)
उच्चिष्ठ एवं निम्निष्ठ के लिये
f'(x) = 0
∴ 12 (x² + 2) (x - 2)= 0
⇒ x² + 2 = 0
∴ x = ± √-2
और x - 2 = 0
x = 2
परन्तु x = ± √-2 सम्भव नहीं है।
क्योंकि यह वास्तविक संख्या नहीं है।
अतः x = 2
अन्तराल [0, 3] पर
f(0) = 25
f(2) = 3(2)⁴ - 8(2)³ + 12(2)² - 48(2) + 25
= 48 – 64 + 48 - 96 + 25 = - 39
तथा f(3) = 3(3)⁴ - 8(3)³ + 12(3)² - 48(3) + 25
= 243 - 216 + 108 - 144 + 25 = 16
∴ निरपेक्ष उच्चतम मान = 25
तथा निरपेक्ष निम्नतम मान = - 39

Class 12 Maths NCERT Solutions Chapter 6 In Hindi प्रश्न 8.
अन्तराल [0, 27] के किन बिन्दुओं पर फलन sin 2x अपना उच्चतम मान प्राप्त करता है?
हल:
प्रश्नानुसार f(x) = sin 2x, [0, 2π] पर
∵ f(x) = 2 cos 2x
f(x) = 0 ⇒ 2 cos 2x = 0

इस प्रकार अधिकतम मान = 1, x = \(\frac{\pi}{4}\) तथा x = \(\frac{5 \pi}{4}\) पर

6.5 Class 12 प्रश्न 9.
फलन sin x + cos x का उच्चतम मान क्या है?
हल:
∵ f(x) = sin x + cos x, [0, 2π] पर
∴ f'(x) = cos x - sin x
f(x) = 0
⇒ cos x - sin x = 0 ⇒ tan x = 1
∴ x = \(\frac{\pi}{4}\), \(\frac{5 \pi}{4}\)
∵ f(x) = sin x + cos x
f(0) = sin 0 + cos 0 = 1

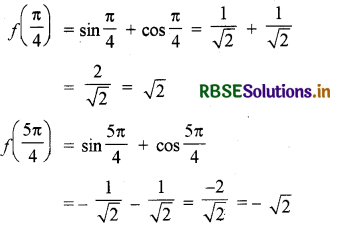
f(2π) = sin 2π + cos 2π = 1
f(x) का उच्चतम मान = √2

प्रश्न 10.
अन्तराल [1, 3] में 2x³ - 24x + 107 का महत्तम मान ज्ञात कीजिए। इसी फलन का अन्तराल [- 3, - 1] में भी महत्तम मान ज्ञात कीजिए।
हल:
हम जानते हैं कि f(x) = 2x³ - 24x + 107 अन्तराल [1, 3] में
∴ f(x) = 6x² - 24
उच्चतम व निम्नतम के लिए
f'(x) = 0
⇒ 6x² - 24 = 0 ⇒ x = ± 2
अन्तराल [1, 3] के लिए, हम x = 1, 2, 3 पर f(x) का मान ज्ञात करते हैं।
f(1) = 2(1)³ - 24 × 1 + 107 = 85
f(2) = 2(2)³ - 24 × 2 + 107 = 75
f(3) = 2(3)³ - 24 × 3 + 107 = 89
इस प्रकार उच्चतम f(x) = 89, x = 3 पर
अन्तराल [-3, - 1] के लिए हम x = - 3, - 2, - 1 पर f(x) का मान ज्ञात करने पर
f(- 3) = 2(-3)³ - 24 (-3) + 107 = 125
f(- 2) = 2(-2)³ - 24 (-2) + 107 = 139
f(- 1) = 2(-1)³ - 24 (- 1) + 107 = 129
इस प्रकार उच्चतम मान f(x) = 139, x = - 2 पर

प्रश्न 11.
यदि दिया है कि अन्तराल [0, 2] में x = 1 पर फलन x⁴ - 62x² + ax + 9 उच्चतम मान प्राप्त करता है, तो a का मान ज्ञात कीजिए।
हल:
मा माना कि
f(x) = x⁴ - 62x² + ax + 9
∴ f(x) = 4x³ - 124x + a
उच्चतम व निम्नतम के लिए, f'(x) = 0
⇒ 4x³ - 124x + a = 0
x = 1 पर, f उच्चतम है = f(1) = 0
∴ 4 . 1³ - 124 . 1 + a = 0; 4 - 124 + a = 0
∴ a = 120
∴ f(x) = x⁴ - 62x² + 120x + 9
f"(x) = 12x² - 124
f"(1) = 12 - 124 = - 112 < 0
∴ x = 1, f उच्चतम है जब a = 120

प्रश्न 12.
[0, 2π] पर x + sin 2x का उच्चतम और निम्नतम मान ज्ञात कीजिए।
हल:
माना कि f(x) = x + sin 2x [0, 2π] पर
∴ f(x) = 1 + 2 cos 2x
उच्चतम व निम्नतम के लिए

f(2π) = 2π + sin 2π = 2π
अतः f(x) का उच्चतम मान = 2π, x = 2π पर उच्चतम तथा f(x) का निम्नतम मान = 0, x = 0 पर निम्नतम

प्रश्न 13.
ऐसी दो संख्याएँ ज्ञात कीजिए जिनका योग 24 है और जिनका गुणनफल उच्चतम हो।
हल:
माना कि वे संख्याएँ x और (24 - x) हैं।
अतः उनका गुणनफल P = x(24 - x) = 24x - x²
उच्चतम व निम्नतम के लिए, \(\frac{d \mathrm{P}}{d x}\) = 0
∴ \(\frac{d \mathrm{P}}{d x}\) = 24 - 2x = 0 ∴ x = 12
⇒ x = 12
\(\frac{d^2 \mathrm{P}}{d x^2}\) = - 2
⇒ P, x = 12 के लिए उच्चतम है।
अतः वे संख्याएँ 12, 12 हैं।

प्रश्न 14.
ऐसी दो धन संख्याएँ x और ' ज्ञात कीजिए ताकि x + y = 60 60 और xy³ उच्चतम हो।
हल:
प्रश्नानुसार x + y = 60 .
∴ x = 60 - y ......... (1)
माना कि xy³ = P
(1) से x का मान 60 - y रखने पर
(60 - y)y³ = P
∴ P = 60y³ - y⁴
⇒ \(\frac{d \mathrm{P}}{d y}\) = 180y² - 4y³ = 4y²(45 - y)
उच्चतम व निम्नतम के लिए \(\frac{d \mathrm{P}}{d y}\) = 0
= 4y²(45 - y) = 0 ⇒ y = 45
\(\frac{d^2 \mathrm{P}}{d y^2}\) = 360y - 12y² = 12y(30 - y)
y = 45 रखने पर \(\frac{d^2 \mathrm{P}}{d y^2}\) = 12 = 12 × 45 (30 - 45) = ऋणात्मक
अतः y = 45 के लिए P उच्चतम है।
अतः x = 15, y = 45, के लिए P = xy³ उच्चतम है।

प्रश्न 15.
ऐसी दो धन संख्याएँ x और y ज्ञात कीजिए जिनका योग 35 हो और गुणनफल x²y⁵ उच्चतम हो।
हल:
प्रश्नानुसार x + y = 35
या y = 35 - x ........ (1)
तथा गुणनफल P = x²y⁵ = x²(35 - x)⁵
[समीकरण (1) का प्रयोग करने पर]
∴ \(\frac{d \mathbf{P}}{d x}\) = x² . 5(35 - x)⁴ (- 1) + (35 - x)⁵ . 2x
= x(35 - x)⁴ - 5x + 2(35 - x)]
= x(35 - x)⁴ (70 - 7x)
∵ \(\frac{d \mathbf{P}}{d x}\) = 0
या x(35 - x)⁴ (70 - 7x)= 0
अतः x = 0, 10, 35
केवल 10 स्वीकृत मान है अतः x = 0, 35 अस्वीकृत करने पर x = 10 पर
जब x, 10 के निकट और 10 की बायीं ओर हो तो,
\(\frac{d \mathrm{P}}{d x}\) = (+) (+) (+) = धनात्मक
जब x, 10 के निकट और 10 की दायीं ओर हो तो,
\(\frac{d \mathrm{P}}{d x}\) = (+) (+) (-) = ऋणात्मक
अर्थात् जैसे x, 10 से होता हुआ आगे बढ़ता है \(\frac{d \mathrm{P}}{d x}\) का चिह्न धनात्मक से ऋणात्मक हो जाता है।
अतः x = 10 पर P उच्चतम है।
∴ समीकरण (1) से y = 35 - 10 = 25
इस प्रकार 10 और 25 अभीष्ट संख्याएँ हैं।

प्रश्न 16.
ऐसी दो धन संख्याएँ ज्ञात कीजिए जिनका योग 16 हो और जिनके घनों का योग निम्नतम हो।
हल:
माना x और 16 - x दो संख्याएँ हैं।
∴ घनों का योग S = x³ + (16 - x)³
∴ \(\frac{d \mathbf{S}}{d x}\) = 3x² + 3(16 - x) . (- 1)
= 3x² - 3(256 - 32x + x²)
= 3(32x - 256)
∵ \(\frac{d \mathrm{~S}}{d x}\) = 0
अतः 3(32x - 256) = 0
या x = \(\frac{256}{32}\) = 8
तथा \(\frac{d^2 \mathrm{~S}}{d x^2}\) = 96 > 0
अत: x = 8 पर S निम्नतम है।
इस प्रकार 8 और (16-8) अर्थात् 8 अभीष्ट संख्याएँ हैं।

प्रश्न 17.
18 cm. भुजा के टिन के किसी वर्गाकार टुकड़े से प्रत्येक कोने पर एक वर्ग काट कर तथा इस प्रकार बने टिन के फलकों को मोड़ कर ढक्कनरहित एक सन्दूक बनाना है। काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे सन्दूक का आयतन उच्चतम हो?
हल:

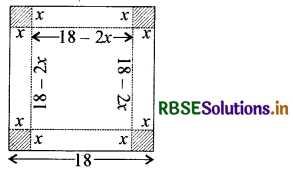
माना वर्ग की प्रत्येक भुजा x cm.
काटी गई है।
∴ सन्दूक के लिए :
l = 18 - 2x,
b = 18 - 2x
और h = x
∴ आयतन = l × b × h
= (18 - 2x) × (18 - 2x) × x
= x (18 - 2x)²
आयतन V = x(18 - 2x)²
\(\frac{d \mathrm{~V}}{d x}\) = x . 2(18 - 2x) (-2) + (18 - 2x)² . 1
= (18 - 2x) (- 4x + 18 - 2x)
= (18 - 2x) (18 - 6x)
अतः x = 3,9
परन्तु x = 9 cm. सम्भव नहीं है।
तथा \(\frac{d^2 \mathrm{~V}}{d x^2}\) = (18 - 2x) (- 6) + (18 - 6x) (- 2)
x = 3 पर, \(\frac{d^2 \mathrm{~V}}{d x^2}\) = (18 - 6) (-6) + (18 - 18) (-2)
= - 72 < 0
∴ x = 3, पर आयतन अधिकतम होगा।
अर्थात् जब वर्ग की भुजा प्रत्येक कोने से 3 cm. काटी गई है तो आयतन उच्चतम होगा।

प्रश्न 18.
45 cm. × 24 cm. की टिन की आयताकार चादर के कोनों पर वर्ग काट कर तथा इस प्रकार बने टिन के फलकों को मोड़ कर ढक्कन रहित एक सन्दूक बनाना है। काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे सन्दूक का आयतन उच्चतम हो।
हल:
माना प्रत्येक कोने से x cm. भुजा काटी गई है।

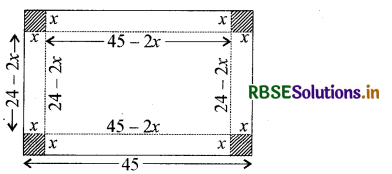
∴ आयताकार सन्दूक की भुजाएँ (45 - 2x), (24 - 2x) और x cm. होंगी।
तब सन्दूक का आयतन
V = (45 - 2x) (24 - 2x) (x)
= 2x(45 - 2x) (12 - x)
= 2(2x³ - 69x² + 540x)
∴ \(\frac{d V}{d x}\) = 2(6x² - 138x + 540)
= 12(x² - 23x + 90)
उच्चतम एवं निम्नतम आयतन के लिए
\(\frac{d V}{d x}\) = 0
या 12(x² - 23x + 90)= 0
या (x - 5) (x - 18) = 0
∴ x = 5, 18
परन्तु x, 12 से अधिक नहीं हो सकता।
∴ x = 5
तथा \(\frac{d^2 \mathrm{~V}}{d x^2}\) = 12(2x - 23)
x = 5 पर \(\frac{d^2 \mathrm{~V}}{d x^2}\) = 12(10 - 23) = ऋणात्मक
∴ V, x = 5 के लिए उच्चतम है।

प्रश्न 19.
सिद्ध कीजिए कि एक दिए वृत्त के अन्तर्गत सभी आयतों में वर्ग का क्षेत्रफल उच्चतम होता है।
हल:
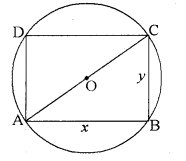
माना त्रिज्या a के वृत्त के अन्तर्गत आयत की लम्बाई और
चौड़ाई क्रमशः x और y है।
∴ x² + y² = (2a)²
या x² + y² = 4a² .... (1)
∴ क्षेत्रफल = xy
अतः A(x) = x\(\sqrt{4 a^2-x^2}\)
∴ A(x) = x


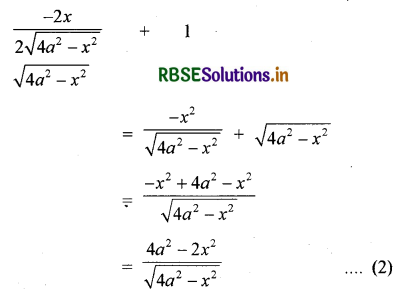
∵ A'(x) = 0
अतः 4a² - 2x² = 0
∴ x = √2a
अब हम x = √2a पर A"(x) का मान ऋणात्मक सिद्ध करेंगे।

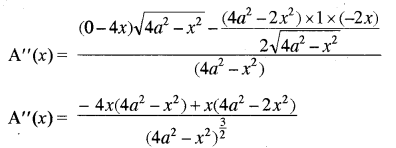
स्पष्ट है कि
x = √2a पर A"(x) = - ve है।
अतः क्षेत्रफल उच्चिष्ठ होगा।
समीकरण (1) से x² + y² = 4a²
(√2a)² + y² = 4a²
∴ y = √2a
∴ आयत का क्षेत्रफल उच्चतम होगा जब x = √2a और y = 2a होगा अर्थात् आयत जब एक वर्ग होगा।

प्रश्न 20.
सिद्ध कीजिए कि प्रदत्त पृष्ठ एवं महत्तम आयतन के बेलन की ऊँचाई, आधार के व्यास के बराबर होती है।
हल:
माना S उस दिए बन्द बेलन का पृष्ठीय क्षेत्रफल है जिसकी त्रिज्या । और ऊँचाई h है। माना इसका आयतन V है तब
पृष्ठीय क्षेत्रफल S = 2πr² + 2πrh

∴ r = \(\frac{h}{2}\); h = 2r पर आयतन अधिकतम है।
इस प्रकार जब बेलन की ऊँचाई, आधार के व्यास के बराबर होती है तो आयतन अधिकतम होता है। (इतिसिद्धम्)

प्रश्न 21.
100 cm³ आयतन वाले डिब्बे सभी बन्द बेलनाकार (लम्ब वृत्तीय) डिब्बों में से न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की 'विमाएँ ज्ञात कीजिए।
हल:
माना बेलनाकार डिब्बों की क्रमशः त्रिज्या r और ऊँचाई h है।
प्रश्नानुसार आयतन = πr²h = 100 cm³
∴ h = \(\frac{100}{\pi r^2}\)
डिब्बे का कुल पृष्ठीय क्षेत्रफल
S = 2πrh + 2πr²

प्रश्न 22.
एक 28 cm. लम्बे तार को दो टुकड़ों में विभक्त किया जाना है। एक टुकड़े से वर्ग तथा दूसरे से वृत्त बनाया जाना है। दोनों टुकड़ों की लम्बाई कितनी होनी चाहिए जिससे वर्ग एवं वृत्त का सम्मिलित क्षेत्रफल न्यूनतम हो?
हल:
माना कि तार के एक भाग की लम्बाई x cm. है तब दूसरा भाग = (28 - x) cm.
माना लम्बाई x वाला भाग त्रिज्या r वाले वृत्त में बदला गया है।
∴ 2πr = x ⇒ r = \(\frac{x}{2 \pi}\)
∴ वृत्त का क्षेत्रफल = πr² = π × \(\frac{x^2}{4 \pi^2}\) = \(\frac{x^2}{4 \pi}\)
अब लम्बाई का दूसरा भाग (28 - x) है जिसे एक - \(\frac{1}{4}\)(28 - x) भुज के वर्ग के रूप में बदला गया है।

अत: तार के एक सिरे से \(\frac{28 \pi}{4+\pi}\) सेमी. की दूरी पर काटा गया है एवं दूसरे टुकड़े की लम्बाई \(\frac{112}{4+\pi}\) सेमी. है।

प्रश्न 23.
सिद्ध कीजिए कि R त्रिज्या के गोले के अन्तर्गत विशालतम शंकु का आयतन गोले के आयतन का \(\frac{8}{27}\) होता है।
हल:
माना VAB विशालतम आयतन का शंकु है जो गोले के अन्तर्गत है। हम जानते हैं कि अधिकतम आयतन के लिए शंकु का अक्ष गोले के व्यास के साथ होना चाहिए।
माना ∠AOC = θ
∴ AC, शंकु के आधार की
त्रिज्या = R sin θ जबकि R गोले की त्रिज्या है।
तथा शंकु की ऊँचाई VC = VO + OC = R + R cos θ

न्यूनतम व अधिकतम के लिए, हम जानते हैं कि
\(\frac{d \mathbf{V}}{d \theta}\) = 0
\(\frac{1}{3}\) πR³ (- 3 sin³θ + 2 sin θ + 2 sin cos θ) = 0
- 3 sin²θ + 2 + 2 cos θ = 0 [∵ sin θ ≠ 0]
- 3(1 - cos²θ) + 2 + 2 cos θ = 0
3 cos² θ + 2 cos θ - 1= 0
(3 cos θ - 1) (cos θ + 1) = 0
cos θ = \(\frac{1}{3}\) or cos θ = -1
परन्तु cos θ ≠ - 1 क्योंकि cos θ = - 1 ⇒ θ = π
जो कि सम्भव नहीं है।

प्रश्न 24.
सिद्ध कीजिए कि न्यूनतम पृष्ठ का दिए आयतन के लम्ब वृत्तीय शंकु की ऊँचाई, आधार की त्रिज्या की √2 गुनी होती है।
हल:
माना एक लम्बवृत्तीय शंकु की ऊँचाई h एवं त्रिज्या r है।
इसलिए शंकु का आयतन V = \(\frac{1}{3}\)πr²h .......... (1)
एवं वक्र पृष्ठ S = πrl .......(2)


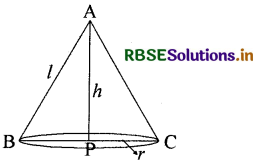
इस प्रकार, न्यूनतम वक्र पृष्ठ वाला लम्ब वृत्तीय शंकु की ऊंचाई त्रिज्या का √2 गुनी होती है।

प्रश्न 25.
सिद्ध कीजिए कि दी हुई तिर्यक ऊँचाई और महत्तम आयतन वाले शंक का अर्द्ध शीर्ष कोण tan^-1√2 होता है।
हल:
माना ABC, अर्द्ध शीर्ष कोण 0 वाला शंकु है। माना तिर्यक ऊँचाई l है।
ऊर्ध्वाधर ऊँचाई = AM = l cos θ
शंकु की त्रिज्या = MC = l sin θ
शंकु का आयतन (V) = \(\frac{1}{3}\)πr²h


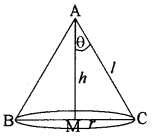
अतः sin θ = 0 या 2 cos² θ - sin² θ = 0
परन्तु θ = 0 सम्भव नहीं है। इस प्रकार,
2 cos²θ - sin²θ = 0

∴ θ = tan^-1 (√2) पर आयतन अधिकतम होगा।
अतः आयतन महत्तम है यदि θ = tan^-1 √2 अर्थात् जब शीर्ष अर्द्धकोण tan^-1 = √2 है तो आयतन महत्तम है।

प्रश्न 26.
सिद्ध कीजिए कि दिए हुए पृष्ठ और महत्तम आयतन वाले लम्ब वृत्तीय शंकु का अर्द्ध शीर्ष कोण sin^-1\(\left(\frac{1}{3}\right)\) होता है।
हल:
माना कि शंकु का पृष्ठीय क्षेत्रफल
S तथा आयतन V है। शंकु की त्रिज्या , ऊँचाई h तथा तिर्यक ऊँचाई 1 है।
∴ शंकु का पृष्ठीय क्षेत्रफल (S)
= πrl + πr²


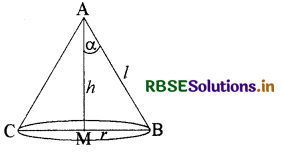
∴ V' = V², S = 4πr² पर उच्चतम है। अतः V, S = 4πr² पर उच्चतम है।
समी. (1) में S का मान रखने पर
l = \(\frac{4 \pi r^2-\pi r^2}{\pi r}\) = \(\frac{3 \pi r^2}{\pi r}\) = 3r
sin α = \(\frac{r}{l}\) ⇒ sin α = \(\frac{1}{3}\)
∴ α = sin^-1\(\left(\frac{1}{3}\right)\)
अतः उच्चतम आयतन के लिए शंकु का अर्द्ध शीर्ष कोण
α = sin^-1 \(\left(\frac{1}{3}\right)\)

प्रश्न संख्या 27 से 29 में सही उत्तर का चुनाव कीजिए.

प्रश्न 27.
वक्र x² = 2y पर (0, 5) से न्यूनतम दूरी पर स्थित बिन्दु है :
(A) (2√2, 4)
(B) (2√2, 0)
(C) (0, 0)
(D) (2, 2)
उत्तर:
(A) (2√2, 4)

हल:
माना P = बिन्दु (x, y) और (0, 5) के बीच की दूरी है,

\(\left(\frac{d^2 \mathrm{P}}{d y^2}\right)_{a t y=4}\) = धनात्मक मान है।
अतः y = 4 पर दूरी न्यूनतम होगी।
जब y = 4 तब x² = 8 ⇒ x = ±2√2
अतः बिन्दु (±2√2, 4) है।
अतः सही विकल्प (A) है।

प्रश्न 28.
x, के सभी वास्तविक मानों के लिए मान है:
(A) 0
(B) 1
(C) 3
(D) \(\frac{1}{3}\)
उत्तर:
(D) \(\frac{1}{3}\)

हल:

अतः न्यूनतम मान = 1
अतः सही विकल्प (D) है।

प्रश्न 29.
[x(x - 1) + 1]^1/3, 0 ≤ x ≤ 1 का उच्चतम मान है:
(A) \(\left(\frac{1}{3}\right)^{\frac{1}{3}}\)
(B) \(\frac{1}{2}\)
(C) 1
(D) 0
उत्तर:
(C) 1

हल:

अतः सही विकल्प (C) है।