RBSE Solutions for Class 12 Maths Chapter 6 Application of Derivatives Ex 6.3

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 6 Application of Derivatives Ex 6.3 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 6 Application of Derivatives Ex 6.3

Question 1.
Find the slope of the tangent to the curve y = 3x⁴ - 4x at x = 4.
Answer:
Differentiating y = 3x⁴ - 4x w.r.t x
\(\frac{d y}{d x}\) = 3 × 4x³ - 4 = 12x³ - 4
At x = 4, \(\frac{d y}{d x}\) = 12 × (4)³ - 4 = 12 × 64 - 4
= 768 - 4 = 764
∴ \(\left(\frac{d y}{d x}\right)_{(x=4)}\) = 764 ⇒ m = 764
Thus, slope of the tangent at x = 4 is 764.

Question 2.
Find the slope of the tangent to the curve
y = \(\frac{x-1}{x-2}\), x ≠ 2 at x = 10
Answer:
Differentiating y = \(\frac{x-1}{x-2}\) w.r.t. x

Question 3.
Find the slope of the tangent to the curve y = x³ - x + 1 at the point whose x-coordinate is 2.
Answer:
Differentiating y = x³ - x + 1 w.r.t. x
\(\frac{d y}{d x}\) = 3x² - 1
At x = 2, \(\frac{d y}{d x}\) = 3(2)² - 1 = 12 - 1 = 11
∴ \(\left(\frac{d y}{d x}\right)_{(x=2)}\) = 11
Thus, at x = 2 slope of tangent is 11.

Question 4.
Find the slope of the tangent to the curve y = x³ - 3x + 2 at the point whose x-co-ordinate is 3.
Answer:
Differentiating y = x³ - 3x + 2 w.r.t. x
\(\frac{d y}{d x}\) = 3x² - 3
At x = 3, \(\frac{d y}{d x}\) = 3 × 3² - 3 = 27 - 3 = 24
∴ \(\left(\frac{d y}{d x}\right)_{(x=3)}\) = 24 ⇒ m = 24
Thus, at x = 3 slope of tangent is 24.

Question 5.
Find the slope of the normal to the curve x = a cos³ θ, y = a sin³ θ at θ = π/4.
Answer:
We have x = a cos³ θ and y = a sin³ θ.
Differentiating x and y w.r.t. θ

Question 6.
Find the slope of the normal to the curve x = 1 - a sin θ, y = b cos²θ at θ = \(\frac{\pi}{2}\).
Answer:
We have x = 1 - a sin θ, y = b cos² θ.
Differentiating x and y w.r.t. θ

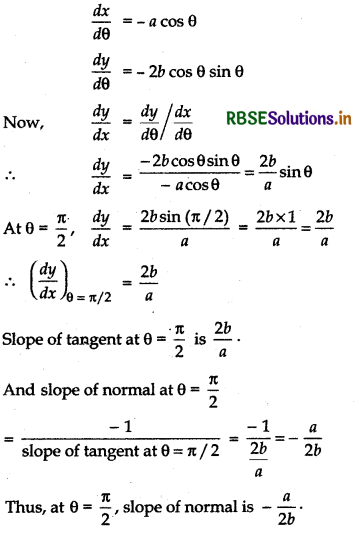
Question 7.
Find points at which the tangent to the curve y = x³ - 3x² - 9x + 7 is parallel to the x-axis.
Answer:
We have y = x³ - 3x² - 9x + 7
Differentiating w.r.t. x
\(\frac{d y}{d x}\) = 3x² - 6x - 9
Since, tangents are parallel to x-axis
∴ \(\frac{d y}{d x}\) = 0
⇒ 3x² - 6x - 9 = 0
⇒ 3(x² - 2x - 3) = 0
⇒ (x - 3) (x + 1) = 0
⇒ x - 3 = 0 or x + 1 = 0
⇒ x = 3 or x = - 1
Putting x = 3 and x = - 1 in equation y = x³ - 3x² - 9x + 7
y = (3)³ - 3(3)² - 9 × 3 + 7
⇒ y = 27 - 27 - 27 + 7
⇒ y = - 20
and y = (- 1)³ - 3(- 1)² - 9(- 1) + 7
⇒ y = - 1 - 3 + 9 + 7
⇒ y = 12
Hence, required points are (3, - 20) and (- 1, 12).

Question 8.
Find a point on the curve y = (x - 2)² at which the tangent is parallel to the chord joining the points (2, 0) and (4, 4).
Answer:
Slope of line joining the points (2, 0) and(4, 4)
m = \(\frac{4-0}{4-2}=\frac{4}{2}\) = 2
Differentiating y = (x - 2)² w.r.t. x
\(\frac{d y}{d x}\) = 2(x - 2) ......... (1)
Since, tangent is parallel to the line joining the points (2, 0) and (4, 4).
∴ Slope of tangent = Slope of line joining the points (2, 0) and (4, 4)
⇒ \(\frac{d y}{d x}\) = 2 ........ (2)
From equations (1) and (2)
2(x - 2) = 2 ⇒ x - 2 = 1
⇒ x = 1 + 2 = 3
Putting x = 3 in y = (x - 2)²
y = (3 - 2)² = 1² = 1
Hence, required points is (3, 1).

Question 9.
Find the point on the curve y = x³ - 11x + 5 at which the tangent is y = x - 11.
Answer:
Differentiating y = - x³ - 11x + 5 w.r.t. x
\(\frac{d y}{d x}\) = 3x² - 11 ...... (i)
Given, slope of tangent = 1 ...... (ii)
From Eqs. (i) and (ii)
∴ 1 = 3x² - 11 ⇒ 3x² = 12
⇒ x² = 4 ⇒ x = ±2
When x = 2, then y = 2³ - 11 × 2 + 5 = - 9
When x = - 2, then y = (- 2)³ - 11(- 2) + 5 = 19
y = x - 11 is not the tangent at point (- 2, 19).
Since LHS. = 19
R.H.S. = - 2 - 11 = - 13
19 ≠ - 13
Hence, y = x - 11 is tangent at point (2, - 9).

Question 10.
Find the equation of all lines having slope - 1 that are tangents to the curve
y = \(\frac{1}{x-1}\), x ≠ 1
Answer:

∴ At (0, - 1) and (2, 1) slope of tangent is - 1.
Equation of tangent at point (0, - 1)
y - (- 1) = - 1(x - 0)
⇒ y + 1 = - x ⇒ x + y + 1 = 0
And at point (2, 1), equation of tangent
y - 1 = - 1(x - 2) ⇒ y - 1 = - x + 2
⇒ x + y = 2 + 1 ⇒ x + y - 3 = 0
Hence, x + y + 1 = 0 and x + y - 3 = 0 are required tangents.

Question 11.
Find the equation of all lines having slope 2 which are tangents to the curve
y = \(\frac{1}{x-3}\), x ≠ 3
Answer:
Differentiating y = \(\frac{1}{x-3}\) w.r.t. x
\(\frac{d y}{d x}=-\frac{1}{(x-3)^{2}}\) ...... (1)
Given, slope of tangent = 2 ......... (2)
From equations (1) and (2),
2 = - \(\frac{1}{(x-3)^{2}}\)
⇒ 2(x - 3)² = - 1 ⇒ (x - 3)² = - \(\frac{1}{2}\)
which is not possible since square of real number cannot be negative (x ∈ R, x² > 0).
Hence, curve has no tangent with slope 2.

Question 12.
Find the equations of all lines having slope 0 which are tangent to the curve
y = \(\frac{1}{x^{2}-2 x+3}\)
Answer:

Hence, required equation of tangent is 2y - 1 = 0 at point \(\left(1, \frac{1}{2}\right)\).

Question 13.
Find points on the curve \(\frac{x^{2}}{9}+\frac{y^{2}}{16}\) = 1 at which the tangents are (i) parallel to x-axis (ii) parallel to y-axis
Answer:
Differentiating \(\frac{x^{2}}{9}+\frac{y^{2}}{16}\) = 1 w.r.t. x

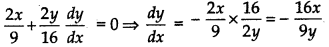
(i) When tangent is parallel to x-axis
\(\frac{d y}{d x}\) = 0 ⇒ - \(\frac{16 x}{9 y}\) = 0 ⇒ x = 0
Putting x = 0 in equation \(\frac{x^{2}}{9}+\frac{y^{2}}{16}\) = 1
y² = 16 ⇒ y = ±4
Thus, at points (0, ±4) tangents are parallel to x-axis.

(ii) When tangent is parallel toy-axis, i.e., perpendicular to x-axis, then

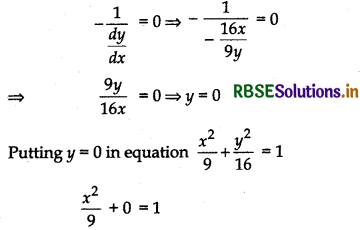
⇒ x² = 9 ⇒ x = ± 3
Thus, at points (±3, 0) tangents are parallel to y-axis.

Question 14.
Find the equation of the tangent and normal to the given curves at the indicated points:
(i) y = x⁴ - 6x³ + 13x² - 10x + 5 at (0, 5)
Answer:
Given, y = x⁴ - 6x³ + 13x⁴ - 10x + 5
Differentiating w.r.t. x
\(\frac{d y}{d x}\) = 4x³ - 18x² + 26x - 10
At(0, 5), \(\frac{d y}{d x}\) = 4 × 0 - 18 × 0 + 26 × 0 - 10 = - 10
∴ \(\left(\frac{d y}{d x}\right)_{(0,5)}\) = - 10
∴ At (0, 5) slope of tangent = - 10
∴ Equation of tangent at (0, 5) is
y - 5 = - 10(x - 0) ⇒ y - 5 = - 10x
⇒ y + 10x - 5 = 0 ⇒ 10x + y - 5 = 0
∴ At point (0, 5) slope of normal
= \(\frac{-1}{\text { Slope of tangent }}=\frac{-1}{-10}=\frac{1}{10}\)
Thus, at (0, 5) equation of normal is
y - 5 = \(\frac{1}{10}(x - 0)\)
⇒ 10(y - 5) = x ⇒ 10y - 50 = x
⇒ 10y - x - 50 = 0 ⇒ x - 10y + 50 = 0
Thus, equation of tangent is 10x + y - 5 = 0
And equation of normal is x - 10y + 50 = 0

(ii) y = x⁴ - 6x⁴ + 13x² - 10x + 5 at (1, 3)
Answer:
Given, y = x⁴ - 6x³ + 13x² - 10x + 5
Differentiating w.r.t. x
\(\frac{d y}{d x}\) = 4x³ - 18x² + 26x - 10
At(1, 3), \(\frac{d y}{d x}\) = 4 × 1³ - 18 × 1² + 26 × 1 - 10 = 2
∵ \(\left(\frac{d y}{d x}\right)_{(1,3)}\) = 2
∴ At (1, 3), slope of tangent = 2
And at (1,3) slope of normal
= \(\frac{-1}{\text { Slope of tangent at point }(1,3)}=-\frac{1}{2}\)
Now, equation of tangent at point (1, 3) is
y - 3 = 2(x - 1) ⇒ y - 3 = 2x - 2
⇒ y - 2x = 3 - 2 = 1 ⇒ 2x - y + 1 = 0
And equation of normal at point (1, 3) is
y - 3 = - \(\frac{1}{2}(x - 1)\) ⇒ 2(y - 3) - 1(x - 1)
⇒ 2y - 6 - x + 1 = x + 2y - 6 - 1 = 0
⇒ x + 2y - 7 = 0
Thus, equation of tangent is 2x - y + 1 = 0
and equation of normal is x + 2y - 7 = 0

(iii) y = x³ at (1, 1)
Answer:
Given, y = x³
Differentiating y = x w.r.t. x
\(\frac{d y}{d x}\) = 3x²
At point (1, 1), \(\frac{d y}{d x}\) = 3 × 1² = 3
∴ \(\left(\frac{d y}{d x}\right)_{(1,1)}\) = 3
∴ At point (1, 1) slope of tangent = 3
And at point (1, 1) slope of normal
= \(\frac{-1}{\text { Slope of normal at point }(1,1)}=-\frac{1}{3}\)
Slope of normal at point (1, 1) =
At point (1, 1), equation of tangent
y - 1 = 3(x - 1) ⇒ y - 1 = 3x - 3
⇒ y - 3x + 3 - 1 = 0 ⇒ y - 3x + 2 = 0
⇒ 3x - y - 2 = 0
And equation of normal at (1, 1)
y - 1 = - \(\frac{1}{3}\)(x - 1) ⇒ 3(y - 1) = - 1(x - 1)
⇒ 3y - 3 - x + 1
⇒ x + 3y - 3 - 1 = 0
⇒ x + 3y - 4 = 0
Thus, equation of tangent is 3x - y - 2 = 0
And equation of normal is x + 3y - 4 = 0

(iv) y = x² at (0, 0)
Answer:
Given, y = x²
Differentiating y = x² w.r.t. x
\(\frac{d y}{d x}\) = 2x
At (0, 0), \(\frac{d y}{d x}\) = 2 × 0 = 0
∴ \(\left(\frac{d y}{d x}\right)_{(0,0)}\) = 0
At (0, 0) slope of tangent = 0
And at (0, 0) equation of tangent is
y - 0 = 0(x - 0) ⇒ y = 0
Since normal is ⊥^r to tangent.
Hence, equation of normal, x = 0

Note.: Here tangent is x-axis (y = 0) and normal is y-axis (x = 0).

(v) x = cos t, y = sin t at t = π/4
Answer:
Given, x = cos t, y = sin t
Differentiating x and y w.r.t. t

y = x
Thus, equation of tangent is x + y - √2 = 0
and equation of normal is y = x

Question 15.
Find the equation of the tangent line to the curve y = x² - 2x + 7 which is
(a) parallel to the line 2x - y + 9 = 0
Answer:
Differentiating y = x² - 2x + 7 w.r.t. x
\(\frac{d y}{d x}\) = 2x - 2
For slope of line 2x - y + 9 = 0
2x + 9 = y ⇒ 2x - y + 9 = 0
∴ Slope of line = -\(\frac{a}{b}=-\frac{2}{(-1)}\) = 2
Thus, slope of line 2x - y + 9 is 2.
Since, tangent is parallel to line 2x - y + 9 = 0.
Thus, slope of tangent = slope of line
∴ \(\frac{d y}{d x}\) = 2 ⇒ 2x - 2 = 2
⇒ 2(x - 1) = 2 ⇒ x - 1 = 1
⇒ x = 1 + 1 = 2
Putting x = 2 in y = x² - 2x + 7
y = 2² - 2 × 2 + 7 = 4 - 4 + 7 = 7
∴ Point is (2, 7).
∴ At point (2, 7), equation of tangent is
y - 7 = 2(x - 2) ⇒ y - 7 = 2x - 4
⇒ 2x - y - 4 + 7 = 0 ⇒ 2x - y + 3 = 0
Hence, equation of tangent is 2x - y + 3 = 0

(b) perpendicular to the line 5y - 15x = 13
Answer:
For slope of line 5y - 15x = 13
5y = 15x + 13 ⇒ y = 3x + \(\frac{13}{5}\)
∴ Slope of given line = 3
∵ Tangent is perpendicular to line
5y - 15x = 13
∴ Slope of tangent = \(\frac{1}{\text { slope of given line }}=-\frac{1}{3}\)
But slope of tangent = 2x - 2

⇒ 36y - 217 = - 12(x - 5/6)
(Multiplying both sides by 36)
⇒ 36y - 217 = - 12x + 12 × 5/6
⇒ 36y - 217 - 12x + 10
⇒ 12x + 36y - 10 - 217 = 0
⇒ 12x + 36y - 227 = 0
Thus, 12x + 36y - 227 = 0 is the required equation of tangent.

Question 16.
Show that the tangents to the curve y = 7x³ + 11 w.r.t at the points where x = 2 and x = - 2 are parallel.
Sol.
Differentiating y = 7x³ + 11 w.r.t. x
\(\frac{d y}{d x}\) = 7 × 3x²
At point x = 2 slope of tangent
\(\frac{d y}{d x}\) = 7 × 3(2)² = 7 × 3 × 4 = 84
At x = - 2 slope of tangent
\(\frac{d y}{d x}\) = 7 × 3(- 2)² = 7 × 3 × 4 = 84
Thus, at x = 2 and x = - 2, slope of tangent are same.
∴ At point x = 2 and x = - 2, tangents are parallel.
Hence Proved.

Question 17.
Find the points on the curve y = x³ at which the slope of the tangent is equal to the y-coordinate of the point.
Answer:
Differentiating y = x³, w.r.t. x
\(\frac{d y}{d x}\) = 3x²
At point (x₁, y₁), slope of tangent = 3x₁²
We have, 3x₁² = y₁ ..... (1)
Again (x₁, y₁) lies on curve y = x³
∴ y₁ = x₁³ ........ (2)
From equations (1) and (2)
x₁³ = 3x₁² ⇒ x₁³ - 3x₁² = 0
⇒ x₁²(x₁ - 3) = 0 ⇒ x₁ = 0 or x₁ = 3
For x₁ = 0, y₁ = 0³ = 0
For x₁ = 3, y₁ = 3¹ = 27
Thus, (0, 0) and (3, 27) are required points.

Question 18.
For the curve y = 4x³ - 2x⁵, find all the points at which the tangent passes through the origin.
Answer:
Let the point be (x₁, y₁).
y = 4x₃ - 2x₅ ........ (i)
∵ Differentiating equation (1), w.r.t. x .
\(\frac{d y}{d x}\) = 4 × 3x² - 2 × 5x⁴
∴ \(\frac{d y}{d x}\) = 12x² - 10x⁴
∴ Slope of tangent at point (x₁, y₁)
\(\left(\frac{d y}{d x}\right)_{\left(x_{1}, y_{1}\right)}\) = 12x₁² - 10x₁⁴
∵ Point (x₁, y₁) lies on curve y = 4x³ - 2x⁵
∴ y₁ = 4x₁³ - 2x₁⁵ ......... (2)
Now, at point (x₁, y₁) equation of tangent
y - y₁ = (12x₁² - 10x₁⁴) (x - x₁)
Since, tangent passes through (0, 0)
∴ 0 - y₁ = (12x₁² - 10x₁⁴) (0 - x₁)
⇒ - y₁ = - x₁(12x₁² - 10x₁⁴)
⇒ y₁ = 12x₁³ - 10x₁⁵ ........ (3)
From equations (2) and (3),
12x₁³ - 10x₁⁵ = 4x₁³ - 2x₁⁵
⇒ 12x₁³ - 4x₁³ = 10x₁⁵ - 2x₁⁵
⇒ 8x₁³ = 8x₁⁵ ⇒ 8x₁³ - 8x₁⁵ = 0
⇒ 8x₁³ (1 - x₁²) = 0 ⇒ x₁ = 0, 1 - x₁² = 0
⇒ x₁ = 0, x₁² = 1 ⇒ x₁ = 0, x₁ = ±1
Equation of curve y = 4x³ - 2x⁵
x₁ = 0, y₁ = 0
For x₁ = 1, y₁ = 4 × 1³ - 2 × 1⁵ = 2
For x₁ = - 1, y₁ = 4(- 1)³ - 2(- 1)⁵ = - 4 + 2 = - 2
Hence, required points are (0, 0), (1, 2) and (- 1, - 2).

Question 19.
Find the points on the curve x² + y² - 2x - 3 = 0 at which the tangents are parallel to the x-axis.
Answer:
Differentiating x² + y² - 2x - 3 = 0 w.r.t. x
2x + 2y\(\frac{d y}{d x}\) - 2 = 0
⇒ 2y\(\frac{d y}{d x}\) = 2 - 2x
⇒ \(\frac{d y}{d x}=\frac{2(1-x)}{2 y}=\frac{1-x}{y}\)
Since, tangent is parallel to x-axis
∴ \(\frac{d y}{d x}\) = 0 ⇒ \(\frac{1-x}{y}\) = 0
⇒ 1 - x = 0 ⇒ x = 1
Putting x = 1 in equation, x² + y² - 2x - 3 = 0
1² + y² - 2 × 1 - 3 = 0
⇒ y² + 1 - 2 - 3 = 0
⇒ y² - 4 = 0
⇒ y² = 4
⇒ y = ± 2
Thus, required points are (1, 2), (1, - 2).

Question 20.
Find the equation of the normal at the point (am², am³) for the curve ay² = x³.
Answer:
Differentiating ay² = x³, w.r.t. x

∴ Equation of normal at point (am², am³)
y - am³ = - \(\frac{2}{3 m}\) (x - am²)
⇒ 3my - 3am⁴ - 2x + 2am²
⇒ 2x + 3my - 3am⁴ - 2am² = 0
⇒ 2x + 3my - am²(3m² + 2) = 0

Question 21.
Find the equation of the normals to the curve y = x³ + 2x + 6 which are parallel to the line x + 14y + 4 = 0.
Answer:
Differentiating y = x³ + 2x + 6, w.r.t. x
\(\frac{d y}{d x}\) = 3x² + 2 (Slope of tangent)
Since, normal is parallel to x + 14y + 4 = 0.
Thus, - \(\frac{1}{\frac{d y}{d x}}\) = slope of tine x + 14y + 4 = 0
⇒ - \(\frac{1}{3 x^{2}+2}\) = - \(\frac{1}{14} \)(Slope of normal)
⇒ 3x² + 2 = 14 ⇒ 3x² = 12
⇒ x² = 4⇒ x = ±2
Putting x = 2 in y = x³ + 2x + 6,
y = 2³ + 2 × 2 + 6 = 8 + 4 + 6 = 18
∴ Point is (2, 18).
At x = - 2, y = (- 2)³ + 2 × (- 2) + 6 = - 6
∴ Point is ( - 2, - 6).
∴ Equation of normal at point (2, 18) is
y - 18 = - \(\frac{1}{14}\)(x - 2)
⇒ 14(y - 18) = - 1(x - 2)
⇒ 14y - 252 = - x + 2
⇒ x + 14y - 252 - 2 = 0
⇒ x + 14y - 254 = 0
And equation of normal at point (- 2, - 6) is
y - (- 6) = - \(\frac{1}{14}\) {x - (- 2)}
⇒ y + 6 = - \(\frac{1}{14}\) (x + 2)
⇒ 14(y + 6) = - (x + 2)
⇒ 14y + 84 = - x - 2
⇒ x + 14y + 84 + 2 = 0
⇒ x + 14y + 86 = 0
Thus, equation of normals are x + 14y - 254 = 0 and x + 14y + 86 = 0.

Question 22.
Find the equations of the tangent and normal to the parabola y² = 4ax at the point (at², 2at).
Answer:
Differentiating y² = 4ax, w.r.t. x
2y\(\frac{d y}{d x}\) = 4a ⇒ \(\frac{d y}{d x}=\frac{4 a}{2 y}=\frac{2 a}{y}\)
At point (at², 2at), \(\frac{d y}{d x}=\frac{2 a}{2 a t}=\frac{1}{t}\)
Slope of tangent of point (at², 2at) = \(\frac{1}{t}\)
∴ Equation of tangent at point (at², 2at) is
y - 2at = \(\frac{1}{t}\)(x - at²)
⇒ ty - 2at² = x - at²
⇒ ty = x + 2at² - at² ⇒ ty = x + at²
Now, slope of normal at point (at², 2at)
= -\(\frac{1}{\frac{1}{t}}\) = - t
∴ Equation of normal at point (at², 2at) is
y - 2at ⇒ - t(x - at²)
⇒ y - 2at = - tx + at³
⇒ y = - tx + 2at + at³
Thus, equation of tangent is ty = x + at²
And equation of normal is y = - tx + 2at + at³

Question 23.
Prove that the curves x = y² and xy = k cut at right angles, if 8k² = 1.
Answer:
Solving x = y² and xy = k, we get
y² × y = k ⇒ y³ = k
⇒ y = k^1/3 ⇒ x = (k^1/3)² = k^2/3
Thus, curves x = y² and xy = k cut each other at point (k^2/3, k^1/3).
Differentiating x = y², w.r.t. x

Question 24.
Find the equations of the tangent and normal to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 at the point (x₀, y₀).
Answer:

Question 25.
Find the equations of the tangent to the curve Y = \(\sqrt{3 x-2}\) which is parallel to the line 4x - 2y + 5 = 0.
Answer:
Differentiating y = \(\sqrt{3 x-2}\) w.r.t. x

⇒ 6(4y - 3) = 8x × 6 - 41 ⇒ 24y - 18 = 48x - 41
⇒ 48x - 24y - 41 + 18 = 0 ⇒ 48x - 24y - 23 = 0
Thus, equation of tangent is 48x - 24y - 23 = 0

Choose the correct answer in Q. 26 and Q. 27.

Question 26.
The slope of the normal to the curve y = 2x² + 3 sin x at x = 0 is
(A) 3
(B) \(\frac{1}{3}\)
(C) - 3
(D) - \(\frac{1}{3}\)
Answer:
Differentiating y = 2x² + 3 sin x, w.r.t. x
\(\frac{d y}{d x}\) = 4x + 3 cos x
At x = 0 at \(\frac{d y}{d x}\) = 4 × 0 + 3 × cos 0 = 3 × 1 = 3
At x = 0 slope of tangent = 3
∴ At x = 0 slope of normal
= \(\frac{-1}{\text { slope of tangent }}=-\frac{1}{3}\)
Thus, (D) is correct.

Question 27.
The line y = x + 1, is a tangent to the curve y² = 4x at the point
(A) (1, 2)
(B) (2, 1)
(C) (1, - 2)
(D) (- 1, 2)
Answer:
Differentiating y² = 4x, w.r.t. x
2y.\(\frac{d y}{d x}\) = 4 ⇒ \(\frac{d y}{d x}=\frac{4}{2 y}\)
∴ \(\frac{d y}{d x}=\frac{2}{y}\) (slope of tangent) ....... (1)
And slope of line y = x + 1 = 1 ........ (2)
From equation (1) and (2), \(\frac{2}{y}\) = 1 ⇒ y = 2
Putting value of y in y² = 4x,
2² = 4x = 4 ⇒ 4x ⇒ x = 1
∴ Point is (1, 2)
∴ Line y = x + 1 is tangent of curve at point (1, 2)
Thus, (A) is correct.