RBSE Solutions for Class 12 Maths Chapter 6 अवकलज के अनुप्रयोग Ex 6.3

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 6 अवकलज के अनुप्रयोग Ex 6.3 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 6 अवकलज के अनुप्रयोग Ex 6.3

प्रश्न 1.
वक्र y = 3x⁴ - 4x के x = 4 पर स्पर्श रेखा की प्रवणता ज्ञात कीजिए।
हल:
प्रश्नानुसार
y = 3x⁴ - 4x, x = 4
∴ \(\frac{d y}{d x}\) = 12x³ - 4 = 4(3x³ - 1)
x = 4 रखने पर
\(\left.\frac{d y}{d x}\right]_{x=4}\) = 4 [3 × 64 - 1] = 4[192 - 1]
= 4 × 191 = 764

प्रश्न 2.
वक्र y = \(\frac{x-1}{x-2}\), x ≠ 2 के x = 10 पर स्पर्श रेखा की प्रवणता ज्ञात कीजिए।
हल:

प्रश्न 3.
वक्र y = x³ - x + 1 की स्पर्श रेखा की प्रवणता उस बिन्दु पर ज्ञात कीजिए जिसका x-निर्देशांक 2 है।
हल:
प्रश्नानुसार y = x³ - x + 1
∴ \(\frac{d y}{d x}\) = 3x² - 1
x = 2 रखने पर \(\left.\frac{d y}{d x}\right]_{x=2}\) = 3 × 4 - 1 = 11

प्रश्न 4.
वक्र y = x³ - 3x + 2 की स्पर्श रेखा की प्रवणता उस बिन्दु पर ज्ञात कीजिए जिसका x-निर्देशांक 3 है।
हल:
प्रश्नानुसार y = x³ - 3x + 2
∴ \(\frac{d y}{d x}\) = 3x² - 3 = 3(x² - 1)
x = 3 रखने पर \(\left.\frac{d y}{d x}\right]_{x=3}\) = 3 (9 - 1) = 24

प्रश्न 5.
वक्र x = a cos³ θ, y = a sin³ θ के θ = \(\frac{\pi}{4}\) पर अभिलम्ब की प्रवणता ज्ञात कीजिए।
हल:
प्रश्नानुसार y =a sin³ θ, x = a cos³ θ

∴ अभिलम्ब की प्रवणता = \(\frac{-1}{m}\) = \(\frac{-1}{-1}\) = 1

प्रश्न 6.
वक्र x = 1 - a sin θ, y = b cos² θ के θ = \(\frac{\pi}{2}\) पर अभिलम्ब की प्रवणता ज्ञात कीजिए।
हल:
प्रश्नानुसार x = 1 - a sin θ, y = b cos² θ

प्रश्न 7.
वक्र y = x³ - 3x² - 9x + 7 पर उन बिन्दुओं को ज्ञात कीजिए जिन पर स्पर्श रेखाएँ x-अक्ष के समान्तर हैं।
हल:
प्रश्नानुसार y = x³ - 3x² - 9x + 7
∴ \(\frac{d y}{d x}\) = 3x² - 6x - 9 = 3 (x² - 2x - 3)
= 3 (x - 3) (x + 1)
स्पर्श रेखा x-अक्ष के समान्तर होती है यदि \(\frac{d y}{d x}\) = 0
अर्थात् 3 (x - 3) (x + 1) = 0
या x = - 1, 3
यदि x = - 1, y = (- 1)³ - 3 (- 1)² - 9(- 1) + 7
= - 1 - 3 + 9 + 7 = 12
जब x = 3, y = 3³ - 3.3² - 9.3 + 7 .
= 0 - 27 + 7 = - 20
इस प्रकार (- 1, 12), (3, - 20) पर स्पर्श रेखा x-अक्ष के समान्तर है।

प्रश्न 8.
वक्र y = (x - 2)² पर एक बिन्दु ज्ञात कीजिए जिस पर स्पर्श रेखा, बिन्दुओं (2, 0) और (4, 4) को मिलाने वाली रेखा के समान्तर है।
हल:
प्रश्नानुसार y = (x - 2)²
∴ \(\frac{d y}{d x}\) = 2 (x - 2)
माना कि बिन्दु P(2, 0), Q(4, 4) को मिलाने वाली रेखा की।
प्रवणता
= \(\frac{4-0}{4-2}\) = \(\frac{4}{2}\) = 2
स्पर्श रेखा की प्रवणता = \(\frac{d y}{d x}\) = 2 (x - 2)
स्पर्श रेखा जीवा PQ के समान्तर है
∴ 2(x - 2) = 2 या x - 2 = 1, x = 3
जब x = 3 y = (3 - 2)² = 1
बिन्दु (3, 1) पर स्पर्श रेखा जीवा के समान्तर होगी।

प्रश्न 9.
वक्र y = x³ - 11x + 5 पर उस बिन्दु को ज्ञात कीजिए जिस पर स्पर्श रेखा y = x - 11 है।
हल:
प्रश्नानुसार y = x³ - 11x + 5
∴ \(\frac{d y}{d x}\) = 3x² - 11 ......... (1)
स्पर्श रेखा y = x - 11 की प्रवणता = 1 ............ (2)
(1) और (2) से, 3x² - 11 = 1
या 3x² = 12, x² = 4, x = ± 2
जब x = 2, y = 2³ - 11.2 + 5 = 8 - 22 + 5 = - 9
जब x = - 2, y = (- 2)³ - 11 (-2) + 5 = - 8 + 22 + 5 = 19
(- 2, 19) स्पर्श रेखा y = x - 11 पर नहीं है।
∴ बिन्दु (2, - 9) पर स्पर्श रेखा y = x - 11 है।

प्रश्न 10.
प्रवणता - 1 वाली सभी रेखाओं का समीकरण ज्ञात कीजिए जो वक्र y = \(\frac{1}{x-1}\), x ≠ - 1 को स्पर्श करती है।
हल:

∴ (0, - 1) और (2, 1) पर स्पर्श रेखा की प्रवणता = - 1 है।
अतः (0, - 1) पर स्पर्श रेखा का समीकरण
y + 1 = (- 1) (x - 0)
y + 1 = - x या x + y + 1 = 0
तथा (2, 1) पर स्पर्श रेखा का समीकरण
y - 1 = (- 1) (x - 2) = - x + 2
या x + y - 3 = 0
∴ अभीष्ट स्पर्श रेखाएँ
x + y + 1 = 0 और x + y - 3 = 0

प्रश्न 11.
प्रवणता 2 वाली सभी रेखाओं का समीकरण ज्ञात कीजिए जो वक्र y = \(\frac{1}{x-3}\), x ≠ 3 को स्पर्श करती है।
हल:
प्रश्नानुसार y = \(\frac{1}{x-3}\), ∴ \(\frac{d y}{d x}=-\frac{1}{(x-3)^2}\) ......... (1)
स्पर्श रेखा की प्रवणता = 2 ............ (2)
(1) और (2) से
- \(\frac{1}{(x-3)^2}\) = 2 ∴ (x - 3)² = - \(\frac{1}{2}\)
यह सम्भव नहीं है। चूंकि (x - 3)² का मान सदैव धनात्मक ही प्राप्त होगा।
∴ दिए गए वक्र पर ऐसी कोई स्पर्श रेखा नहीं है जिसकी प्रवणता 2 हो।

प्रश्न 12.
प्रवणता 0 वाली सभी रेखाओं का समीकरण ज्ञात कीजिए जो वक्र y = \(\frac{1}{x^2-2 x+3}\) को स्पर्श करती है।
हल:

प्रश्न 13.
वक्र \(\frac{x^2}{9}+\frac{y^2}{16}\) = 1 पर उन बिन्दुओं को ज्ञात कीजिए जिन पर स्पर्श रेखाएँ
(i) x-अक्ष के समान्तर हैं
(ii) y-अक्ष के समान्तर हैं।
हल:
वक्र का समीकरण \(\frac{x^2}{9}+\frac{y^2}{16}\) = 1
x के सापेक्ष अवकलन करने पर \(\frac{2 x}{9}+\frac{2 y}{16} \frac{d y}{d x}\) = 0

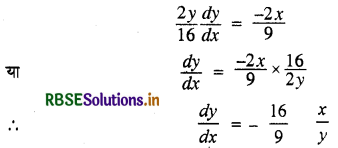
(i) जब स्पर्श रेखा x-अक्ष के समान्तर है तो \(\frac{d y}{d x}\) = 0
अर्थात् \(\frac{16}{9} \cdot \frac{x}{y}\) = 0 ∴ x = 0
\(\frac{x^2}{9}+\frac{y^2}{16}\) = 1 में x = 0 रखने से y = ± 4
x-अक्ष के समान्तर स्पर्श रेखाओं के बिन्दु = (0, ± 4)

(ii) जब स्पर्श रेखा y-अक्ष के समान्तर हो तो

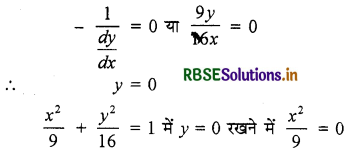
∴ x = ± 3
∴ y अक्ष के समान्तर स्पर्श रेखाओं के बिन्दु = (± 3, 0)

प्रश्न 14.
दिए वक्रों पर निर्दिष्ट बिन्दुओं पर स्पर्श रेखा और अभिलम्ब के समीकरण ज्ञात कीजिए:
(i) y = x⁴ - 6x³ + 13x² - 10x + 5 के (0, 5) पर
हल:
प्रश्नानुसार y = x⁴ - 6x³ + 13x² - 10x + 5
∴ \(\frac{d y}{d x}\) = 4x³ - 18x² + 26x - 10
(0, 5) पर \(\frac{d y}{d x}\) = - 10
स्पर्श रेखा की प्रवणता = - 10 = m
∴ स्पर्श रेखा का समीकरण
y - 5 =- 10(x - 0) या 10x + y - 5 = 0
⇒ 10x + y = 5
अभिलम्ब की प्रवणता = - \(\frac{1}{m}\) = - \(\frac{1}{-10}\) = \(\frac{1}{10}\)
∴ अभिलम्ब का समीकरण
y - 5 = \(\frac{1}{10}\) (x - 0) या 10(y - 5) = x
या x - 10y + 50 = 0

(ii) y = x⁴ + - 6x³ + 13x² - 10x + 5 के (1, 3) पर
हल:
प्रश्नानुसार y = x⁴ - 6x³ + 13x² - 10x + 5
∴ \(\frac{d y}{d x}\) = 4x³ - 18x² + 26x - 10
(1, 3) पर, x = 1 पर रखने से \(\left.\frac{d y}{d x}\right]_{x=1}\)
= 4 - 18 + 26 - 10 = 2
∴ स्पर्श रेखा की प्रवणता m = 2
बिन्दु (1, 3) पर स्पर्श रेखा का समीकरण .
y - 3 = 2(x - 1) = 2x - 2
या 2x - y + 3 - 2 = 0
या 2x - y + 1 = 0 ⇒ y = 2x + 1
∵ अभिलम्ब की प्रवणता = - \(\frac{1}{m}\) = - \(\frac{1}{2}\)
(1, 3) पर अभिलम्ब का समीकरण
y - 3 = - \(\frac{1}{2}\) = (x - 1) या 2y - 6
= - x + 1
या x + 2y - 6 - 1 = 0
⇒ x + 2y - 7 = 0

(iii) y = x³ के (1, 1) पर
हल:
प्रश्नानुसार y = x² ∴ \(\frac{d y}{d x}\) = 3x²
(1, 1) पर, x = 1 रखने से स्पर्श रेखा की प्रवणता = m = 3.1² = 3
∴ (1, 1) पर स्पर्श रेखा का समीकरण
y - 1 = 3(x - 1) या y - 1 = 3x - 3
या 3x -y - 3 + 1 = 0 ⇒ 3x - y - 2 = 0
या y = 3x - 2
∵ अभिलम्ब की प्रवणता = - \(\frac{1}{m}\) = - \(\frac{1}{3}\)
∴ अभिलम्ब का समीकरण
y - 1 = - \(\frac{1}{3}\)(x - 1) या 3y - 3 = - x + 1
या x + 3y - 3 - 1 = 0 या x + 3y - 4 = 0

(iv) y = x² के (0, 0) पर
हल:
प्रश्नानुसार y = x² ∴ \(\frac{d y}{d x}\) = 2x
(0, 0) पर (x = 0 रखने) से स्पर्शों की ढाल = m = 2 × 0 = 0
∴ स्पर्श रेखा का समीकरण
y - 0 = 0 (x - 0) ∴ y = 0
अभिलम्ब इसके लम्ब हैं और (0, 0) से होकर जाता है।
∴ अभिलम्ब का समीकरण x = 0

(v) x = cos t, y = sin t के t = \(\frac{\pi}{4}\) पर।
हल:
प्रश्नानुसार x = cos t, y = sin t

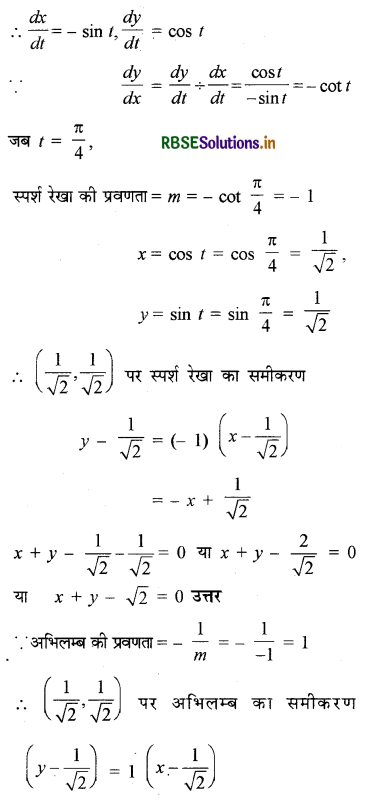
अतः y = x या x = y
इस प्रकार स्पर्श रेखा का समीकरण x + y - √2 = 0 तथा अभिलम्ब का समीकरण y = x

प्रश्न 15.
वक्र y = x² - 2x + 7 की स्पर्श रेखा का समीकरण ज्ञात कीजिए जो
(a) रेखा 2x - y + 9 = 0 के समान्तर है।
(b) रेखा 5y - 15x = 13 पर लम्ब है।
हल:
प्रश्नानुसार y = x² - 2x +7
∴ \(\frac{d y}{d x}\) = 2x - 2 = स्पर्श रेखा की प्रवणता

(a) स्पर्श रेखा, 2x - y + 9 = 0 के समान्तर है
इसकी प्रवणता = - \(\frac{a}{b}\) = \(\frac{-2}{-1}\) = 2
अतः 2x - 2 = 2 या 2x = 4
या x = 2
x = 2 वक्र के समीकरण में रखने पर
y = x² - 2x + 7 = 2² - 2 × 2 + 7
= 4 - 4 + 7 = 7
∴ (2, 7) पर स्पर्श रेखा का समीकरण
y - 7 = 2(x - 2) = 2x - 4
2x - y - 4 + 7 = 0 या 2x - y + 3 = 0
या y - 2x - 3 = 0

(b) रेखा 5y - 15x = 13 की प्रवणता = \(\frac{15}{5}\) = 3
स्पर्श रेखा 5y - 15x = 13 पर लम्ब है
∴ स्पर्श रेखा की प्रवणता = - \(\frac{1}{3}\) ∴ 2x - 2 = - \(\frac{1}{3}\)

36 से गुणा करने पर
36y - 217 = - 12x + 10
या 12x + 36y - 10 - 217 = 0
या 12x + 36y - 227 = 0 या 36y + 12x - 227 = 0

प्रश्न 16.
सिद्ध कीजिए कि वक्र y = 7x³ + 11 के उन बिन्दुओं पर स्पर्श रेखाएँ समान्तर हैं जहाँ x = 2 तथा x = - 2 है।
हल:
प्रश्नानुसार y = 7x³ + 11
∴ \(\frac{d y}{d x}\) = 21x²
जब x = 2, स्पर्श रेखा की प्रवणता = 21 × 2² = 84
जब x = - 2 स्पर्श रेखा की प्रवणता = 21 × (-2)² = 84
x = 2 और x = - 2 स्पर्श रेखा की प्रवणता समान है।
∴ इन बिन्दुओं पर स्पर्श रेखाएँ समान्तर हैं।

प्रश्न 17.
वक्र y = x³ पर उन बिन्दुओं को ज्ञात कीजिए जिन पर स्पर्श रेखा की प्रवणता बिन्दु के y-निर्देशांक के बराबर है।
हल:
वक्र का समीकरण y = x³ ∴ \(\frac{d y}{d x}\) = 3x²
बिन्दु (x₁, y₁) पर स्पर्श रेखा की प्रवणता = 3x₁²
दिया है 3x₁² = y₁ ........ (1)
(x₁, y₁) वक्र y = x³ पर स्थित है
y₁ = x₁³ ...... (2)
(1) और (2) से 31 को लुप्त करने से
x₁³ = 3x₁² ∴ x₁ = 3, 0
जब x₁ = 0, y = x³ में x = 0 रखने पर y₁ = 0
जब x₁ = 3, y₁ = 3³ = 27
∴ अभीष्ट बिन्दु (0, 0) और (3, 27) है।

प्रश्न 18.
वक्र y = 4x³ - 2x⁵, पर उन बिन्दुओं को ज्ञात कीजिए जिन पर स्पर्श रेखाएँ मूल बिन्दु से होकर जाती हैं।
हल:
वक्र का समीकरण y = 4x³ - 2x⁵ ....... (1)
x के सापेक्ष अवकलन करने पर \(\frac{d y}{d x}\) = 12x² - 10x⁴
(x₁, y₁) पर स्पर्श रेखा की प्रवणता = 12x₁² - 10x₁⁴ ..... (2) (x₁, y₁) वक्र पर भी स्थित है
∴ y₁ = 4x₁³ - 2x₁⁵ .... (3)
(x₁, y₁) पर स्पर्श रेखा का समीकरण
y - y₁ = (12x₁² - 10x₁⁴) (x - x₁)
यह (0, 0) से होकर जाती है अतः
x = 0, y = 0 रखने पर - y₁ = (12x₁² - 10x₁⁴) (-x₁)
(3) से y₁ का मान रखने पर
(4x₁³ - 2x₁⁵) = x₁ (12x₁² - 10x₁⁴)
या x₁³(4 - 2x₁²) = x₁³ (12 - 10x₁²)
∴ 8x₁² = 8 ∴ x₁ = + 1, x₁ = 0
वक्र का समीकरण है y = 4x³ - 2x⁵
जब x₁ = 0, y₁ = 0
जब x₁ = 1, y₁ = 4 - 2 = 2
जब x₁ = - 1, y₁ = - 4 + 2 = - 2
इस प्रकार अभीष्ट बिन्दु = (0, 0), (1, 2), (- 1, - 2)

प्रश्न 19.
वक्र x² + y² - 2x - 3 = 0 के उन बिन्दुओं पर स्पर्श रेखाओं के समीकरण ज्ञात कीजिए जहाँ पर वे x-अक्ष के समान्तर हैं।
हल:
वक्र का समीकरण
x² + y² - 2x - 3 = 0
x के सापेक्ष अवकलन करने पर
2x + 2y\(\frac{d y}{d x}\) - 2 = 0 ∴ \(\frac{d y}{d x}=\frac{1-x}{y}\)
∵ स्पर्श रेखा x-अक्ष के समान्तर है ∴ ढाल = 0
⇒ \(\frac{1-x}{y}\) = 0 ∴ x = 1
x = 1, वक्र के समीकरण x² + y² - 2x - 3 = 0 में रखने पर
1 + y² - 2 - 3 = 0 y² = 4, y = ± 2
∴ अभीष्ट बिन्दु (1, 2), (1, - 2) = (1, ±2)

प्रश्न 20.
वक्र ay² = x³ के बिन्दु (am², am³) पर अभिलम्ब का समीकरण ज्ञात कीजिए।
हल:
वक्र का समीकरण ay² = x³
x के सापेक्ष अवकलन करने पर,

अतः अभिलम्ब का समीकरण
y - am³ = - \(\frac{2}{3 m}\) (x - am²)
या 3my - 3am⁴ = - 2x + 2am²
या 2x + 3my - am² (2 + 3m²) = 0

प्रश्न 21.
वक्र y = x³ + 2x + 6 के उन अभिलम्बों के समीकरण ज्ञात कीजिए जो रेखा x + 14y + 4 = 0 के समान्तर है।
हल:
वक्र का समीकरण
y = x³ + 2x + 6
x के सापेक्ष अवकलन करने पर \(\frac{d y}{d x}\) = 3x² + 2
स्पर्श रेखा की बिन्दु (x₁, y₁) पर प्रवणता = 3x₁² + 2
अतः अभिलम्ब की प्रवणता = - \(\frac{1}{m}\) = - \(\frac{1}{3 x_1^2+2}\) ..... (1)
अभिलम्ब x + 14y + 4 = 0 के समान्तर है
इसकी प्रवणता = - \(\frac{1}{14}\) ....... (2)
(1) और (2) से- \(\frac{1}{3 x_1^2+2}\) = - \(\frac{1}{14}\)
∴ 3x₁² + 2 = 14, 3x₁² = 12, x₁² = 4
अतः x₁ = ± 2
जब x₁ = 2, y₁ = x₁³ + 2x₁ + 6 = 8 + 4 + 6 = 18
जब x₁ = - 2, y₁ = - 8 - 4 + 6 = - 6
(2, 18) पर अभिलम्ब का समीकरण
y - 18 = - \(\frac{1}{14}\) (x - 2)
या 14y - 252 = - x + 2
या x + 14y - 254 = 0
(- 2, - 6) पर अभिलम्ब का समीकरण
y + 6 = - \(\frac{1}{14}\) (x + 2)
या 14y + 84 = - x - 2
या x + 14y + 86 = 0
इन अभिलम्बों के समीकरण x + 14y - 254 = 0, x + 14y + 86 = 0 है।

प्रश्न 22.
परवलय y² = 4ax के बिन्दु (at², 2at) पर स्पर्श रेखा और अभिलम्ब के समीकरण ज्ञात कीजिए।
हल:
वक्र का समीकरण y² = 4ax
अवकलन करने पर 2y\(\frac{d y}{d x}\) = 4a
∴ \(\frac{d y}{d x}=\frac{4 a}{2 y}=\frac{2 a}{y}\)
बिन्दु (at², 2at) पर स्पर्श रेखा की प्रवणता
= \(\frac{2 a}{2 a t}=\frac{1}{t}\)
स्पर्श रेखा का समीकरण y - 2at = \(\frac{1}{t}\) (x - at²)
या yt - 2at² = x - at², yt = x + at²
⇒ ty = x + at²
अब अभिलम्ब की प्रवणता= - \(\frac{1}{m}\) = - t
∴ अभिलम्ब का समीकरण
y - 2at = - t (x - at²)
∴ y = - tx + 2at + at³

प्रश्न 23.
सिद्ध कीजिए कि वक्र x = y² और xy = k एक-दूसरे को समकोण पर काटती हैं, यदि 8k² = 1 है।
हल:
दिए हुए वक्र हैं x = y² ....(1)
xy = k ....(2)
समी. (1) एवं (2) को हल करने पर
y² = \(\frac{k}{y}\) ⇒ y³ = k

प्रश्न 24.
अतिपरवलय \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 के बिन्दु (x₀, y₀) पर स्पर्श रेखा तथा अभिलम्ब के समीकरण ज्ञात कीजिए।
हल:
वक्र है \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1
x के सापेक्ष अवकलन करने पर,
\(\frac{2 x}{a^2}-\frac{2 y}{b^2} \frac{d y}{d x}\) = 0
∴ \(\frac{d y}{d x}=\frac{b^2}{a^2} \cdot \frac{x}{y}\)

(i)

(ii)

प्रश्न 25.
वक्र y = \(\sqrt{3 x-2}\) की उन स्पर्श रेखाओं के समीकरण ज्ञात कीजिए जो रेखा 4x - 2y + 5 = 0 के समान्तर हैं।
हल:
वक्र का समीकरण y = \(\sqrt{3 x-2}\) .... (1)
x के सापेक्ष अवकलन करने पर
\(\frac{d y}{d x} = \frac{1}{2 \sqrt{3 x-2}}\) × 3 = \(\frac{3}{2 \sqrt{3 x-2}}\)
स्पर्श रेखा 4x - 2y + 5 = 0 के समान्तर है
∴ स्पर्श रेखा की प्रवणता = रेखा की प्रवणता = \(\frac{4}{2}\) = 2

24y - 18 = 48x - 41
या 48x - 24y - 41 + 18 = 0
या 48x - 24y - 23 = 0 या 48x - 24y = 23

प्रश्न 26 और 27 में सही उत्तर का चुनाव कीजिए:

प्रश्न 26.
वक्र y = 2x² + 3 sin x के x = 0 पर अभिलम्ब की प्रवणता
(A) 3
(B) \(\frac{1}{3}\)
(C) - 3
(D) - \(\frac{1}{3}\)
उत्तर:
(D) - \(\frac{1}{3}\)

हल:
दिया गया वक्र का समीकरण
y = 2x² + 3 sin x
\(\frac{d y}{d x}\) = 4x + 3 cos x
\(\left(\frac{d y}{d x}\right)_{x=0}\) = 0 + 3 cos 0
= 0 + 3 × 1 = 0 + 3 = 3
अतः अभिलम्ब की प्रवणता = - \(\frac{1}{3}\)
अतः सही विकल्प (D) है।

प्रश्न 27.
किस बिन्दु पर y = x + 1, वक्र 12 = 4x की स्पर्श रेखा है?
(A) (1, 2)
(B) (2, 1)
(C) (1, - 2)
(D) (- 1, 2)
उत्तर:
(A) (1, 2)

हल:
माना वह बिन्दु (x₁, y₁) है जिस पर y = x + 1, वक्र y² = 4x की स्पर्श रेखा है। अतः y₁² = 4x₁

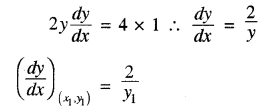
दी गयी रेखा का ढाल m = 1 होगा
प्रश्नानुसार \(\frac{2}{y_1}\) = 1 [∴ y₁ = 2]
y₁² = 4x₁ से
(2)² = 4x [∴ x₁ = 1']
अतः बिन्दु (1, 2)
अतः सही विकल्प (A) है।