RBSE Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 5 Continuity and Differentiability Miscellaneous Exercise

Question 1.
(3x² - 9x + 5)⁹
Answer:
Let y = (3x² - 9 + 5)²
Differentiating both sides wr.t. x
\(\frac{d y}{d x}\) = 9(3x² - 9x + 5)⁸ . \(\frac{d}{d x}\) (3x² - 9x + 5)
= 9(3x² - 9x + 5)⁸.(6x - 9)
= 9(6x - 9) (3x² - 9x + 5)⁸
= 9 × 3(2x - 3) (3x² - 9x + 5)⁸
= 27(2x - 3) (3x² - 9x + 5)⁸

Question 2.
sin³ x + cos⁶ x
Answer:
Let y = sin³ x + cos⁶ x
Differentiating both sides w.r.t. x
\(\frac{d y}{d x}\) = 3 sin² x . \(\frac{d}{d x}\) (sin x) + 6 cos⁵ x . \(\frac{d}{d x}\) (cos x)
= 3 sin² x cos x + 6 cos⁵ x (- sin x)
= 3 sin² x cos x - 6 cos⁵ x sin x
= 3 sin x cos x (sin x - 2 cos⁴ x)

Question 3.
(5x)^{3 cos 2x}
Answer:
Let y = (5x)^{3 cos 2x}
Taking logarithm on both sides, we get
log y = 3 cos 2x log (5x)
Now, differentiating both sides w.r.t x

Question 4.
sin^-1 (x√x), 0 ≤ x < 1
Answer:
Let y = sin^-1 (x√x) ⇒ y = sin^-1 (x)^3/2
Differentiating both sides w.r.t. x

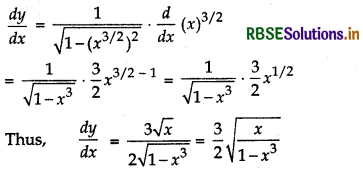
Question 5.
\(\frac{\cos ^{-1} \frac{x}{2}}{\sqrt{2 x+7}}\), - 2 < x < 2
Answer:

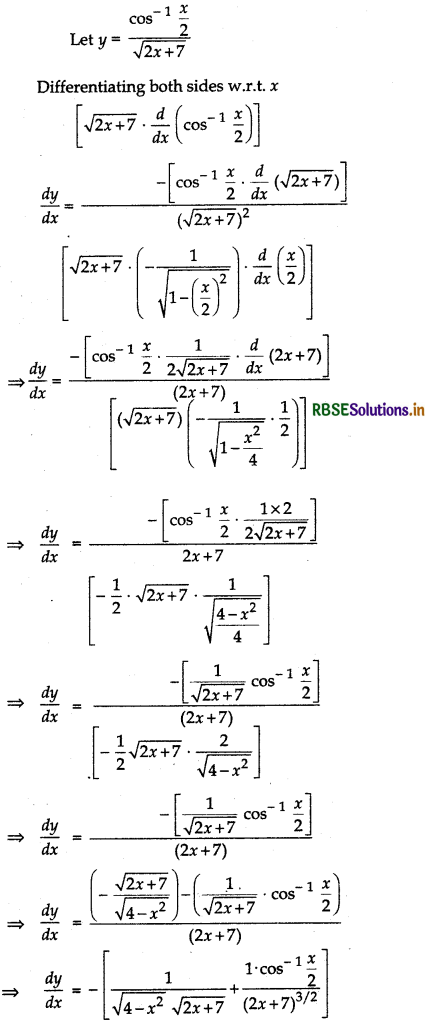
Question 6.
cot^-1\(\left[\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right]\), 0 < x < \(\frac{\pi}{2}\)
Answer:

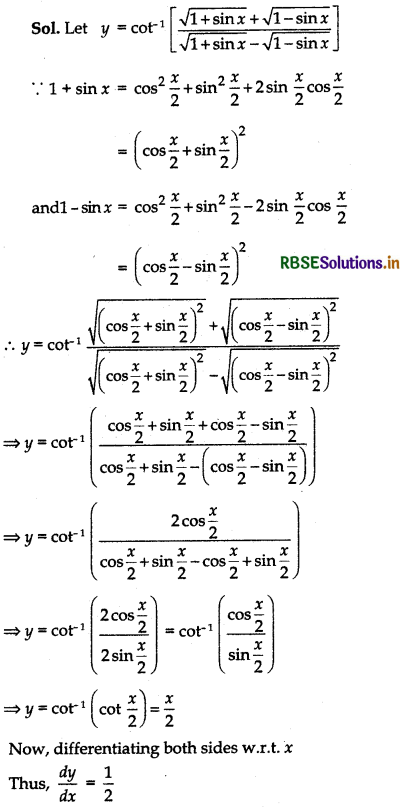
Question 7.
(log x)^{log x}, x > 1
Answer:
Let y = (log x)^{log x}
log y = log x.{log (log x)}
Now, differentiating both sides w.r.t. x

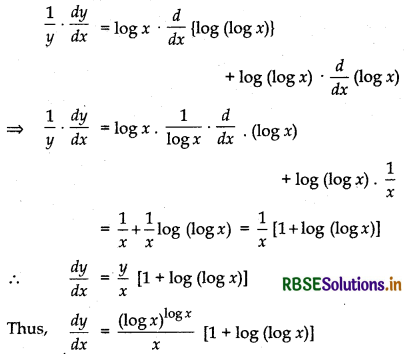
Question 8.
cos (a cos x + b sin x), for some constants a and b.
Answer:
Let y = cos (a cos x + b sin x)
Differentiating both sides w.r.t. x
\(\frac{d y}{d x}\) = - sin(a cos x + b sin x) × \(\frac{d}{d x}\)(a cos x + b sin x)
⇒ \(\frac{d y}{d x}\) = - sin(a cos x + b sin x) × {- a sin x + b cos x}
Thus, \(\frac{d y}{d x}\) = (a sin x - b cos x) × (a cos x + b sin x)

Question 9.
(sin x - cos x)^{(sin x - cos x)}, \(\left(\frac{\pi}{4}<x<\frac{3 \pi}{4}\right)\)
Answer:
Let y = (sin x - cos x)^{(sin x - cos x)}
Taking logarithm on both sides
log y = (sin x - cos x) log (sin x - cos x)
Now, differentiating both sides w.r.t. ‘x’

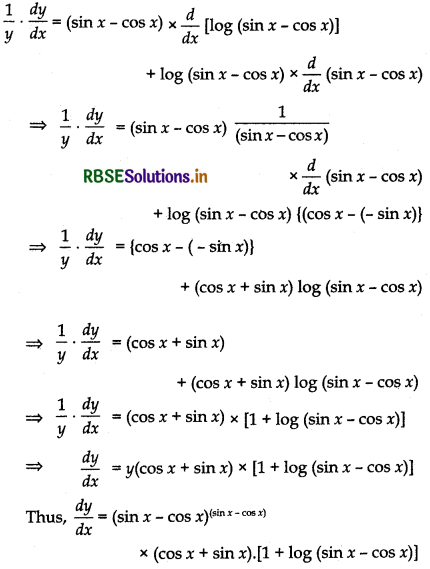
Question 10.
x^x + x^a + a^x + a^a, for same fixed a > 0 and x > 0
Answer:
Let y = x^x + x^a + a^x + a^a
Differentiating both sides w.r.t. x

Question 11.
x^x2 - 3 + (x - 3)^x2 for x > 3
Answer:
Let y = x^x2 - 3 + (x - 3)^x2
and u = x^x2 - 3, y = (x - 3)^x2
∴ y = u + v
Differentiating both sides w.r.t. x
\(\frac{d y}{d x}=\frac{d u}{d x}-\frac{d v}{d x}\) ........ (1)
Now, taking logarithm on both sides of u = x^x2 - 3
log u = (x² - 3)log x
Differentiating both sides of w.r.t. x
Now, taking logarithm on both sides of u = x^x2 - 3
log u = (x² - 3)log x
Differentiating both sides of w.r.t. x

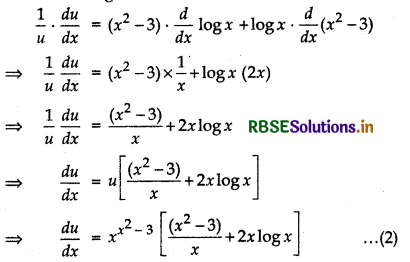
Again, taking logarithm on both sides of v = (x - 3)^x2
log v = x²log(x - 3)
Differentiating both sides w.r.t. z

Question 12.
If y = 12(1 - cos t), x = 10(t - sin t), - \(\frac{\pi}{2}\) < t < \(\frac{\pi}{2}\), then find \(\frac{d y}{d x}\).
Answer:
We have,
y = 12(1 - cos t) and x = 10(t - sin t)
Differentiating x and y wr.t. t
\(\frac{d y}{d t}\) = 12{0 - (- sin t)} = 12 sin t

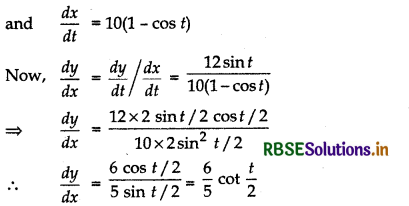
Question 13.
If y = sin^-1x + sin^-1 \(\sqrt{1-x^{2}}\), 0 < x < 1 then find \(\frac{d y}{d x}\).
Answer:
Given, y = sin^-1 x + sin^-1 \(\sqrt{1-x^{2}}\)
Putting sin^-1 x = θ ⇒ x = sin θ
∴ y = θ + sin^-1 (\(\sqrt{1-\sin ^{2} \theta}\))
⇒ y = θ + sin^-1 (cos θ)
⇒ y = θ + sin^-1 \(\left[\sin \left(\frac{\pi}{2}-\theta\right)\right]\)
⇒ y = θ + \(\frac{\pi}{2}\) - θ ⇒ y = \(\frac{\neq}{2}\)
Differentiating both sides w.r.t. x
\(\frac{d y}{d x}\) = 0

Question 14.
If x\(\sqrt{1+y}\) + y\(\sqrt{1+x}\) = 0 for - 1 < x < 1, then prove that \(\frac{d y}{d x}=-\frac{1}{(1+x)^{2}}\).
Answer:
We have x\(\sqrt{1+y}\) + y\(\sqrt{1+x}\) = 0
⇒ x\(\sqrt{1+y}\) = - y\(\sqrt{1+x}\)
Squaring both sides
(x\(\sqrt{1+y}\))² = (- y\(\sqrt{1+x}\))²
⇒ x²(1 + y) = y²(1+ x)
⇒ x² + x²y = y² + xy²
⇒ x² + x²y - y² - xy² = 0
⇒ x² - y² + x²y - xy² = 0
⇒ (x - y) (x + y) + xy(x - y) = 0
⇒ (x - y) {(x + y) + xy} = 0
⇒ x + y + xy = 0 [∵ (x - y) ≠ 0 or x ≠ y]
⇒ y(1 + x) - x ⇒ y = -\(\frac{x}{1+x}\)
Differentiating both sides w.r.t. x

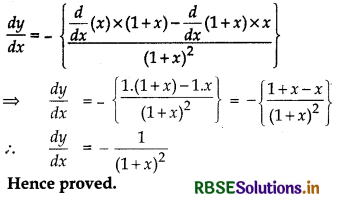
Question 15.
If (x - a)² + (y - b)² = c² for some c > 0, prove that \(\frac{\left\{1+\left(\frac{d y}{d x}\right)^{2}\right\}^{3 / 2}}{\frac{d^{2} y}{d x^{2}}}\), is a constant independent of a and b.
Answer:
We have, (x - a)² + (y - b)² = c² ....... (1)
Differentiating both sides w.r.t. x
2(x - a) + 2(y - b).\(\frac{d y}{d x}\) = 0
⇒ (x - a) + (y - b) \(\frac{d y}{d x}\) = 0 .....(2)
Again, differentiating both sides w.r.t. x

For equation (3) and (4) putting values of (y - b) and (x - a) in equation (1)

which is independent of a and b.
Hence Proved.

Question 16.
If cos y = x cos (a + y), with cos a ≠ ±1, prove that \(\frac{d y}{d x}\) = \(\frac{\cos ^{2}(a+y)}{\sin a}\).
Answer:
We have, cos y = x cos (a + y)
⇒ \(\frac{\cos y}{\cos (a+y)}\) = x
Differentiating both sides w.r.t. x

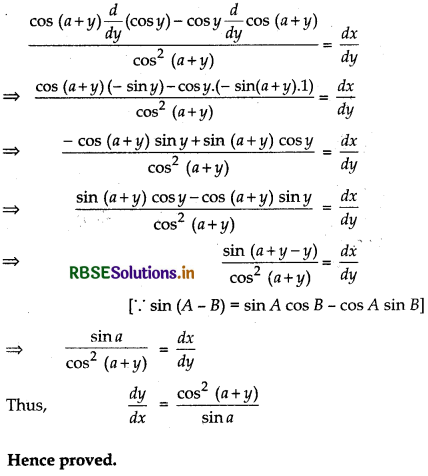
Question 17.
If x = a(cos t + t sin t) and y = a(sin t - t cos t) then find \(\frac{d^{2} y}{d x^{2}}\).
Answer:
We have, x = a(cos t + t sin t)
and y = a(sin t - t cos t)
Differentiating both sides w.r.t t

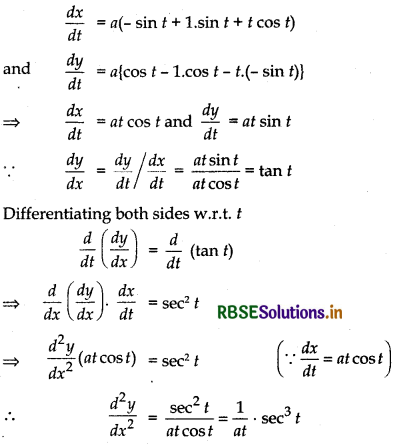
Question 18.
If f(x) = |x|³, show that f”(x) exists for all real x and find it.
Answer:
Let f(x) = x³
If x > 0, |x| = x then f(x) = x³
Differentiating w.r.t. x
\(\frac{d}{d x}\) [f(x)] = \(\frac{d}{d x}\) (x³)
⇒ f'(x) = 3x²
Again, differentiating w.r.t. x
f’(x) = 6x ... (1)
Thus f”(x) exists.
When x < 0, |x| = - x
∴ f(x) = |x|³ = (- x³) = - x³
∴ f(x) = - x³ differentiating w.r.t. x
f'(x) = - 3x²
Again, differentiating w.r.t. x
f''(x) = - 6x ..... (2)
Thus, f”(x) exists
From (1) and (2), we have
f'(x) = 6|x|
Hence, it is proved that f''(x) exists.
Hence proved

Question 19.
Using mathematical induction prove that \(\frac{d}{d x}\)(xⁿ) = nx^{n - 1} for all positive integers n.
Answer:
We have, \(\frac{d}{d x}\)(xⁿ) = nx^{n - 1}
Let P(n): \(\frac{d}{d x}\)(xⁿ) = nx^{n - 1}
Putting n = 1
P(1): \(\frac{d}{d x}\)(x¹) = 1.x^{1 - 1} = 1.x⁰ = 1.1 = 1
Thus, given function is true for n = 1 i.e. true for P(1)
Let statement is true for n = k, then
P(k): \(\frac{d}{d x}\)(x^k) = kx^{k - 1}
Now, we will prove that statement is true for n = k + 1
P(k + 1): \(\frac{d}{d x}\)(x^{k + 1}) = (k + 1)x^k
L.H.S. = \(\frac{d}{d x}\) (x^{k + 1}) = \(\frac{d}{d x}\) (x.x^k)
= 1.x^k + x.(kx^{k - 1})
(∵ \(\frac{d}{d x}\)(x^k+1) = (k + 1)x^k
= x^k + k.x^k
= x^k (k + 1) = (k + 1)x^k = R.H.S.
∴ Statement is true for n = k + 1
Thus, by mathematical induction principle, statement is true for positive integer numbers.

Question 20.
Using the fact that sin (A + B) = sin A cos B + cos A sin B and the differentiation obtain the sum formula for cosines.
Answer:
We have
sin (A + B) = sin A cos B + cos A sin B ..... (1)
Let A and B are function of t then differentiating both sides w.r.t. t
\(\frac{d}{d t}\)[sin (A + B)] = \(\frac{d}{d t}\)[sin A cos B + cos A sin Bl
L.H.S. = \(\frac{d}{d t}\)[sin (A + B)]

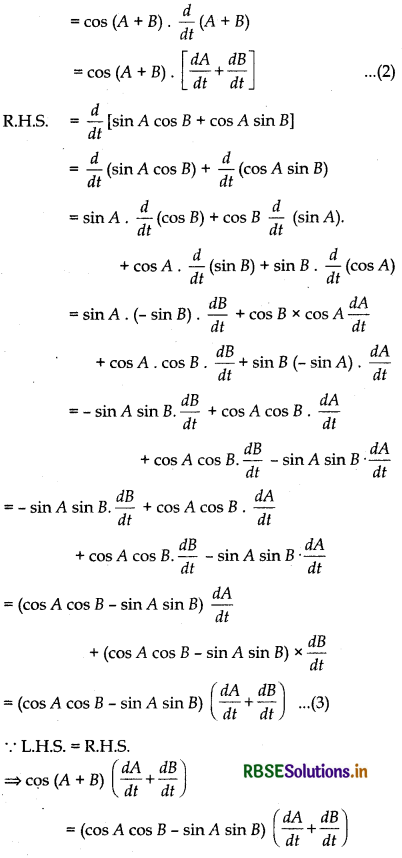
⇒ cos (A + B) = cosA cos B - sin A sin B
Thus, cos (A + B) cos A cos B - sin A sin B

Question 21.
Does there exist a function which is continuous everywhere but not differentiable at exactly two points? Justify your answer.
Answer:
Yes, such function exists which is continuous at each point but not differentiable only at two parts. e.g. function f(x) = |x| + |x - 1|, x ∈ R is continuous at all points but not differentiable at x = 0 and x = 1. Since |x|,is not differentiable at x = 0 similarly |x - 1| is not differentiable at x = 1. Thus, function is not differentiable at two points x = 0, x = 1 whereas it is continuous at all points (where x ∈ R).
Similarly, function f(x) = |x - 2| + |x - 3| x ∈ R, is continuous at all points but not differentiable at x = 2, x = 3.

Question 22.
If y = \(\left|\begin{array}{ccc} f(x) & g(x) & h(x) \\ l & m & n \\ a & b & c \end{array}\right|\), prove that \(\frac{d y}{d x}=\left|\begin{array}{ccc} f^{\prime}(x) & g^{\prime}(x) & h^{\prime}(x) \\ l & m & n \\ a & b & c \end{array}\right|\)
Answer:
We have,

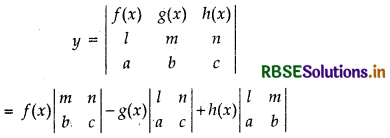
= f(x) (mc - bn) - g(x) (lc - an) + h(x) (lb - am)
⇒ y = (mc - nb) f(x) + g(x) (na - lc) + hx(lb - ma)
Differentiating w.r.t. x

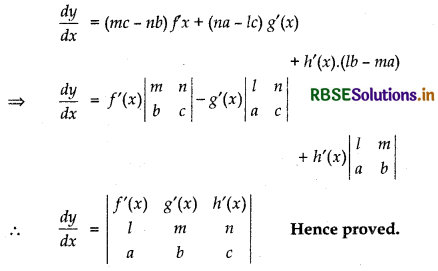
Question 23.
If y = e^{a cos-1 x} - 1 ≤ x ≤ 1, show that
(1 - x²)\(\frac{d^{2} y}{d x^{2}}\) - x\(\frac{d y}{d x}\) - a²y = 0
Answer:
We have
y = e^{a cos-1 x}
Differentiating w.r.t. x