RBSE Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.8

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.8 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 5 Continuity and Differentiability Ex 5.8

Question 1.
Verify Rolle’s theorem for the function
f(x) = x² + 2x - 8, x ∈ [- 4, 2].
Answer:
Given function f(x) = x² + 2x - 8, x ∈ [-4, 2] is a polynomial function.
Polynomial function is continuous so function f(x) is continuous in interval [- 4, 2].
Again, f’(x) = 2x + 2 exists in interval (- 4, 2).
Thus, f(x) is differentiable in interval (- 4, 2).
f(2) = 2² + 2 × 2 - 8 = 4 + 4 - 8 = 0
and f(- 4) = (- 4)² + 2 × (- 4) - 8
= 16 - 8 - 8 = 0
∴ f(2) = f(- 4) = 0
Thus, conditions of Rolle’s theorem satisfied then a point c in interval (- 4, 2) exists such that f'(c) = 0.
∴ f’(c) = 0 ⇒ 2c + 2 = 0 ⇒ 2c = - 2
⇒ c = - 1 ∈ (- 4, 2)
Thus, C = - 1 ∈ (- 4, 2) such that f’(c) = 0
Hence, Rolle’s theorem proved.
Hence Proved.

Question 2.
Examine if Rolle’s theorem is applicable to any of the following functions. Can you say samething about the converse of Rolle’s theorem from these examples?
(i) f(x) = [x] for x ∈ [5, 9]
(ii) f(x) = [x] for x ∈ [-2, 2]
(iii) f(x) = x² - 1 for x ∈ [1, 2].
Answer:
(i) Given, f(x) = [x]
where x ∈ [5,9)
Thus, value of x are 5, 6, 7, Sand 9. Now function is not continuous at these point. i.e., function is not continuous in interval [5, 9] also not differentiable. Thus, Rolle’s theorem will not be verified. Hence Proved.

(ii) Given f(x) = [x], x ∈ [- 2, 2]
Function f(x) = [x] is not continuous in interval [- 2, 2]. Since, greatest function is neither continuous nor differentiable at integer points. Thus, Rolle’s theorem can not be proved. Hence Proved.

(iii) Given, f(x) = x² - 1, x ∈ [1, 2]
Here, f(1) = 1 - 1 = 0 and f(2) = 4 - 1 = 3
∴ f(1) ≠ f(2)
Function f(x) = x² - 1, is polynomial function which is both continuous and differentiable but f(1) ≠ f(2). Thus, Rolle’s theorem cannot be verified.
Hence Proved.

Question 3.
If f: [- 5, 5] → R is a differentiable function and if f’(x) does not vanish anywhere, then prove that f(- 5) ≠ f(5).
Answer:
Given, function f: [- 5, 5] → R which is continuous and differentiable but f’(x) ≠ 0.
Condition of Rolle’s theorem in interval (- 5, 5) are as follows:
If (i) Function f is continuous in interval [- 5, 5].
(ii) Function f is differentiable in interval (- 5, 5).
(iii) f(- 5) = f(5)
then f’(c) = 0 ≠ = c ∈ (- 5, 5)
We have f’(c) ≠ 0
⇒ f(- 5) ≠ f(5)
Hence Proved.

Question 4.
Verify Mean Value Theorem if f(x) = x² - 4x - 3, in the interval [a, b] where a = 1 and b = 4.
Answer:
Given function f(x) = x² - 4x - 3 is a polynomial function. Polynomial function is continuous and differentiable. Thus, function is continuous in interval [1, 4] and differentiable in (1, 4)
Now f’(x) = 2x - 4, exists in interval (1, 4).
∴ There exist a point c is interval (1, 4) such that
f'(c) = \(\frac{f(4)-f(1)}{4-1}\) ......... (1)
f(4) = 4² - 4 × 4 - 3 = 16 - 16 - 3 = - 3
f(1) = 1² - 4 × 1 - 3 = 1 - 4 - 3 = - 6
Putting values of jt4) and fil) in equation (1)
f’(c) = \(\frac{-3-(-6)}{4-1}\)
⇒ (2c - 4) = \(\frac{-3+6}{3}\) = \(\frac{3}{3}\) = 1
⇒ 2c = 4 + 1 ⇒ c = \(\frac{5}{2}\)
⇒ c = \(\frac{5}{2}\) which exists in (1, 4)
f’(c) = \(\frac{f(4)-f(1)}{4-1}\)
Hence, mean value theorem verified.
Hence Proved.

Question 5.
Verify Mean Value Theorem if f(x) = x³ - 5x² - 3x in the interval [a, b] where a = 1 and b = 3. Find all c ∈ (1, 3) for f’(c) = 0.
Answer:
Given function (x) = x³ - 5x² - 3x, x ∈ [1, 3], is a polynomial function since polynomial function is continuous. Thus, function is continuous in interval [1, 3]. Again polynomial function is differentiable also. So, function is differential in (1, 3)
Now f’(x) = 3x² - 10x - 3, exists in x ∈ (1, 3)
In interval (1, 3) a point c exi1s such that
f'(c) = \(\frac{f(b)-f(a)}{b-a}\) ........ (1)
Now, here a = 1 and b = 3 then
f(a) = f(1) = 1³ - 5 × 1² - 3 × 1
= 1 - 5 - 3 = - 7
f(b) = f(3) = 3 - 5 × 3² - 3 × 3
= 27 - 45 - 9 = - 27
Putting values of f(a) and f(b) in equation (1)
f'(c) = \(\frac{f(3)-f(1)}{3-1}\) = \(\frac{-27-(-7)}{3-1}\)
⇒ 3c² - 10c - 3 = \(\frac{-27+7}{2}\) = \(\frac{-20}{2}\) = - 10
⇒ 3c² - 10c - 3 + 10 = 0
⇒ 3c² - 10c + 7 = 0
⇒ 3c² - (7 + 3)c + 7 = 0
⇒ 3c² - 7c - 3c + 7 = 0
⇒ c(3c - 7) - (3c - 7) = 0
⇒ (3c - 7) (c - 1) = 0
⇒ 3c - 7 = 0 or c - 1 = 0

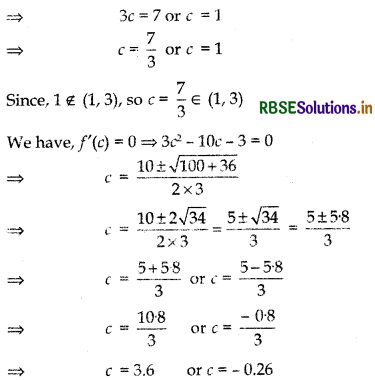
3.6 ∉ (1, 3) and c = - 0.26 ∉ (1, 3)
Thus, for f'(c) = 0 there does not exist any point in interval (1, 3)
Hence Proved.

Question 6.
Examine the applicability of Mean Value Theorem for all three functions given in the above question 2.
(i) f(x) = [xI, x ∈ [5, 9].
Answer:
Given function f(x) = [x], x ∈ [5, 9] is greatest integer function which neither continuous nor differentiable at integer point. Thus function f(x) = [x] is neither continuous nor differentiable in interval [5, 9] since at x = 6 Left hand limit

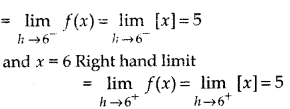
∴ L.H.L. ≠ R.H.L.
Thus, mean value theorem is not verified in interval [5, 9]

(ii) f(x) = [x], x ∈ [- 2, 2]
Answer:
Given function f(x) = [x], x ∈ [- 2, 2] is greatest integer function and function is neither continuous nor differentiable at any integer point of interval [- 2, 2]. Thus mean value theorem is not verified.

(iii) f(x) = x² - 1, x ∈ [1, 2]
Answer:
It is polynomial function which is continuous in interval [1, 2] and is differentiable in interval (1, 2).
Again f(1) = 1² - 1 = 0
and f(2) = 2² - 1 = 4 - 1 = 3
f’(x) = 2x exists in interval (1, 2)
∴ f(x) = x² - 1 is differentiable in interval (1, 2).
Then, in interval (1, 2) a point c exists such that

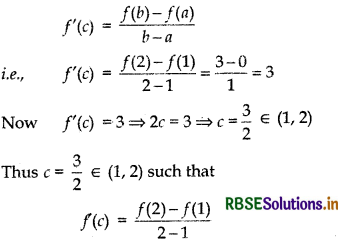
Hence, mean value theorem is verified.