RBSE Solutions for Class 12 Maths Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.7
Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.7 Textbook Exercise Questions and Answers.
Rajasthan Board RBSE Solutions for Class 12 Maths in Hindi Medium & English Medium are part of RBSE Solutions for Class 12. Students can also read RBSE Class 12 Maths Important Questions for exam preparation. Students can also go through RBSE Class 12 Maths Notes to understand and remember the concepts easily.
RBSE Class 12 Maths Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.7
प्रश्न संख्या 1 से 10 तक में दिए फलनों के द्वितीय कोटि के अवकलज ज्ञात कीजिए :
प्रश्न 1.
x2 + 3x + 2
हल:
माना कि y = x2 + 3x + 2
\(\frac{dy}{dx}\) = 2x + 3
और \(\frac{d^2 y}{d x^2}=\frac{d}{d x}\)(2x + 3) = 2
प्रश्न 2.
x20
हल:
माना कि
y = x20
∴ \(\frac{d y}{d x}\) = 20x20-1 = 20x19
∴ \(\frac{d^2 y}{d x^2}\) = 20\(\frac{d}{d x}\)(x19) = 20 × 19x18
= 380x18
प्रश्न 3.
x. cos x
हल:
माना कि
y = x. cos x
\(\frac{d y}{d x}\) = 1 . (cos x) - x . sin x
पुनः अवकलन करने पर
\(\frac{d^2 y}{d x^2}\) = - sin x - (1 . sin x + x cos x)
= - 2 sin x - x cos x

प्रश्न 4.
log x
हल:
माना कि y = log x
\(\frac{d y}{d x}=\frac{1}{x}\) = x-1
पुनः अवकलन करने पर
\(\frac{d^2 y}{d x^2}=\frac{d}{d x}\)(x-1) = -1. x-2 = -\(\frac{1}{x^2}\)
प्रश्न 5.
x3log x
हल:
माना कि y = x3 log x
अवकलन करने पर
\(\frac{d y}{d x}\) = 3x2 log x + x3 \(\frac{1}{x}\) = 3x2 log x + x2
पुनः अवकलन करने पर
\(\frac{d^2 y}{d x^2}\) = 3 . 2x log x + 3x2 \(\frac{1}{x}\) + 2x
= 6x log x + 2x + 3x
= 6x log x + 5x = x (5 + 6 log x)
प्रश्न 6.
ex sin 5x
हल:
माना कि y = ex sin 5x
अवकलन करने पर
\(\frac{d y}{d x}\) = e (sin 5x) + ex . cos 5x . 5
= e (sin 5x + 5 cos 5x)
पुनः अवकलन करने पर
\(\frac{d^2 y}{d x^2}\) = ex (sin 5x + 5 cos 5x) + (ex) \(\frac{d}{dx}\) (sin 5x + 5 cos 5x)
= ex (sin 5x + 5 cos 5x) + ex (5 cos 5x - 25 sin 5x)
= ex (- 24.sin 5x + 10 cos 5x)
= 2ex (5 cos 5x - 12 sin 5x)
प्रश्न 7.
e6x cos 3x
हल:
माना कि y = e6x cos 3x
अवकलन करने पर
\(\frac{dy}{dx}\) = 6e6x (cos 3x) + (e6x) (- 3 sin 3x)
= e6x (6 cos 3x - 3 sin 3x)
पुनः अवकलन करने पर
\(\frac{d^2 y}{d x^2}\) = 6e6x (6 cos 3x - 3 sin 3x) + e6x \(\frac{dy}{dx}\) (6 cos 3x - 3 sin 3x)
= 6e6x (6 cos 3x - 3 sin 3x) + e6x (-18 sin 3x - 9 cos 3x)
= e6x (36 - 9) cos 3x + e6x (- 18 - 18) sin 3x
= e6x [27 cos 3x - 36 sin 3x]
= 9e6x (3 cos 3x - 4 sin 3x)

प्रश्न 8.
tan-1 x
हल:
माना कि y = tan-1x
अवकलन करने पर
\(\frac{d y}{d x}=\frac{1}{1+x^2}\) = (1 + x2)-1
पुनः अवकलन करने पर
\(\frac{d^2 y}{d x^2}\) = (-1) (1 + x2)-1-1 \(\frac{d}{d x}\)(1 + x2)
= -(1 + x2)-2 . 2x = \(\frac{-2 x}{\left(1+x^2\right)^2}\)
प्रश्न 9.
log(log x)
हल
माना कि y = log (log x)
अवकलन करने पर

प्रश्न 10.
sin (log x)
हल:
माना कि
y = sin (log x)
log x = t रखने पर, y= sin t, t = log x
t के सापेक्ष अवकलन करने पर

प्रश्न 11.
यदि y = 5 cos x - 3 sin x है तो सिद्ध कीजिए कि \(\frac{d^2 y}{d x^2}\) + y = 0.
हल
प्रश्नानुसार y = 5 cos x - 3 sin x
अवकलन करने पर
\(\frac{dy}{dx}\) = - 5 sin x - 3 cos x
पुनः अवकलन करने पर
\(\frac{d^2 y}{d x^2}\) = - 5 cos x + 3 sin x
= – (5 cos x – 3 sin x)
= -y
या \(\frac{d^2 y}{d x^2}\) + y = 0 ( इतिसिद्धम्)

प्रश्न 12.
यदि y = cos-1x है तो \(\frac{d^2 y}{d x^2}\) को केवल y के पदों में ज्ञात कीजिए।
हल:
y = cos-1x ∴ x = cos y
x के सापेक्ष अवकलन करने पर
1 = – sin y \(\frac{dy}{dx}\)
\(\frac{d y}{d x}=-\frac{1}{\sin y}\) = - cosec y .... (1)
x के सापेक्ष पुनः अवकलन करने पर
\(\frac{d^2 y}{d x^2}\) = cosec y cot y . \(\frac{d y}{d x}\)
(1) से \(\frac{d y}{d x}\) का मान रखने पर
= cosec y cot y (- cosec y)
= - cosec y cot y
प्रश्न 13.
यदि y = 3 cos (log x) + 4 sin (log x) है तो दर्शाइए कि x2y2 + xy1 + y = 0.
हल:
y = 3 cos (log x) + 4 sin (log x)
अवकलन करने पर
∴ \(\frac{d y}{d x}\) = -3 sin (log x) \(\frac{d}{dx}\) (log x) + 4 cos (log x) \(\frac{d}{dx}\) (log x)
= -3 sin (log x) . \(\frac{1}{x}\) + 4 cos (log x). \(\frac{1}{4}\)
x से गुणा करने पर

प्रश्न 14.
यदि y = Aemx + Benx है तो दर्शाइए कि \(\frac{d^2 y}{d x^2}\) - (m + n) \(\frac{dy}{dx}\) + mny = 0
हल:
y = Aemx + Benx
अवकलन करने पर
\(\frac{dy}{dx}\) = A. memx + B
पुनः अवकलन करने पर
\(\frac{d^2 y}{d x^2}\) = A . m2emx + B. n2enx
प्रश्नानुसार L.H.S. = \(\frac{d^2 y}{d x^2}\) - (m + n) \(\frac{dy}{dx}\) + mny
= A m2emx + B nm2enx - (m + n) × (A memx+ B nenx) + mn (A emx + B enx)
= Aemx [m2 - m (m+n) + mn] + Benx [n2 - n(m + n) + mn]
=Aemx 0 + Benx 0 = 0 = R.H.S
प्रश्न 15.
यदि y = 500 e7x + 600 e-7x है तो दर्शाइए कि \(\frac{d^2 y}{d x^2}\) = 49y
हल:
y = 500 e7x + 600 e-7x
अवकलन करने पर
\(\frac{d y}{d x}\) = 500 × 7e7x + 600 (- 7) e-7x
= 3500 e7x - 4200 e-7x
पुनः अवकलन करने पर
\(\frac{d^2 y}{d x^2}\) = 3500 x 7e7x - 4200 x (- 7) e-7x
= 500 . 49 . e7x + 600 . 49e-7x
= 49 (500 e7x + 600 e-7x) = 49y
∴ \(\frac{d^2 y}{d x^2}\) = 49y

प्रश्न 16.
यदि ey(x + 1) = 1 है तो दर्शाइए कि \(\frac{d^2 y}{d x^2}=\left(\frac{d y}{d x}\right)^2\) है
हल:
ey(x + 1) = 1 या (x + 1) ey = 1
अवकलन करने पर

प्रश्न 17.
यदि y = (tan-1x) है तो दर्शाइए कि (x2 + 1)2 y2 + 2x (x-1 + 1) y1 = 2 है।
हल:
y = (tan-1x)2
अवकलन करने पर
\(\frac{dy}{dx}\) = 2 tan-1x \(\frac{d}{dx}\) (tan-1x)
= \(\frac{2 \tan ^{-1} x}{1+x^2}\)
(1 + x2) से गुणा करने
= (1 + x2)\(\frac{dy}{dx}\) = 2 tan-1x
पुनः अवकलन करने पर
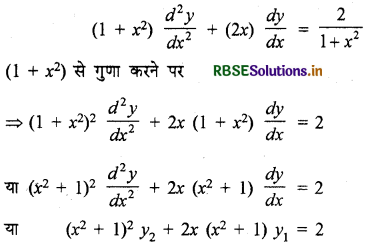

- RBSE Class 12 Maths Notes Chapter 13 Probability
- RBSE Class 12 Maths Notes Chapter 12 Linear Programming
- RBSE Class 12 Maths Notes Chapter 11 Three Dimensional Geometry
- RBSE Class 12 Maths Notes Chapter 10 Vector Algebra
- RBSE Class 12 Maths Notes Chapter 9 Differential Equations
- RBSE Class 12 Maths Notes Chapter 8 Application of Integrals
- RBSE Class 12 Maths Notes Chapter 7 Integrals
- RBSE Class 12 Maths Notes Chapter 6 Application of Derivatives
- RBSE Class 12 Maths Notes Chapter 5 Continuity and Differentiability
- RBSE Class 12 Maths Notes Chapter 4 Determinants
- RBSE Class 12 Maths Notes Chapter 3 Matrices