RBSE Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.7

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.7 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 5 Continuity and Differentiability Ex 5.7

Question 1.
x² + 3x + 2
Answer:
Let y = x² + 3x + 2
Differentiating w.r.t. x
\(\frac{d y}{d x}\) = 2x + 3
Again, differentiating w.r.t. x
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}(2x + 3)\) = 2
Thus, \(\frac{d^{2} y}{d x^{2}}\) = 2

Question 2.
x²⁰
Answer:
Let y = x²⁰
Differentiating w.r.t. x

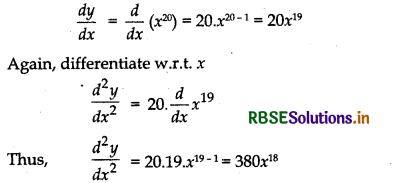
Question 3.
x cos x
Answer:
Let y = x cos x
Differentiating w.r.t x

Question 4.
log x
Answer:
Let y = log x
Differentiating w.r.t. x
\(\frac{d y}{d x}\) = \(\frac{1}{x}\) = x^-1
Again, differentiating w.r.t. x
\(\frac{d^{2} y}{d x^{2}}\) = (- 1)x^-1-1 = (- 1)x^-2
∴ \(\frac{d^{2} y}{d x^{2}}=-\frac{1}{x^{2}}\)

Question 5.
x³ log x
Answer:
Let y = x³ log x
Differentiating w.r.t. x

Question 6.
e^x sin 5x
Answer:
Let y = e^x sin 5x
Differentiating w.r.t. x

Question 7.
e^6x cos 3x
Answer:
Let y = e^6x cos 3x
Differentiating w.r.t. x

Question 8.
tan^-1 x
Answer:
Let y = tan^-1 x
Differentiating w.r.t. x

Question 9.
log (log x)
Answer:
Let y = log(log x)
Differentiating w.r.t. x

Question 10.
sin (log x)
Answer:
Let y = sin (log x)
Differentiating w.r.t. x

Question 11.
If y = 5 cos x - 3 sin x then show that \(\frac{d^{2} y}{d x^{2}}\) + y = 0.
Answer:
Given y = 5 cos x - 3 sin x
Differentiating w.r.t. x
\(\frac{d y}{d x}\) = 5 \(\frac{d}{d x}\) cos x - 3 \(\frac{d}{d x}\) sin x
⇒ \(\frac{d y}{d x}\) = 5(- sin x) - 3 cos x
⇒ \(\frac{d y}{d x}\) = - 5 sin x - 3 cos x
Again, differentiating w.r.t. x
\(\frac{d^{2} y}{d x^{2}}\) = - 5 cos x - 3(- sin x)
= -5 cos x + 3 sin x
= - (5 cos x - 3 sin x) = - y [From (1)]
Thus, \(\frac{d^{2} y}{d x^{2}}\) + y = 0
Hence proved.

Question 12.
If y = cos^-1 x then find \(\frac{d^{2} y}{d x^{2}}\) only in terms of y.
Answer:
Differentiating y = cos^-1x w.r.t. x

Question 13.
If y = 3 cos (log x) + 4 sin (log x) then show that x²y₂ + xy₁ + y = 0.
Answer:
y = 3 cos(log x) + 4 sin(log x)
Differentiating both sides w.r.t. x

Question 14.
If y = Ae^mx + Be^nx then show that
\(\frac{d^{2} y}{d x^{2}}\) - (m + n)\(\frac{d y}{d x}\) + mny = 0
Answer:
Differentiating y = Ae^mx + Be^nx w.r.t. x
\(\frac{d y}{d x}\) = mAe^mx + nBe^nx
Again, differentiating w.r.t. x
\(\frac{d^{2} y}{d x^{2}}\) = m²Ae^mx + n²Be^nx
Now L.H.S. = \(\frac{d^{2} y}{d x^{2}}\) - (m + n)\(\frac{d y}{d x}\) + mny
= m²Ae^mx + n²Be^nx - (m + n)(mAe^mx + nBe^nx)
= m²Ae^mx + n²Be^nx - m²Ae^mx - mnBe^nx - mnAe^mx - n²Be^nx + mnAe^mx+ mnBe^nx)
= 0 = R.HS.
Thus, \(\frac{d^{2} y}{d x^{2}}\) -(m + n)\(\frac{d y}{d x}\) + mny = 0
Hence Proved.

Question 15.
If y = 500e^7x + 600e^-7x then show that \(\frac{d^{2} y}{d x^{2}}\) = 49y
Answer:
Given y = 500e^7x + 600e^-7x
Differentiating both sides w.r.t. x

Question 16.
If e^y (x + 1) = 1 then show that \(\frac{d^{2} y}{d x^{2}}=\left(\frac{d y}{d x}\right)^{2}\)
Answer:
Given e^y (x + 1) = 1 ⇒ (x + 1)e^y = 1
Differentiating both sides w.r.t. x

Question 17.
If y = (tan^-1 x)² then show that
(x² + 1)² y₂ + 2x(x² + 1)y₁ = 2
Answer:
Given, y = (tan^-1 x)² Differentiating both sides w.r.t. x