RBSE Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.5

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.5 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 5 Continuity and Differentiability Ex 5.5

Question 1.
cos x.cos 2x.cos 3x
Answer:
Let y = cos x.cos 2x.cos 3x
Taking logarithm on both sides, we have
log y = log {cos x.cos 2x.cos 3x}
log y = log (cos x) + log (cos 2x) + log (cos 3x)
Differentiating both sides w.r.t. x, we get

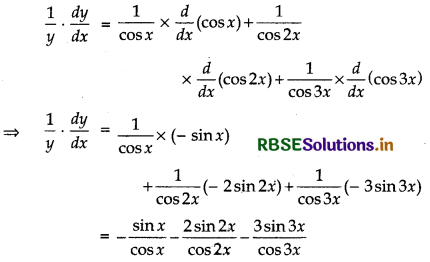
= - tan x - 2 tan 2x - 3 tan 3x
∴ \(\frac{d u}{d x}\) = - y[tan x + 2 tan 2x + 3 tan 3x]
∴ \(\frac{d}{d x}\) (cos x.cos 2x.cos 3x) = - cos x cos 2x cos 3x × [tan x + 2 tan 2x + 3 tan 3x]

Question 2.
\(\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}\)
Answer:

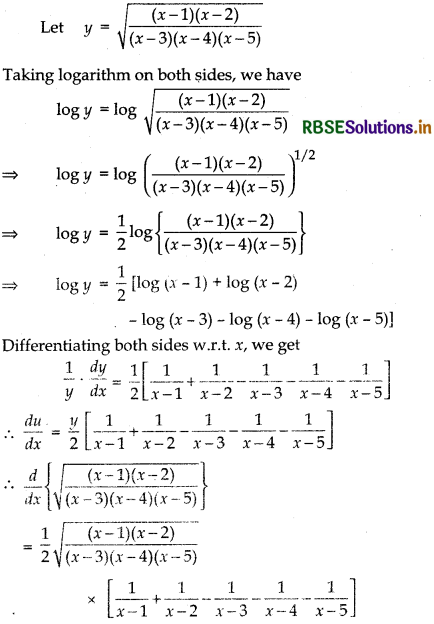
Question 3.
(log x)^{cos x}
Answer:
Let y = (log x)^{cos x}
Taking logarithm on both sides, we have
log y = log {(log x)^{cos x}}
⇒ log y = cos x log(log x)
Differentiating both sides w.r.t. x, we get

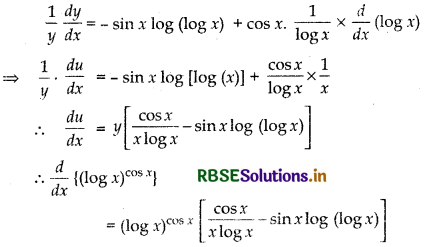
Question 4.
x^x - 2^{sin x}
Answer:
Let y = x^x - 2^{sin x}
and u = x^x, v = 2^{sin x}
∴ y = u - v
Differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}=\frac{d u}{d x}-\frac{d v}{d x}\)
Now, in u = x^x and v = 2 ^{sin x} taking logarithm both sides
log u = x log x
and log v = sin x(log 2)
Now, differentiating both sides w.r.t x, we have

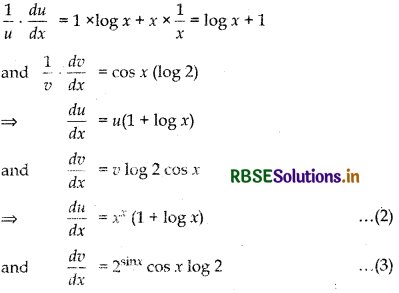
From equations (1), (2) and (3)
\(\frac{d u}{d x}\) = (1 + log x)x^x - 2^{sin x} cos x 2 log 2
∴ \(\frac{d y}{d x}\) (x^x - 2^{sin x}) = (1 + log x)x^x - 2^{sin x} cos x log 2

Question 5.
(x + 3)².(x + 4)³.(x + 5)⁴
Answer:
Let y = (x + 3)².(x + 4)³.(x + 5)⁴
Taking logarithm on both sides, we have
log y = log {(x + 3)².(x + 4)³ (x + 5)⁴)
⇒ log y = log(x + 3)² + log(x + 4)³ + log(x + 5)⁴
⇒ log y = 2 log (x + 3) + 3 log (x + 4) + 4 log (x + 5)
Differentiating both sides w.r.t. x, we get

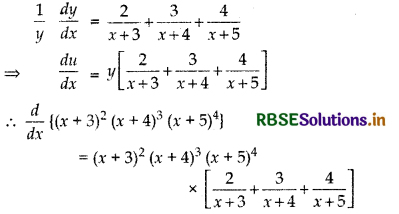
Question 6.
\(\left(x+\frac{1}{x}\right)^{x}+x^{\left(1+\frac{1}{x}\right)}\)
Answer:

Question 7.
(log x)^x + x ^{log x}
Answer:
Let y = (log x)^x + x ^{log x}
and u = (log x)^x, v = x^{log x}
∴ y = u + v
Differentiating both sides w.r.t x, we get
\(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) ....... (1)
In u = (log x)^x taking logarithm on both sides
log u = x log (log x)
Differentiating both sides w.r.t x, we get

Question 8.
(sin x)^x + sin^-1 √x
Answer:
Let y = (sin x)^x + sin^-1 √x
and u = (sin x)^x, v = sin^-1 √x
∴ y = u + v
Differentiating both sides w.r.t x, we get
\(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) ....... (1)
In u = (sin x)^x taking logarithm in both sides.
log u = x log sin x
Differentiating both sides w.r.t x, we get

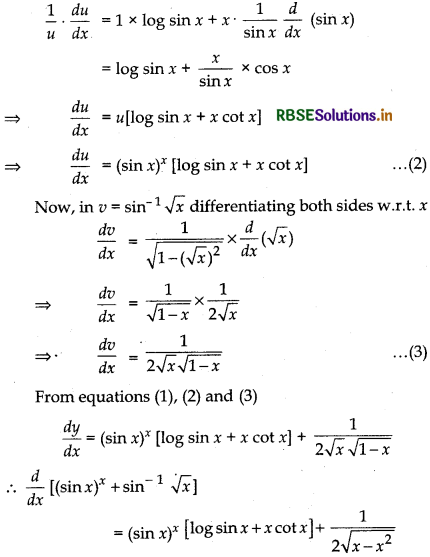
Question 9.
Answer:
Let y = x^{sin x} + (sin x)^{cos x}
and u = x^{sin x} y = (sin x)^{cos x}
∴ y = u + v
Differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) ....... (1)
Again, in u = x^{sin x} taking logarithm in both sides
log u = sin x log x
Differentiating both sides w.r:t. x, we get

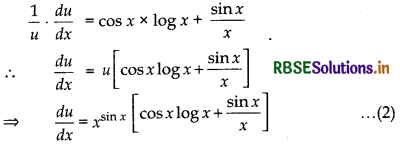
Now, in v = (sin x)^{cos x} taking logarithm in both sides
log v = cos x log sin x
Differentiating both sides w.r.t. x, we get

Question 10.
x^{x cos x} + \(\frac{x^{2}+1}{x^{2}-1}\)
Answer:
Let u = x^{x cos x} and v = \(\frac{x^{2}+1}{x^{2}-1}\)
then y = u + v
Differentiating both sides w.r.t x, we get
\(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\)
Consider, u = (x cos x)^x
Taking logarithm on both sides
log u = x log(x cos x)
⇒ log u = x[log x + log cos x]
⇒ log u = x log x + x log cos x
Differentiating both sides w.r.t. x

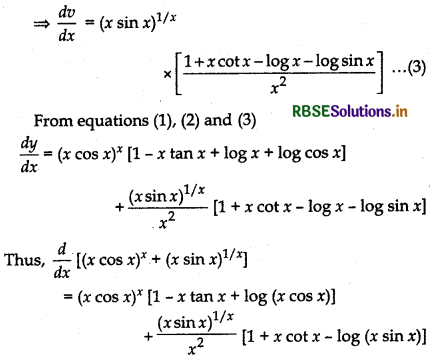
Find \(\frac{d y}{d x}\) of the function given in Q.12 to Q.15

Question 12
x^y + y^x = 1
Answer:
Let u = x^y and v = y^x
Then u + v = 1
In u = x^y and v = y^x taking logarithm on both sides
log u = y log x and log v = x log y
Now, differentiating w.r.t x, we get

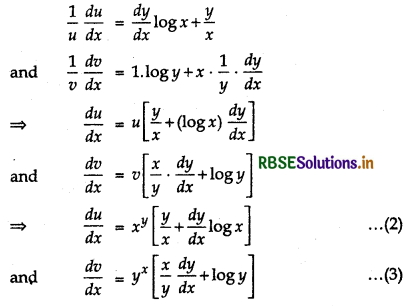
Now, differentiating both sides of (1) w.r.t. x, we get
\(\frac{d u}{d x}+\frac{d v}{d x}\) = 0 ....... (4)
Putting the value of \(\frac{d u}{d x}\) and \(\frac{d v}{d x}\) from equation (4) in (2) and (3)

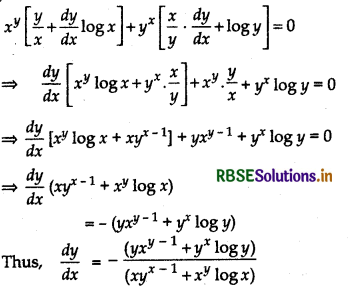
Question 13.
y^x = x^y
Answer:
y^x = x^y
Taking logarithm on both sides
x log y = y log x
Differentiating both sides w.r.t. x

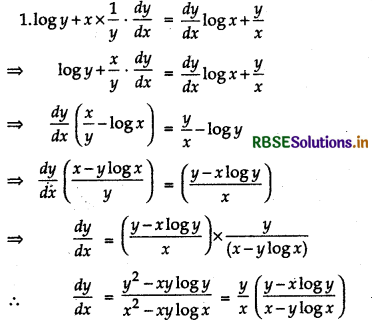
Question 14.
(cos x)^y = (cos y)^x
Answer:
Given, (cos x)^y = (cos y)^x
Taking logarithm on both sides
y log (cos x) = x log (cos y)
Differentiating both sides w.r.t. x, we get

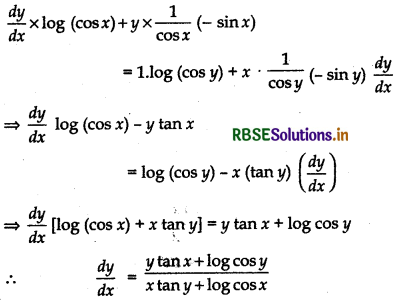
Question 15.
xy = e^{(x - y)}
Answer:
Given, xy = e^{(x - y)}
Taking logarithm on both sides, we have
log(xy) = log e^{(x - y)}
⇒ log x + log y = (x - y) log e
⇒ log x + logy(x - y) (∵ log_e e = 1)
Now, differentiating both sides w.r.t. x, we get

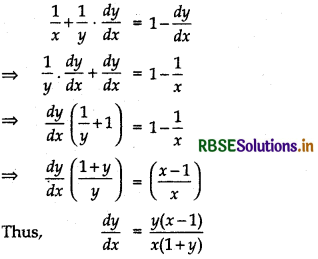
Question 16.
Find the derivative of the function given by
f(x) = (1 + x) (1 + x²) (1 + x⁴) (1 + x⁸) and hence find f'(1).
Answer:
Given, f(x) = (1 + x) (1 + x²) (1 + x⁴) (1 + x⁸)
Taking logarithm on both sides, we have
log [f(x)] = log {(1 + x) (1 + x²) (1 + x⁴) (1 + x⁸)}
⇒ log [f(x) = log(1 + x) + log(1 + x²) + log(1 + x⁴) + log(1 + x⁸)
Differentiating both sides w.r.t. x, we get

Question 17.
Differentiate (x² - 5x + 8) (x³ + 7x + 9) in three ways mentioned below:
(i) By using product rule
(ii) By expanding the product to obtain a single polynomial
(iii) By logarithm differentiation Do they all give the same answer?
Answer:
(i) Use of product rule
Let y = (x² - 5x + 8) (x³ + 7x + 9)
Differentiating both sides w.r.t. x, we get

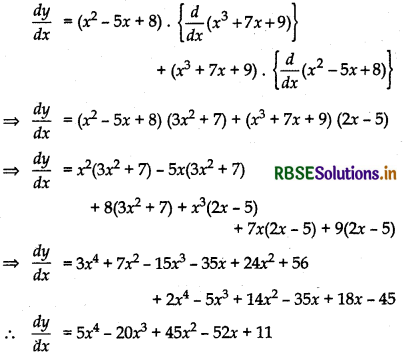
(ii) To get single polynomial by expanding product
y = (x² - 5x + 8) (x³ + 7x + 9)
⇒ y = x²(x³ + 7x + 9) - 5x(x³ + 7x + 9) + 8(x³ + 7x + 9)
⇒ y = x⁵ + 7x³ + 9x² - 5x⁴ - 35x² - 45x + 8x³ + 56x + 72
⇒ y = x⁵ - 5x⁴ + 15x³ - 26x² + 11x + 72
Differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}\) = 5x⁴ - 20x³ + 45x² - 52x + 11

(iii) By logarithmic differentiation
y = (x² - 5x + 8) (x³ + 7x + 9)
Taking logarithm on both sides, we have
log y = log {(x² - 5x +8) (x³ + 7x + 9)}
⇒ log y = log(x² - 5x + 8) + log(x³ + 7x + 9)
Differentiating both sides w.r.t. x, we get

All the three answers obtained from (i), (ii) and (iii) are same.

Question 18.
If u, v and w, are function of x, then show that
\(\frac{d}{d x}(uvw)\) = \(\frac{du}{d x}\)u.w + u.\(\frac{dv}{d x}\).w + u.v \(\frac{d w}{d x}\)
in two ways first by repeated application of product rule, second by logarithm differentiation.
Answer:
(i) Let y = uvw u.(v.w)
By taking u as first function and (v, w) as second function differentiating w.r.t. x, we get

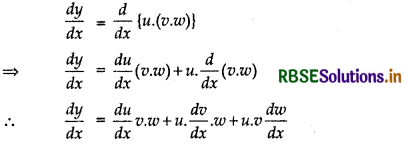
(ii) Taking logarithm of both sides of y = uvw
log y = log(uvw)
⇒ log y = log u + log v + log w
Differentiating both sides w.r.t. x, we get