RBSE Solutions for Class 12 Maths Chapter 4 Determinants Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 4 Determinants Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 4 Determinants Miscellaneous Exercise

Question 1.
Prove that the determinant x \(\left|\begin{array}{ccc} x & \sin \theta & \cos \theta \\ -\sin \theta & -x & 1 \\ \cos \theta & 1 & x \end{array}\right|\) is independent of θ.
Answer:

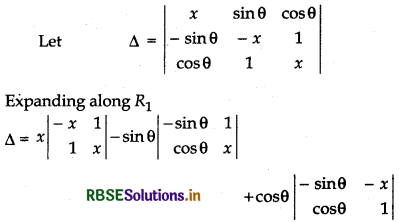
= x(- x² - 1) - sin θ (- x sin θ - cos θ) + cos θ (- sin θ + x cos θ)
= x(- x² - 1) + x sin² θ + sin θ cos θ - cos θ sin θ + x cos² θ
= - x³ - x + x(sin² θ + cos² θ)
= - x³ - x + x × 1 = - x³
Clearly, ∆ is independent of θ.
Hence Proved.

Question 2.
Without expanding the determinant, prove that
\(\left|\begin{array}{ccc} a & a^{2} & b c \\ b & b^{2} & c a \\ c & c^{2} & a b \end{array}\right|\)=\(\left|\begin{array}{ccc} 1 & a^{2} & a^{3} \\ 1 & b^{2} & b^{3} \\ 1 & c^{2} & c^{3} \end{array}\right|\)
Answer:

Question 3.
Evaluate
\(\left|\begin{array}{ccc} \cos \alpha \cos \beta & \cos \alpha \sin \beta & -\sin \alpha \\ -\sin \beta & \cos \beta & 0 \\ \sin \alpha \cos \beta & \sin \alpha \sin \beta & \cos \alpha \end{array}\right|\)
Answer:

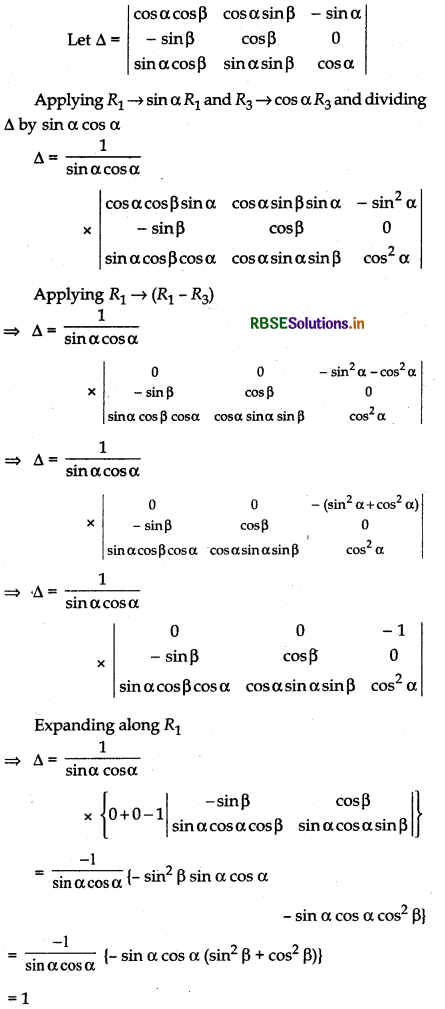
Question 4.
If a, b and c are real numbers and
Δ = \(\left|\begin{array}{lll} b+c & c+a & a+b \\ c+a & a+b & b+c \\ a+b & b+c & c+a \end{array}\right|\) = 0
then show that either a + b + c = 0 and a = b = c.
Answer:
Given determinant is:

⇒ 2(a + b + c) {(b - c) × (c - b) - (c - a) (b - a)} = 0
⇒ 2(a + b + c) {- (b - c)² - (cb - ca - ab + a²)} = 0
⇒ 2(a + b + c) {- b² - c² + 2bc - bc + ca + ab - a²} = 0
⇒ 2(a + b + c) × {- a² - b² - c² + bc + ca + ab} = 0
⇒ - 2(a + b + c) × {a² + b² + c² - ab - bc - ca] = 0
⇒ -(a + b + c) {2a² + 2b² + 2c² - 2ab - 2bc - 2ca] = 0
⇒ - (a + b + c) {(a² + b² - 2ab + b² + c² - 2ab + c² + a² - 2ac} = 0
⇒ - (a + b + c) × {(a - b)² + {b - c)² + (c - a)²} = 0
⇒ a + b + c = 0
or (a - b)² + (b - c)2² + (c - a)² = 0
⇒ a - b = 0, b - c = 0, c - a = 0
⇒ a = b, b = c, c = a
⇒ a = b = c
Hence a + b + c = 0
or a = b = c
Hence Proved.

Question 5.
If a ≠ 0 then, solve
\(\left|\begin{array}{ccc} x+a & x & x \\ x & x+a & x \\ x & x & x+a \end{array}\right|\) = 0
Answer:

Question 6.
Prove that
\(\left|\begin{array}{ccc} a^{2} & b c & a c+c^{2} \\ a^{2}+a b & b^{2} & a c \\ a b & b^{2}+b c & c^{2} \end{array}\right|\) = 4a²b²c²
Answer:

= 2a²b²c {(a + c) (1 - 0) - 1(a + b -b - c)}
= 2a²b²c{a + c - a - b + b + c}
= 2a²b²c(2c)
= 4a²b²c²
Hence Proved.

Question 7.
If A^-1 = \(\left[\begin{array}{rrr} 3 & -1 & 1 \\ -15 & 6 & -5 \\ 5 & -2 & 2 \end{array}\right]\) and B = \(\left[\begin{array}{rrr} 1 & 2 & -2 \\ -1 & 3 & 0 \\ 0 & -2 & 1 \end{array}\right]\) then find the value of (AB)^-1.
Answer:
We have,

= 1(3 - 0) - 2(-1 - 0) - 2(2 - 0)
= 3 + 2 - 4 = 1
∴ |B| = 1 ≠ 0
Since, B is non-singular so B^-1 exists.
If B_ij is cofactor of b_ij in B, then
B₁₁ = + [3 × 1 - (- 2) × 0] = 3
B₁₂ = (- 1) (- 1) - 0 = 1
B₁₃ = + [(- 1) × (- 2) - 0 × 3] = 2
B₂₁ = (- 1) (2 - 4) = (- 1) (- 2) = 2
B₂₂ = + [1 × 1 - 0 (- 2) = 1
B₂₃ = (- 1) [1 × (- 2) - 0 × 2] = 2
B₃₁ = + [2 × 0 - 3 × (- 2)] = 6
B₃₂ = (- 1) [0 - (- 1) (- 2)] = 2
B₃₃ = + [1 × 3 - (-1) × 2] = 3 + 2 = 5

Question 8.
Let A = \(\left[\begin{array}{rrr} 1 & -2 & 1 \\ -2 & 3 & 1 \\ 1 & 1 & 5 \end{array}\right]\), then verify that
(i) (adj A)^-1 = (adj) A^-1
Answer:
Given, A = \(\left[\begin{array}{rrr} 1 & -2 & 1 \\ -2 & 3 & 1 \\ 1 & 1 & 5 \end{array}\right]\)
Determinant of matrix A,
|A| = \(\left|\begin{array}{rrr} 1 & -2 & 1 \\ -2 & 3 & 1 \\ 1 & 1 & 5 \end{array}\right|\)
= (15 - 1) + 2(- 10 - 1) + (- 2 - 3)
= 14 + 2(- 11) + (- 5)
= 14 - 22 - 5 = - 13
∴ | A | = - 13 ≠ 0
Since, matrix A is non-singular so A^-1 exists.
If A_ij is cofactor of a_ij in A, then
A₁₁ = + [3 × 5 - 1 × 1] = 15 - 1 = 14
A₁₂ = (- 1) [- 10 - 1] = 11
A₁₃ = + [- 2 × 1 - 1 × 3] = - 2 - 3 = - 5
A₂₁ = (- 1) [- 10 - 1] = (- 1) × (- 11) = 11
A₂₂ = + [1 × 5 - 1 × 1] = 5 - 1 = 4
A₂₃ = (- 1) [1 + 2] = (- 1) × 3 = - 3
A₃₁ = + [- 2 × 1 - 3 × 1] = - 2 - 3 = - 5
A₃₂ = (- 1) [1 + 2] = (- 1) (3) = - 3
A₃₃ = + [1 × 3 - (- 2) × (- 2)] = 3 - 4 = - 1

= 14(- 4 - 9) - 11(- 11 - 15) - 5(- 33 + 20)
= 14(- 13) - 11(- 26) - 5 (-13)
= - 182 + 286 + 65 = 169
∴ |B| = 169 ≠ 0
Since, matrix B is non-singular so B^-1 exists.
If B_ij is cofactor of b_ij in B, then
B₁₁ = + [4 × (-1) - (- 3) × (- 3)] = - 4 - 9 = -13
B₁₂ = (- 1) (- 11 - 15)] = (- 1) (- 26) = 26
B₁₃ = + [11 × (- 3) - (- 5) × 4] = - 33 + 20 = - 13
B₂₁ = (- 1) [- 11 - 15)] = (- 1) (- 26) = 26
B₂₂ = + [14 × (- 1) - (- 5) × (- 5)] = -14 - 25 = - 39
B₂₃ = (- 1) (- 42 + 55) = (- 1) (13) = - 13
B₃₁ = + [11 × (- 3) - 4 × (- 5)] = - 33 + 20 = - 13
B₃₂ = (- 1) [- 42 + 55] = (- 1) (13) = - 13
B₃₃ = + [14 × 4 - 11 × 11] = 56 - 121 = - 65

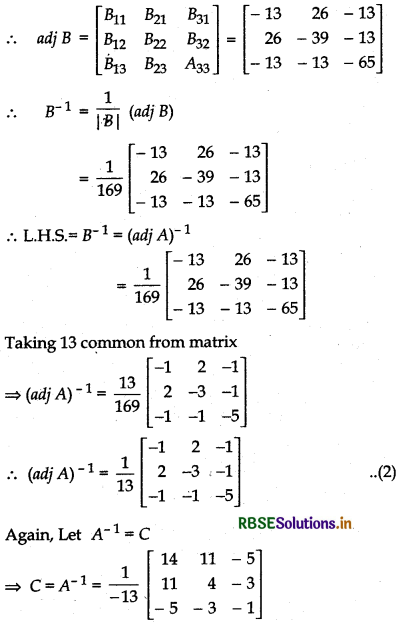
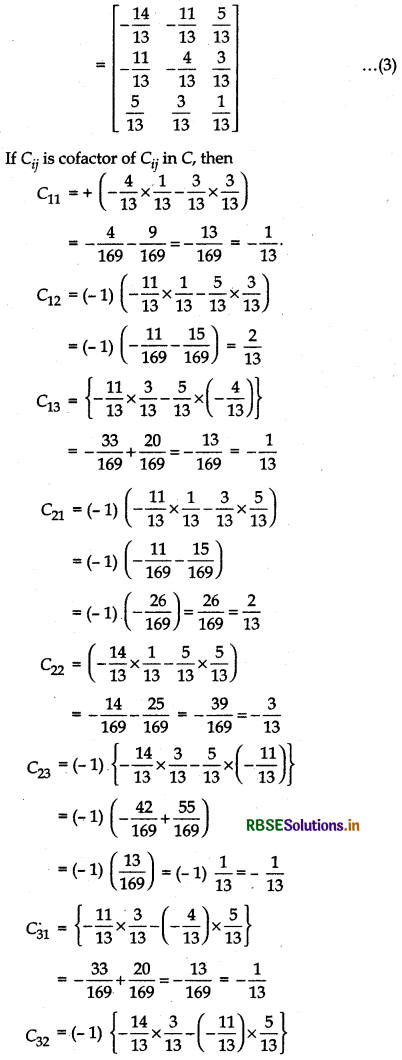
(ii) (A^-1)^-1 = A
Answer:

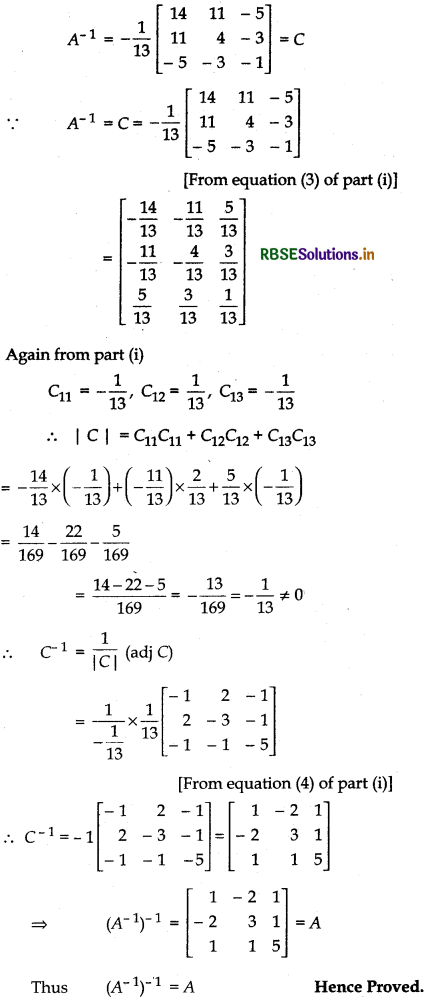
Question 9.
Evaluate: \(\left|\begin{array}{ccc} x & y & x+y \\ y & x+y & x \\ x+y & x & y \end{array}\right|\)
Answer:

= 2(x + y) {x × (- x) - (x - y) × (- y)}
= 2(x + y) {- x² + xy - y²}
= - 2(x + y) (x² - xy + y²)
= - 2(x³ + y³)

Question 10.
\(\left|\begin{array}{ccc} 1 & x & y \\ 1 & x+y & y \\ 1 & x & x+y \end{array}\right|\)
Answer:

Using properties of determinants in Question 11 to 15. Prove that

Question 11.
\(\left|\begin{array}{ccc} \alpha & \alpha^{2} & \beta+\gamma \\ \beta & \beta^{2} & \gamma+\alpha \\ \gamma & \gamma^{2} & \alpha+\beta \end{array}\right|\) = (β - γ) (γ - α) (α - β) (α + β + γ)
Answer:

Applying R₂ → R₂ - R₁ and R₃ → R₃ - R₁

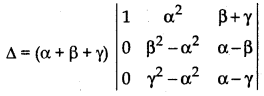
Taking common (β - α) and (γ - α) from R₂ and R₃ respectively

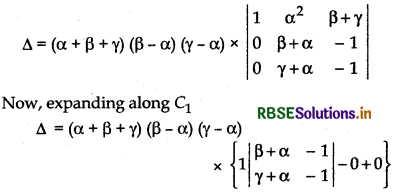
⇒ ∆ = (α + β + γ) (β - α) (γ - α) × {(β - α) (- 1) - (γ + α) (- 1)}
⇒ ∆ = (α + β + γ) (β - α) (γ - α) × (- β - α + γ + α)
⇒ ∆ = (α + β + γ) (β - α) (γ - α) (- β + γ)
⇒ ∆ = (α + β + γ) (α - β) (γ - α) (γ - β) [∵ (β - α) = - (α - β), (γ - β) = - (β - γ)]
⇒ ∆ = (α + β + γ) (α - β) (β - γ) (γ - α)
= R.H.S
Hence Proved.

Question 12.
\(\left|\begin{array}{ccc} x & x^{2} & 1+p x^{3} \\ y & y^{2} & 1+p y^{3} \\ z & z^{2} & 1+p z^{3} \end{array}\right|\) = (1 + pxyz) (x - y) (y - z) (z - x), where p is any scalar.
Answer:

Now, in ∆₁, applying R₂ → R₂ - R₁ and R₃ → R₃ - R₁
∆₁ = \(\left|\begin{array}{ccc} x & x^{2} & 1 \\ y-x & y^{2}-x^{2} & 0 \\ z-x & z^{2}-x^{2} & 0 \end{array}\right|\)
Taking factor (y - z) and (z - x) common from R₂ and R₃ respectively

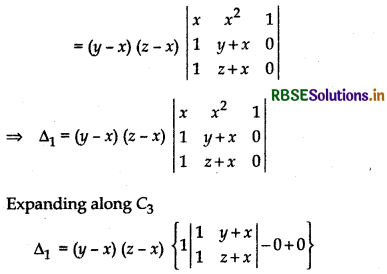
⇒ ∆₁ = (y - x) (z - x) {1(z + x) - 1 × (y + x)}
⇒ ∆₁ = (y - x) (z - x) {z + x - y - x}
⇒ ∆₁ = (y - x) (z - x) (z - y)
⇒ ∆₁ = (x - y) (y - z) (z - x)
[∵ (y - x) = - (x - y) and (z - y) = - (y - z)]
∴ ∆₁ = (x - y) (y - z) (z - x) ...... (2)
Now ∆₂ = \(\left|\begin{array}{ccc} x & x^{2} & p x^{3} \\ y & y^{2} & p y^{3} \\ z & z^{2} & p z^{3} \end{array}\right|\)
Taking x, y, z common from R₁, R₂ and R₃ respectively and p from C₃

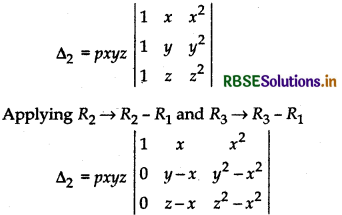
Again, taking common (y - x) and (z - x) from R₂ and R₃ respectively,
∆₂ = pxyz(y - x) (z - x) \(\left|\begin{array}{ccc} 1 & x & x^{2} \\ 0 & 1 & y+x \\ 0 & 1 & z+x \end{array}\right|\)
Now, expanding ∆₂ along C₁
⇒ ∆₂ = pxyz(y - x) (z - x) × \(\left\{1\left|\begin{array}{ll} 1 & y+x \\ 1 & z+x \end{array}\right|-0+0\right\}\)
⇒ ∆₂ = pxyz(y - x) (z - x) × {1 × (z + x) - 1 × (y + x)}
⇒ ∆₂ = pxyz{y - x) (z - x) (z + x - y - x)
⇒ ∆₂ = pxyz(y - x) (z - x) (z - y)
⇒ ∆₂ = pxyz(x - y) (y - z) (z - x)
[∵ (y - x) = -(x - y) and (z - y) = - (y - z)]
∴ ∆₂ = pxyz(x - y) (y - z) (z - x) ....... (3)
Now, substituting the values of ∆₁ and ∆₂ in equation (1), we get
∆ = (x - y) (y - z) (z - x) + pxyz(x - y) (y - z) (z - x)
⇒ ∆ = (x - y) (y - z) (z - x) (1 + pxyz)
∴ ∆ = (1 + pxyz) (x - y) (y - z) (z - x)
= R.H.S.
Hence Proved.

Question 13.
\(\left|\begin{array}{ccc} 3 a & -a+b & -a+c \\ -b+a & 3 b & -b+c \\ -c+a & -c+b & 3 c \end{array}\right|\) = 3(a + b + c) (ab + bc + ca)
Answer:

⇒ ∆ = (a + b + c) {(a + 2b) (2c + a) - (- c + a) (- b + a)}
⇒ ∆ = (a + b + c) {2ca + a² + 4bc + 2ba - (bc - ac- ab + a²)}
⇒ ∆ = (a + b + c) {(2ca + a² + 4bc - bc + ac + ab - a² + 2ab}
⇒ ∆ = (a + b + c) {3ab + 3bc + 3ca}
⇒ ∆ = (a + b + c) × 3 (ab + bc + ca)
⇒ ∆ = 3 (a + b + c) (ab + bc + ca)
∴ ∆ = 3 (a + b + c) (ab + bc + a)

Question 14.
\(\left|\begin{array}{ccc} 1 & 1+p & 1+p+q \\ 2 & 3+2 p & 4+3 p+2 q \\ 3 & 6+3 p & 10+6 p+3 q \end{array}\right|\) = 1
Answer:

Question 15.
\(\left|\begin{array}{ccc} \sin \alpha & \cos \alpha & \cos (\alpha+\delta) \\ \sin \beta & \cos \beta & \cos (\beta+\delta) \\ \sin \gamma & \cos \gamma & \cos (\gamma+\delta) \end{array}\right|\) = 0
Answer:

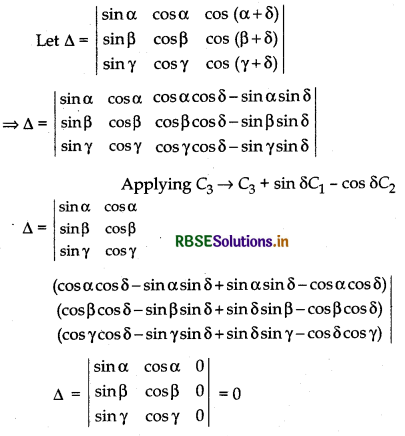
Thus, ∆ = 0 (all elements of C₃ are zero)
Hence Proved.

Question 16.
Solve the following equations :
\(\frac{2}{x}+\frac{3}{y}+\frac{10}{z}\) = 4
\(\frac{4}{x}-\frac{6}{y}+\frac{5}{z}\) = 1
\(\frac{6}{x}+\frac{9}{y}-\frac{20}{z}\) = 2
Answer:
Given system of equation is
\(\frac{2}{x}+\frac{3}{y}+\frac{10}{z}\) = 4
\(\frac{4}{x}-\frac{6}{y}+\frac{5}{z}\) = 1
\(\frac{6}{x}+\frac{9}{y}-\frac{20}{z}\) = 2
Let u = \(\frac{1}{x}\), v = \(\frac{1}{y}\) and w = \(\frac{1}{z}\) then
2u + 3v + 10 w = 4
4u - 6v + 5w = 1
6u + 9v - 20w = 2
Writing in matrix form
AX = B ....... (1)

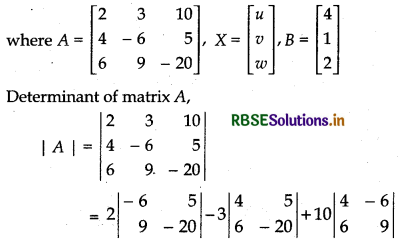
⇒ |A| = 2 × 75 - 3 × (- 110) + 10 x× 72
⇒ |A| = 150 + 330 + 720 = 1200
∴ |A| = 1200 ≠ 0
Since, matrix A is non-singular so A^-1 exists.
If A_ij is cofactor of a_ij in A, then
A₁₁ = + [- 6 × (- 20) - 9 × 5] = 120 - 45 = 75
A₁₂ = (- 1) [- 80 - 30] = (- 1) (- 110) = 110
A₁₃ = + [4 × 9 - 6 × (- 6)] = 36 + 36 = 72
A₂₁ = (- 1) (- 60 - 90) = (- 1) (- 150) = 150
A₂₂ = + [- 40 - 60] = - 100
A₂₃ = (- 1) [18 - 18] = 0
A₃₁ = + [3 × 5 - (- 6) × 10] = 15 + 60 = 75
A₃₂ = (- 1) (10 - 40) = (-1) (- 30) = 30
A₃₃ = + [2 × (- 6) - 4 × 3] = - 12 - 12 = - 24

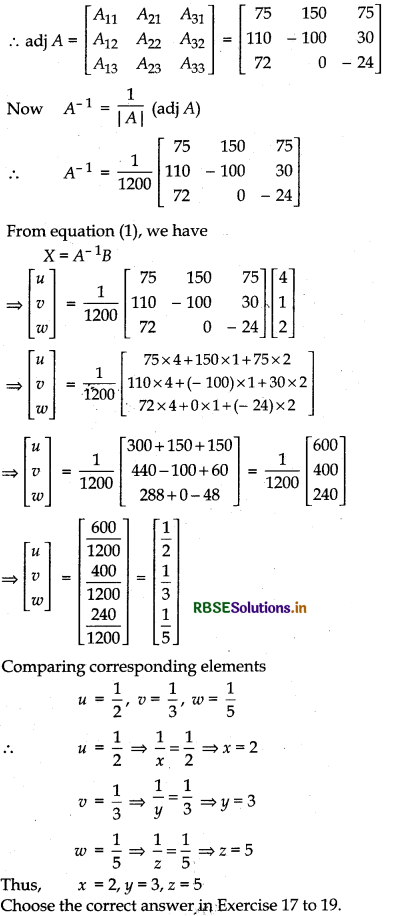
Question 17.
If a,b,c are in A.P., then the determinant \(\left|\begin{array}{lll} x+2 & x+3 & x+2 a \\ x+3 & x+4 & x+2 b \\ x+4 & x+5 & x+2 c \end{array}\right|\) is:
(A) 0
(B) 1
(C) x
(D) 2x
Answer:

All element of R₂ are zero.
Thus, option (A) is correct.

Question 18.
If x, y, z are non-zero real numbers, then the inverse of matrix A = \(\left[\begin{array}{lll} x & 0 & 0 \\ 0 & y & 0 \\ 0 & 0 & z \end{array}\right]\) is:

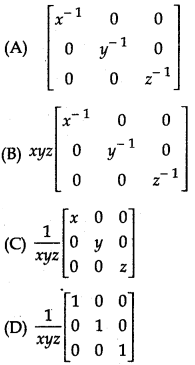
Answer:
Let A = \(\left[\begin{array}{ccc} x & 0 & 0 \\ 0 & y & 0 \\ 0 & 0 & z \end{array}\right]\)
∴ Determinant of matrix A is
|A| = x\(\left|\begin{array}{ll} y & 0 \\ 0 & z \end{array}\right|\) - 0 + 0
= x(yz - 0) = xyz
∴ |A| = xyz ≠ 0
If A_ij is cofactor of a_ij in A, then
A₁₁ = + [yz - 0] = yz
A₁₂ = (- 1) (0 × z - 0 × 0) = 0
A₁₃ = + [0 × 0 - 0 × y = 0]
A₂₁ = (- 1) (0 × z - 0 × 0) = 0
A₂₂ = + [xz - 0 × 0] = xz
A₂₃ = (- 1) (x × 0 - 0 × 0) = 0
A₃₁ = + [0 × 0 - 0 × y] = 0
A₃₂ = (- 1) [x × 0 - 0 × 0] = 0
A₃₃ = + [x × y - 0 × 0] = xy

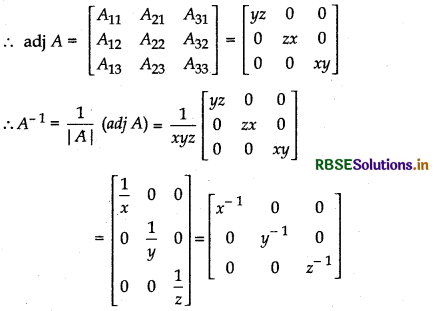
Thus, option (A) is correct.

Question 19.
If A = \(\left[\begin{array}{ccc} 1 & \sin \theta & 1 \\ -\sin \theta & 1 & \sin \theta \\ -1 & -\sin \theta & 1 \end{array}\right]\), where 0 ≤ θ ≤ 2π, then
(A) Det (A) = 0
(B) Det (A) ∈ (2, ∞)
(C) Det (A) ∈ (2, 4)
(D) Det (A) ∈ [2, 4]
Answer:

⇒ (1 + sin²θ) + (sin²θ - sin²θ) + (sin²θ + 1)
⇒ |A| = 1 + sin²θ + sin²θ + 1
⇒ |A| = 2(1 + sin²θ)
Now θ = 0, |A| = 2
θ = \(\frac{\pi}{2}\),
|A| = 2(1 + 1) = 4
∴ det (A) ∈ [2, 4]
Thus, option (D) is correct.