RBSE Solutions for Class 12 Maths Chapter 4 Determinants Ex 4.6

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 4 Determinants Ex 4.6 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 4 Determinants Ex 4.6

Question 1.
x + 2y = 2
2x + 3 y = 3
Answer:
Given system of equations is :
x + 2y = 2
2x + 3y = 3
Given system of equations can be written in matrix form as:

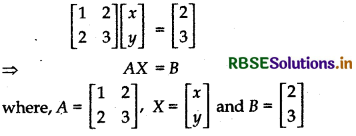
Determinant of matrix A is
|A| = \(\left|\begin{array}{ll} 1 & 2 \\ 2 & 3 \end{array}\right|\)
= 1 × 3 - 2 × 2
= 3 - 4 = - 1
∴ |A| = - 1 ≠ 0
Thus, given system of equations is consistent.

Question 2.
2x - y = 5
x + y = 4
Answer:
Given system of equations is :
2x - y = 5
x + y = 4
In matrix form, the given system of equations can be written as
AX = B

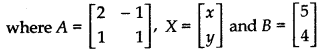
Determinant of matrix A is
|A| = \(\left|\begin{array}{rr} 2 & -1 \\ 1 & 1 \end{array}\right|\) = 2 × 1 - 1 × (- 1) = 2 + 1 = 3
i.e., |A| ≠ 0
Thus, given system of equations is consistent.

Question 3.
x + 3y = 5
2x + 6y = 8
Answer:
Given system of equations is :
x + 3y = 5
2x + 6y = 8
In matrix form, the given system of equations can be written as:
AX = B

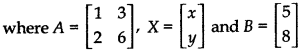
Determinant of matrix A
|A| = \(\left|\begin{array}{ll} 1 & 3 \\ 2 & 6 \end{array}\right|\) = (1 × 6) - 2 × (3) = 6 - 6 = 0
∴ |A| = 0
i.e., matrix A is singular.
Thus, the given system of equations is in-consistent.

Question 4.
x + y + z = 1
2x + 3y + 2z = 2
ax + ay + 2az = 4
Answer:
Given system of equations is:
x + y + z = 1
2x + 3y + 2z = 2
ax + ay + 2az = 4
In matrix form, this can be written as:
AX = B

It means A is non-singular so given system of equations is consistent.

Question 5.
3x - y - 2z = 2
2y - z = - 1
3x - 5y = 3
Answer:
Given system of equations is :
3x - y - 2z = 2
0x + 2y - z = - 1
3x - 5y + 0z = 3
Above system can be expressed in matrix form as
AX = B

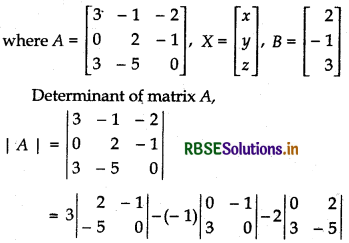
= 3{2 × 0 - (- 5) × (- 1)} + 1{0 × 0 - 3 × (- 1)} - 2{0 × (- 5) - 3 × 2}
= 3(- 5) + 1(3) - 2(- 6)
= - 15 + 3 + 12 = 0
⇒ |A| = 0
So, matrix A is singular.
Thus, given system of equations is in-consistent.

Question 6.
5x - y + 4z = 5
2x + 3y + 5z = 2
5x - 2y + 6z = - 1
Answer:
Given system of equations is:
5x - y + 4z = 5
2x + 3y + 5z = 2
5x - 2y + 6z = - 1
We can write the above system in matrix form as :
AX = B

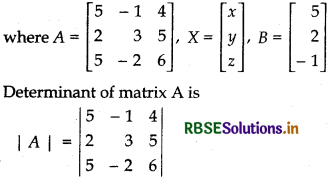
= 5{3 × 6 - (- 2) × 5} + 1(2 × 6 - 5 × 5) + 4{2 × (- 2) - 5 × 3}
= 5(18 + 10) + 1(12 - 25) + 4(- 4 - 15)
= 5 × 28 - 13 + 4 × (- 19)
= 140 -13 - 76 = 140 - 89 = 51
∴ | A | = 51 ≠ 0
Thus, given system of equations is consistent.

Solve system of linear equations, using matrix method in questions 7 to 14:

Question 7.
5x + 2y = 4
7x + 3y = 5
Answer:
Given system of equations is :
5x + 2y = 4
7x + 3y = 5
Writing the given system of equations in matrix form
AX = B

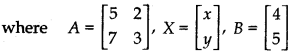
Determinant of matrix |A| is
|A| = \(\left|\begin{array}{ll} 5 & 2 \\ 7 & 3 \end{array}\right|\)
= 5 × 3 - 7 × 2 = 15 - 14 = 1
∴ |A| = 1 ≠ 0
Since, matrix A is non-singular so A^-1 exists and system is consistent.
If A_ij is cofactor of a_ij in A, then
A₁₁ = (- 1)^{1 + 1}(3) = 3
A₁₂ = (- 1)^{1 + 2} = 7 = - 7
A₂₁ = (- 1)^{2 + 1}2 = - 2
A₂₂ = (- 1)^{2 + 2}5 = 5
Matrix formed by the cofactors of |A| is:

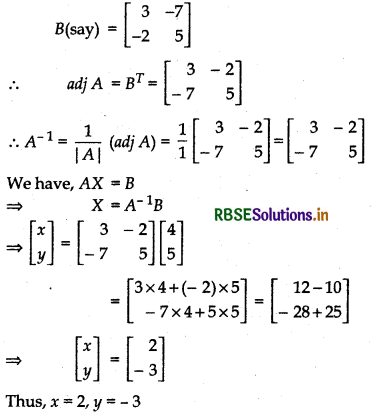
Question 8.
2x - y = - 2
3x + 4y = 3
Answer:
Given system of equations is:
2x - y = - 2
3x + 4y = 3
Writing the given system of equations in matrix form,
AX = B ........ (1)

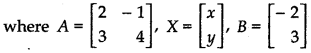
Determinant of matrix A is
|A| = \(\left|\begin{array}{rr} 2 & -1 \\ 3 & 4 \end{array}\right|\)
= 2 × 4 - 3 × (- 1) = 8 + 3 = 11
∴ |A| = 1 ≠ 0
Since, matrix A is non-singular so A^-1 exists, and system is consistent.
If A_ij is cofactor of a_ij in A
A₁₁ = (- 1)^{1 + 1} 4 = 4
A₁₂ = (- 1)^{1 + 2} 3 = - 3
A₂₁ = (- 1)^{2 + 1} (- 1) = (- 1) (- 1) = 1
A₂₂ = (- 1)^{2 + 2} 2 = 2
Matrix formed by the cofactor of |A| is:

Question 9.
4x - 3y = 3
3x - 5y = 7
Answer:
Given system of equations is:
4y - 3 y = 3
3x - 5y = 7
Writing the given system of equations in matrix form
AX = B .......... (1)

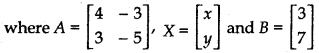
Determinant of matrix A,
|A| = \(\left|\begin{array}{rr} 4 & -3 \\ 3 & -5 \end{array}\right|\)
= 4 × (- 5) - 3 × (- 3) = - 20 + 9 = - 11
∴ |A| = - 11 ≠ 0
Since, matrix A is non-singular so A^-1 exists and given system is consistent.
If A_ij is cofactor of a_ij in A, then
A₁₁ = (- 1)^{1 + 1} (- 5) = - 5
A₁₂ = (- 1)^{1 + 2} (3) = (- 1) × 3 = - 3
A₂₁ = (- 1)^{2 + 1} (- 3) = (- 1) (- 3) = 3
A₂₂ = (- 1)^{2 + 2} 4 = 4
Matrix formed by the cofactor of |A| is:

Question 10.
5x + 2y = 3
3x + 2y = 5
Answer:
Given system of equations is:
5x + 2y = 3
3x + 2y = 5
Writing the given system of equations in matrix form
AX = B .......... (1)

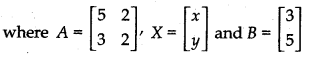
Determinant of matrix A,
|A| = \(\left|\begin{array}{ll} 5 & 2 \\ 3 & 2 \end{array}\right|\)
= 5 × 2 - 3 × 2 = 10 - 6 = 4
∴ |A| = 4 ≠ 0
Since, matrix A is non-singular so A^-1 exists and given, system is consistent.
If A_ij is cofactor of a_ij in A, then
A₁₁ = (- 1)^{1 + 1} (2) = 2
A₁₂ = (- 1)^{1 + 2} (3) = - 3
A₂₁ = (- 1)^{2 + 1} (2) = - 2
A₂₂ = (- 1)^{2 + 2} (5) = 5

Question 11.
2x + y + 2 = 1
x - 2y - z = 3/2
3y - 5z = 9
Answer:
Given system of equations is :
2x + y + z = 1
x - 2y - z = 3/2
0x + 3y - 5z = 9
Writing the given system of equations in matrix form
AX = B ...(1)

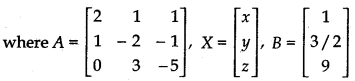
Determinant of matrix A,
|A| = \(\left|\begin{array}{rrr} 2 & 1 & 1 \\ 1 & -2 & -1 \\ 0 & 3 & -5 \end{array}\right|\)
= 2{- 2 × (- 5) - 3 × (- 1)} - 1(1 × (- 5) - 0 × (-1)} + 1{1 × 3 - 0 × (- 2)}
= 2{(10 + 3) -1(- 5 + 0) + 1(3 + 0)}
= 2 × 13 - 1 × (- 5) + 1 × 3 = 26 + 5 + 3 = 34
∴ |A| = 34 ≠ 0
Since, matrix A is non-singular so A^-1 exists and given system of equations is consistent.
If A_ij is cofactor of a_ij in A, then
A₁₁ = + [2 × (- 5) - 3 × ( - 1)] = 10 + 3 = 13
A₁₂ = (- 1) [(- 5 + 0)] = ( - 1) (- 5) = 5
A₁₃ = [1 × 3 - 0 × (- 2)] = 3 + 0 = 3
A₂₁ = (- 1) [- 5- 3] = (- 1) (- 8) = 8
A₂₂ = + [2 × ( - 5) - 0 × 1] = - 10 - 0 = - 10
A₂₃ = (- 1) [6 - 0] = - 6
A₃₁ = +[1 × (- 1) - (- 2) × 1] = - 1 + 2 = 1
A₃₂ = (- 1) [- 2 - 1] = (- 1) (- 3) = 3
A₃₃ = + [2 × (- 2) - 1 × 1] = - 4 - 1 = - 5

Question 12.
x - y + z = 4
2x + y - 3z = 0
x + y + z = 2
Answer:
Given system of equations is:
x - y + z = 4
2x + y - 3z = 0
x + y + z = 2
Writing it in matrix form
AX = B ...... (1)

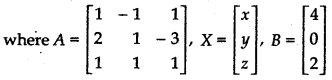
= (1 + 3) + (2 + 3) + (2 - 1) = 4 + 5 + 1 = 10
∴ |A| = 10 ≠ 0
Since, matrix A is non-singular so A^-1 exists and given tern is consistent.
If A_ij is cofactor of in a_ij, then
A₁₁ = +[1 × 1 - 1 × (- 3)] = 1 + 3 = 4
A₁₂ = (- 1) [2 + 3] = (- 1)5 = - 5
A₁₃ = +[2 × 1 - 1 × 1] = 2 - 1 = 1
A₂₁ = (- 1) [ - 1 - 1] = (- 1) (- 2) = 2
A₂₂ = + [1 × 1 - 1 × 1] = 1 - 1 = 0
A₂₃ = - 1[1 + 1] = - 2
A₃₁ = +[(- 1) × (- 3) - 1 × 1] = 3 - 1 = 2
A₃₂ = (- 1) [- 3 - 2] = (- 1) (- 5) = 5
A₃₃ = +[1 × 1 - 2 × (- 1)] = 1 + 2 = 3

Question 13.
2x + 3y + 3z = 5
x - 2y + z = - 4
3x - y - 2z = 3
Answer:
Given system of equations is:
2x + 3y + 3z = 5
x - 2y + z = - 4
3x - y - 2z = 3
Writing it in matrix form
AX = B ........ (1)

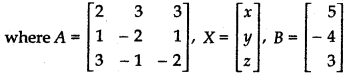
Determinant of matrix A is
|A| = \(\left|\begin{array}{rrr} 2 & 3 & 3 \\ 1 & -2 & 1 \\ 3 & -1 & -2 \end{array}\right|\)
= 2(4 + 1) - 3 (- 2 - 3) + 3(- 1 + 6)
= 2 × 5 - 3 × (- 5) + 3 × 5 = 10 + 15 + 15 = 40
∴ |A| = 40 ≠ 0
Since, matrix A is non-singular so A^-1 exists and system of equations is consistent.
If A_ij is cofactor of a_ij in A, then
A₁₁ = + [- 2 × (- 2) - (- 1) × 1] = 4 + 1 = 5
A₁₂ = (- 1) [- 2 - 3] = (- 1) (- 5) = 5
A₁₃ = + [1 × (- 1) - 3 × (- 2)] = - 1 + 6 = 5
A₂₁ = (- 1) [- 6 + 3] = (- 1) (- 3) = 3
A₂₂ = + [2 × (- 2) - 3 × 3] = - 4 - 9 = - 13
A₂₃ = (- 1) [- 2 - 9] = (- 1) (- 11) = 11
A₃₁ = + [3 × 1 - (- 2) × 3] = 3 + 6 = 9
A₃₂ = (- 1) [2 - 3] = - 1(- 1) = 1
A₃₃ = + [2 × (- 2) - 1 × 3] = - 4 - 3 = - 7

Question 14.
x - y + 2z = 7
3x + 4y - 5z = - 5
2x - y + 3z = 12
Answer:
Given system of equations is:
x - y + 2z = 7
3x + 4y - 5z = - 5
2x - y,+ 3z = 12
Writing it in matrix form
AX = B

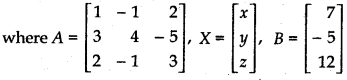
Determinant of matrix A,
|A| = \(\left|\begin{array}{rrr} 1 & -1 & 2 \\ 3 & 4 & -5 \\ 2 & -1 & 3 \end{array}\right|\)
= (12 - 5) + (9 + 10) + 2(- 3 - 8)
= 7 + 19 + 2(- 11) = 26 - 22 = 4
∴ |A| = 4 ≠ 0
Since, matrix A is non-singular so A^-1 exists and system of equations is consistent.
If A_ij is cofactor of a_ij in A, then
A₁₁ = + [4 × 3 - (- 1) × (- 5)] = 12 - 5 = 7
A₁₂ = (- 1) [9 + 10] = (- 1) (19) = -19
A₁₃ = + [3 × (- 1) - 2 × 4] = - 3 - 8 = - 11
A₂₁ = (- 1) [- 3 + 2] = (-1) (- 1) = 1
A₂₂ = + [1 × 3 - 2 × 2] = 3 - 4 = - 1
A₂₃ = (-1)[- 1 + 2] = (- 1)(1) = - 1
A₃₁ = + [(- 1) × (- 5) - 4 × 2] = 5 - 8 = - 3
A₃₂ = (- 1) [- 5 - 6] = (- 1) (- 11) = 11
A₃₃ = + [1 × 4 - 3 × (- 1)] = 4 + 3 = 7

Question 15.
If A = \(\left[\begin{array}{rrr} 2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2 \end{array}\right]\), find A^-1. Using A^-1 solve the following system of equations:
2x - 3y + 5z = 11
3x + 2y - 4z = - 5
x + y - 2z = - 3
Answer:
Given, A = \(\left[\begin{array}{rrr} 2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2 \end{array}\right]\)
Determinant of matrix A is
|A| = \(\left|\begin{array}{rrr} 2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2 \end{array}\right|\)
⇒ |A| - 2(- 4 + 4) + 3(- 6 + 4) + 5(3 - 2)
= 2 × 0 + 3(- 2) + 5 × 1 = - 6 + 5 = - 1
∴ |A| = 4 ≠ 0
So, matrix A is non-singular so A^-1 exist.
If A_ij is cofactor of a_ij then
A₁₁ = + [2 × (- 2) -1 × (- 4)] = - 4 + 4 = 0
A₁₂ = (-1) [- 6 + 4] = (-1) (- 2) = 2
A₁₃ = + [3 × 1 -1 × 2] - 3 - 2 = 1
A₂₁ = (- 1) [6 - 5] = - 1
A₂₂ = + [2 × (- 2) - 1 × 5] = - 4 - 5 = - 9
A₂₃ = (- 1) [2 + 3] = - 5
A₃₁ = + [- 3 × (- 4) - 2 × 5] = 12 - 10 = 2
A₃₂ = (-1) [- 8 - 15] = (- 1) (- 23) = 23
A₃₃ = + [2 × 2 - 3 × (- 3)] = 4 + 9 = 13

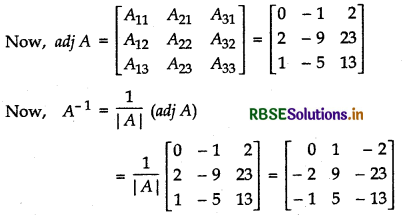
Writing the given system of equations in matrix form, we get

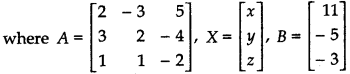
Since, matrix A is non-singular so A^-1 exists.
since, A × B ⇒ x = A^-1B

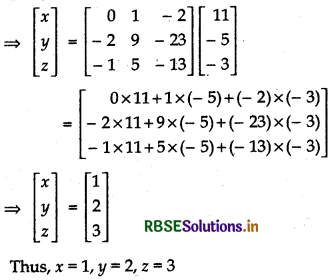
Question 16.
The cost of 4 kg onion, 3 kg wheat and 2 kg rice is ₹ 60. The cost of 2 kg onion, 4 kg wheat and 6 kg rice is ₹ 90. The cost of 6 kg onion, 2 kg wheat and 3 kg rice is ₹ 70. Find the cost of each item (per kg) by matrix method
Answer:
Let cost of 1 kg onion = ₹ x
cost of 1 kg wheat = ₹ y
And cost of 1 kg rice = ₹ z
We have,
cost of 4 kg onion = ₹ 4x
cost of 3 wheat = ₹ 3y
And cost of 2 kg rice = ₹ 2z
∴ 4x + 3y + 2z = 60 .......... (1)
Again cost of 2 kg onion = ₹ 2x
cost of 4 kg wheat = ₹ 4y
and cost of 6 kg rice = ₹6z
∴ 2x + 4y + 6z = 90 ........... (2)
Now cost of 6 kg onion = ₹ 6x
cost of 2 kg wheat = ₹2y
and cost of 3 kg rice = ₹3z
∴ 6x + 2y + 3z = 70 ........... (3)
Thus, system of equations is :
4x + 3y + 2z = 60
2x + 4y + 6z = 90
6x + 2y + 3z = 70
or
4x + 3y + 2z = 60
x + 2y + 3z = 45
6x + 2y + 3z = 70
Writing in matrix form
AX = B ......... (4)

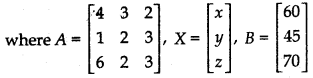
Determinant of matrix A is
|A| = \(\left|\begin{array}{lll} 4 & 3 & 2 \\ 1 & 2 & 3 \\ 6 & 2 & 3 \end{array}\right|\)
= 4(2 × 3 - 2 × 3) - 3(1 × 3 - 6 × 3) + 2(1 × 2 - 6 × 2)
= 4(6 - 6) - 3(3 - 18) + 2(2 - 12)
= 4 × 0 - 3(- 15) + 2(- 10)
= 0 + 45 - 20 = 25
∴ |A| = 25 ≠ 0
If A_ij is cofactor of a_ij in A, then
A₁₁ = + [2 × 3 - 2 × 3] = 0
A₁₂ = (- 1) [1 × 3 - 6 × 3] = (- 1) (3 - 18) = (- 1) (- 15) = 15
A₁₃ = + [1 × 2 - 6 × 2] = 2 - 12 = - 10
A₂₁ = (- 1) [3 × 3 - 2 × 2] = (- 1) (9 - 4) = (- 1)5 = - 5
A₂₂ = [4 × 3 - 6 × 2] = 12 - 12 = 0
A₂₃ = (- 1) [4 × 2 - 6 × 3] = (-1) (8 - 18) = (-1) (-10) = 10
A₃₁ = +[3 × 3 - 2 × 2] = 9 - 4 = 5
A₃₂ = (- 1) [12 - 2] = - 10
A₃₃ = + [4 × 2 - 1 × 3] = 8 - 3 = 5

⇒ x = 5, y = 8, z = 8
Thus, Onion = ₹ 5, Wheat = ₹ 8, Rice = ₹ 8