RBSE Solutions for Class 12 Maths Chapter 4 Determinants Ex 4.3

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 4 Determinants Ex 4.3 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 4 Determinants Ex 4.3

Question 1.
Find the area of the triangle with vertices at the point given in each of the following:
(i) (1, 0), (6, 0), (4, 3)
Answer:
(1, 0), (6, 0), (4, 3)
Here x₁ = 1, x₂ = 6, x₃ = 4, y₁ = 0, y₂ = 0, y₃ = 3
Area of triangle

(ii) (2, 7), (1, 1), (10, 8)
Answer:
Here x₁ = 2, x₂ = 1, x₃ = 10, y₁ = 7, y₂ = 1, y₃ = 3
Area of triangle

= \(\frac{1}{2}\) {- 1 × 1 - (- 6 × 8) - 0 + 0} = \(\frac{1}{2}\) {- 1 + 48}
= \(\frac{47}{2}\) sq.units = 23\(\frac{1}{2}\) sq.units

(iii) (- 2, - 3) (3, 2), (- 1, - 8)
Answer:
Here x₁ = - 2, x₂ = 3, x₃ = - 1, y₁ = - 3, y₂ = 2, y₃ = - 8
Area of triangle

Question 2.
Show that point A (a, b + c), B(b, c + a) and C(c, a + b) are collinear.
Answer:
Three points will be collinear if area of ∆ ABC is zero.
Area of triangle

(Since C₁ and C₃ are identical)
Thus, given points are collinear.
Hence Proved.

Question 3.
Find values of k if area of triangle is 4 sq. units, and vertices are:
(i) (k, 0), (4, 0), (0, 2)
Answer:
Area of triangle

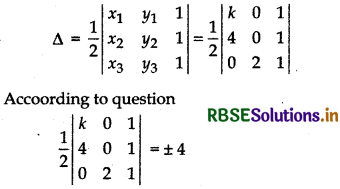
Expanding along C₂
⇒ \(\frac{1}{2}\) {- 2(k - 4)} = ± 4
Taking positive sign
- (k - 4) = 4 ⇒ k = 0
Taking negative sign
- (k - 4) = - 4 ⇒ k = 8
Thus, k = 0 or k = 8

(ii) (- 2, 0), (0, 4), (0, k)
Answer:

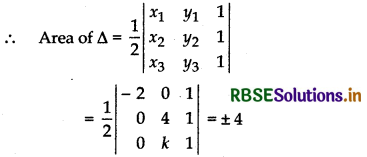
Expanding along C1
\(\frac{1}{2}\) {- 2(4 - k)} = ±4 ⇒ - (4 - k) = ± 4
Taking positive sign
- (4 - k) = 4 ⇒ k = 0
Taking negative sign
- (4 - k) = - 4 ⇒ k = 8
Thus, k = 8 or k = 0

Question 4.
Using determinants find the equation of line joining the points
(i) (1, 2) and (3, 6)
Answer:
(1, 2) and (3, 6) are given points.
Let (x, y) be any point on line joining the points (1, 2) and (3, 6). Thus, point (1, 2), (3, 6) and (x, y) are collinear so area of triangle so formed will be zero.

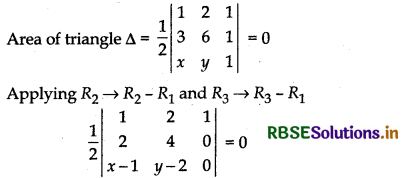
Expanding along C₃
⇒ 2(y - 2) - (x - 1) × 4 = 0
⇒ 2y - 4 - 4x + 4 = 0
⇒ 2y - 4x = 0
⇒ y - 2x = 0
⇒ y = 2x
which is required equation of line.

(ii) (3, 1) and (9, 3)
Answer:
Given points are (3, 1) and (9, 3)
Let (x, y) be any point on line joining the points (3, 1) and (9, 3) then points (3, 1), (9, 3) and (x, y) will be collinear.
So area of triangle so formed will be zero. Thus

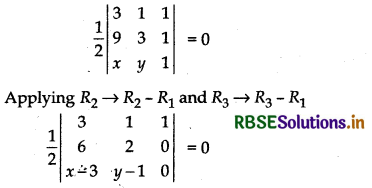
Expanding along C₃
⇒ 1{6 × (y - 1) - (x - 3) × 2} = 0
⇒ 6y - 6 - 2x + 6 = 0
⇒ 6y - 2x = 0
⇒ 3y - x = 0
⇒ x - 3y = 0
⇒ x = 3y
which is required equation of line.

Question 5.
If (2, - 6), (5, 4) and (k, 4) are vertices of a triangle whose area is 35 sq. units, then the value of k is:
(A) 12
(B) - 2
(C) - 12, - 2
(D) 12, - 2
Answer:
(2, - 6), (5, 4) and (k, 4) are vertices.
Here x₁ = 2, x₂ = 5, x₃ = k, y₃ = - 6, y₂ = 4, y₃ = 4
Given that, area of triangle is 35 sq. units.

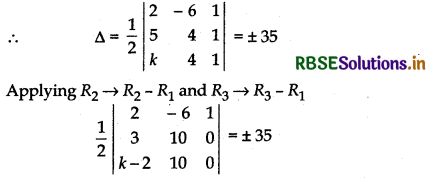
Expanding along C₃
⇒ {3 × 10 - (k - 2) × 10} = ± 70
⇒ 30 - 10k + 20 = ± 70
⇒ 50 - 10k = ± 70
Take positive sign
50 - 10k = 70 ⇒ k = - 2
Taking negative sign
50 - 10k = - 70 ⇒ k = 12
Thus k = - 2 or k = 12
Thus (D) is correct.