RBSE Solutions for Class 12 Maths Chapter 3 आव्यूह Ex 3.2

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 3 आव्यूह Ex 3.2 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 3 आव्यूह Ex 3.2

प्रश्न 1.
मान लीजिए कि A = \(\left[\begin{array}{ll} 2 & 4 \\ 3 & 2 \end{array}\right]\), B = \(\left[\begin{array}{cc} 1 & 3 \\ -2 & 5 \end{array}\right]\), C = \(\left[\begin{array}{cc} -2 & 5 \\ 3 & 4 \end{array}\right]\), तो निम्नलिखित ज्ञात कीजिए:
(i) A + B
हल:

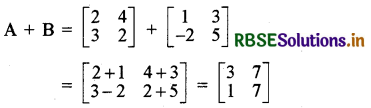
(ii) A - B
हल:

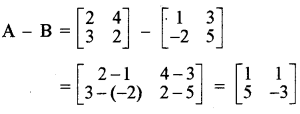
(iii) 3A - C
हल:

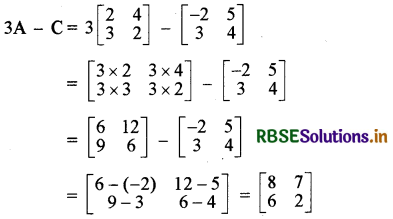
(iv) AB
हल:

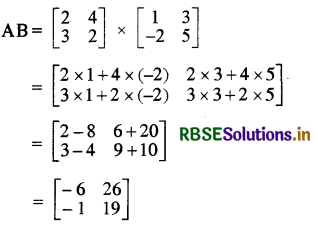
(v) BA
हल:

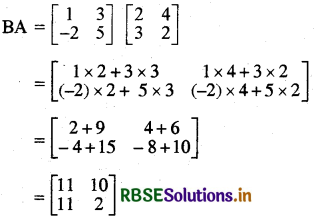
प्रश्न 2.
निम्नलिखित को परिकलित कीजिए:
(i) \(\left[\begin{array}{cc} a & b \\ -b & a \end{array}\right]+\left[\begin{array}{ll} a & b \\ b & a \end{array}\right]\)
हल:

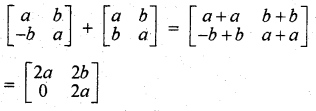
(ii) \(\left[\begin{array}{ll} a^2+b^2 & b^2+c^2 \\ a^2+c^2 & a^2+b^2 \end{array}\right]+\left[\begin{array}{cc} 2 a b & 2 b c \\ -2 a c & -2 a b \end{array}\right]\)
हल:

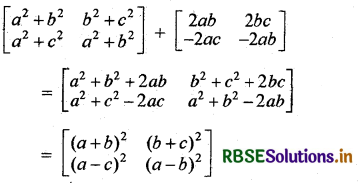
(iii) \(\left[\begin{array}{ccc} -1 & 4 & -6 \\ 8 & 5 & 16 \\ 2 & 8 & 5 \end{array}\right]+\left[\begin{array}{ccc} 12 & 7 & 6 \\ 8 & 0 & 5 \\ 3 & 2 & 4 \end{array}\right]\)
हल:

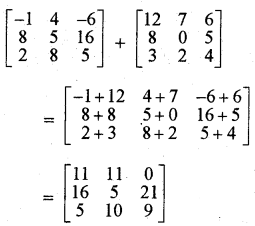
(iv) \(\left[\begin{array}{cc} \cos ^2 x & \sin ^2 x \\ \sin ^2 x & \cos ^2 x \end{array}\right]+\left[\begin{array}{ll} \sin ^2 x & \cos ^2 x \\ \cos ^2 x & \sin ^2 x \end{array}\right]\)
हल:

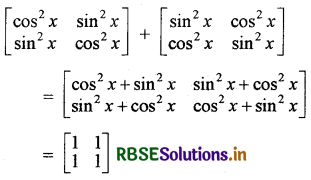
प्रश्न 3.
निदर्शित गुणनफल परिकलित कीजिए:
(i) \(\left[\begin{array}{cc} a & b \\ -b & a \end{array}\right]\left[\begin{array}{cc} a & -b \\ b & a \end{array}\right]\)
हल:

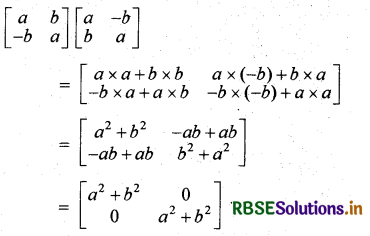
(ii) \(\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right]\) [2 3 4]
हल:

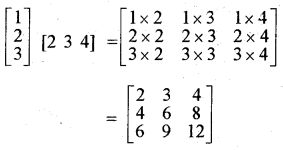
(iii) \(\left[\begin{array}{cc} 1 & -2 \\ 2 & 3 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 3 \\ 2 & 3 & 1 \end{array}\right]\)
हल:

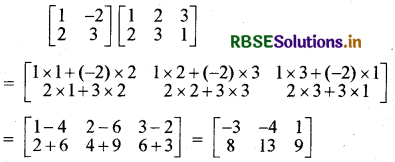
(iv) \(\left[\begin{array}{lll} 2 & 3 & 4 \\ 3 & 4 & 5 \\ 4 & 5 & 6 \end{array}\right]\left[\begin{array}{ccc} 1 & -3 & 5 \\ 0 & 2 & 4 \\ 3 & 0 & 5 \end{array}\right]\)
हल:

(v) \(\left[\begin{array}{cc} 2 & 1 \\ 3 & 2 \\ -1 & 1 \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 1 \\ -1 & 2 & 1 \end{array}\right]\)
हल:

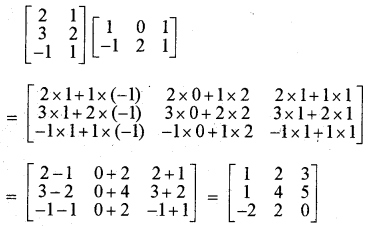
(vi) \(\left[\begin{array}{ccc} 3 & -1 & 3 \\ -1 & 0 & 2 \end{array}\right]\left[\begin{array}{cc} 2 & -3 \\ 1 & 0 \\ 3 & 1 \end{array}\right]\)
हल:

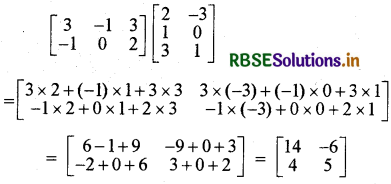
प्रश्न 4.
यदि A = \(\left[\begin{array}{ccc} 1 & 2 & -3 \\ 5 & 0 & 2 \\ 1 & -1 & 1 \end{array}\right]\), B = \(\left[\begin{array}{ccc} 3 & -1 & 2 \\ 4 & 2 & 5 \\ 2 & 0 & 3 \end{array}\right]\) C = \(\left[\begin{array}{ccc} 4 & 1 & 2 \\ 0 & 3 & 2 \\ 1 & -2 & 3 \end{array}\right]\) तो (A + B) तथा (B - C) परिकलित कीजिए। साथ ही सत्यापित कीजिए कि A + (B - C) = (A + B) – C.

(i) A = \(\left[\begin{array}{ccc} 1 & 2 & -3 \\ 5 & 0 & 2 \\ 1 & -1 & 1 \end{array}\right]\), B = \(\left[\begin{array}{ccc} 3 & -1 & 2 \\ 4 & 2 & 5 \\ 2 & 0 & 3 \end{array}\right]\)
हल:

(ii) B = \(\left[\begin{array}{ccc} 3 & -1 & 2 \\ 4 & 2 & 5 \\ 2 & 0 & 3 \end{array}\right]\) , C = \(\left[\begin{array}{ccc} 4 & 1 & 2 \\ 0 & 3 & 2 \\ 1 & -2 & 3 \end{array}\right]\)
हल:

(iii)

प्रश्न 5.
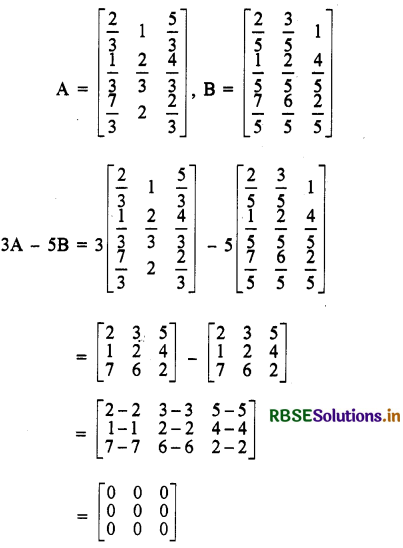
यदि A = \(\left[\begin{array}{ccc} \frac{2}{3} & 1 & \frac{5}{3} \\ \frac{1}{3} & \frac{2}{3} & \frac{4}{3} \\ \frac{7}{3} & 2 & \frac{2}{3} \end{array}\right]\) तथा B = \(\left[\begin{array}{ccc} \frac{2}{5} & \frac{3}{5} & 1 \\ \frac{1}{5} & \frac{2}{5} & \frac{4}{5} \\ \frac{7}{5} & \frac{6}{5} & \frac{2}{5} \end{array}\right]\), तो 3A - 5B परिकलित कीजिए।
हल:
प्रश्नानुसार

प्रश्न 6.
सरल कीजिए
cos θ \(\left[\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\) + sin θ \(\left[\begin{array}{cc} \sin \theta & -\cos \theta \\ \cos \theta & \sin \theta \end{array}\right]\)
हल:
प्रश्नानुसार

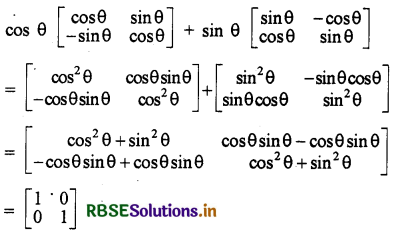
प्रश्न 7.
X तथा Y ज्ञात कीजिए यदि
(i) X + Y = \(\left[\begin{array}{ll} 7 & 0 \\ 2 & 5 \end{array}\right]\) तथा X - Y = \(\left[\begin{array}{ll} 3 & 0 \\ 0 & 3 \end{array}\right]\)
हल:

(ii) 2X + 3Y = \(\left[\begin{array}{ll} 2 & 3 \\ 4 & 0 \end{array}\right]\) तथा 3x + 2x = \(\left[\begin{array}{ll} 2 & - 2 \\ - 1 & 5 \end{array}\right]\)
हल:
मान लीजिए \(\left[\begin{array}{ll} 2 & 3 \\ 4 & 0 \end{array}\right]\) = P, \(\left[\begin{array}{cc} 2 & -2 \\ -1 & 5 \end{array}\right]\) = Q
अतः 2x + 3Y = P ........... (1)
3x + 2Y = Q ........... (2)
(1) को 2 से तथा (2) को 3 से गुणा करने पर
4X + 6Y = 2P ........... (3)
9X + 6Y = 3Q ........... (4)
(4) में से (3) घटाने पर
9X - 4X = 30 - 2P
⇒ 5X = 30 - 2P

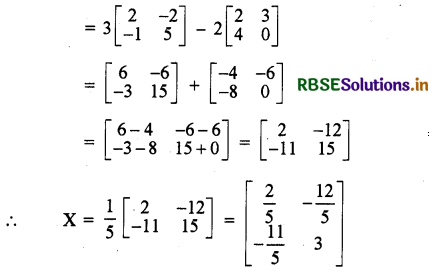
अब समीकरण (1) से
3Y = P - 2x

प्रश्न 8.
x ज्ञात कीजिए यदि Y = \(\left[\begin{array}{ll} 3 & 2 \\ 1 & 4 \end{array}\right]\) तथा 2x + Y = \(\left[\begin{array}{cc} 1 & 0 \\ -3 & 2 \end{array}\right]\)
हल:
हमें दिया है

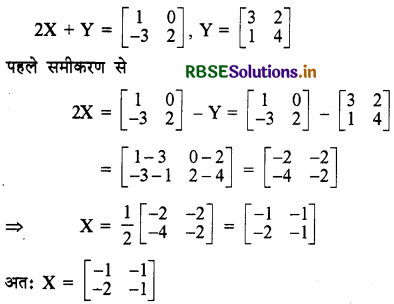
प्रश्न 9.
तथा ज्ञात कीजिए यदि 2\(\left[\begin{array}{ll} 1 & 3 \\ 0 & x \end{array}\right]\)+\(\left[\begin{array}{ll} y & 0 \\ 1 & 2 \end{array}\right]\)=\(\left[\begin{array}{ll} 5 & 6 \\ 1 & 8 \end{array}\right]\)
हल:

⇒ 2 + y = 5 ∴ y = 5 - 2 = 3
⇒ 2x + 2 = 8 ∴ 2x = 8 - 2 = 6
∴ x = 3
अतः x = 3, y = 3

प्रश्न 10.
प्रदत्त समीकरण को x, y, z तथा t के लिए हल कीजिए यदि
\(2\left[\begin{array}{ll} x & z \\ y & t \end{array}\right]+3\left[\begin{array}{cc} 1 & -1 \\ 0 & 2 \end{array}\right]=3\left[\begin{array}{ll} 3 & 5 \\ 4 & 6 \end{array}\right]\)
हल:
प्रश्नानुसार

2x = 6 ∴ x = 3
2y = 12 ∴ y = 6
2z = 18 ∴ z = 9
2t = 12 ∴ t = 6
अतः x = 3, y = 6, z = 9, t = 6

प्रश्न 11.
यदि x\(\left[\begin{array}{l} 2 \\ 3 \end{array}\right]\)+y\(\left[\begin{array}{c} -1 \\ 1 \end{array}\right]\)=\(\left[\begin{array}{c} 10 \\ 5 \end{array}\right]\) है तो x तथा y के मान ज्ञात कीजिए।
हल:
प्रश्नानुसार

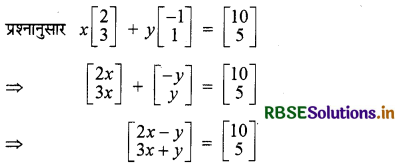
⇒ 2x - y = 10 ............ (1)
3x + y = 5 ........... (2)
(1) और (2) को जोड़ने पर
5x = 15 ⇒ x = \(\frac{15}{5}\) = 3
x का मान (1) में रखने पर
6 - y = 10
∴ y = 6 - 10 = - 4
आत: x = 3, y = - 4

प्रश्न 12.
यदि 3\(\left[\begin{array}{ll} x & y \\ z & w \end{array}\right]\)=\(\left[\begin{array}{cc} x & 6 \\ -1 & 2 w \end{array}\right]\)+\(\left[\begin{array}{cc} 4 & x+y \\ z+w & 3 \end{array}\right]\) है तो x, y, z तथा w के मानों को ज्ञात कीजिए।
हल:

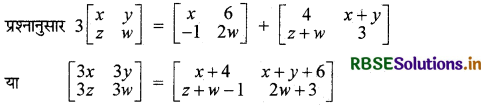
3x = x + 4 या 2x = 4 ∴ x = 2
3y = x + y + 6 या 2y = x + 6 = 2 + 6 = 8
∴ y = 4 (x का मान रखने पर)
3w = 2w + 3 या w = 3
3z = z + w - 1
या 2z = w - 1 = 3 - 1 = 2 (w का मान रखने पर)।
∴ z = 1
अतः x = 2, y = 4, z = 1, w = 3.

प्रश्न 13.
यदि F(x) = \(\left[\begin{array}{ccc} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{array}\right]\) है, तो सिद्ध कीजिए कि
F(x) F(y) = F (x + y)
हल:

(1) व (2) से
F(x) F(y) = F(x + y)

प्रश्न 14.
दर्शाइए कि
(i) \(\left[\begin{array}{cc} 5 & -1 \\ 6 & 7 \end{array}\right]\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right] \neq\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right]\left[\begin{array}{cc} 5 & -1 \\ 6 & 7 \end{array}\right]\)
हल:

(ii)
\(\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]\left[\begin{array}{ccc} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right] \neq\left[\begin{array}{ccc} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]\)
हल:
सिद्ध करना है।

प्रश्न 15.
यदि A = \(\left[\begin{array}{ccc} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{array}\right]\) है तो A² - 5A + 6I का मान ज्ञात कीजिए।
हल:

प्रश्न 16.
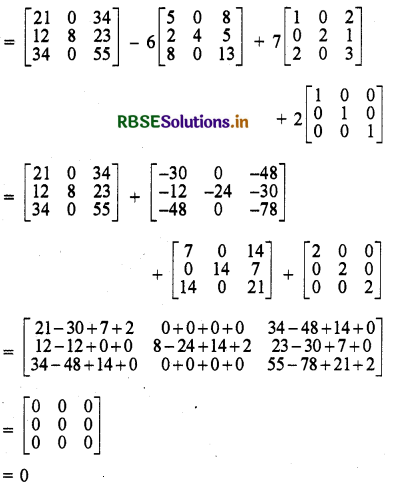
यदि A = \(\left[\begin{array}{lll} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{array}\right]\) है तो सिद्ध कीजिए कि A³ - 6A² + 7A + 2I = 0
Answer:

बायाँ पक्ष = A³ - 6A² + 7A + 2I में A³, A², A, I का मान रखने पर

प्रश्न 17.
यदि A = \(\left[\begin{array}{ll} 3 & -2 \\ 4 & -2 \end{array}\right]\) तथा I = \(\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\) एवं A² = kA - 2I हो तो k ज्ञात कीजिए।
हल:

संगत अवयवों को समान रखने पर
1 = 3k - 2
- 2 = - 2k,
4 = 4k,
- 4 = - 2k - 2,
इन सभी समीकरणों से k = 1 प्राप्त होता है।
⇒ k = 1

प्रश्न 18.
यदि A = \(\left[\begin{array}{cc} 0 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 0 \end{array}\right]\) तथा I कोटि 2 का एक तत्समक आव्यूह है तो सिद्ध कीजिए कि I + A = (I - A) \(\left[\begin{array}{cc} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]\)
हल:
सिद्ध करना है I + A = (I - A) \(\left[\begin{array}{cc} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]\)

अन्य विधि:

प्रश्न 19.
किसी व्यापार संघ के पास 30,000 रुपयों का कोष है जिसे दो भिन्न-भिन्न प्रकार के बाण्डों में निवेश करना है। प्रथम बाण्ड पर 5% वार्षिक तथा द्वितीय बाण्ड पर 7% वार्षिक ब्याज प्राप्त होता है। आव्यूह गुणन के प्रयोग द्वारा यह निर्धारित कीजिए कि 30,000 रुपयों के कोष को दो प्रकार के बाण्डों में निवेश करने के लिए किस प्रकार बाँटें जिससे. व्यापार संघ को प्राप्त कुल वार्षिक ब्याज
(a) Rs. 1,800 हो
(b) Rs. 2,000 हो।
हल:
(a) मान लीजिए 30,000 रु. के दो भाग x रु. तथा (30,000 - x) रु. हैं।
इसे आव्यूह A = [x (30,000 - x)] से व्यक्त कर सकते हैं।
ब्याज दरें 5% वार्षिक अर्थात् 0.05 वार्षिक एवं 7% वार्षिक अर्थात् 0.07 वार्षिक है।
इसे R = \(\left[\begin{array}{l} 0.05 \\ 0.07 \end{array}\right]\) से व्यक्त करेंगे।
कुल ब्याज = AR = [x (30,000 - x)] \(\left[\begin{array}{l} 0.05 \\ 0.07 \end{array}\right]\)
= [1,800] (दिया है)
⇒ [x (30,000 - x)] \(\left[\begin{array}{l} 0.05 \\ 0.07 \end{array}\right]\) = [1,800]
[x × 0.05 + (30,000 - x) × 0.07] = [1,800]
[0.05x + 0.07 (30,000 - x)] = [1,800]
2,100 - (0.07 - 0.05) x = 1,800
∴ 0.02 x = 2,100 - 1,800 = 300
x = \(\frac{300}{0.02}\) = \(\frac{30,000}{2}\) = 15,000 रु.
∴ 30,000 - x = 30,000 - 15,000
= 15,000 रु.
अतः 1800 रु. ब्याज पाने के लिए प्रत्येक बाण्ड 15,000 रु. के खरीदने चाहिए।

(b) 2000 रु. ब्याज पाने के लिए समीकरण हैं :
[x (30,000 - x)] \(\left[\begin{array}{l} 0.05 \\ 0.07 \end{array}\right]\) = [2000]
या 0.05 x + 0.07 (30,000 – r) = 2000
या (0.05 - 0.07) x + 2100 = 2000
या - 0.02 x + 2100 = 2000
या 0.02 x = 2100 - 2000 = 100
∴ x = \(\frac{100}{0.02}\) = \(\frac{10,000}{2}\)
= 5,000
2000 रु. ब्याज पाने के लिए 30,000 रु. के दो भाग 5,000 रु. व 25,000 रु. करने होंगे।

प्रश्न 20.
किसी स्कूल की पुस्तकों की दुकान में 10 दर्जन रसायन विज्ञान, 8 दर्जन भौतिक विज्ञान तथा 10 दर्जन अर्थशास्त्र की पुस्तकें हैं। इन पुस्तकों का विक्रय मूल्य क्रमश रु. 80, रु. 60 तथा रु. 40 प्रति पुस्तक है। आव्यूह बीजगणित के प्रयोग द्वारा ज्ञात कीजिए कि सभी पुस्तकों को बेचने से दुकान को कुल कितनी धनराशि प्राप्त होगी?
हल:
विद्यालय में पुस्तकों की संख्या इस प्रकार है:
रसायन विज्ञान : 10 दर्जन = 120 पुस्तकें
भौतिक विज्ञान : 8 दर्जन = 96 पुस्तकें
अर्थशास्त्र : 10 दर्जन = 120 पुस्तकें
इसे आव्यूह A से निम्नानुसार व्यक्त करेंगे:
A = [120 96 120]
रसायन विज्ञान, भौतिक विज्ञान व अर्थशास्त्र की प्रत्येक पुस्तक का मूल्य क्रमशः 80 रु., 60 रु. और 40 रु. है।
इस तथ्य को आव्यूह R से निम्नानुसार व्यक्त करेंगे :
R = \(\left[\begin{array}{l} 80 \\ 60 \\ 40 \end{array}\right]\)
60
सभी पुस्तकें बेचने पर प्राप्त राशि
AR = [120 96 120] \(\left[\begin{array}{l} 80 \\ 60 \\ 40 \end{array}\right]\)
= [120 × 80 + 96 × 60 + 120 × 40]
= [9600 + 5760 + 4800] = [20160]
कुल प्राप्त राशि = Rs. 20160.
मान लीजिए कि X, Y, Z, W तथा P क्रमशः 2 × n, 3 × k, 2 × p, n × 3, p × k, कोटियों के आव्यूह हैं।
नीचे दिए प्रश्न 21 तथा 22 में सही उत्तर चुनिए

प्रश्न 21.
PY + WY के परिभाषित होने के लिए n, k तथा p पर क्या प्रतिबन्ध होगा?
(A) k = 3, p = n
(B) k स्वेच्छ है, p = 2.
(C) p स्वेच्छ है, k = 3
(D) k = 2, p = 3
उत्तर:
(A) k = 3, p = n

हल:
दिया गया है कि
आव्यूह P की कोटि = p × k
आव्यूह Y की कोटि = 3 × k
आव्यूह W की कोटि = n × 3
आव्यूह PY परिभाषित होने के लिए P के स्तम्भों की संख्या = Y की पंक्तियों की संख्या
∴ k = 3
इसी तरह से WY परिभाषित होने के लिए
w के स्तम्भों की संख्या = Y की पंक्तियों की संख्या अर्थात् ।
3 = 3
अब PY + WY परिभाषित होने के लिए
PY की कोटि = p × k = p × 3
तब WY की कोटि = n × k
अतः PY + WY परिभाषित होने के लिए PY तथा WY की कोटि समान होनी चाहिये।
∴ p = n तथा k = 3
अतः सही विकल्प (A) है।

प्रश्न 22.
यदि n = p, तो आव्यूह 7X - 5Z की कोटि है-
(A) p × 2
(B) 2 × n
(C) n × 3
(D) p × n
उत्तर:
(B)

हल:
X की कोटि = 2 × n
z की कोटि = 2 × p
∵ p = n
अतः 7X - 5Z की कोटि 2 × n है।
अतः सही विकल्प (B) है।