RBSE Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.2

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.2 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 3 Matrices Ex 3.2

Question 1.
Let
A = \(\left[\begin{array}{ll} 2 & 4 \\ 3 & 2 \end{array}\right],\) B = \(\left[\begin{array}{rr} 1 & 3 \\ -2 & 5 \end{array}\right]\), C = \(\left[\begin{array}{rr} -2 & 5 \\ 3 & 4 \end{array}\right]\)
Find each of the following:
(i) A + B
Answer:

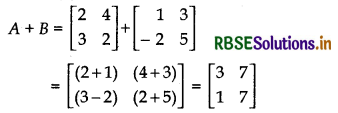
(ii) A - B
Answer:

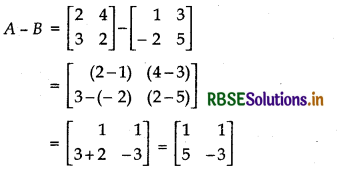
(iii) 3A - C
Answer:

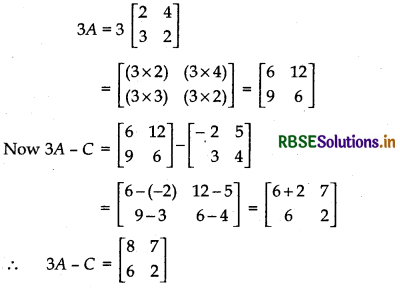
(iv) AB
Answer:

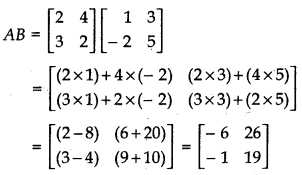
(v) BA
Answer:

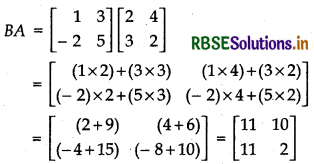
Question 2.
Compute the following:
(i) \(\left[\begin{array}{rr} a & b \\ -b & a \end{array}\right]\) + \(\left[\begin{array}{ll} a & b \\ b & a \end{array}\right]\)
Answer:

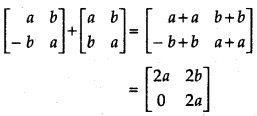
(ii) \(\left[\begin{array}{ll} a^{2}+b^{2} & b^{2}+c^{2} \\ a^{2}+c^{2} & a^{2}+b^{2} \end{array}\right]+\left[\begin{array}{rr} 2 a b & 2 b c \\ -2 a c & -2 a b \end{array}\right]\)
Answer:

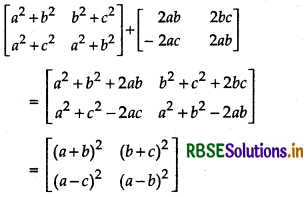
(iii) \(\left[\begin{array}{rrr} -1 & 4 & -6 \\ 8 & 5 & 16 \\ 2 & 8 & 5 \end{array}\right]+\left[\begin{array}{ccr} 12 & 7 & 6 \\ 8 & 0 & 5 \\ 3 & 2 & 4 \end{array}\right]\)
Answer:

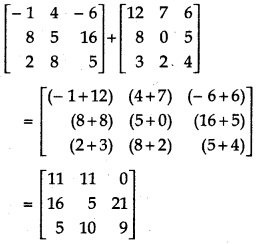
(iv) \(\left[\begin{array}{cc} \cos ^{2} x & \sin ^{2} x \\ \sin ^{2} x & \cos ^{2} x \end{array}\right]+\left[\begin{array}{ll} \sin ^{2} x & \cos ^{2} x \\ \cos ^{2} x & \sin ^{2} x \end{array}\right]\)
Answer:

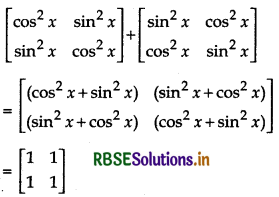
Question 3.
Compute the indicated products:
(i) \(\left[\begin{array}{rr} a & b \\ -b & a \end{array}\right]\left[\begin{array}{rr} a & -b \\ b & a \end{array}\right]\)
Answer:

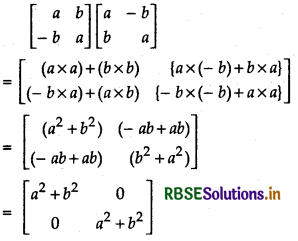
(ii) \(\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right]\left[\begin{array}{lll} 2 & 3 & 4 \end{array}\right]\)
Answer:

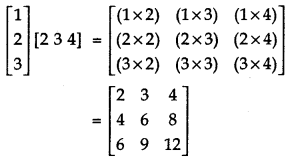
(iii) \(\left[\begin{array}{rr} 1 & -2 \\ 2 & 3 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 3 \\ 2 & 3 & 1 \end{array}\right]\)
Answer:

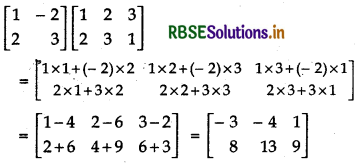
(iv) \(\left[\begin{array}{lll} 2 & 3 & 4 \\ 3 & 4 & 5 \\ 4 & 5 & 6 \end{array}\right]\left[\begin{array}{rrr} 1 & -3 & 5 \\ 0 & 2 & 4 \\ 3 & 0 & 5 \end{array}\right]\)
Answer:

(v) \(\left[\begin{array}{rr} 2 & 1 \\ 3 & 2 \\ -1 & 1 \end{array}\right]\left[\begin{array}{rrr} 1 & 0 & 1 \\ -1 & 2 & 1 \end{array}\right]\)
Answer:

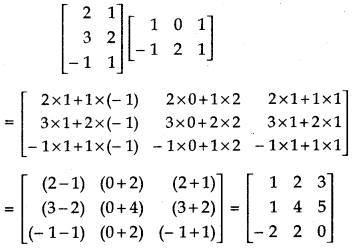
(vi) \(\left[\begin{array}{rrr} 3 & -1 & 3 \\ -1 & 0 & 2 \end{array}\right]\left[\begin{array}{rr} 2 & -3 \\ 1 & 0 \\ 3 & 1 \end{array}\right]\)
Answer:

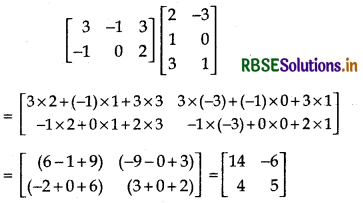
Question 4.
If A = \(\left[\begin{array}{rrr} 1 & 2 & -3 \\ 5 & 0 & 2 \\ 1 & -1 & 1 \end{array}\right]\), B = \(\left[\begin{array}{rrr} 3 & -1 & 2 \\ 4 & 2 & 5 \\ 2 & 0 & 3 \end{array}\right]\) and C = \(\left[\begin{array}{rrr} 4 & 1 & 2 \\ 0 & 3 & 2 \\ 1 & -2 & 3 \end{array}\right]\), then compute (A + B) and (B - C). Also verify that A + (B - C) = (A + B) - C.
Answer:

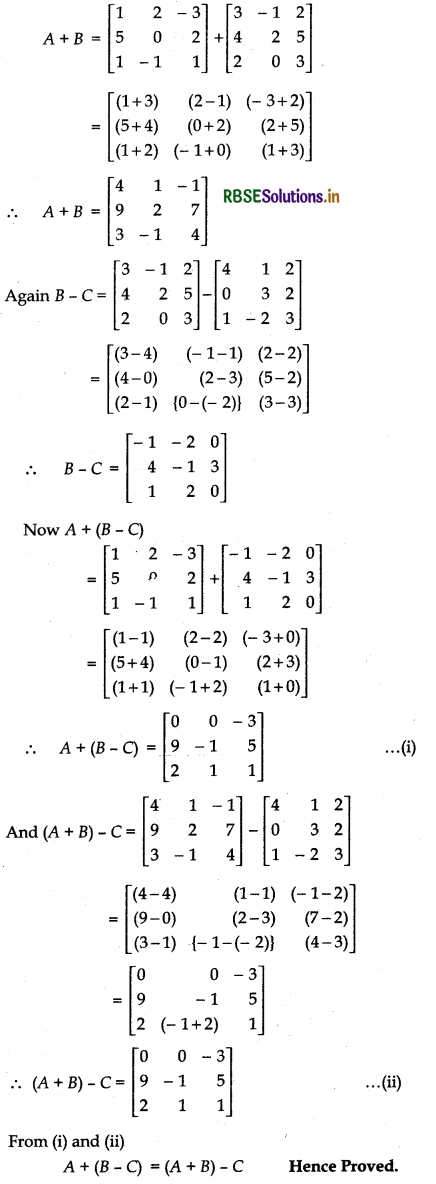
Question 5.
If A = \(\left[\begin{array}{ccc} \frac{2}{3} & 1 & \frac{5}{3} \\ \frac{1}{3} & \frac{2}{3} & \frac{4}{3} \\ \frac{7}{3} & 2 & \frac{2}{3} \end{array}\right]\) and B = \(\left[\begin{array}{ccc} \frac{2}{5} & \frac{3}{5} & 1 \\ \frac{1}{5} & \frac{2}{5} & \frac{4}{5} \\ \frac{7}{5} & \frac{6}{5} & \frac{2}{5} \end{array}\right]\) then compute 3A - 5B.
Answer:

Question 6.
Simplify:
cos θ \(\left[\begin{array}{rr} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\) + sin θ \(\left[\begin{array}{rr} \sin \theta & -\cos \theta \\ \cos \theta & \sin \theta \end{array}\right]\)
Answer:

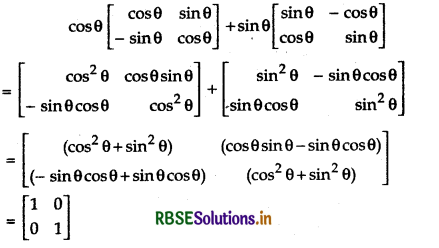
Question 7.
(i) X + Y = \(\left[\begin{array}{ll} 7 & 0 \\ 2 & 5 \end{array}\right]\) and X - Y = \(\left[\begin{array}{ll} 3 & 0 \\ 0 & 3 \end{array}\right]\)
Answer:

(ii) 2X + 3Y = \(\left[\begin{array}{ll} 2 & 3 \\ 4 & 0 \end{array}\right]\) and 3X + 2Y = \(\left[\begin{array}{rr} 2 & -2 \\ -1 & 5 \end{array}\right]\)
Answer:

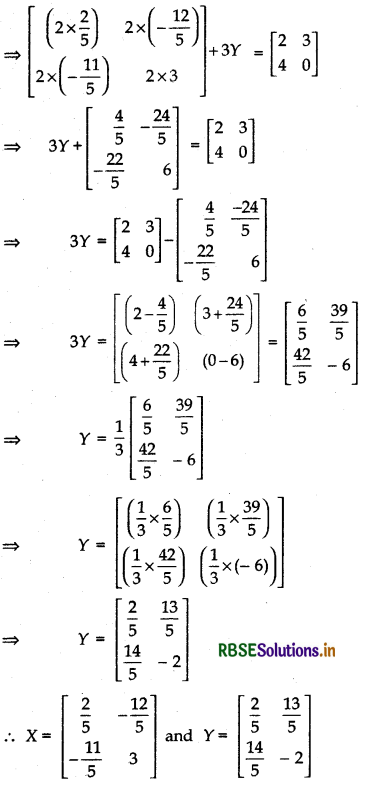
Question 8.
Find X if Y = \(\left[\begin{array}{ll} 3 & 2 \\ 1 & 4 \end{array}\right]\) and 2X + Y = \(\left[\begin{array}{rr} 1 & 0 \\ -3 & 2 \end{array}\right]\).
Answer:

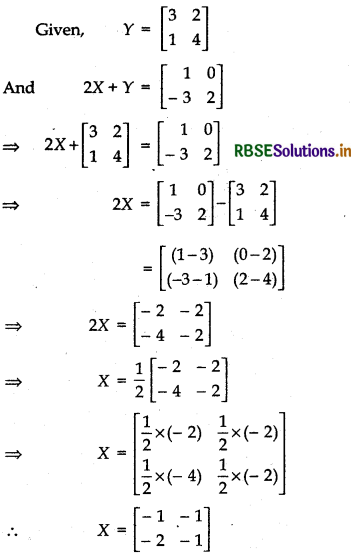
Question 9.
Find x and y if
2\(\left[\begin{array}{ll} 1 & 3 \\ 0 & x \end{array}\right]+\left[\begin{array}{ll} y & 0 \\ 1 & 2 \end{array}\right]=\left[\begin{array}{ll} 5 & 6 \\ 1 & 8 \end{array}\right]\)
Answer:

Comparing corresponding elements, we get
2 + y = 5,
⇒ y = 5 - 2,
⇒ y = 3,
∴ y = 3,

2x + 2 = 8
⇒ 2x = 8 - 2
⇒ 2x = 6
∴ x = 3

Question 10.
Solve the equation for x, y, z and t, if
2\(\left[\begin{array}{ll} x & z \\ y & t \end{array}\right]+3\left[\begin{array}{rr} 1 & -1 \\ 0 & 2 \end{array}\right]=3\left[\begin{array}{ll} 3 & 5 \\ 4 & 6 \end{array}\right]\)
Answer:

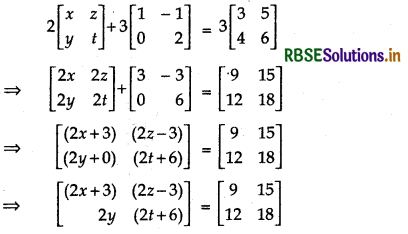
Comparing corresponding elements, we get
2x + 3 = 9, 2z - 3 = 15, 2y = 12, 2t + 6 = 18
⇒ 2x = 9 - 3, 2z = 15 + 3, y = \(\frac{12}{2}\), 2t = 18 - 6
⇒ 2x = 6, 2z = 18, y = 6, 2t = 12
∴ x = 3, z = 9, y = 6, t = 6

Question 11.
If x\(\left[\begin{array}{l} 2 \\ 3 \end{array}\right] \)+ y\(\left[\begin{array}{r} -1 \\ 1 \end{array}\right]\) = \(\left[\begin{array}{c} 10 \\ 5 \end{array}\right]\), then find the values of x and y.
Answer:

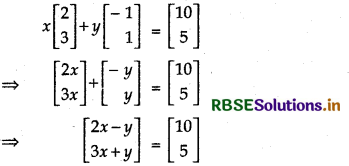
⇒ 2x - y = 10 ........ (i)
3x + y = 5 .......... (ii)
Adding equation (i) and (ii), we get

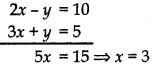
Putting value of x in euqation (i), we get
2 × 3 - y = 10 ⇒ 6 - y = 10
⇒ - y = 10 - 6 ⇒ y = 4
⇒ y = - 4
Thus, x = 3, y = - 4

Question 12.
Given
3\(\left[\begin{array}{cc} x & y \\ z & w \end{array}\right]=\left[\begin{array}{cc} x & 6 \\ -1 & 2 w \end{array}\right]+\left[\begin{array}{cc} 4 & x+y \\ z+w & 3 \end{array}\right]\)
find the value of x, y, z and w.
Answer:

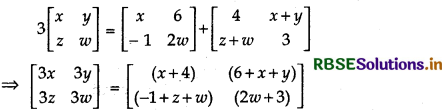
Comparing corresponding elements, we get
3x = x + 4,
3z = - 1 + z + w,
⇒ 3x - x = 4
⇒ 2x = 4,
3z - z = w - 1,
2z = w - 1,

3y = 6 + x + y
3w = 2w + 3
3y - y = 6 + x
2y = 6 + x
3w - 2w = 3
w = 3

∴ x = 2,
2y = 6 + 2, ⇒ 2y = 8,
y = 4

And w = 3, then 2z = w - 1
⇒ 2z = 3 - 1
⇒ 2z = 2
∴ z = 1
Thus, x = 2, y = 4, z = 1, w = 3

Question 13.
If F(x) = \(\left[\begin{array}{ccc} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{array}\right]\), show that F(x) F(y) = F(x + y).
Answer:

Question 14.
Show that
(i) \(\left[\begin{array}{rr} 5 & -1 \\ 6 & 7 \end{array}\right]\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right] \neq\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right]\left[\begin{array}{rr} 5 & -1 \\ 6 & 7 \end{array}\right]\)
Answer:

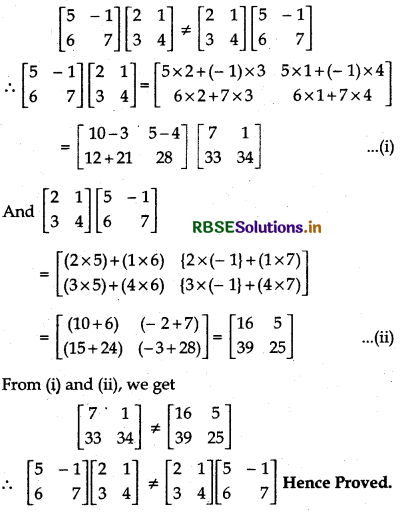
(ii)
\(\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]\) ≠ \(\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]\)
Answer:

Question 15.
If A = \(\left[\begin{array}{rrr} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{array}\right]\), then find the value of A² - 5A + 6I
Answer:
Here, A² = AA

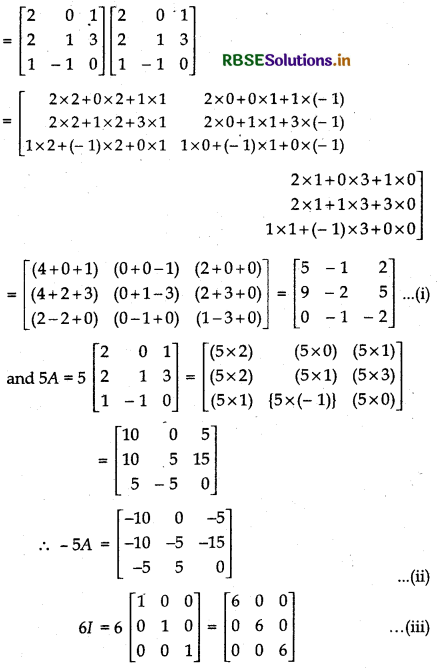
Question 16.
If A = \(\left[\begin{array}{lll} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{array}\right]\), then prove that:
A³ - 6A² + 7A + 2I = 0
Answer:

Question 17.
If A = \(\left[\begin{array}{ll} 3 & -2 \\ 4 & -2 \end{array}\right]\) and I = \(\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\) and A² = KA - 2I, then find k.
Answer:

⇒ 1 = 3k - 2, - 2 = - 2k
4 = 4k, - 4 = - 2k - 2
⇒ 3k = 2 + 1, 2k = 2
4k = 4, - 2k = - 4 + 2
⇒ 3k = 3, 2k = 2
4k = 4, - 2k = - 2
⇒ k = 1, k = 1

Question 18.
If \(\left[\begin{array}{cc} 0 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 0 \end{array}\right]\) and I is the identity matrix of order 2, show that I + A = (I - A)\(\left[\begin{array}{rr} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]\)
Answer:

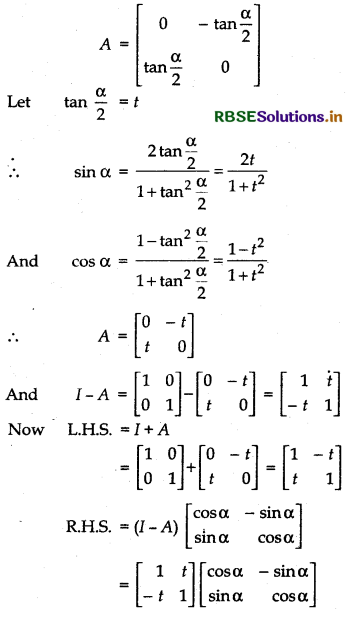
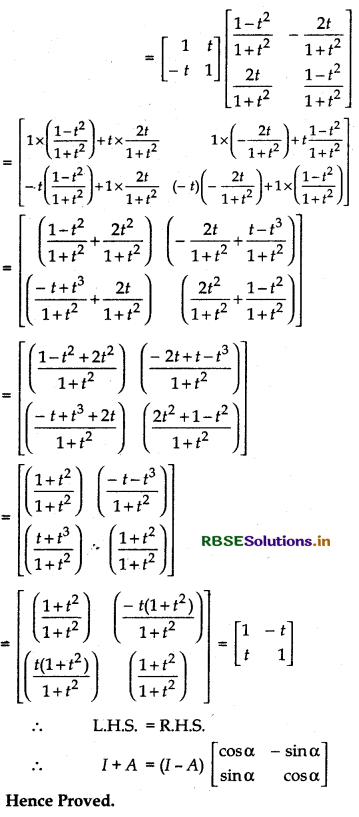
Question 19.
A trust fund has ₹ 30,000 that must be invested in two different types of bonds. The first bond pays 5% interest per year and the second bond pays 7% interest per year. Using matrix multiplication determine how to divide ₹ 30,000 among the two types of bonds. If the trust fund must obtain an annual total interest of:
(a) ₹ 1,800
(b) ₹ 2,000
Answer:
Let x and (30000 - x) are two parts of ₹ 30,000.
Then matrix A = [x (30000 - x)]
Rate of interest are 5% and 7% or 0.05 and 0.07
Let matrix of rate R = \(\left[\begin{array}{l} 0.05 \\ 0.07 \end{array}\right]\)

(a) We have, total interest = ₹ 1800
= [x (30000 - x)] \(\left[\begin{array}{l} 0.05 \\ 0.07 \end{array}\right]\) = [1800]
⇒ [x × 0.05 + (30000 - x) × 0.07] - [1800]
⇒ [0.05x + (30000 × 0.07) - 0 07 × x] = [1800]
⇒ 0.05x + 2100 - 0.07× = 1800
⇒ 0.05x - 0.07x = 1800 - 2100
⇒ - 0.02x = - 300
⇒ x = \(\frac{-300}{-0.02}\) = \(\frac{30000}{2}\) = 15000
First bond = ₹ 15,000
Now 30000 - x = 30000 -15000
∴ Second bond = ₹ 15,000
Thus, each bond should be bought for ₹ 15,000 so that interest of ₹ 1800 is received.

(b) For interest ₹ 2,000, matrix equation will be of the following type
[x (3000 - x)] \(\left[\begin{array}{l} 0.05 \\ 0.07 \end{array}\right]\) = [2000]
⇒ [x × 0.05 + (30000 - x) × 0.07] = [2000]
⇒ [0.05x + (30000 × 0.07) - (x × 0.07]) = [2000]
⇒ 0.05x + 2100.00 - 0.07x = 2000
⇒ 0.05x - 0.07x = 2000 - 2100
⇒ - 0.02x = - 100
⇒ x = \(\frac{-100}{-0.02}\) = \(\frac{10000}{2}\) = 5000
∴ First bond = ₹ 5,000
Thus 30000 - x = 30000 - 5000 = 25000
∴ Second bond = ₹ 25,000
To get ₹ 2,000 as interest two bonds should be divided into ₹ 5,000 and ₹ 25,000.

Question 20.
The bookshop of a particular school has 10 dozen chemistry books, 8 dozen physics books, 10 dozen economics books. Their selling prices are ₹ 80, ₹ 60 and ₹ 40 each respectively. Find the total amount the book shop will receive from selling all the books using matrix algebra.
Answer:
Number of books in school is as follows:

Subject	Number of books
Chemistry	10 dozen = 10 × 12 = 120
Physics	8 dozen = 8 × 12 = 96
Economics	10 dozen = 10 × 12 = 120

Let number of books are represented by A
∴ A = [120 96 120]
And selling prices are represented by R then
∴ R = \(\left[\begin{array}{l} 80 \\ 60 \\ 40 \end{array}\right]\)
Money obtained by selling the books
= AR = [120 96 120] \(\left[\begin{array}{l} 80 \\ 60 \\ 40 \end{array}\right]\)
= [(120 × 80) + (96 × 60) + (120 × 40)]
= [9600 + 5760 + 4800] = [20160]
Total money obtained = ₹ 20,160
Assume X, Y, Z, W and P are matrices of order 2 × n, 3 × k, 2 × p, n × 3 and p × k respectively. Choose the correct answer in exercises 21 and 22.

Question 21.
The restriction on n, k and p so that PY + WY will defined are:
(A) k = 3, p = n
(B) k is arbitary, p = 2
(C) p is arbitrary, k = 3
(D) k = 2, p = 3
Answer:
Order P matrix P = p × k
Order of martix Y = 3 × k
Order of matrix W = n × 3
Then for PY defined
Number of columns in P = number of rows in Y
k =3
and WY defined
Number of columns in W = number of rows in Y
(w = 3)
Now PY + WY defined
order of PY = p × k = p × 3
Then order of WY = n × k
Thus, PY + WY is defined if order of PY and WY are same
∴ p = n and k = 3
Thus (A) is correct.

Question 22.
If n = p, then order of matrix 7X - 5Z.
(A) p × 2
(B) 2 × n
(C) n × 3
(D) p × n
Answer:
X Order of X = 2 × n
Z Order of Z = 2 × p
∵ p = n
Thus, order of 7X - 5Z = 2 × n,
Hence, choice (B) is correct.