RBSE Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.1

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.1 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 3 Matrices Ex 3.1

Question 1.
In the matrix A = \(\left[\begin{array}{cccc} 2 & 5 & 19 & -7 \\ 35 & -2 & 5 / 2 & 12 \\ \sqrt{3} & 1 & -5 & 17 \end{array}\right]\)
Write:
(i) the order of the matrix
Answer:
There are 3 rows and 4 columns in matrix A. So order of matrix A is 3 × 4.

(ii) the number of elements
Answer:
Since, number of rows = 3 and number of columns = 4
∴ Number of elements = 3 × 4 = 12

(iii) the elements a₁₃, a₂₁, a₃₃, a₂₄, a₂₃
Answer:
a₁₃ = Common element of first row and third column = 19
a₂₁ = Common element of second row and first column = 35
a₃₃ = Common element of third row and third column = - 5
a₂₄ = Common element of second row and fourth column = 12
a₂₃ = Common element of second row and third column = 5/2

Question 2.
If a matrix has 24 elements, what are the possible orders it can have ? What if it has 13 elements ?
Answer:
Matrix has 24 elements. So, its possible orders are as follows:
1 × 24, 24 × 1, 2 × 12, 12 × 2, 3 × 8, 8 × 3, 4 × 6, 6 × 4.
When elements are 13 then orders are 1 × 13 and 13 × 1.

Question 3.
If a matrix has 18 elements, what are the possible oders it can have ? What if it has 5 elements?
Answer:
When matrix has 18 elements, then possible orders are as follows:
1 × 18, 18 × 1, 2 × 9, 9 × 2, 3 × 6, 6 × 3
It it has 5 elements then oders are 1 × 5 and 5 × 1.

Question 4.
Construct a 2 × 2 matrix, A = [a_ij], whose elements are given by:
(i) a_ij = \(\frac{(i+j)^{2}}{2}\)
Answer:

(ii) a_ij = \(\frac{i}{j}\)
Answer:

(iii) a_ij = \(\frac{(i+2 j)^{2}}{2}\)
Answer:

Question 5.
Construct a 3 × 4 matrix, whose elements are obtained in the following way:
(i) a_ij = \(\frac{1}{2}\) |- 3i + j |
Answer:

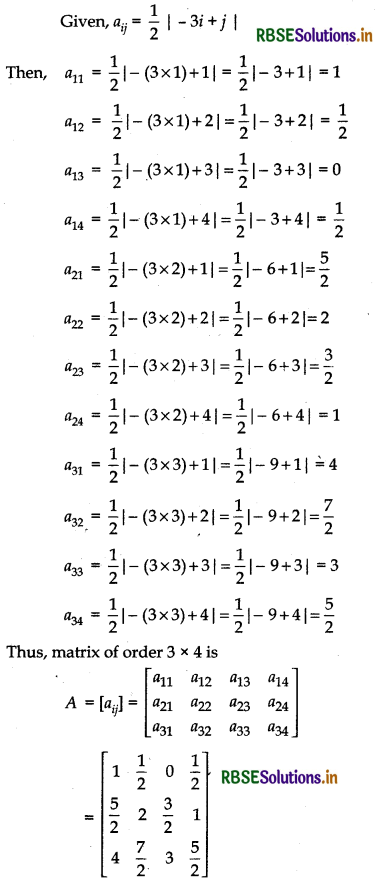
(ii) a_ij = 2i - j
Answer:
Given, a_ij = 2i - j
Then
a₁₁ = 2 × 1 - 1 = 2 - 1 = 1
a₁₂ = 2 × 1 - 2 = 2 - 2 = 0
a₁₃ = 2 × 1 - 3 = 2 - 3 = - 1
a₁₄ = 2 × 1 - 4 = 2 - 4 = - 2
a₂₁ = 2 × 2 - 1 = 4 - 1 = 3
a₂₂ = 2 × 2 - 2 = 4 - 2 = 2
a₂₃ = 2 × 2 - 3 = 4 - 3 = 1
a₂₄ = 2 × 2 - 4 = 4 - 4 = 0
a₃₁ = 2 × 3 - 1 = 6 - 1 = 5
a₃₂ = 2 × 3 - 2 = 6 - 2 = 4
a₃₃ = 2 × 3 - 3 = 6 - 3 = 3
a₃₄ = 2 × 3 - 4 = 6 - 4 = 2
Thus, matrix of order 3 × 4 is

Question 6.
Find the values of x, y and z from the following equations:
(i) \(\left[\begin{array}{ll} 4 & 3 \\ x & 5 \end{array}\right]=\left[\begin{array}{ll} y & z \\ 1 & 5 \end{array}\right]\)
Answer:
Given, \(\left[\begin{array}{ll} 4 & 3 \\ x & 5 \end{array}\right]=\left[\begin{array}{ll} y & z \\ 1 & 5 \end{array}\right]\)
On comparing corresponding elements, we get
4 = y, 3 = z, x = 1
Thus, x = 1, y = 4, z = 3

(ii) \(\left[\begin{array}{cc} x+y & 2 \\ 5+z & x y \end{array}\right]=\left[\begin{array}{cc} 6 & 2 \\ 5 & 8 \end{array}\right]\)
Answer:
Given \(\left[\begin{array}{cc} x+y & 2 \\ 5+z & x y \end{array}\right]=\left[\begin{array}{cc} 6 & 2 \\ 5 & 8 \end{array}\right]\)
On comparing corresponding elements, we get
x + y = 6 .... (i)
5 + z = 5 ..... (ii)
and xy = 8 ..... (iii)
From equation (iii) putting, y = \(\frac{8}{x}\) in equation (i), we get
x + \(\frac{8}{x}\) = 6 ⇒ x² + 8 = 6x
⇒ x² - 6x + 8 = 0 ⇒ (x - 4) (x - 2) = 0
∴ x = 4, x = 2
Putting x = 4 in equation (i), we get
4 + y = 6 ⇒ y = 6 - 4 = 2
∴ y = 2
When x = 2, then from equation (i), we get
2 + y = 6 ⇒ y = 6 - 2 = 4
∴ y = 4
and 5 + z = 5 ∴ z = 5 - 5 = 0
Thus, x = 2, y = 4, z = 0

(iii) \(\left[\begin{array}{c} x+y+z \\ x+z \\ y+z \end{array}\right]=\left[\begin{array}{l} 9 \\ 5 \\ 7 \end{array}\right]\)

Answer:
Given, \(\left[\begin{array}{c} x+y+z \\ x+z \\ y+z \end{array}\right]=\left[\begin{array}{l} 9 \\ 5 \\ 7 \end{array}\right]\)
On comparing corresponding elements, we get
x + y + z = 9 ...... (i)
x + z = 5 ....... (ii)
y + z = 7 ...... (iii)
From equation (i) and (ii)
y = 9 - 5 = 4
From equation (i) and (iii)
x = 9 - 7 = 2
In equation (i) putting y = 4, x = 2
2 + 4 + z = 9 ⇒ z = 9 - 6
∴ z = 3
Thus, x = 2, y = 4, z = 3

Question 7.
Find the values of a, b, c and d from equation:
\(\left[\begin{array}{cc} a-b & 2 a+c \\ 2 a-b & 3 c+d \end{array}\right]=\left[\begin{array}{rr} -1 & 5 \\ 0 & 13 \end{array}\right]\)
Answer:
Given, \(\left[\begin{array}{cc} a-b & 2 a+c \\ 2 a-b & 3 c+d \end{array}\right]=\left[\begin{array}{rr} -1 & 5 \\ 0 & 13 \end{array}\right]\)
Comparing corresponding elements, we get
a - b = - 1 ..... (i)
2a + c = 5 ..... (ii)
2a - b = 0 ...... (iii)
3c + d = 13 ...... (iv)
Solving equation (i) and (ii), we get

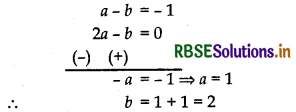
Putting a = 1 in equation (ii), we get
2 × 1 + c = 5 ⇒ c = 5 - 2 = 3
Putting c = 3 in equation (iv), we get
3 × 3 + d = 13 ⇒ d = 13 - 9
∴ d = 4
Thus, a = 1, b = 2, c = 3, d = 4

Question 8.
A = [a_ij]_{m × n} is a square matrix, if
(A) m < n (B) m > n
(C) m = n
(D) None of these
Answer:
Number of rows and columns are equal in a square matrix, i.e.,
Number of rows = Number of columns (m = n)
Thus, option (C) is correct.

Question 9.
Which of the given values of x and y make the following pair of matrices are equal:
\(\left[\begin{array}{cc} 3 x+7 & 5 \\ y+1 & 2-3 x \end{array}\right],\left[\begin{array}{cc} 0 & y-2 \\ 8 & 4 \end{array}\right]\)
(A) x = - \(\frac{1}{3}\), y = 7
(B) Not impossible to find
(C) y = 7, x = -\(\frac{2}{3}\)
(D) x = - \(\frac{1}{3}\), y = -\(\frac{2}{3}\)
Answer:
In two equal matrices, corresponding elements are equal i.e.,
3x + 7 = 0 and 2 - 3x = 4
On solving these equations, we get
x = - \(\frac{7}{3}\) and x = - \(\frac{2}{3}\)
Here, x has two values, which is not possible.
Thus, (B) is correct.

Question 10.
What will be the number of matrices of order 3 × 3 matrices whose each entry is 0 or 1 ?
(A) 27
(B) 18
(C) 81
(D) 512
Answer:
There will be 9 elements in matrix of order 3 × 3, so we can place either 0 or 1 at each place.
Total number of ways to fill places of 0 = 2⁹ = 512
∴ Possible number of matrices = 512
Thus (D) is correct.