RBSE Solutions for Class 12 Maths Chapter 2 प्रतिलोम त्रिकोणमितीय फलन विविध प्रश्नावली

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 2 प्रतिलोम त्रिकोणमितीय फलन विविध प्रश्नावली Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन विविध प्रश्नावली

प्रश्न 1.
cos^-1 \(\left(\cos \frac{13 \pi}{6}\right)\)
हल:
cos^-1 की मुख्य मान शाखा का परिसर {0, π} है

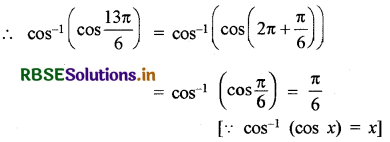
प्रश्न 2.
tan^-1\((tan \frac{7 \pi}{6})\)
हल:
∵ tan^-1 की मुख्य मान शाखा का परिसर \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) है

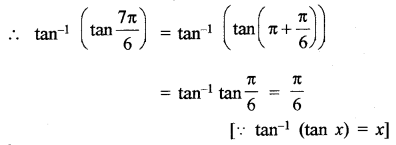
प्रश्न 3.
2 sin^-1 \(\frac{3}{5}\) = tan^-1 \(\frac{24}{7}\)
हल:

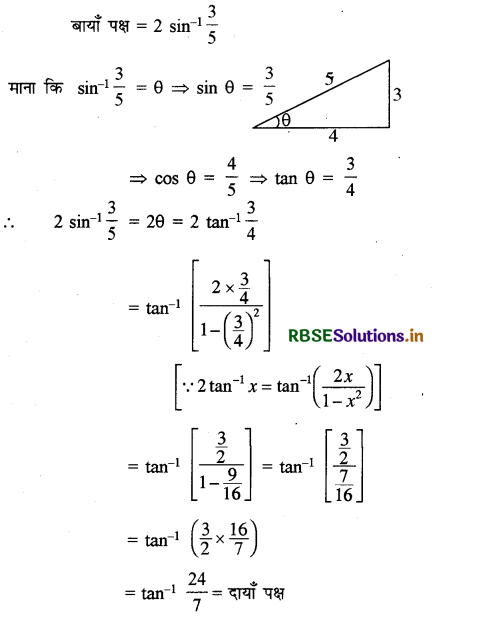
प्रश्न 4.
sin^-1\(\left(\frac{8}{17}\right)\) + sin^-1\(\left(\frac{3}{5}\right)\) = tan^-1 \(\left(\frac{77}{36}\right)\)
हल:

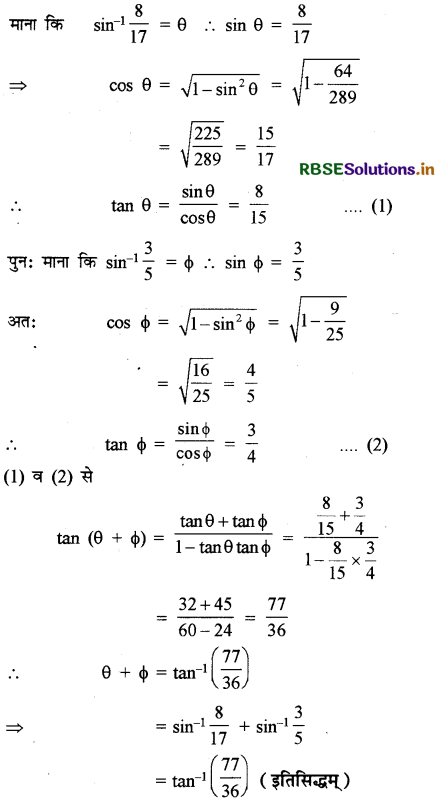
प्रश्न 5.
cos^-1\(\frac{4}{5}\) + cos^-1\(\frac{12}{13}\) = cos^-1 \(\frac{33}{65}\)
हल:

प्रश्न 6.
cos^-1\(\frac{12}{13}\) + sin^-1\(\frac{3}{5}\) = sin^-1\(\frac{56}{65}\)
हल:

प्रश्न 7.
tan^-1\(\frac{63}{16}\) = sin^-1 \(\frac{5}{13}\) + cos^-1\(\frac{3}{5}\)
हल:

प्रश्न 8.
tan^-1\(\frac{1}{5}\) + tan^-1\(\frac{1}{7}\) + tan^-1\(\frac{1}{3}\) + tan^-1\(\frac{1}{8}\) = \(\frac{\pi}{4}\)
हल:

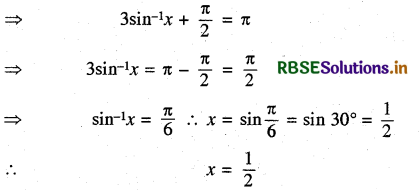
प्रश्न 9.
tan^-1 √x = \(\frac{1}{2}\) cos^-1, x ∈ [0, 1]
हल:

प्रश्न 10.
cot^-1 \(\left(\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right)\) = \(\frac{x}{2}\), x ∈ \(\left(0, \frac{\pi}{4}\right)\)
हल:

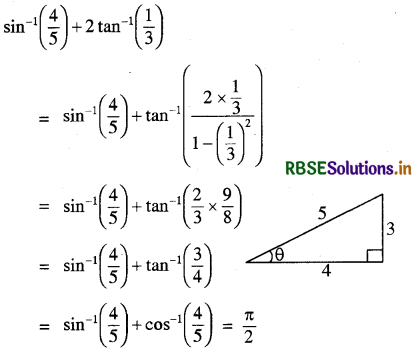
प्रश्न 11.
tan^-1\(\left(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\right)\) = \(\frac{\pi}{4}-\frac{1}{2}\) cos^-1 x - \(\frac{1}{\sqrt{2}}\) ≤ x ≤ 1
हल:
मान लिया x = cos 2θ
1 + x = 1 + cos 2θ = 2 cos²θ
और 1 - x = 1 - cos 2θ = 2 sin²θ

प्रश्न 12.
\(\frac{9 \pi}{8}-\frac{9}{4} \sin ^{-1} \frac{1}{3}=\frac{9}{4} \sin ^{-1} \frac{2 \sqrt{2}}{3}\)
हल:

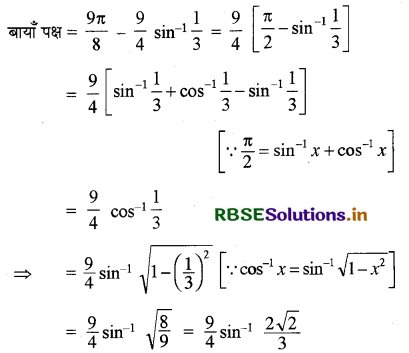
प्रश्न 13.
2 tan^-1 (cos x) = tan^-1 (2 cosec x)
हल:
दी गई समीकरण है

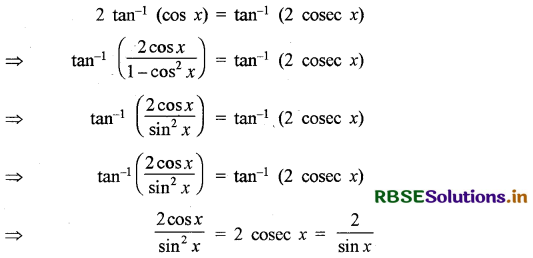
या 2 sin x cos x = 2 sin² x
या sin x cos x = sin² x
sin x cos x - sin² x = 0
या sin x (cos x - sin x) = 0
sin x = 0 ⇒ x = 0 जो कि दिए
गए समीकरण को संतुष्ट नहीं करता। अत: x ≠ 0
और cos x - sin x = 0 या tan x = 1
∴ x = \(\frac{\pi}{4}\)

प्रश्न 14.
tan^-1 \(\frac{1-x}{1+x}\) = \(\frac{1}{2}\) tan^-1 x, (x > 0)
हल:

प्रश्न 15.
sin (tan^-1 x), |x| < 1 बराबर होता है
(A) \(\frac{x}{\sqrt{1-x^2}}\)
(B) \(\frac{1}{\sqrt{1-x^2}}\)
(C) \(\frac{1}{\sqrt{1+x^2}}\)
(D) \(\frac{x}{\sqrt{1+x^2}}\)
हल:
sin (tan^-1 x), |x| < 1
माना tan^-1 x = θ
∴ x = tan θ
tan θ = \(\frac{x}{1}\)

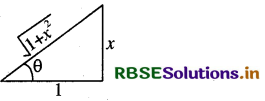
∴ sin θ = \(\frac{x}{\sqrt{1+x^2}}\) ⇒ sin (tan^-1 x) = \(\frac{x}{\sqrt{1+x^2}}\)
अतः सही विकल्प (D) है।

उत्तरः
(D) \(\frac{x}{\sqrt{1+x^2}}\)

प्रश्न 16.
यदि sin^-1 (1 - x) - 2 sin^-1 x = \(\frac{\pi}{2}\), का मान बरबर है
(A) 0, \(\frac{1}{2}\)
(B) 1, \(\frac{1}{2}\)
(C) 0
(D) \(\frac{1}{2}\)
हल:
यदि sin^-1 (1 - x) - 2 sin^-1 x = \(\frac{\pi}{2}\)
हम जानते हैं कि sin^-1 (1 - x) + cos^-1 (1 - x) = \(\frac{\pi}{2}\)
∴ sin^-1 (1 - x) = \(\frac{\pi}{2}\) - cos^-1 (1 - x)
मान रखने पर
\(\frac{\pi}{2}\) - cos^-1 (1 - x) - 2 sin^-1 x = \(\frac{\pi}{2}\)
⇒ - 2 sin^-1 x = cos^-1 (1 - x)
माना sin^-1 x = θ तब x = sin θ
⇒ - 2 θ = cos^-1 (1 - x)
⇒ cos (- 2θ) = 1 - x
⇒ cos 2θ = 1 - x
⇒ 1 - 2 sin² θ = 1 - x [∵ x = sin θ]
⇒ 1 - 2x² = 1 - x
⇒ 2x² - x = 0
⇒ x (2x - 1) = 0
∴ x = 0, \(\frac{1}{2}\) लेकिन x = \(\frac{1}{2}\) दिये गये समीकरण को संतुष्ट नहीं करता है।
\(\left[\because \sin ^{-1}\left(1-\frac{1}{2}\right)-2 \sin ^{-1}\left(\frac{1}{2}\right)=\frac{\pi}{6}-2 \times \frac{\pi}{6}=\frac{\pi}{2}\right]\)
अतः सही विकल्प (C) है।

प्रश्न 17.
tan^-1\(\left(\frac{x}{y}\right)\) - tan^-1\(\frac{x-y}{x+y}\) का मान:
(A) \(\frac{\pi}{2}\) है
(B) \(\frac{\pi}{3}\) है
(C) \(\frac{\pi}{4}\) है
(D) \(\frac{-3 \pi}{4}\) है
हल:

उत्तरः
(C) \(\frac{\pi}{4}\) है