RBSE Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions Ex 2.1

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions Ex 2.1 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 2 Inverse Trigonometric Functions Ex 2.1

Question 1.
Find the principal value of sin^-1 \(\left(-\frac{1}{2}\right)\).
Answer:

Question 2.
Find the principal value of cos^-1 \(\left(\frac{\sqrt{3}}{2}\right)\).
Answer:

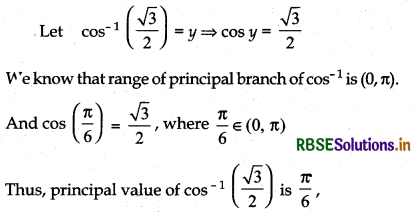
Question 3.
Find the principal value of cosec^-1 (2).
Answer:
Let cosec^-1 (2) = y ⇒ cosec y = 2
We know that range of principal branch of cosec^-1 is \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) - {0}
And cosec \(\left(\frac{\pi}{6}\right)\) = 2, where \(\frac{\pi}{6} \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]-\{0\}\)
Thus, principal value of cosec^-1 (2) is \(\frac{\pi}{6}\).

Question 4.
Find the principal value of tan^-1 (- √3).
Answer:

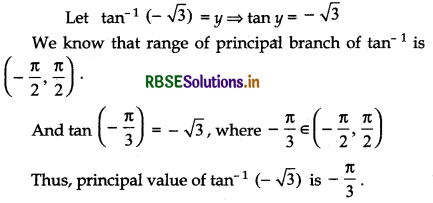
Question 5.
Find the principal value of cos^-1 \(\left(-\frac{1}{2}\right)\).
Answer:

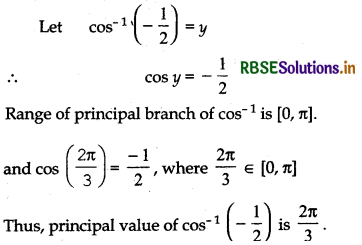
Question 6.
Find the principal value of tan^-1 (- 1).
Answer:
Let tan^-1 (- 1) = y ⇒ tan y = - 1
We know that range of principal branch of tan^-1 is \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\).

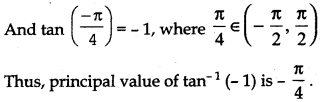
Question 7.
Find the principal value of sec^-1 \(\left(\frac{2}{\sqrt{3}}\right)\).
Answer:

Question 8.
Find the principal value of cot^-1 (√3).
Answer:
Let cot^-1 (√3) = y
∴ cot y = √3
We know that range of principal branch of cot^-1 is (0, π).
And cot \(\left(\frac{\pi}{6}\right)\) = √3, where \(\frac{\pi}{6}\) ∈ (0, π)
Thus, principal value of cot^-1 (√3) is \(\frac{\pi}{6}\).

Question 9.
Find the principal value of cos^-1\(\left(-\frac{1}{\sqrt{2}}\right)\).
Answer:

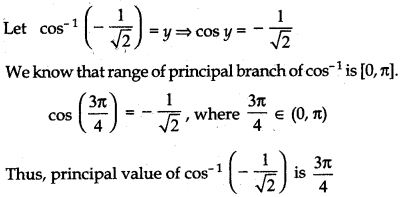
Question 10.
Find the principal value of:
cosec^-1 (- √2).
Answer:

Question 11.
Find the value of tan^-1 (1) + cos^-1 \(\left(-\frac{1}{2}\right)\) + sin^-1\(\left(-\frac{1}{2}\right)\)
Answer:

Question 12.
Find the value of:
cos^-1\(\left(\frac{1}{2}\right)\) + 2 sin^-1\(\left(\frac{1}{2}\right)\)
Answer:
Range of cos^-1 and sin^-1 are (0, π) and (- π/2, π/2) respectively.

Question 13.
If sin^-1 x = y, then:
(A) 0 ≤ y ≤ π
(B) - \(\frac{\pi}{2}\) ≤ y ≤ \(\frac{\pi}{2}\)
(C) 0 < y < π
(D) - \(\frac{\pi}{2}\) < y < \(\frac{\pi}{2}\)
Answer:

Question 14.
tan^-1 √3 - sec^-1 (- 2) is equal to:
(A) π
(B) - \(\frac{\pi}{3}\)
(C) \(\frac{\pi}{3}\)
(D) \(\frac{2 \pi}{3}\)
Answer: