RBSE Solutions for Class 12 Maths Chapter 13 प्रायिकता Ex 13.4

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 13 प्रायिकता Ex 13.4 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 13 प्रायिकता Ex 13.4

प्रश्न 1.
बताइए कि निम्नलिखित प्रायिकता बंटनों में कौनसे एक यादृच्छिक चर के लिए सम्भव नहीं है। अपना उत्तर कारण सहित लिखिए
(i)

हल:
प्रायिकताओं का योग = 0.4 + 0.4 + 0.2 = 1.0
दिया गया बंटन प्रायिकता बंटन है।

(ii)

हल:
यहाँ पर P(3) = - 0.1, प्रायिकता कभी भी ऋण नहीं हो सकती।

(iii)

हल:
प्रायिकताओं का योग = 0.6 + 0.1 + 0.2 = 0.9
प्रायिकताओं का योगफल एक होना चाहिए।
यह बंटन प्रायिकता बंटन नहीं है।

(iv)

हल:
प्रायिकताओं का योग = 0.3 + 0.2 + 0.4 + 0.1 + 0.05 = 1.05 > 1
प्रायिकताओं का योगफल 1 से अधिक नहीं हो सकता।
अर्थात् यह बंटन प्रायिकता बंटन नहीं है।

प्रश्न 2.
एक कलश में 5 लाल और 2 काली गेंदें हैं। दो गेंदें यादृच्छया निकाली गईं। मान लीजिए X काली गेंदों की संख्या को व्यक्त करता है। X के सम्भावित मान क्या हैं? क्या X यादृच्छिक चर है?
हल:
काली गेंदों की संख्या 2 है।
X के मान 0, 1 और 2 हो सकते हैं।
इनके संगत प्रायिकता P(x) ज्ञात की जा सकती है।
∴ X एक यादृच्छिक चर है।

प्रश्न 3.
मान लीजिए x चितों की संख्या और पटों की संख्या में अन्तर को व्यक्त करता है। जब एक सिक्के को 6 बार उछाला जाता है। X के सम्भावित मूल्य क्या हैं?
हल:
जब एक सिक्के को 6 बार उछाला जाता है तो सिक्कों पर चितों और पटों की संख्याएँ इस प्रकार हैं-

की संख्या का अन्तर
अर्थात् X = 6, 4, 2, 0

प्रश्न 4.
निम्नलिखित के प्रायिकता बंटन ज्ञात कीजिए
(i) एक सिक्के की दो उछालों में चितों की संख्या का
हल:
एक सिक्के की दो उछालों में प्रतिदर्श समष्टि
S = {HH, HT, TH, TT} है।
यहाँ पर चितों की संख्या 0, 1, 2 हो सकती है।
P(0) = \(\frac{1}{4}\), P(1) = \(\frac{2}{4}\) = \(\frac{1}{2}\), P(2) = \(\frac{1}{4}\)
अतः प्रायिकता बंटन इस प्रकार होगा-

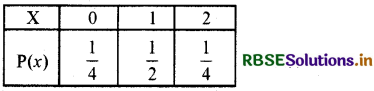
(ii) तीन सिक्कों के एक साथ एक बार उछालने पर पटों की संख्या का
हल:
तीन सिक्कों को एक साथ फेंकने पर प्रतिदर्श समष्टि
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
पटों की संख्या 0, 1, 2, 3 हो सकती है।

(iii) एक सिक्के की चार उछालों में चितों की संख्या का।
हल:
एक सिक्के को चार बार उछालने पर चितों की संख्या
0, 1, 2, 3, 4 हो सकती है।
n(S) = 2⁴ = 16
S = {HHHH, HHHT, HHTH, HTHH, HTTH, THHH, HHTT, HTHT, THHT, THTH, TTHH, HTTT, THTT, TTHT, TTTH, TTTT;
X = चित्तों की संख्या

प्रश्न 5.
एक पासा दो बार उछालने पर सफलता की संख्या का प्रायिकता बंटन ज्ञात कीजिए जहाँ
(i) 4 से बड़ी संख्या' को एक सफलता माना गया है।
(ii) 'पासे पर संख्या 6 प्रकट होना' को एक सफलता माना गया है।
हल:
(i) जब दो पासे फेंके जाते हैं तो n(S) = 6 × 6 = 36
एक पासे पर 4 से अधिक संख्या 5, 6 .:. सफलता की प्रायिकता अर्थात् पासे पर 4 से अधिक संख्या आने
की प्रायिकता = 2_1
P(असफलता) = पासे पर 4 से अधिक संख्या न आने की प्रायिकता
= 1 - \(\frac{1}{3}\) = \(\frac{2}{3}\)
अब P(0) = P(पासे पर दोनों बार 5, 6 नहीं आता)

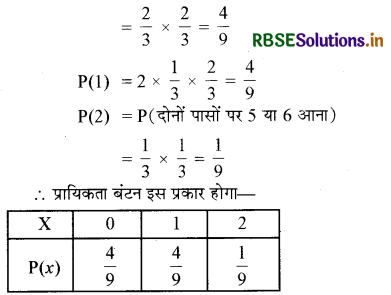
(ii) माना कि A: 'न्यूनतम 1 पासे पर संख्या 6 आना'
⇒ A = {(1,6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5)}
एक पासे पर 6 प्राप्त होने की प्रायिकता = \(\frac{1}{6}\)
पासे पर 6 न आने की प्रायिकता = 1 - \(\frac{1}{6}\) = \(\frac{5}{6}\)
दो पासों पर 6 न आने की प्रायिकता = \(\frac{5}{6} \times \frac{5}{6}\) = \(\frac{25}{36}\)
दो पासों पर कम से कम एक 6 आने की प्रायिकता
= 1 - \(\frac{25}{36}\) = \(\frac{11}{36}\)
∴ कम से कम 6 आने का प्रायिकता बंटन इस प्रकार होगा|

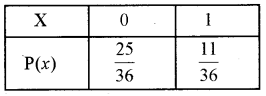
प्रश्न 6.
30 बल्बों के एक ढेर से, जिसमें 6 बल्ब खराब हैं, 4 बल्बों का एक नमूना (प्रतिदर्श) यादृच्छया बिना प्रतिस्थापन के निकाला जाता है। खराब बल्बों की संख्या का बंटन ज्ञात कीजिए।
हल:
30 बल्बों के ढेर में 6 बल्ब खराब हैं।
∴ सही बल्ब = 30 - 6 = 24
एक खराब बल्ब चुनने की प्रायिकता = \(\frac{6}{30}\) = \(\frac{1}{5}\)
एक अच्छा बल्ब चुनने की प्रायिकता = 1 - \(\frac{1}{5}\) = \(\frac{4}{5}\)
यदि X खराब बल्बों की संख्या को व्यक्त करता हो तो
X = 0, 1, 2, 3, 4

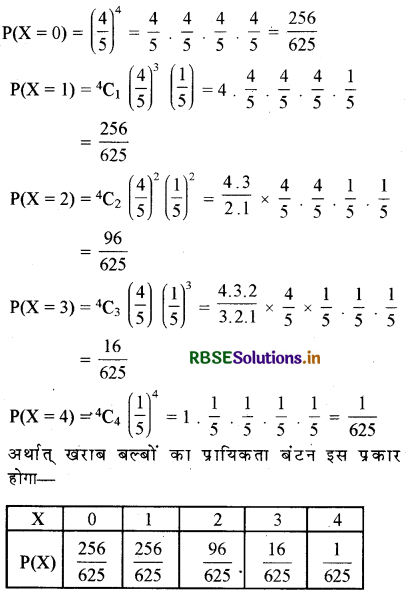
प्रश्न 7.
एक सिक्का समसर्वय सन्तुलित नहीं है, जिसमें चित प्रकट होने की सम्भावना पट प्रकट होने की सम्भावना की तीन गुनी है। यदि सिक्का दो बार उछाला जाता है तो पटों की संख्या का प्रायिकता बंटन ज्ञात कीजिए।
हल:
प्रश्नानुसार चित और पट आने की प्रायिकता का अनुपात = 3 : 1
अर्थात् यदि पट x बार आता है तो चित 3x बार आएगा।

प्रश्न 8.
एक यादृच्छिक चर X का प्रायिकता बंटन नीचे दिया गया है-

ज्ञात कीजिए
(i) k
हल:
प्रायिकताओं का योगफल ΣP(X) =1
या 0 + k + 2k + 2k + 3k + k² + 2k² + 7K² + k = 1
या 10k² + 9k = 1
या 10k² + 9k - 1 = 0
या (k + 1) (10k - 1) = 0,
k = \(\frac{1}{10}\) ∴ k ≠ - 1

(ii) P(X < 3)
हल:
अतः प्रायिकता बंटन इस प्रकार होगा-

P(X < 3) = P(0) + P(1) + P(2) = 0 + \(\frac{1}{10}+\frac{2}{10}=\frac{3}{10}\)

(iii) P(X > 6)
हल:
P(X > 6) = P(7) = \(\frac{7}{100}+\frac{1}{10}=\frac{17}{100}\)

(iv) P(0 < X < 3)
हल:
P(0 < X < 3) = P(1) + P(2) = \(\frac{1}{10}+\frac{2}{10}=\frac{3}{10}\)

प्रश्न 9.
एक यादृच्छिक चर X का प्रायिकता फलन P(x) निम्न प्रकार से है, जहाँ x कोई संख्या है-

(a) k का मान ज्ञात कीजिए।
हल:
(a) प्रायिकताओं का योगफल = ΣP(X) = 1
∴ k + 2k + 3k + 0 = 1 या 6k = 1
या k = \(\frac{1}{6}\)

(b) P(X < 2), P(X ≤ 2), P(X ≥ 2) ज्ञात कीजिए।
हल:
(i) P(X < 2) = P(0) + P(1) = \(\frac{1}{6}+\frac{2}{6}=\frac{3}{6}\)
= \(\frac{1}{2}\)

(ii) P(X ≤ 2) = p(0) + p(1) + P(2)
= \(\frac{1}{6}+\frac{2}{6}+\frac{3}{6}=\frac{6}{6}\) = 1

(iii) P(X ≥ 2) = P(2) = \(\frac{3}{6}\) = \(\frac{1}{2}\)

प्रश्न 10.
एक न्याय्य सिक्के की तीन उछालों पर प्राप्त चितों की संख्या का माध्य ज्ञात कीजिए।
हल:
एक न्याय्य सिक्के को तीन बार उछालने पर प्रतिदर्श समष्टि
s = {TTT, THT, TTH, HTT, HHT, HTH, THH, HHH}
(i) P(0) = कोई चित न आने की प्रायिकता = \(\frac{1}{8}\)
(ii) P(1) = P(एक चित का आना) = \(\frac{3}{8}\)
(i) P(2) = P(दो चित का प्राप्त होना) = \(\frac{3}{8}\)
(iv) P(3) = P(तीन चित प्राप्त होना) = \(\frac{1}{8}\)
अतः प्रायिकता बंटन इस प्रकार होगा|

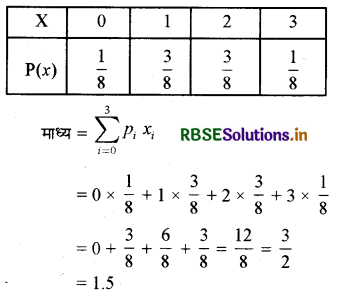
प्रश्न 11.
दो पासों को युग्मत् उछाला गया। यदि X, छक्कों की संख्या को व्यक्त करता है, तो X की प्रत्याशा ज्ञात कीजिए।
हल:
एक पासा उछालने से प्रतिदर्श समष्टि S = {1, 2, 3, 4, 5, 6}
एक पासे पर छक्का प्राप्त होने की प्रायिकता = \(\frac{1}{6}\)
पासे पर छक्का न प्राप्त होने की प्रायिकता = 1 - \(\frac{1}{6}\) = \(\frac{5}{6}\)
जब दो पासे उछाले जाते हैं n(S) = 36.

प्रश्न 12.
प्रथम छ: धन पूर्णांकों में से दो संख्याएँ यादृच्छया (बिना प्रतिस्थापन) चुनी गईं। मान लें X दोनों संख्याओं में से बड़ी संख्या को व्यक्त करता है। E(X) ज्ञात कीजिए।
हल:
माना कि प्रथम छः धन पूर्णांक = {1, 2, 3, 4, 5, 6} हैं।
इनमें एक अंक 6 तरीकों से चुना जा सकता है।
इस अंक को निकालने के बाद पांच अंक शेष रह जाते हैं। इनमें से एक अंक 5 तरीकों से चुना जा सकता है।
बिना प्रतिस्थापन के 1, 2, 3, 4, 5, 6 से दो अंक 5 × 6 = 30 तरीकों से चुन सकते हैं।

प्रश्न 13.
मान लीजिए दो पासों को फेंकने पर प्राप्त संख्याओं के योग को X से व्यक्त किया गया है। X का प्रसरण और मानक विचलन ज्ञात कीजिए।
हल:
दो पासों को फेंकने पर प्रतिदर्श समष्टि है
S = {(x, y) : x, y ∈ {1, 2, 3, 4, 5, 6}}
n(S) = 36
यहाँ X = x + y जहाँ x, y ∈ {1, 2, 3, 4, 5, 6}
X के मान 2, 3, 4, 5, .......12 तक हो सकते हैं।
अतः X का प्रायिकता बंटन

प्रश्न 14.
एक कक्षा में 15 छात्र हैं जिनकी आयु 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 और 20 वर्ष है। एक छात्र को इस प्रकार चुना गया कि प्रत्येक छात्र के चुने जाने की सम्भावना समान है और चुने गए छात्र की आयु (X) को लिखा गया। यादृच्छिक चर X का प्रायिकता बंटन ज्ञात कीजिए। X का माध्य, प्रसरण व मानक विचलन भी ज्ञात कीजिए।
हल:
प्रत्येक बच्चे के चुने जाने की प्रायिकता = \(\frac{1}{15}\)
दिए हुए बंटन का प्रायिकता बंटन इस प्रकार है-


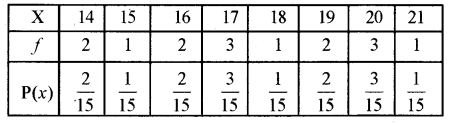
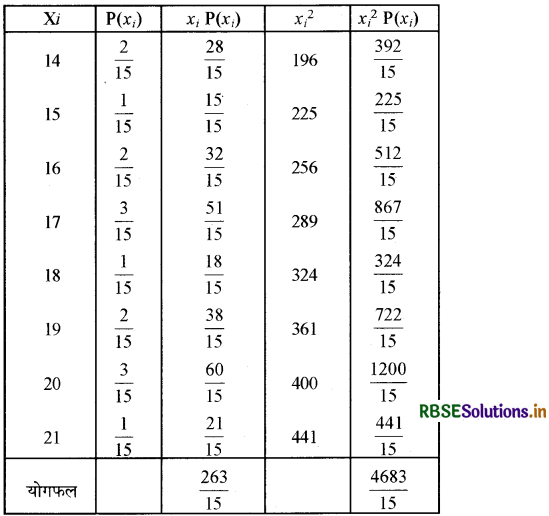
माध्य
µ = Σx_i P_i = \(\frac{263}{15}\)
= 17.533
प्रसारण = var X = ΣE(X²) - |ΣE(X²)|
= Σp_i x_i² - |Σp_i x_i|²
= 312.20 - (17.533)²
= 312.20 - 307.418
= 4.782
मानक विचलन σ = √var X = √4.782
= 2.19

प्रश्न 15.
एक बैठक में 70% सदस्यों ने किसी प्रस्ताव का अनुमोदन किया और 30% सदस्यों ने विरोध किया। एक सदस्य को यादृच्छया चुना गया और यदि उस सदस्य ने प्रस्ताव का विरोध किया हो तो X = 0 लिया गया जब कि उसने प्रस्ताव का अनुमोदन किया हो तो X = 1 लिया गया। E(X) और var (X) ज्ञात कीजिए।
हल:
x = 0, प्रायिकता = 30% = 0.3
X = 1, प्रायिकता = 70% = 0.7

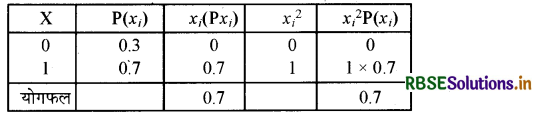
E(X_i) = Σx_i p_i = 0.7
Var (X) = E(x²) - (E(X))²
= Σx_i² p(x_i) - (Σx_i P(x_i))²
= 0.7 - (0.7)²
= 0.7 - 0.49
= 0.21

निम्नलिखित में से प्रत्येक में सही उत्तर चुनें:

प्रश्न 16.
ऐसे पासे जिसके तीन फलकों पर 1, अन्य दो फलकों पर 2 और एक फलक पर 5 लिखा गया है, को उछालने पर प्राप्त संख्याओं का माध्य
(A) 1
(B) 2
(C) 5
(D) \(\frac{8}{3}\)
उत्तर:
(B) 2

हल:
माना किं X पासों की संख्या को निरूपित कर रहा है तब X के मान 1, 2 और 5 लेंगे

अतः सही विकल्प (B) है।

प्रश्न 17.
मान लीजिए ताश की एक गड्डी से यादृच्छया दो पत्ते निकाले जाते हैं। मान लीजिए X इक्कों की संख्या प्रकट करता है। तब E(X) का मान है
(A) \(\frac{37}{221}\)
(B) \(\frac{5}{13}\)
(C) \(\frac{1}{13}\)
(D) \(\frac{2}{13}\)
उत्तर:
(D) \(\frac{2}{13}\)

हल:
n(S) = 52
n(A) = 4

अतः सही विकल्प (D) है।