RBSE Solutions for Class 12 Maths Chapter 12 Linear Programming Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 12 Linear Programming Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 12 Linear Programming Miscellaneous Exercise

Question 1. 
A. dietician has to develop a special diet using two foods P and Question Each packet (containing 30 g) of food P contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food Q contains 3 units of calcium, 20 units of iron, 4 units of cholesterol and 3 units of vitamin A. The diet requires atleast 240 units of calcium, atleast 460 units of iron and atmost 300 units of cholesterol. How many packets of each food should be used to maximize the amount of vitamin A in the diet? What is the maximum amount of vitamin A in the diet?
Answer:
Let the dietician uses x packets of food P and y packets of food Q.

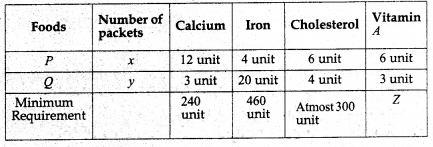
∴ Objective function:
Z = 6x + 3y and 
Subject to constraints
12x + 3y ≥ 240,
4x + 20y ≥ 460
6x + 4y ≤ 0
x, y ≥ 0 
or 4x + y ≥ 80,
x + 5y ≥ 115
3x + 2y ≤ 150
x, y ≥ 0
(i) Graph of 4x + y ≥ 80: Line 4x + y = 80 passes through points A(20, 0) and B(0, 80).
Putting x =0, y =0 in iñequality 4x + y ≥ 80
0 ≥ 80 which is not true.
The points of region 4x + y ≥ 80 lies on the line AB and above it.

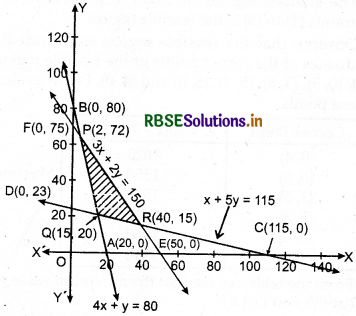
(ii) Graph of x + 5y ≥ 115 : Line x + 5y = 115 passes through points 0(115, 0) and D(0, 23).
Putting x = 0, y = 0 in inequality x + 5y ≥ 115 0 ≥ 115 which is not true.
⇒ The points of region x + 5y ≥ 115 lies on the line CD and above it.

(iii) Graph of 3x + 2y ≤ 150: Line 3x + 2y = 150 passes through points E(50, 0) and F(0, 75).
Putting x = 0, y = 0 in inequality 3x + 2y ≤ 150 0 ≤ 150 which is true.
⇒ The points of region 3x + 2y ≤ 150 lies on the line EF and below it.

(iv) The points of region x ≥ 0 lies on y-axis and right side of y-axis.
 
(v) The points of region y ≥ 0 lies on x-axis and above x-axis.
(vi) Intersection point of line AB : 4x + y = 80 and line CD : x + 5y = 115 is Q(15, 20).
(vii) Intersection point of line CD : x + 5y = 115 and line EF : 3x + 2y = 150 is R(40,15).
(viii) Intersection point of line AB : 4x + y = 80 and line EF : 3x + 2y = 150 is P(2, 72).
∴ The feasible region of this problem is PQR.
Now objective function :
Z = 6x + 3y
At point P(2, 72),
Z = 6 × 2 + 3 × 72 = 12 + 216 = 228
At point Q(15, 20),
Z = 6 × 15 + 3 × 20 = 90 + 60 = 150
At point R(40,15),
Z = 6 × 40 + 3 × 15 = 240 + 45 = 285
Hence, maximum amount of vitamin is 285 units when 40 packets of food P and 15 packets of food Q is used.

 

Question 2.
A farmer mixes two brands P and Q of cattle feed. Brand P, costing ₹ 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing ₹ 200 per bag contains 1.5 units of nutritional element A, 11.25 units of elements B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
Answer:
Let the farmer mixes x bags of brand P and y bags of brand Q.
Given:

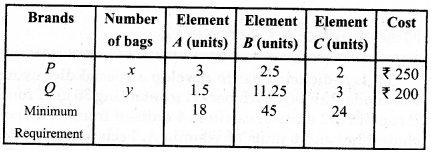
Z = 250x + 200y and
Subject to constraints 3x + 1.5y ≥ 18, 2.5x + 11.25y ≥ 45, 
2x + 3y ≥ 24 and x, y ≥ 0. 
or 2x + y ≥ 12, 2x + 9y ≥ 36, 2x + 3y ≥ 24, x, y ≥ 0.

(i) Graph of 2x + y ≥ 12 : Line 2x + y = 12 passes through the points A(6, 0) and B(0,12).
Putting x = 0, y = 0 in inequality 2x + y ≥ 12 0 ≥ 12 which is not true.
⇒ The points of region 2x + y ≥ 12 lies on the line AB and above it.

(ii) Graph of 2x + 9y ≥ 36 : Line 2x + 9y ≥ 36 passes through the points C(18,0) and (0,4).
∴ Putting x = 0, y = 0 in inequality 2x + 9y ≥ 36 0 ≥ 36 which is not true.
⇒ The points of region 2x + 9y > 36 lies on the line CD and above it.

(iii) Graph of 2x + 3y ≥ 24 : Line 2x + 3y = 12 passes through the points A (12, 0) and B(0,12).
Putting x = 0, y = 0 in inequality 2x + 3y ≥ 24 0 ≥ 24 which is not true.
⇒ The points of region 2x + 3y ≥ 24 lies on the line EF and above it.

(iv) The'points of region x ≥ 0 lies on y-axis and right side of y-axis.

(v) The points of region y ≥ 0 lies on x-axis and above x-axis.

(vi) Intersection point of line AB : 2x + y = 12 and line EF :2x + 3y = 24 is P(3, 6).

(vii) Intersection point of line CD : 2x + 9y = 36 and line EF : 2x + 3y = 24 is R(9,2).
The feasible region of this problem is YBPRCX.
 
Now objective function:
Z = 250x + 200y

At point B(0,12),
Z = 250 × 0 + 200 × 12 = 0 + 2400 = 2400

At point P(3, 6),
Z = 250 × 3 + 200 × 6 = 750 + 1200 = 1950

At point R(9,2),
Z = 250 × 9 + 200 × 2 = 2250 + 400 = 2650

At point C(18,0),
Z = 250 × 18 + 0 = 4500
Minimum value of Z is 1950 but feasible region is unbounded inequality 250x + 200y ≤ 1950 or 5x + 4y ≤ 39.

This line passes through the points (\(\frac{39}{0}\), 0) and (0, \(\frac{39}{4}\)) and lies at point (3, 6)
Putting x = 0, y = 0 in this line
0 < 39, which is true.
The points of region 5x+ 4y ≤ 39 lies below line 5x + 4y = 39 whose any point is not common with feasible region.
Hence, the minimum value of Z is ₹ 1950 and 3 bags of brand P and 6 bags of brand Q are mixed.

Question 3.
A dietician wishes to mix together two kinds of food X and V in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below:
One kg of food X costs ₹ 16 and one kg of food Y costs ₹ 20. Find the least cost of the mixture which will produce the required diet?

Answer:
Let the dietician mixes x kg of food X and y kg of food Y.
Given : Cost of food X is ₹ 16 per kg and cost of food Y is ₹ 20 per kg. Then cost of mixture = 16x + 20y 
∴ Objective function : Z = 16x + 20y and Subject to constraints : x + 2y ≥ 10, 2x + 2y ≥ 12 or x + y ≥ 6, 3x + y ≥ 8, x, y ≥ 0.

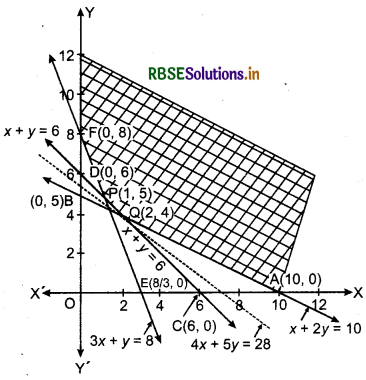
(i) Graph of x + 2y ≥ 10 : Line x + 2y = 10 passes through points A(10, 0) and B(0, 5).
Putting x = 0, y = 0 in inequality x + 2y ≥ 10 0 ≥ 10 which is not true.
⇒ The points of region x + 2y ≥ 10 lies on the line AB and above it.

(ii) Graph of x + y ≥ 6 : Line x + y = 6 passes through points C(0, 6) and D(0, 6).
∴ Putting x = 0, y = 0 in inequality x + y ≥ 6 0 ≥ 6 which is not true.
⇒ The points of region x + y ≥ 6 lies on the line CD and above it.

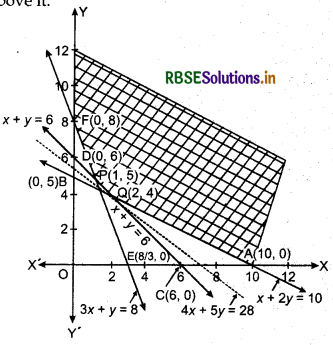
(iii) Graph of 3x + y ≥ 8: Line 3x + y = 8 passes through points.E(J,0J andF(0,8).
∴ Putting x = 0, y = 0 in inequality 3x + y ≥ 8 0 ≥ 8 which is not true.
⇒ The points of region 3x + y ≥ 8 lies, on the line EF and above it.

(iv) The points of region x ≥ 0 lies on y-axis and right side of y-axis

(v) The point of region y ≥ 0 lies on x-axis and above x-axis.

(vi) Intersection point of line CD : x + y = 6 and line EF : 3x + y = 8 is P(1, 5).

(vii) Intersection point of line AB : x + 2y - 10 and line CD : x + y = 6 is Q(2,4).
∴ The feasible region of this problem is YFPQAX.
 
Now objective function:
Z = 16x + 20 y
At point F(0,8), Z = 0 + 20 × 8 = 160
At point P(l, 5), Z = 16 × 1 + 20 × 5 = 16 + 100 = 116
At point Q(2,4), Z = 16 × 2 + 20 × 4 = 32 + 80 = 112
At point A(10,0), Z = 16 × 10 + 0 = 160
∴ Minimum value of Z is ₹ 112 but feasible region is unbounded.
Any point of 16x + 20y ≤ 112 is not common with feasible region.
Hence, minimum value of Z is ₹ 112 for which the mixture should contain 2 kg of food X and 4 kg of food Y.

Question 4.
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:

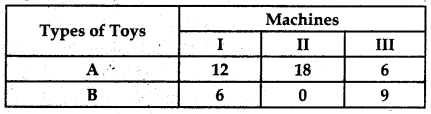
Each machine is available for a maximum of 6 hours per day. If the profit on each toy A is ₹ 7.50 and that on each toy of type B is ₹ 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
Answer:
Let the manufacturer makes x toys of type A and y toys of type B.
∴ Objective function:
Z = 7.5x + 5y and
Subject to constraints
12x + 6y ≤ 360,18x ≤ 360, . ....
6x + 9y ≤ 360, x, y ≥ 0.
or 2x + y ≤ 60, x ≤ 20, 2x + 3y ≤ 120, x, y ≥ 0.

(i) Graph of 2x + y ≤ 60 : Line 2x + y = 60, passes . through points A(30,0) and B(0, 60)
∴ Putting x = 0, y = 0 in inequality 2x + y ≤ 60 .
0 ≤ 60 which is true.
⇒ The points of region 2x + y ≤ 60 lies on the line AB and below it.

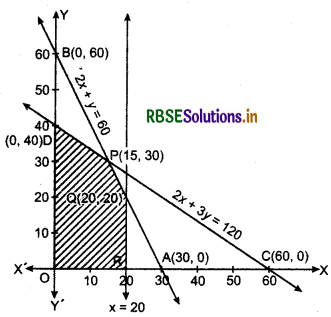
(ii) Points of x ≤ 20 lies between x = 0 and x = 20.
(iii) Graph of 2x + 3y ≤ 120: Line 2x + 3y = 120 passes through C(60,0) and D(0,40).
Putting x = 0, y = 0 in inequality 2x + 3y ≤ 120 0 ≤ 120 which is true.
⇒ The points of region 2x + 3y ≤ 120 lies on the line CD or below it.

(iv) The points of region x ≥ 0 lies on y-axis and right side of y-axis.
(v) The points of region y ≥ 0 lies on x-axis and above x-axis.
(vi) Intersection point of line AB : 2x + y = 60 and CD : 2x + 3y = 120 is P(15,30)
(vii) Intersection point of line x = 20 and line AB : 2x + y = 60 is Q(20,20).

The feasible region of this problem is ODPQR.
Now, objective function:
Z = 7.5x + 5y
At point D(0,40),
Z = 0 + 5 × 40 = 200

At point P(15, 30),
Z = 7.5 × 15 + 5 × 30 = 112.5 + 150 = 262.50

At point Q(20,20),
Z = 7.5 × 20 + 5 × 20 = 150 + 100 = 250

At point R(20, 0),
Z = 7.5 × 20 + 0 = 150
Hence, maximum profit is ₹ 262.50. When 15 toys of type A and 30 toys of type B will be made.

Question 5.
An aeroplane can carry a maximum of 200 passengers. A profit of ₹ 1000 is made on each executive class ticket and a profit of ₹ 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit for the airline. What is the maximum profit?
Answer:
Let x passengers travel by executive class and y passengers travel by economy class.
Given : Profit of ₹ 1000 is made on each executive class ticket and a profit of 1600 is made on each economy class ticket.
∴ Objective function:
Z = 1000x + 600y and
Subject to constraints x ≥ 20, x + y ≤ 200, y ≥ 4x, x, y ≥ 0. 
(i) Graph of x + y ≤ 200 : Line x + y = 200 passes through points (200, 0) and (0,200).
Putting x = 0, y = 0 in inequality x + y ≤ 200 0 ≤ 200 which is true.
⇒ The points of region x + y ≤ 200 lies on the line x + y = 200 and below it.

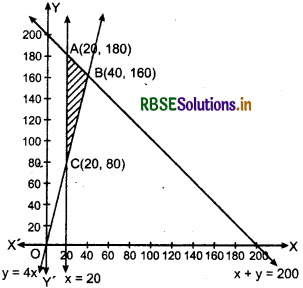
(ii) The points of region x ≥ 20 lies on the line x = 20 and right side of it.

(iii) Graph of y ≥ 4x : Line y = 4x passes through the points 0(0, 0) and B(40, 160).
∴ Putting x = 0, y = 0 in inequality y - 4x ≥ 0
40 ≥ 0 which is true.
⇒ The points of region y - 4x ≥ 0 lies on OB and above it.

(iv) The points of region x ≥ 0 lies on y-axis and right side of y-axis.

(v) The point of region y ≥ 0 lies on x-axis and above x-axis.

(vi) Intersection point of line x = 20 and y = 4x is C(20,80).

(vii) Intersection point of line y = 4x and x + y = 200 is B(40,160).

(viii) Intersection point of line x = 20 and x + y = 200 is A(20,180).

The feasible region of this problem is ABC which is shaded.
Now, objective function:
Z = 1000x + 600y 
At point A(20,180),
Z = 1000 × 20 + 600 × 180 = 20000 + 108000 =128000 

At point B(40,160),
Z = 1000 × 40+ 600 × 160 = 40000 + 96000 = 136000 

At point C(20, 80),
Z = 1000 × 20 + 600 × 80 = 20000 + 48000 = 68000
Hence, 40 tickets of executive class and 160 tickets of economy class should be sold to maximize profit and maximum profit of ₹ 1,36,000.

Question 6.
Two godowns A and B have grain capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F whose requirements are 60,50 and 40 quintals respectively. The cost of transportation per qunital from the godowns to the shops are given in the following table :

Transportation cost per quintal (in ₹)
From/To	A	B
D	6	4
E	3	2
F	2.50	3

How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?
Answer:
Let godown A supplies x and y quintals of grain to the shops D and E respectively. The capacity of godown A is 100 qunitals.
So, the grain transported from shop A to F = 100 - (x + y) quintals.
Only 60 quintals grains is transported to shop D.
Similarly, the grain transported from godown B to shop D = (60 - x) quintals
In the same way the grains transported from godown B to shop E = (50 - y) quintals
Total capacity of godown B is 50 quintals.
∴ Grain transported to shop £ from godown B = 50 - (60 - x + 50 - y)
= (x + y - 60) quintals
The grain transported to shop, D, E, F from godowns A and B as follows, which is shown in the following table :

Shop/Godown	A	B
D	X	60 - x
E	y	50 - y
F	100 = x - y	50 - (60 - x) - (50 - y) = x + y — 60

∴ Subject to constraints x ≥ 0, y ≥ 0, 100 - x - y ≥ 0, x + y ≤ 100
60 - x ≥ 0 or x ≤ 60, 
50 - y ≥ 0 or y ≤ 50
x + y - 60 ≥ 0 or x + y ≥ 60.

Total transportation cost
= 6x + 3y + 2.5(100 - x - y) + 4(60 - x) + 2(50 -y) + 3(x + y - 60)
= 6x + 3y + 250 - 2.5x - 2.5y + 240 - 4x + 100 - 2y + 3x + 3y - 180
= 2.5x + 1.5y + 410
(i) The points of region x ≥ 0 lies on y-axes and right side of it.
(ii) The points of y ≥ 0 lies on x-axes and above it.
(iii) Graph of x + y ≤ 100 : Line x + y = 100 passes through points (100, 0) and (0,100)
∴ Putting x = 0, y = 0 in inequality x + y ≤ 100 0 ≤ 100 which is true.

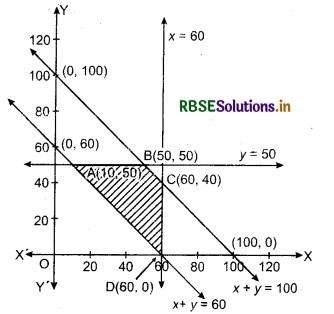
⇒ The points of region x + y ≤ 100 lies on the line x + y = 100 or below it.

(iv) The points of region x ≤ 60 lies on the line x = 60 and right side of it.

(v) The points of region y ≤ 50 lies on the line y = 50 and below it.

(vi) Graph of x + y ≥ 60 : Line x + y = 60 passes through the points (60, 0) and (0, 60).
∴Putting x = 0, y = 0 in inequation x + y ≥ 60  0 ≥ 60 which is not true.
⇒ The points of region x + y ≥ 60 lies on the line x + y = 60 and above it.

The feasible region on this problem is ABCD.
(1) Intersection point of line AB : y = 50 and line AD : x + y = 60 is A(10, 50).
(2) Intersection point of line BC : x + y = 100 and AB : y = 50 is B(50, 50).
(3) Intersection point of line BC : x + y = 100 and AD : x = 60 is C(60, 40).
(4) Intersection point of line CD : x = 60 and AD : x + y = 60 is D(60, 60).

Now, objective function:
Z = 2.5x + 1.5y + 410
At point A (10, 50),
Z = 2.5 × 10 + 1.5 × 50 + 410 = 25 + 75 + 410 = 510

At point B(50, 50),
Z = 2.5 × 50 + 1.5 × 50 + 410
= 125 + 75 + 410 = 610

At point C(60,40),
Z = 2.5 × 60 + 1.5 × 40 + 410
= 150 + 60 + 410 = 620

At point D(60, 0),
Z = 2.5 × 60 + 0 + 410
= 150 + 410 = 560
Thus minimum value of Z is ₹ 510 when the amount of grain transported from A to D, E and F is 10 quintals, 50 quintals and 40 quintals respectively and from B to D, E and F is 50 quintals, 0 quintal and 0 quintal respectively.

Question 7.
An oil company has two depots A and B with capacities of 7000 L and 4000 L respectively. The company is to supply oil to three petrol pumps, D, E and F whose requirements are 4500 L, 3000 L and.3500 L respectively. The distances (in km) between the depots and the petrol pumps is given in the following table :
Distance in (km)

From/To	A	B
D	7	3
E	6	4
F	3	2

Assuming that the transportation cost of 10 litres of oil is ₹ 1 per km, how should the delivery be scheduled in order that the transportation cost is minimum? What is the minimum cost?
Answer:
Suppose x litres of petrol be supplied to petrol pump D and y litres of petrol be supplied to petrol pump E from depot A.
Total capacity of depot A is 7000 litres Petrol supply from depot A to petrol pump F is [7000 - (x + y)] litres.
⇒ 7000 - (x + y) > 0
∴ x + y ≤ 7000 ...(1)
The requirement of petrol pump D is 4500 litres
∴ Petrol supply from depot B is (4500 - x) litres
 4500 - x ≥ 0 or x ≤ 4500 .. .(2)

The requirement of petrol pump E is 3000 litres,
∴ Petrol supply to petrol pump E by depot B is (3000 - y) litres.
 3000 - y ≥ 0 or y ≤ 3000

The requirement of petrol pump F is 3500 litres Petrol supplied to pump F by depot A is 7000 - (x + y) litres
Petrol supplied to F by depot B is 3500 - (7000 - x - y)
= - 3500 + x - y litres.
 - 3500 + x + y ≥ 0 or x + y ≥ 3500
Y Subject to.constraints x + y < 7000, x ≤ 4500, y < 3000, x + y ≥ 3500, x, y ≥ 0
Transportation cost of 10 litres of petrol is ₹ 1 per km. 
⇒ Transportation cost per litre is ₹ 0.1 per km
From transportation cost table :

Z = 0.7x + 0.6y + 0.3(7000 - x - y) + 0.3(4500 - x) + 0.4(3000 - y) + 0.2(x + y - 3500)
or Z = 0.3x + 0.1y + 3950

(i) Graph of x + y ≤ 7000 : Line x + y = 7000 passes through points A(7000,0) and B(0, 7000).
∴ Putting x = 0, y = 0 in inequality x + y ≤ 7000 0 ≤ 7000, which is true.
⇒ x + y ≤ 7000 lies on line x + y = 7000 and below it.

(ii) The points of region x ≤ 4500 lies on x = 4500 and right side of it.

(iii) The point of region y ≤ 3000 lies on y = 3000 and below it.

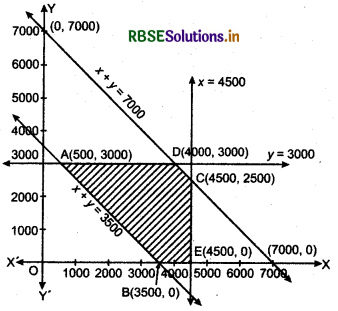
(iv) Graph of x + y ≥ 3500 : Line x + y = 3500 passes through the points (3500,0) and (0,3500)
∴ Putting x = 0, y = 0 in inequality x + y ≥ 3500 0 ≥ 3500 which is not true.
⇒ The points of region x + y ≥ 3500 lies on x + y = 3500 or above it.

(v) The points or region x ≥ 0 lies on y-axes and right side of it.

(vi) The points of region y ≥ 0 lies on x-axes and above it.

(vii) Intersection points of lines x + y- 3500, y = 0 and y = 3000 are 6(3500,0) and A(500,3000) respectively.

(viii) Intersection point of lines x + y = 7000, x = 4500 and y = 3000 are C(4500, 2500) and D(4000, 3000) respectively.

(ix) Line x = 4500 meets on x-axes at point £(4500,0).
∴ The feasible region of this problem is ABECD.
Now objective function:
Z = 0.3x + 0.1y + 3950
At point A(500,3000),
Z = 0.3 × 500 + 0.1 × 3000 + 3950 = 150 + 300 + 3950 = 4400
At point 6(3500,0),
Z = 0.3 × 3500 + 0 + 3950 = 1050 + 3950 = 5000
At point E(4500,0),
Z = 0.3 × 4500 + 0 + 3950 = 1350 + 3950 = 5300
At point C(4500,2500),
Z = 0.3 × 4500 + 0.1 × 2500 + 3950 -1350 + 250 + 3950 = 5550
 
At point D(4000,3000),
Z = 0.3 × 4000 + 0.1 × 3000 + 3950 - 1200 + 300 + 3950 = 5450
Hence, minimum transportation cost is ₹ 4400 when the oil supplied from depot A is 500 L, 3000L and 3500L and from depot 6 is 4000 L, 0 L and 0 L to petrol pumps D, E and F respectively. 

Question 8. 
A fruit grower can use two types of fertilizer in his garden, brand P and brand Question The amount (in kg)' of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.
If the grower wants to minimise the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?

kg per bag
	Brand P	Brand Q
Nitrogen	3	3.4
Phosphoric acid	1	2
Potash	3	1.5
Chlorine	1.5	2

Answer:
Let the fruit grower mixes x bags of brand P and y bags of brand Q. Total amount of nitrogen in bags = 3x + 3.5y
∴ Objective function: Z = 3x + 3.5y
(To find minimum value)
Amount of phosphoric acid in mixture = (x + 2y) kg
⇒ x + 2y ≥ 240
Amount of potash in mixture = 3x + 1.5y
⇒ 3x + 1.5y ≥ 270
Amount of chlorine in mixture = 1.5x + 2y
⇒ 1.5x + 2y ≤ 310

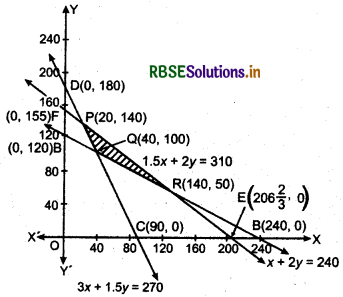
Subject to constraints in the problem :
x + 2y ≥ 240, 3x + 1.5y ≥ 270,1.5x + 2y ≤ 310, x, y ≥ 0.
(i) Graph of x + 2y ≥ 240 : Line x + 2y = 240 passes through the points A(240,0) and B(0,120).
Putting x = 0, y = 0 in inequality x + 2y ≥ 240
0 ≥ 240 which is not true.
⇒ The points of region x + y ≥ 240 lies on AB and above it.
(ii) Graph of 3x + 1.5y ≥ 270 : Line 3x + 1.5y = 270 passes through the points C(90, 0) and D(0,180)
∴ Putting x = 0, y = 0 in inequality 3x + 1.5y ≥ 270
0 ≥ 270 which is not true

⇒ The points of region 3x + 1.5y ≥ 270 lies on CD or above it. 
(iii) Graph of 1.5x + 2y ≤ 310 : Line 1.5x + 2y = 310 passes through the points E (206 \(\frac{2}{3}\), 0) and F(0, 155).
∴ Putting x = 0, y = 0 in in equation 1.5x + 2y ≤ 310 0 ≤ 310 which is true
⇒ The points of region 1.5x + 2y ≤ 310 lies on EF or below it.

(iv) The points of region x ≥ 0 lies on y-axis and right side of it.

(v) The points of region y ≥ 0 lies on x-axis and above it.

(vi) Intersection points of line AB : x + 2y = 240 and CD: 3x + 1.5 y = 270 is Q(40,100)

(vii) Intersection points of lines AB : x + 2y = 240 and EF: 1.5 x + 2y = 310 is R(140, 50)

(viii) Intersection points of lines CD : 3x + 1.5y = 270 and EF: 1.5x + 2y = 310 is P(20,140).
The feasible region of this problem is APQR.
Now, objective function:
Z = 3x + 3.5y

At point P(20,140),
Z = 3 × 20 + 3.5 × 140
= 60 + 490 = 550

At point Q(40,100),
Z = 3x40 + 3.5x100
= 120 + 350 = 470

At point R(140,50),
Z = 3 × 140 + 3.5 × 50
=420 + 175 = 595
Hence Z is minimum at x = 40, y = 100 and minimum amount of nitrogen is 470 kg.

Question 9.
Refer to Question 8. If the grower wants to maximise the amount of nitrogen added to the garden, how many bags of each brand should be added? What is the maximum amount of nitrogen added?
Answer:
Let the fruit grower mixes x bags of brand P and y bags of brand Q. Total amount of nitrogen in bags = 3x + 3.5y
∴ Objective function: Z = 3x + 3.5y
(To find minimum value)
Amount of phosphoric acid in mixture = (x + 2y) kg
⇒ x + 2y ≥ 240
Amount of potash in mixture = 3x + 1.5y
⇒ 3x + 1.5y ≥ 270
Amount of chlorine in mixture = 1.5x + 2y
⇒ 1.5x + 2y ≤ 310

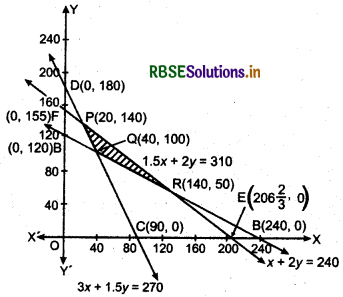
Subject to constraints in the problem :
x + 2y ≥ 240, 3x + 1.5y ≥ 270,1.5x + 2y ≤ 310, x, y ≥ 0.
(i) Graph of x + 2y ≥ 240 : Line x + 2y = 240 passes through the points A(240,0) and B(0,120).
Putting x = 0, y = 0 in inequality x + 2y ≥ 240
0 ≥ 240 which is not true.
⇒ The points of region x + y ≥ 240 lies on AB and above it.
(ii) Graph of 3x + 1.5y ≥ 270 : Line 3x + 1.5y = 270 passes through the points C(90, 0) and D(0,180)
∴ Putting x = 0, y = 0 in inequality 3x + 1.5y ≥ 270
0 ≥ 270 which is not true

⇒ The points of region 3x + 1.5y ≥ 270 lies on CD or above it. 
(iii) Graph of 1.5x + 2y ≤ 310 : Line 1.5x + 2y = 310 passes through the points E (206 \(\frac{2}{3}\), 0) and F(0, 155).
∴ Putting x = 0, y = 0 in in equation 1.5x + 2y ≤ 310 0 ≤ 310 which is true
⇒ The points of region 1.5x + 2y ≤ 310 lies on EF or below it.

(iv) The points of region x ≥ 0 lies on y-axis and right side of it.

(v) The points of region y ≥ 0 lies on x-axis and above it.

(vi) Intersection points of line AB : x + 2y = 240 and CD: 3x + 1.5 y = 270 is Q(40,100)

(vii) Intersection points of lines AB : x + 2y = 240 and EF: 1.5 x + 2y = 310 is R(140, 50)

(viii) Intersection points of lines CD : 3x + 1.5y = 270 and EF: 1.5x + 2y = 310 is P(20,140).
The feasible region of this problem is APQR.
Now, objective function:
Z = 3x + 3.5y

At point P(20,140),
Z = 3 × 20 + 3.5 × 140
= 60 + 490 = 550

At point Q(40,100),
Z = 3x40 + 3.5x100
= 120 + 350 = 470

At point R(140,50),
Z = 3 × 140 + 3.5 × 50
=420 + 175 = 595

Z = 3x + 3 5y
Z is maximum at point R(140, 50) maximum amount of nitrogen is 595 kg when 140 bags of brand P and 50 bags of brand Q be added.

Question 10.
A toy company manufactures two types of dolls, A and B. Market research and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is atmost half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of other type by atmost 600 units. If the company makes profit of ₹ 12 and ₹ 16 per doll respectively on dolls A and B, how many of each should be produced weekly in order to maximise the profit?
Answer:
Suppose a toy company manufactures x dolls of type A and y dolls of type B. Company makes profit of ₹ 12 and ₹ 16 per. dolls respectively on dolls of type A and type B.
Total profit = 12x + 16y
Now, objective function :
Z = 12x + 16y
(To find maximum value)
Maximum production of both types of dolls = 1200
x + y ≤ 1200

The production level of dolls of type A can exceed three times the production of dolls of type B by atmost 600 units. '
⇒ x - 3y ≤ 600
The demand for dolls of type B is atmost half of that for dolls of type A.
⇒ y ≥ \(\frac{x}{2}\) or x ≤ 2y or x - 2y ≤ 0
Thus, subject to constraints :
x + y ≤ 1200, x - 3y ≤  600, y ≥ \(\frac{x}{2}\), y ≥ 0.
(i) Graph of x + y ≤  1200 : Line x + y = 1200 passes through the points A(1200, 0) and B(0, 1200)
∴ Putting x = 0, y = 0 in inequality x + y ≤  1200
0 ≤  1200, which is true.

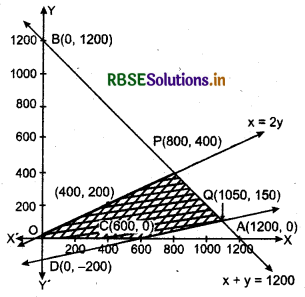
⇒ The points of region x + y ≤ 1200 lies on AB and below it.
(ii) Graph of x - 3y ≤ 600 : Line x - 3y = 600 passes through the points C(600, 0) and D(0, - 200).
∴ Putting x = 0, y = 0 in inequality x - 3y ≤ 600 0 ≤ 600, which is true.
⇒ The points of region x - 3y ≤ 600 lies on CD and above it.

(iii) Graph of y ≥ \(\frac{x}{2}\) or x ≥ 2y or x - 2y ≤ 0: Line x-2y = 0 passes through the points origin O and P(800,400).
∴ Putting x = 0, y = 0 in inequality x-2y<Q
200 ≤ 0 which is true.
⇒ The points of region x - 2y ≤ 0 lies on OP and below it. 

(iv) The points of region x ≥ 0 lies on y-axes and right side of it.

(v) The points of region y ≥ 0 lies on x-axes and above it.

(vi) Intersection points of lines AB : x + y = 120 and x = 2y is P(800,400).

(vii) Intersection points of lines CD : x - 3y = 600 and AB:x + y = 1200is Q(1050,150)
∴ The feasible region of this problem is OPQC.
Now, objective function:
Z = 12x + 16y
At point P(800,400),
Z = 12 × 800 + 16 × 400 = 9600 + 6400 = 16000
At point Q(1050,150),
Z = 12 × 1050 + 16 × 150 = 12600 + 2400 =15000
At point C(600, 0),
Z = 12 × 600 + 0 = 7200
Thus, maximum profit is ₹ 16000 which is at x = 800, y = 400.
Hence, 800 and 400 dolls of type A and type B should be produced respectively to get the maximum profit of ₹ 16000.