RBSE Solutions for Class 12 Maths Chapter 12 रैखिक प्रोग्रामन Ex 12.2

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 12 रैखिक प्रोग्रामन Ex 12.2 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 12 रैखिक प्रोग्रामन Ex 12.2

प्रश्न 1.
रेशमा दो प्रकार के भोज्य P और Q को इस प्रकार मिलाना चाहती है कि मिश्रण में विटामिन अवयवों में 8 मात्रक विटामिन A तथा 11 मात्रक विटामिन B हों। भोज्य P की लागत Rs. 60/kg और भोज्य Q की लागत Rs. 80/kg है। भोज्य P में 3 मात्रक/kg विटामिन A और 5 मात्रक/kg विटामिन B है जबकि भोज्य Q में 4 मात्रक/kg विटामिन A और 2 मात्रक/kg विटामिन B है। मिश्रण की न्यूनतम लागत ज्ञात कीजिए।
हल:
माना कि रेशमा x kg भोज्य P और y kg भोज्य Q मिश्रण बनाती है। प्रश्नानुसार प्रदत्त आँकड़ों से निम्न सारणी बना सकते हैं-

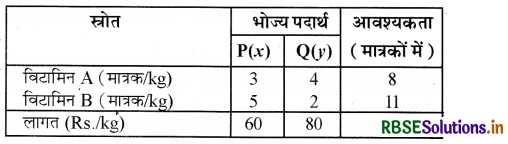
दोनों भोज्यों का लागत मूल्य = 60x + 80y
∴ उद्देश्य फलन Z = 60x + 80y
विटामिन A की कुल मात्रा 3x +4y जो कि कम से कम 8 मात्रक है।
अर्थात् 3x + 4y ≥ 8
विटामिन B की कुल मात्रा 5x+2y जो कि कम से कम 11 मात्रक है।
अर्थात् 5x + 2y ≥ 11
इस प्रकार Z = 60x + 80y का न्यूनतमीकरण करना है जबकि अवरोध 3x + 4y ≥ 8; 5x + 2y ≥ 11, x, y ≥ 0 है।

(i) 3x + 4y ≥ 8 का क्षेत्र
रेखा 3x + 4y = 8 बिन्दु A\(\left(\frac{8}{3}, 0\right)\) और B(0, 2) से गुजरती है। 3x + 4y ≥ 8 में x = 0, y = 0 रखने पर 0 ≥ 8 जो सत्य नहीं है।
अर्थात् 3x + 4y ≥ 8 के क्षेत्र बिन्दु रेखा AB पर और उसके ऊपर हैं।

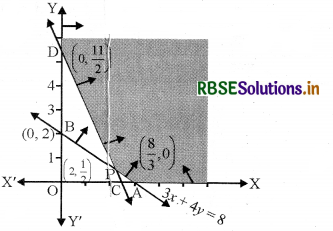
(ii) 5x + 2y > 11 का क्षेत्र
रेखा 5x + 2y = 11, बिन्दु C\(\left(\frac{11}{5}, 0\right)\) और D\(\left(0, \frac{11}{2}\right)\) से होकर जाती है।
∴ 5x + 2y ≥ 11 में x = 0, y = 0 रखने पर 0 ≥ 11 जो सत्य नहीं है।
अर्थात् 5x + 2y ≥ 11 के क्षेत्र बिन्दु रेखा CD पर या उसके ऊपर है।

(iii) x ≥ 0 के क्षेत्र बिन्दु -अक्ष पर और उसके दायीं ओर हैं।

(iv) y ≥ 0 के क्षेत्र के बिन्दु :-अक्ष पर और उसके ऊपर स्थित हैं। इस प्रकार समस्या का सुसंगत क्षेत्र YDPAX है।
बिन्दु P रेखा AB = 3x + 4y = 8 और CD = 5x + 2y = 11 का प्रतिच्छेदन बिन्दु है जिसके निर्देशांक \(\left(2, \frac{1}{2}\right)\) हैं।
अर्थात् कोनीय बिन्दु हैं D\(\left(0, \frac{11}{2}\right)\), P\(\left(2, \frac{1}{2}\right)\) तथा A\(\left(\frac{8}{3}, 0\right)\)|
अब इन बिन्दुओं पर Z का मान निम्नांकित सारणी के अनुसार ज्ञात करेंगे-

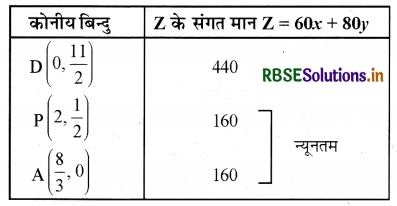
कोनीय बिन्दु z के संगत मान Z = 60x + 80p
∴ Z का न्यूनतम मान 160 परन्तु सुसंगत क्षेत्र अपरिबद्ध है। असमिका 60x + 80y < 160 पर विचार करने पर है।
60x + 80y < 160 या 3x + 4y < 8 के क्षेत्र और सुसंगत क्षेत्र में कोई भी बिन्दु उभयनिष्ठ नहीं है।
∴ Z का न्यूनतम मान 160 है जो AP के प्रत्येक बिन्दु पर है।

प्रश्न 2.
एक प्रकार के केक को 200 g आटा तथा 25 g वसा (fat) की आवश्यकता होती है तथा दूसरी प्रकार के केक के लिए 100 g आटा तथा 50g वसा की आवश्यकता होती है । केकों की अधिकतम संख्या बताओ जो 5 किलो आटे तथा 1 किलो वसा से बन सकते हैं, यह मान लिया गया है कि केकों को बनाने के लिए अन्य पदार्थों की कमी नहीं रहेगी।
हल:
माना कि पहले प्रकार के x केक और दूसरे प्रकार के) केक बनाए जाते हैं।
इनको बनाने में आटे और वसा की आवश्यकता इस प्रकार है-

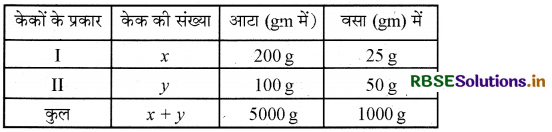
कुल संख्या = x + y
∴ उद्देश्य फलन Z = x + y
आटे की आवश्यकता = 200x + 100y
उपलब्ध आटा = 5000g
अर्थात् 200x + 100y ≤ 5000
या 2x + y ≤ 50
वसा की आवश्यकता = 25x + 50y
उपलब्ध वसा = 1000g
अर्थात् 25x + 50 ≤ 1000
या x + 2 ≤ 40
अब उद्देश्य Z = x + y का अधिकतमीकरण करना है जबकि 2x + y ≤ 50; x + 2y ≤ 40, x, y ≥ 0 अवरोध है।

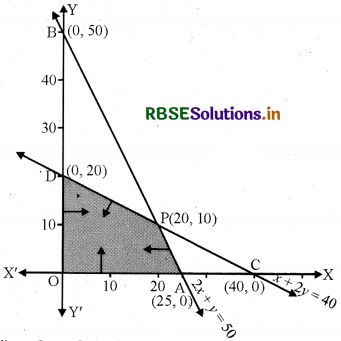
(i) 2x + 2y ≤ 50 का क्षेत्र-
रेखा 2x + y = 50 बिन्दु A(25, 0) और B(0, 50) से गुजरती है।
2x + y ≤ 50 में x = 0, y = 0 रखने पर 0 ≤ 50 जो सत्य है।
अर्थात् 2x + 4y ≤ 50 के क्षेत्र बिन्दु AB पर और उसके नीचे है।

(ii) x + 2y ≤ 40 का क्षेत्र-
रेखा x + 2y = 40, बिन्दु C(40, 0) और D(0, 20) से होकर जाती है।
x + 2y ≤ 40 में x = 0, y = 0 रखने पर 0 ≤ 40 जो सत्य है।
अर्थात् x + 2y ≤ 40 के क्षेत्र बिन्दु रेखा CD पर और उसके नीचे हैं।

(iii) x ≥ 0 के क्षेत्र बिन्दु y-अक्ष पर और उसके दायीं ओर हैं।

(iv) y ≥ 0 के क्षेत्र के बिन्दु x-अक्ष पर और उसके ऊपर हैं। अतः समस्या का सुसंगत क्षेत्र OAPD है। जबकि बिन्दु P, AB = 2x + y = 50, CD = x + 2y = 40 के प्रतिच्छेदन बिन्दु हैं । इसके निर्देशांक (20, 10) हैं।
अर्थात् कोनीय बिन्दु हैं A(25, 0), P(20, 10) तथा D(10, 20)।
अब इन बिन्दुओं पर Z का मान निम्नांकित सारणी के अनुसार ज्ञात करेंगे

कोनीय बिन्दु	z का संगत मान Z = x + y
O (0, 0)	0
A (25,0)	25
P(20, 10)	30 → अधिकतम
D (10, 20)	20

∴ Z का अधिकतम मान 30 बिन्दु P(20, 10) पर है।
पहले प्रकार के 20 और दूसरे प्रकार के 10 केक बनाने चाहिए।

प्रश्न 3.
एक कारखाने में टेनिस के रैकेट तथा क्रिकेट के बल्ले बनते हैं। एक टेनिस रैकेट बनाने के लिए 1.5 घण्टा यांत्रिक समय तथा 3 घण्टे शिल्पकार का समय लगता है। एक क्रिकेट बल्ले को तैयार करने में 3 घण्टे यांत्रिक समय तथा 1 घण्टा शिल्पकार का समय लगता है। एक दिन में कारखाने में विभिन्न यन्त्रों पर उपलब्ध समय के 42 घण्टे और शिल्पकार समय के 24 घण्टे से अधिक नहीं हैं।
(i) रैकेटों और बल्लों को कितनी समय में बनाया जाए ताकि कारखाना पूरी क्षमता से कार्य करे।
(ii) यदि रैकेट और बल्ले पर लाभ क्रमश: ₹20 तथा ₹10 हों तो कारखाने का अधिकतम लाभ ज्ञात कीजिए यदि कारखाना पूरी क्षमता से कार्य करे।
हल:
माना कि कारखाना एक दिन में x टेनिस के रैकेट और / क्रिकेट के बल्ले बनाता है।
हमें दिया है:

कुल समय मशीनी 1.5x + 3y जो अधिकतम 42 घण्टे हैं
या 1.5x + 3y ≤ 42
x + 2y ≤ 28
कुल शिल्पकार का समय 3x + y जो 24 घण्टे तक उपलब्ध है
∴ 3x + y ≤ 24
x रैकेट और बल्लों पर लाभ = 20x + 10y
अब समस्या के उद्देश्य फलन Z = 20x + 10y का अधिकतमीकरण करना है जबकि अवरोध हैं: x + 2y ≤ 28, 3x + y ≤ 24, x, y ≥ 0

(a) x + 2 ≤ 28 का क्षेत्र
रेखा x + 2y = 28 बिन्दु A(28, 0) और B(0, 14) से होकर जाती है। x + 2y < 28 में x = 0, y = 0 रखने पर 0 ≤ 28 जो सत्य है। अर्थात् x + 2y ≤ 28 के क्षेत्र बिन्दु AB पर और उसके नीचे हैं।

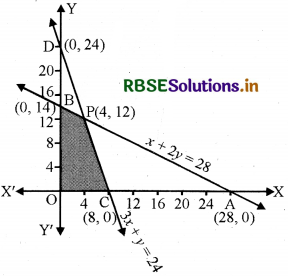
(b) 3x + y ≤ 24 का क्षेत्र
रेखा 3x + y = 24, बिन्दु C(8, 0) और D(0, 24) से होकर जाती है।
3x + y ≤ 24 में x = 0, y = 0 रखने पर 0 ≤ 24 जो सत्य है।
अर्थात् 3x + y ≤ 24 के क्षेत्र बिन्दु रेखा CD पर या उसके नीचे स्थित हैं।

(c) AB = x + 2y = 28, CD = 3x + y = 24 बिन्दु P(4, 12) पर प्रतिच्छेदन करती है।

(d) x ≥ 0 क्षेत्र के बिन्दु y-अक्ष पर और उसकी दायीं ओर हैं।

(e) y ≥ 0 क्षेत्र के बिन्दु :-अक्ष पर और उसके ऊपर हैं।
(i) रैकेट और बल्लों की अधिकतम संख्या प्राप्त करने के लिए उद्देश्य फलन Z = x + y है।
अर्थात् कोनीय बिन्दु हैं C(8, 0), P(4, 12) तथा D(0, 14)। अब इन बिन्दुओं पर Z का मान निम्नांकित सारणी के अनुसार ज्ञात करेंगे

कोनीय बिन्दु	Z के संगत मान Z = x + y
O(0, 0)	0
C(8, 0)	6
P(4, 12)	16→ अधिकतम
D(0, 14)	14

∴ Z का अधिकतम मान 16 है जबकि रैकेट की संख्या 4 है, बल्लों की संख्या 12 है।

(ii) उद्देश्य Z = 20x + 10y लाभ फलन का अधिकतमीकरण
करने पर C(8, 0) पर Z = 20 × 8 + 0 = 160
P(4, 12) पर Z = 20 × 4 + 10 × 12 = 80 + 120 = 200
D(0, 14) पर Z = 20 × 0 + 10 × 14 = 140
इस प्रकार अधिकतम मान ₹ 200 है जब 4 रैकेट और 12 बल्ले बनाए जाते हैं।

प्रश्न 4.
एक निर्माणकर्ता नट और बोल्ट का निर्माण करता है। एक पैकेट नटों के निर्माण में मशीन A पर एक घण्टा और मशीन B पर 3 घण्टे काम करना पड़ता है, जबकि एक पैकेट बोल्ट के निर्माण में 3 घण्टे मशीन A पर और 1 घण्टा मशीन B पर काम करना पड़ता है। वह नटों से ₹ 17.50 प्रति पैकेट और बोल्टों पर ₹ 7.00 प्रति पैकेट लाभ कमाता है। यदि प्रतिदिन मशीनों का अधिकतम उपयोग 12 घण्टे किया जाए तो प्रत्येक (नट और बोल्ट) के कितने पैकेट उत्पादित किए जाएँ ताकि अधिकतम लाभ कमाया जा सके ?
हल:
माना कि x पैकेट नट के और " पैकेट बोल्ट का उत्पादन किया जाता है। अतः प्रश्नानुसार दिए आँकड़ों से-

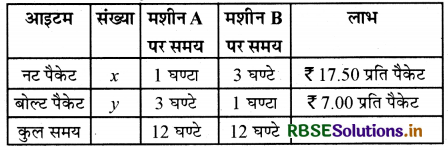
मशीन A के उपयोग का समय = x + 3 घण्टे
उपलब्ध समय = 12 घण्टे
अतःx + 3y ≤ 12
तथा मशीन B के उपयोग का समय = 3x + 1 घण्टे
उपलब्ध समय = 12 घण्टे।
अतः 3x + y ≤ 12
कुल लाभ = 17.50x + 7.00y
उद्देश्य फलन = 17.5x + 7y
अवरोध x + 3y ≤ 12, 3x + y ≤ 12, x, y ≥ 0

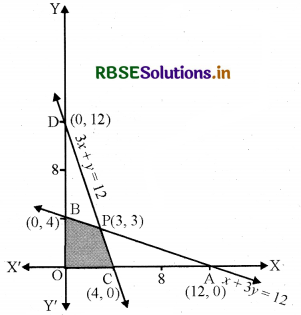
(i) x + 3y ≤ 12 का क्षेत्र -
रेखा x + 3y = 12 बिन्दु A(12, 0) और B(0, 4) से होकर जाती है।
x = 3y ≤ 12 में x = 0, y= 0 रखने पर 0 ≤ 12 जो सत्य है।
अर्थात् x + 3y ≤ 12 क्षेत्र के बिन्दु AB पर और उसके नीचे स्थित हैं।

(ii) 3x + y ≤ 12 का क्षेत्र
रेखा 3x + y = 12 बिन्दु C(4, 0) और D(0, 12) से होकर जाती है।
3x + y ≤ 12 में x = 0, y = 0 रखने पर 0 ≤ 12 जो सत्य है।
अर्थात् 3x + y ≤ 12 के क्षेत्र बिन्दु रेखा CD या उसके नीचे स्थित हैं।

(iii) x ≥ 0 क्षेत्र के बिन्दु y-अक्ष पर और उसकी दायीं ओर हैं।

(iv) y ≥ 0 क्षेत्र के बिन्दु x-अक्ष पर और उसके ऊपर हैं।

(v) रेखा AB = x + 3y = 12 और रेखा CD = 3x + y = 12 बिन्दु P(3, 3) पर प्रतिच्छेदित करती है।
समस्या का सुसंगत क्षेत्र OCPB है।
अर्थात् कोनीय बिन्दु हैं C(4, 0), P(3, 3) तथा B(0, 4)।
अब इन बिन्दुओं पर Z का मान निम्नांकित सारणी के अनुसार ज्ञात करेंगे

कोनीय बिन्दु	Z का संगत मान Z = 17.5x + 7y |
O(0, 0)	0
C(4,0)	70
P(3, 3)	73.5 → अधिकतम
B(0,4)	28

अधिकतम लाभ ₹ 73.5 है जब 3 नट और 3 बोल्ट के पैकेट का उत्पादन किया जाए।

प्रश्न 5.
एक कारखाने में दो प्रकार के पेंच A और B बनते हैं। प्रत्येक के निर्माण में दो मशीनों के प्रयोग की आवश्यकता होती है, जिसमें एक स्वचालित और दूसरी हस्तचालित है। एक पैकेट पेंच A के निर्माण में 4 मिनट स्वचालित और 6 मिनट हस्तचालित मशीन तथा एक पैकेट पेंच B के निर्माण में 6 मिनट स्वचालित और 3 मिनट हस्तचालित मशीन का कार्य होता है। प्रत्येक मशीन किसी भी दिन के लिए अधिकतम 4 घण्टे काम के लिए उपलब्ध है । निर्माता पेंच A के प्रत्येक पैकेट पर रुपये 7 और पेंच B के प्रत्येक पैकेट पर ₹10 का लाभ कमाता है। यह मानते हुए कि कारखाने में निर्मित सभी पेंचों के पैकेट बिक जाते हैं, ज्ञात कीजिए कि प्रतिदिन कितने पैकेट विभिन्न पेंचों के बनाए जाएँ जिससे लाभ अधिकतम हो तथा अधिकतम लाभ ज्ञात कीजिए ।
हल:
माना कि x, A प्रकार के और y, B प्रकार के पेंचों का उत्पादन होता है। प्रश्नानुसार दिए गए आँकड़ों से

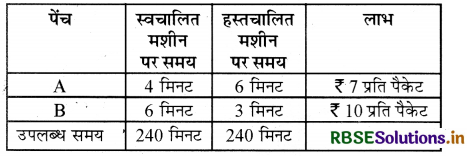
उद्देश्य फलन = 7x + 10y ∴ Z = 7x + 10y
अवरोध 4x + 6y ≤ 240, 6x + 3y ≤ 240, x, y ≥ 0
या 2x + 3y ≤ 120, 2x + y ≤ 80, x, y ≥ 0

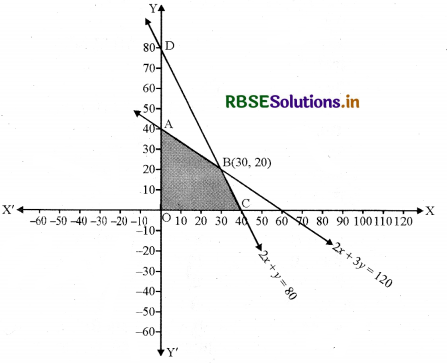
(i) 2x + 3y ≤ 120 का क्षेत्र-
रेखा 2x + 3y = 120, बिन्दु A (0, 40 ) और B (30, 20) से होकर जाती है।

2x + 3y ≤ 120 में x = 0, y = 0 रखने पर 0 ≤ 120 जो सत्य.
अर्थात् 2x + 3y ≤ 120 के क्षेत्र बिन्दु AB पर और उसके नीचे स्थित हैं।

(ii) 2x + y ≤ 80 का क्षेत्र-
रेखा 2x + y = 80 बिन्दु C(40, 0) और D(0, 80) से होकर जाती है।
2x + y ≤ 80 में x = 0, 1 = 0 रखने पर (0 ≤ 80 जो सत्य है।
अर्थात् 2x + y ≤ 80 क्षेत्र के बिन्दु CD पर या इसके नीचे हैं।

(iii) x ≥ 20 क्षेत्र के बिन्दु y-अक्ष पर और उसके दायीं ओर हैं।

(iv) y ≥ 0 क्षेत्र के बिन्दु x-अक्ष पर और उसके ऊपर हैं।

(v) रेखा AB = 2x + 3y = 120, CD = 2x + y = 80 बिन्दु B(30, 20) पर मिलती है।
समस्या का सुसंगत क्षेत्र OABC है।
अर्थात् कोनीय बिन्दु हैं A(0, 40), B(30, 20) तथा C(40, 0)।अब
इन बिन्दुओं पर Z का मान निम्नांकित सारणी के अनुसार ज्ञात करेंगे-

कोनीय बिन्दु	Z का संगत मान Z = 7x+ 10y
0(0, 0)	0
A(0, 40)	400
B(30, 20)	410 → अधिकतम
C(40, 0)	280

इस प्रकार अधिकतम लाभ ₹ 410 है जब 30, A प्रकार के पेंचों के पैकेट और 20, B प्रकार के पेंचों के पैकेटों का उत्पादन होता है।

प्रश्न 6.
एक कुटीर उद्योग निर्माता पैडेस्टल लैंप और लकड़ी के शेड बनाता है। प्रत्येक के निर्माण में एक रगड़ने/काटने और एक स्प्रेयर की आवश्यकता पड़ती है। एक लैंप के निर्माण में 2 घण्टे रगड़ने/काटने और 3 घण्टे स्प्रेयर की आवश्यकता होती है, जबकि एक शेड के निर्माण में 1 घण्टा रगड़ने/काटने और 2 घण्टे स्प्रेयर की आवश्यकता होती है। स्प्रेयर की मशीन प्रतिदिन अधिकतम 20 घण्टे और रगड़ने/काटने की मशीन प्रतिदिन अधिकतम 12 घण्टे के लिए उपलब्ध है। एक लैंप की बिक्री पर ₹ 5 और एक शेड की बिक्री पर ₹ 3 का लाभ होता है। यह मानते हुए कि सभी निर्मित लैंप और शेड बिक जाते हैं, तो बताइए वह निर्माण की प्रतिदिन कैसी योजना बनाए कि लाभ अधिकतम हो?
हल:
मानां कि x लैंप और " शेड उत्पादित किए जाते हैं। प्रश्नानुसार दिए गए आँकड़ों से

उद्देश्य फलन = 5x + 3y
अवरोध 2x + y ≤ 12, 3x + 2y ≤ 20, x, y ≥ 0

(i) 2x + y ≤ 12 का क्षेत्र
रेखा 2x + y = 12 बिन्दु A(6, 0) और B(0, 12) से होकर जाती है। 2x + y ≤ 12 में x = 0, y = 0 रखने पर 0 ≤ 12 जो सत्य है।
अर्थात् 2x + y ≤ 12 के क्षेत्र बिन्दु रेखा AB पर और उसके नीचे स्थित हैं।

(ii) 3x + 2 ≤ 20 का क्षेत्र-
रेखा 3x + 2y = 20 बिन्दु C\(\left(\frac{20}{3}, 0\right)\) और D(0, 10) से होकर जाती है।
3x + 2y ≤ 20 में x = 0, y = 0 रखने पर 0 ≤ 20 जो
अर्थात् 3x + 2y ≤ 20 रेखा CD पर और इसके नीचे का क्षेत्र

(iii) x ≥ 0 क्षेत्र के बिन्दु y-अक्ष पर और उसके दायीं ओर सत्य है।

(iv) y ≥ 0 क्षेत्र के बिन्दु x-अक्ष पर और उसके ऊपर हैं।

(v) AB = 2x + y = 12, CD = 3x + 2y = 20 बिन्दु P(4, 4) पर मिलती है।
समस्या का सुसंगत क्षेत्र OAPD है।

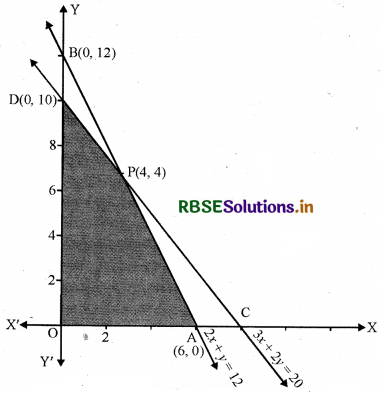
अर्थात् कोनीय बिन्दु हैं A(6, 0), P(4, 4) तथा D(0, 10)। अब इन बिन्दुओं पर Z का मान निम्नांकित सारणी के अनुसार ज्ञात करेंगे

कोनीय बिन्दु	Z के संगत मान Z = 5x + 3y
O(0, 0)	0
A(6, 0)	30
P(4, 4)	32 → अधिकतम
D(0, 10)	30

अधिकतम लाभ 32 है यदि निर्माता 4 लैंप और 2 शेड प्रतिदिन का उत्पादन करे।

प्रश्न 7.
एक कम्पनी प्लाईवुड के अनूठे स्मृति चिह्न का निर्माण करती है। A प्रकार के प्रति स्मृति चिह्न के निर्माण में 5 मिनट काटने और 10 मिनट जोड़ने में लगते हैं। B प्रकार के प्रति स्मृति चिह्न के लिए 8 मिनट काटने और 8 मिनट जोड़ने में लगते हैं। दिया गया है कि काटने के लिए कुल समय 3 घण्टे 20 मिनट तथा जोड़ने के लिए 4 घण्टे उपलब्ध हैं। प्रत्येक A प्रकार के स्मृति चिह्न पर ₹5 और प्रत्येक B प्रकार के स्मृति चिह्न पर ₹6 का लाभ होना है। ज्ञात कीजिए कि लाभ के अधिकतमीकरण के लिए प्रत्येक प्रकार के कितने-कितने स्मृति चिह्नों का कम्पनी द्वारा निर्माण होना चाहिए?
हल:
माना कि A प्रकार के स्मृति चिह्न x और B प्रकार के स्मृति चिह्न y कम्पनी द्वारा निर्मित किए जाते हैं। प्रश्नानुसार दिए गए आँकड़ों से

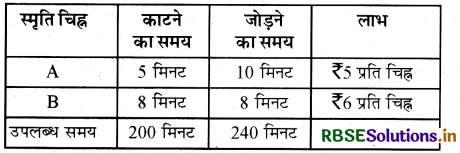
उद्देश्य फलन Z = 5x + 6y
अवरोध 5x + 8y ≤ 200, 10x + 8y ≤ 240, x, y ≥ 0
5x + 8y ≤ 200, 5x + 4y ≤ 120, x, y ≥ 0

(i) 5x + 8y < 200 का क्षेत्र रेखा 5x + 8y = 200 बिन्दुA(40, 0) और B(0, 25) से होकर जाती है। 5x + 8y < 200 में x = 0, } = (0 रखने पर 0 < 200 जो सत्य है। = 5x + 8y< 120 के क्षेत्र बिन्दु AB पर और उसके नीचे स्थित हैं।

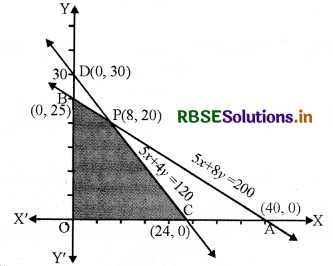
(ii) 5x + 4y ≤ 120 का क्षेत्र रेखा 5x + 4y = 120 बिन्दु C(24, 0) और D(0, 30) से होकर जाती है।
5x + 4y ≤ 120 में x = 0, 3y = 0 रखने पर 0 ≤ 120 जो सत्य है।
⇒ 5x + 4y ≤ 120 रेखा CD पर या उसके नीचे का क्षेत्र है।

(iii) x ≥ 0 क्षेत्र के बिन्दु -अक्ष पर और उसकी दायीं ओर हैं।

(iv) y ≥ 0 क्षेत्र के बिन्दु x-अक्ष पर और उसके ऊपर हैं।

(v) AB : 5x + 8y = 200 और रेखा CD : 5x + 4y = 120 बिन्दु P(8, 20) पर मिलती है।
समस्या का सुसंगत क्षेत्र OBPC है।
अर्थात् कोनीय बिन्दु हैं B(0, 25), P(8, 20) तथा C(24,0)। अब
इन बिन्दुओं पर Z का मान निम्नांकित सारणी के अनुसार ज्ञात करेंगे

कोनीय बिन्दु	Z का संगत मान Z = 5x + 6y
0(0,0)	0
B(0, 25)	150
P(8, 20)	160 → अधिकतम
C(24,0)	120

∴ Z का अधिकतम मान ₹160 है जो 8,A प्रकार के और 20, B प्रकार के स्मृति चिह्न निर्माण करने पर प्राप्त होता है।

प्रश्न 8.
एक सौदागर दो प्रकार के निजी कम्प्यूटर—एक डेस्कटॉप नमूना और दूसरा पोर्टेबल नमूना, जिनकी कीमतें क्रमशः ₹25,000 और ₹40,000 होंगी, बेचने की योजना बनाता है, वह अनुमान लगाता है कि कम्प्यूटर की कुल मासिक माँग 250 नगों से अधिक नहीं होगी। प्रत्येक प्रकार के कम्प्यूटरों के नगों की संख्या ज्ञात कीजिए जिसे सौदागर अधिकतम लाभ प्राप्त करने के लिए संग्रह करे, यदि उसके पास निवेश के लिए ₹70 लाख से अधिक नहीं है और यदि डेस्कटॉप नमूने पर उसका लाभ ₹4,500 और पोर्टेबल नमूने पर ₹5,000 लाभ हो।
हल:
माना कि x डेस्कटॉप और y पोर्टेबल कम्प्यूटर उस सौदागर के पास हैं। प्रश्नानुसार दिए गए आँकड़ों से

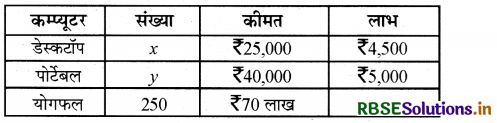
उद्देश्य फलन Z = 4500x + 5000y
उद्देश्य x + y ≤ 250
25000x + 40000y ≤ 70,00,000
या 5x + 8y ≤ 1400
तथा x, y ≥ 0

(i) x + y ≤ 250 का क्षेत्र रेखा x + y = 250 बिन्दु A(250, 0) और B(0, 250) से होकर जाती है।

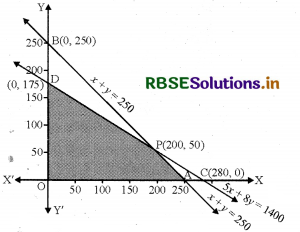
x + y ≤ 250 में x = 0, y = 0 रखने पर 0 ≤ 250 जो सत्य है।
अर्थात् x + y ≤ 250 के क्षेत्र बिन्दु AB पर और उसके नीचे हैं।

(ii) 5x + 8y ≤ 1400 का क्षेत्र-
रेखा 5x + 8y = 1400 बिन्दु C(280, 0) और D(0, 175) से होकर जाती है।
5x + 8y ≤ 1400 में x = 0, y = 0 रखने पर 0 < 1400 जो सत्य है।
अर्थात् 5x + 8y ≤ 1400 क्षेत्र के बिन्दु CD पर या उसके नीचे है।

(iii) x ≥ 0 क्षेत्र के बिन्दु y-अक्ष पर और उसकी दायीं ओर हैं।

(iv) y ≥ 0 क्षेत्र के बिन्दु :-अक्ष पर और उसके ऊपर हैं।

(v) रेखा AB = x + y = 250, CD = 5x + 8y = 1400 बिन्दु P(200, 50) पर मिलती हैं।
समस्या का सुसंगत क्षेत्र OAPD है।
अर्थात् कोनीय बिन्दु हैं A(250, 0), P(200, 50) तथा D(0, 175)। अब इन बिन्दुओं पर Z का मान निम्नांकित सारणी के अनुसार ज्ञात करेंगे

कोनीय बिन्दु	Z का संगत मान Z = 4500x + 5000y
O(0, 0)	0
A(250,0)	1125000
P(200, 50)	1150000 → अधिकतम
D(0, 175)	875000

∴ सौदागर का अधिकतम लाभ 11,50,000 प्राप्त करने के लिए 200 डेस्कटॉप और 50 पोर्टेबल कम्प्यूटर का स्टॉक रखना चाहिए।

प्रश्न 9.
एक भोज्य पदार्थ में कम से कम 80 मात्रक विटामिन A और 100 मात्रक खनिज होना चाहिए। दो प्रकार के भोज्य पदार्थ F₁ और F₂ उपलब्ध हैं। भोज्य F₁ की लागत ₹4 प्रति मात्रक और F₂ की लागत ₹5 प्रति मात्रक है। भोज्य F₁ की एक इकाई में कम से कम 3 मात्रक विटामिन A और 4 मात्रक खनिज है। F₂ की प्रति इकाई में कम से कम 6 मात्रक विटामिन A और 3 मात्रक खनिज हैं। इसको एक रैखिक प्रोग्रामन समस्या के रूप में सूत्रबद्ध कीजिए। उस आहार का न्यूनतम मूल्य ज्ञात कीजिए जिसमें इन दो भोज्यों का मिश्रण है और उसमें न्यूनतम पोषक तत्व हैं।
हल:
माना कि x मात्रक भोज्य F₁ और y मात्रक भोज्य F₂ की है।
प्रश्नानुसार दिए गए आँकड़ों से-

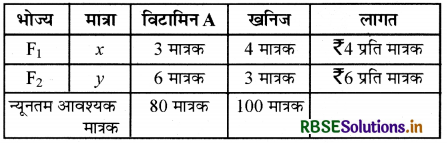
मात्रक रैखिक प्रोग्रामन समस्या इस प्रकार है
उद्देश्य फलन Z = 4x + 6y जिसका न्यूनतमीकरण करना है।

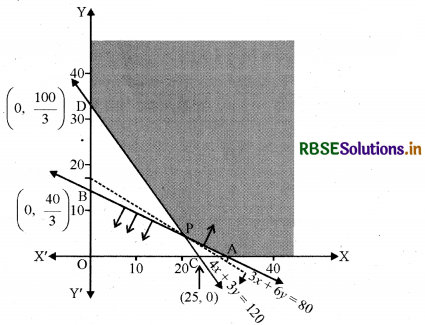
अवरोध 3x + 6y ≥ 80, 4x + 3y ≥ 100, x, y ≥ 0

(i) 3x + 6y > 80 का क्षेत्र-
रेखा 3x + y = 80 बिन्दु A\(\left(\frac{80}{3}, 0\right)\) और B\(\left(0, \frac{40}{3}\right)\) से होकर जाती है। 3x + 6y ≤ 80 में x = 0, y = 0 रखने पर 0 ≤ 80 जो सत्य नहीं है।
अर्थात् 3x + 6y ≥ 80 के क्षेत्र बिन्दु AB पर और उसके ऊपर हैं।

(ii) 4x + 3y ≥ 100 का क्षेत्र-
रेखा 4x + 3y = 100 बिन्दु C(25, 0) और D\(\left(0, \frac{100}{3}\right)\) से होकर जाती है।
4x + 3y ≥ 100 में x = 0, y = 0 रखने पर 0 ≥ 100 जो असत्य है।
अर्थात् 4x + 3y ≥ 100 क्षेत्र के बिन्दु CD पर या उसके ऊपर हैं।

(iii) x ≥ 0 क्षेत्र के बिन्दु y-अक्ष पर और उसकी दायीं ओर हैं।

(iv) y ≥ 0 क्षेत्र के बिन्दु x-अक्ष पर और उसके ऊपर हैं।

(v) रेखा AB = 3x + 6y = 80, CD = 4x + 3y = 100 बिन्दु P\(\left(24, \frac{4}{3}\right)\), पर मिलती है।
समस्या का सुसंगत क्षेत्र YDPAX छायांकित है।
अर्थात् कोनीय बिन्दु हैं D\(\left(0, \frac{100}{3}\right)\), P\(\left(24, \frac{4}{3}\right)\) तथा \(\left(\frac{80}{3}, 0\right)\)।
अब इन बिन्दुओं पर Z का मान निम्नांकित सारणी के अनुसार ज्ञात करेंगे-

अर्थात् Z का न्यूनतम मान = 104 रु. है, जो बिन्दु P\(\left(24, \frac{4}{3}\right)\) पर है। परन्तु सुसंगत क्षेत्र अपरिबद्ध है। रेखा 4x+6y< 104 या 2x + 3y< 52 का कोई बिन्दु सुसंगत क्षेत्र में उभयनिष्ठ नहीं है।
इस प्रकार भोज्यों पर कुल लागत ₹104 है जब भोज्य F₁ की 24 मात्रक और F₂ की \(\frac{4}{3}\) मात्रक प्रयोग की जाए।

प्रश्न 10.
दो प्रकार के उर्वरक F₁ और F₂ हैं। F₁ में 10% नाइट्रोजन और 6% फॉस्फोरिक अम्ल है तथा F₂ में 5% नाइट्रोजन तथा 10% फॉस्फोरिक अम्ल है। मिट्टी की स्थितियों का परीक्षण करने के पश्चात् एक किसान पाता है कि उसे अपनी फसल के लिए 14kg नाइट्रोजन और 14kg फॉस्फोरिक अम्ल की आवश्यकता है। यदि F₁ की कीमत ₹6/kg और F₂ की कीमत ₹5/kg है, प्रत्येक प्रकार का कितना उर्वरक उपयोग के लिए चाहिए ताकि न्यूनतम मूल्य पर वांछित पोषक तत्व मिल सके? न्यूनतम लागत क्या है?
हल:
माना कि x kg, F₁ और ykg, F₂ उर्वरक की आवश्यकता है। .
प्रश्नानुसार दिए गए आँकड़ों से-

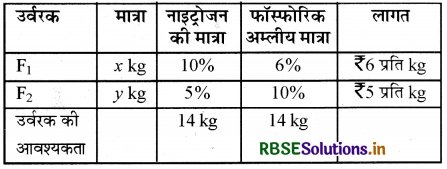
उद्देश्य फलन Z = 6x + 5y
अवरोध \(\frac{10}{100}\) x+\(\frac{5}{100}\) y ≥ 14 या \(\frac{x}{10}+\frac{y}{20}\) ≥ 14
\(\frac{6}{100}\) x+\(\frac{10}{100}\) y ≥ 14, या \(\frac{6 x}{100}+\frac{y}{10}\) ≥ 14
या 2x + y ≥ 280,
3x + 5y ≥ 700, x, y ≥ 0

(i) 2x + y > 280 का क्षेत्र
रेखा 2x + y = 280 बिन्दु A(140, 0) और B(0, 280) से होकर जाती है।
2x + y ≥ 280 में x = 0,y = 0 रखने पर 0 ≥ 280 जो सत्य नहीं है।
अर्थात् 2x + y ≥ 280 के क्षेत्र बिन्दु AB पर और उसके ऊपर है।

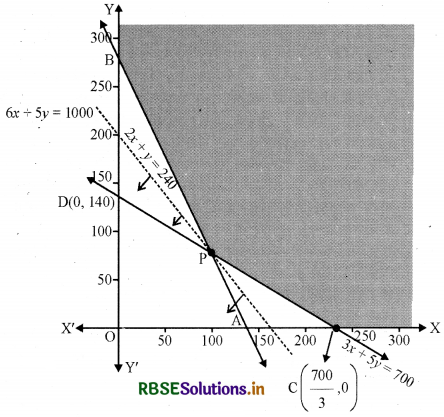
(ii) 3x + 5y ≥ 700 का क्षेत्र-
रेखा 3x + 5y = 700 बिन्दु C\(\left(\frac{700}{3}, 0\right)\) और D(0, 140) से होकर जाती है।
3x + 5y ≥ 700 में x = 0,y= 0 रखने पर 0 ≥ 700 जो सत्य नहीं है।
अर्थात् 3x + 5y ≥ 700 के क्षेत्र बिन्दु CD पर या उसके ऊपर हैं।

(iii) x ≥ 0 क्षेत्र के बिन्दु y-अक्ष पर और उसकी दायीं ओर हैं।

(iv) y ≥ 0 क्षेत्र के बिन्दु x-अक्ष पर और उसके ऊपर हैं।

(v) रेखा AB = 2x + y = 280, CD = 3x + 5y = 700 बिन्दु P(100, 80) पर मिलती है। समस्या का सुसंगत क्षेत्र YBPCX है।
अर्थात् कोनीय बिन्दु हैं B (0, 280), P ( 100, 80) तथा C\(\left(\frac{700}{3}, 0\right)\)|
अब इन बिन्दुओं पर Z का मान निम्नांकित सारणी के अनुसार ज्ञात करेंगे-

कोनीय बिन्दु	Z का संगत मान Z = 6x + 5 y
B(0, 280)	1400   न्यूनतम
P(100, 80)	1000
C\left(\frac{700}{3}, 0\right)	1400

इस प्रकार Z का न्यूनतम मान ₹1000 है। परन्तु सुसंगत क्षेत्र अपरिबद्ध है। 6x + 5y < 1000 के क्षेत्र बिन्दु और सुसंगत क्षेत्र का कोई बिन्दु उभयनिष्ठ नहीं है।
अर्थात् उर्वरक F₁ को 100 kg और उवर्रक F₂ को 80kg मात्रा उपयोग करने से न्यूनतम लागत ₹1000 है।

प्रश्न 11.
निम्नलिखित असमीकरण निकाय 2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 से निर्धारित सुसंगत क्षेत्र के कोनीय बिन्दु (0, 0), (5, 0), (3, 4) और (0, 5) हैं। माना कि Z =px + ay जहाँ p, q> 0, p तथा व के लिए निम्नलिखित में कौन प्रतिबन्ध उचित है ताकि Z का अधिकतम (3, 4) और (0, 5) दोनों पर घटित होता है।
(A) p = q
(B) p = 2q
(C) p = 3q
(D) q = 3p
उत्तर:
(D) q = 3p

हल:
दिया गया है Z = px + qy
A(0, 0) पर Z = p × 0 + q × 0 = 0
B(5, 0) पर Z = 5p + q × 0 = 5P
C(3, 4) पर Z = 3p + 4q
D(0, 5) पर Z = p × 0 + 5q = 0 + 5q = 5q
दिया है Z का अधिकतम मान बिन्दुओं (3,4) और (0, 5) पर घटित होता है।
अतः 3p + 4q = 5q
या q = 3q और q > p
अतः सही विकल्प (D) है।