RBSE Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 11 Three Dimensional Geometry Miscellaneous Exercise

Question 1.
Show that the line joining the origin to the point (2, 1, 1) is perpendicular to the line determined by the points (3, 5, - 1) and (4, 3, - 1).
Answer:
Let direction ratios of the line which passes through the point A(2, 1, 1) and origin B(0, 0, 0) are 2 - 0, 1 - 0, 1 - 0 or 2, 1, 1 and direction ratios of the line which is determined by point C(3, 5, - 1) and D(4, 3, - 1) are 4 - 3, 3 - 5, - 1 + 1 or 1, - 2, 0.
Now AB and CD will be perpendicular, iff
a₁a₂ + b₁b₂ + c₁c₂ = 0
Now, a₁a₂ + b₁b₂ + c₁c₂
= 2 × 1 + 1 × (- 2) + 1 × 0
= 2 - 2 + 0 = 0
Hence, AB and CD are mutually perpendicular.
Hence proved.

Question 2.
If l₁, m₁, n₁ and l₂, m₂, n₂ are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are
m₁n₂ - m₂n₁, n₁l₂ - n₂l₁, l₁,m₂ - l₂m₁.
Answer:
Let AB and CD are two lines, whose direction cosine are l₁, m₁, n₁ and l₂, m₂, n₂ respectively and which are mutually perpendiculars:
l₁l₂ + m₁m₂ + n₁n₂ = 0 ..... (1)
If l₁, m₁, n₁ and l₂, m₂, n₂ are direction cosines, then
l₁² + m₁² + n₁² = 1 ..... (2)
and l₂² + m₁² + n₁² = 1 .... (3)
Let PQ is perpendicular to AB and CD both and its direction cosines are l, m, n, then

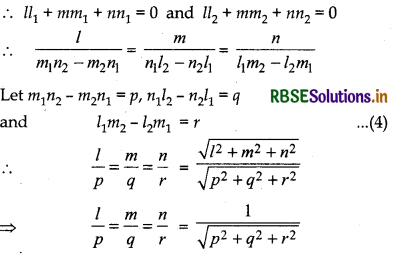
Now (l₁² + m₁² + n₁²) (l₂² + m₂² + n₂²) - (l₁l₂ + m₁m₂ + n₁n₂)²
= (m₁n₂ - m₂n₁)² + (n₁l₂ - n₂l₁)² + (l₁m₂ - l₂m₁)² ....... (5)
From equation (4)
= p² + q² + r²
= (l₁² + m₁² + n₁²) (l₂² + m₂² + n₂₂) - (l₁l₂ + m₁m₂ + n₁n₂)² ....... (6)
From equation (1), (2) and (3),
l₁l₂ + m₁m₂ + n₁n₂ = 0
and l₁² + m₁² + n₁² = 1 and l₂² + m₂² + n₂² = 1
Putting these values in equation (6),
p² + q² + r² = 1 . 1 - 0 = 1

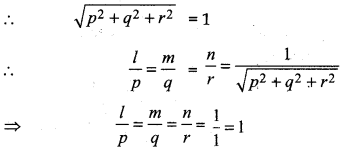
l = p = m₁n₂ - m₂n₁, m = q = n₁l₂ - n₂l₁, n = r = l₁m₂ - l₂m₁
Hence, direction cosines are:
m₁n₂ - m₂n₁, n₁l₂ - n₂l₁, l₁m₂ - l₂m₁
Hence proved.

Question 3.
Find the angle between the lines whose direction ratios are a, b, c and b - c, c - a, a - b.
Answer:
Let angle between those lines is θ whose direction ratios are a, b, c and b - c, c - a, a - b. Then

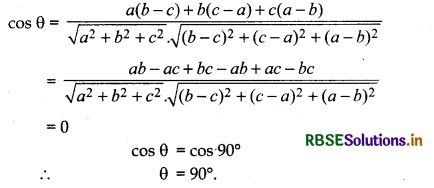
Question 4.
Find the equation of a line parallel to x-axis and passing through the origin.
Answer:
Equation of the line parallel to x-axis and passing through the origin is x-axis. Direction cosines of x-axes are 1, 0, 0.
Hence, equation of x-axis, \(\frac{x}{1}=\frac{y}{0}=\frac{z}{0}\)

Question 5.
if the coordinates of the points A, B, C, and D be (1, 2, 3), (4, 5, 7), (- 4, 3, - 6) and (2, 9, 2) respectively, then find the angle between the lines AB and CD.
Answer:
Let direction ratios of line AB, joining the point A(1, 2, 3) and B(4, 5, 7) are 4 - 1, 5 - 2, 7 - 3 or 3, 3, 4 and direction ratios of line CD joining the point C(- 4, 3, - 6) and D(2, 9, 2) are 2 + 4, 9 - 3, 2 + 6 or 6, 6, 8.
AB || CD
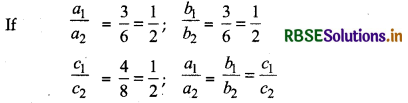So, AB and CD are parallel.
Thus, the angle between them is 0°.

Question 6.
If the lines \(\frac{x-1}{-3}=\frac{y-2}{2 k}=\frac{z-3}{2}\) and \(\frac{x-1}{3 k}=\frac{y-1}{1}=\frac{z-6}{-5}\) are perpendicular, find the value of k.
Answer:
If the given line \(\frac{x-1}{-3}=\frac{y-2}{2 k}=\frac{z-3}{2}\) the direction ratios are - 3, 2k, 2.
and direction ratios of the \(\frac{x-1}{3 k}=\frac{y-1}{1}=\frac{z-6}{-5}\) are 3k, 1, - 5.
Given lines are mutually perpendicular , so
a₁a₂ + b₁b₂ + C₁C₂ = 0
∴ (- 3) × (3k) + 2k × 1 + 2 × (- 5) = 0
⇒ - 9k + 2k - 10 = 0
⇒ - 7k - 10 = 0
⇒ 7k = - 10
∴ k = - \(\frac{10}{7}\)

Question 7.
Find the vector equation of the line passing through (1, 2, 3) and perpendicular to the plane \(\vec{r}\).(î + 2ĵ - 5k̂) + 9 = 0.
Answer:
Perpendicular vector along the plane
\(\vec{r}\).(î + 2ĵ - 5k̂) + 9 = 0 is î + 2ĵ - 5k̂
Hence, equation of the line which passes through the point (1, 2, 3) and along the vector î + 2ĵ - 5k̂ is:
\(\vec{r}\) = (î + 2ĵ + 3k̂) + λ(î + 2kĵ + 5k̂)

Question 8.
Find the equation of the plane passing through (a, b, c) and parallel to the plane \(\vec{r}\).(î + ĵ + k̂) = 2.
Answer:
Equation of any plane parallel to the \(\vec{r}\).(î + ĵ + k̂) = 2 is:
\(\vec{r}\).(î + ĵ + k̂) = λ ...... (1)
This plane passes through the point (a, b, c), then,
∴ (aî + bĵ + ck̂).(î + ĵ + k̂) = λ
⇒ a + b + c = λ
{Put x = a, y = b, z = c in \(\vec{r}\) = xî + yĵ + zk̂
Putting the value of λ in equation (1).
∴ \(\vec{r}\).(î + ĵ + k̂) = a + b + c
This is the required equation of the plane.

Question 9.
Find the shortest distance between the lines
\(\vec{r}\) = 6î + 2ĵ + 2k̂ + λ(î - 2ĵ + 2k̂)
and \(\vec{r}\) = - 4î - k̂ + µ(3î - 2ĵ - 2k̂)
Answer:
Comparing the equation

Question 10.
Find the coordinates of the point where the line passes through (5, 1, 6) and (3, 4, 1) meets the YZ-plane.
Answer:
Equation of the line which passes through the point (5, 1, 6) and (3, 4, 1) is

Question 11.
Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) cross the ZX-plane.
Answer:
Let equation of the line which join the points (x₁, y₁, z₁) and (x₂, y₂, z₂) is:
\(\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}\)
∴ Equation of the line which join the points (5, 1, 6) and (3, 4, 1) is:

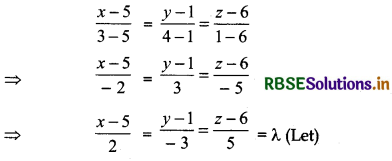
Coordinates of any point on this line
(5 + 2λ, 1 - 3λ, 6 + 5λ)
This point is on the plane YZ i.e., x = 0
5 + 2λ = 0
∴ λ = -5/2
Putting the value of λ in equation (1),

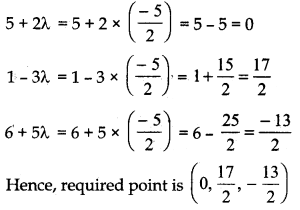
Question 12.
Find the coordinates of the point where the line passes through (3, - 4, - 5) and (2, - 3, 1) and crosses the plane 2x + y + z = 7.
Answer:
Let equation of the line which passes through the points (x₁, y₁, z₁) and (x₂, y₂, z₂) is:

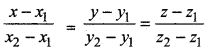
∴ Equation of the line which passes through the point (3, - 4, - 5) and (2, - 3, 1) is:

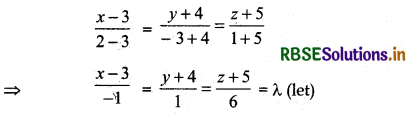
Coordinates of any point on this line
(3 - λ, - 4 + λ, - 5 + 6λ) ....... (1)
This point lids on the plane 2x + y + z =7.
⇒ 2(3 - λ) + (- 4 + λ) + (- 5 + 6λ) = 7
⇒ 6λ - 4 + λ - 5 + 6 = 7
⇒ 5λ - 3 = 7
⇒ 5λ = 10
∴ λ = \(\frac{10}{5}\) = 2
Putting the value of λ in equation (1),
3 - λ = 3 - 2 = 1
- 4 + λ = - 4 + 2 = - 2
- 5 + 6λ = - 5 + 6 × 2
= - 5 + 12 = 7
Hence, required point is (1, - 2, 7).

Question 13.
Find the equation of the plane passing through the point (- 1, 3, 2) and perpendicular to each of the planes
x + 2y + 3z = 5 and 3x + 3y + z = 0.
Answer:
Equation of the plane passing through the point (- 1, 3, 2) is
a(x + 1) + b(y - 3) + c(z - 2) = 0
This plane is perpendicular to x + + 3z 5.
∴ a + 2b + 3c = 0
Equation (1) is perpendicular to 3x + 3y + z = 0
3a + 3b + c = 0
From equation (2) and (3), we get

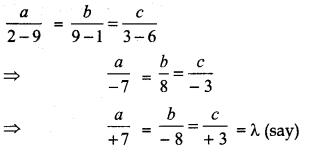
∴ a = 7λ
Putting the values of a, b, c in equation (1), we get
7λ(x + 1) + (- 8λ) (y - 3) + 3λ(z - 2) = 0
⇒ 7(x + 1) - 8(y - 3) + 3(z - 2) = 0
⇒ 7x + 7 - 8y + 24 + 3z - 6 = 0
⇒ 7x - 8y + 3z + 25 = 0
Hence, equation of perpendicular plane is:
7x - 8y + 3z + 25 = 0.

Question 14.
If the points (1, 1, p) and (- 3, 0, 1) be equidistant from the plane \(\vec{r}\) .(3î + 4ĵ - 12k̂) + 13 = 0,then find the value of p.
Answer:
Distance of the plane \(\vec{r} \cdot \vec{n}\) = d from the point \(\vec{r}\) is:

or 20 - 12p = ± 8
Taking +ive sign
20 - 12p = 8
⇒ - 12p = 8 - 20 - 12
∴ p = 1
Taking -ive sign
20 - 12p = - 8
⇒ - 12p = - 8 - 20
⇒ - 12p = - 28
⇒ p = \(\frac{28}{12}\)
∴ p = \(\frac{7}{3}\)
Hence, p = 1, \(\frac{7}{3}\)

Question 15.
Find the equation of the plane passing through the line of intersection of the planes
\(\vec{r}\).(î + ĵ + k̂) = 1 and \(\vec{r}\).(2î + 3ĵ - k̂) + 4 = 0
and parallel to x-axis.
Answer:
Equation of the plane passing through the line of intersection of the planes
\(\vec{r}\).(î + ĵ + k̂) = 1 and \(\vec{r}\).(2î + 3ĵ - k̂) + 4 = 0 is:
\(\vec{r}\).(î + ĵ + k̂) - 1 + λ[\(\vec{r}\).(2î + 3ĵ - k̂) + 4] = 0
⇒ \(\vec{r}\)[(1 + 2λ) + (1 + 3λ) + (1 - λ)] - 1 + 4λ= 0
This plane is parallel to x-axis
∴ Normal of this plane is along x-axis.
Normal vector of the plane is along
[(1 + 2λ)Î + (1 + 3λ)Ĵ + (1 - λ).)k̂]
Direction cosine of x-axis are 1, 0, 0.
⇒ 1.(1 + 2λ) = 0 or λ = -1/2
Putting the value of in equation (1), we get

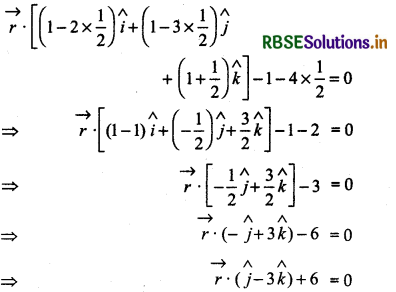
This is the required equation of the plane.

Question 16.
If O be the origin and the coordinates of P be (1, 2, - 3), then find the equation of the plane passing through P and perpendicular to OP.
Answer:
Direction ratios of the line OP which passes
through the point 0(0, 0, 0) and P(1, 2, - 3) are 1 - 0, 2 - 0, - 3 - 0 i.e., 1, 2, - 3.
So, direction ratios of the normal of the plane are (1, 2, -3) and plane passes through the point P(1, 2, -3).
∴ a(x - x₁) + b(y - y₁) + c(z - z₁) = 0
⇒ 1(x - 1) + 2(y - 2) - 3(2z + 3) = 0
⇒ x - 1 + 2y - 4 - 3z - 9 = 0
⇒ x + - 3z - 14 = 0
This is the required equation of the plane.

Question 17.
Find the equation of the plane which contains the line of intersection of the planes \(\vec{r}\). (î + 2ĵ + 3k̂) - 4 = 0, \(\vec{r}\). (2î + ĵ - k̂)+ 5 = 0, and which is perpendicular to the plane \(\vec{r}\) .(5î + 3ĵ - 6k) + 8 = 0.
Answer:
Equation of the plane which contains the line of intersection of the planes
\(\vec{r}\).(î + 2ĵ + 3k̂) - 4 = 0 and r.(2î + ĵ - k̂)+5 = 0 is:
\(\vec{r}\) .(î + 2ĵ + 3k̂) - 4 + [ r .(2î + ĵ - k̂) + 5] = 0
\(\vec{r}\).[(1 + 2λ)î + (2 + λ)ĵ + (3 - λ)k̂] - 4 + 5λ = 0 ..... (1)
Now plane is perpendicular to
\(\vec{r}\).(5î + 3ĵ - 6k̂) + 8 = 0.
∴ Their normal will also be perpendicular.
⇒ (1 + 2λ) × 5 + (2 + λ) × 3 + (3 - λ) × (- 6) = 0
⇒ 5 + 10λ + 6 + 3λ - 18 + 6λ = 0
⇒ 19 λ - 7 = 0
⇒ 19 λ =7
∴ λ = \(\frac{7}{19}\)
Putting the value of λ in equation (1),

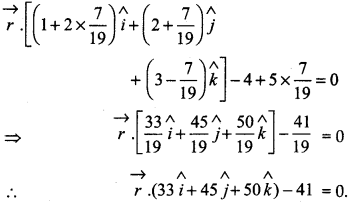
Question 18.
Find the distance of the point (- 1, - 5, - 10) from the point of intersection of the line
\(\vec{r}\) = 2î - ĵ + 2k̂ + λ(3î + 4ĵ + 2k̂) and the plane r.(î - ĵ + k̂) = 5.
Answer:
Given, line \(\vec{r}\) = 2î - ĵ + 2k̂ + λ(3î + 4ĵ + 2k̂) ...... (1)
and plane \(\vec{r}\).(î - ĵ + k̂) = 5 ............ (2)
meets each other.
Putting the value of \(\vec{r}\) in equation (2) from equation
[2î - ĵ + 2k̂ + λ(3î + 4ĵ + 2k̂)].(î - ĵ + k̂) = 5
⇒ (2î - ĵ + 2k̂).(î - ĵ + k̂) + λ(3î + 4ĵ + 2k̂).(î - ĵ + k̂) = 5
⇒ 2 × 1 - 1 × (- 1) + 2 × 1 + λ[(3 × 1 + 4 × (- 1) + 2 × 1] = 5
⇒ 2 + 1 + 2 + λ(3 - 4 + 2) = 5
⇒ 5 + λ = 5
∴ λ = 0
Putting the value of λ in equation (1), point of intersection of line and plane is

Question 19.
Find the vector equation of the line passing through (1, 2, 3) and parallel to the planes \(\vec{r}\).(î - ĵ + 2k̂) = 5 and \(\vec{r}\).(3î + ĵ + k̂) = 6
Answer:
Let equation of the line passing through the point (1, 2, 3)is:
\(\vec{r}\) = î + 2ĵ + 3k̂ + λ(b₁î + b₂ĵ + b₃k̂) ..... (1)
∴ This line is parallel to the plane \(\vec{r}\).(î - ĵ + 2k̂) = 5
Normal of the plane and line (1) is mutually perpendicular.
∴ b₁ - b₂ + 2b₃ = 0 ...(2)
Similarly, line (1) is parallel to the plane
\(\vec{r}\).(3î + ĵ + k̂) = 6.
⇒ Normal of the plane and line (1) is mutually perpendicular.
⇒ 3b₁ + b₂ + b₃ = 0 .... (3)
From equation (2) and (3), we get

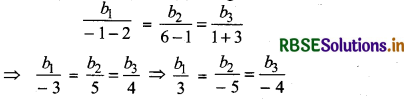
Putting the value of b₁, b₂ and b₃ in equation (1), we get
r = (î + 2ĵ + 3k̂) + λ(3î - 5ĵ - 4k̂).

Question 20.
Find the vector equation of the line passing through the point (1, 2, - 4) and perpendicular to the two lines:
\(\frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7}\) and \(\frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5}\)
Answer:
Let required line be
\(\vec{r}\) = (î + 2ĵ - 4k̂) + λ(b₁î + b₂ĵ + b₃k̂)
Lines \(\frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7}\)
and \(\vec{r}\) = î + 2ĵ - 4k̂+ λ(b₁î + b₂ĵ + b₃k̂)
are mutually perpendicular.
Direction ratios of these lines are 3, - 16, 7 and b₁, b₂, b₃. 
These lines are mutually perpendicular, if
3b₁ - 16b₂; + 7b₃ = 0 ..... (2)
Similarly, direction ratios of lines \(\frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5}\)
and \(\vec{r}\) = î + 2ĵ - 4k̂+ λ(b₁î + b₂ĵ + b₃k̂) are 3, 8, -5 and b₁, b₂, b₃. These lines are mutually perpendicular, if
∴ 3b₁ + 8b₂ - 5b₃ = 0 ..... (3)
From equation (2) and (3),

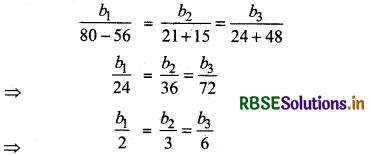
Putting the proportional values of b₁, b₂, b₃ in equation (1)
\(\vec{r}\) = î + 2ĵ - 4k̂+ λ(2î + 3ĵ + 6k̂)
This is the required equation of the line.

Question 21.
Prove that if a plane has the intercepts a, b, c and is at a distance of p units from the origin, then
\(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}=\frac{1}{p^2} \cdot\)
Answer:
Equation of the plane whose intercepts are a, b, c is .

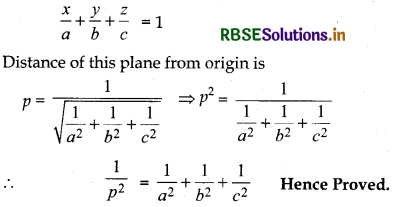
Question 22.
Distance between the two planes 2x + 3y + 4z = 4 and 4x + 6y + 8z = 12is:
(A) 2 units
(B) 4 units
(C) 8 units
(D) units
Answer:
Given, two planes are.
2x + 3y + 4z = 4 ..... (1)
and 4x + 6y + 8z = 12
or 2x + 3y + 4z = 6
Distance between planes ax + by + cz = d₁ and ax + by + cz = d₂ is \(\frac{d_1-d_2}{\sqrt{a^2+b^2+c^2}}\)
∴ Distance between two planes 2x + 3y + 4z = 4 and 2x + 3y + 4z = 6 is
= \(\frac{6-4}{\sqrt{(2)^2+(3)^2+(4)^2}}=\frac{2}{\sqrt{4+9+16}}=\frac{2}{\sqrt{29}}\)
Hence, option (D) is correct.

Question 23.
The planes 2x - y + 4z = 5 and 5x - 2.5y + 10z = 6 are:
(A) Perpendicular
(B) Parallel
(C) Intersect y-axis
(D) Passes through \(\left(0,0, \frac{5}{4}\right)\)
Answer:
Given, planes are
2x - y + 4z =5
and 5x - 2.5y + 10z = 6
Here a₁ = 2, b₁ = - 1, c₁ = 4 and a₂ = 5,