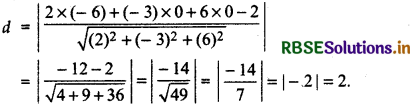RBSE Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry Ex 11.3

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry Ex 11.3 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 11 Three Dimensional Geometry Ex 11.3

Question 1.
In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
(a) z = 2
(b) x + y + z = 1
(c) 2x + 3y - z = 5
(d) 5y + 8 = 0
Answer:
(a) Normal of z = 2 is z-axis. Its direction cosines are cos 90°, cos 90°, cos 0° i.e., 0, 0, 1.
And distance from the origin = 2.

(b) Given, x + y + z = 1
∵ Direction ratios of the normal to the plane is 1,1,1.
Then, direction cosines of the normal to the plane:

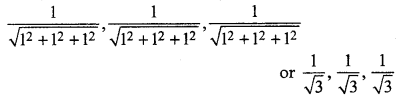
Multiplying by \(\frac{1}{\sqrt{3}}\) to the equation of plane.
\(\frac{1}{\sqrt{3}} x+\frac{1}{\sqrt{3}} y+\frac{1}{\sqrt{3}} z=\frac{1}{\sqrt{3}}\)
Thus, distance of plane from the origin = \(\frac{1}{\sqrt{3}}\)

(c) Given, equation of plane is
2x - 3y - z = 5
∴ Direction ratios of the normal to the plane are 2, - 3,1
∴ Direction cosine of the normal to the plane are:

Multiplying equation of plane by \(\frac{1}{\sqrt{14}}\), we get
\(\frac{2}{\sqrt{14}} x-\frac{3}{\sqrt{14}} y-\frac{1}{\sqrt{14}} z=\frac{5}{\sqrt{14}}\)
Thus, distance of plane from the origin = \(\frac{5}{\sqrt{14}}\)

(d) Given, equation of plane is
5y + 8 = 0 ⇒ 5y = - 8
∴ y = - \(\frac{8}{5}\)
Normal of this plane is y-axis.
Direction cosines are cos 90°, cos 0°, cos 90° i.e., 0, 1, 0
Thus, distance of plane from the origin = \(\left|\frac{-8}{5}\right|=\frac{8}{5}\)

Question 2.
Find the vector equation of a plane which is at a distance of 7 units from the origin and normal to the vector 3î + 5ĵ - 6k̂.
Answer:
Unit vector along vector 3î + 5ĵ - 6k̂ is:

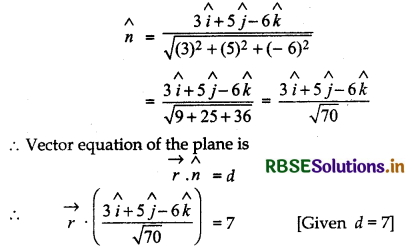
Question 3.
Find the cartesian equation of the following planes:
(a) r. (î + ĵ - k̂) = 2
Answer:
Given, equation \(\vec{r}\). (î + ĵ - k̂) = 2
Putting \(\vec{r}\) = xî + y ĵ + z k̂ in equation (i)
∴ (xî + yĵ + zk̂) (î + ĵ - k̂) = 2
⇒ x × 1 + y × 1 + z × (- 1) = 2
⇒ x + y - z = 2
Hence, cartesian equation of the plane is
x + y - z = 2.

(b) r.(2î + 3ĵ - 4k̂) = 1
Answer:
Given equation \(\vec{r}\).(2î + 3ĵ - 4k̂) = 1
Putting \(\vec{r}\) = xî + y ĵ + z k̂ in equation (i)
∴ (xî + yĵ + zk̂).(2î + 3ĵ - 4k̂) = 1
⇒ x × 2 + y × 3 + z × (- 4) = 1
⇒ 2x + 3y - 4z = 1
Hence, cartesian equation of the plane is
2x + 3y - 4z = 1

(c) r.[(s - 2t)î + (3 - t)ĵ + (2s + t)k̂] = 15.
Answer:
\(\vec{r}\).[(s - 2t)î + (3 - t)ĵ + (2s + t)k̂] = 15
Putting \(\vec{r}\) = xî + y ĵ + z k̂ in equation (i)
∴ (xî + yĵ + zk̂) [(s - 2t)î + (3 - t)ĵ + (2s + t)k̂] = 15
⇒ x × (s - 2t) + y × (3 - t) + z × (2s + t) = 15
Hence, cartesian equation of the plane is
(s - 2t)x + (3 - t)y + (2s + t)z = 15

Question 4.
In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.
(a) 2x + + 4z - 12 = 0
(b) 3y + 4z - 6 = 0
(c) x + y + z = 1
(d) 5y + 8 = 0.
Answer:
Given equation of plane is
2x + + 4z - 12 = 0
Here, \(\sqrt{(2)^2+(3)^2+(4)^2}\) = \(\sqrt{4+9+16}\) = √29
Dividing Eq. (1) by √29
\(\frac{2}{\sqrt{29}} x+\frac{3}{\sqrt{29}} y+\frac{4}{\sqrt{29}} z=\frac{12}{\sqrt{29}}\)
This is the normal form of plane.
∴ Direction cosines (l, m , n) of normal are
\(\frac{2}{\sqrt{29}}, \frac{3}{\sqrt{29}}, \frac{4}{\sqrt{29}}\)
and distance of plane from the origin is (r) = \(\frac{12}{\sqrt{29}}\)
∴ Coordinates of the foot of the perpendicular drawn from the origin:

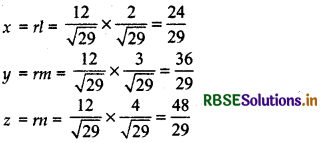
Hence, coordinate of the foot of the perpendicular = \(\left(\frac{24}{29}, \frac{36}{29}, \frac{48}{29}\right)\)

(b) Given equation of plane is
3y + 4z - 6 = 0
Here, \(\sqrt{(3)^2+(4)^2}\) = \(\sqrt{9+16}\) = √25 = 5
Dividing Eq. (1) by S. we get
\(\frac{3}{5} y+\frac{4}{5} z=\frac{6}{5}\)
This is the normal form of plane.
∴ Direction cosines (l, m, n) of normal are
0, \(\frac{3}{5}, \frac{4}{5}\)
Distance of the plane from the origin is
(r) = \(\frac{6}{5}\)
∴ Coordinates of the foot of the perpendicular drawn from the origin:

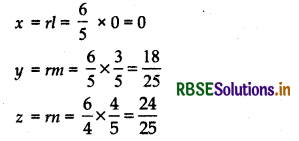
Hence, coordinate of the foot of the perpendicular = \(\left(0, \frac{18}{25}, \frac{24}{25}\right)\)

(c) Given equation of plane is
x + y + z = 1,
Here \(\sqrt{(1)^2+(1)^2+(1)^2}\) = \(\sqrt{1+1+1}\) = √3
Dividing Eq. (i) by, √3, we get
\(\frac{1}{\sqrt{3}} x+\frac{1}{\sqrt{3}} y+\frac{1}{\sqrt{3}} z=\frac{1}{\sqrt{3}}\)
Direction cosines (1, n,, n) of normal are
(l, m, n) = \(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\)
∴ Distance of the plane from the origin is
(r) = \(\frac{1}{\sqrt{3}}\)
∴ Coordinates of the foot of the perpendicular drawn from the origin:

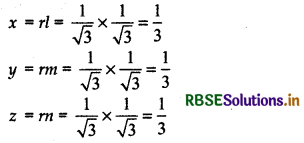
Hence, coordinate of the foot of the perpendicular = \(\left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)\)

(d) Given equation of plane is
5y + 8 = 0 or y = - 8/5 ....... (i)
Direction cosines of plane are 0, 1, 0
∴ Distance from origin = - 8/5
∴ Coordinates of the foot of the perpendicular drawn from the origin

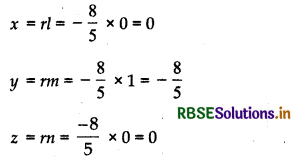
Hence, coordinate of the foot of the perpendicular = \(\left(0,-\frac{8}{5}, 0\right)\)

Question 5.
Find the vector and cartesian equations of the planes that
(a) passes through the point (1, 0, -2) and the normal to the plane is î + ĵ - k̂.
Answer:
(i) Vector equation : Vector equation that passes through the point \(\vec{a}\) and the normal to the plane from vector \(\vec{N}\) is

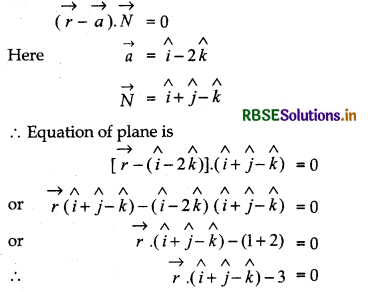
(ii) Cartesian equation: Equation of plane which passes through the point (x₁, y₁, z₁) and direction ratios of perpendicular are a, b, c.
∴ a(x - x₁) + b(y - y₁) + c(z - z₁) = 0
Here, plane passes through the point (1, 0, - 2) and direction ratios of perpendicular are (1, 1, -1).
Equation of plane is
∴ 1(x - 1) + 1(y - 0) - 1(z + 2) = 0
or x - 1 + y - z - 2 = 0
or x + y - z - 3 = 0
x + y - z = 3.

(b) passes through the point (1, 4, 6) and the normal vector to the plane is î - 2ĵ + k̂.
Answer:
Vector equation: Plane passes through the point (1, 4, 6) and along the vector (î - 2ĵ + k̂).
∴ Equation of plane is

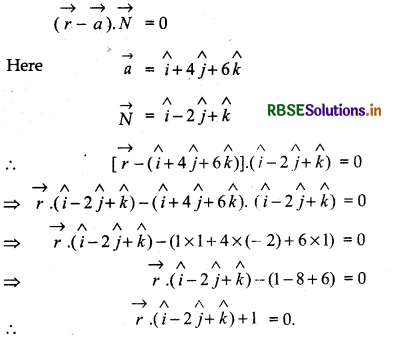
(ii) Cartesian equation: Plane passes through the point (1, 4, 6)
Direction ratios of perpendicular on the plane are 1, - 2, 1
∴ Equation of plane is
1(x - 1) - 2(y - 4) + 1(z - 6) = 0
or x - 1 - 2y + 8 + z - 6 = 0
∴ x - 2y + z + 1 = 0.

Question 6.
Find the equations of the plane that passes through three points.
(a) (1, 1, - 1), (6, 4, - 5), (- 4, - 2, 3)
(b) (1, 1, 0), (1, 2, 1), (- 2, 2, - 1).
Answer:
(a) (1, 1, - 1), (6, 4, - 5), (- 4, - 2, 3)
If direction ratios of perpendicular of the plane are
a, b, c, then equation of the plane which passes through the
point (x₁, y₁, z₁) is
a(x - x₁) + b(y - y₁) + c(z - z₁) = 0
∴ Equation of the plane which passes through the point A(1, 1, - 1)
a(x - 1) + b(y - 1) + c(z - z₁) = 0 ...... (i)
Point B(6, 4, - 5) is on Eq. (1),
⇒ a(6 - 1) + b(4 - 1) + c(- 5 + 1) = 0
∴ 5a + 3b - 4c = 0 ...... (2)
Similarly, point C(- 4, - 2, 3) is on Eq. (i)
a(-4-1)+b(-2-1)+c(3+1) =0
⇒ - 5a - 3b + 4c = 0
∴ 5a + 3b - 4c = 0
Clearly, equation (2) and (3) are same equation.
∴ There will be infinite values of o, h, c which satisfy this equation.
Hence, given points are collinear and there will be infinite number of planes passing through the given points.

(b) (1, 1, 0), (1, 2, 1), (- 2, 2, - 1)
If direction ratios of perpendicular of the plane are a, b, c, then equation of the plane which passes through the point (x₁, y₁, z₁) is
a(x - x₁) + b(y - y₁) + c(z - z₁) = 0
∴ Equation of the plane which passes through the point A(1, 1, 0)
a(x - 1) + b(y - 1) + c(z - 0) = 0 ..... (1)
Point B(1, 2, 1) is on Eq. (i)
∴ a(1 - 1) + b(2 - 1) + c(1 - 0) = 0
⇒ b + c = 0 .......... (2)
Also point C(- 2, 2, 1) is on Eq. (1)
∴ a(- 2 - 1) + b(2 - 1) + c(- 1 - 0) = 0
⇒ - 3a + b - c = 0
∴ 3a - b + c = 0
Eliminating a, b, c from equation (1), (2) and (3)
\(\left|\begin{array}{ccc} x-1 & y-1 & z \\ 0 & 1 & 1 \\ 3 & -1 & 1 \end{array}\right|\) = 0
⇒ (x - 1) [1 + 1] - (y - 1) [0 - 3] + z[0 - 3] = 0
⇒ 2x - 2+ 3y - 3 - 3z = 0
⇒ 2x + 3y - 3z - 5 = 0
Hence, equation of plane is 2x + - 3z = 5.

Question 7.
Find the intercepts cut off by the plane
2x + y - z = 5.
Answer:
Given equation of plane is 2x + y - z = 5
Dividing both sides by 5
\(\frac{2}{5} x+\frac{1}{5} y-\frac{1}{5}\) z = 1
or \(\frac{x}{5 / 2}+\frac{y}{5}+\frac{z}{-5}\) = 1
Hence, intercepts cut off by the plane are 5/2, 5, - 5.

Question 8.
Find the equation of the plane with intercept 3 on the y-axis and parallel to ZOX plane.
Answer:
Let equation of the plane parallel to ZOX plane is,
y = a
Intercept of the plane on the y-axis is 3.
∴ a = 3
Hence, equation of plane is r .
y = 3

Question 9.
Find the equation of the plane which passes through the intersection of the planes 3x - y + 2z - 4 = 0 and x + y + z - 2 = 0 and the point (2, 2, 1).
Answer:
Equation of the plane passes through the intersection of the planes 3x - y + 2z = 0 and x + y + z = 0 is
(3x - y + 2z - 4) + λ(x + y + z - 2) = 0
This plane passes through the point (2, 2, 1).
∴ (3 × 2 - 2 + 2 × 1 - 4) + λ(2 + 2 + 1 - 2) = 0
⇒ (6 - 2 + 2 - 4) + λ(5 - 2) = 0
⇒ 2 + 3λ = 0
⇒ 3λ = - 2
∴ λ = - 2/3
Putting the value of λ in equation (1),
(3x - y + 2z - 4) - \(\frac{2}{3}\)(x + y + z - 2) = 0
⇒ 3(3x - y + 2z - 4) - 2(x + y + z - 2) = 0
⇒ 9x - 3y + 6z - 12 - 2x - 2y - 2z + 4 = 0
⇒ 7x - 5y + 4z - 8 = 0
This is the required equation of the plane.

Question 10.
Find the vector equation of the plane which passes through the intersection of the planes \(\vec{r}\).(2î + 2ĵ - 3k̂) = 7, \(\vec{r}\).(2î + 5ĵ + 3k̂) = 9 and through the point (2, 1, 3).
Answer:
The vector equation of the plane which passes through the intersection of the planes
\(\vec{r}\).(2î + 2ĵ - 3k̂) = 7 and \(\vec{r}\).(2î - 5ĵ + 3k̂) = 9 is \(\vec{r}\).(2î + 2ĵ - 3k̂) - 7 + λ[\(\vec{r}\).(2î + 5ĵ + 3k̂) - 9] = 0 ..... (1)
= \(\vec{r}\).[(2 + 2λ)î + (2 + 5λ)ĵ + (- 3 + 3λ)k̂]- 7 - 9λ = 0
This plane passes through the point (2î + ĵ + 3k̂)
∴ (2î + ĵ + 3k̂).[(2 + 2λ)î + (2 + 5λ)ĵ + (- 3 + 3λ)k̂] - 7 - 9λ = 0
⇒ 2(2 + 2λ) + 1(2 + 5λ) + 3(- 3 + 3λ) - 7 - 9λ = 0
⇒ 4 + 4λ + 2 + 5λ - 9 + 9λ - 7 - 9λ = 0
⇒ 9λ - 10 = 0
⇒ 9λ = 10
∴ λ = \(\frac{10}{9}\)
Putting the value of λ im equation (1), we get

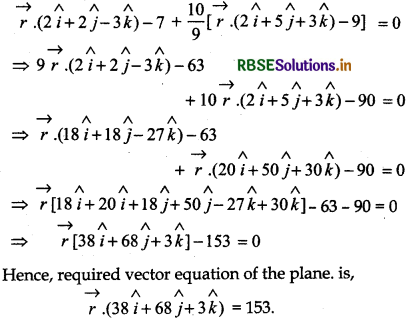
Question 11.
Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x - y + z = 0.
Answer:
Equation of the plane passes through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 is
(x + y + z - 1) + λ(2x + 3y + 4z - 5) = 0
⇒ (1 + 2λ)x + (1 + 3λ)y + (1 + 4λ)z - 1 - 5λ = 0 ..... (1)
Direction ratios of normal of plane (1) are:
(1 + 2λ), (1 + 3λ), (1 + 4λ)
and plane x - y + z = 0 .... (2)
Direction ratios of normal of the plane (2) are 1, -1, 1
∵ Plane (1) and (2) are mutually perpendicular.
∴ a₁a₂ + b₁b₂ + c₁c₂ = 0
⇒ (1 + 2λ).1 + (1 + 3λ).(- 1) (1 + 4λ).1 = 0
⇒ 1 + 2λ - 1 - 3λ + 1 + 4λ = 0
⇒ 3λ + 1 = 0
∴ λ = - 1/3
Putting the value of λ in equation (1),

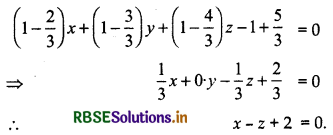
Question 12.
Find the angle between the planes whose vector equations are:
\(\vec{r}\).(2î + 2ĵ - 3k̂) = 5 and \(\vec{r}\).(3î - 3ĵ + 5k̂) = 3
Answer:
Normal of the plane \(\vec{r}\).(2î + 2ĵ - 3k̂) = 5 is a long 2î + 2ĵ - 3k̂ and normal of the plane \(\vec{r}\).(3î + 3ĵ + 5k̂) = 3 is along 3î + 3ĵ - 5k̂.
∴ Angle θ between the planes is equal to the angle between normals.

Question 13.
In the following cases, determine whether the given pair of planes are parallel or perpendicular, and in case they are neither parallel nor perpendicular then find the angle between them.
(a) 7x + 5y + 6z + 30 = 0 and 3x - y - 10z + 4 = 0
(b) 2x + y + 3z - 2 = 0 and x - 2y + 5 = 0
(c) 2x - + 4z + 5 = 0 and 3x - + 6z - 1 = 0
(d) 2x - y + 3z - 1 = 0 and 2x - y + 3z + 3 = 0
(e) 4x + 8y + z - 8 = 0 and y + z - 4 = 0
Answer:
If planes are a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0, then

(i) Condition for parallel
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

(ii) Condition for perpendicular
a₁a₂ + b₁b₂ + c₁c₂ = 0

(a) Given planes are,
7x + 5y + 6z + 30 = 0
and 3x - y - 10z + 4 = 0
Here a₁ = 7, b₁ = 5, c₁ = 6, d₁ = 30
a₂ = 3, b₂ = - 1, c₂ = - 10, d₂ = 4

(i) For parallel
\(\frac{7}{3} \neq \frac{5}{-1} \neq \frac{6}{-10}\)
∴ These planes are not parallel.

(ii) For perpendicular
a₁a₂ + b₁b₂ + c₁c₂ = 7 × 3 + 5 × ( - 1) + 6 × ( - 10) = 21 - 5 - 60 = 21 - 65 = - 44 ≠ 0
∴ These planes are not perpendicular.
If angle between two planes are θ, then

(b) Given plan s are,
2x + y + 3z - 2 = 0
and x - 2y + 5 = 0
Here a₁ = 2, b₁ = 1, c₁ = 3
a₂ = 1, b₂ = - 2, c₂ = 0

(i) For parallel
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\) ⇒ \(\frac{2}{1} \neq \frac{1}{-2} \neq \frac{3}{0}\)
∴ These planes are not parallel.

(ii) For perpendicular
a₁a₂ + b₁b₂ + c₁c₂ = 2 × 1 + 1 × (- 2) + 3 × 0
= 2 - 2 + 0 = 0
∴ Given planes are mutually perpendicular.

(c) Given planes are
2x - 2y + 4z + 5 = 0
and 3x - 3y + 6z - 1 = 0
Here a₁ - 2, b₁ = - 2, c₁ = 4
a₂ = 3, b₂ = - 3, c₂ = 6

(i) For parallel

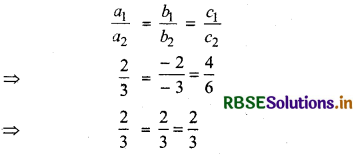
Hence, given planes are parallel.

(d) Given planes are,
2x - y + 3z - 1 = 0
and 2x - y + 3z + 3 = 0
Here a₁ = 2, b₁ = - 1, c₁ = 3
a₂ = 2, b₂ = - 1, c₂ = 3
For parallel

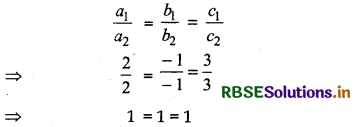
Hence, given planes are parallel.

(e) Given planes are,
4x + 8y + z - 8 = 0
and 0x + y + z - 4 = 0
Here a₁ = 4, b₁ = 8, c₁ = 1
a₂ = 0, b₂ = 1, c₂ = 1

(i) ∴ For parallel
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
⇒ \(\frac{4}{0} \neq \frac{8}{1} \neq \frac{1}{1}\)
Thus, these planes are not parallel.

(ii) For perpendicular
a₁a₂ + b₁b₂ + c₁c₂ = 4 × 0 + 8 × 1 + 1 × 1
= 0 + 8 + 1 = 9 ≠ 0
Thus, given planes are not perpendicular.
If angle between two planes are θ, then

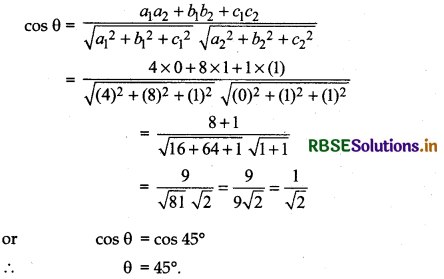
Question 14.
In the following cases, find the distance of each of the given points from the corresponding given plane.

Point	Plane
(a) (0, 0, 0)	3x – 4y + 12z = 3
(b) (3, - 2, 1)	2x – y + 2z + 3 = 0
(c) (2, 3, - 5)	X + 2y – 2z = 9
(d) (- 6, 0, 0)	2x  - 3y + 6z – 2 = 0

Answer:
Let the distance of the plane ax + by + cz + d = 0 from the point (x₁, y₁, z₁) is
d = \(\left|\frac{a x_1+b y_1+c z_1+d}{\sqrt{a^2+b^2+c^2}}\right|\)

(a) Given: Point (0, 0, 0) and plane
3x - 4y + 12z - 3 = 0
Here x₁ = 0, y₁ = 0, z₁ = 0 and a = 3, b = 4, c = 12,d = - 3
Distance of the plane 3x - 4y + 12z = 3 from the point (0, 0, 0) is:

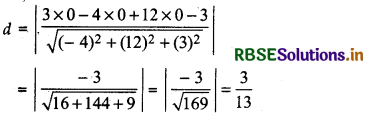
(b) Here x₁ = 3, y₁ = - 2, z₁ = 1 and a = 2, b = - 1, c = 2, d = 3
Distance of the plane 2x - y + 2z + 3 = 0 from the point (3, - 2, 1) is:

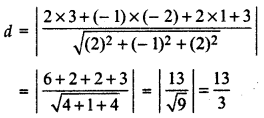
(c)Here x₁ = 2, y₁ = 3, z₁ = - 5 and a = 1, b = 2, c = - 2, d = - 9
∴ Distance of the plane 2x - y + 2z + 3 = 0 from the point (3, - 2, 1) is:

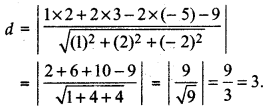
(d) Here x₁ = - 6, y₁ = 0, z₁ = 0 and a = 2, b = - 3, c = 6, d = - 2
∴ Distance of the plane 2x - 3y + 6z - 2 = 0 from the point (- 6, 0, 0) is: